
Взаимное расположение графиков
линейных функций
Цели: продолжить формировать умение строить график линейной функции и определять по графику значение функции по данному аргументу и наоборот; ввести понятие углового коэффициента прямой и выявить случаи взаимного расположения графиков линейных функций в зависимости от значений угловых коэффициентов.
Ход урока
I. Организационный момент
II. Проверочная работа.
Вариант 1
1. Постройте график функции, заданной формулой у = –2х+ 0,5.
2. Линейная функция задана формулой у = 5х – 12. Найдите:
а) значение у, если х = 1,2; –3;
б) значение х, при котором у = 0; –1,5.
Вариант 2
1. Постройте график функции, заданной формулой у = –3х– 1,5.
2. Линейная функция задана формулой у = –4х + 7. Найдите:
а) значение у, если х = –1,3; 8;
б) значение х, при котором у = –2,8; 0.
III. Актуализация знаний.
1. Назовите координаты точек пересечения графиков функций с осями координат. Какие особенности этих точек?
а)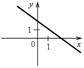 б)
б)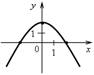 в)
в)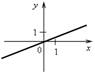 г)
г) 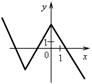 д)
д)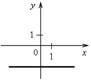 е)
е) 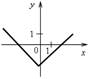
2. № 322, № 324.
№ 322.
Решение:
а) у = –2,4х + 9,6.
Точка пересечения с осью х имеет ординату, равную нулю. Найдем её абсциссу, решив уравнение:
–2,4х + 9,6 = 0;
–2,4х = – 9,6;
х = – 9,6 : (–2,4);
х = 4.
(4; 0) – точка пересечения с осью х.
Точка пересечения с осью у имеет абсциссу, равную нулю. Найдем её ординату по формуле:
Если х = 0, то у = –2,4 · 0 + 9,6 = 9,6.
(0; 9,6) – точка пересечения с осью у.
б) у = –0,7х – 28.
Если у = 0, то –0,7х – 28 = 0;
–0,7х = 28;
х = 28 : (–0,7);
х = –40.
(–40; 0).
Если х = 0, то у = –0,7 · 0 – 28 = –28.
(0; –28).
в) у = 1,2х + 6.
Если у = 0, то 1,2х + 6 = 0;
1,2х = –6;
х = –6 : 1,2;
х = –5.
(–5; 0).
Если х = 0, то у = 1,2 · 0 + 6 = 6.
(0; 6).
г) у = –5х + 2.
Если у = 0, то –5х + 2 = 0;
–5х = –2;
х = –2 : (–5);
х = 0,4.
(0,4; 0).
Если х = 0, то у = –5 · 0 + 2 = 2.
(0; 2).
Ответ: а) (4; 0), (0; 9,6); б) (–40; 0), (0; –28); в) (–5; 0), (0; 6); г) (0,4; 0), (0; 2).
3. № 325.
При выполнении этого задания учащиеся замечают, что для построения графика линейной функции частного вида y = b достаточно построить точку с координатами (0; b) и провести прямую, параллельную оси х (если выполняем задание в тетради в клеточку), либо построить 2 точки с координатами (0; b) и (х0; b), где х0 – любое число, и провести через них прямую.
IV. Объяснение нового материала.
1. Напоминаем, что график прямой пропорциональности y = kx располагается в I и III или в II и IV координатных четвертях в зависимости от знака коэффициента k. Посмотрев в тетради выполненные ранее построения, замечаем, что графики линейных функций пересекают ось х либо под острым углом (с положительным направлением оси х), либо под тупым. Угол зависит от знака k. Если k = 0, то прямая параллельна оси х. Так как от k зависит угол, то k называют угловым коэффициентом прямой.
2. Затем рассматриваем и анализируем рис. 36, 37 со с. 73 учебника. Делаем вывод: если угловые коэффициенты прямых, являющихся графиками двух линейных функций, равны, то эти прямые параллельны, а если угловые коэффициенты различны, то прямые пересекаются.
3. Рассматриваем случай, когда у линейных функций k различны, а b – одинаковые. Во время актуализации знаний мы вспомнили, что графики этих функций все проходят через точку (0; b), значит, они все пересекаются в этой точке.
V. Формирование умений и навыков.
1. Постройте в одной системе координат графики функций:
у = ![]() x + 1; у =
x + 1; у = ![]() x – 2; у
=
x – 2; у
= ![]() x.
x.
Ответьте на вопросы:
1) Чему равен угловой коэффициент каждой прямой?
2) Каково взаимное расположение графиков функций?
3) Каковы координаты точек пересечения каждого графика с осями координат?
2. Пересекаются ли графики функций у = 2х – 4 и у = –4х + 2; у = 2х – 3 и у = 2х + 3?
В том случае, когда графики пересекаются, постройте их. Определите по графику координаты точки пересечения и проверьте результаты вычислением.
3. № 327.
4. Постройте прямую, если её угловой коэффициент равен –0,5 и она проходит через точку (–6; 4). Задайте формулой линейную функцию, график которой параллелен этой прямой и пересекает ось у в точке (0; 5).
VI. Итоги урока.
– Дайте определение линейной функции.
– Что является графиком линейной функции? Как его построить?
– Почему коэффициент k называется угловым? Как от k зависит расположение графика линейной функции?
– В каком случае графики двух линейных функций пересекаются и в каком случае они являются параллельными прямыми?
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.