ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ1

Линейное уравнение с одной переменной

Цель: формировать умение решать по алгоритму уравнения, сводящиеся к линейным.

Ход урока

I. Организационный момент

II. Проверочная работа.

Вариант 1

1. Сколько корней имеет уравнение: а) –2х = 17;                  б) 0 · х = –6;       в) 0 · х = 0?

2. Найдите корень уравнения. а) 26х = –78;                             б) 0,2х = 2,8;      в) x = 24;        г) –3x = .

Вариант 2

1. Сколько корней имеет уравнение: а) 0 · х = –72;                              б) x = 11;                         в) 0 · х = 0?

2. Найдите корень уравнения. а) 21х = 84;                    б) –1,2х = 0,36;           в) x = 21;                        г) –2x = .

III. Формирование умений и навыков.

№ 128 (а; б; е; ж; и); № 129; № 131.

3. № 131, № 132.

№ 131.

Решение:

№ 132.

Решение:

а) (13х – 15) – (9 + 6х) = –3х;

    13х – 15 – 9 – 6х = –3х;

    13х – 6х + 3х = 15 + 9;

    10х = 24;

    х = 24 : 10;

    х = 2,4.

б) 12 – (4х – 18) = (36 + 4х) + (18 – 6х);

    12 – 4х + 18 = 36 + 4х + 18 – 6х;

    – 4х – 4х + 6х = 36 + 18 – 12 – 18;

    – 2х = 24;

    х = 24 : (–2);

    х = –12.

в) 1,6х – (х – 2,8) = (0,2х + 1,5) – 0,7;

    1,6х – х + 2,8 = 0,2х + 1,5 – 0,7;

    1,6х – х – 0,2х = 1,5 – 0,7 – 2,8;

    0,4х = –2;

    х = (–2) : 0,4;

    х = –5.

г) (0,5х + 1,2) – (3,6 – 4,5х) = (4,8 – 0,3х) + (10,5х + 0,6);

    0,5х + 1,2 – 3,6 + 4,5х = 4,8 – 0,3х + 10,5х + 0,6;

    0,5х + 4,5х + 0,3х – 10,5х = 4,8 + 0,6 – 1,2 + 3,6;

    –5,2х = 7,8;

    х = 7,8 : (–5,2);

    х = –1,5.

4. № 134.

Решение:

5. При каком значении t:

а) значение выражения 5t + 11 равно значению выражения 7t + 31;

б) значение  выражения  8t + 3  в  три  раза  больше  значения  выражения 5t – 6;

в) значение  выражения  5t + 1  в два раза меньше значения выражения 10t + 18;

г) значение  выражения  0,25t – 31  на  5  больше  значения  выражения t – 18;

д) значение  выражения  13t – 7  на  8  меньше  значения  выражения
12t + 11;

е) разность выражений 1,5t – 37 и 1,5t – 73 равна 36?

Основную трудность при составлении равенств у учащихся вызывают задания б) – д). Следует разобрать принцип составления равенства с использованием наглядности.

Решение:

б) 8t + 3                                       5t – 6                                    8t + 3                                    3 (5t – 6)

(8t + 3) = 3 (5t – 6);

8t + 3 = 15t – 18;

8t – 15t = – 18 – 3;

–7t = –21;

t = 3.

в) 5t + 1                                       10t + 18                               5t + 1                                    (10t + 18) : 2

5t + 1 = (10t + 18) : 2;

5t + 1 = 5t + 9;

5t – 5t = 9 – 1;

0 · t = 8 – нет решений.

г) 0,25t – 31                               t – 18                              0,25t – 31 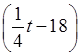                           + 5

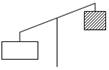
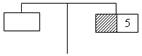
0,25t – 31 = t – 18 + 5;

0,25t – t = – 18 + 5 + 31;

0 · t = 18 – нет решений.

д) 13t – 7 = (12t + 11) – 8   или   (13t – 7) + 8 = 12t + 11.

е) (1,5t – 37) – (1,5t – 73) = 36;

    1,5t – 37 – 1,5t + 73 = 36;

    1,5t – 1,5t = 36 + 37 – 73;

    0 · t = 0                    – t – любое число.

IV. Итоги урока.

Домашнее задание: № 128 (в; г; д; з); № 130; № 133; № 135.