ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ2

Линейное уравнение с одной переменной

Цели: продолжить формировать умение решать уравнения, сводящиеся к линейным.

Ход урока

I. Организационный момент

Устная работа.

1. Показать, что следующие уравнения не имеют решений, и объяснить почему:

а) х + 3 = х;                 в) 2х = 2(х + 1);                д) (–х)² + 1 = 0.

б) х – 1 = х + 1;                         г) х² + 4 = 0;       

2. Определить, равносильны ли уравнения и почему:

а) 5х + 1 = 2                               и             10х + 2 = 4;

б) 2х – 1 = 4                               и             2х = 6;

в) 3х + 1 = 10                             и             х = 3;

г) 2х + 3 = 2х – 4       и             х + 5 = х;

д) 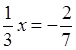                        и             21х = –6.

II. Математический диктант.

Вариант 1

1. Придумайте и запишите какое-нибудь линейное уравнение с одним неизвестным х.

2. Как называется уравнение –2х = 17?

3. При каком условии уравнение сх = 5 имеет единственный корень? Запишите этот корень.

4. Решите уравнение 0,2х = –1.

5. К обеим частям уравнения прибавили число –3. Какими являются полученное и исходное уравнения?

6. Решите уравнение 2х + 1 = 3х – х.

7. Решите уравнение 5 – х = 2х + 2.

Вариант 2

1. Придумайте и запишите какое-нибудь линейное уравнение с одним неизвестным у.

2. Как называется уравнение 17х = –2?

3. При каком условии уравнение ау = 3 не имеет корней?

4. Решите уравнение –0,3х = 1.

5. Обе части уравнения умножим на число –7. Какими являются полученное и исходное уравнения?

6. Решите уравнение х + 3 = 5 + х – 2.

7. Решите уравнение 2 – 2х = –2х + 3.

III. Формирование умений и навыков.

1. Решите уравнение.

а) (5х – 3) + (7х – 4) = 8 – (15 – 11х);

б) (4х + 3) – (10х + 11) = 7 + (13 – 4х);

в) (7 – 5х) – (8 – 4х) + (5х + 6) = 8;

г) (3 – 2х) + (4 – 3х) + (5 – 5х) = 12 + 7х.

Решение:

а) (5х – 3) + (7х – 4) = 8 – (15 – 11х);

    5х – 3 + 7х – 4 = 8 – 15 + 11х;

    5х + 7х – 11х = 8 – 15 + 3 + 4;

    х = 0.

б) (4х + 3) – (10х + 11) = 7 + (13 – 4х);

    4х + 3 – 10х – 11 = 7 + 13 – 4х;

    4х – 10х + 4х = 7 + 13 – 3 + 11;

    –2х = 28;

    х = 28 : (–2);

    х = –14.

в) (7 – 5х) – (8 – 4х) + (5х + 6) = 8;

    7 – 5х – 8 + 4х + 5х + 6 = 8;

    – 5х + 4х + 5х = 8 – 7 + 8 – 6;

    4х = 3;

    х = .

г) (3 – 2х) + (4 – 3х) + (5 – 5х) = 12 + 7х;

    3 – 2х + 4 – 3х + 5 – 5х = 12 + 7х;

    – 2х – 3х – 5х – 7х = 12 – 3 – 4 – 5;

    –17х = 0;

    х = 0.

2. Среди данных уравнений выберите те, которые имеют тот же корень, что и уравнение 2х – 3 = 5х + 6:

а) 19 (2х – 3) = 19 (5х + 6); 

б) 5х – 2х = 6 – 3;

в) .

Решение:

2х – 3 = 5х + 6;

2х – 5х = 6 + 3;

–3х = 9;

х = –3.

а) 19 (2х – 3) = 19 (5х + 6);  | : 19

    2х – 3 = 5х + 6;

    х = –3, так как уравнение равносильно исходному.

При  решении  данного  уравнения  важно  заметить,  что  разделить обе части уравнения на 19 рационально, а выполнить умножение числа на скобку – нет.

б) 5х – 2х = 6 – 3;                    в)    | · 11;

    3х = 3;                                         2х – 3 = 5х + 6;

    х = 1.                                                            2х – 5х = 6 + 3;

                                                                           х = –3,

                                                                       так как уравнение равносильно исходному.

Ответ: а);  в);  х = –3.

3. Среди данных уравнений укажите те, которые не имеют корней:

а) 5х – 10 = 4х;                                         в) 5 – х = 6 – х;                  д) | x | + 1 = 0.

б) 3х + 7 = 3х + 11;                                                 г) | x | = 8;                         

Решение:

а) 5х – 10 = 4х;                                         б) 3х + 7 = 3х + 11;

    5х – 4х = 10;                                              3х – 3х = 11 – 7;

    х = 10.                                         0 · х = 4 – нет корней.

в) 5 – х = 6 – х;                         г) | x | = 8;                                          д) | x | + 1 = 0.

    –х + х = 6 – 5;                           х = 8 или х = –8.              | x | = –1 –

    0 · х = 1 – нет корней.                                                                         нет решений,

                                                                                                                                          так как | x | ≥ 0.

№ 238. Решение:

Если т ¹ 0, то тх = 5 имеет единственный корень х = 5 : т.

Если т = 0, то уравнение примет вид 0 · х = 5, оно не имеет корней.

Не существует такое значение т, чтобы уравнение имело бесконечно много корней.

№ 239. Решение:

Если х = –5, то р · (–5) = 10 – верное равенство.

Найдем р:                  р = 10 : (–5);

                                                       р = –2.

Если х = 1, то                            р · (–1) = 10;

                                                       р = 10 : (–1);

                                                       р = –10.

Если х = 20, то                          р · 20 = 10;

                                                       р = 10 : 20;

                                                       р = 0,5.

Ответ: –2; –10; 0,5.

Обращаем внимание учащихся, что это уравнение с параметром р.

№ 242. Решение:

а) (х + 5) (х + 6) + 9 = 0;

    х² + 6х + 5х + 30 + 9 = 0;

    х² + 11х + 39 = 0;

    х² = –11х – 39.

Слева стоит выражение, значение которого не отрицательно. если х – положительное число, то –11х < 0 и –11х – 39 < 0, значит, х² = –11х – 39 – неверно для любого положительного х, значит, уравнение не может иметь положительный корень.

б) х² + 3х + 1 = 0.

Если х > 0, то каждое слагаемое в левой части уравнения положительно, значит, и вся сумма положительна, следовательно, х > 0 не может являться корнем данного уравнения.

IV. Итоги урока.

Домашнее задание: № 136, № 137, № 138