Линейное уравнение с одной переменной.
Рассмотрим три уравнения:
2x=−3,
0x=0,
0x=2.
второго уравнения является любое число.
Число —1,5 является единственным корнем первого уравнения.
Поскольку произведение любого числа на нуль равно нулю, то корнем
Третье уравнение корней не имеет.
Несмотря на существенное различие полученных ответов, приведённые
уравнения внешне похожи: все они имеют вид ax=b , где x — пере
менная, а и b — некоторые числа.
Уравнение вида ax=b , где x — переменная, а и b — некоторые
числа, называют линейным уравнением с одной переменной.
Приведём ещё примеры линейных уравнений:
1
2
x=7;−0,4x=2,8;−x=0.
Заметим, что, например, уравнения x2=0,(x−2)(x−3)=0,|x|=5
линейными не являются.
Текст, выделенный жирным шрифтом, разъясняет смысл термина
«линейное уравнение с одной переменной». В математике предложение,
раскрывающее суть термина (понятия, объекта), называют определением.
Итак, мы сформулировали (или, говорят, «дали») определение линейного
уравнения с одной переменной.
1) Если a≠0 , то разделив обе части уравнения ах = b на а, получим
x=b
.
a
Отсюда следует: если a≠0 , то уравнение ах = b имеет единcтвенный
b
.
a
корень, равный
2) Если a=0 , то линейное уравнение приобретает такой вид: 0х = b.
Тогда возможны два случая: b = 0 или b≠0 .
В первом случае получаем уравнение 0х = 0. Отсюда: если, а = 0 и b =0,
то уравнение ах = b имеет бесконечно много корней: любое число является
его корнем.
Во втором случае, когда b≠0 , при любом значении х получим невер
ное равенство 0х = b. Отсюда: если а = 0 и b≠0 , то уравнение ax=b
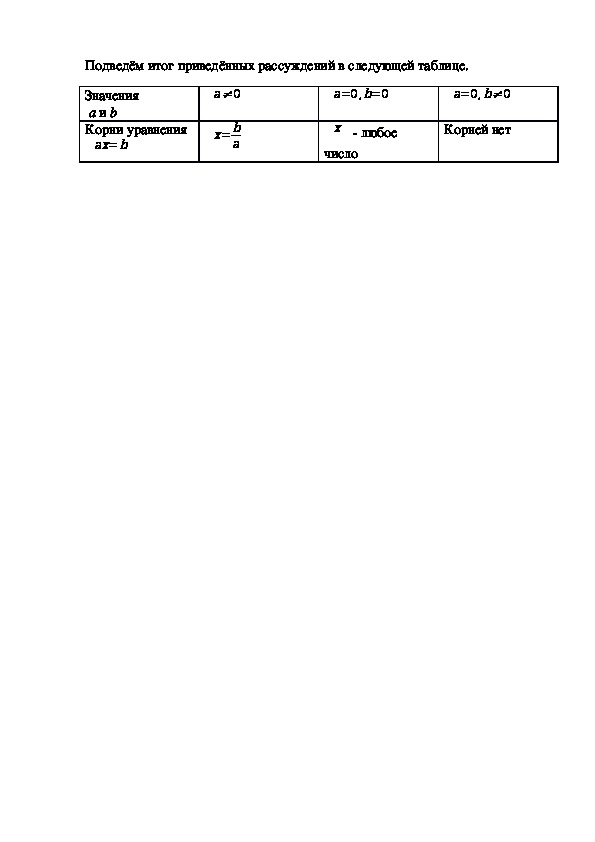
корней не имеет.Подведём итог приведённых рассуждений в следующей таблице.
Значения
а и b
Корни уравнения
ax=b
a≠0
x=b
a
a=0,b=0
a=0,b≠0
x любое
число
Корней нет