Научно-исследовательская работа

по математике

Лобачевский Николай Иванович и его геометрия

Выполнили: 

Сапельнюк Никита Дмитриевич,

Бибикова Анастасия Денисовна

учащиеся  10б класса

МАОУ «Образовательного центра имени

 Героя Советского Союза

 Расковой Марины Михайловны»

Руководитель:

Шатова Ольга Рудольфовна,

учитель математики

МАОУ «Образовательного центра имени

 Героя Советского союза

 Расковой Марины Михайловны»

Содержание:

- Цели и задачи_____________________________________________3

-Введение__________________________________________________4

-Геометрия Лобачевского_____________________________________6

- Применение геометрии Лобачевского в реальной жизни___________11

- Мифы о геометрии Лобачевского и их опровержение_____________13

-Создание модели геометрии Лобачевского_______________________15

-Заключенние_______________________________________________18

- Список используемой литературы_____________________________19

-Приложение_______________________________________________20

Цель: изучить вклад Лобачевского Николая Ивановича в сфере математики; сравнить геометрию Лобачевского и Евклида, создать модели геометрии  Лобачевского.

Задачи:

·                     Подобрать материалы Лобачевском Николае Ивановиче;

·                     Дать представление о нем в презентации;

·                     Выяснить, его главное открытие в сфере геометрии;

·                     Построить модели Лобачевского;

Проблемный вопрос:  Геометрия Лобачевского миф или реальность?

Гипотеза: Применяется геометрия Лобачевского в современной жизни

Методы исследования: сравнительный анализ, теоретический анализ, построение моделей.

Практическая значимость работы: Демонстрация модели геометрия Лобачевского

                                                     Введение:

Детские и юные годы

Николай Иванович Лобачевский родился 20 ноября 1792 г., в Нижнем Новгороде, в семье чиновника геодезического департамента, И. М. Лобачевского.

В 1802 г. поступил в Казанскую гимназию и закончил ее в 1806 г. Особенно хорошие знания он показал в области математики, а также французского, немецкого и латинского языков.

В те годы в гимназии преподавал Г. И. Карташевский. Именно

 благодаря ему у Николая пробудился интерес к математике.

В феврале 1807 г. юный Лобачевский стал студентом Императорского Казанского училища.

Начало научной деятельности

Университет Лобачевский закончил в 1811 г. Получив степень магистра по физике, он был оставлен при университете. Летом 1811 г. он, совместно с И. М. Симоновым, наблюдал комету. В октябре этого же года принялся за изучение работ Гаусса и Лапласа. Это способствовало началу самостоятельных поисков.

В конце 1811 г. Лобачевский Николай Иванович представил свою работу “Теория эллиптического движения небесных тел”.

Начало научной деятельности

Университет Лобачевский закончил в 1811 г. Получив степень магистра по физике, он был оставлен при университете. Летом 1811 г. он, совместно с И. М. Симоновым, наблюдал комету. В октябре этого же года принялся за изучение работ Гаусса и Лапласа. Это способствовало началу самостоятельных поисков.

В конце 1811 г. Лобачевский Николай Иванович представил свою работу “Теория эллиптического движения небесных тел”.

Основные научные открытия

Лобачевский считал Евклидову аксиому параллельности произвольным ограничением. По его мнению, это требование было чересчур жестким. Оно существенно ограничивало возможности теории, которая описывала пространственные свойства.

Николай Иванович изменил существующую аксиому на другую. Она звучит так: “через точку, не лежащую на прямой, может проходить множество прямых параллельных с первой”.

В 1826 г. ученым было сделано устное заявление о своем открытии. После этого он опубликовал несколько трудов, посвященных этой теме.

Современники Лобачевского отнеслись прохладно к его идеям. В 1832 г. он представил свой труд “О началах геометрии”. Эта работа была отрицательно оценена М. В. Остроградским.

Пытаясь найти понимание за границей, в 1837 г. Лобачевский опубликовал свою статью “Воображаемая геометрия” в немецком журнале “Крелле”. Идеи русского ученого удалось продвинуть “королю математиков”, К. Ф. Гауссу. Заинтересованный его трудами, он даже начал изучать русский язык, чтобы ознакомиться с ними в оригинале.

Лобачевский сделал и иные открытия. Независимо от Ж. Данделена, он разработал метод приближенного решения уравнений. В мат.анализе им было получено несколько теорем о тригонометрических рядах. Также Лобачевский дал понятие о признаке сходимости рядов и о непрерывной функции.

Смерть

Николай Иванович Лобачевский ушел из жизни 12 (24) февраля 1856 г. В этот же день тридцать лет назад он впервые опубликовал свою теорию неевклидовой геометрии. Выдающийся русский математик был похоронен на казанском Арском кладбище.

Геометрия Лобачевского

Геометрию Лобачевского называют еще   не­евк­ли­до­вых гео­метрией,

основанная на тех же по­сыл­ках, что и обыч­ная – евк­ли­до­ва гео­мет­рия, за ис­клю­че­ни­ем ак­сио­мы о па­рал­лель­ных, ко­то­рая за­ме­ня­ет­ся на иную. Евк­ли­до­ва ак­сио­ма о па­рал­лель­ных со­сто­ит в том, что че­рез точ­ку, не ле­жа­щую на дан­ной пря­мой, про­хо­дит не бо­лее чем од­на пря­мая, ле­жа­щая с дан­ной пря­мой в од­ной плос­ко­сти и не пе­ре­се­каю­щая её (в евк­ли­до­вой гео­мет­рии та­кие пря­мые на­зы­ва­ют па­рал­лель­ны­ми). В геометрии Лобачевского эта ак­сио­ма за­ме­ня­ет­ся сле­дую­щей: че­рез точ­ку, не ле­жа­щую на дан­ной пря­мой, про­хо­дят по край­ней ме­ре две пря­мые, ле­жа­щие с дан­ной пря­мой в од­ной плос­ко­сти и не пе­ре­се­каю­щие её (дос­та­точ­но, что­бы это бы­ло вы­пол­не­но для од­ной точ­ки и од­ной пря­мой). На­ча­ло этой геометрии бы­ло по­ло­же­но Н. И. Ло­ба­чев­ским, ко­то­рый впер­вые со­об­щил о ней в 1826. Не­сколь­ко позд­нее эту же тео­рию пред­ло­жил Я. Боль­яй; по­это­му ино­гда на­зы­ва­ют гео­мет­ри­ей Ло­ба­чев­ско­го – Боль­яя. Её так­же на­зы­ва­ют не­евк­ли­до­вой гео­мет­ри­ей, хо­тя обыч­но тер­ми­ну «не­евк­ли­до­ва гео­мет­рия» при­да­ют бо­лее ши­ро­кий смысл, вклю­чая сю­да и др. тео­рии, воз­ник­шие вслед за геометрией Лобаческого., а так­же тео­рии, ос­но­ван­ные на из­ме­не­нии по­сы­лок евк­ли­до­вой гео­мет­рии. Ино­гда ее на­зы­ва­ют ги­пер­бо­лической.

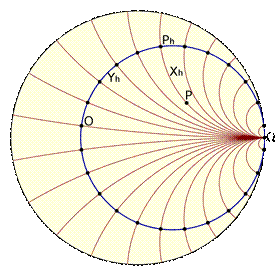
С современной точ­ки зре­ния мож­но дать, например, сле­дую­щее оп­ре­де­ле­ние геометрии Лобачевского на плос­ко­сти: геометрия Лобачевского есть гео­мет­рия внут­ри кру­га на обыч­ной (евк­ли­до­вой) плос­ко­сти, лишь вы­ра­жен­ная осо­бым спо­со­бом. Имен­но, внут­рен­ность кру­га, т. е. круг за ис­клю­че­ни­ем ог­ра­ни­чи­ваю­щей его ок­руж­но­сти, на­зы­ва­ют «плос­ко­стью»(Приложение рис.1). Точ­кой «плос­ко­сти» яв­ля­ет­ся точ­ка внут­ри кру­га. «Пря­мой» на­зы­ва­ют лю­бую хор­ду с ис­клю­чён­ны­ми кон­ца­ми (т. к. ок­руж­ность ис­клю­че­на из «плос­ко­сти»); «дви­же­ни­ем» – лю­бое пре­об­ра­зо­ва­ние кру­га са­мо­го в се­бя, ко­то­рое пе­ре­во­дит хор­ды в хор­ды. Рав­ны­ми на­зы­ва­ют­ся фи­гу­ры внут­ри кру­га, ко­то­рые мож­но пе­ре­вес­ти од­ну в дру­гую та­ки­ми пре­об­ра­зо­ва­ния­ми. Ока­зыва­ет­ся, что лю­бой гео­мет­рической факт, опи­сан­ный на та­ком язы­ке, пред­став­ля­ет тео­ре­му или ак­сио­му геометрии Лобачевского. Ины­ми сло­ва­ми, вся­кое ут­вер­жде­ние геометрии Лобачевского на плос­ко­сти есть не что иное, как ут­вер­ж­де­ние евк­ли­до­вой гео­мет­рии, от­но­ся­ще­еся к фи­гу­рам внут­ри кру­га, лишь пе­ре­ска­зан­ное в ука­зан­ных тер­ми­нах. Евк­ли­до­ва ак­сио­ма о па­рал­лель­ных здесь не вы­пол­ня­ет­ся, т. к. че­рез точ­ку O, не ле­жа­щую на дан­ной хор­де  (т. е. «пря­мой»), про­хо­дит сколь угод­но мно­го не пе­ре­секаю­щих её хорд («пря­мых».) Ана­ло­гич­но геометрия Лобачевского в про­стран­ст­ве мо­жет быть оп­ре­де­ле­на как гео­мет­рия внут­ри ша­ра, вы­ра­жен­ная в со­от­вет­ст­вую­щих тер­ми­нах («пря­мые» – хор­ды, «плос­ко­сти» – пло­ские се­че­ния внут­рен­но­сти ша­ра, «рав­ные» фи­гу­ры – те, ко­то­рые пе­ре­во­дят­ся од­на в дру­гую пре­об­ра­зо­ва­ния­ми, пе­ре­во­дя­щи­ми шар сам в се­бя и хор­ды в хор­ды). Та­ким об­ра­зом, геометрия Лобачевского име­ет со­вер­шен­но ре­аль­ный смысл и столь же не­про­ти­во­ре­чи­ва, как гео­мет­рия Евк­ли­да.

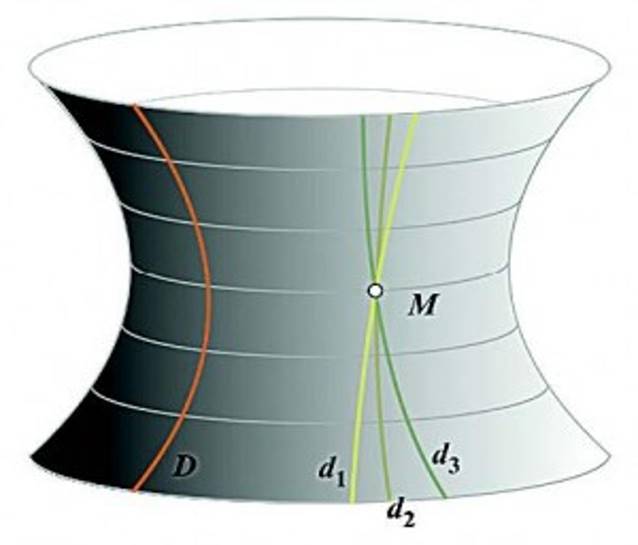
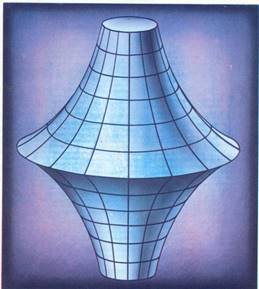
Геометрия Лобачевского изу­ча­ет свой­ст­ва плос­ко­сти Ло­ба­чев­ско­го в пла­ни­мет­рии и про­стран­ст­ва Ло­ба­чев­ско­го в сте­рео­мет­рии. Плос­кость Ло­ба­чев­ско­го – это плос­кость (мно­же­ст­во то­чек), в ко­то­рой оп­ре­де­ле­ны пря­мые ли­нии (а так­же дви­же­ния фи­гур, рас­стоя­ния, уг­лы и пр.), под­чи­няю­щие­ся всем ак­сио­мам евк­ли­до­вой гео­мет­рии, за ис­клю­че­ни­ем ак­сио­мы о па­рал­лель­ных, ко­то­рая за­ме­ня­ет­ся сфор­му­ли­ро­ван­ной вы­ше ак­сио­мой Ло­ба­чев­ско­го. Сход­ным об­ра­зом оп­ре­де­ля­ет­ся про­стран­ст­во Ло­ба­чев­ско­го. За­да­ча вы­яс­не­ния ре­аль­но­го смыс­ла геометрии Лобачевского со­стоя­ла в на­хо­ж­де­нии мо­де­лей плос­кости и про­стран­ст­ва Ло­ба­чев­ско­го, т. е. в на­хо­ж­де­нии та­ких объ­ек­тов, в ко­то­рых реа­ли­зо­вы­ва­лись бы со­от­вет­ст­вую­щим об­ра­зом ис­тол­ко­ван­ные по­ло­же­ния пла­ни­мет­рии и сте­рео­мет­рии геометрии Лобачевского. В 1868 Э. Бельт­ра­ми за­ме­тил, что гео­мет­рия на кус­ке плос­ко­сти Ло­ба­чев­ско­го сов­па­да­ет с гео­мет­ри­ей на по­верх­но­стях по­сто­ян­ной от­ри­ца­тель­ной кри­виз­ны, про­стей­ший при­мер ко­то­рых пред­став­ля­ет псев­до­сфе­ра (Приложение рис. 2). Ес­ли точ­кам и пря­мым на ко­неч­ном кус­ке плос­ко­сти Ло­ба­чев­ско­го со­пос­та­вить точ­ки и крат­чай­шие ли­нии (гео­де­зи­че­ские) на псев­до­сфе­ре и дви­же­нию плос­ко­сти Ло­ба­чев­ско­го со­пос­та­вить пе­ре­ме­ще­ние фи­гу­ры по псев­до­сфе­ре с из­ги­ба­ни­ем, т. е. де­фор­ма­ци­ей, со­хра­няю­щей дли­ны, то вся­кой тео­ре­ме геометрии Лобачевского бу­дет от­ве­чать факт, имею­щий ме­сто на псев­до­сфе­ре. Та­ким об­ра­зом, геометрия Лобачевского по­лу­ча­ет про­стой ре­аль­ный смысл (ин­тер­пре­та­ция Бельт­ра­ми). При этом дли­ны, уг­лы, пло­ща­ди по­ни­ма­ют­ся в смыс­ле ес­те­ст­вен­но­го из­ме­ре­ния их на псев­до­сфе­ре, од­на­ко здесь да­ёт­ся ин­тер­пре­та­ция толь­ко гео­мет­рии на кус­ке плос­ко­сти Ло­ба­чев­ско­го, а не на всей плос­ко­сти и тем бо­лее не в про­стран­ст­ве. В 1901 Д. Гиль­берт до­ка­зал, что в евк­ли­до­вом про­стран­ст­ве не мо­жет су­ще­ст­во­вать ре­гу­ляр­ной по­верх­но­сти, гео­мет­рия на ко­то­рой сов­па­да­ет с гео­мет­ри­ей всей плос­ко­сти Ло­ба­чев­ско­го.

Воз­мож­но чис­то ана­ли­тическое оп­ре­де­ле­ние мо­де­ли геометрии Лобачевского Напр., точ­ки плос­ко­сти мож­но оп­ре­де­лять как па­ры чи­сел, пря­мые мож­но за­да­вать урав­не­ния­ми, дви­же­ния – фор­му­ла­ми, со­пос­тав­ляю­щи­ми точ­кам но­вые точ­ки. Это аб­ст­ракт­но оп­ре­де­лён­ная ана­ли­тическая гео­мет­рия на плос­ко­сти Ло­ба­чев­ско­го, ана­ло­гич­ная ана­ли­тической гео­мет­рии на евк­лидо­вой плос­ко­сти. Ло­ба­чев­ский дал ос­но­вы сво­ей ана­ли­тической гео­мет­рии и тем са­мым фак­ти­че­ски на­ме­тил та­кую мо­дель, хо­тя пол­ное её по­строе­ние вы­яс­ни­лось уже по­сле то­го, как на ос­но­ве ра­бот Ф. Клей­на и др. вы­яви­лось са­мо по­ня­тие о мо­де­ли.

Содержание геометрии Лобачевского

Ло­ба­чев­ский стро­ил свою гео­мет­рию, от­прав­ля­ясь от ос­нов­ных гео­мет­рических по­ня­тий и сво­ей ак­сио­мы, и до­ка­зы­вал тео­ре­мы гео­мет­рическим ме­то­дом, по­доб­но то­му как это де­ла­ет­ся в гео­мет­рии Евк­ли­да. Ос­но­вой слу­жи­ла тео­рия па­рал­лель­ных ли­ний, т. к. имен­но здесь на­чи­на­ет­ся от­ли­чие геометрии Лобачевского от гео­мет­рии Евк­ли­да. Все тео­ре­мы, не за­ви­ся­щие от ак­сио­мы о па­рал­лель­ных, об­щи обе­им гео­мет­ри­ям и об­ра­зу­ют т. н. аб­со­лют­ную гео­мет­рию, к ко­то­рой от­но­сят­ся, напр., тео­ре­мы о ра­вен­ст­ве тре­уголь­ни­ков. Вслед за тео­ри­ей па­рал­лель­ных строи­лись др. раз­де­лы, вклю­чая три­го­но­мет­рию и на­ча­ла ана­ли­ти­че­ской и диф­фе­рен­ци­аль­ной гео­мет­рий. Ни­же пе­ре­чис­ле­ны несколько фак­тов геометрии Лобачевского, ус­та­нов­лен­ных са­мим Н. И. Ло­ба­чев­ским, ко­то­рые от­ли­ча­ют её от гео­мет­рии Евк­ли­да.

1) В геометрии Лобачевского не су­ще­ст­ву­ет по­доб­ных, но не рав­ных тре­уголь­ни­ков; тре­уголь­ни­ки рав­ны, ес­ли их уг­лы рав­ны. По­это­му су­ще­ст­ву­ет аб­со­лют­ная еди­ни­ца дли­ны, т. е. от­ре­зок, вы­де­лен­ный по сво­им свой­ст­вам, по­доб­но то­му как пря­мой угол вы­де­лен свои­ми свой­ст­ва­ми. Та­ким от­рез­ком мо­жет слу­жить, напр., сто­ро­на пра­виль­но­го тре­уголь­ни­ка с дан­ной сум­мой уг­лов.

2) Сум­ма уг­лов вся­ко­го тре­уголь­ни­ка мень­ше π и мо­жет быть сколь угод­но близ­кой к ну­лю. Раз­ность π−(α+β+γ)π−(α+β+γ), где α,β,γ – уг­лы тре­уголь­ни­ка, про­пор­цио­наль­на его пло­ща­ди.

3) Че­рез точ­ку O, не ле­жа­щую на дан­ной пря­мой a, про­хо­дит бес­ко­неч­но мно­го пря­мых, не пе­ре­се­каю­щих a и на­хо­дя­щих­ся с ней в од­ной плос­ко­сти; сре­ди них есть две край­ние b и b', ко­то­рые назы­ва­ют­ся па­рал­лель­ны­ми пря­мой a в смыс­ле Ло­ба­чев­ско­го.

4) Ес­ли пря­мые име­ют об­щий пер­пен­ди­ку­ляр, то они бес­ко­неч­но рас­хо­дят­ся в обе сто­ро­ны от не­го. К лю­бой из них мож­но вос­ста­но­вить пер­пен­ди­ку­ля­ры, ко­то­рые не дос­ти­га­ют др. пря­мой.

5) Ли­ния рав­ных рас­стоя­ний от пря­мой есть не пря­мая, а осо­бая кри­вая, на­зы­вае­мая эк­ви­ди­стан­той или ги­пер­цик­лом.

6) Пре­дел бес­ко­неч­но рас­ту­щих ок­руж­но­стей есть не пря­мая, а осо­бая кри­вая, на­зы­вае­мая пре­дель­ной ок­руж­но­стью или ори­цик­лом.

7) Пре­дел сфер бес­ко­неч­но уве­ли­чи­ваю­ще­гося ра­диу­са есть не плос­кость, а осо­бая по­верх­ность – пре­дель­ная сфе­ра, или ори­сфе­ра; за­ме­ча­тель­но, что на ней име­ет ме­сто евк­ли­до­ва гео­мет­рия. Это по­слу­жи­ло Ло­ба­чев­ско­му ос­но­вой для вы­во­да фор­мул три­го­но­мет­рии.

8) Дли­на ок­руж­но­сти не про­пор­цио­наль­на ра­диу­су, а рас­тёт бы­ст­рее, чем ра­ди­ус.

9) Чем мень­ше об­ласть в про­стран­ст­ве или на плос­ко­сти Ло­ба­чев­ско­го, тем мень­ше мет­рических со­от­но­ше­ния в этой об­лас­ти от­ли­ча­ют­ся от со­от­но­ше­ний евк­ли­до­вой гео­мет­рии. Напр., чем мень­ше тре­уголь­ник, тем мень­ше сум­ма его уг­лов от­ли­ча­ет­ся от π, чем мень­ше ок­руж­ность, тем мень­ше от­но­ше­ние её дли­ны к ра­диу­су от­ли­ча­ет­ся от 2π, и т. п. Умень­ше­ние об­лас­ти фор­маль­но рав­но­силь­но уве­ли­че­нию еди­ни­цы дли­ны, по­это­му при без­гра­нич­ном уве­ли­че­нии еди­ни­цы дли­ны фор­му­лы геометрии Лобачевского пе­ре­хо­дят в фор­му­лы евк­ли­до­вой гео­мет­рии. Евк­ли­до­ва гео­мет­рия есть в этом смыс­ле «пре­дель­ный» слу­чай гео­мет­рии Ло­ба­чев­ско­го.

Ло­ба­чев­ский при­ме­нил свою гео­мет­рию к вы­чис­ле­нию оп­ре­де­лён­ных ин­те­гра­лов. В тео­рии функ­ций ком­плекс­но­го пе­ре­мен­но­го Л. г. по­мог­ла по­стро­ить тео­рию ав­то­морф­ных функ­ций. Связь с Л. г. здесь бы­ла от­прав­ным пунк­том ис­сле­до­ва­ний Пу­ан­ка­ре, ко­то­рый пи­сал, что «не­евк­ли­до­ва гео­мет­рия есть ключ к ре­ше­нию всей за­да­чи». Л. г. на­хо­дит при­ме­не­ние так­же в тео­рии чи­сел, в её геомет­рич. ме­то­дах, объ­е­ди­нён­ных под назв.гео­мет­рия чи­сел. Ус­та­нов­ле­на связь Л. г. с ки­не­ма­ти­кой ча­ст­ной тео­рии от­но­си­тель­но­сти. Эта связь ос­но­ва­на на том, что ра­вен­ст­во, вы­ра­жаю­щее за­кон рас­про­стра­не­ния све­та

Вывод: Геометрия Лобачевского отличается от евклидовой лишь в одной аксиоме – пятой. Но главное различие кроется в понимании самой природы пространства.

Применение геометрии Лобачевского в реальной жизни:

В наши дни геометрия Лобачевского используется в космонавтике для прокладывания дальних маршрутов, вычисления траектории полета, в современной физике и во многих других естественных науках.

Хотелось бы остановиться на эволюции принципа относительности в физике и её связи с геометрией.

Теория относительности – теория, описывающая универсальные пространственно-временные свойства физических процессов. Галилео Галилей, а впоследствии и Исаак Ньютон считали, что если в двух замкнутых лабораториях, одна из которых равномерно прямолинейно (и поступательно) движется относительно другой, провести одинаковый механический эксперимент, результат будет одинаковым. То есть одинаковые опыты протекают одинаково и при разных пространственно-временных условиях. При таком принципе справедлива геометрия Евклида(пространство трехмерное, кривизна пространства-времени не учитывается и скорость движения не сравнима со скоростью света(мала)).До открытия электродинамики, то есть до XIX века, этот принцип мог считаться верным, так как необходимые условия соблюдались(изучаемые тела двигались на малых по сравнению со скоростью света скоростях, у изучаемого пространства кривизна была нулевая).

В электродинамике, открытой как раз в XIX веке, скорости движения частиц были гораздо больше. Назрела необходимость переосмысления принципа относительности.

Бернхард Риман, а за ним и Кингдон Клиффорд предположили, что некоторые физические явления обусловлены кривизной пространства, то есть одинаковые явления в разных условиях(при различной кривизне) могут протекать по-разному.

Не буду углубляться в историю физики. Скажу лишь, что эта гипотеза нашла окончательное обоснование в теории относительности Эйнштейна, в которой пространство было уже четырехмерным(четвертой мерой являлась кривизна пространства-времени) и соответственно эта теория не могла существовать без геометрии Лобачевского аксиомы Лобачевского выполнялись.

При помощи теории относительности были объяснены законы движения небесных тел, явление гравитации, возникновение черных дыр, движение частиц и многое другое. И все это было бы невозможно без геометрии Лобачевского. 

Мифы о геометрии Лобачевского и их опровержение:

Миф первый. Геометрия Лобачевского не имеет ничего общего с Евклидовой.

Не правда. Четыре постулата Евклида в данной геометрии оставлены без изменений. Лобачевский не согласен лишь с пятым, ложность которого была им успешна доказана.

Миф второй. В теории Лобачевского параллельные прямые пересекаются.

Это не так. Пятый постулат Лобачевского звучит так: "На плоскости через точку, не лежащую на данной прямой, проходит более чем одна прямая, не пересекающая данную". В нем не идет речь о пересекающихся прямых. В этом постулате лишь сказано, что существует более, чем одна прямая, проходящая через точку, не лежащую на прямой, и не пересекающая её. Это заблуждение появилось из-за незнания теории великого российского математика.

Миф третий. Геометрия Лобачевского - единственная неевклидова геометрия.

Это также неверно. Неевклидовых геометрий довольно много. Кроме геометрии Лобачевского есть также геометрия Римана, описывающая пространство с положительной кривизной(на сфере).Вот в ней параллельные прямые пересекаются. Как пример можно рассмотреть глобус. Меридианы параллельны, но сходятся у полюсов. Вместе теории Евклида, Лобачевского и Римана называют "три великих геометрии".

Миф четвертый. Геометрия Лобачевского не применима в реальной жизни.

Современная наука считает, что геометрия Евклида- частный случай геометрии Лобачевского и что реальный мир можно описать точнее лишь при помощи детища нашего соотечественника. Сильнейшим толчком к дальнейшему развитию геометрии Лобачевского стала теория относительности Альберта Эйнштейна, которая показала, что само пространство нашей Вселенной не является линейным, а представляет собой гиперболическую сферу. Но ,несмотря ни на что, Лобачевский всю жизнь считал свою геометрию «воображаемой», нереальной.

Миф пятый. Лобачевский первым создал неевклидову геометрию.

Это не совсем так. Венгр Янош Бойяи немец Карл Ф. Гаусс пришли к подобным выводам одновременно с Лобачевским, но по разным причинам не были замечены широкой публикой. Поэтому Николай Иванович считается первым создателем геометрии, отличной от евклидовой. Но есть теория, согласно которой Евклид сам создал геометрию, отличную от своей первоначальной, самокритично опровергая 5 постулат. Подтверждением сторонники этой теории считают то, что многие теоремы Евклид доказал, не

используя V постулат.

Создание моделей Лобачевского.

От теории мы бы хотели перейти к практике, и хотим рассказать о том, как мы создавали данные модели Лобачевского:

1) на основу из узких бутылочных горлышек приклеиваем коричневые рейки. Между ними остаётся просвет, который будет заполнен позже. На нижнюю часть горлышка приклеиваем нарезанные толстые белые рейки по окружности, после чего поверх приклеиваем ещё одну коричневую рейку. (Рис.1)

Заполняем просвет по форме нарезанными коричневыми рейками и покрываем лаком.

2) из двух горлышек бутылки создаём каркас. Покрываем его с верху в низ коричневыми рейками. После же приклеиваем спиралью тонкие белые рейки (Рис.2). Зачищаем наждачной бумагой и покрываем лаком.

2) По аналогии 1 фигурой обклеиваем два бутылочных каркаса коричневыми рейками с верху вниз. У обеих заготовок остаются просветы которые заполним позже. Склеиваем два каркаса и на стыках склеивания с помощью толстых реек приклеенных по окружности делаем возвышение. Соединяем коричневые рейки так чтобы они образовывали угол(Рис.3)

Покрываем лаком.

Основные сложности фигур: изогнутые формы, недостаток эластичности некоторых материалов (наподобие бумаги) и невозможность их использования

Заключение:

Мы изучили вклад Лобачевского Николая Ивановича в сфере математики; сравнили геометрию Лобачевского и Евклида, создали модель геометрии Лобачевского.

С поставленными задачами справились. Убедились, что геометрия Лобачевского это реальность.

Открытие Лобачевского поставило перед наукой по крайней мере два принципиально важных вопроса, не поднимавшихся со времен "Начал" Евклида: "Что такое геометрия вообще? Какая геометрия описывает геометрию реального мира?". До появления геометрии Лобаческого существовала только одна геометрия - евклидова, и, соответственно, только она могла рассматриваться как описание геометрии реального мира. Ответы на оба вопроса дало последующее развитие науки. Лобачевский вошел в историю математики не только как гениальный геометр, но и как автор фундаментальных работ в области алгебры, теории бесконечных рядов и приближенного решения уравнений.

Создание и разработка геометрии Лобачевского поставили вопрос об исследовании всей структуры системы аксиом, как евклидовой геометрии, так и других возникающих к этому времени геометрий и выяснение независимости этих аксиом друг от друга.

Выдающийся вклад Николая Лобачевского в различные математические области были признаны как на родине гения, так и за рубежом.

В наши дни геометрия Лобачевского используется в космонавтике для прокладывания дальних маршрутов, вычисления траектории полета, в современной физике и во многих других естественных науках.

Список литературы:

·          1. Лаптев Б.Л., Великий русский математик, "Вестник высшей школы", 1967, № 12 - с. 8-11;

·          2. Лобачевский Н.И., Сочинения по геометрии, М. - Л., 1946 - 49 (Полн. собр. соч., т. 1 - 3) - с. 59, 72-78 ;

·          3. Элементарное доказательство непротиворечивости планиметрии Лобачевского, М., 1956- с. 7-19;

·          4. Каган В.Ф. Геометрия Лобачевского и ее предистория, М. - Л., 1949 (Основания геометрии, ч. 1) - с. 142-158;

·          5. В.С. Антонов "Энциклопедия по истории России XIX века".

·          6. А.М. Прохоров "Энциклопедический словарь" - с. 163-167.

·          7. Лаптев В.И. Жизнь и деятельность Н.И. Лобачевского // Успехи математических наук. - М., 1951. - Т. 6. - № 3 (43). - с. 10-17.

ПРИЛОЖЕНИЕ

Рис.1                                                           Рис.2

           Н.И.Лобачевский

Скачано с www.znanio.ru