Логарифм. Логарифм числа. Основное логарифмическое тождество. Правила действий с логарифмами.

Лекция № 6

Тема: Логарифм. Логарифм числа. Основное логарифмическое тождество. Правила действий с логарифмами.

Количество часов: 2 часа

Цель: дать новые знания о логарифме числа; добиться усвоения студентами понятий логарифма, свойств логарифмов и формул логарифмирования.

План:

1.       Понятие логарифма числа. Основное логарифмическое тождество.

2.       Свойства логарифмов и формулы логарифмирования.

3.       Правила действий с логарифмами. Переход к новому основанию.

4.       Вычисление логарифма числа.

Логарифмы первоначально использовались исключительно для упрощения вычислений, и это их приложение до сих пор остается одним из самых главных.

ЛОГАРИФМ-это число, применение которого позволяет упростить многие сложные операции арифметики. Использование в вычислениях вместо чисел их логарифмов позволяет заменить умножение более простой операцией сложения, деление – вычитанием, возведение в степень – умножением и извлечение корней – делением.

Свойства и формулы логарифмов незаменимы при решении логарифмических уравнений и функций, упрощении примеров, также они пригодятся при решении интегралов и нахождении производной от логарифмов.

Вопрос 1. Понятие логарифма числа. Основное логарифмическое тождество.

Логарифм числа b по основанию a (log_ab) определяется как показатель степени, в которую надо возвести число a, чтобы получить число b

Внимание! Логарифм существует только у положительных чисел.

Обозначение: логарифм числа b по основанию a: log_ab.

Таким образом, по определению логарифма:

log_ab = x, то a^x = b (a >0, a ≠ 1, b > 0)

Десятичный логарифм – это логарифм по основанию 10, т.е. а = 10.

Обозначение: log₁₀b = lgb

Натуральный логарифм – это логарифм по основанию e, т.е. а = e.

е – число Эйлера, иррациональное число, приближенное значение которого:

Обозначение: log_еb = lnb

Переход от выражения к логарифму называется логарифмированием этого выражения. Переход от логарифма к подлогарифмическому выражению называется потенцированием. Потенцирование в математике — действие обратное логарифмированию по некоторому основанию, то есть возведение в степень с этим основанием.

Примеры.

1) log₃9 = 2, поскольку 3² = 9.

2) , так как .

3) lg1000 = 3, поскольку 10³ = 1000.

4) , так как .

По определению логарифма, если log_ab = x, то a^x = b (a>0, a ≠ 1, b> 0).

Подставляя в последнее равенство вместо х его значение, получаем равенство, которое называется основным логарифмическим тождеством:

, где a>0, a ≠ 1, b> 0.

Например:

1) .

2) 10^lg8 = 8.

3) .

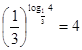Вопрос 2. Свойства логарифмов и формулы логарифмирования

Вопрос 3. Правила действий с логарифмами. Переход к новому основанию.

Логарифмы, как и любые числа, можно складывать, вычитать и всячески преобразовывать, но поскольку логарифмы - это не совсем обычные числа, здесь есть свои правила, которые называются основными свойствами.

Эти правила обязательно надо знать — без них не решается ни одна серьезная логарифмическая задача.

Дополним правила для вынесения показателя степени из логарифма:

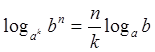
Вопрос 4. Вычисление логарифма числа.

Задача 1.

Вычислите: 1) log₇343;     2) 2lg100 000;      3) ;     4) .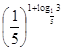

Решение.

1)    log₇343 = log₇7³ = 3 log₇7 = 3;

2)    2lg100000 = 2 lg10⁵ = 10;

3)     = ==  = ;

4)    ==.

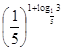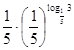Задача 2.

Решите уравнение:

1) log₅125 = х;    5^х = 125;    5^х = 5³;    х = 3;

2)

Вопросы для самопроверки:

1.     Дайте определение понятию логарифм числа.

2.     Перечислите свойства логарифмов и формулы логарифмирования.

3.     Укажите основное логарифмическое тождество.

4.     Как выполняется переход к новому основанию?

Список литературы и ссылки на Интернет-ресурсы, содержащие информацию по теме:

1.            Башмаков М.И., Математика: учебник для студ. учреждений сред. проф. образования / М.И. Башмаков. –7-е изд., стер. – М с.: Издательский центр «Академия», 2020. – 256с.

2.            Григорьев С.Г. Математика: учебник для студ. учреждений сред. проф. организация/ С.Г. Григорьев, С.В. Иволгина; под ред. В.А. Гусева. – 14-е изд., стер. – М.: Издательский центр «Академия», 2019. – 416 с.

3.            Никольский С.М., Потапов М.К., Решетников Н.Н. Шевкин А.В. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. организаций: базовый и углубл. уровни – 5-е изд. - М.: Просвещение, 2018. – 431 с.: ил.

Скачано с www.znanio.ru