Логика и компьютер. Логические операции

Урок 7-8, 10 класс – теория

Учитель: Брух Т.В.

Дата: _____________

Тема: «Логика и компьютер. Логические операции»

Цели урока:

Образовательные:

Ø  Познакомить с определениями: понятие, высказывание и его видами, умозаключение, логические величины, логические переменные.

Ø  Познакомить с основными логическими операциями (инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность), их свойствами и обозначениями;

Ø  Закрепить практические навыки представления логических выражений с помощью формул и таблиц истинности

Развивающие:

Ø  Способствовать развитию логического мышления,

Ø  Способствовать развитию памяти, внимания.

Ø  Научить правильно рассуждать, уметь давать ответы на поставленные вопросы

Воспитательные:

Ø  Способствовать воспитанию аккуратности, терпению.

Ø  Способствовать культурному и интеллектуальному развитию учеников.

Задачи урока:

Образовательные:

Ø  выработка умений самостоятельного применения знаний

Развивающая:

Ø  формирование учебных навыков обобщения имеющейся информации

Воспитательная:

Ø  формирование отношения сотрудничества при групповой работе;

Ø  аккуратность, бережное обращение с техникой.

Ход урока:

1. Организация начала урока. Подготовка учащихся к усвоению.

2. Изучение нового материала.

1.          Как человек мыслит?

2.         Что в нашей обыденной речи является высказыванием, а что - нет? Предложение «Кто последний?» - это высказывание или нет?

3.         Арифметическое умножение и логическое умножения. В чем сходс­тво и различие?

Формы мышления

В основе современной логики лежат учения, созданные еще древ­негреческими мыслителями, хотя первые учения о формах и способах мышления возникли в Древнем Китае и Индии. Основоположником формальной логики является Аристотель, который впервые отделил ло­гические формы мышления от его содержания.

Законы мира, сущность предметов, общее в них мы познаем посредством абстрактного мышления. Логика позволяет строить формальные модели окружающего мира, отвлекаясь от содержательной стороны.

Мышление всегда осуществляется в каких-то формах. Основными формами мышления являются понятие, высказывание и умозаключение.

Имеет две стороны

                                                       Содержание                                                     Объём

Например, понятие “Черное море” – отражает единичный предмет, “Сиамская кошка” – отражает класс сиамских кошек.

Содержание понятия – совокупность существенных признаков множества, отраженных в этом понятии.

 Например, понятие “квадрат” – прямоугольник, имеет равные стороны.

Объем понятия – множество предметов, которые мыслятся в понятии.

Например, под объемом понятия “лев” подразумевается множество всех львов, которые существовали, существуют и будут существовать.

По поводу высказывания можно сказать, истинно оно или ложно. Ис­тинным будет высказывание, в котором связь понятий правильно отражает свойства и отношения реальных вещей. Ложным высказывание будет в том случае, когда оно противоречит реальной действительности.

Например 

истинное высказывание: «Буква «а» - гласная».

ложное высказывание: «Компьютер был изобретен в середине XIX века».

Упражнения (устно):

№1. Какие предложения являются высказываниями?

1.      Москва – столица РФ.

2.      Алуштинский дворец (Ласточкино гнездо) находится в Крыму.

3.      5 – 9 + 8.

4.      5 – 9 + 8 = 4.

5.      На юге Африки живут пингвины.

Ответ: 1, 4, 5.

№2. Определите, какие из следующих предложений являются высказываниями, а какие нет. Какие из высказываний истинные, а какие нет?

1.      Учить второй иностранный язык легче, чем первый.

2.      Обязательно займись каким-либо видом спорта.

3.      Переводчик должен знать хотя бы два языка.

4.      Ты играешь в хоккей?

5.      Отними от неизвестного числа 5 – и получишь 2.

6.      К концу 11 класса хорошо выучу русский язык.

Ответ: 2, 4, 5 – не являются.

Умозаключения бывают:

• Дедуктивные (от общего к частному) – Все ученики ходят в школу. Вася – ученик. Вася ходит в школу.
• Индуктивные (от частного к общему) – Банан и персик – сладкие. Значит, все фрукты сладкие на вкус.
• Аналогия – Наши коровы едят траву и дают молоко. В Австралии есть поля, коровы едят эту траву. Следовательно, австралийские коровы тоже дают молоко.

Например

1. ВСЕ АНТИЛОПЫ СТРОЙНЫЕ.

2. СТРОЙНЫЕ ЖИВОТНЫЕ РАДУЮТ ГЛАЗ.

ВСЕ ________ РАДУЮТ ГЛАЗ.

Первичная проверка усвоения знаний.

Задание 1.

Алгебра высказываний

Алгебра высказываний - это наука об общих операциях, аналогичных сложению и ум­ножению, которые выполняются не только над числами, но и над други­ми математическими объектами, в том числе и над высказываниями. Такая алгебра называется алгеброй логики.

Алгебра логики была разработана для того, чтобы можно было определить истинность и ложность составных высказываний.

Например

А = «Два умножить на два равно четыре»

В = «Два умножить на два равно пять»

В алгебре высказываний над высказываниями можно производить определённые логические операции, в результате которых получается новое составное высказывание.

Для этого используются логические операции.

Составные высказывания на естественном языке образуются с помощью союзов «И», «ИЛИ», «НЕ» которые в алгебре высказываний заменяются на логические операции. Логические операции задаются таблицами истинности

В алгебре логики существуют три основные логические операции, которые соответствуют связкам, употребляемым в высказываниях в естественном языке.

Простые высказывания могут быть связаны между собой словами И, ИЛИ, НЕ.

Получившееся высказывание – сложное высказывание.

В алгебре высказываний, как и в обычной алгебре, вводится ряд операций.

Логические связки И, ИЛИ и НЕ заменяются логическими операциями: конъюнкцией, дизъюнкцией и инверсией. Это основные логические операции, при помощи которых можно записать любую логическую функцию.

Логическое отрицание (инверсия), в качестве логической связки в естественном языке могут служить «не», «неверно, что».

Логическое умножение (конъюнкция), в качестве логической связки в естественном языке могут служить «и», «а», «но», «хотя».

Логическое сложение (дизъюнкция), в качестве логической связки в естественном языке может служить «или».

1. Логическая операция инверсия (отрицание)

соответствует частице НЕ обозначается черточкой над именем переменной или знаком ¬ перед переменной

Инверсия логической переменной истинна, если сама переменная ложна, и, наоборот, инверсия ложна, если переменная истинна.

Таблица истинности инверсии имеет вид:

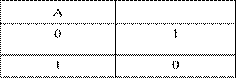
обозначение ¬А или ;

в языках программирования – Not (Нот);

в естественном языке соответствует словам неверно, что... и частице не

2. Логическая операция конъюнкция (логическое умножение)

соответствует союзу И обозначается знаком & или Λ, или * (Амперса́нд (иногда — амперсе́нд; англ. ampersand) — знак &. Он является логограммой, заменяющей слово «и» (в оригинале — and) и возник как лигатура букв et (с лат. — «и»)).

Конъюнкция двух логических переменных истинна тогда и только тогда, когда оба высказывания истинны.
Это определение можно обобщить для любого количества логических переменных, объединенных конъюнкцией.
А & В & С=1, только если А=1, В=1, С=1.
Таблица истинности конъюнкции имеет следующий вид:

·

-              в естественном языке соответствует союзу И;

-              обозначение & («энд») или ^;

-              в языках программирования - And (Энд)

3. Логическая операция дизъюнкция (логическое сложение)

соответствует союзу ИЛИ

обозначается знаком  v  или + или ║

Дизъюнкция двух логических переменных ложна тогда и только тогда, когда оба высказывания ложны.
Это определение можно обобщить для любого количества логических переменных, объединенных дизъюнкцией.
А v В v С =0, только если А=0, В=0, С=0.
Таблица истинности дизъюнкции имеет следующий вид:

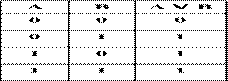
в естественном языке соответствует союзу ИЛИ ;

обозначение «٧»;

в языках программирования обозначение: Or. (Ор)

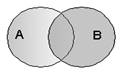Дизъюнкция 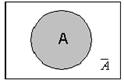   Инверсия 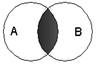Конъюнкция

Операции инверсия, конъюнкция и дизъюнкция являются основными операциями алгебры логики  и называются булевыми операциями.

Существуют другие логические операции. Но они могут быть выражены через основные, поэтому их можно назвать функциями.

3. Контроль и самопроверка знаний.

Заполните таблицы:

4. Подведение итогов урока.

Учитель оценивает работу класса и называет учащихся отличившихся на уроке.

5. Домашнее задание.

1.      Конспект

2.      Составить таблицу по высказыванию (истина, ложь) – 10 примеров.

Кроссворд: Основные понятия логики

По горизонтали:

4. Форма мышления, в которой что-либо утверждается или отрицается.

5. Операция логического умножения.

6. В каком высказывании никакая его часть сама не является высказыванием.

7. Высказывание, которое не соответствует реальной действительности.

8. Как называются высказывания объединенные союзом "или"?

10. Высказывание, построенное на  основании простых высказываний.

12. Одна из сторон понятия, которая составляет совокупность существенных признаков объекта.

13. Наука о  формах и способах мышления.

15. Логические выражения состоят из логических ... и знаков логических операций.

16. Логические выражения, у которых последние  столбцы таблиц  истинности совпадают.

По вертикали:

1. Логическая Функция, которая образуется соединением двух высказываний в одно с помощью оборота речи "… тогда и только тогда, когда…"

2. Логическая функция, которая образуется соединением двух высказываний в одно с помощью оборота речи "если…, то…"

3. Высказывание верно, если оно ...

9. Форма мышления, с помощью которой из одного или нескольких суждений может быть получено новое суждение.

11. Форма мышления, фиксирующая существенные признаки объекта.

14. Одна из сторон понятия, которая определяет совокупность предметов.

17. Она делает истинное высказывание ложным.
Кроссворд с ответами