Ломоносовская олимпиада

1. Копируя векторы, изображенные на данном рис.

 

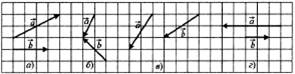
1) построить сумму векторов а+b=m по правилу треугольника, используя рис. б)и г);

2) построить сумму векторов а+b= m по правилу параллелограмма, используя рис. в);

3) построить разность векторов а – b=n, используя рис. а) и г).

2. Даны векторы а(6; 1) и d (5; -3). Найти: 1)координаты вектора a+d ;a -d ;ad; -3а; 7d:

3. А(9;-34),В(75;-38) Найти координаты вектора АВ, длину вектора АВ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5 класс

№1 На скотном дворе гуляли гуси и поросята.
Мальчик сосчитал количество голов, их оказалось 30, а затем он сосчитал количество ног, их оказалось 84.
сколько гусей и сколько поросят было на школьном дворе?

Решение :
1 шаг Представьте, что все поросята подняли по две ноги вверх
2 шаг на земле осталось стоять 30 * 2 = 60 ног
3 шаг подняли вверх 84 - 60 = 24 ноги
4 шаг подняли 24 : 2 = 12 поросят
5 шаг 30 - 12 = 18 гусей
Ответ: 12 поросят и 18 гусей

№2 В пещере старый пират разложил свои сокровища в 3 цветных сундука, стоящих вдоль стены: в один - драгоценные камни, а в другой - золотые монеты, а в третий - оружие. Он помнит, что :
- красный сундук правее, чем драгоценные камни
- оружие правее, чем красный сундук.
В сундуке какого цвета лежит оружие, если зелёный сундук стоит левее, чем синий?
Решение :
ДК - зелёный
ЗC - красный
О – синий

№3 У Гарри Потера имеются двое песочных часов: на 7 минут и на 11 минут. Волшебное зелье должно варится 15 минут. Как сварить его Гарри Потеру, перевернув часы минимальное количество раз?

Решение: 15 = (11 - 7) + 11. Нужно одновременно перевернуть часы, через 7 минут Гарри начинаем варить зелье. После 4 минут (песок в часах на 11 минут закончится) вновь перевернуть часы на 11 минут.Задача решена.

 

№4 Винодел обычно продает свое вино по 30 и по 50 литров и использует для этого кувшины только такого размера. Один из покупателей захотел купить 10 литров. Как винодел отмерил ему 10 литров пользуясь своими кувшинами? 

Ответ: Сначала он наполнил 30-литровый кувшин и вылил его содержимое в 50-литровый. Потом опять наполнил 30-литровый и долил до полного заполнения в 50-литровый. В результате у него в кувшине останется 10 литров.

 

6 класс

№1. ( 2 балла) Используя шесть раз цифру 2, знаки действий и скобки, напишите выражение, значение которого равно 100.

Ответ: возможное решение (222-22) : 2 = 100

2 балла, если записано верное равенство

 

№2. (2 балла) На полке в один ряд стоят книги. Энциклопедия стоит пятой слева и семнадцатой справа. Сколько книг на полке?

Ответ: 21 книга. (4 + 1 + 16 = 21)

2 балла – приведено решение задачи, получен верный ответ.

1 балл – записан верный ответ

 

№3. (3 балла) В коробке 14 белых и 14 чёрных шариков. Какое минимальное количество шариков нужно достать из коробки, чтобы среди них наверняка оказалось 2 черных шарика?

Ответ: 16.(14+2 = 16)

2-3 балла – приведено решение задачи, получен верный ответ.

1 балл – записан верный ответ

 

№4. (5 баллов) В семье четверо детей, им 5,8,13и 15 лет. Детей зовут Аня, Боря, Вера, Галя. Сколько лет каждому ребенку, если одна девочка ходит в детский сад, Аня старше Бори и сумма лет Ани и Веры делится на 3?

Ответ: Вере-5 лет; Боре-8 лет, Ане-13 лет; Гале-15 лет.

5 баллов – приведено верное обоснованное решение задачи

3-4 балла – при верных рассуждениях получен неточный ответ

2 балла – записан верный ответ

 

 

7 класс

 

1. Решите задачу (7 баллов)

На доске написано 4 9 2 5 2 1=100. Поставьте между некоторыми цифрами знаки сложения и вычитания, чтобы получилось верное равенство.

Решение.

4+92+5–2+1=100, 49-2+52+1=100.

Оценивание. За любой верный пример – 7 баллов.

2. Решите задачу (7 баллов)

Путник шел в гору со скоростью v км/час, а с горы 2 v км/час. Какова скорость путника, если он поднимался в гору и возвращался в исходный пункт у подножия горы по одной и той же тропинке?

Решение:

Введем обозначение: s - расстояние, пройденное путником в одном направлении.. - время, затраченное на подъем.. - время, затраченное на спуск. - время, затраченное на подъем и спуск - 2s. Средняя скорость

км/час.

3. Решите задачу (7 баллов)

Даны три натуральных числа. Для каждых двух из них вычислили наибольший общий делитель и наименьшее общее кратное. Полученные шесть чисел сложили. Могло ли получиться число12345?

Решение.

Заметим, что НОД и НОК четных чисел число чётное, а нечётных – нечётное. НОД четного и нечётного чисел – нечётное число, и их НОК – чётное число. Перебирая все случаи (три чётных числа; два чётных, одно нечётное; одно чётное, два нечётных; три нечётных), приходим к выводу, что сумма чисел, о которых говорится в условии задачи, чётна.

Ответ: нет

Оценивание. За верное решение – 7 баллов.

4. Решите задачу (7 баллов)

На клетчатой бумаге нарисован квадрат со стороной 5 клеток. Его требуется разбить на 5 частей одинаковой площади, проводя отрезки внутри квадрата только по линиям сетки. Сделайте это так, чтобы сумма длин всех проведенных отрезков была равна 16 клеткам.

 

Решение.

Один из возможных примеров приведен на рисунке.

Оценивание.

·         Верное решение – 7 баллов.

·         Квадрат разбит на 5 равновеликих частей, но суммарная длина проведенных отрезков больше 16 – 2 балла.

·         Другие случаи – 0 баллов.

 

8 класс

Задача № 1 :

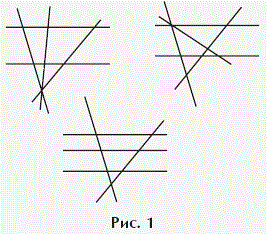
Нарисуйте на плоскости пять различных прямых так, чтобы они пересекались ровно в семи различных точках.

Решение :
Три возможных ответа изображены на рисунке 1.
Можно показать, что других конфигураций из пяти прямых, пересекающихся ровно в семи различных точках, нет

№2

Мальчик пошел с отцом в тир. Отец купил ему 10 пулек.
В дальнейшем отец за каждый промах отбирал у сына одну пульку,
а за каждое попадание давал одну дополнительную пульку.
Сын выстрелил 55 раз, после чего пульки у него кончились. Сколько раз он попал?

Ответ: 50

Решение :
Каждый раз, когда мальчик попадал в цель, число имеющихся у него пулек оставалось прежним
(одну использовал и одну получил от отца).
Каждый раз, когда мальчик промахивался, число имеющихся у него пулек уменьшалось на 2
(одну использовал и одну отобрал отец).
Это значит, что сын за 55 выстрелов промахнулся 10 : 2 = 5 раз, стало быть, попал 55 – 5 = 50 раз.

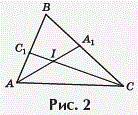
Задача № 3 :

Две биссектрисы треугольника пересекаются под углом 60°.
Докажите, что один из углов этого треугольника равен 60°.

№4

Когда Винни-Пух пришел в гости к Кролику, он съел 3 тарелки меда, 4 тарелки сгущенки и 2 тарелки варенья,
а после этого не смог выйти наружу из-за того, что сильно растолстел от такой еды.
Но известно, что если бы он съел 2 тарелки меда, 3 тарелки сгущенки и 4 тарелки варенья или 4 тарелки меда,
2 тарелки сгущенки и 3 тарелки варенья, то спокойно смог бы покинуть нору гостеприимного Кролика.
От чего больше толстеют: от варенья или от сгущенки?

Ответ : от сгущенки

9 класс

Задание №1. При каких натуральных n частное выражений (n+12-n²) и (n+3) является натуральным числом?

Решение. Разложим на множители многочлен n+12-n²=(n+3)(4-n), сократим на (n+3), получим выражение (4-n). Оно будет являться натуральным числом при n равном 1, 2, 3. Ответ. 1, 2, 3

№2 Автомобиль проехал 600 км. Первую половину пути он двигался со скоростью 100км/ч, а вторую-60км/ч. Найдите среднюю скорость движения автомобиля.

 Решение. Средняя скорость равна отношению общего расстояния на общее время. Каждая половина пути составляет 300 км. 300:100=3(ч)-время, затраченное на первую половину пути; 300:60=5(ч)-время, затраченное на вторую половину пути; 3+5=8(ч)-общее время движения; 600:8=75(км/ч)-средняя скорость движения автомобиля на всем участке.

 Ответ. 75км/ч

№3

Высоты остроугольного треугольника АВС пересекаются в точке Н. Известно, что АВ=СН. Найдите угол АСВ.

Решение. Пусть D –основание высоты, опущенной из вершины А на сторону ВС (рис.) Углы НСВ и DАВ равны как острые углы с взаимно перпендикулярными сторонами. Следовательно, ∆СНD=∆АВD (по гипотенузе и острому углу). Поэтому СD=АD, т.е. треугольник АСD равнобедренный и прямоугольный, следовательно, угол АСВ равен 45 º. Ответ. 45º

 

Задание №4

. В каждой клетке доски 7×7 сидит жук. В какой-то момент времени все жуки взлетают, и после этого каждый из жуков садится в клетку, соседнюю по стороне с той, из которой он взлетел. Докажите, что в какую-то клетку не сядет ни одного жука.

 Решение. Рассмотрим шахматную раскраску доски в черный и белый цвета. Тогда у нас 25 клеток покрашены в черный цвет, а 24 – в белый. Заметим, что жук, взлетевший с белой клетки, сядет на черную клетку, а взлетевший с черной клетки – на белую. Но с белых клеток взлетело 24 жука, и они не смогут сесть на 25 клеток.

10 класс

№1

Условие

Решить в целых числах уравнение  xy + 3x – 5y = – 3.

Решение

xy + 3x – 5y-15 = – 3– 15

(xy– 5y)+( 3x-15 ) = – 18

y (x-5)+3(x-5) = – 18

Запишем уравнение в виде  (x – 5)(y + 3) = – 18.  Его решения соответствуют представлениям числа –18 в виде произведения двух целых чисел.

Ответ

(–13, –2),  (–4, –1),  (–1, 0),  (2, 3),  (3, 6),  (4, 15),  (6, –21),  (7, –12),

(8, –9),  (11, –6),  (14, –5),  (23, –4).

№2

Условие

У нумизмата есть 100 одинаковых по внешнему виду монет. Он знает, что среди них 30 настоящих и 70 фальшивых монет. Кроме того, он знает, что массы всех настоящих монет одинаковы, а массы всех фальшивых – разные, причём каждая фальшивая монета тяжелее настоящей; однако точные массы монет неизвестны. Имеются двухчашечные весы без гирь, на которых можно за одно взвешивание сравнить массы двух групп, состоящих из одинакового числа монет. 
За какое наименьшее количество взвешиваний на этих весах нумизмат сможет гарантированно найти хотя бы одну настоящую монету?

Решение

  Сложим все 100 монет в кучу. Каждым взвешиванием нумизмат будет выбирать две монеты из кучи и сравнивать их. Если их массы равны, то обе монеты настоящие, и требуемая монета найдена. Если же нет, то более тяжёлая монета – фальшивая, и её можно выбросить из кучи.
  Через 70 таких взвешиваний, если равенства никогда не будет, то в куче останется 30 монет, причём все настоящие останутся в куче. Значит, в этом случае нумизмат даже найдёт все 30 настоящих монет. Таким образом, 70 взвешиваний достаточно.

 

№3

Условие

Наконец, у Снежной Королевы появились все квадраты с целыми сторонами, но каждый в единственном экземпляре. Королева пообещала Каю, что он станет мудрым, если сможет из каких-то имеющихся квадратов сложить прямоугольник. Сможет ли он это сделать? Если сможет сделать рисунок.

Решение

Можно составить прямоугольник 33×32 из 9 попарно различных квадратов так, как показано на рисунке. 

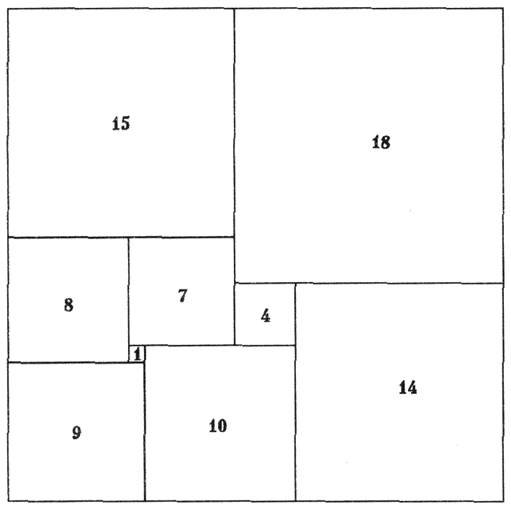
Замечание. Из меньшего числа попарно различных квадратов составить прямоугольник нельзя, но можно это сделать из любого числа квадратов, большего 9. Для этого достаточно приставить квадрат к стороне имеющегося прямоугольника, составленного из n квадратов. 

№4

Условие

В выпуклом четырехугольнике равны длины отрезков, соединяющих середины противоположных сторон, а длины диагоналей равны 4 и 5. Найдите площадь данного четырехугольника.

Решение

Пусть ABCD — данный выпуклый четырехугольник, а K, L, M и N — середины его сторон AB, BC, CD и DA соответственно. Заметим, что отрезки KL и MN являются средними линиями в треугольниках ABC и ACD. Поэтому они оба равны половине диагонали AC и параллельны AC. Значит, четырехугольник KLMN является параллелограммом (1 признак параллелограмма). По условию его диагонали KM и LN равны. Следовательно, четырехугольник KLMN является прямоугольником. Поскольку его сторона KL параллельна диагонали AC и LM параллельна  диагонали BD изначального четырехугольника, то диагонали AC и BD перпендикулярны. По формуле площади четырехугольника : S=1/2⋅AC⋅BD. Таким образом, S=1/2⋅AC⋅BD=10.

Ответ:  S= 10

 

11 класс

 

Задание №1.

Докажите, что 13!-11! кратно 31.

Решение. Так как 13!=123…1213=(123…11) 1213=11!1213, то 13!-11!=11!1213-11!=11!(1213-1)=11!155=11!315, которое кратно 31, что и требовалось доказать.

 

 

Задание № 2.

Три шара радиуса R касаются друг друга, а четвертый шар того же радиуса лежит сверху, при этом касается каждого из трех данных шаров. Определите высоту «горки» из четырех шаров.

Ответ: 2R (+1)

Задание № 3.

Среди n рыцарей каждые двое – либо друзья, либо враги. У каждого из рыцарей ровно три врага, причём враги его друзей являются его врагами. При каких n такое возможно?

Ответ: n = 4  или  n = 6.

 

Задание №4.

Решите уравнение 

Ответ: 

 

Скачано с www.znanio.ru