Мастер – класс по теме: «Реализация технологии деятельностного метода: урок открытия нового знания (ОНЗ)»

Мастер – класс по теме: «Реализация технологии деятельностного метода: урок открытия нового знания (ОНЗ)»

Деятельностные цели:

1) Формирование качеств мышления, необходимых человеку для полноценной жизни и деятельности в современном обществе, и, прежде всего, абстрактного мышления и его дедуктивной составляющей как специфической характеристики математики.

2) Формирование коммуникативных умений и деятельностных способностей, которые позволяют человеку «самостоятельно работать, учиться и переучиваться».

1) Формирование у учащихся системы математических знаний, обеспечивающей непрерывность математической подготовки между начальной школой и обучением математике в любом предпрофиле и профиле на старшей ступени школы.

2) Формирование культурологических представлений, связанных с математикой (ознакомление с ролью математики в развитии человеческой цивилизации и культуры, в современной науке и производстве; знакомство с основами математического языка и математического аппарата как средством постановки и решения проблем реальной действительности).

Не обижайте детей готовыми формулами,

формулы – пустота; обогатите их образами

и картинами, на которых видны связующие

нити. Не отягощайте детей мертвым грузом

фактов; обучите их приемам и способам,

которые помогут их постигать .

Антуан де Сент-Экзюпери

Здравствуйте, уважаемые коллеги!

Разрешите представить вашему вниманию мастер-класс «Реализация технологии деятельностного метода: урок открытия нового знания. (ОНЗ)»

В настоящее время отмечается все больший интерес к проблемам математического образования.

       Как же сформировать у обучающихся интерес к математике? Успех урока целиком зависит от методических приемов, которые выбирает учитель. Как сформировать интерес к предмету у ребенка? Через самостоятельность и активность, через поисковую деятельность на уроке и дома, создание проблемной ситуации, разнообразие методов обучения, через новизну материала, эмоциональную окраску урока.

     В своей педагогической работе я стараюсь использовать разнообразные приёмы, которые активизируют учебную деятельность школьников, воспитывают у них активность, самостоятельность мышления, учат применять знания в процессе обучения.

     На сегодняшний день существует множество авторских программ по преподаванию математики в основной и старшей школе. Одной из самых известных и распространенных является образовательная система  «Учусь учиться», руководителем которой является Людмила Георгиевна Петерсон.

     Основной технологией этой образовательной системы является технология деятельностного метода, с помощью которого реализуется задача формирования функционально грамотной личности. На разном предметном содержании школьник учится получать новые знания, искать ответы на возникающие у него вопросы.

Основные особенности курса математики «УЧУСЬ УЧИТЬСЯ»

Ø  Ребенок не получает знания в готовом виде, а сам открывает их

        на занятиях и уроках

Ø  На каждом уроке у школьников формируется прочная система

        знаний и умение учиться

СХЕМА РЕФЛЕКСИВНОЙ САМООРГАНИЗАЦИИ

1 – выполнение действия, которое привело к

затруднению

2 – фиксирование затруднения («я пока не могу …»)

3 – выход в пространство рефлексии

4 – выявление места затруднения (И – исследование)

5 – выявление причины затруднения (К – критика)

6 – построение проекта выхода из затруднения

7 – реализация построенного проекта

Уроки открытия нового знания (ОНЗ) дают возможность организовать самостоятельную учебно-познавательную деятельность учащихся, целенаправленно и системно формируя у них весь спектр деятельностных способностей. Уроки ОНЗ имеют следующую структуру:

Ø  мотивация к учебной деятельности;

Ø  актуализация знаний и фиксирование индивидуальных затруднений в пробном учебном действии;

Ø  выявление места и причины затруднения;

Ø  построение проекта выхода из затруднения;

Ø  реализация построенного проекта;

Ø  первичное закрепление с проговариванием во внешней речи;

Ø  самостоятельная работа с самопроверкой по эталону;

Ø  включение нового знания в систему знаний и повторение;

Ø  рефлексия учебной деятельности на уроке.

Основной целью этапа мотивации к учебной деятельности является выработка на личностно значимом уровне внутренней готовности выполнения нормативных требований к учебной деятельности.

Для реализации этой цели используется механизм «надо» - «хочу» - «могу»:

Ø  определяется основная цель урока и актуализируются требования к учащимся со стороны учебной деятельности («надо»);

Ø  создаются условия для возникновения у учащихся желания включиться в учебную деятельность («хочу»);

Ø  организовать осознание учащимися тематических рамок урока («могу»).

Урок   (ОНЗ)

Тема: «Сокращение дробей»

Основные цели:

Личностные:

Создавать условие для формирования устойчивого познавательного интереса и становления смыслообразующей функции познавательного мотива.

Метапредметные:

1) Сформировать умение применять основные секреты понимания текста (алгоритм понимания устной и письменной речи).

2) Создать условие для тренинга учащихся по использованию различных способов чтения.

Предметные:

1) Сформировать понятия сократимой и несократимой дроби.

2) Сформировать умение сокращать дроби на основе использования основного свойства дроби.

3) Тренировать умение применять понятия делителя и кратного, признаки делимости, свойства делимости произведения, чтение и нахождение значений буквенных выражений, тренировать умение строить математические модели текстовых задач.

Заметки на полях:

На этом уроке учащиеся знакомятся с понятиями сократимой и несократимой дроби, строят способы сокращения дробей на основе основного свойства дроби и применения алгоритма нахождения НОД чисел, умения представлять число в виде произведения, свойств делимости.

На уроке тренируются умение выполнять следующие виды математических действий:

Ø  сокращают дроби разными способами;

Ø  находят НОД чисел;

Ø  представляют числа в виде произведения множителей;

Ø  определяют, является ли дробь сократимой или нет;

Ø  приводят дроби к заданному знаменателю или числителю;

Ø  строят математические модели текстовых задач.

Основные структурные элементы урока:

1. Новое знание: способы сокращения дробей.

2. Пробное действие: Запишите, несократимы дроби, равные данным  , , ,   и сформулируйте три способа сокращения дробей.

3. Фиксация затруднения: «Я пока не смог записать несократимые дроби, равные данным». «Я пока не могу сформулировать три способа сокращения дробей».

4. Фиксация причины затруднения: «У нас нет способов сокращения дробей».

5. Цель деятельности учащихся: «Построить способы сокращения дробей».

6. Фиксация нового знания: способы сокращения дробей. 

                                                 Ход урока

1.      Мотивация к учебной деятельности.

– Ребята, какую тему вы начали изучать на прошлом уроке? (Основное свойство дроби.)

– Что вы уже узнали? (Числитель и знаменатель можно умножать и делить на одно и то же натуральное число.)

– Сегодня вы продолжите работать с основным свойством дроби.

2.      Актуализация знаний и фиксация индивидуального затруднения в пробном учебном действии.

           На доске карточка с основным свойством дроби

− С чего начнёте урок? (Основное свойство дроби.)

− Какие задания я вам подобрала для повторения? (Задания, которые будут необходимы для открытия новых знаний.)

– Какие способы нахождения НОД и НОК вы знаете? (Методом перебора, методом разложения на простые множители.)

      На доске карточка с заданиями для актуализации знаний

а) 8 и 12;  б) 12 и 36;      в) 9 и 10    7 · 40 · 156

Найдите устно НОД и НОК чисел: а) 8 и 12; б) 12 и 36; в) 9 и 10. (НОД (8; 12) = 4; НОК (8; 12) = 24; НОД (12; 36) = 12; НОК (12; 36) = 36; НОД (9; 10) = 1; НОК (9; 10) = 90.)

– Верно ли, что произведение 7 · 40 · 156 делится на 30? Обоснуйте свой ответ. (Верно, 40 делится на 10, 156 делится на 3.)

− В математике дробь   называют сократимой дробью, как вы думаете, почему? (Числитель и знаменатель можно разделить на одно и то же число.)

− Как тогда можно назвать дробь   ? (Несократимой дробью.)

− Сформулируйте, какие дроби можно назвать сократимыми, а какие несократимыми? (Если числитель и знаменатель дроби можно разделить на одно и то же число, то такая дробь сократимая, а если нет такого числа, на которое можно разделить числитель и знаменатель, то дробь несократимая.)

       На доску вывешивается эталон с понятиями сократимой и несократимой дробью

Если числитель и знаменатель дроби делится на одно и то же число, то такая дробь сократимая.

Если нет такого числа, на которое делится числитель и знаменатель, то дробь несократимая.

− Что вы повторили и узнали?

− Какое следующее задание я приготовила для вас?

− С какой целью вы будете работать с пробным заданием?

       На доску вывешиваются карточки с пробным заданием

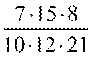
− Запишите, несократимы дроби, равные данным и сформулируйте три способа сокращения дробей.

− У кого нет ответа?

− Что вы не смогли сделать? (Мы пока не смогли записать несократимые дроби, равные данным.)

− У кого есть ответы, способы, которыми вы пользовались для сокращения каждой из дробей.

− Что вы пока не можете сделать? (Мы пока не можем сформулировать способы сокращения дробей.)

− Что теперь вы должны сделать?

3.        Выявление места и причины затруднения

Какое задание вы должны были выполнить?

− Как вы действовали?

− Что вы использовали при выполнении задания?

− В каком месте у вас возникло затруднение? (Затруднение возникло при отборе способов, при  формулировки способов сокращения дробей.)

− Почему у вас возникло затруднение? (У нас нет способов получения несократимых дробей, равных данным (нет способов сокращения дробей).)

− Что дальше необходимо сделать?

4.        Построение проекта выхода из затруднения

Сформулируйте цель вашей деятельности. (Построить способы сокращения дробей.)

– Сформулируйте тему урока. (Сокращение дробей.)

− Вспомните, какие задания вы выполняли на этапе повторения, и определите, что вам поможет при достижении цели. (Основное свойство дроби.)

− Для каждой из дробей у вас будет отдельный план работы по достижении цели

            На доске фиксируются три плана

План 1.

1. Определить на какое число можно разделить числитель и знаменатель дроби.

2. Определить, чем данное число является для числителя и знаменателя.

3. Сформулировать способ сокращения дробей.

4. Уточнить определение сократимой и несократимой дроби.

План 2.

1. Определить, как представлены числитель и знаменатель дроби.

2. Определить, на какие числа можно разделить числитель и знаменатель дроби.

3. Сформулировать второй способ сокращения дробей.

План 3.

1. Вспомнить признаки делимости чисел.

2. Постепенно сократить дробь, используя признаки делимости.

3. Сформулировать третий способ сокращения дробей.

Каждый план зачитывается и уточняется.

5.      Реализация построенного проекта

            Каждой группе дается право выбрать по согласованию один из планов. После выполнения задания три группы представляют результаты своей работы, остальные работают на дополнение и уточнение.

Вариант реализации плана 1:

1. Числитель и знаменатель дроби  можно разделить на 3.

2. Число 3 является наибольшим общим делителем чисел 27 и 36.

3. Найти НОД числителя и знаменателя дроби и разделить числитель и знаменатель дроби на найденное число.

            На доску вывешивается первый способ сокращения дробей

1) Найти для числителя и знаменателя их НОД;

2) Разделить числитель и знаменатель на НОД.

Вариант реализации плана 2:

1. Числитель и знаменатель представлены в виде произведения чисел.

2. Числитель и знаменатель можно разделить на 2, на 3, на 7, на 4, на 5.

3. Если числитель и знаменатель представлены в виде произведения множителей, то сократить можно на общие делители множителей.

            На доске даётся образец сокращения дробей:

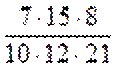
            На доску вывешивается второй способ сокращения дробей

1. Представить числитель и знаменатель в виде произведения чисел.

2. Разделить числитель и знаменатель на общие делители множителей

Вариант реализации плана 3.

На доске:   = 

            На доску вывешивается третий способ сокращения дробей

Делить числитель и знаменатель на числа, используя признаки делимости

Какие способы сокращения дробей вы открыли? (На НОД числителя и знаменателя, последовательно, используя признаки делимости, используя разложение числителя и знаменателя дроби на множители.)

− Что теперь необходимо сделать?

Сопоставить свои варианты с эталоном.

Как это можно сделать, используя учебник?

-Что вы можете сказать о результате своей работы?

- Что дальше необходимо сделать? (Надо научиться сокращать дроби разными способами.)

6. Первичное закрепление во внешней речи

            Задание выполняется у доски с комментарием.

Решение задания:

Первый способ:

Второй способ:               

Третий способ:

7.Самостоятельная работа с самопроверкой по эталону