Математическая статистика - междисциплинарный предмет

 «Математическая статистика – междисциплинарный предмет»

 

                                Авторы работы: учитель математики, Кобаидзе Нина Ивановна, научный руководитель 
и учащиеся – 9 классов.

                                                      Место выполнения работы:

                                                            Школа: МБОУ  гимназии №5

                                                                           ордена «Знак Почета»

                                                                               им. А. В.  Луначарского

                                          Классы:  9 «А», «Г», «Д»  классы

                                                                       Город: Владикавказ,  РСО-Алания

 

                                                       

 

 

План

I. Вступление

II. Математическая статистика – междисциплинарный предмет. 

1. Понятие математической статистики

2. История возникновения математической статистики

3. Элементы математической статистики, характеристики, термины и показатели. Особенности статистики. Классические средние значения. Статистическая вероятность.

III. Примеры различных задач из математической статистики и статистической теории вероятности.  

IV. Выводы

V.  Заключение

VI. Литература

 

Актуальность.

     Сегодня актуальным является междисциплинарный подход в изучении различных наук и предметов. Таким междисциплинарным предметом и стала математическая статистика.
В современном мире математическая статистика занимает важное и надёжное  место в различных науках, областях и сферах деятельности.

     Область применения и использования элементов математической статистики довольно широка и востребована, так как математическая статистика – это инструмент познания и прогнозирования, а статистическая вероятность – это возможность исполнения осуществимости какого-либо события  (дела, явления).

 

Новизна.

     Мы учились правильно формулировать задачи с использованием элементов и формул из математической статистики и ставить к ним вопросы. Обработали  некоторые данные
(по рассматриваемым вопросам), взятые  из статистического управления по республике РСО-А; провели сравнительный анализ некоторых примеров.

 

Цель работы: ознакомиться  с элементами математической статистики и статистической вероятностью; обработать  собранные результаты. Привести примеры и отработать навыки решения статистических задач; выработать умение моделировать задачи на определение классической (статистической) вероятности с использованием основных формул статистики.

Задачи:

1. Сформировать представление о возможности описания и обработки данных с помощью элементов математической статистики: характеристик, терминов и показателей; понимать их практический смысл.

2. Составить различные статистические задачи, правильно формулируя вопросы к ним, для доказательства различных статистических формул, правил и выводов.

3. Рассмотреть различные способы наглядного изображения результатов статистических исследований для оценки действительности. (Составить схемы, таблицы и диаграммы).

Стили и методы.

      Мы пользовались в исследовании следующими стилями:

алгоритмический, визуальный, прикладной, исследовательский, комбинаторный.

Методы.

Ø  Проблемно-поисковые: сбор первичной статистической информации; статистическая сводка и обработка информации;
анализ статистической информации.

Ø  Воспроизводящие методы: анализ и синтез научно-справочной литературы.

Ø  Репродуктивные методы: метод математического моделирования – составление и решение задач; метод статистических группировок и таблиц.

Ø  Исследовательские методы:  (работа с архивной документацией, классификация и систематизация собранного материала).

Объект исследования: математическая статистика.

Предмет исследования: составление и решение статистических задач.

 

I. Вступление

     Статистика имеет многовековую историю и своими корнями уходит в глубокую древность. « Науки математические с самой глубокой древности обращали на себя особое внимание, а в настоящее время они получили еще больше интереса по влиянию своему»  на образование, экономику, промышленность, медицину, демографию и другие науки, области  и сферы деятельности.

        На рубеже третьего тысячелетия становится очевидной универсальность вероятностно-статистических законов;  они стали основой описания научной картины мира. «Числа управляют миром», -  говорили пифагорейцы. Но мы знаем и другое, что  числа дают возможность человеку управлять миром, и в этом нас убеждает статистика.

      В нашу жизнь властно вошли выборы и референдумы, банковские кредиты и страховые полисы, таблицы занятости и диаграммы социологических опросов, которые основываются на элементах математической статистики. Ведь именно изучение и осмысление теории вероятностей и статистических проблем особенно отражают реальность. В настоящее время никто не подвергает сомнению необходимость включения в школьный курс математики изучение элементов статистики и теории вероятностей.

         В своей работе мы попробуем  сформировать представление о возможности описания и обработки  статистических данных, научиться находить элементы статистики, понимать практический смысл, используя  математические формулы и таблицы. Рассмотрим различные способы наглядного изображения результатов нашего исследования по вопросам и задачам из математики, из медицины, из географии и  из других предметов и областей.

II. Математическая статистика – междисциплинарный предмет.

1. Понятие математической статистики

    Математическая статистика – это наука, которая занимается получением, обработкой и анализом количественных данных о разнообразных явлениях, происходящих в природе и обществе.

     Предмет статистической науки составляет статистическая закономерность. Статистическая закономерность – повторяемость, последовательность и порядок изменений в явлениях.

Это понятие  играет большую роль не только в математической статистике, но и вообще в современной науке. Закон больших чисел  -  одна из форм проявления закономерности  массовых количественных отношениях. Суть его заключается в том, что   количественные    закономерности массовых явлений отчетливо проявляются лишь в достаточно большом их числе.

     Одна из основных задач статистики состоит в надлежащей обработке информации. Конечно, у статистики есть много других задач: получение и хранение информации, выработка различных прогнозов, оценка их достоверности и т. д. Ни одна из этих целей не достижима без обработки данных, поэтому, первое, чем стоит заняться — это статистическими методами обработать полученную информацию. Для этого есть много терминов, формул, характеристик, принятых в математической статистике.

     Математическая статистика — раздел математики, посвященный методам и правилам обработки и анализу статистических данных.

2. История возникновения математической статистики.

      Сбор статистических данных начался с самой глубокой древности.

      А к более позднему периоду относятся обработка и анализ статистических данных, т. е. зарождение статистики как науки.
      Вначале под статистикой понимали описания экономического и политического состояния государства или его части. Например, к 1792 г. относится определение: «статистика описывает состояние государства в настоящее время или в некоторый известный момент в прошлом ».

     В настоящее время деятельность государственных статистических служб вполне укладывается в это определение.

     Математическая статистика как наука начинается с работ знаменитого немецкого математика Карла Фридриха Гаусса (1777-1855). В конце XIX в. – начале ХХ в. крупный вклад в математическую статистику внесли английские исследователи, прежде всего К.Пирсон (1857-1936) и Р.А.Фишер (1890-1962). 

В 30-е годы ХХ века поляк Ежи Нейман (1894-1977) и англичанин Э.Пирсон развили общую теорию проверки статистических гипотез, а советские математики академик А.Н. Колмогоров (1903-1987) и член-корреспондент АН СССР Н.В. Смирнов (1900-1966) заложили основы непараметрической статистики.

Математическая статистика бурно развивается и в настоящее время.

 

3. Элементы математической статистики.

     По своему содержанию статистика и математика представляют различные отрасли знания. Математика исследует форму и количественные соотношения явлений и процессов, отвлекаясь от их физического содержания. Поскольку статистика имеет дело с количественными характеристиками, она широко применяет в своих исследованиях положения и методы математики. Особенно широкое применение находят в статистике теория вероятностей и математическая статистика.

     В повседневной жизни мы, не догадываясь, используем такие понятия: как медиана, мода, размах, среднее арифметическое и вероятность.

     Статистика понимается в настоящее время в трех значениях:

1) статистическая наука – вся практическая деятельности человека по сбору, обработке, накоплению и анализу цифровых данных, которые характеризуют образование, экономику страны, ее культуру и другие жизненно важные явления в жизни общества;

2) статистика – наука, которая занимается разработкой технических положений и методов, используемых статистической практикой.

     Существует тесная связь между статистической наукой и статистической практикой. Статистическая практика применяет правила, которые разработала статистическая наука, но в то же время статистическая наука опирается на те материалы, которые были получены статистической практикой, обобщает ее опыт и разрабатывает на основе всего этого свои новые положения;

3) представленные предприятием, организацией статистические данные в виде финансовой отчетности называют статистикой, но статистикой могут быть использованы данные, которые публикуются в справочниках, в периодических изданиях, в сборниках, они и представляют собой результат статистической работы.

     Особенности статистики:

1) в количественном выражении сообщаются статистические данные;

2) статистическую науку интересуют выводы, сделанные в результате анализа собранных и обработанных числовых данных;

3) состояние изучаемого явления на определенной ступени его развития в конкретных условиях места и времени отражают статистические данные.

Математическая статистика занимается как статическим описанием результатов опытов или наблюдений, так и построением и проверкой подходящих математических моделей, содержащих понятия вероятности.

     Классическими средними значениями, составленными из двух положительных чисел a и b, принято считать: среднее арифметическое -  число  (a+b) :2, среднее геометрическое - число ,среднее гармоническое - число 2ab:(a+b).

      Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на их количество. Среднее арифметическое является важной характеристикой ряда чисел, но иногда полезно рассматривать и другие средние.

Средняя величина - это обобщающая количественная характеристика совокупности однотипных явлений, по одному какому- либо  признаку.  В экономической практике используется широкий круг показателей, вычисленных в виде средних величин. Средние величины связаны с законом больших чисел.

     В математической статистике выделяют несколько видов средних величин: по наличию признака-веса, по форме расчета, по охвату совокупности.

     Когда нужно и не нужно среднее арифметическое?

     Имеет смысл вычислять средние траты в семье на продукты, среднюю урожайность картофеля на огороде, средние расходы на продукты, чтобы понять, как поступать в следующий раз, чтобы не было большого перерасхода. Нет смысла вычислять среднюю зарплату моей мамы и бизнесмена Абрамовича, среднюю температуру здорового и больного человека,  средний размер обуви у меня или у моего брата.

     Модой называют число ряда, которое встречается в этом ряду наиболее часто. Можно сказать, что данное число самое «модное» в этом ряду. Такой показатель, как мода, используется не только для числовых данных. Если, например, опросить большую группу учеников, какой школьный предмет им нравится больше всего, то модой этого ряда ответов окажется тот предмет, который будут называть чаще остальных.

     Мода – показатель, который широко используется в статистике. Одним из наиболее частых использований моды является изучение спроса. Например, при решении вопросов, в пачки какого веса фасовать масло, какие открывать авиарейсы и т. п., предварительно изучается спрос и выявляется мода — наиболее часто встречающийся заказ.

Заметим, что в рядах, рассматриваемых в реальных статистических исследованиях, иногда выделяют больше одной моды. Когда в ряду много данных, то интересными бывают все те значения, которые встречаются гораздо чаще других. Их статистики тоже называют модой.

     Когда нужна  мода?

Мода важна для производителей при определении самого популярного размера одежды, обуви, размеров бутылки сока, пачки чипсов, популярного фасона одежды

     Однако нахождение среднего арифметического или моды далеко не всегда позволяет делать надежные выводы на основе статистических данных. Если есть ряд данных, то, помимо средних значений, надо еще указать, насколько используемые данные различаются между собой.

     Одним из статистических показателей различия или разброса данных является размах.

Размах — это разность между наибольшим и наименьшим значениями ряда данных.
     Когда нужен и не нужен размах?

Размах ряда находят тогда, когда хотят определить, как велик разброс данных в ряду. 

     Еще одной важной статистической характеристикой ряда данных является его медиана. Обычно медиану ищут в случае, когда числа в ряду являются какими-либо показателями и надо найти, например, фирму со средней годовой прибылью, авиакомпанию, предлагающую средние цены на билеты, и т. д.

     Медианой ряда, состоящего из нечетного количества чисел, называется число данного ряда, которое окажется посередине, если этот ряд упорядочить.      Медианой ряда, состоящего из четного количества чисел, называется среднее арифметическое двух стоящих посередине чисел этого ряда.

Когда нужна и не нужна медиана?

     Медиана чаще применяется с другими статистическими характеристиками, но по ней одной можно отбирать результаты, выше или ниже медианы.

    

     III. Примеры статистических задач из математики, медицины, экономики, географии и др.  

( Из математической статистики ).

Пример№1: Найти выборочную среднюю по данному распределению выборки объема n=8:

Введем обозначения:

     х₁, х₂ ,х₃  ,…,х_n –выборка;

     n – объем выборки;

     х_i – вариант признака «х» (последовательность вариант, записанных в возрастающем порядке, называется вариационным рядом);

     n_i – частота выборки (сумма всех частот равна объему выборки);

     w_i – относительная частота;

     х_в – несмещенная оценка генеральной средней (выборочная средняя);

     u_i =  х_i   – с – условная варианта (при х_i больших);

 

х_i 2 5 9

n_i 3 1 4.

Решение:

Пример №2. Как изменяется АД (артериальное давление) у учителей в зависимости проведённых уроков (проверялось АД до урока и после урока). Наблюдались учителя следующих предметов: математика - 5, осетинский язык - 3, английский язык - 3. Найти выборочную среднюю по данному распределению выборки объема.

АД до уроков	Кол-во учителей	АД – верхнее (ср.)	АД - нижнее (ср.)
Математика	5	118	85
Английский яз.	2	115	80
Осетинский яз.	3	119	88

АД после уроков	Кол-во учителей	АД – верхнее (ср.)	АД - нижнее (ср.)
Математика	5	140	91
Английский яз.	2	126	90
Осетинский яз.	3	130	86

 

Найдем выборочную среднюю по данному распределению выборки объема n=10 для  АД – верхнего (до уроков):  

1) Данная выборка:   х_i 115   118   119

                                    n_i     2      5       3.

2)

3)

u_i     -3     0     1

n_i     2     5     3;

АД - верхнее (до уроков)  118

Определим АД - нижнее (до уроков)

1) Данная выборка:

 х_i         80   85   88

n_i             2    5    3.

2)

3)

u_i     -5    0      3

n_i     2     5     3;

АД - нижнее (до уроков)  84,9

Аналогично вычислим АД после уроков и получим АД – верхнее: 132;

АД – нижнее: 89.

Ответ: АД до уроков: 11885; АД после уроков: 13289

Пример №3.

( Тестовые баллы ЕГЭ  по математике  )

а) Определить средний тестовый балл участников ЕГЭ по математике (в гендорном соотношении) за 2012-2013. Итоговые данные занести в таблицу и построить диаграмму.

 

ЕГЭ математика (по населенным пунктам городского типа).	мальчики	девочки
2012	45	44,3
2013	49,8	48,9

 

 

 

 

 

 

 

 

 

 

 

 

 

 

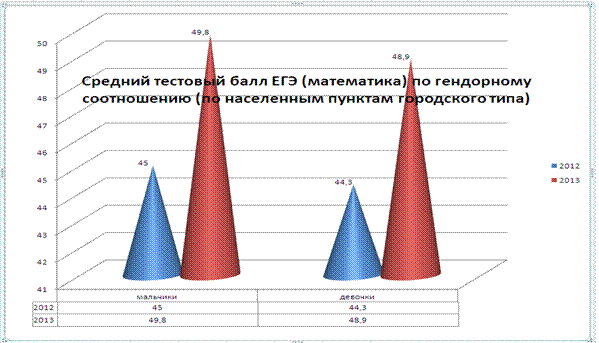
б) Определить количество участников ЕГЭ по РФ и РСО-Алании, из них-стобальников по математике 2012-2013. Составить таблицу и построить диаграмму.

в) Какой процент составляют стобальники РФ в 2012 г. по сравнению с 2013 г.?

 

 

 

	Количество Участников ЕГЭ по РСО-Алании	Количество Участников ЕГЭ по РФ	Количество стобалльников ЕГЭ по математике по РФ	Количество стобалльников ЕГЭ по математике по РСО-Алании
2012	26614	3032121	56	1
2013	27053	2952132	538	2

в) Решение.

56 – х%                                   

538 – 100%;

Пример №4. Привести некоторые статистические данные по употреблению наркотиков во всем мире. Показать различные диаграммы и таблицы о распространении наркотиков и обращаемости граждан в медучреждения.

Предисловие к задаче: Известно что в настоящее время перед молодежью встала страшная проблема употребления наркотиков. По всему миру гибнут и подростки, и взрослые.

Из всемирного доклада ООН о наркотиках известно, что одного килограмма героина достаточно для производства 200 тыс. доз.

Согласно официальной статистике, в России насчитывается около 500 000 хронических наркоманов. В странах Запада доля преступлений, связанных с наркотиками, составляет 67% от общего их числа.

По данным экспертов, в России от передозировки наркотиками ежедневно погибает минимум 200 человек. До 80% российских наркоманов — несовершеннолетние и молодежь. Наркотики – это невероятное зло, но его надо искоренить. Надо всемирно объявить войну наркотикам и вести активную борьбу с теми, кто вовлекает в эту трясину молодежь. Наркотики – это угроза 21 века!

Распространенность (%) употребления инъекционных наркотиков среди населения в возрасте 15-64 лет (на карте мира).

Основные виды проблемных наркотиков (по фактору обращаемости за наркологической помощью), 2007 год (или последний год, по которому имеются данные)

 

 

 

 

 

 

 

 

 

 

 

 

     Вывод: Статистические данные помогают нам ознакомиться с ужасающей действительностью и побуждают к принятию эффективных мер по борьбе с наркотиками.

Математическая вероятность.

     Однако в жизни чаще встречаются события, сравнить и оценить которые, основываясь только на интуиции и на сомнительные (неверные) цифры, невозможно и трудно. Каждое событие обладает определенной степенью возможности наступления, т.е. определенной оценкой. Такую оценку называют вероятностью события. Это мы изучаем в школе по алгебре в разделах: приближенные вычисления и случайные события или величины.
     Основатель современной теории вероятностей А.Н.Колмогоров: «Вероятность математическая – это числовая характеристика степени возможности появления какого-либо определенного события в тех или иных определенных, могущих повторяться неограниченное число раз условиях».

Классическое определение.
Определение: вероятность события (Р (А)) – это численная мера объективной возможности его появления.
Теория вероятностей даёт способ числового нахождения вероятности события:

А – некоторое событие;

m – количество исходов, при которых событие А появляется;

n – конечное число равновозможных исходов.

     Вероятностью Р наступления случайного события А называется отношение m/n, где n – число всех возможных исходов эксперимента, а m – число всех благоприятных исходов: Р(А)= m/n.

Формула полной вероятности: P(A) = P(H₁) •P(A/H₁)+P(H₂) •P(A/H₂) + … +

+ P(H_n) • P(A/H_n).

Формула суммы вероятностей: P(A + B) = P(A) + P(B) - P(A) • P(B).

Задача из ЕГЭ – В₆.

В торговом центре стоит два одинаковых кофейных автомата. Вероятность того, что в автомате к концу дня закончится кофе, равна 0,3.

Вероятность того, что к концу дня кофе закончится в обоих автоматах, равна 0,12.

Найти вероятность того, что к концу дня кофе останется в обоих автоматах.

Искомое событие равно: .

P(A + B) = P(A) + P(B) - P(A) • P(B);

0,3+0,3-0,12=0,48.

отсюда

P()=1- P(A + B)=1-0,48=0,52

Ответ: 0,52

Формула произведения независимых событий: P(A • B) = P(A) • P(B).

Формула суммы несовместимых событий: P(A + B) = P(A) + P(B).

 

Задача№4. В нашей школе 1300 человек, из  них 5 человек – трудные подростки.

Какова вероятность того, что один из них попадётся директору на глаза?

     Решение:

Задача №5. Из карточек составили слово «статистика». Карточку с какой буквой вероятнее всего вытащить? Какие события равновероятные?

 Решение: Всего 10 букв.

Буква «с» встречается 2 раза – P(с) = 2/10 = 1/5;

буква «т» встречается 3 раза – P(т) = 3/10;

буква «а» встречается 2 раза – P(а) = 2/10 = 1/5;

буква «и» встречается 2 раза – P(и) = 2/10 = 1/5;

буква «к» встречается 1 раз – P(к) = 1/10.
Задача№6. Случайно нажимают три клавиши из одной октавы. Найдите вероятность того, что:

1)      звучат ноты «си» и «до»;

2)      не звучит нота «фа»;

3)      звучит нота «ля»;

4)      получится до-мажорное звучание.

     Решение. Исходами являются все наборы по 3 клавиши из 7 имеющихся в октаве; порядок расположения клавиш в наборе не учитывается. Общее количество исходов

;    = ;    .

1)      А={звучат ноты «си» и «до»}. К двум клавишам добавляют третью – любую из 5 оставшихся,

2)      В={ не звучит нота «фа»}. Выбираем три клавиши из шести, исключая «фа»,

3)      С={звучит нота «ля»}. Выбираем две клавиши из шести, исключая «ля»,

4)      D={получилось до-мажорное звучание};  (должны быть нажаты три соседние клавиши в начале октавы, единственный вариант).

Статистическое определение вероятности.
     Статистическая вероятность – относительная частота, с которой событие проявляются внутри класса событий.

     Задача №7. По статистике в городе Владикавказе за год из каждой 1000 автомобилистов два попадают в аварию. Какова вероятность того, что автомобилист в этом городе весь год проездит без аварий?

     Решение.
Задача №8.
Чтобы определить, какой цвет волос встречается в городе чаще, а какой реже, мы, школьники за полчаса провели следующий эксперимент. Каждый выбрал свой маршрут и записывал по пути следования цвет волос каждого пятого встречного. Результаты были занесены в следующую таблицу:

Оцените вероятность того, что выбранный наугад житель этого города будет:
а) шатеном; б) рыжим; в) не рыжим.

     Решение.

а) ;  б)

в)
Задача № 9. Из озера в городе Моздок  выловили 86 рыб, которых пометили и отпустили обратно в озеро. Через неделю произвели повторный отлов, на этот раз поймали 78 рыб, среди которых оказалось 6 помеченных. Сколько приблизительно рыб живет в озере?

     Решение: 

Оказывается, найти ответ на этот неожиданный вопрос совсем несложно.

В самом деле: обозначим неизвестную нам численность рыб в озере через N.

Тогда  вероятность поймать помеченную рыбу в озере будет   86/ N

С другой стороны, эта вероятность должна приближенно равняться полученной во втором улове частоте: 86/N=6/78, отсюда N = 86 ×78/6 =1118. Сравнивая вероятности всех возможных исходов эксперимента, можно только предсказывать.

Задача №10.

А) Определить по статистическим формулам численность населения в некоторых странах мира (18-20 в.), занести данные в таблицу.

1.                  Общая численность населения.

P= P₀ + (N — M) + (V₊ — V_-) = P₀ + E + V_пр (уравнение демографического баланса)

P — общая численность населения

P₀ — численность населения на начало года

N — общее число родившихся

M — общее число умерших

E — естественный прирост населения

V₊ — число прибывших

V_- — число выбывшиих

2.    Общий прирост населения

P₁ — P₀ = P_пр

Р₀ — численность населения на начало периода (обычно год)

Р₁ — на конец периода

3.                  Естественный прирост населения

N — M = E

N — общее число родившихся

M — общее число умерших

4.                  Миграционное сальдо (чистая миграция)

V₊ — V_- = V_пр;  V₊ — число прибывших (иммигранты)

V_- — число выбывших (эмигранты)

V = O — E (косвенный метод); O = P₁ — P₀

 

	Численность населения (млн.чел.)
Годы	1750г.	1800г.	1850г.	1900г.	1950г.	1975г.	2009г.
Мир	791,0	978,0	1,262	1,650	2529	4061	6829
Африка	106,0	107,0	111,0	133,0	227,0	419,0	1010,0
Азия	502,0	635,0	809,0	947,0	1403,0	2379,0	4121,0
Европа	163,0	203,0	276,0	408,0	547,0	676,0	732,0
Латинская Америка и страны Карибского бассейна	16,0	24,0	38,0	74,0	167,0	323,0	582,0
Северная Америка	2,0	7,0	26,0	82,0	172,0	242,0	348,0

 

 Сравнительный анализ: Предположительно численность мирового населения в 2011 году составила 7 миллиардов человек. Хотя с 60-х годов XX века наблюдается снижение уровня роста населения,  удвоение его численности в период с 1950-х по конец 1980-х годов показало, что за последние 50 лет каждый дополнительный миллиард появляется гораздо быстрее,
чем когда-либо ранее:  каждый из двух последних миллиардов появился в рекордный срок — за 12 лет. На пороге – 2015 год…

Б) Приведем пример по плотности населения в РСО-Алании (2013-20104 г.г.)

Вычислить среднюю плотность населения на 1 кв.м. по нашей республике  (Северной Осетии).

Найти моду, медиану и размах.

11,1 ;  17,3;   33,2;   67,2;   73,2;   73,4;   126,1;   320,4;  1134,6

Вычислим среднюю плотность населения на 1 кв. км. по нашей республике.

(1134.6+17,3+73,4+33,2+11,1+67,2+320,4+126,1+73,2):9= 206,3

Медианой данного ряда является число 73,2 , модой число - 73, размах – 1123.5

 

		Всего	Городское	Сельское	Плотность населения чел/кв.км.
1	Владикавказская администрация	330166	327964	2202	1134,6
2	Алагирский район	34971	19665	15306	17,3
3	Ардонский район	27691	16929	10762	73,4
4	Дигорский район	19736	10954	8782	33,2
5	Ирафский район	15171		15171	11,1
6	Кировский район	27375		27373	67,2
7	Моздокский район	86853	40544	46309	320,4
8	Правобережный район	55726	35968	19758	126,1
9	Пригородный район	104767		104767	73,2

   

Задача №11.

Мы провели опрос 8-10 классов с целью определения времени просмотра телевизионных программ (в том числе и по компьютеру). Всего было опрошено 100 человек. 8-А-30уч-ся -2 смена;  9-А-33уч-ся - 1-смена и 10-А- 37 уч-ся - 1 смена.

Показать зависимость числа зрителей от времени суток на гистограмме.

* В какие периоды времени число уч-ся, смотрящих телевизор, превосходит 30 человек?  Какой % всего времени показа составляет время, когда телевизор смотрят более 50 уч-ся?

* Сколько в среднем уч-ся  смотрят телевизор в течение часа в период с 16 до 19 часов?  Сколько  % числа  опрошенных  составляют эти учащиеся?

* Определить, какое число зрителей (в среднем) приходится на час вещания?

Решение:

Время	8-А	9-А	10-А	итого
С 6до7час	5	3	4	12
С8до9час	4	1	1	6
С10до11час	5	1	1	7
С12до13час	1	1	1	3
С14до15час	8	5	5	18
С16до17час	4	5	6	15
С18до19час	1	10	5	16
С20до21час	2	4	7	13
С22до23час	0	3	7	10
итого	30	33	37	100

 

 

 

 

 

 

 

а) более 30 уч-ся смотрят телевизор в периоды с16 часов до 19 часов. Показ передач начинается в 6 часов и заканчивается в 2часа ночи. Таким образом, время телевидения- 20 часов. БОЛЬШЕ 60 УЧ-СЯ НАХОДЯТСЯ У ЭКРАНОВ В ТЕЧЕНИЕ (С 14 ДО 21 ЧАСА)-7 ЧАСОВ. Это составляет 7/20=0,35, т.е. 35% всего времени показа;

б) Воспользуемся данными гистограммы. В течение 9 часов (с 14 до23ч) телевизор смотрят 72 из100. Следовательно, в среднем на этот период приходится72/9=8 уч-ся. Они составляют 72% от 100 человек;

в) За весь период вещания, т. е. за 20 (в нашем случае - 17 часов), на один час в среднем определён результат статистами: 660/20=33,(3); 33чел.

 

IV. Выводы.

1. Показали, что математическая статистика – междисциплинарный предмет. Составили и решили различные задачи, связанные с экономикой, медициной, биологией, физикой, демографией, социологией и другими науками и областями, используя математическую статистику.

2. Сформировали представления о статистических исследованиях; обработали собранные  результаты с помощью элементов математической статистики (характеристик, терминов и показателей) и научились  понимать их практический смысл.

 3.  Математическая статистика дает цифровое и содержательное освещение некоторых явлений и процессов. (Рассмотрели различные статистические  задачи , чтобы показать, что статистика дает доказательную силу формулам и выводам).

4. Рассмотрели различные способы наглядного изображения результатов статистических исследований. (Составили  схемы, таблицы и диаграммы). Статистика служит самым надёжным прогнозом оценки действительности.

V. Заключение

     Мы, выходя из школы в большой  и непредсказуемый мир, должны отличать истинную информацию от ложной и уметь ее анализировать. Во взрослой жизни надо уметь прогнозировать исход предстоящей ситуации, а также использовать результаты статистических обработок для своего благополучия и в целях развития общества. Статистика –  это наука будущего.

     Рекомендуем всем школьникам изучать математическую статистику и применять ее в различных задачах, ведь на экзаменах встречаются стохастические и вероятностные задачи, в которых используются формулы  математической статистики. Мы надеемся, что математическая статистика  в жизни тоже очень помогает.

 

VI. Список литературы

1. Шмойлова Р.А. Теория статистики. М.,2005г.- С.208, 210, 211.

2. Колмогоров А.Н. Введение в теорию вероятностей. Москва, 1982 г. Изд. «Наука»

3. «Всемирный доклад ООН о наркотиках». 2009 г.