МАТЕМАТИЧЕСКИЕ МЕТОДЫ ПРИ РЕШЕНИИ

ФИЗИЧЕСКИХ ЗАДАЧ

Топчий А. А.

учитель физики,

МАОУ «Лицей №29», г. Тамбов

Данная работа посвящена рассмотрению  математических приёмов при решении физических задач. Изучая математику, мы не всегда задаёмся вопросом: в каких конкретных случаях нам предстоит применять полученные знания? А решая задачи по физике, считаем, что кроме физических законов нам ничего не потребуется. Но физика тесно связана с математикой: при решении задач применяются преобразования формул; геометрические построения;  устанавливаются функциональные зависимости, связывающие физические величины. Для физика-исследователя математическая и физическая части решения задачи не являются отдельными и независимыми, физик должен в совершенстве владеть математическим аппаратом.

Цель работы – выявление класса задач по физике, тесно связанных с математикой. В школьной программе данные задачи рассматриваются на уроках физики с 8 по 10 класс, но они могли бы решаться и на уроках математики, демонстрируя межпредметные связи и помогая усвоить одновременно материал по двум предметам.

Работа должна быть интересна учащимся, готовящимся к углубленному изучению физики, а также учителям – для внеурочной работы по предмету.

§1. Векторные величины. Действия над векторами

Мы знаем, что в физике много векторных величин. Выбрав систему отсчёта, мы сможем выполнять действия над векторами: складывать, вычитать, находить проекции на оси. При выполнении этих действий нам поможет знание правил работы с геометрическим вектором, а также теоремы геометрии.

Задача 1

С какой скоростью и по какому курсу должен лететь самолёт, чтобы за время, равное 1 часу, пролететь точно на север путь 180 км, если во время полёта дует северо-западный ветер под углом 30 градусов к меридиану и со скоростью 8м/с?

Дано:

t = 1ч = 3600с

S = 180км = 1,8 ∙

α = 30°

 =8 м/с

Найти:

 -?

∠ OMN - ?

Решение:

Самолёт участвует в двух движениях: со скоростью V относительно воздуха и со скоростью вместе с воздухом относительно земли. По условию задачи, скорость  направлена на юго-восток под углом 30° к меридиану.

Скорость самолета относительно Земли =50м/с.

Вектор скорости направлен на север (по условию).

По правилу сложения векторов: .

Из чертежа видно, что самолет должен держать курс на северо-запад под углом OMN к меридиану.

Применим теорему косинусов для треугольника OMN:

 = += +∙

м/с

Теперь вычислим угол OMN (курс самолёта) по теореме синусов:

Ответ: м/с, .

Задача 2

Самолёт летит горизонтально со скоростью 360 км/ч на высоте 490 м. Когда он пролетает над точкой А, с него сбрасывают груз. На каком расстоянии от точки А груз упадёт на Землю? С какой скоростью и под каким углом к горизонту груз упадёт на землю?

Дано: = 360км/ч

 = 490м

Найти: АВ - ?

 V - ?

 α - ?

Решение:

Направим ось ОX – горизонтально, ОY – вертикально, начало координат поместим в точку А.

 Уравнения движения груза:

OX: x = t

OY: y = ,где = h

Т.е. движение груза состоит из равномерного движения в горизонтальном направлении и свободного падения в вертикальном направлении.

С точки зрения математики, мы решаем систему уравнений.

Для точки В уравнения примут вид:

Теперь найдём скорость падения:  (выполнили переход от векторных величин к скалярным), при этом

 .

Угол падения на землю определяется из соотношения в прямоугольном треугольнике:

≈45°.

Вывод: при решении задачи нам пригодилось знание законов движения и правила работы с векторными величинами, а также нахождение угла в прямоугольном треугольнике.

Ответ: расстояние АВ = м/с, α = 45°.

Рассмотрим ещё одну задачу, в которой также требуется разложение вектора и расчёт углов.

Задача 3

Бомбардировщик пикирует на цель под углом 60 градусов к горизонту со скоростью =540 км/ч и сбрасывает бомбу на высоте h = 600 м.

На каком расстоянии S от цели в горизонтальном направлении надо сбросить бомбу, чтобы она попала в цель? Сопротивление воздуха не учитывать.

Дано: = 540 км/ч

 h = 600м

 α = 60°

Найти: S – ?

Решение:

Выберем систему координат, как показано на рисунке.

Начальные условия:  = 0,  = 0, =, =.

Как и в предыдущей задаче, зависимость координат бомбы от времени можно выразить системой уравнений:

Бомба попадет в цель в некоторый момент времени , при этом y = h, x = S.

Получим: h =t +  ,

с точки зрения математики, нами получено квадратное уравнение относительно переменной t.

g + 2- 2h = 0

Решая его, получим:

 (нам подходит только данный корень, т.к. )

Подставив полученное значение в первое уравнение системы, получим:

 x = S = 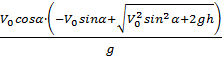 ≈ 490 м

Ответ: S ≈ 490 м.

При решении физической задачи нам могут потребоваться формулы площадей и объёмов геометрических фигур.

Задача 4

Определить скорость и ускорение точки, находящейся на поверхности Земли на широте 54 градуса, принимая во внимание только вращение Земли вокруг оси. Радиус Земли – 6400 км.

Дано:

R = 6400 км = 6.4 м

φ = 54°

T = 24 ч = 86400 с

Найти: V – ? а – ?

Решение:

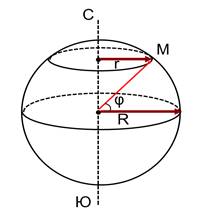
Пусть данная точка М находится на окружности радуиса r, тогда

V = , r – радиус окружности сечения земной сферы плоскостью, проходящей через точку М с широтой 54° перпендикулярно вращению оси Земли;  - траектория движения; Т – время одного полного оборота Земли.

По рисунку: r = R cos φ.

Тогда V ==м/с.

Ускорение точки М: а ==  м/с².

При решении задачи мы использовали геометрический материал: сечением сферы является окружность. Т.к. к любому такому сечению существует перпендикулярный ему радиус сферы, то есть формула, выражающая радиус сечения через радиус сферы.

Ответ: .

§2. Математический анализ в физике

При решении задач по физике мы также сталкиваемся с исследованием функции.

Задачи на нахождение наибольшего и наименьшего значений функции из математического анализа являются прикладными. Чаще всего мы их встречаем с геометрическим или экономическим содержанием, но есть также задачи с физическим смыслом, которые легко решаются средствами высшей математики.

Задачи, которые будут представлены, можно решить и без применения понятия производной и определённого интеграла. Но в старших классах можно представить данные решения, как альтернативные и более удобные.

Задача 5

Санки с грузом общей массой m нужно сдвинуть с места. Какую наименьшую силу необходимо приложить?

Дано:

m – масса санок

Найти:

Решение:

Отложим векторы всех сил, действующих на санки, от их центра масс, как показано на рисунке. Чтобы санки сдвинулись с места, силы должны уравновешивать друг друга, сила F – результирующая.

Выберем координатные оси, как показано на рисунке, и найдём проекции силы F на данные оси:

 = F cos α,

 = F sin α.

F_тр – сила трения, N – сила реакции опоры, mg – сила тяжести.

Получим уравнения относительно каждой из координатных осей:

OX: F cos α – F_тр = 0,

OY: F sin α + N – mg = 0.

По формуле F_тр = kN выразим N из второго уравнения: N = mg – F sin α.

Тогда F_тр = kN (mg – F sin α) и подставим в первое уравнение:

F cos α – kmg + k F sin α = 0.

Получим функцию для силы F, относительно угла, под которым она приложена:

F .

Областью определения функции служит отрезок .

Исследуем функцию на наименьшее значение с помощью производной

Воспользуемся формулой сложения гармонических колебаний:

.

На области определения производная может обратиться в ноль только

при .

Если изобразить график функции , можно заметить, что функция принимает отрицательные значения на промежутке (0; т.е.

α =  является точкой минимума функции, и т.к. она единственная на области определения, то наименьшее значение будет достигаться в ней.

Вывод , т. е. силу F необходимо приложить под углом  к положительному направлению оси OX.

Ответ:

Задача 6

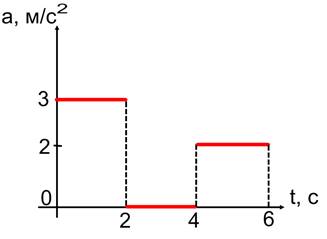Зависимость ускорения тела от времени показана на рисунке.

Начертите графики зависимости скорости, перемещения тела от времени, если начальная скорость тела х₀ = - 3 м/с, и начальная координата тела х₀ = 2 м.

Пользуясь графиками, найдите среднюю скорость перемещения V_ср и среднюю путевую скорость V за время t = 6 с движения.

Решение:

Рассмотрим каждый из временных промежутков:

1)  

2)

3)

 Средняя скорость вычисляется по правилу: весь путь делится на всё затраченное на него время. Также заметим, что путь вычисляется как площадь фигуры, полученной под графиком скорости. Т. к. путь – это скорость, умноженная на время, получается, что каждая ординта равна перемещению в данный момент времени, а сумма таких ординат на каждом отрезке и образует площадь фигуры (т.е. при подсчёте применяется понятие определённого интеграла на указанном отрезке).

 Теперь построим графики зависимостей скорости и перемещения от времени: законы для скорости – линейные зависимости, для перемещения – квадратичные функции.

)

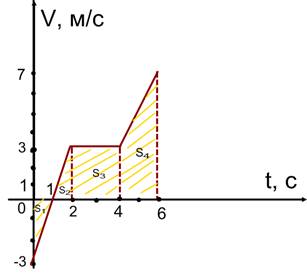
Ответ: 3, 2м/с; 2,7 м/с.

Заключение

В работе на примере небольшого набора задач показано, насколько широко применяется математика в физике; как можно проанализировать физическую задачу и решить её математическим путём. В работе намерено берутся задачи среднего уровня сложности, при решении которых не требуется знаний углубленного курса изучения математики, но необходимо понимание физических процессов с точки зрения математики и её законов. Тем самым, наглядно демонстрируются элементарные приёмы решения.

Рассмотрение таких вопросов позволяет в комплексе подходить к изучению наук естественно-математического цикла, углублять знания, не выучивать алгоритмы решения, а понимать суть процессов.

Цели, поставленные в начале исследования, были достигнуты: обозначен круг задач по физике, которые решаются с помощью элементарных знаний по математике; также показано применение средств математического анализа для решения более сложных задач.

При работе над данной темой были использованы сборники задач и методические пособия по физике, учебник по алгебре и математическому анализу для углубленного изучения, статьи и методические рекомендации.

Вопросы, которые возникают при решении физических задач, остаются открытыми: насколько математика проникает в физику, а физика в математику? В каких учебниках и на уроках по какому предмету они должны решаться? В работе показана лишь небольшая часть того, что зачастую остаётся вне школьных уроков.

 Эта работа позволяет внимательнее подойти к изучению практико-ориентированных задач более высокого уровня сложности, заинтересовать учащихся в дальнейшем исследовании и углублении знаний. Полученные результаты рекомендуется рассмотреть на занятиях математического кружка.

Список использованных источников

1.                 Кузнецов, А.П. Анализ в физике / А.П. Кузнецов, С.П. Савин, Н.В. Станкевич. – Саратов: Научная книга, 2008. – 90 с.

2.                 Стасенко, А.Л. Интегралы и производные в физике: учебно-методическое пособие для старшеклассников / А.Л. Стасенко. – М.: ФАЛТ МФТИ, 2006. – 108 с.

3.                 Турчина, Н.В. Физика: 3800 задач для школьников и поступающих в вузы / Н.В. Турчина, Л.И. Рудакова, О.И. Суворов и др. – М.: Дрофа, 2000. – 672 с.

4.                 Физика. Решение задач: В 2 кн: Кн. 1. – Мн.: Литература, 1997. – 576с.

5.                 Шабунин, М.И. Алгебра. Начала математического анализа. Профильный уровень: учебник для 10 класса / М.И. Шабунин, А.А. Прокофьев. – М.: БИНОМ. Лаборатория знаний, 2007. – 424 с.