Математические состязания, как средство формирования творческой активности учащихся

Юзеева И.П.

МАОУ «Академический лицей»

города Магнитогорска

Математические состязания, как средство
формирования творческой активности учащихся

Итоги работы предприятий во многом зависят от того, насколько развито творческое мышление их работников. В связи с этим в современном обществе возникла потребность в личности, которая обладает данным качеством. Участие обучающихся в различного рода математических турнирах, правильно организованная деятельность по подготовке к ним, специальным образом подобранные формы и содержание математических соревнований способствуют формированию их творческой активности, значительно повышая интерес к математике.

В последние годы проводится много различных математических состязаний, которые делятся на личные и командные.

К личным видам относятся: устные, письменные олимпиады, математический экспресс; к командным – математическая регата, математический бой, математическая карусель и другие.

Целью математического боя является развитие культуры мышления и математической речи, умения вести дискуссию и оппонировать; воспитание уважительного отношения к окружающим. Для формирования умения слушать и слышать друг друга можно проводить командное соревнование «математическая регата». Целью математического экспресса и письменной олимпиады является формирование навыков самопроверки и самоконтроля, развитие изобретательности и смекалки, умения нестандартно мыслить. Опираясь на их цели, можно разработать содержание различных видов математических соревнований. Рассмотрим одно из этих состязаний, например, математическую регату.

Одной из традиционных тем математических олимпиад является тема «Задачи на раскраску». Каждая из задач этого типа содержит в своем решении что-то неожиданное, какую-то «изюминку», поэтому именно они составили содержание данного математического соревнования.

Задачи для математической регаты подбирались с использованием дидактических принципов составления задач: индивидуального подхода, последовательного преодоления трудностей, сравнения, доступности, полноты. Применение последних помогает углублять понимание изучаемой темы, а также существенным образом активизирует мыслительную деятельность обучающихся. Например, использование принципа сравнения позволяет подбирать задачи, при решении которых учащимся приходится внимательно анализировать условия задач, сравнивать, то есть искать общее и различия, переносить некоторые идеи решения одних задач на другие. Несмотря на то, что формулировки некоторых задач различны, способ их решения может быть один.

Представляю содержание разработанного математического соревнования.

 Математическая регата

1 тур (стоимость каждой задачи 3 балла)

1. На белые клетки доски покрашенной в шахматном порядке (см. рис.1) поставлены три шашки. Каждую из шашек нужно передвинуть на соседнюю по стороне клетку. Доказать, что это всегда можно сделать так, что на одной клетке окажется не менее двух шашек.

Рис.1

2. Рома, Сема и Тома взяли по квадрату клетчатой бумаги 55 клеток. Каждый закрасил 16 клеток черными, а остальные оставил белыми. На всех трех получившихся картинках каждая черная клетка имела ровно 2 черные соседки (по стороне). Рома хотел пройти по всем черным клеткам, переходя из клетки в соседнюю, но на его картинке такой переход оказался невозможным. На чертеже Семы это сделать было можно, но некоторые черные клетки оказались без белых соседок. Наконец, рисунок Томы позволял пройти по всем черным клеткам, переходя от соседки к соседке, а каждая черная клетка имела белую соседку. Восстановите чертежи.

3. Некоторые клетки квадрата 44 белые, а остальные черные. Соседними считаются клетки, у которых общая сторона. Известно, что у каждой белой клетки ровно три черные соседки, а у каждой черной клетки – ровно одна соседка. Восстановите раскраску по этим условиям.

2 тур (стоимость каждой задачи 4 балла)

1. Шахматный конь вышел с поля а1 и через несколько ходов вернулся на него. Докажите, что он сделал четное число ходов.

2. Можно ли все клетки доски 9×9 обойти конем по одному разу и вернуться в исходную клетку?

3. Фигура «верблюд» ходит по доске 1010 ходом типа (1;3) (т.е. она сдвигается сначала на соседнее поле, а затем сдвигается еще на три поля в перпендикулярном направлении; конь, например, ходит ходом типа (1;2)). Можно ли пройти ходом «верблюда» с какого-то исходного поля на соседнее с ним?

3 тур ( стоимость каждой задачи 5 баллов)

1. В каждой клетки доски 55 сидит жук. В некоторый момент все жуки переползают на соседние (по горизонтали или вертикали) клетки. Как вы думаете, останутся ли при этом пустые клетки?

2. Докажите, что шахматную доску 88 нельзя замостить 15 прямоугольными фигурками 14 и одной фигуркой, указанной на рисунке 2. (Квадраты шахматной доски и фигурки одинаковы.)

Рис.2

3. Клетки прямоугольной доски размером 1530 раскрашены в белый и черный цвета. У каждой белой клетки, не граничащей со сторонами прямоугольника, среди восьми ее соседей ровно пять окрашены в черный цвет, а у каждой черной клетки, не граничащей со сторонами прямоугольника, - ровно четыре белых соседних клетки. Сколько всего белых клеток на этой доске?

4 тур

( стоимость каждой задачи 6 баллов)

1. Какое наибольшее количество прямоугольников 41 можно разместить в квадрате 66 (не нарушая границ клеток)?

2. Можно ли во всех клетках бесконечной клетчатой плоскости расставить по одному все целые числа (каждое целое число – ровно в одной клетке) так, чтобы у каждого числа все четыре соседние (по стороне) числа были либо только больше, либо только меньше.

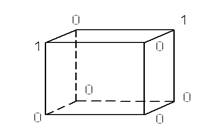3. В каждой вершине куба записано число (рис. 3). За один шаг к двум числам, размещенным на одном (любом) ребре, прибавляется по единице. Можно ли за несколько таких шагов сделать все восемь чисел равными между собой?

Рис.3

Если рассматривать письменную олимпиаду, то целесообразно в ее содержание включать задачи, затрагивающие вопросы стереометрии многогранников. Это дает обучающимся хорошую возможность повторить их свойства, а также познакомиться с некоторыми из них.

Рассмотренные математические соревнования и разработанное содержание одного из них могут быть полезны для учителей, которые желают заниматься подготовкой обучающихся к различным математическим турнирам, например к олимпиадам.

Литература

1.                 Андреев В. И. Диалектика воспитания и самовоспитания творческой личности. Казань, 1988.

2.                 Богоявленская Д. Б. Пути к творчеству. - М: Знание,1981.-96с.-(Новое в жизни, науке, технике. Сер.»Педагогика и психология»;№10)

3.                 Гингулис Э.Ж. Развитие математических способностей учащихся.// Математика в школе.-1990, № 1.

4.                 http://math4school.ru/sites.html

Скачано с www.znanio.ru