Добавить материал

и получить 10 документов
и свидетельство СМИ

Шамхалова Аминат Микаиловна

Математический квест: "Покорение логарифма"

docx
29.04.2025

Публикация в СМИ для учителей

Бесплатное участие. Свидетельство СМИ сразу.
Мгновенные 10 документов в портфолио.

Добавить материал

Математический квест на тему.docx

Математический квест на тему: "Покорение Логарифма"

Цели урока: способствование проявлению творческих умений, познавательного интереса студентов к математике

Задачи: образовательные: обобщение и систематизация понятия и свойств логарифма; закрепление навыков вычисления логарифмических выражений; выполнение заданий ЕГЭ базового уровня ; развивающие: развитие логического мышления учащихся; развитие находчивости, сообразительности, а также интереса к математике; воспитательные: воспитание познавательной активности, чувства ответственности, культуры общения, диалога.

Тип урока: урок повторения, закрепления пройденного материала.

Форма урока: урок-игра

Структура урока: 1. Организационный момент

2. Постановка целей урока – игры

3. Командная работа учеников

А)представление команд

Б)актуализация опорных знаний

В)прохождение маршрута

4.Подведение итогов. Рефлексия.

Оборудование: интерактивная доска, мультимедийный проектор, компьютер, листы (отдельно для каждой команды), конверты с заданиями.

Ход урока.

1. Организационный момент.

2. Постановка целей игры. Правила игры

Учитель: Здравствуйте, уважаемые участники математического квеста «Покорение логарифма». Само слово «квест» английского происхождения и означает - поиск чего-либо. И в конце нашей игры вы сможете ответить на вопрос: «Что вы смогли найти на сегодняшнем нашем интересном уроке - игре?» Ваша задача пройти все испытания и дойти до конечного пункта нашего маршрута. Капитаны команд берут конверт с заданием и ключом. Только после выполнения упражнений вы можете воспользоваться ключом и узнать, где находится следующая точка маршрута. И запомните, что квест – это командная игра, двигаться по маршруту и решать задания необходимо вместе, сообща!

3. Командная работа учеников:

Для начала я предлагаю командам представиться.

А) Приветствие команд

На данном этапе команды представляются: название, эмблема, девиз.

Максимальное число баллов – 3б..

Б)Актуализация опорных знаний

Собираем багаж – основные знания по данной теме:

определение логарифма;
свойства логарифмов;
основное логарифмическое тождество;
свойства логарифмической функции.

Б) Прохождение маршрута

Для каждой команды составлен свой путь выполнения заданий:

1команда: АКТОВЫЙ ЗАЛ ШКОЛЬНЫЙ ДВОРСТОЛОВАЯ

КАБИНЕТ №4.

2КОМАНДА: БИБЛИОТЕКА ШКОЛЬНЫЙ ДВОРФОЙЕ КОРПУСА НАЧАЛЬНЫХ КЛАССОВ КАБИНЕТ №4.

Чтобы понять, где находится конверт с ключом необходимо решить следующее задание:

1. Вычислите логарифм:

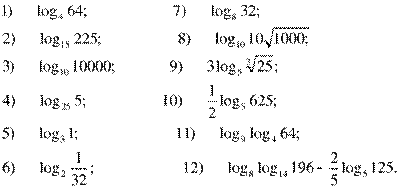
Для первой команды конверт с ключом спрятан в АКТОВОМ ЗАЛЕ.

1. Вычислите логарифм:

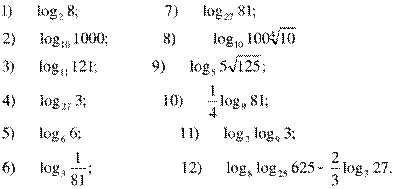
Для второй команды конверт с ключом спрятан в БИБЛИОТЕКЕ.

Как только справляются с заданием команды открывают конверт с ключом и бегут дальше за следующими заданиями.

1 и 2 КОМАНДЫ, ЧТОБЫ НАЙТИ КЛЮЧ К СЛЕДУЮЩЕМУ ПУНКТУ ВАМ НЕОБХОДИМО РАЗГАДАТЬ РЕБУСЫ. КАЖДЫЙ РЕБУС НА ОБОРОТНОЙ СТОРОНЕ ПРОНУМЕРОВАН. ВОЗЬМИТЕ С ПЕРВЫХ РЕБУСОВ ЧЕТВЕРТЫЕ БУКВЫ, СО ВТОРОГО ВТОРУЮ БУКВУ, С ТРЕТЬЕГО ВСЕ ЦИФРЫ КОТОРЫЕ ВЫ ИСПОЛЬЗОВАЛИ В ПОРЯДКЕ ВОЗРАСТАНИЯ. ЭТО БУДЕТ ВАШ КЛЮЧ.

ВЫ ИМЕЕТЕ ПРАВО ВОСПОЛЬЗОВАТЬСЯ КЛЮЧОМ ТОЛЬКО ТОГДА, КОГДА РАСШИФРУЕТЕ ВСЕ АНАГРАММЫ.

Следующая точка маршрута обеих команд в ШКОЛЬНОМ ДВОРЕ.

1 КОМАНДА, ЧТОБЫ НАЙТИ КЛЮЧ К СЛЕДУЮЩЕМУ ПУНКТУ ВАМ НЕОБХОДИМО решить следующие уравнения:

1. Найдите корень уравнения ${{\log }_{2}}(7-x)~=~6$ .

2. Найдите корень уравнения ${{\log }_{2}}(8+x)~=~3$ .

3. Найдите корень уравнения ${{\log }_{13}}(17-x)~=~{{\log }_{13}}12$ .

4. Найдите корень уравнения ${{\log }_{4}}(8-5x)~=~2{{\log }_{4}}3$ .

5. Решите уравнение $\log_4 (x^2 +x)=\log_4 (x^2 +6)$ .

Впишите все ответы – это будет ваш ключ:


СТОЛОВАЯ

2 КОМАНДА, ЧТОБЫ НАЙТИ КЛЮЧ К СЛЕДУЮЩЕМУ ПУНКТУ ВАМ НЕОБХОДИМО решить следующие уравнения ЕГЭ базового уровня:

1. Найдите корень уравнения ${{\log }_{6}}(3-x)~=~2$ .

2. Найдите корень уравнения ${{\log }_{2}}(3+x)~=~5$ .

3. Найдите корень уравнения ${{\log }_{3}}(14-x)~=~{{\log }_{3}}5$ .

4. Найдите корень уравнения ${{\log }_{2}}(4-x)~=~2{{\log }_{2}}5$ .

5. Решите уравнение $\log_3 (x^2 +4x)=\log_3 (x^2 +4)$ .

Впишите все ответы – это будет ваш ключ:

ФОЙЕ КОРПУСА НАЧ.КЛАССОВ

Испокон веков целью математической науки было помочь людям узнать больше об окружающем мире, познать его закономерности и тайны. Математики, выделяя самые существенные черты того или иного наблюдаемого в природе явления, вводя числовые характеристики и связывая эмпирические данные с помощью различных математических зависимостей, тем самым составляют математическую модель явления. Изучение этой модели позволяет людям больше узнать о природном явлении, глубже уяснить его природу и свойства. Ряд явлений природы помогает описать именно логарифмическая зависимость. Иначе говоря, математики, пытаясь составить математическую модель того или иного явления, достаточно часто обращаются именно к логарифмической функции. Одним из наиболее наглядных примеров такого обращения является логарифмическая спираль.

Какие из следующих графиков могут быть графиком функции y = log₂х

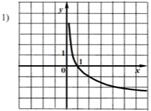
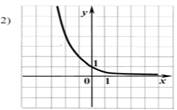
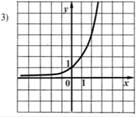
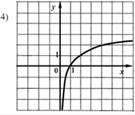
Команды получают задание. Необходимо ответить устно на 5 вопросов. Учитель следит за правильностью ответов и дает следующий ключ.

Верно ли, что логарифмическая функция y =log_ab: (слайд 12 )

1) определена при любом х (нет)

2) принимает все действительные значения (да)

3) является четной (нет)

4) имеет наибольшее и наименьшее значение (нет)

5) не имеет экстремумов (да)

6) непрерывна (да)

7) имеет график, проходящий через точку (0;1) (нет)

8) убывает при 0<a<1 (да)

9) возрастает при а>0 (нет)

10) график функции находится 1 и 4 четвертях (да)

Ответы: нет, да, нет, нет, да, да, нет, да, нет, да.

Обе команды встречаются в кабинете №4. И та команда, которая была быстрее, находчивее и умнее получает конверт с поздравлениями и призами.

4.Подведение итогов игры. Рефлексия:

что нужно знать, чтобы успешно решать задачи по этой теме?
что нового узнали на уроке?
как вы оцените свою работу на уроке?
понравился ли вам урок?

Математический квест на тему: "Покорение

Только после выполнения упражнений вы можете воспользоваться ключом и узнать, где находится следующая точка маршрута

Чтобы понять, где находится конверт с ключом необходимо решить следующее задание: 1

ТРЕТЬЕГО ВСЕ ЦИФРЫ КОТОРЫЕ ВЫ ИСПОЛЬЗОВАЛИ

Ряд явлений природы помогает описать именно логарифмическая зависимость

Подведение итогов игры. Рефлексия: что нужно знать, чтобы успешно решать задачи по этой теме? что нового узнали на уроке? как вы оцените свою работу на…

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

Посмотрите также