математика

Учитель математики Никитина Н.Н

Предмет: алгебра

Класс: 8 класс,

Тема урока: Квадратичная функция.

Тип урока: Урок закрепления пройденного материала.

Цели урока: Обучающая цель: систематизировать знания о различных видах преобразований графиков функций; закрепить ранее приобретенные знания о квадратичной функции, навыков построения ее графиков, умения применять свойства функции при решении задач; познакомиться с алгоритмом построения  графика функции с помощью математического ПО ADVANCED GRAPHER.

Развивающая цель: совершенствовать умения логически мыслить и выражать свои мысли вслух, развить логическое мышление, волю, эмоции;

Воспитательная цель: воспитывать у обучающихся стремление к совершенствованию своих знаний; воспитывать интерес к предмету.

Оборудование урока: видео проектор, презентация PowerPoint (PP),  , чертёжные инструменты, карточки с заданиями.

Ход урока.

I.       Организационный момент. Вступительное слово учителя.

Здравствуйте, ребята!

/Далее на доске появляется изображение лягушонка/

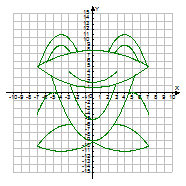/На экране компьютера медленно вырисовываются в разных цветах части парабол, которые в итоге дают изображение лягушки./(слайд 1)

Учитель: Заметили ли вы, что детали для рисунка предоставила нам очень интересная функция? Какая?

Ученики: Это квадратичная функция.

Учитель: Да, это квадратичная функция, построение графиков которой – одна из целей нашего урока.

   Наша жизнь полна различными явлениями, процессами, событиями и во всем этом мы хотим увидеть какую-то закономерность, или представить информацию в удобном для нас виде. Как раз в этом нам и помогают функции. В 8 классе мы существенно пополнили запас функций, графики которых умеем теперь не только строить, но и исследовать, т.е. читать. После освоения материала (на него уйдет не один урок) каждый сможет сам рисовать с помощью графиков функций (и не только квадратичной), а проверять свои художества можно, используя компьютер.

Итак, цели нашего урока:

1)      Систематизировать знания о различных видах преобразований графиков функций (уметь по графику определить, какое выполнено преобразование и, зная порядок преобразований, построить график этой функции);

2)      Закрепить ранее приобретенные знания о квадратичной функции, навыков построения ее графиков, умения применять свойства функции при решении задач.

Ставлю перед вами задачу: показать умение строить графики по формуле, определять основные элементы параболы, по графику задавать функцию формулой.

II.    Повторение.

1.      Математический диктант с последующей самопроверкой (8 мин.)

Учитель. Итак, первый этап – математический диктант. На карточке № 1 по вертикали указаны номера заданий, по горизонтали – номера ответов.

Вы должны внимательно послушать задание, посмотреть на экран выбрать номер правильного ответа, затем в строке с номером задания под номером выбранного вами ответа поставить знак «+».

Задания математического диктанта.

Задание. Укажите график функции. Читает учитель.

Через 5 минут верхняя часть карточки № 1 сдается, а нижняя остается у учащихся для самопроверки (слайд …). Ученики выставляют отметки за математический диктант.

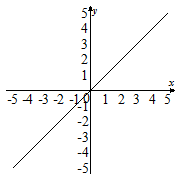
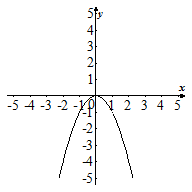
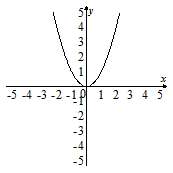
Фронтальный опрос (8 мин.)

Для определения степени освоения учащимися знаний правил построения графиков функций у =ах²  выполняется следующее задание (письменно):

1.      Соотнесите графики с  формулами соответствующих функций.

/  у = - 0,5х²; у = 1,5х²; у = -2х²; у = 0,25х²  /

Ответы заслушать с места.

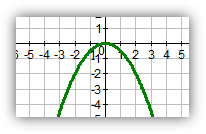
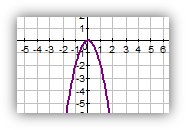
2.      Устная работа с классом( Итак, виды функций вспомнили. А сейчас устный опрос.)

1)      Что является графиком квадратичной функции?

2)      Графиком какой функции является гипербола?

3)      Какое значение принимает функция  в точке   ?

4)      При каком значении переменной   x   значение функции  равно  6  ?

5)      Принадлежит ли графику функции точка  с координатами   (-1;3) ?

Ответьте  на вопрос: при помощи каких преобразований можно получить график функции, если исходная функция у = х² . прокомментируйте  динамические слайды.

1.      Как построить график функции   , зная график функции  ?

2.      Как построить график функции   , зная график функции  ?

3.      Как построить график функции   , зная график функции  ?

4.      Как построить график функции   , зная график функции  ?

5.      Как построить график функции  , зная график функции  ?

6.      Как построить график функции  , зная график функции  ?

Обобщите, что нужно знать, чтобы построить график данной функции:

у = а(х + l )² + m.

Работа в парах на раздаточных  листах

Пока учитель заслушивает ответы по карточкам, остальные учащиеся выполняют задания 1,2,3 по раздаточным листам с последующей самопроверкой на экране

      Работа в тетрадях

      На отвороте доски подготовлены 3 системы координат и около каждой написаны задания №4, №5, №6 из «Дополнительные задания учащимся».

      Первый ряд  выполняет задание №4, второй ряд - №5, третий ряд – №6.

К доске так же вызывается 3 человека.  (Работа стоящих у доски оценивается с  

последующим выставлением в журнал.)

Задание №4:     Решить систему уравнений графически:

                                            ,

                                             . 

Задание №5:     Решить уравнение графически:

Задание №6:      Найдите координаты точек пересечения графиков функций

                                      и      

Вопросы к классу: 

·         Что общего во всех этих примерах?

·         Чем они отличаются?

Пока дети работают в тетрадях, проверить МД

III.             Выполнение рисунков с помощью парабол. Самостоятельная работа. (Научить учащихся выполнять построение с помощью парабол на различных примерах.) Работы сдаются учителю.

Задание 7:

Графиками функций  сделать рисунок, дать ему название.

Например. Даны функции:

1. [- 9; - 1]

2. 

3. 

4. 

5. 

6. 

7. 

Учащиеся строят графики, получают рисунок. Если не сделано ошибок, он должен выглядеть так, как показано:

Задание 3. После завершения работы над заданием 2, проверить правильность его выполнения на компьютере.

Итог урока.

Доклад.

Домашним заданием к этому уроку для отдельных учащихся было подготовить небольшие сообщения на тему  «Практическое применение функций». Заслушаем доклад  Крят Валерии «Квадратичная функция»

Рефлексия

Итак, Как вы думаете, вы справились с данной задачей?

Что было нового на уроке?

Что было интересно? А что не  очень?

Все ли у вас получилось?

Подведение итогов

Вы видели, ребята, как часто приходиться встречаться в жизни с графиками квадратичных функций. Умение владеть их преобразованием нужно и архитектору, и дизайнеру, и артиллеристу, и астроному. Вы сегодня успешно справились с поставленной перед вами в начале урока задачей. Успешно справились :                      . Я поставлю вам следующие оценки –(после проверки самостоятельной работы)---.

Домашнее задание:Нарисуйте графиками кусочных функций по готовым заданиям картину.

1.  У = -2(х-3)² +9              1,5≤х ≤5
2.   У = -2(х+3)² +9             -5≤х ≤-1,5
3.    У = -2(х-1,5)² +2,5       0,5≤х ≤2,5
4.     У = -2(х+1,5)² +2,5    -2,5≤х ≤-0,5
5.     У = - 0,5 –х                -2≤х ≤-1
6.     У = 2,5 –х                      1≤х ≤2
7.     У= 0,2 х² -2,5              -1,5≤х ≤1,5
8.     У = х² - 3,5                   -1≤х ≤1
9.      У = 0,5                        -2,5≤х ≤-0,5.    

10.    У = 0,5                        0,5≤х ≤2,5

Задание 2. Перед Вами тюльпан.  Напишите формулы функций, которые их определили, если они выполнены с помощью только трафарета графика функции  .