
СЦЕНАРНЫЙ ПЛАН ИЗУЧЕНИЯ ТЕМЫ
«Квадратные уравнения»
(алгебра 8 класс)
Составила учитель математики Бакланова Н.И., ГБОУ СОШ №10 "ОЦ ЛИК" г.о.Отрадный Самарской области
Календарно-тематическое планирование (10 часов)
|
№ п/п |
Кол-во уроков |
Дата |
Форма проведения |
Тема |
Результат |
Характеристика познавательных универсальных учебных действий |
|
§3. Решение квадратных уравнений – 10ч |
||||||
|
36-37 |
2 |
|
Диалогическая лекция с ИКТ |
Неполные квадратные уравнения. Решение квадратных уравнений по формуле. Теорема Виета. Разложение квадратного трёхчлена на множители. Сокращение дробей. Решение задач с помощью квадратных уравнений. |
Ученик научится: - решать неполные квадратные уравнения любого вида; - решать полные квадратные уравнения с использованием формулы корней; - исследовать квадратные уравнения по дискриминанту и коэффициентам; - раскладывать квадратный трёхчлен на множители и сокращать дроби. Ученик получит возможность научиться: владеть специальными приёмами решения квадратных уравнений и систем уравнений; уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики. |
Распознавать квадратные уравнения классифицировать квадратные уравнения по внешнему виду; обосновывать выбор данного алгоритма решения квадратного уравнения; моделировать ход решения уравнения; строить и обосновывать ход решения данного квадратного уравнения; обосновывать рациональность выбранного способа решения.
|
|
38-39 |
2 |
|
Урок-семинар |
Семинар по теме: «Решение квадратных уравнений. Решение задач с помощью квадратных уравнений» |
||
|
40-42 |
3 |
|
Урок-практикум |
Практикум по теме: «Решение квадратных уравнений» |
||
|
43 |
1 |
|
Проверочная работа |
Проверочная работа по теме: «Решение квадратных уравнений» |
||
|
44 |
1 |
|
Повторно-обобщающий |
Обобщение по теме: «Решение квадратных уравнений» |
||
|
45 |
1 |
|
Урок контроля |
Контрольная работа: «Решение квадратных уравнений» |
||
I. Структура темы
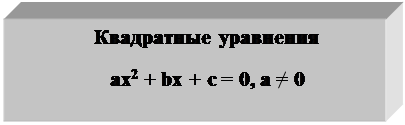 |
· а=0
bх + с = 0
(линейное уравнение); · b=0
· с=0
· b=0
и с=0 ·
ах2 + bх
+ с = 0, где а, b
и с отличны от нуля.


![]() ах2
+ с = 0;
ах2
+ с = 0;![]() ах2
+ bх = 0;
ах2
+ bх = 0;![]() ах2 = 0.
ах2 = 0.
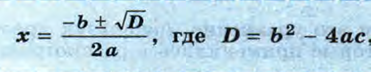
![]()
![]()
|
Алгоритм решения квадратного уравнения
|
Квадратное уравнение |
1.Найти D |
2.Сравнить значение D c 0 |
3.Найти корни квадратного уравнения |
|
ах2 + bx + с = 0 |
D = b2 – 4ac |
D>0
D=0 D<0 |
корней нет |
|
2х2 – 5х – 3 = 0 |
D = (-5)2 – 4 . 2 . (-3) = 49 |
D>0 |
|
2.
Полные квадратные уравнения а) х2 - 7х
+ 10 = 0; б) х2 - 10х
+ 25 = 0; в) -х2 +
х +3= 0; г) 2х2
– х = 3; д) 5х2 -
18х + 3 = 0. 1.
Неполные квадратные уравнения а) 2х2 -
18х = 0; б) - х2
+ 2х = 0; в) 4х2 =
0; г) 4х2
– 11 = х2 – 11+ 9х; д) х2 –
4х +4 =0; е) 16 - х2 =
0; ж) х2 + 81
= 0.
Ключевые
задачи
 |
|||||
 |
|||||
а) х2 +
16х +63 = 0; б) х2 + 2х - 48 = 0. а) В уравнении х2
+ pх - 35 = 0 один из
корней равен 7. Найдите другой корень и коэффициент p. б) Один из корней
уравнения х2 - 13х +q
= 0 равен 12,5. Найдите другой корень и коэффициент q.
Ключевые
задачи
 |
![]()
![]()
![]()




8m2n
– 4mn3 = =
4mn(2m – n2) 16x2−9=(4x)2−32
= = (4x−3)(4x+3); 4x2 – 4x + 1 = (2x – 1)2
= = (2x – 1) (2x – 1). (5x +5y ) + (m x +my) = = x(5 +m)
+ y (5 +m) = = (x
+y) (5 +m)
|

II. Задачи для совместной деятельности

III. Задания для самостоятельной деятельности
 |
 |
IV. Проверочная работа по теме: «Решение квадратных уравнений»
|
1 вариант
1). Решите уравнение: а). 2х2+7х – 9 = 0; б). 3х2 = 18х; в). 100 х2 – 16 = 0; г). х2 – 16х + 63 = 0.
2). Периметр прямоугольника равен 20 см. Найдите его стороны, если известно, что площадь прямоугольника равна 24 см2.
3) Разложите на множители:
4) Сократите:
5). В уравнении х2 + рх – 18 = 0 один из корней равен – 9. Найдите другой корень и коэффициент р. |
2 вариант
1). Решите уравнение: а). 3х2+13х – 10 = 0; б). 2х2 – 3х = 0; в). 16 х2 = 49; г). х2 – 2х – 35 = 0.
2). Периметр прямоугольника равен 30 см. Найдите его стороны, если известно, что площадь прямоугольника равна 56 см2.
3) Разложите на множители:
4) Сократите:
5). В уравнении х2 + 11х + q = 0 один из корней равен – 7. Найдите другой корень и свободный член q.
|
Контрольная работа по теме: «Решение квадратных уравнений»
|
1 вариант.
1). Решите уравнения:
2). Решите задачу: Когда от квадратного листа фанеры отрезали прямоугольную полосу шириной 2 м, площадь оставшейся части листа составила 24 м2. Найдите первоначальную площадь листа.
3). Сократите дробь:
4). Один из корней уравнения х 2 + kx + 45 = 0 равен 5. Найдите другой корень и коэффициент k.
|
2 вариант.
1). Решите уравнения:
2). Решите задачу: От прямоугольного листа картона длиной 16 см отрезали квадрат, сторона которого равна ширине листа. Площадь оставшегося прямоугольника равна 60 м2. Найдите ширину листа картона.
3). Сократите дробь:
4). Один из корней уравнения х 2 – 26x + q = 0 равен 12. Найдите другой корень и свободный член q.
|
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.