математика

Учитель Карпилло И.Ю.

МБОУ «СОШ имени А.М.Горького», г.Карачев Брянской области

Математика  8 класс

Тема урока :  «Квадратный корень из произведения и дроби»

Базовый учебник  Алгебра 8 : учебник для 8 кл. образоват. учреждений/ Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова – М.: Просвещение, 2013.

Цели урока:

Образовательные:

-  усвоение приемов упрощения вычисления корней,

 -  сформировать умение применять их для преобразования выражений, содержащих квадратные корни,

Воспитательные:

-  воспитывать внимательность, аккуратность, настойчивость.

-  воспитывать интерес к математике.

Развивающие:

-  развивать память,

-  развивать умений преодолевать трудности,

- развивать логическое мышление

-  развивать навыки работы с учебником, справочными материалами.

Задачи: 
в направлении личностного развития: 
- уметь ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи; 
- воспитание способности принимать самостоятельные решения; 
- уметь осознавать и понимать личную ответственность за будущий результат; 
в метапредметном направлении: 
-уметь использовать математическую терминологию; 
- уметь использовать эталон для самопроверки; 
- уметь воспринимать устную речь; 
в предметном направлении: 
- владеть математическими знаниями и умениями, необходимыми для продолжения образования; 
- уметь использовать математическую терминологию; 
-уметь применять теоремы о квадратных корнях из произведения и дроби для вычисления значений выражений, содержащих квадратные корни. 

Оборудование: учебник, компьютер, мультимедийный проектор, презентация «Арифметический квадратный корень из произведения и дроби», выполненная с помощью программы Microsoft Power Point 2010.

Тип урока:

комбинированный.

                                                Ход урока

I . Организационный момент :постановка  цели и задачи урока.

II. Актуализация знаний

1). Фронтальный опрос (используется презентация   «Арифметический квадратный корень из произведения и дроби» (Слайд №2, №3)

 Учащиеся дают ответы на поставленные вопросы. )  

1.     Сформулируйте определение арифметического квадратного корня

2.     При каких значениях а выражение имеет смысл?

3.     Продолжите запись: ()² = …

4.     Продолжите запись:= …                                                        

5.     Сформулируйте теорему о квадратном корне из произведения

6.     Продолжите запись: = …                             

7.     Сформулируйте теорему о квадратном корне из дроби

  2) Устный счет (Выполняется фронтальная работа, в ходе которой учащиеся дают ответы, и происходит обсуждение ответов (слайд №4, №5):

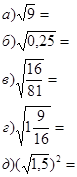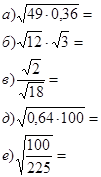III. Совершенствование навыков и способов деятельности

Работа с учебником:

1)    №374- формирование приема перекомбинации множителей при вычислении квадратных корней.

2)    №387-формирование приема вычисления квадратных корней с использованием обратных свойств квадратного корня.

3)    №376-отработка приема использования формулы разности квадратов при вычислении корней.( слайд №9)

IV. Физкультминутка (Логическая миниатюра)

VI. Контроль знаний Самостоятельная работа с самопроверкой          (слайд №9)

VII. Домашнее задание

№ 375,377(а-г),387 (б,г,е,з)

VIII Итог урока.

Сегодня на уроке мы с вами, я надеюсь убедились, что не всегда , для решения сложных, на первый взгляд, задач, требуется приложить много усилий.

Какие новые приемы, позволяющие упрощать вычисления корней мы использовали?

Приложение №1

1. № 374,

Р е ш е н и е

Это задание может вызвать затруднения у учащихся. Раньше им встречались выражения вида , в которых  и  извлекались. При выполнении данного номера это свойство корней напрямую применять нецелесообразно.

Необходимо подкоренное выражение представить в виде произведения таких множителей, из которых корень извлекается.

а) ;

б) ;

в) ;

г) ;

д) ;

е) ;

ж) ;

з) .

3. № 376.( Слайд №9)

Данное упражнение еще раз заостряет внимание учащихся на свойствах квадратных корней.

Если в примерах а) и б) учащиеся просто могут вычислить значение подкоренного выражения и извлечь корень, то в следующих примерах это  сделать можно «увидев» формулу  разности  квадратов.

в) ;

д)

    .

Приложение №2: Миниатюра, которую разыгрывают ученики.

За столом сидит ученик, он в роли учителя математики. К столу прикреплен плакат «Экзамен по математике».

   Вбегает ученик.

    - Извлекать корни умеешь? – спрашивает экзаменатор.

Ученик:

    - Да. Конечно. Нужно потянуть за стебель растения посильнее, и корень его извлечется из почвы.

    - Нет, я имел в виду другой корень, например, из девяти.

     - Это будет «девя», так как в слове «девять» суффиксом является «ть».

    - Вы меня не совсем поняли, я имел в виду корень квадратный.

    - Квадратных корней не бывает. Они бывают мочковатые и стержневые.

    - Арифметический квадратный корень из девяти?

    - Три, так как три в квадрате равно девяти.

При этом ученик берет со стола плакат с записью    и показывает его аудитории.