
ТЕМА УРОКА:
ВОЗВЕДЕНИЕ В КВАДРАТ СУММЫ И РАЗНОСТИ ДВУХ ВЫРАЖЕНИЙ». Слайд 1
Тип урока: урок изучения нового материала (урок-исследование)
Вид урока: проблемно-поисковый.
Цели урока: Слайд 2
Образовательные:
-вывести формулы квадратов суммы и разности двух чисел.
-сформировать умение учащихся практически применять эти формулы для упрощения выражений.
Развивающие :
-развивать логическое мышление, внимание, память, сообразительность, культуру математической речи и культуру общения;
Воспитывающие:
-воспитывать ответственное отношение к деятельности, высокой познавательной активности и самостоятельности;
-воспитывать интерес к математике как учебному предмету через современные технологии преподавания;
- воспитывать чувство ответственности, культуры диалога.
Формы организации познавательной деятельности:
фронтальная, индивидуальная, групповая, коллективная.
Методы и приёмы обучения: объяснительно-иллюстративный, проблемно-поисковый, исследовательский, словесный, наглядный (демонстрация компьютерной презентации), практический.
Оборудование :
-компьютер, мультимедийный проектор, экран, портрет Евклида, набор геометрических фигур, раздаточный материал.
Средства обучения:
Программное обеспечение:
Microsoft Office Word 2007 Microsoft Office Word 2010
Microsoft Office Power Point 2007 Microsoft Office Power Point 2010
План урока Слайд 3
Ход урока.
I. Организационный момент. Вступительное слово учителя.
Эпиграф урока:
Знание только тогда знание,
когда оно приобретено усилиями
своей мысли, а не памятью.
Слайд 4 (Л.Н.Толстой)
«Ещё в глубокой древности было подмечено, что некоторые многочлены можно умножать короче, быстрее, чем остальные. Так появились формулы сокращённого умножения. Их несколько. Сегодня вам предстоит сыграть роль исследователей и «открыть» две из этих формул».
Итак, тема нашего урока квадрат суммы и квадрат разности двух выражений. Чтобы открыть формулы нам необходимо, вспомнить, что мы знаем и умеем.
II. Актуализация опорных знаний (устные упражнения)
1.Прочитайте выражения. Слайд 5
а) а + b ; г) x – у ; б) n2 + m2 ; д) (z –a)2;
в) (c + d)2 ; е) b2 – c2; ж) 2ху.
- что значит: (c + d)2 ; (z –a)2 (значит, выражение умножается на себя два раза)
2. Найдите квадраты выражений: a; - 2 ; 5b ; 4х2, 6х2 у3. Слайд 6
(вспомнить правило возведения в степень произведения).
3. Представьте в виде квадрата: 64; 100; 36а2; 25x4 ; 49 b2c2; х6с8. Слайд 7
4. Найдите удвоенное произведение выражений: Слайд 8
а) а и b; б) 3b и -5с; в) 0,4х и 2х2; г)
![]() и 6 .
и 6 .
(вспомнить правило умножения степеней с одинаковыми степенями).
5. Перемножьте данные многочлены: Слайд 9
а) (x +2) ·(y - 1) б) ( 3 – c) · (4 + b)
(вспомнить правило умножения многочлен на многочлен)
6.Вычислить значения выражений 25²+250+5²; 13²- 78+3². Слайд 10
2 ученика считают у доски. Учитель предлагает вычислить, используя калькулятор.
- Возможно ли сосчитать устно? (В конце урока ответим на этот вопрос)
III. Изучение нового материала (Исследовательская работа).
1. Упростите выражения I столбца, запишите ответы в III столбце, проанализируйте результат. Слайд 11
1 вариант -1), 2), 3) 2 вариант - 4), 5), 6)
Ученики раскрывают скобки по правилу умножения многочлена на многочлен (столбец I), полученные ответы записывают в Ш столбце таблицы. II часть таблицы закрыта.
|
№ |
I |
II |
III |
|
1) 2) 3) 4) 5) 6) 7) 8) |
(y + b) (y +b) (с + d ) (c +d) (х + 2)(х+2) (x – y) (x – y) (m - n) (m- n) (a – 2) (a – 2) (6х +y) (6x+y) (5 – 4b) (5 – 4b) |
(y +b)2 (c + d)2 (х+2)2 (x – y)2 (m-n)2 (a – 2)2
|
y 2 + 2yb + b2 c2 + 2cd + d2 х2 + 4х + 4 x2 – 2xy + y2 m2 – 2mn + n2 a2 – 4a + 4
|
-Ребята, посмотрите внимательно на I и III столбики. Слайд 12
-Есть ли в них нечто общее? Можно ли выражения I cтолбца записать короче? (Ответы учащихся) (Открыть II столбец). Слайд 12
-Что получается в результате умножения суммы и разности двух выражений?
-Результатом умножения является трехчлен, у которого:
1-й член – квадрат первого выражения;
2-й член – удвоенное произведение первого и второго выражений;
3-й член – квадрат второго выражения.
- Мы с вами нашли наиболее простой способ умножения суммы и разности двух выражений на себя, т.е. вывели формулы возведения в квадрат суммы и разности двух выражений.
-Записать ответы заданий 7) и 8) столбца I в столбцах II и III найденным способом. Слайд 13
-Скажите, как проще и быстрее вам было работать: перемножая многочлен на многочлен или применяя формулы?
-Попробуйте записать формулы, которыми будем пользоваться для возведения в квадрат суммы и разности двух выражений. Слайд 14
(а+b)2 =а2+2аb+b2 (a-b)2=a2-2ab+b2
- Чем они отличаются? (знаком перед удвоенным произведением).
-Сформулируйте эти формулы словесно. Слайд 15
-Эти формулы называются формулами сокращенного умножения, они применяются для упрощения выражений, для рационального решения некоторых числовых выражений.
Примеры применения формул. Слайд 16
2. Чтение правил по учебнику, парный пересказ правил .
3. Первичное закрепление .
Заполнить таблицу. Слайд 17
|
Выражение
|
Квадрат 1 выражения |
Удвоенное произведение |
Квадрат 2 выражения |
Итог
|
|
(а + 4)2 |
|
|
|
|
|
(8 - х)2 |
|
|
|
|
|
(2y + 1)2 |
|
|
|
|
|
(0,5b - 2)2 |
|
|
|
|
4. . Вставьте пропущенные одночлены: Слайд 18
( * – 1)2 = 9х2 - * х + 1; (5а + * )2 = * а2 + 40а + 16
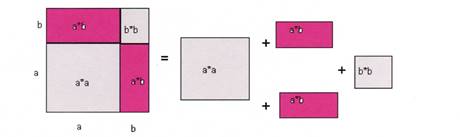
5. Геометрическое истолкование формулы (а+b)2. Слайд 19
-Некоторые правила сокращённого умножения были известны ещё около 4 тыс. лет тому назад. Их знали вавилоняне и другие народы древности. Тогда они формулировались словесно или геометрически.
У древних греков величины обозначались не числами или буквами, а отрезками прямых. Они говорили не «а2», а «квадрат на отрезке а», не «а∙b», а «прямоугольник, содержащийся между отрезками а и b». Например, тождество (а + b)2 = а2 + 2аb + b2 во второй книге «Начал» Евклида (3 в до н.э.) формулировалось так: «Если отрезок как-либо разбит на два отрезка, то площадь квадрата, построенного на всем отрезке, равна сумме площадей квадратов, построенных на каждом из двух отрезков, и удвоенной площади пря-моугольника, сторонами которого служат эти два отрезка». Доказательство опиралось на геометрическое соображение.
А теперь давайте и мы с помощью рисунка объясним геометрический смысл формулы (а + b)2 = а2 + 2аb + b2.
-Объясните геометрический смысл выражения (а+в)2 (квадрат со стороной a+b). (У каждого ученика – вырезанные из бумаги 2 квадрата со сторонами а и b и 2 прямоугольника со сторонами a и b). Каждый моделирует свой квадрат.
- Чему равна площадь полученного квадрата? (Сумме площадей квадрата со стороной а, двух площадей прямоугольника со сторонами а и в и площади квадрата со стороной в).
III. Физминутка. Слайд 20
IV.Закрепление изученного материала. Слайд 21 Работа у доски и в тетрадях. При выполнении заданий - проговаривать правила.
1 .№ 862 (а, г, е, з).
2.Вычислить:
(30+1)2 ; 512 ; (30-1)2 ; 492 . Слайд 22
3. Преобразовать выражения : (а-7)2 ; (7-а)2 ; (5+х)2 ; (-5-х)2
Учащиеся сами приходят к выводу: (а - b)2 =(b - а) 2 , (-а - b)2 =(а + b) 2 Слайд 23
4. А теперь вернемся к числовым выражениям, которые в начале урока вычислялись учащимися с помощью калькулятора и решались по действиям в тетради. Делается вывод, что рационально можно найти значения данных выражений используя выведенные на уроке формулы сокращенного умножения. Слайд 24 (гиперссылка к слайду 10)
V. Этап предварительного контроля. (карточки)
1.Соедините пары тождественно равных выражений. Слайд 25 (вспомнить определение тождественно равных выражений)
|
1. |
( 3а + с) 2 |
5. |
( y - в) 2 |
|
2. |
( а – 2в) 2 |
6. |
x2 – 2xв + в2 |
|
3. |
( x – в) 2 |
7. |
а2 – 4ав + 4в2 |
|
4. |
y 2 – 2yв + в2 |
8. |
9а2 + 6ас + с2 |
2. Выбрать правильный ответ. Слайд 26
|
|
(y - 9)2 |
(5x+4y)2 |
(2a – 0,5x)2 |
|
|
1 |
y2 - 9y +81 |
25x2 - 20xy +16 y2 |
4a2 - 2ax +0,25 x2 |
|
|
2 |
y2 + 18y +81 |
25x2 + 40xy +16 y2 |
4a2 + 2ax +0,25 x2 |
|
|
3 |
y2 -18y +81 |
25x2 +20xy +16 y2 |
4a2 - ax +0,25 x2 |
|
|
4 |
y2 + 9y +81 |
25x2 - 40xy +16 y2 |
4a2 + ax +0,25 x2 |
|
3. Вычислить : 612, 592 Слайд 27
VI. Домашнее задание: п. 31, доказать геометрический смысл формулы (a-b)2,
№863(а, б, в, д); 866, №869(д, е). Слайд 28
VII. Итог урока. Слайд 29
-С какими формулами мы познакомились сегодня на уроке?
-Почему эти формулы называются формулами сокращенного умножения?
-Чему равен квадрат суммы двух выражений?
-Чему равен квадрат разности двух выражений?
-Как вы думаете, зачем нужны нам эти формулы и стоит ли их запоминать?
(С помощью формул результат можно получить гораздо проще и быстрее).
Рефлексия. Выставление отметок.
Учащиеся анализируют свою работу на уроке, обсуждают, высказывают свое мнение.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.