
Любой прогресс невозможен без математики. Сегодня покажем на уроке какова роль математики для полета в космос.
В астрономии математика помогла сделать многие открытия. Новые алгоритмы, разработанные математиками, переходили на службу астрономам.
Законы движения планет Солнечной системы основаны на математических законах Иоганна Кеплера – великого немецкого ученого начала XVII века.
В наши дни с помощью математики предсказываются многие астрономические явления. Например, математическими методами рассчитали, что в 1982 году состоится 4 солнечных затмения, а 16 октября 2126 года в Москве произойдёт полное солнечное затмение.
Изучение перспектив космических исследований показывает, что уже в ближайшие десятилетия станут реальными космические путешествия человека на другие планеты.
Об этом и многом другом мы поговорим сегодня на уроке, но для начала надо вспомнить азы тригонометрии которое позволить ответить на многие вопросы сегодня и в будущем.
Задач перед нами много и сегодня вы сможете попробовать себя в роли математика художника ,математика экономиста, математика астронавта
Устно:
Какому
выражению соответствует значение ![]() ?
?
А)
![]() В)
В) ![]()
Выбрать верное равенство:
А)
![]() Б)
Б)![]() В)
В) ![]()
Какой из углов является углом 2 четверти?
А)
![]() Б) -145
Б) -145![]()
В
каких четвертях ![]() имеют разные знаки?
имеют разные знаки?
А) 2 и 4 Б) 1 и 3 В) 1 и 4
Каким
выражением можно заменить ![]() +
+![]() ?
?
А)
![]() Б)
Б) ![]() В)
В) ![]()
Определите
знак выражения ![]()
Вычислить
![]()
Назовите угол α из промежутка [0; π/2], для которого sinα = ½
Используя основные формулы тригонометрии, упростите выражение:
1. (sin a – 1) (sin a + 1)
2. sin2 a – 1 + cos2 a
3. sin2 a + tg a ctg a + cos2 a
4. ![]()
Продолжим решать тригонометрические уравнения, применяя нужный метод.
Задание №1.
Решить уравнение sin2 х + 5 sin х - 6 =0.
Задание №2
Решите уравнение 2sinx cos5x – cos5x = 0;
Задание №3
Решите уравнение 2 sin2 х - 3 sinх cos х - 5 cos2х =0
Учащиеся решают уравнение
2 sin2 х - 3 sinх cos х - 5 cos2х =0
2 sin2 х - 3 sinх cos х - 5 cos2х =0 | : cos2х ≠ 0
2 tg 2x - 3 tg x - 5 = 0
замена tg x = t
2 t2 – 3 t – 5 =0
t1 = -1; t2 = 2,5
Выполняем обратную замену и решаем уравнения
1) tg х = -1
х
= -π/2 + πk , k ![]() Z.
Z.
2) tg х = 2,5
х
= arctg 2,5+ πn, n ![]() Z.
Z.
Ответ:
-π/2 + πk , arctg 2,5+ πn, n, k ![]() Z.
Z.
Задание №4.
Решить
уравнение ![]() sin x + cos x = 1
sin x + cos x = 1
Учащиеся решают уравнение
![]() sin x + cos x = 1 │ :2
sin x + cos x = 1 │ :2
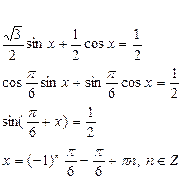
Ответ:
![]()
Сегодня в день науки очень важно говорить об открытиях и ученных . Мы готовились к этому дню и провели некоторые исследования в группах, котрые сейчас дети представят .
3. Самостоятельная работа учащихся с последующей проверкой результатов работы
Учитель: А теперь выберите два уравнения и самостоятельно решите их.
*Работа выполняется под копирку. Оригинальный вариант сдается учителю для проверки и выставления отметки, а второй - остается у учащихся для самопроверки.
На экране проецируется задание.
|
На оценку |
1 вариант |
2 вариант |
|
«3»
«4»
«5»
|
3 sin x+ 5 cos x = 0 5 sin2 х - 3 sinх cos х - 2 cos2х =0 3 cos2х + 2 sin х cos х =0 5 sin2 х + 2 sinх cos х - cos2х =1 2 sin x - 5 cos x = 3 1- 4 sin 2x + 6 cos2х = 0 |
2 cos x+ 3 sin x = 0 6 sin2 х - 5 sinх cos х + cos2х =0 2 sin2 x – sin x cosx =0 4 sin2 х - 2sinх cos х - 4 cos2х =1 2 sin x - 3 cos x = 4 2 sin2 х - 2sin 2х +1 =0 |
Учитель: Ребята, проверьте свое решение с ответами и поставьте оценку.
*Ответы записываются на доске с обратной стороны, пока учащиеся работают. После того, как собраны работы, проводится самопроверка, и учащиеся выставляют себе предварительную оценку.
|
|
1 вариант |
2 вариант |
|
«3»
«4»
«5»
|
- arctg
5/3+ πk, k
π/4
+ πk; - arctg
0,4 + πn, k,
n
π/2
+ πk;
- arctg 1,5 + πn,
k, n π/4
+ πk;
- arctg 0,5 + πn,
k, n
arctg
( - 1 ± √5) + πk,
k π/4
+ πk;
arctg 7 + πn,
k, n |
-
arctg 2/3+ πk,
k arctg
1/3+ πk;
arctg 0,5 + πn,
k, n
πk;
arctg 0,5 + πn,
k, n -π/4
+ πk;
- arctg 5/3 + πn,
k, n
arctg
( 2 ± √11) + πk,
k π/4
+ πk;
arctg 1/3 + πn,
k, n |
*Дифференцированное домашнее задание. Задание выводится на экран, в электронном журнале загружается файлом
Решите уравнения
Оценка «3»:
1.
![]()
2.
![]()
3.
![]()
Оценка «4»:
4. ![]()
5. ![]()
Оценка «5»:
6. ![]()
7. Найдите наибольший отрицательный корень уравнения
![]()
Учитель: Подведем итоги урока. Сегодня на уроке мы вспомнили числовые значения тригонометрических функций, вспомнили формулы решения простейших тригонометрических уравнений, рассмотрели общие подходы решения тригонометрических уравнений, закрепили навыки и проверили умения решать тригонометрические уравнения, познакомились со способом отбора корней при решении тригонометрических уравнений.
Я уверена, что у вас сложилось более полное представление о тригонометрических уравнениях и разнообразии способов их решения, и с решением тригонометрических уравнений большинство из вас справится.
- Что нового узнали на уроке?
- Испытывали ли вы затруднения при выполнении самостоятельной работы?
- Испытывали ли вы затруднения при выборе самостоятельной работы?
- Какие проблемы у вас возникли по окончании урока?
Учитель: Спасибо вам за насыщенную работу на уроке. Я благодарю всех, кто принял активное участие в работе. Урок окончен. До свидания!
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.