Поделиться
Математика_10класс_2 урок_рабочий лист ученика.docx
Рабочий лист ученика №2. Тригонометрические формулы суммы и разности углов.
Цель урока: Учащиеся выведут тригонометрические формулы суммы и разности углов, применят формулы для упрощения тригонометрических выражений.
Критерии оценивания: Учащийся
· выводит тригонометрические формулы суммы и разности углов;
· применяет формулы для упрощения тригонометрических выражений.
«Самостоятельная работа».
Вывод тригонометрические формулы суммы и разности углов.
1. Заполните пропуски в выводе формулы:
В прямоугольники впишите пропущенную информацию.
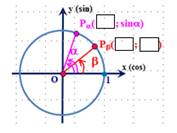
Заполните пропуски:
2. Заполните пропуски в выводе формулы:
3. Заполните пропуски в выводе формулы:
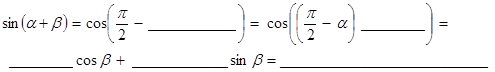
4. Заполните пропуски в выводе формулы:
5. Заполните пропуски в выводе формулы:
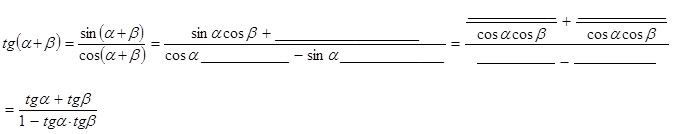
6.
Заполните пропуски в выводе формулы: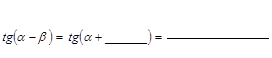 
Решение задач.
№1. Вычислите:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
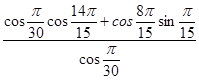
№2. Упростите выражение:
1. 
2. 
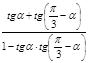
3. 
4. 
5. 
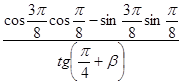
6. 
7. 
№3. Вычислите:
1. 
, если 
;
2. 
, если 
;
3. 
,
если 
и 
;
4. 
, если 
, 
;
5. 
если 
6. 
,
если 
7. 
– острые углы;
Рефлексия. «Незаконченное предложение».
Домашний тест:
1. sin
105
А)
В)
С)
D)
Е)
1
2. cos 5βcosβ + sin 5βsinβ
А) cos 2β В) sin 2β С) cos 4β D) sin 4β Е) cosβ
3. sin51cos21– cos51sin21
А)
В) 1 С) 0 D) –1
Е) 
4. cos79cos34+sin79sin34
А) 
В) 
С) 
D) 
Е) 1
5. sin 5αcos 4α–cos 5αsin 4α+sinα
А) 2cosα В) –2sinα С) sinα D) cosα Е) 2sinα
6. Вычислите
tg
(α+β),
если tgα=
,
tgβ=
А)
В) 
С)
D)
4 Е)
7.
A) 0 B) –1
C) 
D) 1 E) 
8. 
A) ctg 15° B) tg 35° C) tg 15° D) ctg 35° E) cos 20°
9. 
А)ctgα В) tgα С) –tgα D)– ctgα Е) 1
10. Вычислите
tg(α–β), если tgα=
, tgβ=
,
А) 
В)
С) 
D) 1 Е) –1
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
