МЕДИАНА УПОРЯДОЧЕННОГО РЯДА

Медиана упорядоченного ряда

Цели: ввести понятие медианы как статистической характеристики упорядоченного ряда; формировать умение находить медиану для упорядоченных рядов с четным и нечетным числом членов; формировать умение интерпретировать значения медианы в зависимости от практической ситуации.

Ход урока

I. Устная работа.

Даны ряды:

1) 4; 1; 8; 5; 1; 7.

2) ; 9; 3; 0,5; .

3) 6; 0,2; ; 4; 6; 7,3; 6.

Найдите:

а) наибольшее и наименьшее значения каждого ряда;

б) размах каждого ряда;

в) моду каждого ряда.

II. Объяснение нового материала.

Объяснение  проводить  согласно  пункту  10  учебника.  Следует подчеркнуть, что перед нахождением медианы нужно всегда упорядочить ряд данных.

На доску следует вынести правила нахождения медианы для рядов с четным и нечетным числом членов:

Особое внимание следует уделить интерпретации значений медианы для различных задач. Учитель должен прививать критическое отношение к статистическим выводам и обобщениям.

III. Формирование умений и навыков.

1-я группа. Упражнения на применение формул нахождения медианы упорядоченного и неупорядоченного ряда.

1. № 186.

Решение:

а) число членов ряда п = 9; медиана есть среднее в упорядоченном ряду значение варианта Ме = 41;

б) п = 7, ряд упорядочен, Ме = 207;

в) п = 6, ряд упорядочен, Ме = 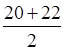 = 21;

г) п = 8, ряд упорядочен, Ме = 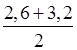 = 2,9.

Ответ: а) 41; б) 207; в) 21; г) 2,9.

3. № 188 (устно).

Решение:

а) Может, если сумма членов не кратна числу членов.

б) Не может, так как разность двух натуральных чисел,
из которых уменьшаемое больше вычитаемого, есть натуральное число.

в) Не может, так как мода – один из членов ряда, а все члены ряда – натуральные числа.

г) Может, если число членов ряда четное и числа  и  не равны между собой.

Ответ: да; б) нет; в) нет; г) да.

4. Зная, что в упорядоченном ряду содержится т чисел, где т – нечетное число, укажите номер члена, являющегося медианой, если т равно:

а) 5;     б)     17;     в) 47;      г) 201.

Решение:

Номер находим как  + 1, где  – целая часть числа.

а)  + 1 = 2 + 1 = 3;                        в)  + 1 = 23 + 1 = 24;

б)  + 1 = 8 + 1 = 9;                     г) 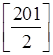 + 1 = 100 + 1 = 101.

Ответ: а) 3; б) 9; в) 24; г) 101.

2-я группа. Практические задачи на нахождение медианы соответствующего ряда и интерпретацию полученного результата.

1. № 189.

Решение:

Число членов ряда п = 12. Для нахождения медианы ряд нужно упорядочить:

136, 149, 156, 158, 168, 174, 178, 179, 185, 185, 185, 194.

Медиана ряда Ме = 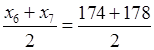 = 176.

Выработка  за  месяц  была  больше  медианы  у  следующих  членов артели:

1) Квитко;                                       4) Бобков;

2) Баранов;                    5) Рылов;

3) Антонов;                    6) Астафьев.

Ответ: 176.

2. № 192.

Решение:

Упорядочим ряд данных:

30, 31, 32, 32, 32, 32, 32, 32, 33, 35,

35, 36, 36, 36, 38, 38, 38, 40, 40, 42;

число членов ряда п = 20.

Размах A = x_max – x_min = 42 – 30 = 12.

Мода Мо = 32 (это значение встречается 6 раз – чаще других).

Медиана Ме = 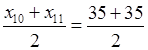 = 35.

Размах показывает наибольший разброс времени на обработку детали; мода показывает наиболее типическое значение времени обработки; медиана – время обработки, которое не превысили половина токарей.

Ответ: 12; 32; 35.

IV. Итоги урока.

– Что называется медианой ряда чисел?

– Может  ли  медиана  ряда  чисел  не  совпадать  ни  с  одним  из  чисел ряда?

– Какое  число  является  медианой  упорядоченного  ряда,  содержащего 2п чисел? 2п – 1 чисел?

– Как найти медиану неупорядоченного ряда?

Домашнее задание: № 187, № 190, № 191, № 254.