МЕТОДИ РІШЕННЯ МАТРИЧНИХ ІГОР

МЕТОДИ РІШЕННЯ МАТРИЧНИХ ІГОР.

Відомість матричної гри до завдання лінійного програмування.

Розглянемо m х п гру із платіжною матрицею

Без обмеження спільності будемо вважати, що всі елементи матриці А позитивні (цього завжди можна домогтися, користуючись афінним  правилом, що перетворить задану матрицю гри, але не змінює оптимальних змішаних стратегій гравців).

Тим самим, шукана ціна гри v – позитивне число.

Інтереси гравця А

З теореми про властивості оптимальних змішаних стратегій гравців випливає, що при будь-якій чистій стратегії B_k гравця В, k = 1, 2, ... , п, оптимальна змішана стратегія  гравця А забезпечує його середній виграш, не менший v. Іншими словами, виконуються співвідношення

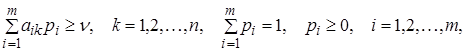
які з урахуванням позначень

можна записати так

Оскільки гравець А прагне зробити свій гарантований виграш максимально можливим, то завдання відшукання рішення матричної гри зводиться до наступного завдання:

знайти ненегативні величини , що задовольняють нерівностям

і такі, що їхня сума мінімальна

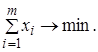
Інтереси гравця В

Аналогічним чином укладаємо, що оптимальна змішана стратегія гравця В при будь-якій чистій стратегії Аi гравця А, i = 1, 2,... ,т, забезпечує його середній програш, не більший v. Іншими словами, виконуються співвідношення

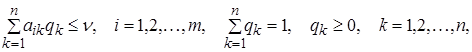
які з урахуванням позначень

можна записати так

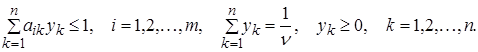
Оскільки гравець В  прагне зробити свій гарантований програш мінімально можливим, то завдання відшукання рішення матричної гри зводиться до наступного завдання:

знайти ненегативні величини , що задовольняють нерівностям

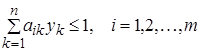
і такі, що їхня сума максимальна

Тим самим, ми одержуємо наступний важливий результат.

Теорема. Рішення матричної гри з позитивною платіжною матрицею  рівносильна рішенню двоїстих завдань лінійного програмування

(A)           

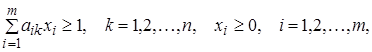
(B)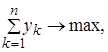        

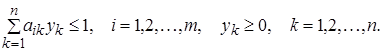
При цьому ціна гри

де  – величина, зворотна загальному значенню оптимальних сум,

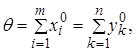
а оптимальні значення  й  пов'язані з оптимальними  й  за допомогою рівностей

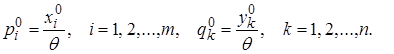
Алгоритм рішення матричної гри

1-й крок. До всіх елементів вихідної матриці гри додається одне й теж позитивне число  так, щоб всі елементи нової матриці були строго позитивні.

2-й крок. Вирішуються двоїсті завдання лінійного програмування (А) і (В) (наприклад, симплексом-методом, або як-небудь інакше).

Перебувають набори , і число .

3-й крок. Будуються оптимальні змішані стратегії гравців А и В відповідно

4-й крок. Обчислюється ціна гри