Методич реком к уроку (1)

Методические рекомендации к уроку   №5 на тему  «Решение текстовых задач»

Цель обучения:

8.4.2.2 решать текстовые задачи с помощью дробно-рациональных уравнений.

На данном уроке будут применены формулы процента и решены задачи на движение.

Методические рекомендации по организации урока.

Урок можно начать с активизации знаний учащихся и повторить дробно-рациональное уравнение, определение процента числа.  Учащиеся ранее рассматривали квадратные и дробно-рациональные уравнения. Учащиеся должны уметь составить уравнение по условию задачи. Знают определение дробно-рационального уравнения. Знают алгоритм составления дробно-рационального уравнения. Знают и умеют решать дробно-рациональное уравнение. Каждый ученик демонстрирует знания по решению дробно-рационального уравнения.

Активизация уже имеющихся знаний осуществляется через повторение пройденного материала.

Критерии оценивания:

- Верно названы проценты числа;

-  Верно записаны проценты числа;

Учитель дает обратную связь на выполненное задание, указывая на правильные ответы и активность учащихся. 

Решению текстовых задач предшествует достаточно долгое время, отводимое на отработку решения уравнений. Решения  некоторых задач на проценты практически сводятся к решению дробных рациональных уравнений, которые, в свою очередь, включают чаще всего решение квадратных уравнений.

Вместе с учащимися повторите задачи, приводящие к решению дробных рациональных уравнений. используя  формулы процента.

Разоберите с учащимися  примеры 1,2. Обратите внимание учащихся на составление таблицы, используя математическую модель задачи.

Для работа в парах,  объедините учащихся в пары. Каждая пара  получает одинаковый  набор заданий. После выполнения заданий пары сверяют полученные ответы с ответами других.  Взаимооценивают и самоценивают друг друга.

Критерии оценивания:

1.Верно использована математическая модель.

2.Верно использована формула процента.

3. Верно составлено уравнение.

4. Верно решено дробно-рациональное уравнение.

5. Верно интерпретированы корни уравнения соответствующие условию задачи.

            Более способным учащимся предлагается дополнительные дифференцированные задания. Учащиеся самостоятельно находят неизвестные элементы, используя данные задачи. Менее способным учащимся оказывается помощь в виде подмостков.

Рекомендации по оцениванию уровня достижения учебной цели.

В конце урока учитель может оценить уровень достижения учебной цели с помощью упражнения «Муравейник». Предложите учащимся записать на стикере один вопрос, который для них остался непонятным по новой теме. Если у учащихся нет затруднений, то они могут придумать интересный вопрос для одноклассников. По завершению задания организуйте предоставление обратной связи по уровню ответов учащихся.

Ответы и решения.

Приложение 1

1.      Моторная лодка, скорость которой в стоячей воде 15 км/ч, прошла по течению реки 35 км, а против течения 25 км. По течению она шла столько же времени, сколько против течения. Какова скорость течения реки?

t₁= t₂ ,

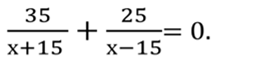
2.      Катер, развивающий в стоячей воде скорость 20 км/ч, прошел 36 км против течения и 22 км по течению, затратив на весь путь 3 ч. Найдите скорость течения реки.

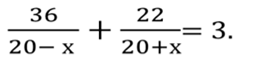
3.      Один из лыжников прошел расстояние в 20 км на 20 мин быстрее, чем другой. Найдите скорость каждого лыжника, зная, что один из них двигался со скоростью, на 2 км/ч большей, чем другой

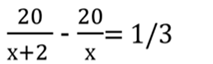
4.      Из города в село, находящееся от него на расстоянии 120 км, выехали одновременно два автомобиля. Скорость одного была на 20 км/ч больше скорости другого, и поэтому он пришел к месту назначения на 1 ч раньше. Найдите скорость каждого автомобиля.

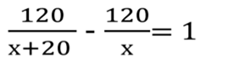
Приложение 2

1.      Из города в село, находящееся от него на расстоянии 120 км, выехали одновременно два автомобиля. Скорость одного была на 20 км/ч больше скорости другого, и поэтому он пришел к месту назначения на 1 час раньше. Найдите скорость каждого автомобиля.

Пусть V₁=x км/ч, тогда V₂=х+20 км/ч

Так как 1-ый пришел на 1 час раньше 2-ого, то составим уравнение:

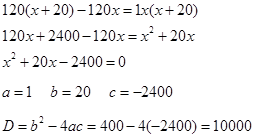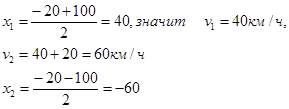2.      Сплав меди и цинка, содержащий 5 кг цинка, сплавили с 15 кг цинка, после чего процентное содержание цинка в сплаве повысилось на 30%. Какова первоначальная масса сплава, если известно, что меди в нём было больше, чем цинка?

Решение. Составление математической модели:

х кг меди было в сплаве;

(х +5) кг – масса первоначального сплава;

 - первоначальное процентное содержание цинка;

 - процентное содержание цинка в полученном сплаве.

Согласно условию,

.

Работа с составленной моделью.

Решив полученное уравнение, находим , . Оба корня удовлетворяют составленному уравнению.

Ответ на вопрос задачи.

По условию в первоначальном сплаве было 5 кг цинка, а меди – больше, чем цинка. Поэтому из найденных значений выбираем значение 20. тогда масса сплава – 25 кг.

Ответ: 25 кг.

После решения задачи необходимо ещё раз объяснить ход решения и поинтересоваться у учащихся, понятно ли им данное решение. Так же необходимо заметить, что в некоторых случаях целесообразно создавать геометрические модели для лучшего восприятия условия задачи. Чаще всего такие модели составляются к задачам на движение. ( Как пример разобрать задачу 

Приложение 3

Два автомобиля выезжают одновременно из одного города в другой. Скорость первого на 10 км/ч больше скорости второго, и поэтому первый автомобиль приезжает на место на 1 ч раньше второго. Найдите скорость  каждого автомобиля, зная, что расстояние между городами равно 560 км.

Критерии оценивания к заданиям для классной работы:

Учащиеся достигнут целей обучения если:

грамотно записывают краткое условие к задаче;

правильно составляют дробно-рациональное уравнение по условию задачи;

правильно решают составленное дробно-рациональное уравнение;

правильно записывают ответ к задаче;

Литература:

Алгебра.8 класс: учебник для общеобразовательных учреждений/ [Ю.Н.Макарычев, Н.Г.Миндюк, К.И. Нешков, С.Б.Суворова]; под редакцией С.А. Теляковского. – М.:Просвещение, 2013.