Методическая копилка при подготовке к ОГЭ части геометрия

Дополнительные теоремы, свойства фигур, используемые на экзамене при решении геометрических задач

1.     В равных треугольниках биссектрисы соответствующих углов равны.

2.     В равных треугольниках медианы, проведенные к соответственным сторонам, равны.

3.     Все точки одной из двух параллельных прямых равноудалены от другой.

4.     Если медиана СМ треугольника АВС равна половине стороны АВ,  то треугольник АВС – прямоугольный.

5.     Если две высоты треугольника равны, то треугольник равнобедренный.

6.     Если через данную точку к окружности проведены две касательные, то отрезки касательных, соединяющих данную точку с точками касания равны.

7.     Радиус окружности, вписанной в прямоугольный треугольник, определяется по формуле

8.     В треугольник АВС вписана окружность, касающаяся стороны АВ в точке М, ВС = а. Докажите, что АМ = р-а, где р- полупериметр треугольника АВС.

9.     Прямые, содержащие высоты треугольника, пересекаются в одной точке.

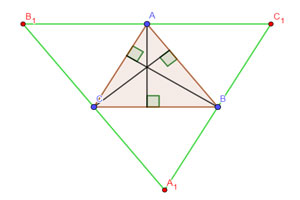
10.  В треугольнике АВС на продолжении медианы АМ за точку М отложили отрезок МК, равный отрезку АМ. То четырехугольник АВКС параллелограмм.

11.  Медиана прямоугольного треугольника, проведённая к гипотенузе, равна её половине.

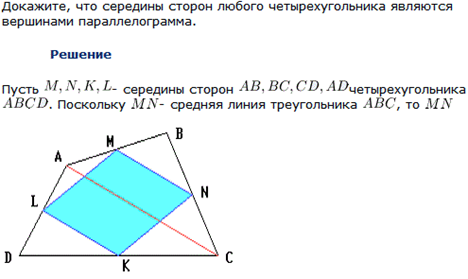
12.  Середины сторон параллелограмма являются вершинами параллелограмма.

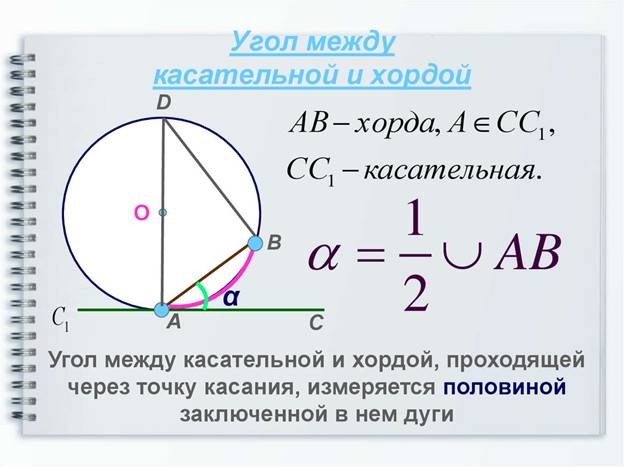
13.  Свойство угла между касательной и хордой:  угол САВ =1/2 дуги АВ, а угол С₁ АВ = ½ дуги АDB

14.   Хорды АВ и CD  равны, тогда и дуги АМВ =дуге CND.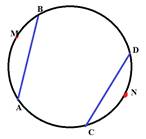

15.  Если две дуги окружности равны, то равны и хорды, их стягивающие.

16.  Хорды AB и CD окружности пересекаются в точке М, то рисунок  97                        

17.  Хорды AB и CD окружности не пересекаются, то рисунок  98                        

18.  Признак принадлежности четырех точек одной окружности

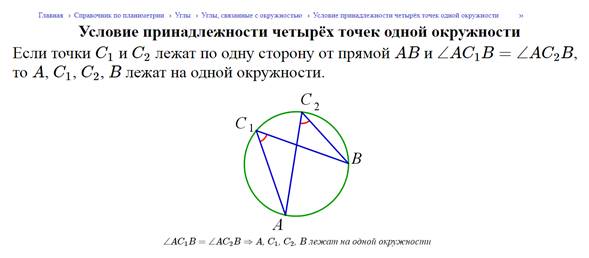
19.  Средняя линия трапеции делит ее диагонали пополам.

20. Отрезок, соединяющий середины диагоналей трапеции, параллелен её основаниям и равен их полуразности.

21.  Отношение периметров подобных треугольников равно коэффициенту подобия.

22.  Свойство пересекающихся хорд: Если хорды AB и CD окружности пересекаются в точке М, АМ*МВ=DM*MC.

23.  Свойство касательной и секущей: если через точку А к окружности проведены касательная АМ (м точка касания) и прямая (секущая), пересекающая окружность в точках В и С, .

24.  В подобных треугольниках биссектрисы, проведенные из вершин соответственных углов, относятся как соответственные стороны.

25.  Теорема Менелая

26.  Теорема Птолемея

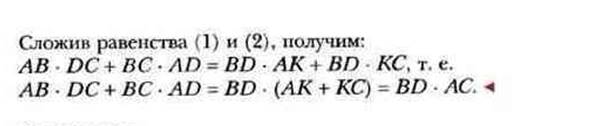
27. Площадь выпуклого четырехугольника, диагонали которого перпендикулярны, равна половине их произведения.

28.  Медиана треугольника разбивает его на два равновеликих треугольника.

29.  На стороне AC треугольника ABC отмечена точка M так, что . Докажите, что .

30.   Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

31.  Биссектриса треугольника делит его сторону на отрезки, длины которых пропорциональны прилежащим сторонам.

32.  Площади треугольников ABC и A₁B₁C₁ соответственно равны S₁ и S₂. Известно, что углы равны при вершинах А и А₁ равны. Докажите, что .

33.  Прямые перпендикулярны если K₁*k₂= -1

34.