Методическая разработка «О воспитании эстетического вкуса учащихся на уроках математики»

Муниципальное бюджетное  учреждение

                                                     «Школа №82»

г.о. Тольятти Самарской области.

Методическая разработка

«О воспитании эстетического вкуса учащихся на уроках математики»

Предмет: математика

Класс  5-11

Автор: Родионова Галина Михайловна,

 учитель математики

МБУ  «Школа № 82»,

  г.о. Тольятти  Самарской области

                                                  2021

О воспитании эстетического вкуса учащихся

Формирование и развитие познавательных интересов – часть широкой проблемы  воспитания всесторонней развитой личности.

Математика  всегда была неотъемлемой и существенной составной частью человеческой культуры,  она является ключом к познанию окружающего мира. Важно развивать в человеке способность понимать смысл поставленной перед ним задачи, умение правильно рассуждать, навыки алгоритмического мышления. Школьников необходимо научить самостоятельно  работать, высказывать и проверять предположения, уметь делать обобщения изученных фактов, творчески применять знания в новых ситуациях.

Учитель должен удивляться красоте и моще математических методов и заражать этим своих учеников. В равной степени он должен быть терпеливым, поскольку не вправе ожидать мгновенных результатов. Однако если все делать профессионально и честно, то рано или поздно, ученик себя проявит и поймет, что  математика – наука «замечательная».

Известно, что решение задач – одно из основных средств математического развития школьников. Каждая математическая задача служит конкретным  целям обучения, но ее основная цель – развитие творческого и математического мышления учащихся, повышение их интереса к математике. Этому  способствуют прежде всего так называемые красивые  задачи.

В понятие «красивая задача» всегда присутствует элемент субъективизма. Тем не менее, понятия «изящное решение» задачи, «красивый» вывод и т.д. являются в математике общепринятыми. Известный математик Н.Г.Чеботарев утверждал: «Красота в математике идет рука об руку с целесообразностью: мы редко называем изящными рассуждения, не приводящие к законченной цели или более длинные, чем это представляется необходимым».

Чтобы помочь школьникам осознать эстетику задачи, необходимо с первых уроков геометрии знакомить учеников с различными способами решения одной и той же  задачи, различными приемами доказательствам одной и той же теоремы.

Но более широкие возможности в формировании эстетического вкуса представляют учителю математики внеклассные занятия. Здесь можно показать красоту геометрических задач во всей полноте.

Восприятие эстетической стороны планиметрической задачи начинается для школьников с условия и чертежа. Поэтому содержание  условия должно вызывать интерес (тут важна и форма подачи условия, и его занимательность). В геометрических задачах большую роль играет чертеж (достаточно вспомнить задачи о вычерчивании фигур одним росчерком, задачи на разрезание и др.). Чертеж должен соответствовать значению слова «красивый». Иными словами рисунок «доставляющий наслаждение, приятный внешним видом, гармоничностью, стройностью».

Приведу несколько задач, условия которых соответствуют данному выше определению.

Задача 1.  Постройте с помощью циркуля и линейки фигуры, изображенные на  рис.1

Эта задача привлекает внимание учащихся  прежде всего условием (красивый узор). Но замечательно еще и то, что этот узор дают простейшие построения циркулем и линейкой, изучаемые в школе (проведение перпендикулярных прямых, деление отрезка пополам и др.) 

Далее школьникам можно предложить самостоятельно придумать геометрические узоры, построение которых возможно выполнить циркулем и линейкой. Например,  при изучении темы «Правильные многоугольники», геометрия 9 класс.

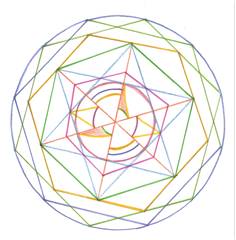
Хан Диана, 9 «Г» класс                                Рамазанова Регина, 9 «Г»  класс

Созидательное  путешествие хорд.

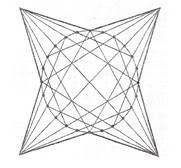
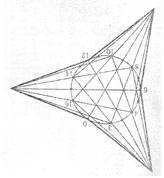
Красивая задача – это задача устанавливающая интересный факт и предполагающая красивое. А красивое решение – это, пожалуй, основное в понятии  «красивая задача».  Оно наглядно, неожиданно, просто.

 Задачи, удовлетворяющие этому требованию, неизменно вызывают интерес учащихся, побуждая их искать более короткие и более простые пути решения.  Математическая (планиметрическая) задача способствует формированию и развитию эстетического вкуса учащихся в том случае, если она отвечает определенным требованиям, а именно:

1)    Условие задачи должно быть интересно школьнику; если задача геометрическая, то чертеж к ней – красивый;

2)    Задача может устанавливать интересный факт, порой неожиданный;

3)    Такая задача обладать большой степенью общности;

4)    Наконец, основное: в решение задачи обязательно нужно спрятать «изюминку», чтобы оно было наглядно и удивительно просто.

 Желательно также, чтобы задача предполагала несколько способов решения. Формируя и развивая эстетический вкус при решении планиметрических задач, учитель помогает более полно воспринимать красоту геометрии, повышает их общую культуру.   

Простые, но творческие задания для пятиклассников способствуют интеллектуальному развитию, раскрепощению  их мысли, проявлению инициативы и смелости при поиске решения.

Казалось бы простое задание: « Начертить  прямоугольник,  ширина которого 1 клетка, длина 10 клеток. И заштриховать  1/10 его часть».  Но сколько простора для творчества!  Стоит лишь поддержать ребят,  и учитель получит смелые, нешаблонные  решения.

 Интересно и такое задание: «Нарисуйте квадрат, сторона которого 10 клеток. Заштрихуйте половину  квадрата разными способами. 

При введении понятия дроби  решалась такая задача: заштриховать некоторую часть прямоугольника или квадрата. Обычно оно выполняется с большим желанием на уроке, и если попросить закончить их дома, то  многие ребята находят   интересные решения. Или построить фигуру, если известна её часть. 

В 11 классе  учащимся можно  предложить творческое задание: составить карточку – задание по теме  «Площадь криволинейной трапеции»,  в которой содержится условие задачи на нахождение площади криволинейной трапеции. К заданию  предполагается карточка с решением (рисунком).  Ученики проявляют к этому заданию  большой интерес, каждый  захочет  отличиться оригинальностью решения. Коллективное обсуждение выполненных заданий стимулирует деятельность школьников и  развивает  интерес к изучению  математики.

Творческие работы учащихся на тему

« Когда теория скучна, а рисовать хочется»

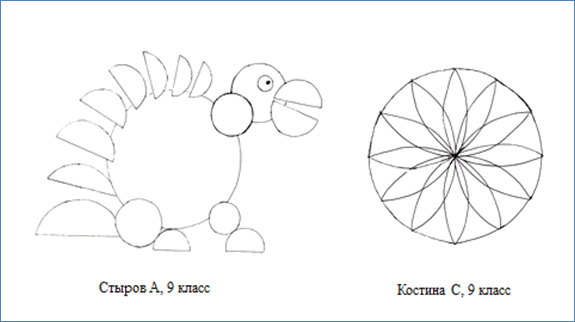
Гребенникова А., 9 класс

Список литературы:

Журнал «Математика в школе» № 2,1997 г, стр.4.

Кордемский Б.А. «Математические завлекалки». – М.: Оникс: ООО « Мир и Образование»,  2005.