Методическая разработка открытого урока по математике на тему: «Сравнение отрезков и углов»

Методическая разработка открытого урока по математике на тему: «Сравнение отрезков и углов»
Цель урока:
1.Ввести понятие сравнения отрезков и углов; ввести понятие середины отрезка; ввести понятие биссектрисы угла; отработать навыки сравнения фигур, в частности отрезков и углов.
2. Развитие умений применять полученные теоретические знания при выполнении практических заданий.
3. Воспитание интереса к изучению математики, дисциплинированности, самостоятельности, целеустремленности и трудолюбия
Оборудование: компьютер, проектор, интерактивная доска, презентация, видеоурок, геометрические фигуры, чертежные инструменты, веревка, макеты углов.
Ход урока.
1. Организационный момент.
2. Проверка домашнего задания. (Слайд2).
3. Повторение через фронтальный опрос (Слайд 3):
- Что такое отрезок? Как он обозначается?
- Что такое луч? Как он обозначается?
- Что такое угол? Как он обозначается?
- Как называется общая точка, из которой выходят лучи? А как называются сами лучи?
- Какой угол называется развернутым?
- Что делает любой угол с плоскостью? Если угол неразвернутый, то, как называются части плоскости, на которые угол разделяет плоскость?
1 задача(Слайд 4). Проведите прямую a и отметьте на ней точки А и В. Отметьте: а) точки M и N, лежащие на отрезке АВ; б) точки P и Q, лежащие на прямой а , но не лежащие на отрезке АВ; в) точки R и S, не лежащие на прямой а.
2 задача (Слайд 5). Проведите прямую и отметьте на ней три точки. Сколько отрезков получилось на прямой?
3 задача (Слайд6). Начертите неразвернутый угол. Отметьте точки А, В, М и N так, чтобы все точки отрезка АВ лежали внутри угла, а все точки отрезка MN лежали вне угла.
4.
Изучение
нового материала (Видеоурок).
-Среди окружающих нас
предметов встречаются такие, которые имеют одинаковую форму и размер.
-Посмотрите вокруг, найдите и назовите одинаковые предметы (по форме и
размеру)…
-Посмотрите на доску, на ней начерчены две фигуры и в руках у меня также
находятся две фигуры. О каких фигурах можно сказать, что они равны? Что нужно
сделать?
Вывод:две геометрические фигуры называются
равными, если их можно совместить наложением.
2. Сравнение отрезков
Выполним рисунок:

Рис. 3. Отрезки АВ и МN
Рассмотрим отрезки АВ и МN. Если точку А совместить с точкой М, а B – с точкой N, то такие отрезки называются равными.
В данной ситуации может быть другой случай:
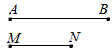
Рис. 4. Отрезки АВ и MN
Точка М совпадает с точкой А, а точка N лежит во внутренней части отрезка АВ. В таком случае делаем вывод о том, что MN<AB.
Однако существует третий случай:
![]()
Рис. 5. Отрезки АВ и MN
Точка А совпадает с точкой М, а точка В лежит между точками М и N. В таком случае отрезок АВ является частью отрезка MN. Именно поэтому MN>AB.
Определение: Точка, которая делит отрезок пополам, называется серединой отрезка.
Рассмотрим рисунок:
![]()
Рис. 6. Точка Р – середина отрезка MN.
3. Сравнение углов
В данный момент рассмотрим равенство углов. В этой ситуации также имеется три случая:
1. Случай:
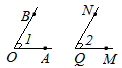
Рис. 7. Углы ∠AOB, ∠MQN равны
Если луч MQ совпадает с лучом ОА, а луч QN совпадает с лучом ОВ, то углы ∠AOB, ∠MQN равны.
2. Случай:
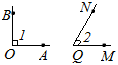
Рис. 8. Углы ∠AOB >∠MQN
Если луч MQ совпадает с лучом ОА, а луч QN не совпадает с лучом ОВ, а лежит во внутренней области угла ∠AOB, то ∠AOB > ∠MQN.
3. Случай:
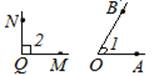
Рис. 9. Углы ∠AOB <∠MQN
Луч MQ совпадает с лучом ОА, а луч QN не совпадает с лучом ОВ, а лежит во внешней области угла ∠AOB, в таком случае ∠AOB <∠MQN.
4. Биссектриса угла
Определение: Луч, который выходит из вершины угла и делит его пополам, называется биссектрисой.
На рисунке 10 обозначена биссектриса ОМ
угла ∠АОВ.
Заметим, что, по определению, ![]() .
.
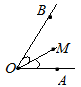
Рис. 10. ОМ – биссектриса угла ∠AOB
— У вас на столах лежат заготовки углов. Как, не имея транспортира провести
биссектрису? (сложить угол пополам и провести карандашом прямую, исходящую из
вершины угла) .
5.Закрепление.
А сейчас давайте решим несколько задач устно по готовым чертежам..
№19. Точка О – середина отрезка АВ. Можно ли совместить отрезки: а) ОА и ОВ; б) ОА и АВ? Сравните эти отрезки.
Решение.
Поскольку точка О является серединой отрезка АВ, то ОА=ОВ (по определению).Следовательно, отрезок АО можно совместить наложением с отрезком ОВ.
Отрезки ОА и АВ совместить нельзя, так как ОА является частью отрезка АВ, соответственно, ОА<AB.
Ответ: ОА и АВ совместить нельзя, АО и ОВ совместить можно.
№20 по рис 25 учебника.
№21. Луч ОС делит угол АОВ на два угла. Сравните углы АОВ и АОС.
Решение:
∠АОC<∠AOB, так как луч ОС проходит внутри угла ∠АОВ, соответственно, угол
∠АОС является частью угла ∠АОВ.
Ответ: ∠АОC<∠AОB
№22. Луч l – биссектриса угла hk. Можно ли наложением совместить углы: а) hl и lk; б) hl и hk?
Решение:
Вспомним, что такое биссектриса. Данный луч – это часть прямой, которая делит угол пополам. Соответственно, углы ∠hl и ∠lk равны между собой, поэтому их можно совместить наложением.
Угол ∠hl является частью угла ∠hk, так как ∠hl меньше ∠hk . Следовательно, данные углы совместить нельзя.
Ответ: Углы ∠hl и ∠lk совместить можно, углы ∠hl и ∠hk совместить нельзя.
Дополнительные задачи: см. методичку стр.10-11 (тоненькая)
6.Итог урока.
Итак, что нового мы сегодня узнали на уроке? Что такое середина отрезка? Что такое биссектриса угла? Какие фигуры называются равными в геометрии? Как сравнить отрезки? Как сравнить углы?
7.Домашнее задание.
§3 п. 5, 6, № 18, 23.
8. Оценки за урок
Скачано с www.znanio.ru
© ООО «Знанио»
С вами с 2009 года.
![]()

