
Бахтеева Венера Ахматовна,
Учитель МБОУ СОШ с.Красная Горка
МР Нуримановский р-н Республики Башкортостан
Методическая разработка по математике по теме "Преобразования тригонометрических функций"
(10-й класс)
1. Место данного урока в теме, разделе курсе.
Данный урок обобщающий по теме “Преобразования графиков”. Урок разработан с использованием теории и технологии исследования.
2. Связь с предыдущими уроками, темами, на что в них опирается.
На данном уроке используются знания:
– свойства тригонометрических функций;
– преобразования различных функций;
– графики функций y=cosx, y=sinx, y=tgx, y=ctgx;
Урок является основополагающим в данной теме: на нем исследуются и развиваются пространственное воображение и логика учащихся.
|
Методическая разработка урока |
|
|
Предмет: |
Математика |
|
Класс: |
10 |
|
Учебник: |
Мордкович А.Г., Семёнов П.В. |
|
Тема: |
Преобразования графиков тригонометрических функций |
|
Вид деятельности: |
Исследовательская |
|
Объект исследования: |
Тригонометрические функции |
|
Предмет исследования: |
Преобразования |
|
Цель: |
Создать условия для развития умений получать знания посредством проведения исследовательской деятельности и анализа ситуации. |
|
Задачи: |
1. Повторить различные виды преобразований. 2. Повторить свойства тригонометрических функций. 3. Выполнять преобразования с тригонометрическими графиками. 4. Выполнять построения с помощью Microsoft Excel графиков тригонометрических функций |
|
Оборудование: |
Проектор, компьютеры, компетентностно – ориентированные заданиями для работы в группах, учебник “Алгебра и начала анализа,10-11” под редакцией А.Г.Мордковича, П.В.Семёнова, презентация к уроку, лист самооценки, лист оценки малой группы. |
|
Средства достижения результата урока: |
1. Мотивация учащихся; 2. Актуализация знаний: · мониторинг умений определять свойства тригонометрических функций (работа в группах); · мониторинг знаний построения тригонометрических функций. 2. Обобщение и систематизация полученных выводов. 3. Подведение итогов урока, задание на дом. |
|
Результат |
К концу занятия учащиеся смогут: · Выполнять любые преобразования тригонометрических функций; · Выявить свои пробелы с помощью прохождения тренажера и теста на компьютере; · Сформулировать проблему и выявить пути её решения; · Применять полученные знания при построении различных графиков функции; · Сформулировать алгоритм построения графика любой тригонометрической функции с преобразованиями; · Представить результат деятельности группы в соответствии с заданной целью коммуникации; · Попрактиковаться работе с компьютером; · Оценить результаты своей деятельности по заданным критериям. |
Ход занятия
I. Контрольно-оценочный. Актуализация знаний.(15 мин)
1. Организованное начало урока.
Объявляется начало урока, учащиеся занимают свои места. Делается установка на работу, раздаётся оценочный лист урока, в который учащиеся будут фиксировать свою успешность на уроке с помощью баллов. Работа в группах организуется путем выполнения компетентностно – ориентированных заданий. (слайды на свойства функции, преобразования функций)
2. Выполнение работы в группах по два человека.
Учащимся предлагается выполнить работу, которая предполагает анализ предложенных заданий, построить тригонометрическую функцию и описать ее свойства. Время на выполнение работы –7 минут.
3. Самопроверка.
II. Представление и обсуждение исследовательской работы (20 мин)
2. Закрепления изученного материала. Построение графиков тригонометрических функций с помощью программы Microsoft Excel
IV. Рефлексивно-оценочный (3 мин)
1. Подведение итога урока, оценивание деятельность группы в целом и каждого учащегося в отдельности по оценочным листам, выделяя удавшиеся моменты. Поставить оценки за заработанные баллы. Выслушивание комментариев учителя. Ученики высказывают свою оценку деятельности на уроке, определяют свой уровень усвоения материала.
2. Постановка домашнего задания. Предоставить возможность каждому учащемуся проверить при выполнении дом. работы, степень усвоения материала.
Задание:
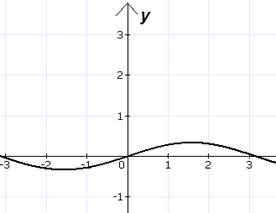
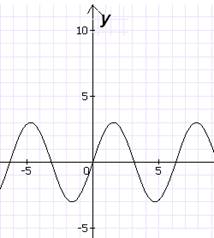
Определите, какая графическая модель, соответствует каждой из данных функций:
|
у = |
у = |
у = - 3sinx |
у =3sinx |
у =
2sin(x - |
|
|
|
|
|
|
Буквы, обозначающие графики, запишите рядом с формулой.(тест прилагается)
Если работа выполнена правильно, то вы прочтете имя ученого математика, который содействовал развитию аналитической теории тригонометрических функций.
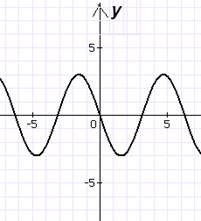
Л Э
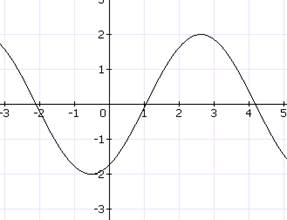
Е Р
Й
Самостоятельная работа на 5 вариантов по карточкам.
Вариант 1.
1.Постройте график функции
y=3sin(x-![]() ).
).
По графику найдите:
А) область значений функции;
Б) промежутки возрастания, убывания функции.
Вариант 2.
1.Постройте график функции y= 2cosx+1.
По графику найдите:
А) область значений функции;
Б) промежутки возрастания, убывания функции.
Вариант 3.
1.Постройте график функции
y= - 0,5cos(x+![]() ).
).
По графику найдите:
А) область значений функции;
Б) промежутки возрастания, убывания функции.
Вариант 4.
1.Постройте график функции y=-2,5sinx – 0,5
По графику найдите:
А) область значений функции;
Б) промежутки возрастания, убывания функции.
Вариант 5.
1.Постройте график функции
y= - 0,5sin(x-![]() ).
).
По графику найдите:
А) область значений функции;
Б) промежутки возрастания, убывания функции.
· Вопрос 1.
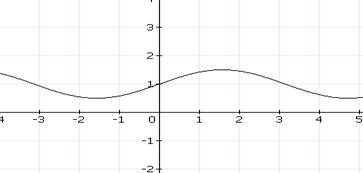
Задать формулой функцию, график которой изображен на рисунке:
Ваш ответ:
![]()
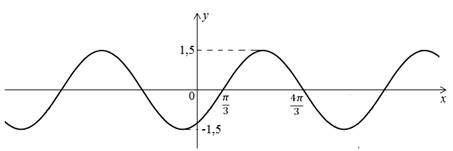
· Вопрос 2.
Задать формулой функцию, график которой изображен на рисунке:
Ваш ответ:
![]()
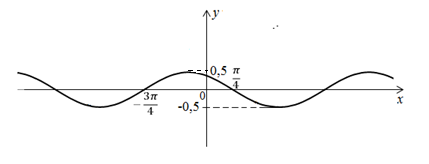
· Вопрос 3.
Найти наименьшее значение
функции ![]() на
промежутке
на
промежутке ![]()
Ваш ответ:
-3
· Вопрос 4.
Указать формулу функции, график
которой получают из графика функции ![]() сжатием
его к оси х в три раза.
сжатием
его к оси х в три раза.
Ваш ответ:
![]()
· Вопрос 5.
Найти наибольшее значение
функции ![]() на
промежутке
на
промежутке ![]()
Ваш ответ:
![]()
· Вопрос 6.
Областью значений функции y=f(x) является промежуток [-2; 2]. Найти область значений функции y=4f(x)-3.
Ваш ответ:
[-11; 5]
Оценочный лист ученика(цы) 10 м класса
|
Построение графиков функции |
Выполнение теста тренажера |
Построение графиков функции с помощью ME |
Средняя оценка |
Итоговая оценка |
|
|
|
|
|
|
|
|
|
|
|
|
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.