ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ И МОЛОДЁЖНОЙ ПОЛИТИКИ ХМАО-ЮГРЫ

БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ

  ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ХМАО-ЮГРЫ

НЯГАНСКИЙ ТЕХНОЛОГИЧЕСКИЙ КОЛЛЕДЖ

 

 

 

 

 

 

 

 

 

МАТЕМАТИКА

Методические указания

для преподавателей математики и студентов

средних специальных учебных заведений

по теме:

«Основы теории вероятностей и математической статистики»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Составитель

П.М. Ажулаева

 

 

 

 

 

Нягань, 2018

Согласовано: на заседании     ПЦК «Информатика и вычислительная техника»   Протокол №______    от «______» ____________20____г. Председатель ПЦК ________________     А. К. Гайнетдинова

Утверждаю: Зам. директора по УМР БУ «Няганский технологический  колледж»                                                                                                                                             __________________ М.Г. Штепина

 

Разработчик: Преподаватель БУ «Няганский технологический  колледж»

_________________ П.М.Ажулаева

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Аннотация

В данной работе    рассмотрены темы раздела «Основы теории вероятностей и математической  статистики» по дисциплине «Математика» из рабочей программы учебной дисциплины «Математика».

В предлагаемой    разработке рассматриваются основные понятия теории по темам данного раздела рассматриваемых на лекциях, практических занятиях, самостоятельных работах. Данная работа может быть использована преподавателями и студентами всех специальностей, как первых курсов, так и вторых курсов.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 Содержание

 

Введение	5
Основные понятия	6
1.Вероятность. Теоремы сложения и умножения вероятностей	7
1.1.Основные понятия комбинаторики	7
1.2.Решение комбинаторных задач	10
1.3.Понятие о случайном событии. Виды событий. Вероятность события	12
1.4.Классическое определение вероятности	12
1.5.Теорема сложения вероятностей несовместных событий	14
1.6.Теорема умножения вероятностей несовместных событий	15
2. Случайная величина, её функция распределения	17
2.1.Случайная величина, способы её задания	17
2.2.Дитскретная и непрерывная случайные величины	17
2.3.Закон распределения случайной величины	18
2.4.Биномиальное распределение	20
3.Математическое ожидание и дисперсия случайной величины	22
3.1.Математическое ожидание дискретной случайной величины	22
3.2.Среднее квадратичное отклонение и дисперсия случайной величины	23
4. Практические задания для самоконтроля	25
5. Ответы	28
Список литературы	29
Приложение	30

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВВЕДЕНИЕ

 

 

Основная цель изучения математики в средних специальных учебных заведениях состоит в том, чтобы дать студентам набор математических знаний и навыков, необходимых для изучения других программных дисциплин, использующих в той или иной мере математику, для умения выполнять практические расчеты, для формирования и развития логического мышления.

В данной работе последовательно вводятся все базовые понятия раздела математики: «Основы теории вероятностей и математической статистики», предусмотренные программой и ФГОС, формулируются основные теоремы, большая часть которых не доказывается. Рассматриваются  основные задачи и методы их решения и технологии применения этих методов к решению практических задач. Изложение сопровождается подробными комментариями и   примерами.

Методические указания могут быть использованы для первичного ознакомления с изучаемым материалом, при конспектировании лекций, для подготовки к практическим занятиям, для закрепления полученных знаний, умений и навыков. Кроме того, пособие будет полезно и студентам- старшекурсникам как справочное пособие, позволяющее быстро восстановить в памяти то, что было изучено ранее.

В конце работы приведены примеры и задания, которые студенты могут выполнять в режиме самоконтроля.

Методические указания предназначены для преподавателей и студентов любой  формы обучения.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ОСНОВНЫЕ ПОНЯТИЯ

Многие, столкнувшись с понятием «теория вероятностей», «математическая статистика» пугаются, думая, что это нечто непосильное, очень сложное. Но всё на самом деле не так трагично. Мы рассмотрим основное понятие теории вероятностей, комбинаторики, математической статистики, изучим основные формулы, рассмотрим задачи и их решения.

Что же изучает такой раздел математики, как теория вероятностей, математическая статистика и комбинаторика. Впервые этим вопросом заинтересовались ученые ещё в 18 веке, когда изучали азартные игры.

Основное понятие теории вероятностей – событие. Это любой факт, который констатируется опытом или наблюдением. Но что же такое опыт? Ещё одно основное понятие теории вероятностей. Оно означает, что этот состав обстоятельств создан не случайно, а с определённой целью.

Теория вероятностей изучает объективные закономерности массовых случайных событий. Она является теоретической базой для математической статистики. Математическая статистика  занимается разработкой методов сбора, описания и обработки результатов наблюдений. Путем наблюдений (испытаний, экспериментов), т.е. опыта в широком смысле слова, происходит познание явлений действительного мира.

В своей практической деятельности мы часто встречаемся с явлениями, исход которых невозможно предсказать, результат которых зависит от случая.

Случайное явление можно охарактеризовать отношением числа его наступлений к числу испытаний, в каждом из которых при одинаковых условиях всех испытаний оно могло наступить или не наступить.

Теория вероятностей есть раздел математики, в котором изучаются случайные явления (события) и выявляются закономерности при массовом их повторении.

Математическая статистика - это раздел математики, который имеет своим предметом изучения методов: сбора, систематизации, обработки и использования статистических данных для получения научно обоснованных выводов и принятия решений.

При этом под статистическими данными понимается совокупность чисел, которые представляют количественные характеристики интересующих нас признаков изучаемых объектов. Статистические данные получаются в результате специально поставленных опытов, наблюдений.

Статистические данные по своей сущности зависят от многих случайных факторов, поэтому математическая статистика тесно связана с теорией вероятностей, которая является ее теоретической основой.

 

 

 

 

 

I. ВЕРОЯТНОСТЬ. ТЕОРЕМЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ

1.1. Основные понятия комбинаторики

Прикладной аспект теории связан с необходимостью подсчитывать количества различных объектов, учитывая или не учитывая их порядок. Например, метеорологу для составления прогноза погоды на 10 января этого года приходится анализировать не только характер последних данных о природных явлениях, но и варианты характеристик погоды на 10 января в предыдущие годы.

Раздел математики, занимающийся подсчётами количества различных комбинаций между объектами, называется комбинаторикой.

Группы, составленные из каких–либо элементов,  называются соединениями. Различают три основных вида соединений: размещения, перестановки и сочетания.

Задачи,  в которых производится подсчет возможных различных соединений, составленных из конечного числа элементов по некоторому правилу, называются комбинаторными. Раздел математики, занимающийся  их решением, называется комбинаторикой.

В разделе математики, который называется комбинаторикой, решаются некоторые задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств. Например, если взять 10 различных цифр 0, 1, 2, 3,… , 9 и составлять из них комбинации, то будем получать различные числа, например 143, 431, 5671, 1207, 43 и т.п.

Мы видим, что некоторые из таких комбинаций отличаются только порядком цифр (например, 143 и 431), другие - входящими в них цифрами (например, 5671 и 1207), третьи различаются и числом цифр (например, 143 и 43).

Таким образом, полученные комбинации удовлетворяют различным условиям. В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания.

Предварительно познакомимся с понятием факториала.

Произведение всех натуральных чисел от 1 до n включительно называют

n - Факториалом и пишут

Пример 1. Вычислить: a) 3!; б) 7! – 5!; в) .

Решение. а)  .

б) Так как  , то можно вынести за скобки  5!.

Тогда получим

 

 

в)

 

 

1.     Перестановки

Комбинация из n элементов, которые отличаются друг от друга только порядком элементов, называются перестановками.

Перестановки обозначаются символом Р_n, где n - число элементов, входящих в каждую перестановку. (Р - первая буква французского слова permutation- перестановка).

Число перестановок можно вычислить по формуле

 или с помощью факториала:

Запомним, что 0!=1 и 1!=1.

Пример 2. Сколькими способами можно расставлять на одной полке шесть различных книг?

Решение. Искомое число способов равно числу перестановок из 6 элементов, т.е.

.

    Примеры

1.На собрании пожелали выступить 4 человека. Сколькими способами можно расположить список докладчиков?

Решение: .

2.Сколько шестизначных чисел, кратных пяти, можно составить из цифр1,2,3,4,5,6 при условии, что в числе цифры не повторяются?

Решение: цифра 5 должна стоять на последнем месте (кратные пяти). Остальные пять цифр могут стоять на оставшихся пяти местах в любом порядке, .

 

2.     Размещения

Размещениями из n элементов по m в каждом называются такие соединения, которые отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком из расположения.

Размещения обозначаются символом  , где n- число всех имеющихся элементов, m - число элементов в каждой комбинации. (А-первая буква французского слова arrangement, что означает «размещение, приведение в порядок»).

При этом полагают, что mn.

Число размещений можно вычислить по формуле

         (1)

Запишем эту формулу в факториальной форме:

     (2)

Пример 3. Сколько вариантов распределения трех путевок в санатории различного профиля можно составить для пяти претендентов?

Решение. Искомое число вариантов равно числу размещений из 5 элементов по 3 элемента, т.е.

.

Примеры

1.     В группе 20 студентов. Сколькими способами могут быть выбраны староста  и его заместитель при условии, что каждый студент может быть выбран только на одну должность?

Решение:  (способов).

2.     Группа изучает 7 учебных дисциплин. Сколькими способами можно составить расписание занятий на понедельник, если в этот день должно быть 3 различных пары?

Решение:

3.     Сколько различных двузначных чисел можно образовать из цифр 1,2,3,4?  

Решение: .

Итого 12+4=16.

4.     Сколько различных двузначных чисел можно образовать из цифр 1,2,3,4 при условии, что в каждом числе нет одинаковых цифр?

Решение:   .

5.     В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить 4 фотографии. Сколькими способами это можно сделать, если ни одна страница газеты не должна содержать более одной фотографии?

Решение:

 

3.     Сочетания

Сочетаниями называются все возможные комбинации из n элементов по m, которые отличаются друг от друга, по крайней мере, хотя бы одним элементом (здесь m и n-натуральные числа, причем m  n).

Число сочетаний из n элементов по m обозначаются  (С-первая буква французского слова combination- сочетание).

В общем случае число из n элементов по m равно числу размещений из n элементов по m, деленному на число перестановок из n элементов:

                     

Используя для чисел размещений и перестановок факториальные формулы, получим:

 

Пример 4. В бригаде из 25 человек нужно выделить четырех для работы на определенном участке. Сколькими способами это можно сделать?

Решение. Так как порядок выбранных четырех человек не имеет значения, то это можно сделать  способами.

Находим по первой формуле

Кроме того, при решении задач используются следующие формулы, выражающие основные свойства сочетаний:

  

(по определению полагают  и );

.

Примеры

1.     Группу студентов колледжа должны экзаменовать по математике комиссия из двух преподавателей. Сколькими способами может быть составлена такая комиссия, если в колледже пять преподавателей математики?

Решение:

2.     Сколько матчей будет сыграно в футбольном чемпионате с участием 16 команд, если каждые две команды встречаются между собой один раз?

Решение: .

 

1.2. Решение комбинаторных задач

Задача 1. На факультете изучается 16 предметов. На понедельник нужно в расписание поставить 3 предмета. Сколькими способами можно это сделать?

Решение. Способов постановки в расписание трех предметов из 16 столько, сколько можно составить размещений из 16 элементов по 3.

.

Задача 2. Из 15 объектов нужно отобрать 10 объектов. Сколькими способами это можно сделать?

Решение.

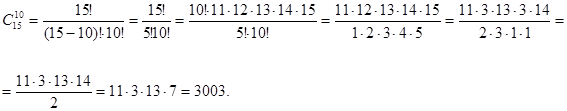
Задача 3. В соревнованиях участвовало четыре команды. Сколько вариантов распределения мест между ними возможно?

Решение.

.

Задача 4. Сколькими способами можно составить дозор из трех солдат и одного офицера, если имеется 80 солдат и 3 офицера?

Решение. Солдат в дозор можно выбрать

способами, а офицеров  способами. Так как с каждой командой из солдат может пойти любой офицер, то всего имеется  способов.

Задача 5. Найти , если известно, что .

Решение.

Так как  ,  то получим

,

,

,

, .

По определению сочетания следует, что , . Т.о. .

                                                                                                         Ответ: 9

Упражнения

1.     Найти число размещений:

 1) из 10 элементов по 4;

 2) из  (n + 4)  элементов  по (n – 2).

2.     Составить все возможные перестановки из элементов:

1) 1; 2) 5;6; 3) a, b, c.

3.     Вычислить значения выражений:

1)5! + 6! 2)

4.       Решить уравнение

 

Ответы и решения

1.     1) 5040;

2) (n+4)(n+3)…(n+4  –(n–2)+1) = (n+4)(n+3)….

2. 

n(n-1)(n-2) …(n-4) = 30(n-2)(n-3)(n-4)(n-5)

n(n-1) = 30(n-5),

n = 6, n = 25

4.  840; 2652; 105; 16

Дополнительно

Вычислите: 1)

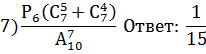
1.3. Понятие о случайном событии. Виды событий. Вероятность события

 Всякое действие, явление, наблюдение с несколькими различными исходами, реализуемое при данном комплексе условий, будем называть испытанием.

 Результат этого действия или наблюдения называется событием.

 Если событие при заданных условиях может произойти или не произойти, то оно называется случайным. В том случае, когда событие должно непременно произойти, его называют достоверным, а в том случае, когда оно заведомо не может произойти,- невозможным.

События называются несовместными, если каждый раз возможно появление только одного из них.

События называются совместными, если в данных условиях появление одного из этих событий не исключает появление другого при том же испытании.

События называются противоположными, если в условиях испытания они, являясь единственными его исходами, несовместны.

События принято обозначать заглавными буквами латинского алфавита: А, В, С, Д, … .

Полной системой событий А₁, А₂, А₃, … , А_n называется совокупность несовместных событий, наступление хотя бы одного из которых обязательно при данном испытании.

Если полная система состоит из двух несовместных событий, то такие события называются противоположными и обозначаются А и .

Пример. В коробке находится 30 пронумерованных шаров. Установить, какие из следующих событий являются невозможными, достоверными, противоположными:

достали пронумерованный шар (А);

достали шар с четным номером (В);

достали шар с нечетным номером (С);

достали шар без номера (Д).

Какие из них образуют полную группу?

Решение. А - достоверное событие; Д - невозможное событие;

В и С - противоположные события.

Полную группу событий составляют  А и Д, В и С.

Вероятность события, рассматривается как мера объективной возможности появления случайного события.

 

1.4. Классическое определение вероятности эгс -16

Число, являющееся выражением меры объективной возможности наступления события, называется вероятностью этого события и обозначается символом Р(А).

Определение. Вероятностью события А называется отношение числа исходов m, благоприятствующих наступлению данного события А, к числу n всех исходов (несовместных, единственно возможных и равновозможных), т.е.

.

Следовательно, для нахождения вероятности события необходимо, рассмотрев различные исходы испытания, подсчитать все возможные несовместные исходы n, выбрать число интересующих нас исходов m и вычислить отношение m к n.

Из этого определения вытекают следующие свойства:

1.     Вероятность любого испытания есть неотрицательное число, не превосходящее единицы.

Действительно, число m искомых событий заключено в пределах . Разделив обе части на n, получим

.

2. Вероятность достоверного события равна единице, т.к. .

3. Вероятность невозможного события равна нулю, поскольку .

Задача 1. В лотерее из 1000 билетов имеются 200 выигрышных. Вынимают наугад один билет. Чему равна вероятность того, что этот билет выигрышный?

Решение. Общее число различных исходов есть n=1000. Число исходов, благоприятствующих получению выигрыша, составляет m=200. Согласно формуле, получим

                                       .         

Задача 2. В партии из 18 деталей находятся 4 бракованных. Наугад выбирают 5 деталей. Найти вероятность того, что из этих 5 деталей две окажутся бракованными.

Решение. Число всех равновозможных независимых исходов n равно числу сочетаний из 18 по 5 т.е.

 

 

Подсчитаем число m, благоприятствующих событию А. Среди 5 взятых наугад деталей должно быть 3 качественных и 2 бракованных. Число способов выборки двух бракованных деталей из 4 имеющихся бракованных равно числу сочетаний из 4 по 2:

.

Число способов выборки трех качественных деталей из 14 имеющихся качественных равно

.

Любая группа качественных деталей может комбинироваться с любой группой бракованных деталей, поэтому общее число комбинаций m составляет

.

Искомая вероятность события А равна отношению числа исходов m, благоприятствующих этому событию, к числу n всех равновозможных независимых исходов:

.

 

 1.5. Теорема сложения вероятностей несовместных событий

Суммой конечного числа событий называется событие, состоящее в наступлении хотя бы одного из них.

Сумму двух событий обозначают символом А+В, а сумму n событий символом А₁+А₂+ … +А_n.

Теорема сложения вероятностей.

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

 или

Следствие 1. Если событие А₁, А₂, … ,А_n образуют полную систему, то сумма вероятностей этих событий равна единице.

.

Следствие 2. Сумма вероятностей противоположных событий  и  равна единице.

.

Задача 1. Имеется 100 лотерейных билетов. Известно, что на 5 билетов попадает выигрыш по 20000 руб., на 10 - по 15000 руб., на 15 - по 10000 руб., на 25 - по 2000 руб. и на остальные ничего. Найти вероятность того, что на купленный билет будет получен выигрыш не менее 10000 руб.

Решение. Пусть А, В, и С- события, состоящие в том, что на купленный билет падает выигрыш, равный соответственно 20000, 15000 и 10000 руб. так как события А, В и С несовместны, то

.

Задача 2. На заочное отделение техникума поступают контрольные работы по математике из городов А, В и С. Вероятность поступления контрольной работы из города А равна 0,6, из города В - 0,1. Найти вероятность того, что очередная контрольная работа поступит из города С.

Решение. События «контрольная работа поступила из города А», «контрольная работа поступила из города В» и «контрольная работа поступила из города С» образуют полную систему, поэтому сумма их вероятностей равна единице:

, т.е. .

Задача 3. Вероятность того, что день будет ясным, . Найти вероятность  того, что день будет облачным.

Решение. События «день ясный» и «день облачный» противоположные, поэтому

, т.е .

 

1.6. Теорема умножения вероятностей независимых событий

При совместном рассмотрении двух случайных событий А и В возникает вопрос:

Как связаны события А и В друг с другом, как наступление одного из них влияет на возможность наступления другого?

Простейшим примером связи между двумя событиями служит причинная связь, когда наступление одного из событий обязательно приводит к наступлению другого, или наоборот, когда наступление одного исключает возможность наступления другого.

Для характеристики зависимости одних событий от других вводится понятие условной вероятности.

Определение. Пусть А и В - два случайных события одного и того же испытания. Тогда условной вероятностью события А или вероятностью события А при условии, что наступило событие В, называется число .

Обозначив условную вероятность , получим формулу

, .

Задача 1. Вычислить вероятность того, что в семье, где есть один ребенок- мальчик, родится второй мальчик.

Решение. Пусть событие А состоит в том, что в семье два мальчика, а событие В - что один мальчик.

Рассмотрим все возможные исходы: мальчик и мальчик; мальчик и девочка; девочка и мальчик; девочка и девочка.

Тогда ,  и по формуле находим

.

Событие А называется независимым от события В, если наступление события В не оказывает никакого влияния на вероятность наступления события А.

Теорема умножения вероятностей

Вероятность одновременного появления двух независимых событий равна произведению вероятностей этих событий:

.

Вероятность появления нескольких событий, независимых в совокупности, вычисляется по формуле

.

Задача 2. В первой урне находится 6 черных и 4 белых шара, во второй- 5 черных и 7 белых шаров. Из каждой урны извлекают по одному шару. Какова вероятность того, что оба шара окажутся белыми.

Решение. Пусть  - из первой урны извлечен белый шар; - из второй урны извлечен белый шар. Очевидно, что события   и  независимы.

Так как , , то по формуле  находим

.

Задача 3. Прибор состоит из двух элементов, работающих независимо. Вероятность выхода из строя первого элемента равна 0,2; вероятность выхода из строя второго элемента равна 0,3. Найти вероятность того, что: а) оба элемента выйдут из строя; б) оба элемента будут работать.

Решение. Пусть событие А- выход из строя первого элемента, событие В- выход их строя второго элемента. Эти события независимы (по условию).

а) Одновременное появление А и В есть событие АВ. Следовательно,

.

б) Если работает первый элемент, то имеет место событие  (противоположное событию А- выходу этого элемента из строя); если работает второй элемент- событие В. Найдем вероятности событий  и :

;

.

Тогда событие, состоящее в том, что будут работать оба элемента, есть  и, значит,

.

 

 

 

 

 

 

 

 

 

 

 

 

 

II. СЛУЧАЙНАЯ ВЕЛИЧИНА, ЕЕ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ

2.1. Случайная величина, способы ее задания

Случайной называется величина, которая в результате испытания может принять то или иное числовое значение, причем заранее неизвестно, какое именно.

Если для какой - либо величины ее измерение повторять многократно в практически одинаковых условиях, то обнаружится, что всякий раз получаются несколько отличные друг от друга результаты. Это складывается влияние причин двух видов: 1) основных, определяющих главное значение результата; 2) второстепенных, обуславливающих их расхождение.

При совместном действии этих причин понятия необходимости и случайности оказываются тесно связанными между собой, но необходимое преобладает над случайным.

Таким образом, возможные значения случайных величин принадлежат некоторым числовым множествам.

Случайным является то, что на этих множествах величины могут принять любое значение, но какое именно, заранее сказать нельзя.

Случайная величина связана со случайным событием.

Если случайное событие - качественная характеристика испытаний, то случайная величина - его количественная характеристика.

Случайные величины обозначают заглавными латинскими буквами  а их значение – прописными- .

Вероятность того, что случайная величина  примет значение  обозначают:

 и т.д.

Случайные величины задают законами распределения.

Закон распределения случайной величины - это соответствие, установленное между возможными значениями случайной величины и их вероятностями.

Законы распределения могут быть заданы тремя способами: табличным, графическим, аналитическим. Способ задания зависит от типа случайной величины.

Различают два основных типа случайных величин: дискретные и непрерывно распределенные случайные величины.

 

2.2. Дискретная и непрерывная случайные величины

 Если значения, которые может принимать данная случайная величина , образует дискретный (конечный или бесконечный) ряд чисел  то и сама случайная величина  называется дискретной.

Если же значения, которые может принимать данная случайная величина ,  заполняют конечный или бесконечный промежуток (а, в) числовой оси Ох, то случайная величина называется непрерывной.

Каждому значению случайной величины дискретного типа  отвечает определенная вероятность ; каждому промежутку (а, в) из области значений случайной величины непрерывного типа также отвечает определенная вероятность того, что значение, принятое случайной величиной, попадает в этот промежуток.

 

2.3. Закон распределения случайной величины

Соотношение, устанавливающее тем или иным способом связь между возможными значениями случайной величины и их вероятностями, называется законом распределения случайной величины.

Закон распределения дискретной случайной величины обычно задается рядом распределения:

				…
				…

 

При этом , р₁+р₂+…+р_n=1, где суммирование распространяется на все (конечное или бесконечное) множество возможных значений данной случайной величины .

Закон распределения непрерывной случайной величины удобно задавать с помощью функции плотности вероятности .

Вероятность того, что значение, принятое случайной величиной , попадет в промежуток (а, в), определяется равенством 

.

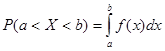График функции называется кривой распределения.

Геометрически вероятность попадания случайной величины в промежуток (а,b) равна площади соответствующей криволинейной трапеции, ограниченной кривой распределения, осью Ох и прямыми х=а, х=b.

 

Задача1. Даны вероятности значений случайной величины : значение 10 имеет вероятность 0,3; значение 2 – вероятность 0,4; значение 8 – вероятность 0,1; значение 4 – вероятность 0,2.

Построить ряд распределения случайной величины .

 

Решение. Расположив значения случайной величины в возрастающем порядке, получим ряд распределения:

	2	4	8	10
	0,4	0,2	0,1	0,3

 

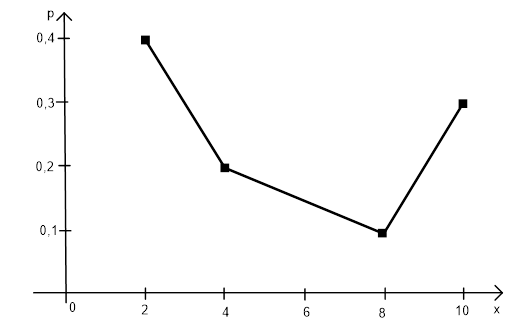
Возьмем на плоскости хОр точки (2; 0,4), (4; 0,2), (8; 0,1) и (10; 0,3). Соединив последовательные точки прямолинейными отрезками, получим многоугольник (или полигон) распределения случайной величины

	х

 

Задача 2. Разыгрываются две вещи стоимостью по 5000 руб. и одна вещь стоимостью 30000 руб. Составить закон распределения выигрышей для человека, купившего один билет из 50.

Решение. Искомая случайная величина  представляет собой выигрыш и может принимать три значения: 0, 5000 и 30000 руб. Первому результату благоприятствует 47 случаев, второму результату - два случая и третьему – один случай. Найдем их вероятности:

;     ;     .

Закон распределения случайной величины имеет вид:

 

	0	5000	30000
	0,94	0,04	0,02

 

В качестве проверки найдем

.

Задача 3. Случайная величина подчинена закону распределения с плотностью , причем

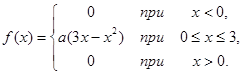
Требуется: 1) Найти коэффициент a; 2) построить график распределения плотности ; 3) найти вероятность попадания в промежуток (1; 2).

Решение. 1) Так как все значения данной случайной величины заключены на отрезке [0; 3], то

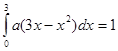, откуда

, или

, т.е. .

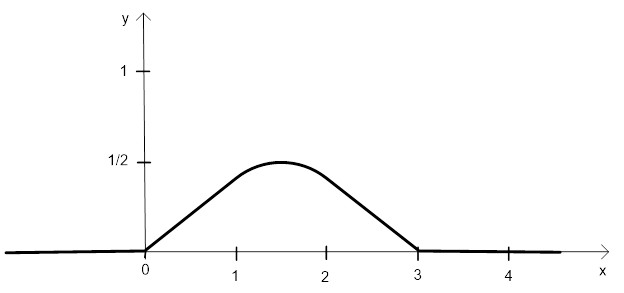
2) Графиком функции в интервале [0; 3] является парабола , а вне этого интервала графиком служит сама ось абсцисс.

 

3) Вероятность попадания случайной величины в промежуток (1; 2) найдется из равенства

.

 

2.4. Биномиальное распределение

Пусть производится определенное число n независимых опытов, причем в каждом из них с одной и той же вероятностью может наступить некоторое событие Р. Рассмотрим случайную величину X, представляющую собой x_i - число наступлений событий A в n опытах. Закон ее распределения имеет вид

Значения	0	1	2	…	n
Вероятности

 

Где , вычисляется по формуле Бернулли.

Закон распределения, который характеризуется такой таблицей, называется биноминальным.

Задача. Монету подбрасывают 5 раз. Составить закон распределения случайной величины - числа выпадения герба.

Решение. Возможны следующие значения случайной величины: 0, 1, 2, 3, 4, 5. Зная, что вероятность выпадения герба в одном испытании равна , найдем вероятности значений случайной величины  по формуле Бернулли:

;

;

;

;

;

.

 

 

Закон распределения имеет вид

 

Значения	0	1	2	3	4	5
Вероятности

 

Сделаем проверку:

.

 

 

 

 

 

 

 

 

 

 

III. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ И ДИСПЕРСИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

3.1. Математическое ожидание дискретной случайной величины

Наиболее исчерпывающей характеристикой случайной величины является ее закон распределения вероятностей. Однако не всегда обязательно знать весь закон распределения. Иногда можно обойтись одним или несколькими числами, отражающими наиболее важные особенности закона распределения, например, числом, имеющим смысл «среднего значения» случайной величины, или же числом, показывающим средний размер отклонения случайной величины от своего среднего значения. Такого рода числа называются числовыми характеристиками случайной величины. Оперируя числовыми характеристиками, можно решать многие задачи, не пользуясь законом распределения.

Одна из самых важных числовых характеристик случайной величины есть математическое ожидание.

Если известна дискретная случайная величина , закон распределения которой имеет вид

 

Значения			…
Вероятности			…

 

то математическим ожиданием (или средним значением) дискретной величины  называется число

.

Таким образом, математическое ожидание дискретной случайной величины  равно сумме произведений возможных значений этой величины на их вероятности.

Пример 1. Найти математическое ожидание случайной величины , зная закон ее распределения

	-1	0	1	2	3
	0,2	0,1	0,25	0,15	0,3

Решение.

.

Свойства математического ожидания.

1.     Постоянный множитель можно выносить за знак математического ожидания:

2.     Математическое ожидание постоянной величины С равно самой этой величине:

3.     Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:

.

4.     Математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий этих величин:

.

3.2. Среднее квадратичное отклонение и дисперсия случайной величины.

Пример 2. Найдем математическое ожидание случайных величин  и , зная законы их распределения

1)

	-8	-4	-1	1	3	7

2)

	-2	-1	0	1	2	3

 

Решение:

,

.

a)

Получили любопытный результат: законы распределения величин и разные, а их математические ожидания одинаковы.

 

 

 

 

 

 

 

                                                             

б)

 

 

Из рисунка б видно, что значение величины более сосредоточены около математического ожидания , чем значения величины , которые разбросаны (рассеяны) относительно ее математического ожидания (рисунок а).

Основной числовой характеристикой степени рассеяния значений случайной величины  относительно ее математического ожидания является дисперсия, которая обозначается через .

Определение. Отклонением называется разность между случайной величиной и ее математическим ожиданием , т.е. .

Отклонение и его квадрат также являются случайными величинами.

Определение. Дисперсией дискретной случайной величины называется математическое ожидание квадрата ее отклонения:

.

Свойства дисперсии.

1.     Дисперсия постоянной величины С равна 0:

.

2.     Если - случайная величина, а С – постоянная, то

.

3.     Если  и - независимые случайные величины, то

.

Для вычисления дисперсий более удобной является формула

.

Пример 3. Дискретная случайная величина распределена по закону:

 

	-1	0	1	2
	0,2	0,1	0,3	0,4

 

Найти .

Решение. Сначала находим .

,

а затем .

.

По формуле  имеем

.

Средним квадратичным отклонением случайной величины называется корень квадратный из ее дисперсии:

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

IV. ПРАКТИЧЕСКИЕ ЗАДАНИЯ ДЛЯ САМОКОНТРОЛЯ

Комбинаторика

1.     Сколько различных пятизначных чисел можно составить из цифр 1, 3, 5, 7, 9 при условии, что ни одна цифра в числе не повторяется?

 

2.     Сколько существует вариантов распределения трех призовых мест, если в розыгрыше участвуют 7 команд?

 

3.     Сколькими способами можно выбрать двух студентов на конференцию, если в группе 33 человека?

 

4.     Решить уравнения

а) . б) .

5.     Сколько четырехзначных чисел, делящихся на 5, можно составить из цифр 0, 1, 2, 5, 7, если каждое число не должно содержать одинаковых цифр?

 

6.     Из группы в 15 человек должны быть выделены бригадир и 4 члена бригады. Сколькими способами это можно сделать?

 

7.     Буквы азбуки Морзе состоят из символов (точек и тире). Сколько букв можно изобразить, если потребовать, чтобы каждая буква содержала не более пяти символов?

 

8.     Сколькими способами можно составить четырехцветные ленты из семи лент различных цветов.

 

9.     Сколькими способами можно выбрать четырех лиц на четыре различные должности из девяти кандидатов?

 

10. Сколькими способами можно выбрать 3 из 6 открыток?

 

11. Перед выпуском группа учащихся в 30 человек обменялась фотокарточками. Сколько всего было роздано фотокарточек.

 

12. Сколькими способами можно рассадить 10 гостей по десяти местам за праздничным столом?

 

13. Сколько всего игр должны провести 20 футбольных команд в одно круговом  чемпионате?

 

14. Сколькими способами можно распределить 12 человек по бригадам, если в каждой бригаде по 6 человек?

 

 

 

Теория вероятностей

1.     В урне находиться 7 красных и 6 синих шаров. Из урны одновременно вынимают два шара. Какова вероятность того, что оба шара красные (событие А)?

 

2.     Девять различных книг расставлены наудачу на одной полке. Найти вероятность того, что четыре определенные книги окажутся поставленными рядом (событие С).

 

3.     Из 10 билетов выигрышными являются 2. Определить вероятность того, что среди взятых наудачу 5 билетов, один выигрышный.

 

4.     из колоды карт (52 карты) наудачу извлекают 3 карты. Найти вероятность того, что это тройка, семерка, туз.

 

5.     Ребенок играет с пятью буквами разрезной азбуки А, К, Р, Ш, Ы. Какова вероятность того, что при случайном расположении букв в ряд он получит слово «Крыша».

 

6.     В ящике находятся 6 белых и 4 красных шара. Наудачу берут два шара. Какова вероятность того, что они окажутся одного цвета?

 

7.     В первой урне находятся 6 черных и 4 белых шара, во второй – 5 черных и 7 белых шаров. Из каждой урны извлекают по одному шару. Какова вероятность того, что оба шара окажутся белыми?

 

 

Случайная величина, математическое ожидание и дисперсия случайной величины

1.     Составить закон распределения числа попаданий в цель при шести выстрелах, если вероятность попадания при одном выстреле равна 0,4.

 

2.     Вероятность того, что студент найдет в библиотеке нужную ему книгу, равна 0,3. Составить закон распределения числа библиотек, которые он посетит, если в городе четыре библиотеки.

 

3.     Охотник стреляет по дичи до первого попадания, но успевает делать не более четырех выстрелов. Найти дисперсию числа промахов, если вероятность попадания в цель при одном выстреле равна 0,7.

 

4.     Найти математическое ожидание и дисперсию случайной величины X, если закон ее распределения задан таблицей:

Найти М(Х) и D(Х)

Х	1	2	3	4
р	0,3	0,1	0,2	0,4

 

5.     На заводе работают четыре автоматические линии. Вероятность того, что в течении рабочей смены первая линия не потребует регулировки, равна 0,9, вторая – 0,8, третья – 0,75, четвертая – 0,7. найти математическое ожидание числа линий, которые в течение рабочей смены не потребуют регулировки.

6.     Найти дисперсию и математическое ожидание случайной величины Х, зная закон ее распределения:

 

Х	0	1	2	3	4
р	0,2	0,4	0,3	0,08	0,02

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

V. ОТВЕТЫ

 

Комбинаторика

1. . 2. . 3. . 4. а) , 5; б) . 5. . 6.. 7. . 8. . 9.. 10.. 11. . 12. . 13. 190. 14. 924.

 

Теория вероятностей

1.  2. 3.  4. 5. 6. 7.

 

Случайная величина, математическое ожидание и дисперсия случайной величины.

1.

0	1	2	3	4	5	6
0,046656	0,186624	0,311040	0,276480	0,138240	0,036864	0,004096

 

     2.

1	2	3	4
0,3	0,21	0,147	0,343

 

3.  4.  5. 6..

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

СПИСОК ЛИТЕРАТУРЫ

Основная:

1.     Богомолов Н.В. Практические занятия по математике. – М.: Высшая школа, 1990. –  495 с.

2.     Соловейчик И.Л. Сборник задач по математике для техникумов / И.Л.Соловейчик, В.Т. Лисичкин. – М.: Оникс 21 век, 2003. – 464 с.

3.     Валуцэ И.И. Математика для техникумов / И.И. Валуцэ, Г.Д. Дилигул. -  М.: Наука, 1989. – 575 с.

4.     Данко П.Е. Высшая математика в упражнениях и задачах. В двух частях. Часть II / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. –  М.: Высшая школа, 1986. – 415 с.

5.     Выгодский М.Я. Справочник по высшей математике. – М.: Наука, 1975. – 872 с.

Дополнительная:

6.     Григулецкий В.Г. Математика для студентов экономических специальностей. Часть 2 / В.Г. Григулецкий, И.В. Лукьянова, И.А. Петунина. –  Краснодар, 2002. – 348 с.

7.     Малыхин В.И.  Математика в экономике. – М.: Инфра-М, 1999. – 356 с.

8.     Гусак А.А. Высшая математика. В 2-х т., Т.2. –  учебное пособие для студентов вузов. –  М.: ТетраСистемс, 1988. – 448 с.

9.     Григулецкий В.Г. Высшая математика / В.Г. Григулецкий,  З.В. Ященко. – Краснодар, 1998.-186 с.

10.  Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 2000. – 400 с.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Приложение

При решении комбинаторных задач в первую очередь будем применять два важных правила: правило суммы и правило произведения.

Правило суммы

Обозначения: А и В – конечное множество, n(A), n(B) – число элементов множества А и В.

Если А и В не содержит общих элементов, то

Например, если в группе 13 юношей и 12 девушек, то преподаватель может вызвать к доске одного студента 12+13 =25 способами.

Если А и В  содержит общие элементы, то

 Пример. Сколько человек в группе занимается спортом, если 9 человек занимаются лыжами и плаванием, а 12 человек – плаванием и волейболом, причем в секцию по плаванию ходят 4 человека из группы.

Решение. Имеем: n(A)=9, n(B)= 12,

 

Правило суммы А, В и С.

Пример

Из 35 студентов, побывавших на каникулах в Москве, все, кроме двоих, делились впечатлениями. О посещении Большого театра с восторгом вспоминали 12 человек, Кремля – 14 , а 16  –  о концерте, по три студента запомнили посещение театра и Кремля, а также театра и концерта, а четверо   –  концерта и пребывания в Кремле. Сколько студентов сохранили воспоминания одновременно о театре, концерте и Кремле?

Решение: обозначим:

А – число студентов, вспоминающих о театре, n(A) =12;

B – о Кремле, n(B) = 14;

C – о концерте, n(С) = 16;

D – число студентов, побывавших в поездке.

 (35 – 2=33) – делились впечатлениями, обозначим через: х =

 =33=12+14+16 – 3 – 3 – 4 – x,

x=3.

ОТВЕТ: Всего три студента рассказывали о трёх культурных мероприятиях поездки.

Упражнение. В результате социологического опроса студентов факультета программирования о занятиях в свободное от занятий время выяснилось, что из 100 человек:

18 – любят читать книги;

24 – читают книги, но не ходят в театр;

7   – читают книги и посещают театр;

28 – читают книги;

47 – ходят на дискотеки;

9 – посещают театр и дискотеки;

13 – лежат на диване перед телевизором, занимаются только просмотром всех возможных каналов телевидения.

1.Сколько студентов любят ходить в театр?

2.Сколько студентов читают книги, посещают театр, но не дискотеки?

3.Сколько студентов посещают либо дискотеки, либо театр?

4.Сколько студентов, посещая дискотеки и театр, не любят читать книги?

5.Сколько студентов предпочитают только дискотеки?

6.Сколько студентов посещают либо дискотеки, либо театр, либо читают книги?

Правило произведения. Если элемент b можно выбрать k способами, а элемент с можно выбрать m способами, то пару (b, c) можно выбрать km способами.

Пример. В колледже есть три варианта занятий по интересам: творческие объединения (ТО), спортивные секции (СС) и научное студенческое общество (НСО). Каждое направление содержит по четыре вида коллективов: ТО – театральный, музыкальный, танцевальный и КВН; СС – лёгкая атлетика лыжи, спортивные игры и плавание; НСО – естественно – математическое, гуманитарное, техническое и информационное направление. Сколькими способами студенты могут разнообразить свой досуг в колледже после занятий, выбрав коллектив по интересам?

Решение. Так как надо учесть и три основных направления, и то, что в каждом из них по четыре коллектива, то  для подсчёта общего числа вариантов их нужно перемножить: n(A) = 3, n(B) = 4,

Частным случаем правила произведения является число размещений с повторениями  .

Пример. Сколькими способами из различных нечетных цифр можно составить различные трёхзначные числа? (

Пример. Сколькими способами могут взойти 3 зерна пшеницы, если посажено 7 зёрен?

Решение, так как порядок не важен, то

Перестановки с повторениями

Если имеются соединения с повторяющимися элементами, то формула уже неприменима, так как при переставлении одинаковых элементов соединение не изменится. Соединения, имеющие повторяющиеся элементы, называются перестановками с повторениями.

Пример

1.Сколькими способами можно расставить белые фигуры на первой линии шахматной доски?

Решение: на первой линии могут находиться король, ферзь, 2 ладь, 2 коня, 2 слона. Длина 8, состав(1,1,2,2,2). Тогда число перестановок с размещениями найдём по формуле: .

Решение задач, связанных с перебором  вариантов, требует анализа комбинаторных вычислений.

2.Сколько слов можно получить, переставляя буквы в слове математика?

Решение: слово имеет длину 10; состав (2;3;2;1;1;1), т. е.

«и» - 2 раза; «а» - 3 раза, «м» - 2 раза …

 

3.Сколько различных перестановок можно образовать из букв следующих слов: а) зебра; б) баран; в) водород; г) абракадабра.

Ответ: 120; 60; 420; 83160.

(

).

Упражнение. Составьте различные новые слова из букв слова: а) апельсин; б) норматив; в) стационар; г) ромашка; д) множества; е) ратификация.

Задачи подсчёта возможных комбинаций объектов, удовлетворяющих определённым условиям, часто встречаются в практической деятельности и получили название комбинаторных.

Многообразие таких задач не всегда удается описать с помощью математических формул. Однако для стандартных распространенных ситуаций способы подсчёта вариантов определены.

Пример

Разложить n различных деталей в m ящиков. Сколько вариантов таких размещений можно перебрать?

Решение: так как все n деталей могут поместиться и в один ящик, то на языке функции можно установить связь: между количеством n деталей и количеством ящиков m: n.

Такое часто встречающееся число подсчётов вариантов называют размещением с повторением и обозначают . Так как каждую из n деталей можно разместить в m ящиков, то необходимо n раз умножить число m, то есть .

Пример

Сколько различных двоичных чисел длиной 6 можно записать с помощью цифр 0 и 1?

Решение: размещаем две цифры 0 и 1 на 6 мест, то есть на каждом из шести мест (m=6) может быть одна из двух двоичных цифр. Всего таких вариантов будет  двоичных чисел: на каждом из шести мест по два варианта цифр.

Пример

1.Сколько проводится матчей в Чемпионате РФ по футболу в премьер – лиге (16 команд) за сезон?

Решение: поскольку один матч проводится между двумя командами, каждый матч состоит из двух элементов (одна команда играет дома, вторая на выезде), количество матчей вычисляется по формуле:

 .

2.     В больнице берутся десять историй болезней пациентов, которым понадобилось переливание крови за последний месяц, и устанавливается группа крови, которая была перелита каждому из них. Среди этих пациентов у четверых человек оказалась первая группа крови, у трёх – вторая, у двух – третья, у одного – четвертая группа крови. Какова вероятность того, что у выбранного наугад пациента окажется первая группа крови?

Решение: обозначим через А- событие, которое заключается в том, что у выбранного пациента окажется первая группа крови. Общее число исходов равно 10, исходов которые благоприятствуют нашему событию 4. Значит, Р(А) = 4/10= 0,4= 40% 91 группа крови).  Ответ:0,4

(Краткое оформление задачи):

 А – событие, что окажется 1 группа крови; m=4, n=10;P(A)=4/10=0,4

3.     На книжной полке находятся 2 книги по микробиологии, 3 книги по химии, 1 книга по математике. Чему равна вероятность того, что случайным образом будет извлечена книга по химии или математике?

Решение: А – событие, которое заключается в том, что наугад возьмут книгу по химии, через В – событие, которое заключается в том, что наугад возьмут книгу по математике.

Р(А)=3/6=1/2, Р(В)=1/6. По теореме сложения Р(АилиВ)=3/6+1/6=4/6=2/3. Ответ: 2/3

4.В коробке находится 15медицинских инструментов, среди которых 10 пинцетов. Лаборант случайным образом извлекает 3 инструмента. Найти вероятность того, что все они окажутся пинцетами.

Решение: А – событие, которое состоит в том, что все 3 извлечённых инструмента оказались пинцетами.

  (количество всех исходов)

 , Р(А)=m/n=120/455=24/91.

 

5.В бригаде из 20 рабочих выбирается бригадир, хозяйственник и общественный кассир. Сколько вариантов выбора имеется в распоряжении рабочих?

Решение: Здесь n = 20, k = 3.

Число вариантов выбора будет равно  = 20  19  18 = 6840.

6.В бригаде из 20 рабочих требуется выбрать троих для направления в командировку. Сколько существует вариантов выбора?

Решение. Последовательность выбора в данном случае не имеет значения. Комбинации: «Иван, Пётр, Николай» и «Пётр, Николай, Иван» по условию задачи являются не различными. Значит число вариантов выбора равно числу сочетаний из 20 объектов (рабочих) по 3:

  

7.На 6 карточках написаны цифры 2, 2, 3, 4, 4, 4. Сколько различных шестизначных чисел можно получить, располагая эти карточки последовательно?

Решение. Здесь n = 6, r = 3, при этом n₁ = 2, n₂ = 1, n₃ = 3. Перестановки с повторением. Следовательно, можно составить указанным в задаче способом 60 различных шестизначных чисел.

 

8.Найти х, если известно что

Решение:

[]

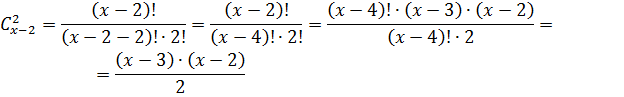
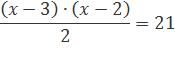
По условию сочетания  

Значит, х = 9

Ответ:9.

9.В партии из 18 деталей находятся 4 бракованных. Наугад выбирают 5 деталей. Найти вероятность того, что из этих 5 деталей две окажутся бракованными.

Решение. Число всех равновозможных независимых исходов n равно числу сочетаний из 18 по 5 т.е.

Подсчитаем число m, благоприятствующих событию А. Среди 5 взятых наугад деталей должно быть 3 качественных и 2 бракованных. Число способов выборки двух бракованных деталей из 4 имеющихся бракованных равно числу сочетаний из 4 по 2:

.

Число способов выборки трех качественных деталей из 14 имеющихся качественных равно

.

Любая группа качественных деталей может комбинироваться с любой группой бракованных деталей, поэтому общее число комбинаций m составляет     .

Искомая вероятность события А равна отношению числа исходов m, благоприятствующих этому событию, к числу n всех равновозможных независимых исходов:

.

10. Имеется 100 лотерейных билетов. Известно, что на 5 билетов попадает выигрыш по 20000 руб., на 10 - по 15000 руб., на 15 - по 10000 руб., на 25 - по 2000 руб. и на остальные ничего. Найти вероятность того, что на купленный билет будет получен выигрыш не менее 10000 руб.

Решение. Пусть А, В, и С- события, состоящие в том, что на купленный билет падает выигрыш, равный соответственно 20000, 15000 и 10000 руб., так как события А, В и С несовместны, то

.

11. На заочное отделение техникума поступают контрольные работы по математике из городов А, В и С. Вероятность поступления контрольной работы из города А равна 0,6, из города В - 0,1. Найти вероятность того, что очередная контрольная работа поступит из города С.

Решение. События "контрольная работа поступила из города А", "контрольная работа поступила из города В" и "контрольная работа поступила из города С" образуют полную систему, поэтому сумма их вероятностей равна единице: 0,6+,01+р=1, т.е. р = 1-0,7=0,3

12.Вероятность того, что день будет ясным, р=0,85. Найти вероятность  g  того, что день будет облачным.

Решение. События "день ясный" и "день облачный" противоположные, поэтому p+g=1, g=1-p=1-0?85=0?15.

Определение. Пусть А и В - два случайных события одного и того же испытания. Тогда условной вероятностью события А или вероятностью события А при условии, что наступило событие В, называется числo:

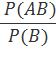
Обозначив условную вероятность  , получим формулу

 

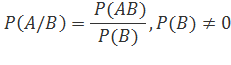
13.Вычислить вероятность того, что в семье, где есть один ребенок- мальчик, родится второй мальчик.

Решение. Пусть событие А состоит в том, что в семье два мальчика, а событие В - что один мальчик.

Рассмотрим все возможные исходы: мальчик и мальчик; мальчик и девочка; девочка и мальчик; девочка и девочка.

Тогда ,  и по формуле находим

.

Событие А называется независимым от события В, если наступление события В не оказывает никакого влияния на вероятность наступления события А.

Вероятность появления нескольких событий, независимых в совокупности, вычисляется по формуле

.

14.В первой урне находится 6 черных и 4 белых шара, во второй- 5 черных и 7 белых шаров. Из каждой урны извлекают по одному шару. Какова вероятность того, что оба шара окажутся белыми.

Решение. Пусть  - из первой урны извлечен белый шар; - из второй урны извлечен белый шар. Очевидно, что события  и  независимы.

Так как

 ,

, 

то по формуле

 

 находим

.

15.Прибор состоит из двух элементов, работающих независимо. Вероятность выхода из строя первого элемента равна 0,2; вероятность выхода из строя второго элемента равна 0,3. Найти вероятность того, что: а) оба элемента выйдут из строя; б) оба элемента будут работать.

Решение. Пусть событие А- выход из строя первого элемента, событие В- выход их строя второго элемента. Эти события независимы (по условию).

а) Одновременное появление А и В есть событие АВ. Следовательно,

.

б) Если работает первый элемент, то имеет место событие  (противоположное событию А- выходу этого элемента из строя); если работает второй элемент- событие В. Найдем вероятности событий  и :

;

.

Тогда событие, состоящее в том, что будут работать оба элемента, есть  и, значит,

.

16.Найти математическое ожидание числа очков,

выпадающих при подбрасывании игральной кости.

Решение

1	2	3	4	5	6
1/6	1/6	1/6	1/6	1/6	1/6

 

МХ=

Ответ: МХ=3,5.

  17.Случайные величины Х и У

имеют следующие законы распределения:             

х	-1	1
р	0,5	0,5

у	-2	2
р	0,5	0,5

 

 

 

 

 

Найти ДХ и ДУ.

Решение

МХ=(-1)0,5+10,5=0    МУ=(-2)0,5+20,5=0.

ДХ=10,5+10,5=1         ДУ=40,5+40,5=4.

18. Законы распределения случайных величин заданы таблицами.

 

-2	-1	1	2
1/6	1/3	1/3	1/6

                           И

-2	-1	1	2
1/4	1/4	1/4	1/4

Найти ДХ и ДУ.

Решение.

МХ= (-2)1/6+(-1)1/3+11/3+21/6=0,

МУ=(-2)1/4+(-1)1/4+11/4+21/4=0.

ДХ= 41/6+11/3+11/3+41/6=2,

ДУ=41/4+11/4+11/4+41/4=2,5.

 

Упражнения

1.Случайная величина Х имеет следующий закон распределения

1	2	3
0,3	0,2	0,5

Найти МХ и ДХ.                                         

2. Случайная величина Х распределена по закону

2	4	6	8	10
1/4	1/8	1/4	1/8	1/4

Найти МХ и ДХ.                                                  

  3. Может ли распределение какой – либо случайной величины задаваться таблицей:

а)

0	½	10
0,1	0,5	0,1	0,3

б)

1	2	3	4
0	0,4	0,2	0,3

 

4.Монета подбрасывается три раза. Рассматривается случайная величина Х – число проявлений герба.  Найти распределение случайной величины.

Решение

0	1	2	3
0,125	0,375	0,375	0,125

 

 5.  Случайная величина Х – квадрат числа очков, появившихся при подбрасывании игральной кости. Найти закон распределения.

Решение

1	4	9	16	25	36
1/6	1/6	1/6	1/6	1/6	1/6

 

6.  Найти МХ для случайной величины

1	4	9	16	25	36
1/6	1/6	1/6	1/6	1/6	1/6

                Ответ: 91/6

 

 

 

 

 

Комбинаторный анализ, или комбинаторика, одна из наиболее успешно применяемых в настоящее время областей математики.

Прикладной характер комбинаторики, теории вероятностей и математической статистики проявляется  при математической обработке результатов измерений, задачах экономики, страхового дела, массового обслуживания, в авиации, спутниковой навигации, в операционных исследованиях, эксплуатационно-технических  характеристиках, в статистике и др. В операционных исследованиях она применятся для составления расписаний, определения последовательности промышленных операций, распределения материала, маршрутов транспортных средств и так далее.

Существует версия, что теория вероятностей  как раздел математики возникла в 1654 г. из переписки между Б. Паскалем И П. Ферма по поводу одной задачи. Попытки с помощью чисел описать случайные явления, оценить шансы их появления, измерить возможные результаты будущих событий, конечно, предпринимались гораздо раньше.

Можно выделить два главных источника теории вероятностей – азартные игры и статистическая обработка результатов наблюдений.

Необходимо отметить ещё один важный для теории вероятностей источник статистических данных – отчеты страховых компаний.

 

Скачано с www.znanio.ru