

![]()
УДК 372.8:[512+517]
ББК 74.262.21
П64
Серия «МГУ — школе» основана в 1999 году
Потапов М. К.
П64 Алгебра и начала математического анализа. Методические рекомендации. 11 класс : пособие для учителей общеобразоват. организаций / М. К. Потапов, А. В. Шевкин. — М. : Просвещение, 2013. — 256 с. : ил. — (МГУ — школе).
В книге рассмотрены концепция и структура учебника «Алгебра и начала математического анализа. 11 класс» авторов С. М. Никольского, М. К. Потапова, Н. Н. Решетникова, А. В. Шевкина, приведены 4 варианта примерного тематического планирования, даны методические рекомендации по изучению курса и комментарии к решению наиболее трудных задач, а также рекомендации по использованию дидактических материалов к данному учебнику (авторы: М. К. Потапов, А. В. Шевкин).
Книга предназначена учителям, работающим по учебнику «Алгебра и начала математического анализа, 11» С. М. Никольского и др.
УДК 372.8:[512+517]
ББК 74.262.21
Учебное издание
Серия «МГУ — школе»
Потапов Михаил Константинович
Шевкин Александр Владимирович
Методические рекомендации
11 класс
Пособие для учителей общеобразовательных организаций
Зав. редакцией Т. А. Бурмистрова. Редактор Л. В. Кузнецова.
Младший редактор Е. А. Андреенкова. Художники П. С. Барбаринский, О. П. Богомолова. Компьютерная графика: Г. М. Дмитриев.
Техническое редактирование и компьютерная верстка Е. В. Саватеевой.
Корректоры М. А. Терентьева, Л. С. Александрова, А. К. Райхчин
Подписано в печать 27.08.13. Формат 60 × 901/16. Гарнитура Школьная. Печ. л. 16. Заказ №
Открытое акционерное общество «Издательство «Просвещение».
127521, Москва, 3-й проезд Марьиной рощи, 41.
© Издательство «Просвещение», 2013 © Художественное оформление.
Издательство «Просвещение», 2013
Все права защищены
Данная книга адресована учителям, работающим по учебнику «Алгебра и начала математического анализа, 11» (авторы: С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин). Этот учебник предназначен как для базового, так и для углубленного уровня и является частью учебно-методического комплекта для 10—11 классов. Он продолжает серию учебников «МГУ — школе» тех же авторов для 5—10 классов и нацелен на подготовку учащихся к поступлению в вуз и к обучению в вузе.
В учебно-методический комплект для 11 класса входят: 1. Алгебра и начала математического анализа. 11 класс. Учебник для общеобразоват. организаций: базовый и углубленный уровни (С. М. Н и к о л ь с к и й, М. К. П о т а п о в, Н. Н. Р е ш е т н и к о в, А. В. Ш е в к и н. — М.: Просвещение, 2008—2013).
2. Алгебра и начала математического анализа. Дидактические материалы. 11 класс (М. К. П о т а п о в, А. В. Ш е вк и н. — М.: Просвещение, 2007—2013).
3.
 |
4. Алгебра и начала математического анализа. Методические рекомендации. 11 класс. Пособие для учителей общеобразоват. организаций (М. К. П о т а п о в, А. В. Ш е вк и н. — М.: Просвещение, 2009—2013).
В данной книге рассмотрены концепция учебников алгебры и начал математического анализа для 10 и 11 классов, их структура, приведены 4 варианта примерного тематического планирования в 11 классе, даны методические рекомендации по изучению основных тем курса 11 класса и комментарии к решению некоторых трудных задач, а также рекомендации по использованию дидактических материалов. Практически для всех пунктов учебника в книге для учителя имеются рубрики: Решения и комментарии, Промежуточный контроль и Дополнения. В первой из них приведены условия многих задач и их решения или даны рекомендации, помогающие найти решение. При этом даны пояснения, помогающие обучению школьников. Во второй рубрике указаны номера самостоятельных и контрольных работ по дидактическим материалам. В третьей рубрике содержится обсуждение дополнительных вопросов, которые необходимо знать учителю, чтобы суметь дать обоснованные ответы на вопросы любознательных учащихся.
Здесь же приведены примеры задач из материалов ЕГЭ по рассматриваемой теме.
Отметим, что в книге для учителя разобрано большое число сложных задач, предлагавшихся на различных экзаменах.
Авторы выражают благодарность профессору МГУ им. М. В. Ломоносова, члену-корреспонденту РАН Ю. В. Нестеренко, доценту Самарского университета С. В. Дворянинову, учителям математики В. И. Гридасову (г. Воронеж), В. Е. Рочеву (г. Протвино) за ценные замечания и предложения по совершенствованию первых изданий учебников и дидактических материалов для 10 и 11 классов.
Авторами учебников разработана концепция многоуровневых учебников математики. Приведем основные положения этой концепции.
• Математика едина и может быть изложена в одном учебнике для работы по разным программам. Содержание учебника должно соответствовать научной точке зрения на изучаемые вопросы.
• Учебник должен сочетать в себе научность, стройность, экономность и логичность изложения материала с доступностью для учащихся его текстов.
• Учебник не должен ограничиваться интересами среднего ученика, он обязан удовлетворять интересам всех учащихся — от слабых до сильных.
• Учебник должен обеспечивать не только организацию дифференцированного обучения, но и любой уровень изучения материала.
• Способ изложения материала в учебнике, организация учебных текстов и системы упражнений должны обеспечивать достижение различных целей обучения при работе по разным программам.
Структура учебников алгебры и начал математического анализа для 10 и 11 классов и их методический аппарат отвечают основным положениям этой концепции. Авторы учебников серии «МГУ — школе» считают принципиально важным обучать школьников разных профилей по одним и тем же учебникам. Тогда учащиеся, заинтересованные в более глубоком изучении математики, могут углублять свои познания в математике самостоятельно или под руководством учителя, который получает реальную возможность для организации дифференцированного обучения и подготовки школьников к поступлению в вузы. Кроме того, переход с одной программы обучения на другую не будет вызывать трудностей ни у учащихся, ни у учителей.
Эти особенности учебников в полной мере отвечают требованиям ФГОС, нацеливающим учебный процесс на формирование у учащихся в процессе изучения курса математики общеучебных (надпредметных) умений при выполнении универсальных учебных действий, предусмотренных ФГОС.
Каждый из двух учебников обладает цельностью и завершенностью своего содержания, а вместе они составляют единый курс. Для каждого из учебников разработана авторская рабочая программа, соответствующая ФГОС.
В учебниках пункты без звездочки соответствуют базовому уровню. Эти же пункты, а также пункты со звездочкой и специально выделенный в пунктах без звездочки материал соответствуют ФГОС для обучения на углубленном уровне.
Каждая глава учебников для 10 и 11 классов завершается историческими сведениями. В конце каждого учебника помещен раздел «Задания для повторения», содержащий задания для повторения изученного материала в 10 и 11 классах и за предыдущие годы. В этот раздел включены задания школьных выпускных экзаменов и конкурсных экзаменов в различные вузы страны прошлых лет, а также задания Единого государственного экзамена (ЕГЭ). Это позволит учителю организовать целенаправленную подготовку учащихся к экзаменам.
На базовом уровне дополнительные материалы и сложные задачи, специально выделенные в учебниках, можно не рассматривать. Пропуск необязательных пунктов и задач не нарушает целостности курса. Снижается лишь уровень погружения учащихся в теоретические тонкости, уменьшается число доказываемых фактов, технически или идейно сложных задач. Учебники позволяют заинтересованному ученику, не обучающемуся в профильном классе, изучить необходимый ему материал по учебнику самостоятельно или под руководством учителя.
При углубленном обучении за счет дополнительных пунктов и отдельных задач со звездочкой содержание изучаемого материала расширяется и углубляется до объема, соответствующего требованиям ФГОС для углубленного обучения.
Учебник для 11 класса содержит все вопросы программы, связанные с исследованием функций и построением их графиков, с производной и первообразной, с решением уравнений, неравенств и их систем, с комплексными числами. Здесь углубляются знания учащихся по ранее изученным вопросам до уровня, необходимого для поступления в вузы, предъявляющие повышенные требования к математической подготовке школьников.
Учебник для 11 класса включает три главы: I. Функции. Производные. Интегралы. II. Уравнения. Неравенства. Системы.
III. Комплексные числа.
Материал первой и второй глав можно изучать параллельно с начала учебного года, так как содержание этих глав практически не связано друг с другом. В то же время техника решения сложных уравнений и неравенств требует продолжительного времени на ее овладение. Такой порядок изучения этих глав позволяет своевременно подготовиться к различным олимпиадам и конкурсам.
Первая глава учебника для 11 класса посвящена функциям, производным, интегралам. Сначала повторяется и систематизируется весь ранее изученный материал об элементарных функциях, рассматривается исследование функции элементарными средствами. Затем на интуитивной основе вводится понятие предела функции в точке и на бесконечности, изучаются свойства пределов, понятие непрерывности функции.
Изложение в учебнике материала, связанного с производной и первообразной, достаточно традиционно, а вот понятие определенного интеграла вводится не как разность значений первообразной в точках a и b, а с помощью интегральных сумм. Это дает учащимся возможность ощутить естественно-исторический путь формирования важных понятий курса математического анализа. До изучения формулы Ньютона — Лейбница определенные интегралы вычисляются на основе их геометрического смысла. В учебнике рассмотрены все приложения производных и интегралов (исследование функций и построение их графиков, задачи на максимум и минимум, вычисление площадей, ограниченных графиками функций), предусмотренные стандартом для обучения на базовом уровне.
В первой главе учебника для 11 класса также имеется материал, предусмотренный стандартом для обучения на профильном уровне. Это построение графиков функций, связанных с модулями, графиков сложных функций, обратные тригонометрические функции, непрерывность функции, имеющей производную, производная обратной функции, теоремы о среднем, выпуклость графика вверх (вниз), асимптоты, дробно-линейная функция, формула и ряд Тейлора, замена переменной при интегрировании и интегрирование по частям, применение определенных интегралов в геометрии и физике, дифференциальные уравнения.
Содержание второй главы учебника для 11 класса существенно отличает учебники серии «МГУ — школе» от аналогичных учебников. Впервые в школьной практике учащимся столь подробно излагается материал, связанный с решением сложных уравнений и неравенств, которые в учебнике классифицируются не по «внешнему виду» (логарифмические, тригонометрические, иррациональные и т. п.), а по способам их решения. Авторы считают это принципиальным, так как большинство уравнений и неравенств, предлагаемых на экзаменах, трудно отнести к какому-то одному виду. Чаще всего они смешанные, там присутствуют и тригонометрия, и логарифмы, и иррациональность и т. д. Поэтому так важно знать общие способы решения уравнений (неравенств), т. е. знать, что происходит с уравнением (неравенством) при возведении в степень, при применении некоторых формул и т. д. Так как все простейшие уравнения (неравенства) изучены в предыдущих классах, то теперь можно решать любые уравнения (неравенства).
Если при решении уравнения применяется преобразование, приводящее к неравносильному уравнению, то возможны три способа оформления решения:
1) переход к уравнению-следствию;
2) переход к системе, равносильной исходному уравнению;
3) переход к уравнению, равносильному исходному на некотором множестве.
Все эти способы изучаются поэтапно.
Сначала рассматриваются такие уравнения, для которых уравнение-следствие имеет корни, легко проверяемые подстановкой в исходное уравнение. При этом рассматриваются не только традиционные иррациональные уравнения, но и большой класс уравнений, содержащих логарифмы, корни, тригонометрические функции. Это первый этап освоения умения решать сложные уравнения. На нем, возможно, должна остановиться бо€льшая часть учащихся, которые не планируют сдавать вступительный экзамен в вуз с повышенными требованиями по математике.
На втором этапе осуществляется переход от исходного уравнения к равносильной ему системе. Этот способ решения уравнений особенно важен для учащихся, которые планируют сдавать экзамен в вуз с повышенными требованиями к математической подготовке абитуриентов.
Только на последнем, третьем этапе изучается переход к уравнению, равносильному исходному уравнению на некотором множестве. Этот способ решения уравнений труднее остальных: он изучается только при углубленном изучении математики и позволяет подготовить учащихся к решению сложных задач из ЕГЭ. Этот этап важен еще и потому, что ситуации, в которых решить уравнение можно только переходом к уравнению, равносильному исходному на некотором множестве, достаточно распространены (например, решение уравнений с модулями).
Аналогичная работа ведется в учебнике и при обучении решению неравенств с разницей в том, что для неравенств не используется понятие «неравенство-следствие».
Во второй главе учебника имеется параграф «Использование свойств функций при решении уравнений и неравенств», материал которого широко используется при решении некоторых заданий из ЕГЭ. В классах с углубленным изучением математики изучаются те же методы, что и в обычных классах, но на более сложных задачах и с рассмотрением большего количества случаев.
Во второй главе также содержится материал для углубленного изучения математики, связанный с освоением техники решения уравнений, неравенств, систем.
Завершает теоретическую часть учебника для 11 класса третья глава «Комплексные числа».
Следует учесть, что провести все самостоятельные работы из дидактических материалов со всем классом, скорее всего, не удастся, да это и не требуется. Некоторые из них можно использовать как домашние задания на отметку или как дополнительные задания для заинтересованных учащихся (на уроке или дома). Самостоятельные работы отнесены к соответствующим темам, но могут использоваться и при изучении других тем (например, для организации повторения изученного ранее материала).
Многие самостоятельные работы и все контрольные работы избыточны по объему. Предполагается, что учитель самостоятельно отберет из них часть заданий с учетом уровня подготовки учащихся по предмету и времени, отводимого на выполнение работы. Некоторые задания вариантов III и IV несколько сложнее соответствующих заданий вариантов I и II. Так как в классах с углубленным изучением математики контрольных работ должно быть больше, чем в обычных классах, то отдельные самостоятельные работы, отмеченные звездочкой, можно провести как контрольные работы.
Справа от параграфа или пункта указано число часов, отведенных на его изучение при каждом из вариантов планирования I, II, III, IV, рассчитанных соответственно на 2,5, 3, 4, 5 недельных часов в течение года. Тексты контрольных работ приведены в дидактических материалах.
|
I |
II |
III |
IV |
||
|
§ 1. Функции и их графики |
6 |
6 |
9 |
11 |
|
|
1.1. Элементарные функции |
1 |
1 |
1 |
1 |
|
|
1.2. Область определения и область изменения функции. Ограниченность функции |
1 |
1 |
1 |
1 |
|
Продолжение
|
I |
II |
III |
IV |
||
|
1.3. Четность, нечетность, периодичность функций |
1 |
1 |
2 |
2 |
|
|
1.4. Промежутки возрастания, убывания, знакопостоянства и нули функции |
1 |
1 |
2 |
2 |
|
|
1.5. Исследование функций и построение их графиков элементарными методами |
1 |
1 |
1 |
1 |
|
|
1.6. Основные способы преобразования графиков |
1 |
1 |
1 |
2 |
|
|
1.7. Графики функций, содержащих модули |
— |
— |
1 |
1 |
|
|
1.8. Графики сложных функций |
— |
— |
— |
1 |
|
|
§ 2. Предел функции и непрерывность |
5 |
5 |
5 |
6 |
|
|
2.1. Понятие предела функции |
1 |
1 |
1 |
1 |
|
|
2.2. Односторонние пределы |
1 |
1 |
1 |
1 |
|
|
2.3. Свойства пределов функций |
1 |
1 |
1 |
1 |
|
|
2.4. Понятие непрерывности функции |
1 |
1 |
1 |
1 |
|
|
2.5. Непрерывность элементарных функций |
1 |
1 |
1 |
1 |
|
|
2.6. Разрывные функции |
— |
— |
— |
1 |
|
|
§ 3. Обратные функции |
3 |
3 |
6 |
6 |
|
|
3.1. Понятие обратной функции |
2 |
2 |
1 |
1 |
|
|
3.2. Взаимно обратные функции |
— |
— |
1 |
1 |
|
|
3.3. Обратные тригонометрические функции |
— |
— |
2 |
2 |
|
|
3.4. Примеры использования обратных тригонометрических функций |
— |
— |
1 |
1 |
|
|
Контрольная работа № 1 |
1 |
1 |
1 |
1 |
|
|
§ 4. Производная |
8 |
9 |
11 |
12 |
|
|
4.1. Понятие производной |
2 |
2 |
2 |
2 |
|
|
4.2. Производная суммы. Производная разности |
1 |
1 |
2 |
2 |
|
|
4.3. Непрерывность функции, имеющей производную. Дифференциал |
— |
— |
1 |
1 |
|
|
4.4. Производная произведения. Производная частного |
2 |
2 |
2 |
2 |
|
|
4.5. Производные элементарных функций |
1 |
1 |
1 |
1 |
|
|
4.6. Производная сложной функции |
1 |
2 |
2 |
2 |
|
|
4.7. Производная обратной функции |
— |
— |
— |
1 |
|
|
Контрольная работа № 2 |
1 |
1 |
1 |
1 |
|
|
§ 5. Применение производной |
15 |
15 |
16 |
19 |
|
|
5.1. Максимум и минимум функции |
2 |
2 |
2 |
2 |
|
|
5.2. Уравнение касательной |
2 |
2 |
2 |
2 |
|
|
5.3. Приближенные вычисления |
1 |
1 |
1 |
1 |
|
|
5.4. Теоремы о среднем |
— |
— |
— |
1 |
|
|
5.5. Возрастание и убывание функции |
2 |
2 |
2 |
2 |
|
|
5.6. Производные высших порядков |
1 |
1 |
1 |
1 |
|
|
5.7. Выпуклость графика функции |
— |
— |
— |
1 |
|
Продолжение
|
I |
II |
III |
IV |
5.8. Экстремум функции с единственной 2 2 2 2
критической точкой
5.9. Задачи на максимум и минимум 2 2 2 2
5.10. Асимптоты. Дробно-линейная функция — — 1 1
5.11. Построение графиков функций 2 2 2 2
с применением производных
5.12. Формула и ряд Тейлора — — — 1
Контрольная работа № 3 1 1 1 1
§ 6. Первообразная и интеграл 8 11 13 18
6.1. Понятие первообразной 2 3 3 3
6.2. Замена переменной. Интегрирование — — — 1
по частям
6.3. Площадь криволинейной трапеции 1 1 1 1
6.4. Определенный интеграл 1 2 2 2
6.5. Приближенное вычисление — — 1 1
определенного интеграла
6.6. Формула Ньютона — Лейбница 2 3 3 3
6.7. Свойства определенных интегралов 1 1 1 2
6.8. Применение определенного интеграла — — 1 2
в геометрических и физических задачах
6.9. Понятие дифференциального уравнения — — — 1
6.10. Задачи, приводящие — — — 1
к дифференциальным уравнениям
Контрольная работа № 4 1 1 1 1
§ 7. Равносильность уравнений и неравенств 4 4 4 4
7.1. Равносильные преобразования 2 2 2 2
уравнений
7.2. Равносильные преобразования 2 2 2 2
неравенств
§ 8. Уравнения-следствия 4 7 8 9
8.1. Понятие уравнения-следствия 1 1 1 1
8.2. Возведение уравнения в четную степень 1 2 2 2
8.3. Потенцирование логарифмических 1 1 2 2
уравнений
8.4. Другие преобразования, приводящие 1 1 1 2
к уравнению-следствию
8.5. Применение нескольких — 2 2 2
преобразований, приводящих
к уравнению-следствию
§ 9. Равносильность уравнений и неравенств 5 6 13 13
системам
9.1. Основные понятия 1 1 1 1
9.2. Решение уравнений с помощью систем 1 2 2 2
9.3. Решение уравнений с помощью систем 1 1 2 2
(продолжение)
Продолжение
|
I |
II |
III |
IV |
9.4. Уравнения вида f (α (x)) = f (β (x)) — — 2 2
9.5. Решение неравенств с помощью систем 1 1 2 2
9.6. Решение неравенств с помощью систем 1 1 2 2
(продолжение)
9.7. Неравенства вида f (α (x)) > f (β (x)) — — 2 2
§ 10. Равносильность уравнений 3 3 7 11
на множествах
10.1. Основные понятия 1 1 1 1
10.2. Возведение уравнения в четную 1 1 2 2
степень
10.3. Умножение уравнения на функцию — — 1 2
10.4. Другие преобразования уравнений — — 1 2
10.5. Применение нескольких — — 1 2
преобразований
10.6. Уравнения с дополнительными — — — 1
условиями
Контрольная работа № 5 1 1 1 1
§ 11. Равносильность неравенств 2 2 6 9
на множествах
11.1. Основные понятия 1 1 1 1
11.2. Возведение неравенства в четную 1 1 1 2
степень
11.3. Умножение неравенства на функцию — — 1 1
11.4. Другие преобразования неравенств — — 1 1
11.5. Применение нескольких — — 1 1
преобразований
11.6. Неравенства с дополнительными — — — 1
условиями
11.7. Нестрогие неравенства — — 1 2
§ 12. Метод промежутков для уравнений 1 4 4 5
и неравенств
12.1. Уравнения с модулями 1 1 1 1
12.2. Неравенства с модулями — 1 1 1
12.3. Метод интервалов для непрерывных — 1 1 2
функций
Контрольная работа № 6 — 1 1 1
§ 13. Использование свойств функций 2 5 5 6
при решении уравнений и неравенств
13.1. Использование областей существования 1 1 1 1
функций
13.2. Использование неотрицательности 1 1 1 1
функций
13.3. Использование ограниченности — 1 1 2
функций
Продолжение
|
I |
II |
III |
IV |
||
|
13.4. Использование монотонности и экстремумов функций |
— |
1 |
1 |
1 |
|
|
13.5. Использование свойств синуса и косинуса |
— |
1 |
1 |
1 |
|
|
§ 14. Системы уравнений с несколькими неизвестными |
5 |
7 |
8 |
8 |
|
|
14.1. Равносильность систем |
2 |
2 |
2 |
2 |
|
|
14.2. Система-следствие |
1 |
2 |
2 |
2 |
|
|
14.3. Метод замены неизвестных |
2 |
2 |
2 |
2 |
|
|
14.4. Рассуждения с числовыми значениями при решении систем уравнений |
— |
— |
1 |
1 |
|
|
Контрольная работа № 7 |
— |
1 |
1 |
1 |
|
|
§ 15. Уравнения, неравенства и системы с параметрами |
— |
— |
4 |
7 |
|
|
15.1. Уравнения с параметром |
— |
— |
1 |
2 |
|
|
15.2. Неравенства с параметром |
— |
— |
1 |
2 |
|
|
15.3. Системы уравнений с параметром |
— |
— |
1 |
2 |
|
|
15.4. Задачи с условиями |
— |
— |
1 |
1 |
|
|
§ 16. Алгебраическая форма и геометрическая интерпретация комплексных чисел |
— |
— |
— |
5 |
|
|
16.1. Алгебраическая форма комплексного числа |
— |
— |
— |
2 |
|
|
16.2. Сопряженные комплексные числа |
— |
— |
— |
2 |
|
|
16.3. Геометрическая интерпретация комплексного числа |
— |
— |
— |
1 |
|
|
§ 17. Тригонометрическая форма комплексных чисел |
— |
— |
— |
3 |
|
|
17.1. Тригонометрическая форма комплексного числа |
— |
— |
— |
2 |
|
|
17.2. Корни из комплексных чисел и их свойства |
— |
— |
— |
1 |
|
|
§ 18. Корни многочленов. Показательная форма комплексных чисел |
— |
— |
— |
2 |
|
|
18.1. Корни многочленов |
— |
— |
— |
1 |
|
|
18.2. Показательная форма комплексного числа |
— |
— |
— |
1 |
|
|
Повторение |
14 |
15 |
17 |
16 |
|
|
Повторение курса алгебры и начал математического анализа 10—11 классов |
12 |
13 |
15 |
14 |
|
|
Итоговая контрольная работа № 8 |
2 |
2 |
2 |
2 |
|
|
§ 1. |
Функции и их графики
В предыдущих классах учащиеся уже изучали многие перечисленные ниже понятия. В 11 классе эти понятия уточняются, приводятся в систему, готовятся к использованию при исследовании функций — сначала элементарными средствами, а потом с помощью производной.
В данном пункте учебника напоминаются определения
функции, сложной функции как функции от функции (ее называют также
суперпозицией функций), определены основные объекты изучения — основные
элементарные функции: ![]() N, n ≥ 2), y = xα (α ∈ R+), y = x−α (α ∈ R+), y = sin x, y = cos x, y = tg x, y = ctg x, y = ax (a
> 0, a ≠ 1), y = loga x (a
> 0, a ≠ 1).
N, n ≥ 2), y = xα (α ∈ R+), y = x−α (α ∈ R+), y = sin x, y = cos x, y = tg x, y = ctg x, y = ax (a
> 0, a ≠ 1), y = loga x (a
> 0, a ≠ 1).

Затем к основным элементарным функциям добавляются элементарные функции,
полученные из основных элементарных функций с помощью конечного числа
арифметических операций и конечного числа суперпозиций. Элементарными
функциями, например, являются функции y =
sin x + cos
x, y =
−sin2 (x −
5).
При обучении на базовом, а тем более на профильном уровне понятие сложной функции должно быть хорошо отработано, так как оно будет использоваться в дальнейшем, например при нахождении производной функции, где нельзя ограничиться только производной от функции f (kx + l). Такой отработке будут способствовать задания из самостоятельной работы С—1, в которой есть задания на решение уравнений, где суперпозиция двух элементарных функций равна числу.
Решения и комментарии
1.2. б) Выпишите основные элементарные функции f (x) и g (x), с помощью которых задана сложная функция f (g (x)) = ln x4.
Ответ. f (x) = ln x, g (x) = x4.
![]() 1.3.
б) Выпишите основные элементарные функции f (x), g (x)
и ϕ (x),
с помощью которых задана сложная функция f (g (ϕ (x))) = (
sin x)3.
1.3.
б) Выпишите основные элементарные функции f (x), g (x)
и ϕ (x),
с помощью которых задана сложная функция f (g (ϕ (x))) = (
sin x)3.
Ответ. f (x) = x3, g x( ) = x, ϕ (x) = sin x.
1.4. Заданы элементарные функции: f (x) = 7х, ϕ (x) = x2, g (x) = log5 x. Задайте формулой функцию: в) f (g (x)); г) g (g (x)); д) g (ϕ (f (x))); е) ϕ (g (f (x))); ж) f (g (ϕ (x)));
з) f (g (f (x))).
Решение. Для лучшего понимания учащимися решения можно выполнить следующие шаги, приводящие к ответу в задании в): записать функцию f (x) = 7х, затем функцию f (g x( )) = 7g x( ) = 7 log5 x.
Аналогично получим ответы в следующих заданиях: г) g (g (x)) = log5 (log5 x);
д) g (ϕ (f (x))) = log5 (7x)2;
е) ϕ (g (f (x))) = (log5 7х)2;
ж) f (g (ϕ (x))) = 7 log5 x2;
з) f (g (f (x))) = 7 log5 7x.
Промежуточный контроль. C—1.
1.2. Область определения и область изменения
В п. 1.2 учебника вводится понятие области существования функции. Под областью существования функции y = f (x) понимают множество всех действительных чисел x, для каждого из которых существует действительное число y, равное f (x). Это множество называют еще и полной областью определения функции. Область определения функции может быть любой частью области существования функции или может совпадать с ее областью существования. Область определения функции задается условиями или смыслом решаемой задачи.
Например, если функция у = x2 выражает зависимость площади у квадрата от длины его стороны x, то область определения функции есть множество (0; +∞). Но функция, заданная формулой у = x2, имеет область существования — множество всех действительных чисел R.
Подчеркнем, что если функция задана формулой и явно не указана ее область определения, то областью определения такой функции считают ее область существования. Область определения функции часто обозначают D (f). В п. 2 дидактических материалов рассмотрен ряд примеров на нахождение области определения функции.
Здесь же вводится понятие области изменения (области значений) функции. Во всех примерах, разобранных в этом пункте учебника, явно выписана область изменения E (f) функции y = f (x). В п. 3 дидактических материалов приведены дополнительные примеры нахождения области изменения функции.
В этом же пункте учебника вводятся понятия ограниченной функции, ограниченной сверху функции, ограниченной снизу функции, наименьшего и наибольшего значений функции на множестве X. Эти понятия тесно связаны с понятием области изменения функции, поскольку область изменения функции можно найти, зная ее наибольшее (наименьшее) значение либо зная, что она не ограничена сверху (снизу) на множестве X.
Решения и комментарии
1.12. Покажите, что на полной области определения функция:
а) у = х2 не является ограниченной сверху;
б) y = − 12 не является ограниченной снизу; x
в) у = log2 x не является ограниченной.
![]() Решение. а)
Для любого сколь угодно большого числа M >
0 найдется число x0 =
M +1,
такое, что у0 =
х20 =
Решение. а)
Для любого сколь угодно большого числа M >
0 найдется число x0 =
M +1,
такое, что у0 =
х20 =
= M + 1 > M. Это означает, что на полной области определения функция y = х2 не является ограниченной сверху.
![]() б) Для любого
сколь угодно большого числа M >
0 найдется число x0 = 1 , такое, что y 0
=
− 12
=
− 1 2 =
б) Для любого
сколь угодно большого числа M >
0 найдется число x0 = 1 , такое, что y 0
=
− 12
=
− 1 2 =
![]() 2M x0 ⎛ 1 ⎞
2M x0 ⎛ 1 ⎞
⎜ ⎟
⎝ 2M ⎠
= −2M < −M. Это означает, что на полной области определения функция y = − x12 не является ограниченной снизу.
в) Для любого сколь угодно большого числа M > 0 найдется число x0 = 2M + 1, такое, что | у0 | = | log2 x0 | = = | log2 2M + 1 | = M + 1 > M. Это означает, что на полной области определения функция у = log2 x не является ограни-
ченной.
1.13. Докажите, что если функция y = f (x), определенная на множестве Х, ограничена и сверху, и снизу на этом множестве, то она ограничена на данном множестве.
Решение. Так как функция y = f (x), определенная на множестве Х, ограничена и снизу, и сверху на этом множестве, то существуют числа A и B, такие, что для каждого x ∈ Х верно неравенство
A ≤ f (x) ≤ B. (1)
Возможны только три следующих случая:
1) Если A > 0, то из неравенства (1) следует, что B > 0 и f (x) > 0, поэтому | f (x) | = f (x) ≤ B для каждого x ∈ Х. 2) Если B < 0, то из неравенства (1) следует, что A < 0 и f (x) < 0, поэтому | f (x) | = −f (x) ≤ −A = | A | для каждого x ∈ Х.
3) Если A ≤ 0, а B ≥ 0, то из неравенства (1) следует, что −С < f (x) < С, где С = 1 + max (| A |, B), т. е. что | f (x) | < С для каждого x ∈ Х.
Итак, во всех случаях показано: существует число M > 0, такое, что | f (x) | ≤ M для каждого x ∈ Х. Это означает, что функция y = f (x) ограничена на множестве Х, что и требовалось доказать.
![]() 1.14. г)
Имеет ли наибольшее (наименьшее) значение функция y = 2 sin x ?
Если имеет, то укажите точку (точки), в которой (в которых) оно достигается.
1.14. г)
Имеет ли наибольшее (наименьшее) значение функция y = 2 sin x ?
Если имеет, то укажите точку (точки), в которой (в которых) оно достигается.
![]()
![]()
![]()
![]() Решение. Область
существования этой функции находится из условия sin x ≥ 0. Это
множество D (f), состоящее из отрезков [2πn; π + 2πn],
n ∈ Z.
Для любого x ∈
D (f) имеем 0 ≤
sin x ≤
1, причем sin x =
0 для x = xn
= πn,
n ∈ Z,
а sin x = 1
для x
Решение. Область
существования этой функции находится из условия sin x ≥ 0. Это
множество D (f), состоящее из отрезков [2πn; π + 2πn],
n ∈ Z.
Для любого x ∈
D (f) имеем 0 ≤
sin x ≤
1, причем sin x =
0 для x = xn
= πn,
n ∈ Z,
а sin x = 1
для x ![]() x k, k ∈ Z.
Так как функция y =
2t возрастает на R, то она возрастает и
на отрезке [0; 1]. Но функция, возрастающая на отрезке [0; 1], принимает
наименьшее значение в точке t0 =
0, а наибольшее значение в точке t1 = 1. Поэтому 2 sin
x = 1
для x = xn
и 2 sin x =
2 для x = xk.
x k, k ∈ Z.
Так как функция y =
2t возрастает на R, то она возрастает и
на отрезке [0; 1]. Но функция, возрастающая на отрезке [0; 1], принимает
наименьшее значение в точке t0 =
0, а наибольшее значение в точке t1 = 1. Поэтому 2 sin
x = 1
для x = xn
и 2 sin x =
2 для x = xk.
Следовательно, функция имеет
наименьшее значение 1 (оно достигается в точках xn = πn, n ∈ Z)
и наибольшее значение 2 (оно достигается в точках xk ![]() k,
k ∈ Z).
k,
k ∈ Z).
Промежуточный контроль. C—2, C—3.
Дополнения
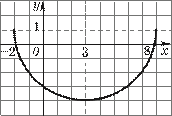
1. Отметим, что функция на своей области существования может принимать наибольшее (наименьшее) значение не в одной точке. Например, функция y = {x} принимает наименьшее значение в бесконечном числе точек, а именно в точках x ∈ Z. Функция с областью определения
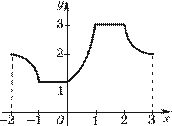 [−2; 3], график
которой изображен на рисунке 1, имеет наименьшее значение 1 в каждой точке
отрезка [−1;
0] и наибольшее значение 3 в каждой точке отрезка [1; 2].
[−2; 3], график
которой изображен на рисунке 1, имеет наименьшее значение 1 в каждой точке
отрезка [−1;
0] и наибольшее значение 3 в каждой точке отрезка [1; 2].
2. В п. 1.2 учебника и в п. 3 дидактических материалов приведены примеры нахождения E (f) — области изменения функции f (x). Это простые примеры, цель которых — пояснить, что Рис. 1 же такое E (f). На самом деле нахождение E (f) надо проводить в конце исследования функции f (x), так как для нахождения E (f) необходимо знать многие свойства этой функции.
Приведем более сложные примеры нахождения E (f).
Пример 1. Найдем E (f) — область изменения функции f x( ) = x + 1 .
x
Решение. Область существования этой функции — все x, кроме x = 0. Эта функция нечетная, поэтому, определив сначала E (f) для x > 0, легко найти E (f) для всех x ∈ D (f). Пусть x > 0. Применяя числовое неравенство a + 1 ≥ 2, справедливое для любого a > 0, получаем, что
a
f (x) ≥ 2 для любого x > 0. Так как f (1) = 2, то область изменения функции f (x) для x > 0 есть [2; +∞).
Так как функция f (x) нечетная, то E (f) = (−∞; −2] ∪ ∪ [2; +∞).
Конечно, для x < 0 область изменения функции можно найти и так. Пусть x < 0. Применяя числовое неравенство a + 1 ≤ −2, справедливое для любого a < 0, получаем, что
a
f (x) ≤ −2 для любого x < 0. Так как f (−1) = −2, то область изменения функции f (x) для x < 0 есть (−∞; −2]. Следовательно, E (f) = (−∞; −2] ∪ [2; +∞).
Пример 2. Найдем E (f) — область изменения функции
f x(
) = x2
+1 + ![]() 21 .
21 .
x + 1
Решение. Область существования этой функции —
D (f) = R. Применяя числовое неравенство a + 1 ≥ 2, спра-
a
ведливое для любого a > 0, получаем, что f (x) ≥ 2 для любого x ∈ R. Так как f (0) = 2, то E (f) = [2; +∞).
Пример 3. Найдем E (f) — область изменения функции
f x(
) = x2
+ 2 + ![]() 21 .
21 .
x + 2
Решение. Область существования этой функции —
D (f) = R. Применяя числовое неравенство a + 1 ≥ 2, спраa
ведливое для любого a > 0, получаем, что f (x) ≥ 2 для любого x ∈ R. Но здесь нельзя утверждать, что E (f) = [2; +∞).
Так как функция f (x) четная, то область изменения функции E (f) на всей области существования D (f) совпадает с областью изменения этой функции для x ∈ [0; +∞).
Рассмотрим функцию ![]() 0. Она возрастающая на
промежутке [0; +∞).
0. Она возрастающая на
промежутке [0; +∞).
Действительно, если 0 ≤
x1 <
x2, то f x( 2) ![]() f x( 1) x2 x
f x( 1) x2 x
![]() =
=![]() − +
− + ![]() =
=
( ) ( )
=
(x2 − x1) (x2 + x1) ⎜⎛⎝1
− ![]() 1 2 +
2) ⎞⎟⎠ > 0.
1 2 +
2) ⎞⎟⎠ > 0.
(![]() x + 2) (x
x + 2) (x
Но возрастающая на промежутке [0; +∞) функция принимает свое наименьшее значение в точке x0 = 0. Итак, f (0) = 2,5, f (x) > f (0) для любого x > 0, и поэтому
E (f) = [2,5; +∞).
Отметим, что в примерах 2 и 3, используя одно и то же неравенство a + 1 ≥ 2 (a > 0), получаем, что f (x) ≥ 2 для a
любого x, но в примере 2 функция достигает значения 2 в точке x0 = 0, а в примере 3 нет. Поэтому в примере 3 было проведено дополнительное исследование.
3. Обычно решение задач на нахождение области изменения функции ограничивается указанием соответствующего множества и некоторых соображений, похожих на приведенные выше, о том, почему это и есть E (f). Но бывают (хотя и достаточно редко) ситуации, когда требуется доказать, что выписанное множество и есть область изменения функции. Учитель должен уметь проводить доказательство, но может не требовать этого от учащихся. Приведем лишь один пример.
![]() Пример 4. Найдем
E (f) — область изменения функции f x( ) = 1 − x2 .
Пример 4. Найдем
E (f) — область изменения функции f x( ) = 1 − x2 .
![]() Решение.
Область существования этой функции находится из условия 1 − x2 ≥ 0, т. е. D (f)
= [−1; 1]. Далее
обычно пишут: так как f (1) =
f (−1)
= 0, f (0)
= 1, 0 ≤ 1 − x2 ≤ 1 для x ∈ [−1; 1], то E (f)
= [0; 1]. Однако
в этом рассуждении пропущен следующий шаг: надо доказать, что для любого числа y0
∈ D
(f) существует хотя бы одно число x0 ∈ D (f),
такое, что y0 =
f (x0). Приведем два способа доказательства
этого утверждения.
Решение.
Область существования этой функции находится из условия 1 − x2 ≥ 0, т. е. D (f)
= [−1; 1]. Далее
обычно пишут: так как f (1) =
f (−1)
= 0, f (0)
= 1, 0 ≤ 1 − x2 ≤ 1 для x ∈ [−1; 1], то E (f)
= [0; 1]. Однако
в этом рассуждении пропущен следующий шаг: надо доказать, что для любого числа y0
∈ D
(f) существует хотя бы одно число x0 ∈ D (f),
такое, что y0 =
f (x0). Приведем два способа доказательства
этого утверждения.
1-й способ. Докажем, что для любого фиксированного числа y0 ∈ [0; 1] уравнение
![]() y
0 = 1
− x2 (1)
y
0 = 1
− x2 (1)
имеет хотя бы один корень x0 ∈ [−1; 1].
![]()
![]() Решив уравнение (1) (используя
материалы второй главы учебника), получим, что оно имеет два корня: x1
= 1 − y20
и x2 =
− 1 −
y20 , такие, что x1 ∈ [0; 1] и x2
∈ [−1; 0] (x1
= x2
= 0 при y0
= 1 и при y0
= −1).
Итак, доказано существование чисел x1 и x2 из
D (f), таких, что y0 = f (x1) и y0
= f (x2),
а это и означает, что E (f) =
[0; 1].
Решив уравнение (1) (используя
материалы второй главы учебника), получим, что оно имеет два корня: x1
= 1 − y20
и x2 =
− 1 −
y20 , такие, что x1 ∈ [0; 1] и x2
∈ [−1; 0] (x1
= x2
= 0 при y0
= 1 и при y0
= −1).
Итак, доказано существование чисел x1 и x2 из
D (f), таких, что y0 = f (x1) и y0
= f (x2),
а это и означает, что E (f) =
[0; 1].
![]() 2-й способ.
Так как функция f (x) четная, то это означает, что E (f)
— область изменения функции на всей области существования D (f)
совпадает с областью изменения этой функции для x ∈ [0; 1]. Найдем E
(f1), если f1 ( )x = 1 − x2 ,
x ∈ [0;
1].
2-й способ.
Так как функция f (x) четная, то это означает, что E (f)
— область изменения функции на всей области существования D (f)
совпадает с областью изменения этой функции для x ∈ [0; 1]. Найдем E
(f1), если f1 ( )x = 1 − x2 ,
x ∈ [0;
1].
Функция f1 (x) непрерывна на отрезке [0; 1], f1 (1) = 0, f1 (0) = 1. Поэтому по теореме из п. 2.5 она принимает все значения между f1 (1) и f1 (0), т. е. для функции f1 (x) имеем E (f1) = [0; 1]. Следовательно, E (f) = [0; 1].
4. Приведем примеры задач из ЕГЭ, в которых используются понятия, рассмотренные в п. 1.2. Здесь и далее в ответах к заданиям части А указан номер верного ответа.
A6 (2007). Укажите множество значений функции y = 2x + 5.
1) (5; +∞); 2) (0 +∞); 3) (−∞; +∞); 4) (7; +∞).
Решение. Для любого x ∈ R имеем 2x > 0, следовательно, 2x + 5 > 5. (В тесте проводить какие-либо доказательства не требуется.) Ответ. 1.
A8 (2007). Найдите область определения функции
![]() 25 f x( ).
25 f x( ).
x
1) [0; 3) ∪ (3; +∞); 2) [0; +∞);
3) [0; 81) ∪ (81; +∞); 4) (−∞; 81) ∪ (81; +∞).
Решение. Область определения функции находим из двух
условий: x![]() .
.
Ответ. 3.
![]() A10 (2005).
Укажите область определения функции y =
3 − lg
x.
A10 (2005).
Укажите область определения функции y =
3 − lg
x.
1) (0; 3]; 2) (0; 1000]; 3) (3; 1000]; 4) [1000; +∞).
Решение. Область определения функции находим из условия 3 − lg x ≥ 0.
Ответ. 2.
B8 (2005). Найдите наибольшее целое значение функции
y = 25 ⋅ 3cos 4x cos 3x + sin 4x sin 3x − 2.
Решение. Данную функцию можно задать формулой y = 25 ⋅ 3cos (4x − 3x) − 2 или формулой y = 25 ⋅ 3cos x − 2. Так как для любого x ∈ R имеем −1 ≤ cos x ≤ 1, то −3 ≤ cos x − 2 ≤ −1. Тогда в силу возрастания на R функции 3t справедливо двойное неравенство 3−3 ≤ 3cos x − 2 ≤ 3−1, откуда следует, что для любого x ∈ R имеем
![]() .
.
![]() Так
как
Так
как ![]() =
8
=
8 ![]() , то наибольшее целое значение функции
равно 8.
, то наибольшее целое значение функции
равно 8.
Ответ. 8.
В данном пункте вводится понятие четности (нечетности) функции. Отметим, что учащимся в изучении этого свойства функций «мешает» предыдущий опыт. Они знают, что целые числа бывают двух типов — четные и нечетные, и часто полагают, что и функции бывают только четные и нечетные. Поэтому при введении понятий «четная функция» и «нечетная функция» нужно сразу сообщить, что существуют четные функции, нечетные функции, а также функции, которые не являются ни четными, ни нечетными, и функции, которые являются одновременно и четными, и нечетными. Соответствующие примеры приведены в учебнике и в дидактических материалах. Рассмотрим другие примеры.
Функция f (x) = 0 одновременно является и четной, и нечетной, так как ее можно записать в виде f (x) = 0 ⋅ x. Тогда для любого x верны равенства f (−x) = 0 ⋅ (−x) = = −0 ⋅ x = 0 ⋅ x, т. е. для любого x верны равенства f (−x) = = −f (x) и f (−x) = f (x).
Эта функция иногда может быть задана замысловатой формулой, например такой: f (x) = (| x | − x) (| x | + x).
Действительно, f (x) = | x |2 − x2 = x2 − x2 = 0 при каждом x ∈ R.
Приведем пример еще одной функции, являющейся одновременно и четной, и нечетной:
| x | x
g x( ) = ![]() − . x | x |
− . x | x |
Действительно, g (x) = 0 при каждом x ≠ 0, поэтому для каждого x ≠ 0
g (−x) = −g (x) и g (−x) = g (x).
Вообще если функция f (x) = 0 определена на множестве M, симметричном относительно начала координат, и не определена вне множества M, то она является и четной, и нечетной. Таким свойством обладает, например, функция
![]() log2 (1 −
| x |) (| x |
−
2 )
log2 (1 −
| x |) (| x |
−
2 )
,
так как D (p) = (−2; −1) ∪ (1; 2), и на D (p) имеем p (x) = 0.
Приведем пример нечетной функции
![]() f x(
) = lg (
x2 +1
− x),
f x(
) = lg (
x2 +1
− x),
которая на первый взгляд не является ни четной, ни нечетной (доказательство приведено в п. 4 дидактических материалов).
В п. 5 дидактических материалов приведены примеры использования четности функций для решения задач с параметром.
В п. 1.3 учебника даны определения периодической функции, периода и главного периода функции, приведены примеры периодических функций.
Отметим, что если периодом функции f (x) является число T, то график функции y = f (x + T), полученный сдвигом графика функции y = f (x) вдоль оси Ox на | T |, совпадает с графиком функции y = f (x).
Подчеркнем, что в примере 1в из п. 1.3 учебника функция y = {x} имеет период T = m — любое целое, отличное от нуля число, так как для любого числа x верно равенство {x + m} = {x}.
Ниже в Дополнении 3 показано, что T = 1 — главный период этой функции.
Отметим, что при нахождении периода функции обычно ограничиваются отысканием какого-либо периода, по возможности наименьшего положительного. Но если не приведено доказательство, что найденный период является наименьшим положительным периодом, то нельзя утверждать, что этот период является главным периодом функции. Доказательства того, что функции y = sin x и y = cos x имеют главный период T = 2π, а функции y = tg x и y = ctg x имеют главный период T = π, приведены в учебнике 10 класса.
В п. 1.3 учебника утверждается, что функция f (x) = = sin x + cos x имеет главный период T = 2π, а функция g (x) = sin x cos x имеет главный период T = π.
Докажем это.
![]() 1) Вводя
вспомогательный угол, получаем, что f x( ) =2 sin ⎛⎜⎝x + π4⎞⎟⎠.
1) Вводя
вспомогательный угол, получаем, что f x( ) =2 sin ⎛⎜⎝x + π4⎞⎟⎠.
Пусть число T есть период функции f (x), тогда, так как D (f) = R, то для любого x должно выполняться равенство f (x + T) = f (x), т. е. равенство
![]()
![]() 2 sin ⎜⎝⎛x
+ T + π4⎞⎟⎠ =2 sin ⎛⎜⎝x + π4⎞⎟⎠.
2 sin ⎜⎝⎛x
+ T + π4⎞⎟⎠ =2 sin ⎛⎜⎝x + π4⎞⎟⎠.
В частности, при x =
![]()
![]() должно
выполняться равенство
должно
выполняться равенство
![]()
![]() 2 sin ⎜⎝⎛ 2π
+ T⎞⎟⎠ =2 sin 2π,
откуда следует, что sin ⎝⎜⎛ 2π
+ T⎞⎟⎠ = 1.
2 sin ⎜⎝⎛ 2π
+ T⎞⎟⎠ =2 sin 2π,
откуда следует, что sin ⎝⎜⎛ 2π
+ T⎞⎟⎠ = 1.
Но так как sin u = 1 только для uk
![]() k, k ∈ Z, то T есть
одно из чисел 2πk,
k ∈ Z
(k ≠
0), т. е. периодом функции f (x) является любое число 2πk, k ∈ Z (k
≠ 0).
Наименьшее положительное среди них 2π,
следовательно, главный период функции f (x) есть 2π.
k, k ∈ Z, то T есть
одно из чисел 2πk,
k ∈ Z
(k ≠
0), т. е. периодом функции f (x) является любое число 2πk, k ∈ Z (k
≠ 0).
Наименьшее положительное среди них 2π,
следовательно, главный период функции f (x) есть 2π.
2) Применяя формулу синуса
двойного угла, получаем, что g x( ) =
![]()
![]() sin 2x.
sin 2x.
Пусть число T есть период
функции g (x), тогда, так как D (f) = R, то
для любого x должно выполняться равенство g (x + T) = g (x),
т. е. равенство ![]()
![]() sin 2 (x + T) =
sin 2 (x + T) = ![]()
![]() sin 2x.
sin 2x.
В частности, при x ![]() должно выполняться равенство
должно выполняться равенство
1
![]()
![]() π
π ![]() π,
откуда следует, что
π,
откуда следует, что ![]() .
.
2 2 2 2
Но так как sin u =
1 только для uk ![]() k, k ∈ Z,
то
k, k ∈ Z,
то
2T есть одно из чисел 2πk, k ∈ Z, т. е. периодом функции g (x) является любое число πk, k ∈ Z. Наименьшее положительное среди них π. Следовательно, главный период функции g (x) есть π.
К нахождению периодов функций, составленных с помощью нескольких периодических функций, надо подходить аккуратно, так как, например, при сложении периодических функций может получиться непериодическая функция.
В Дополнении 4 доказано, что при сложении периодических функций y = sin x и y = sin πx получается функция y = sin x + sin πx, не являющаяся периодической. Это доказательство можно рассматривать в классах с углубленным изучением математики.
Решения и комментарии
1.20. а) Определите, является ли четной или нечетной функция
x2 − 2x + 4 x2 + 2x + 4
![]() f x( ) = x2 − 3x +
8 + x2 + 3x + 8 .
f x( ) = x2 − 3x +
8 + x2 + 3x + 8 .
Решение. Так как знаменатели дробей не обращаются в нуль ни при каком x ∈ R, то D (f) = R. Для каждого x ∈ R верны равенства
![]() f
(−x)
=
f
(−x)
= ![]() + =
+ =
x2 + 2x + 4 x2 − 2x + 4
![]() = 2 + 3x +
8 + x2 − 3x +
8 = f x( ),
= 2 + 3x +
8 + x2 − 3x +
8 = f x( ),
x
следовательно, функция f (x) четная.
1.23. Докажите, что если функция y = f (x) определена на множестве Х и для любого х ∈ Х число (−x) ∈ Х, то функция:
f x( ) + f (−x)
а) ϕ ( )x =четная;
2
![]() f x( ) − f (−x)
f x( ) − f (−x)
б) ψ ( )x =нечетная.
2
Решение. а) Так как функция y = f (x) определена на множестве Х, для любого х ∈ Х число (−x) ∈ Х и справед-
ливы равенства ![]() , то функция ϕ (x)
четная.
, то функция ϕ (x)
четная.
б) Так как функция y = f (x) определена на множестве
X и для любого х ∈
Х число (−x)
∈ Х и
справедливы равенства ![]() , то функция ψ (x) нечетная.
, то функция ψ (x) нечетная.
1.24. Докажите, что если функция y = f (x) определена на множестве Х и для любого х ∈ Х число (−x) ∈ Х, то эту функцию можно представить в виде суммы двух функций, каждая из которых определена на том же множестве Х и одна из которых четная, а другая нечетная.
Решение. Если функция y = f (x) удовлетворяет условиям задачи, то
f x( ) +
f (−x) f x( ) −
f (−x) f x( ) = ![]() + ,
+ ,
где функция ϕ ( )x = четная, а функция
2
f x(
) −
f (−x) ψ
( )x = ![]() нечетная (задание 1.23).
нечетная (задание 1.23).
2
1.25. Представьте функцию y = 2x, определенную на всей оси, в виде суммы четной и нечетной функций.
Решение. Функция y = 2x удовлетворяет условиям задачи 1.24, поэтому
x 2x + 2−x 2x − 2−x
2 = ![]() + ,
+ ,
где функция ϕ ( )x = четная, а функция
2
2x − 2−x
ψ ( )x = ![]() нечетная.
нечетная.
2
1.30. Докажите, что если число Т есть период функции f, то число mT, где m ∈ N, также будет периодом этой функции.
Доказательство. Так как число Т есть период функции f, то Т ≠ 0 и для каждого x ∈ D (f) числа x + Т и x − Т принадлежат D (f) и верно равенство f (x + Т) = f (x).
Докажем, что тогда число mТ, где m ∈ N, также является периодом функции f.
При m = 1 число mТ является периодом функции f по условию задачи.
Предположим, что при m = k число kТ является периодом функции, и докажем, что при m = k + 1 число (k + 1) Т также является периодом функции f.
По нашему предположению числа x + kТ и x − kТ принадлежат D (f) и верно равенство f (x + kТ) = f (x). Так как число T — период функции f, то числа
(x + kТ) + Т = x + (k + 1) Т и (x − kТ) − Т = x − (k + 1) Т также принадлежат D (f) и верны равенства f (x + (k + 1) Т) = f ((x + kТ) + Т) = f (x + kТ) = f (x),
а это означает, что число (k + 1) Т является периодом функции f. Но тогда согласно принципу математической индукции число mТ, где m ∈ N, является периодом функции f, что и требовалось доказать.
Определите, является ли функция периодической. Если да, то укажите ее период (1.33—1.34).
1.33. д) у = sin | x |; е) у = cos | x |.
Решение. д) Функция у = sin | x | определена на множестве R и не является периодической, так как график функции y = sin | x + T |, полученный сдвигом графика функции y = sin | x | вдоль оси Ox на | T | единиц, не совпадает с графиком функции y = sin | x | ни для какого числа T ≠ 0 (рис. 2).
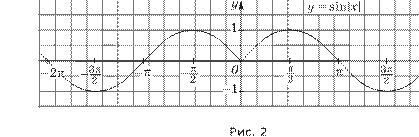
е) Функция у = cos | x | определена на множестве R, она периодическая, ее главный период T = 2π, так как при любом x ее значение совпадает со значением функции у = cos x, которая является периодической функцией с главным периодом T= 2π.
![]()
![]() 1.34. в)
y ={ }x
− 1.
1.34. в)
y ={ }x
− 1.
2
Решение. Так как для любого целого числа m, такого, что m ≠ 0, и любого x ∈ R числа x + m и x − m принад-
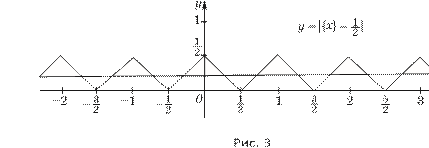
лежат множеству R и верно равенство {x + m} = {x}, то любое целое число m, m ≠ 0, является периодом функции
![]() y ={ }x − 1 .
y ={ }x − 1 .
2
Отметим, что функция {x} не является непрерывной,
![]()
![]() а функция y = { }x
− 1является примером
непрерывной
а функция y = { }x
− 1является примером
непрерывной
2
периодической функции, не связанной явно с тригонометрическими функциями. Ее график изображен на рисунке 3. Построение аналогичных графиков будет рассмотрено в п. 1.6.
1.36. Определите период функции:
а) y = sin 3x + cos 8x; в) y = sin 4x + cos 10x.
Решение. а) Функция y = sin 3x + cos 8x определена на множестве R и имеет период T = 2π, так как для любого x ∈ R верны равенства sin 3 (x + 2π) + cos 8 (x + 2π) = sin (3x + 6π) + cos (8x + 16π) = = sin 3x + cos 8x.
в) Функция y = sin 4x + cos 10x определена на множестве R и имеет период T = π, так как для любого x ∈ R верны равенства sin 4 (x + π) + cos 10 (x + π) =
= sin (4x + 4π) + cos (10x + 10π) = sin 4x + cos 10x.
Промежуточный контроль. C—4, C—5.
Дополнения
1. Отметим, что в определении четной (нечетной) функции условие (−x) ∈ D (f), вообще говоря, является лишним, так как если мы требуем для каждого x ∈ D (f) выполнения равенства f (−x) = f (x) (или f (−x) = −f (x)), то тем самым мы требуем, чтобы для каждого x ∈ D (f) существовало число f (−x), а это означает, что число (−x) ∈ D (f). Но это условие помогает в определении функций, которые не являются ни четными, ни нечетными, если области определения этих функций не симметричны относительно нуля.
Например, функция f x( ) = 1 + 1 не является ни четx x− 5
ной, ни нечетной, так как для числа x = −5, принадлежащего D (f), число −x = 5 не принадлежит D (f), и не надо проверять справедливость равенств f (−x) = −f (x) и f (−x) = −f (x) для любого x ∈ D (f).
2. ![]() Покажем, что в приведенном
определении периода функции нельзя опускать условия (x + T) ∈ X и (x
− T)
∈ X.
Рассмотрим, например, функцию f x( ) =
tg(
x)2.
Ее область существования состоит из всех неотрицательных целых чисел x,
кроме x =
Покажем, что в приведенном
определении периода функции нельзя опускать условия (x + T) ∈ X и (x
− T)
∈ X.
Рассмотрим, например, функцию f x( ) =
tg(
x)2.
Ее область существования состоит из всех неотрицательных целых чисел x,
кроме x = ![]()
![]() +
πk, k =
0, 1, 2, ... . График этой
+
πk, k =
0, 1, 2, ... . График этой
функции изображен на рисунке 4. Для любого x ∈ D (f) имеем: (x + T) ∈ D (f) и f (x + π) = f (x), но (x − π) ∉ D (f) для x ∈ [0; π). Такую функцию не принято считать периодической.

Приведем еще один пример, показывающий необходимость условий (x + T) ∈ X и (x − T) ∈ X в определении периодической функции.
Рассмотрим функцию f (x) = sin x, x ∈ [0; π]. Для любого x ∈ [0; π] верны равенства sin (x + 2π) = sin (x − 2π) = = sin x, но ни одно из чисел x + 2π и x − 2π не принадлежит области определения функции [0; π].
Таким образом, если в определении периодической функции опустить одно или оба условия (x + T) ∈ X и (x − T) ∈ X, то под такое определение попадают такие функции, которые на самом деле не являются периодическими.
3. Докажем, что функция f (x) = {x} имеет главный период T = 1, т. е. покажем, что нет числа T ∈ (0; 1), такого, что для любого числа x верно равенство {x + T} = {x}.
Предположим, что такое число есть, тогда (для x = 0) должно выполняться равенство {T} = {0}.
Так как {T} = T ≠ 0 для T ∈ (0; 1), а {0} = 0, то полученное противоречие означает: предположение, что функция f (x) имеет положительный период, меньший 1, неверно. Следовательно, T = 1 — главный период функции f (x) = {x}.
4. Докажем, что функция
у = sin x + sin πx (1)
не является периодической.
Функция (1) определена на множестве R. Предположим, что эта функция периодическая, т. е. существует такое не равное нулю число T, что для любого числа x справедливо равенство
sin (x + T) + sin π (x + T) = sin x + sin πx. (2)
Тогда это равенство справедливо, в частности, для х = 0 и х = 2, т. е. справедливы числовые равенства sin T + sin πT = 0,
sin (2 + T) + sin πT = sin 2.
Вычитая из второго равенства первое, получаем, что справедливо равенство sin (2 + T) − sin T = sin 2,
которое, используя формулы разности синусов и синуса двойного угла, перепишем в виде
2 sin 1 cos (1 + T) = 2 sin 1 cos 1,
или (так как sin 1 ≠ 0) в виде cos (1 + T) = cos 1.
Перенеся cos 1 в левую часть и применив формулу разности косинусов, перепишем это равенство в виде
−2 sin T2 sin ⎛⎜⎝1 + T2 ⎞⎟⎠ = 0. (3)
Равенство (3) справедливо в двух случаях: либо
T
sin = 0, (4)
2
либо
sin ⎜⎝⎛1 + T2 ⎞⎟⎠ = 0. (5)
Справедливость равенства (4) означает, что существует отличное от нуля (так как Т ≠ 0) целое число k, такое, что T = 2πk.
Справедливость равенства (5) означает, что существует целое число n, такое, что T = −2 + 2πn. Следовательно, если число T — период функции (1), то либо T = 2πk, либо T = −2 + 2πn, где k ∈ Z, n ∈ Z.
Покажем, что никакое из этих чисел не является периодом функции (1).
1. Если число Т = 2πk (k ≠ 0 — целое число) есть период функции (1), то, в частности, в точке x = 0 должно быть справедливо равенство (2), т. е. равенство
sin 2π2k = 0. (6)
Но равенство (6) выполняется лишь при условии, что найдется такое целое число m, для которого верно равенство
2π2k = πm. (7)
Но равенство (7) не выполняется ни при каких целых числах k (k ≠ 0) и m, так как в противном случае было бы справедливо равенство π = m , которое невозможно, так
2k
как число π иррациональное.
Таким образом, нашлось такое число x (x = 0), для которого при T = 2πk не справедливо равенство (2), а это означает, что число T не является периодом функции (1).
2. Если число Т = −2 + 2πk (k — целое число) есть период функции (1), то, в частности, в точке x = 1 должно быть справедливо равенство (2), т. е. должно быть справедливо равенство sin (−1) + sin (−π + 2π2n) = sin 1,
которое можно переписать в виде
sin 2π2n = −2 sin 1. (8)
Так как −2
sin 1 < −2
sin ![]()
![]() < −1, то
равенство (8) невоз-
< −1, то
равенство (8) невоз-
можно. Таким образом, нашлось такое число х (х = 1), для которого при Т = −2 + 2πk не справедливо равенство (2), а это означает, что число T не является периодом функции (1).
Итак, получилось противоречие с предположением о том, что функция (1) периодическая. Следовательно, функция (1) не является периодической, что и требовалось доказать.
5. Приведем примеры задач из ЕГЭ, связанных с понятиями четности (нечетности) и периодичности.
А4 (2007). На одном из следующих рисунков изображен график нечетной функции. Укажите этот рисунок.

Рис. 5
Решение. На рисунке 5 (4) изображен график нечетной функции, так как этот график симметричен относительно начала координат.
Ответ. 4.
B8 (2007). Периодическая функция определена для всех действительных чисел. Ее период равен 2 и f (1) = 5. Найдите значение выражения 3f (7) − 4f (−3).
Решение. 3f (7) − 4f (−3) = 3f (1 + 3 ⋅ 2) − 4f (1 − 2 ⋅ 2) = = 3f (1) − 4f (1) = −f (1) = −5.
Ответ. −5.
B8 (2006). Нечетная функция y = f (x) определена на всей числовой прямой. Для всякого неотрицательного значения переменной x ее значение совпадает со значением функции g (x) = x (2x + 1) (x − 2) (x − 3).
Сколько корней имеет уравнение f (x) = 0?
Решение. На множестве неотрицательных чисел значения функций f (x) и g (x) совпадают, поэтому на множестве неотрицательных чисел функция f (x) имеет те же нули, что и функция g (x), т. е. функция не имеет других нулей, кроме 0, 2 и 3. Так как функция y = f (x) нечетная, то f (−2) = −f (2) = 0, f (−3) = −f (3) = 0, f (−x0) = −f (−x0) ≠ 0 для числа x0 ∈ (0; +∞), отличного от 2 и 3. Следовательно, функция f (x) имеет всего 5 нулей, поэтому уравнение f (x) = 0 имеет 5 корней.
Ответ. 5.
1.4. Промежутки возрастания, убывания,
В данном пункте учебника даны определения возрастающей на промежутке функции, убывающей на промежутке функции, строго монотонной на промежутке функции, неубывающей на промежутке функции, невозрастающей на промежутке функции, монотонной на промежутке функции. Подчеркнем, что каждое из этих понятий рассматривается на промежутке.
По определению если для любых x1 и x2 из промежутка X из неравенства x1 < x2 следует неравенство f (x1) < f (x2), то функцию f (x) называют возрастающей на промежутке X. Обратим внимание на то, что из определения следует, что из справедливости неравенства x1 < x2 следует справедливость неравенства f (x1) < f (x2). Многие считают, что из определения также следует, что из неравенства f (x1) < f (x2) следует неравенство x1 < x2. Это действительно так, но не указывается в определении. Это надо уметь доказывать.
Аналогичное замечание можно сделать и для убывающей функции. Поэтому в учебнике дана задача 1.40 (ее решение приведено ниже). Отметим, что утверждения, сформулированные в этом задании, используются при решении уравнений и неравенств.
Отметим, что отыскание нулей функции и промежутков знакопостоянства функции сводится к решению уравнений и неравенств, часть из которых рассматривается в учебнике для 10 класса, а остальные — во второй главе учебника для 11 класса. В п. 6 дидактических материалов приведены примеры на отыскание промежутков монотонности и знакопостоянства функции.
Решения и комментарии
1.39. а) Докажите, что сумма возрастающих на промежутке Х функций является функцией, также возрастающей на промежутке Х.
Доказательство. а) Пусть дана функция ϕ (x) = f (x) + + g (x), где функции f (x) и g (x) возрастающие на промежутке Х. Это означает, что для чисел x1 и x2 из промежутка Х из справедливости неравенства x1 > x2 следует справедливость неравенств f (x1) > f (x2) и g (x1) > g (x2), а поэтому и справедливость цепочки равенств и неравенств ϕ (x1) = f (x1) + g (x1) > f (x2) + g (x1) > f (x2) + g (x2) = ϕ (x2).
Это означает, что функция ϕ (x) является возрастающей на промежутке X.
Утверждения из задания 1.39 часто используются при решении задач.
1.40. а) Докажите, что если функция y = f (x) определена на промежутке Х и возрастает на нем, то для любой пары чисел x1 и x2 из промежутка Х из справедливости неравенства f (x1) > f (x2) следует справедливость неравенства x1 > x2.
б) Докажите, что если функция y = f (x) определена на промежутке Х и убывает на нем, то для любой пары чисел x1 и x2 из промежутка Х из справедливости неравенства f (x1) > f (x2) следует справедливость неравенства x1 < x2.
в) Докажите, что если функция y = f (x) определена и строго монотонна на промежутке Х, то для любой пары чисел x1 и x2 из промежутка Х из справедливости равенства f (x1) = f (x2) следует справедливость равенства x1 = x2.
Доказательство. а) Для чисел x1 и x2 возможны только три соотношения: x1 = x2, x1 > x2 и x1 < x2.
Предположим, что x1 = x2, тогда f (x1) = f (x2), что противоречит условию f (x1) > f (x2).
Предположим, что x1 < x2, тогда из возрастания функции f (x) на промежутке X следует, что f (x1) < f (x2), что противоречит условию f (x1) > f (x2).
Это означает, что на самом деле x1 > x2, что и требовалось доказать.
Доказательства в заданиях б) и в) проводятся аналогично, поэтому здесь не приводятся.
Замечание. Часто определения и утверждения, приведенные в задании 1.40, формулируют иначе:
а) Если функция y = f (x) определена на промежутке Х и возрастает на нем, то для любой пары чисел x1 и x2 из промежутка Х равносильны неравенства f (x1) > f (x2) и x1 > x2.
б) Если функция y = f (x) определена на промежутке Х и убывает на нем, то для любой пары чисел x1 и x2 из промежутка Х равносильны неравенства f (x1) > f (x2) и x1 < x2.
в) Если функция y = f (x) определена и строго монотонна на промежутке Х, то для любой пары чисел x1 и x2 из промежутка Х равносильны равенства f (x1) = f (x2) и x1 = x2.
1.51. При каких значениях b и c функция у = x2 + bx + c принимает отрицательные значения только при х ∈ (−4; −2)?
Решение. Так как функция у = x2 + bx + c принимает отрицательные значения только при х ∈ (−4; −2), то нули функции x1 = −4 и x2 = −2. Тогда b = −(x1 + x2) = 6, с = x1 ⋅ x2 = 8. Промежуточный контроль. C—6.
1.5. Исследование функций и построение их графиков
В этом пункте приведена схема исследования функции, напоминаются определения графика функции, разъясняется на интуитивном уровне понятие функции, непрерывной на промежутке. Подчеркнем, что график функции только иллюстрирует свойства функции, но не доказывает их.
Отметим, что исследование функций элементарными средствами является первым этапом изучения свойств функций. После изучения производной описанный выше порядок исследования не изменяется, просто появятся новые средства доказательства возрастания, убывания функции, поиска наибольшего (наименьшего) значения функции.
Решения и комментарии
2 − x2
1.56. а) Исследуйте функцию y
= ![]() 2 + 1 и постройте ее x
2 + 1 и постройте ее x
график.
2 − x2
Решение. 1) Функция f x(
) = ![]() 2 + 1 определена для люx
2 + 1 определена для люx
бых действительных чисел, так как х2 + 1 ≠ 0, т. е. область ее существования есть R.
![]()
![]() 2) Так как f (x)
= 0 при x1
= −2 и
x2 =2,
то у этой функции есть два нуля: x1 и x2.
2) Так как f (x)
= 0 при x1
= −2 и
x2 =2,
то у этой функции есть два нуля: x1 и x2.
![]()
Рис. 6
4) f (x) > 0 при 3) Эта функция четная, так
![]() 2 − (−x)2 2 − x2 как (−x)2 + 1 = x2 + 1 для любых х ∈ R,
т. е. график функции y =
f (x) симметричен относительно оси Oy.
2 − (−x)2 2 − x2 как (−x)2 + 1 = x2 + 1 для любых х ∈ R,
т. е. график функции y =
f (x) симметричен относительно оси Oy.
![]() x ∈ (− 2; 2), f
(x) < 0 при
x ∈ (− 2; 2), f
(x) < 0 при
![]() x ∈ (− ∞; − 2)
(∪ 2;
+∞)
(рис. 6).
x ∈ (− ∞; − 2)
(∪ 2;
+∞)
(рис. 6).
5) На промежутке [0; +∞) функция f x( ) = −1 + 23
x + 1
убывающая, так как при 0 ≤ x1 < x2 справедливо
неравенство ![]() .
.
6)
Так как ![]() и f (x) убывает на проме-
и f (x) убывает на проме-
жутке [0; +∞), то она на этом промежутке имеет наибольшее значение −1 + 3 = 2, достигаемое в точке х = 0. Так как f (x) — четная функция, то и на R она принимает наибольшее значение 2 в точке х = 0. Функция f (x) не имеет наименьшего значения, так как f (x) > −1 при всех х.
7) Область изменения функции y = f (x) есть промежуток Y = (−1; 2], так как y принимает все значения из промежутка (−1; 2].
Вычислим координаты нескольких точек графика:
|
х |
0 |
0,5 |
1 |
|
2 |
3 |
7 |
|
у |
2 |
1,4 |
0,5 |
0 |
−0,4 |
−0,7 |
−0,94 |
Учитывая перечисленные свойства функции f (x), построим ее график сначала для x > 0, а потом отразим его симметрично относительно оси Oy (рис. 7).

Рис. 7
В данном пункте учебника обобщаются рассмотренные ранее на примерах способы преобразования графиков функций. Здесь изучаются пункты:
1) симметрия относительно осей координат;
2) сдвиг (параллельный перенос) вдоль осей координат;
3) растяжение и сжатие графиков вдоль осей координат;
4) построение графика функции y = A (k (x − a)) + B по графику функции y = f (x);
5) симметрия относительно прямой y = x.
Изложение п. 1—5 близко к традиционному, оно содержит обоснования, проведенные для произвольной точки M0 (x0; y0). Пункт 5, посвященный симметрии относительно прямой y = x, учащимся нужно обязательно усвоить, если в программу их обучения входит изучение обратной функции.
Следует обратить внимание на задания 1.68, 1.69, 1.73, в которых используется уравнение окружности. В классах с углубленным изучением математики этот материал должен быть хорошо проработан, так как он будет дальше часто использоваться.
В п. 7 дидактических материалов приведены примеры построения графиков функций с использованием этих способов их преобразования.
Решения и комментарии
1.68. Уравнение окружности с центром O (0; 0) радиуса R имеет вид х2 + у2 = R2, поэтому графиком функции
![]()

 y
= R2
− x2
является верхняя полуокружность (рис. 8). Постройте график функции: а) y
= 4 − x2 ;
y
= R2
− x2
является верхняя полуокружность (рис. 8). Постройте график функции: а) y
= 4 − x2 ;
б) y = − 4 − x2 ;
в) y = 9 − (x − 1)2 ;
е) y = − 25 − (x − 3)2 +1.
Решение. а) Графиком функ-
ции y = 4 − x2 является верх- Рис. 8 няя полуокружность окружности х2 + у2 = 4 (см. рис. 8, R = 2).
 б)
График функции y =
− 4 −
x2 симметричен графику
б)
График функции y =
− 4 −
x2 симметричен графику
![]() функции y = 4 − x2 относительно
оси Ox (рис. 9).
функции y = 4 − x2 относительно
оси Ox (рис. 9).
в) Графиком функции y = 9 − x2 является верхняя полуокружность окружности х2 + у2 = 9. График функции
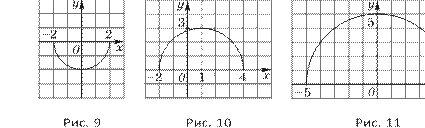
![]() y = 9 − (x − 1)2 получим
переносом графика функции y =
9 − x2
на 1 единицу вправо (рис. 10).
y = 9 − (x − 1)2 получим
переносом графика функции y =
9 − x2
на 1 единицу вправо (рис. 10).
![]()
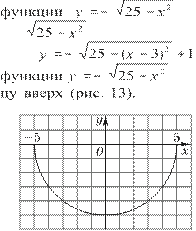
 е)
Графиком функции y =
25 − x2
является верхняя полуокружность окружности х2 + у2 = 25 (рис. 11). График
симметричен графику функции
е)
Графиком функции y =
25 − x2
является верхняя полуокружность окружности х2 + у2 = 25 (рис. 11). График
симметричен графику функции
y = относительно оси Ox (рис. 12). График функции получим переносом графика
на 3 единицы вправо и на 1 едини-
Рис. 12 Рис. 13
![]() В сложном случае
е) перед приведенным выше построением полезно показать следующее: если
уравнение переписать в виде y −
1 = − 25
− (x − 3)2 и
возвести полученное уравнение в квадрат, то получится уравнение окружности (х
− 3)2
+ (у − 1)2 = 25. Теперь становится
понятным, что графиком исходной функции является нижняя полуокружность
окружности (х −
3)2 + (у
− 1)2
= 25 (см.
рис. 13) и для ее построения надо выполнить приведенные выше шаги.
В сложном случае
е) перед приведенным выше построением полезно показать следующее: если
уравнение переписать в виде y −
1 = − 25
− (x − 3)2 и
возвести полученное уравнение в квадрат, то получится уравнение окружности (х
− 3)2
+ (у − 1)2 = 25. Теперь становится
понятным, что графиком исходной функции является нижняя полуокружность
окружности (х −
3)2 + (у
− 1)2
= 25 (см.
рис. 13) и для ее построения надо выполнить приведенные выше шаги.
1.70. Постройте график функции:
а) x = 2y; б) x = 2y2, y ≥ 0; в) x = 2y; г) x = ⎛⎝⎜ 21⎟⎠⎞ y;
![]() д)
x
д)
x ![]() ; е) x = 1 −
y2 .
; е) x = 1 −
y2 .
 Решение. В заданиях а)—е) требуется построить график
функции x = f
(y), зная график функции y =
f (x). Такие графики уже строились в 10 классе по точкам,
при этом значения аргумента y откладывались по оси Oy, а значения
функции x — по оси Ox. В учебнике доказано, что графики функций x
= f (y)
и y = f
(x) симметричны относительно прямой y = x, поэтому теперь графики можно
строить с помощью симметрии относительно прямой y = x.
Решение. В заданиях а)—е) требуется построить график
функции x = f
(y), зная график функции y =
f (x). Такие графики уже строились в 10 классе по точкам,
при этом значения аргумента y откладывались по оси Oy, а значения
функции x — по оси Ox. В учебнике доказано, что графики функций x
= f (y)
и y = f
(x) симметричны относительно прямой y = x, поэтому теперь графики можно
строить с помощью симметрии относительно прямой y = x.
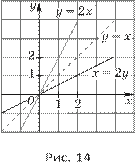
а) График функции x = 2y, y ≥ 0, построим, отразив симметрично относительно прямой y = x график функции y = 2x (рис. 14).
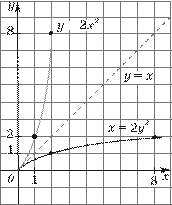 б) График функции x =
2y2, y ≥
0, построим, отразив симметрично относительно прямой y = x график
функции y = 2x2,
x ≥ 0
б) График функции x =
2y2, y ≥
0, построим, отразив симметрично относительно прямой y = x график
функции y = 2x2,
x ≥ 0
(рис. 15).
в) График функции x = 2y построим, отразив симметрично относительно прямой y = x график функции y = 2x (рис. 16).
г) График функции x = ⎛⎜⎝ 21⎞⎟⎠ y
построим, отразив симметрично относительно прямой y = x график функции y = ⎛⎜⎝ 21⎞⎟⎠ x (рис. 17).
Рис. 15
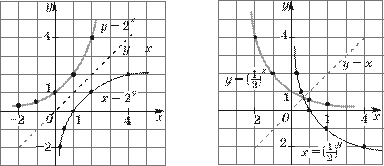
Рис. 16 Рис. 17

Рис. 18 Рис. 19
![]() д) График
функции x = sin
y,
д) График
функции x = sin
y, ![]() , построим, отразив симметрично
относительно прямой y =
x график функции y (рис. 18).
, построим, отразив симметрично
относительно прямой y =
x график функции y (рис. 18).
![]() е) График
функции x = 1
− y2
построим, отразив симметрично относительно прямой y = x график
функции y = 1
− x2
. Получится правая полуокружность окружности х2 + у2 = 1 (рис. 19).
е) График
функции x = 1
− y2
построим, отразив симметрично относительно прямой y = x график
функции y = 1
− x2
. Получится правая полуокружность окружности х2 + у2 = 1 (рис. 19).
1.72. Придумайте пример функции y = f (x), график которой совпадает с графиком функции х = f (у) при построении их в одной системе координат xOy.
Решение. Примеры таких функций: y = x и x = y; y = 1 x
и x = 1; y = − 2 и x = − 2 ; y = 1 − x и x = 1 − y; y = 2 − x и y x y x = 2 − y.
1.74. На рисунке 20, а—е изображена парабола. Является ли эта парабола графиком функции y = f (x) или x = ϕ (y)? Если да, то задайте эту функцию формулой.
Решение. а) На рисунке 20, а изображена парабола y = ax2, проходящая через точку (1; 2). Так как 2 = a ⋅ 12 при a = 2, то это парабола y = 2x2.
б) На рисунке 20, б изображена парабола y = ax2, проходящая через точку (1; −2). Так как −2 = a ⋅ 12 при a = −2, то это парабола y = −2x2.
в) На рисунке 20, в изображена парабола x = ay2, проходящая через точку (2; 1). Так как 2 = a ⋅ 12 при a = 2, то это парабола x = 2y2.
г) На рисунке 20, г изображена парабола y = ax2, проходящая через точку (−2; 1). Так как −2 = a ⋅ 12 при a = −2, то это парабола x = −2y2.

д) На рисунке 20, д изображена парабола y = a (x − 1)2 + 1, так как ее вершина (x0; y0) имеет координаты (1; 1). Парабола проходит через точку (0; 3), поэтому из равенства 3 = a (0 − 1)2 + 1 следует, что a = 2. Итак, это парабола y = 2 (x − 1)2 + 1.
е) На рисунке 20, е изображена парабола y = a (x − 1)2 + 2, так как ее вершина (x0; y0) имеет координаты (1; 2). Парабола проходит через точку (0; 0), поэтому из равенства 0 = a (0 − 1)2 + 2 следует, что a = −2. Итак, это парабола y = −2 (x − 1)2 + 2.
Дополнение. В качестве дополнительного задания можно предложить учащимся задать формулой параболу, изображенную на рисунке 21, а.
Решение. На рисунке 21, а изображена парабола x = a (y − 1)2 + 2, так как ее вершина (x0; y0) имеет координаты (2; 1). Парабола проходит через точку (0; 0), поэтому из равенства 0 = a (0 − 1)2 + 2 следует, что a = −2. Итак, это парабола x = −2 (y − 1)2 + 2.

Заметим, что парабола, изображенная на рисунке 21, а, симметрична относительно прямой y = x (рис. 21, б) параболе y = −2 (x − 1)2 + 2 (задание 1.74), поэтому формулу, которой задана парабола, изображенная на рисунке 21, а, можно получить с помощью замены x на y и y на x из формулы y = −2 (x − 1)2 + 2.
Промежуточный контроль. C—7.
1.8*. Графики сложных функций
Пункты 1.7—1.8 учебника необязательны при обучении на базовом уровне. Здесь показано, как строить графики функций, содержащих модули, и графики сложных функций. В п. 1.7 показывается, как с помощью графика функции у = f (x) строить графики функций у = | f (x) | и у = f (| x |). На большом числе примеров здесь обобщаются рассмотренные ранее для частных случаев способы преобразования графиков функций, содержащих модули.
В п. 8 дидактических материалов рассмотрены примеры построения графиков функций, содержащих модули.
В п. 1.8 рассматривается на конкретных примерах построение графиков суперпозиции, суммы, произведения двух функций, графиков кусочно-заданных функций.
В п. 9 дидактических материалов рассмотрены задачи на применение графиков при решении задач с параметром.
Решения и комментарии
1.81. Постройте график функции:
а) y = x2 − 5 | x − 1 | + 1; б) y = | x2 − 3x + 2 | + 2x − 3. Решение. а) Построим график исходной функции на двух промежутках: (−∞; 1] и [1; +∞).
1) Если x ≥ 1, то x2 − 5 | x − 1 | + 1 = x2 − 5 (x − 1) + 1 = x2 − 5x + 6.
Графиком функции y = x2 − 5x + 6 является парабола с вершиной (2,5; −0,25). Определим координаты некоторых точек этой параболы:
|
x |
1 |
2 |
2,5 |
3 |
4 |
|
y |
2 |
0 |
−0,25 |
0 |
2 |
Графику исходной функции принадлежат лишь точки параболы из промежутка [1; +∞).
2) Если x ≤ 1, то x2 − 5 | x − 1 | + 1 = x2 + 5 (x − 1) + 1 = x2 + 5x − 4.
Графиком функции y = x2 + 5x − 4 является парабола с вершиной (−2,5; −10,25). Определим координаты некоторых точек этой параболы:
|
x |
−4 |
−3 |
−2,5 |
−2 |
−1 |
|
y |
−8 |
−10 |
−10,25 |
−10 |
−8 |
Графику исходной функции принадлежат лишь точки параболы из промежутка (−∞; 1].
График исходной функции изображен жирной линией на рисунке 22.
б) Исходную функцию можно задать формулой y = | (x − 1) (x − 2) | + 2x − 3. Построим ее график на промежутках (−∞; 1], [1; 2] и [2; +∞).

1) Если 1 ≤ x ≤ 2, то
| x2 − 3x + 2 | + 2x − 3 = − (x2 − 3x + 2) + 2x − 3 = −x2 + 5x − 5.
Графиком функции y = −x2 + 5x − 5 является парабола с вершиной (2,5; 1,25). Определим координаты некоторых точек этой параболы:
|
x |
1 |
2 |
2,5 |
3 |
4 |
|
y |
−1 |
1 |
1,25 |
1 |
−1 |
Графику исходной функции принадлежат лишь точки параболы из промежутка [1; 2].
2) Если x ≤ 1 или x ≥ 2, то
| x2 − 3x + 2 | + 2x − 3 = x2 − 3x + 2 + 2x − 3 = x2 − x − 1.
Графиком функции y = x2 − x − 1 является парабола с вершиной (0,5; −1,25). Определим координаты некоторых точек этой параболы:
|
x |
−4 |
−3 |
−2,5 |
−2 |
−1 |
|
y |
−8 |
−10 |
−10,25 |
−10 |
−8 |
Графику исходной функции принадлежат лишь точки параболы из промежутков (−∞; 1] и [2; +∞).
График исходной функции изображен жирной линией на рисунке 23.
Замечание. Чтобы убедиться, что графиком функции является непрерывная линия, границы промежутков включены в каждый из рассматриваемых промежутков.
1.82. Постройте график функции:
а) y = [sin x]; б) y = {sin x};
в) y = [cos x]; г) y = {cos x}.
Решение. а) Здесь учащимся можно напомнить, что целая часть числа a, обозначаемая [a], есть наибольшее число, не превосходящее a. Поэтому если sin x = 1, то [sin x] = 1; если sin x = −1, то [sin x] = −1; если 0 < sin x < 1, то [sin x] = 0; если −1 < sin x < 0, то
[sin x] = −1. График функции y = [sin x] изображен на рисунке 24, а.
б) Дробная часть числа a, обозначаемая {a}, есть разность этого числа и его целой части: {a} = a − [a]. Поэтому если sin x равен −1, 0 или 1, то {sin x} = 0; если 0 < sin x < 1, то {sin x} = sin x; если −1 < sin x < 0, то {sin x} = sin x − (−1) = = sin x + 1. График функции y = {sin x} изображен на рисунке 24, б.
в), г) Так как cos x = sin ⎛⎜⎝x + 2π ⎞⎟⎠, то графики функций y = [cos x] и y = {cos x} можно получить сдвигом вдоль
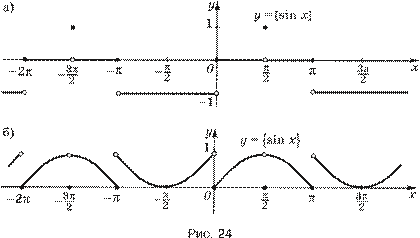
оси Ox графиков функций y = [sin x] и y
= {sin x}
соответственно на ![]()
![]() влево.
влево.
Замечание. В заданиях д)—з) по каждому графику функции y = f (x), построенному в заданиях а)—г), надо построить график функции y = | f (x) |.
1.83. Постройте график функции: sin x cos x
а) y = ![]() ; б) y =
; б) y = ![]() .
.
| sin x | | cos x |
Решение. а) Функция определена в тех точках x, где sin x ≠ 0. Если sin x > 0, то y = 1; если sin x < 0, то y = −1. sin x
График
функции y = ![]() изображен на рисунке 25.
изображен на рисунке 25.
| sin x |
б) Так как cos x = sin ⎛⎜⎝x + 2π ⎞⎟⎠, то график функции cos x
y =можно получить сдвигом графика функции
| cos x |
![]() y = sin x на π
влево.
y = sin x на π
влево.
Рис. 25
1.87. Постройте график функции:
![]() а)
y = x2
+ 2x +1 + x2 − 6x + 9;
а)
y = x2
+ 2x +1 + x2 − 6x + 9;
б) y = x2 − 2x +1 − x2 + 6x + 9.
Решение. а) Данную функцию можно записать в виде y = | x + 1 | + | x − 3 |. Построим ее график на каждом из промежутков: x ≥ 3, −1 ≤ x ≤ 3, x ≤ −1.
1) Если x ≤ −1, то | x + 1 | + | x − 3 | = −x − 1 − x + 3 = = −2x + 2. График функции — часть прямой y = −2x + 2, для точек которой выполнено условие x ≤ −1.
2) Если −1 ≤ x ≤ 3, то | x + 1 | + | x − 3 | = x + 1 − x + 3 = 4. График функции — часть прямой y = 4, для точек которой выполнено условие −1 ≤ x ≤ 3.
3) Если x ≥ 3, то | x + 1 | + | x − 3 | = x + 1 + x − 3 = 2x − 2. График функции — часть прямой y = 2x − 2, для точек которой выполнено условие x ≥ 3.
График исходной функции изображен на рисунке 26.

Рис. 26 Рис. 27
б) Исходную функцию можно записать в виде y = | x − 1 | − | x + 3 |. Построим ее график на каждом из промежутков: x ≥ 1, −3 ≤ x ≤ 1, x ≤ −3.
1) Если x ≤ −3, то | x − 1 | − | x + 3 | = −x + 1 + x + 3 = 4. График функции — часть прямой y = 4, для точек которой выполнено условие x ≤ −3.
2) Если −3 ≤ x ≤ 1, то | x − 1 | − | x + 3 | = −x + 1 − x − 3 = = −2x − 2. График функции — часть прямой y = −2x − 2, для точек которой выполнено условие −3 ≤ x ≤ 1.
3) Если x ≥ 1, то | x − 1 | − | x + 3 | = x − 1 − x − 3 = −4. График функции — часть прямой y = −4, для точек которой выполнено условие x ≥ 1.
График исходной функции изображен на рисунке 27.
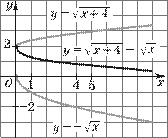 1.88. а) Постройте график функции y = x + 4 − x.
1.88. а) Постройте график функции y = x + 4 − x.
![]() Решение. В одной системе
координат построим графики двух функций y =
x + 4
и y = − x
(на общей части их областей существования, т. е. для x ≥ 0). Затем для
каждого значения x сложим соответствующие значения функций и получим
ординату точки
Решение. В одной системе
координат построим графики двух функций y =
x + 4
и y = − x
(на общей части их областей существования, т. е. для x ≥ 0). Затем для
каждого значения x сложим соответствующие значения функций и получим
ординату точки
![]() графика исходной функции. Рис.
28 Так как функцию y =
x + 4
−
графика исходной функции. Рис.
28 Так как функцию y =
x + 4
−
− x можно записать в виде y = , то очевидно,
что эта функция убывающая на промежутке [0; +∞), причем при неограниченном возрастании x значения y стремятся к нулю, оставаясь положительными.
График исходной функции изображен на рисунке 28. Промежуточный контроль. C—8, C—9.
|
§ 2. |
Предел функции и непрерывность
Понятие предела функции является одним из основных понятий в курсе алгебры и начал математического анализа. Однако практика введения этого понятия в школе показала, что оно с трудом усваивается учащимися. Поэтому при обучении на базовом уровне даже не используют знак предела. Мы считаем, что вполне достаточно интуитивного понимания предела функции, и пользуемся знаком предела.
В данном пункте из рассмотрения многочисленных примеров на интуитивном уровне вводится понятие предела функции сначала при х → +∞, затем при х → −∞. При этом никак не формализуются слова «x неограниченно возрастает» и «значения функции f (x) стремятся к A», где A — действительное число, +∞ или −∞. Вводится соответствующая символика (знак предела), объясняется смысл употребления слова «равен» и знака «=» перед знаками +∞, −∞, ∞, не являющимися действительными числами. Затем дается понятие предела функции в точке также на интуитивном уровне.
Решения и комментарии 2.2. Объясните, что означает запись:
а) lim ⎜⎝2 x
x → +∞ ⎛ + 1 ⎞⎠⎟ = 2; б) xlim→ −3 x2 = 9; г) xlim→ 5 x 1− 5 = ∞.
Решение. а) Эта запись означает, что при неограниченном возрастании x (при х → +∞) соответствующие значения функции y = 2 + 1 стремятся к числу 2. x
б) Эта запись означает, что при х → −3 соответствующие значения функции y = х2 стремятся к числу 9.
![]()
![]() 1
1
г) Эта запись означает, что lim= +∞, т. е. x → 5x − 5
![]() при х → 5
соответствующие значения функции y =1
при х → 5
соответствующие значения функции y =1
x − 5
стремятся к +∞, т. е. неограниченно возрастают.
2.3. Объясните, почему верно равенство:
![]() а)
xlim→
1
а)
xlim→
1 ![]() 1 =
+∞; б) xlim→
− 1 (x +−11)2 = −∞;
1 =
+∞; б) xlim→
− 1 (x +−11)2 = −∞;
в) xlim 3 = ∞.
→ 2 (x − 2)
Решение. а) Функция y = ![]() 1 определена для всех x,
1 определена для всех x,
| x − 1|
кроме x = 1. Для всех x ≠ 1 соответствующие значения этой функции положительны, и при х → 1 они неограниченно возрастают, а это и означает справедливость равенства.
![]() б) Функция y
б) Функция y ![]() определена
для всех x, кроме
определена
для всех x, кроме
x = −1. Для всех x ≠ −1 соответствующие значения этой функции отрицательны, а их модули при х → −1 неограниченно возрастают, а это и означает справедливость равенства.
![]() в) Так как lim= +∞, то это и
означает спра-
в) Так как lim= +∞, то это и
означает спра-
x → 2
ведливость равенства.
2.5. Определите, чему равен предел:
а) lim (−1)[ x] ⋅ x3 ; д) lim (−2)[ x] . x → +∞ x → +∞
Решение. а) Так как lim | (−1)[ x] ⋅ x3 | = +∞, то lim (−1)[ x] ⋅ x3 = ∞. x → +∞
x → +∞
д) Так как lim | (−2)[ x] | = +∞, то lim (−2)[ x] = ∞. x → +∞ x → +∞
В данном пункте учебника рассматривается понятие одностороннего предела.
sin x
Сначала рассматривается функция y = ![]() . Она опреx
. Она опреx
делена для всех действительных x, кроме x = 0, ее график изображен на рисунке 62 учебника.
Из рассмотрения положительных значений x, близких sin x
к нулю (х → 0, x > 0), делается вывод, что lim = 1,
![]() x → 0 x x > 0
x → 0 x x > 0
sin x
т. е. находится односторонний предел функции при x, x
стремящемся к нулю справа.
Затем с помощью замены переменной x = −u показываsin x
ется, что и lim ![]() =
1. Тем самым доказано, что и при x, x → 0 x x < 0
=
1. Тем самым доказано, что и при x, x → 0 x x < 0
sin x
стремящемся к нулю слева, предел функции ![]() сущестx
сущестx
вует и тоже равен 1.
Наконец, приводятся определения правого и левого пределов функции f (x) в точке.
Далее после рассмотрения ряда примеров в учебнике дано определение:
Если существуют левый и правый пределы функции y = f (x) в точке a и оба они равны A, то говорят, что эта функция имеет предел в точке a, равный A, и пишут: lim f x( ) = A. x → a
Для обучения на профильном уровне в учебнике приведены также определения предела функции «на языке ε − δ» и «на языке последовательностей».
Следует подчеркнуть, что пределы, найденные по разным определениям, совпадают.
Решения и комментарии
2.7. Найдите левый и правый пределы функции y = f (x) при x → a, если:
а) f x( ) = x 1+
2 , a = −2; б)
f x( ) = ![]() 1 2 , a =
2.
1 2 , a =
2.
Решение. а) При x → −2 и x < −2 дробь 1 отриx + 2
цательна и стремится к −∞, т. е. lim 1 = −∞. При
![]() x
x
x
x → −2 и x > −2 дробь 1 положительна и стремится к x + 2
![]() +∞, т. е..
+∞, т. е..
x
x > −2
б) При x → 2 и x < 2 дробь ![]() 1 2 стремится к
+∞,
1 2 стремится к
+∞,
т. е. xlim→
2 (![]() x 1 =
+∞. При x →
2 и x >
2 дробь
x 1 =
+∞. При x →
2 и x >
2 дробь ![]() 1 2
1 2
− 2)2 (x − 2)
x < 2 стремится к +∞,
т. е. lim ![]() 1 2
= +∞.
1 2
= +∞.
2.11. Найдите левый и правый пределы функции y = f (x) при x → a, если:
x x2 − 4
а) f x( ) = , a = 0; б) f x(
) = ![]() , a = −2.
, a = −2.
| x | x + 2
Решение. а) При x → 0 и x < 0 дробь x равна −1, по-
| x |
этому lim x = −1. При x → 0 и x > 0 дробь x равна 1, x → 0 | x | | x | x < 0
x поэтому lim = 1.
x → 0 | x |
x > 0
x2 − 4
б) При x → −2 и x
< −2 верны равенства ![]() =
=
x + 2
(x − 2) (x + 2) x2 − 4
=
![]() =
x − 2,
поэтому lim
=
x − 2,
поэтому lim ![]() =
lim (x −
2) = −4.
x +
2 x → −2 x + 2 x → −2 x < −2 x <
−2
=
lim (x −
2) = −4.
x +
2 x → −2 x + 2 x → −2 x < −2 x <
−2
x2 − 4
При x → −2 и x
> −2
верно равенство ![]() =
x − 2,
поx +
2
=
x − 2,
поx +
2
x2 −
4 этому lim ![]() =
lim (x −
2) = −4.
=
lim (x −
2) = −4.
x → −2 x + 2 x → −2 x > −2 x > −2
2.12. Вычислите:
sin 2x sin πx
а) lim ![]() ; в) lim
; в) lim ![]() . x → 0 2x x → 0 πx
. x → 0 2x x → 0 πx
Решение. а) При x → 0 переменная u = 2x также стреsin 2x sin u
мится к 0 (u → 0), поэтому lim
![]() =
lim
=
lim ![]() =
1. x →
0 2x u → 0 u
=
1. x →
0 2x u → 0 u
в) При x → 0 переменная u = πx также стремится к 0 sin πx sin u
(u →
0), поэтому lim ![]() = lim
= lim ![]() = 1.
= 1.
x → 0 πx u → 0 u
2.13. а) Докажите, используя определение предела «на языке ε − δ» или «на языке последовательностей», что
lim (3x − 7) = 5. x → 4
Доказательство. 1-й способ. Функция y = 3x − 7 определена в любой окрестности точки x0 = 4, включая и саму точку x0 = 4. Возьмем произвольное положительное число ε и выясним, для каких значений x выполняется неравенство | 3x − 7 − 5 | < ε. Поскольку равносильны нера-
венства
| 3x −
7 − 5
| < ε,
| 3x − 12
| < ε, |
x − 4|
< ![]()
![]() , (1) то это означает, что для
любого числа ε >
0 нашлось число δ
=
, (1) то это означает, что для
любого числа ε >
0 нашлось число δ
= ![]()
![]() > 0, такое, что из справедливости неравенства
| x − 4
| < δ следует
справедливость неравенств (1). По определению предела «на языке ε − δ» это означает, что
> 0, такое, что из справедливости неравенства
| x − 4
| < δ следует
справедливость неравенств (1). По определению предела «на языке ε − δ» это означает, что
lim (3x − 7) = 5, что и требовалось доказать. x → 4
2-й способ. Рассмотрим произвольную последовательность {xn} значений переменной x, имеющую пределом чис-
1 ло 4. Пусть, например, xn = 4 + . Тогда последователь-
n
ность {f (xn)} соответствующих значений функции f (x) = 3x − 7 задается формулой общего члена f x( n) = 3xn − 7 = 5 + 3 . Эта последовательность имеет преn
делом при n → +∞ число 5. По определению предела «на языке последовательностей» это означает, что lim (3x − 7) = 5, что и требовалось доказать. x → 4
Дополнение. В учебнике утверждается, что можно доказать, что
1 1
lim (1 + x)x = e и lim (1 + x)x = e, (2)
x → 0 x → 0 x > 0 x < 0 где e — иррациональное число, приближенно равное
2,71828... .
Докажем это. Как показано в учебнике для 10 класса,
nlim→ +∞ ⎜⎝⎛1 + n1 ⎞⎟⎠ n = e, (3)
если n ∈ N и n → +∞.
Покажем, что
⎛ + 1 ⎞⎟ α
αlim→ +∞ ⎜⎝1 α ⎠ = e, (4)
если α → +∞, принимая любые положительные значения, необязательно натуральные.
Обозначим через [α] целую часть числа α. Для любого положительного числа α выполняются очевидные неравенства
[α] ≤ α < [α] + 1.
Но тогда для α ≥ 1 имеем
⎛⎜⎝1 [α]+11 ⎞ [α] + 1 ⎛ + 1 ⎞⎟⎠ [α] + 1 < ⎝⎛⎜1+ α1 ⎞⎟⎠α + 1 ≤ ⎛⎜⎝1+ [α]1 ⎠⎟⎞α + 1 < ⎛⎝⎜1+ [α]1 ⎞⎠⎟ [α]+ 2.
+ ⎟⎠ < ⎜⎝1 α
Разделив на ![]() все члены этих неравенств, получим, что
справедливы неравенства
все члены этих неравенств, получим, что
справедливы неравенства
⎛ 1 ⎞ [α] + 1 ⎛ 1 ⎞ 2
![]() ⎜⎝
1 +
[α]
+ 1⎟ α ⎜⎝
1 +
[α]⎟⎠ ⎛ 1 ⎞ [α]
⎜⎝
1 +
[α]
+ 1⎟ α ⎜⎝
1 +
[α]⎟⎠ ⎛ 1 ⎞ [α]
![]() ⎠ < ⎛⎜⎝1
+ 1 ⎞⎟⎠⋅ ⎜⎝1
+ [α]⎟⎠ . (5)
⎠ < ⎛⎜⎝1
+ 1 ⎞⎟⎠⋅ ⎜⎝1
+ [α]⎟⎠ . (5)
![]() α
α
Пусть α → +∞. Тогда m = [α] + 1 и m1 = [α] таковы, что m ∈ N и m1 ∈ N, m → +∞ и m1 → +∞. Используя равенство (3), получим, что
⎛ 1 ⎞ α] + ⎛
α → +∞lim ⎜⎝1 + [α] + 1⎟⎠ [ 1 = m lim→ +∞ ⎝⎜1 + m1 ⎟⎠⎞ m = e,
⎛ 1 ⎞ [α] ⎛ 1 ⎞ m1
α → +∞lim ⎜⎝1 + [α]⎟⎠ = m1lim→ +∞ ⎜⎝1 + m1 ⎟⎠ = e.
Так как при α → +∞ знаменатель левой части соотношения (5) стремится к 1 и дробь в правой части также стремится к 1, то левая и правая части в соотношении (5) стремятся к e. Но тогда и средняя часть соотношения (5) стремится к e. Справедливость равенства (4) доказана.
Пусть теперь α → −∞, принимая любые отрицательные значения, необязательно натуральные. Тогда β = −α → +∞, принимая любые положительные значения, следовательно, α −β β
α
→ −∞lim ⎜⎝⎛1
+ α1 ⎟⎠⎞ = β
lim→
+∞ ⎜⎝⎛1
− β1⎟⎠⎞ = β
lim→
+∞ ⎝⎛⎜β![]() β− 1⎠⎞⎟ =
β− 1⎠⎞⎟ =
= β lim→ +∞ ⎛⎜⎝⎜⎛⎜⎝1 + β 1− 1⎠⎟⎞β − 1 ⎛⎜⎝1 + β 1− 1⎟⎠⎞⎟⎟⎠⎞ = e ⋅ 1 = e.
Таким образом, доказано, что
αlim→ −∞ ⎛⎜⎝1 + α1 ⎞⎟⎠ α = e, (6)
если α → −∞, принимая любые отрицательные значения.
Если в формуле (4) положить x ![]() , то получим, что x
→ 0 и x
> 0 при α → +∞ и
α > 0,
следовательно,
, то получим, что x
→ 0 и x
> 0 при α → +∞ и
α > 0,
следовательно,
lim
(![]()
![]() x) e.
x) e.
xx > 0
Аналогично если в формуле (6) положить x ![]() ,
то получим, что x →
0 и x <
0 при
,
то получим, что x →
0 и x <
0 при ![]() 0, следовательно,
0, следовательно,
![]() lim ( +
x)x =
e.
lim ( +
x)x =
e.
x
x < 0
Тем самым мы доказали, что справедливы равенства (2).
В данном пункте учебника рассматриваются свойства пределов функций и применение этих свойств для вычисления пределов. При этом свойства пределов не доказываются.
В п. 10 дидактических материалов приведены примеры вычисления пределов функций.
Решения и комментарии
2.15. Вычислите:
x3 − 1
а) lim (sin x + cos x); в) lim ; x →x → 1 x − 1
1
![]() −
cos 2x
−
cos 2x
 г) lim; д) lim;
x →
−2 x
→
0 x2
г) lim; д) lim;
x →
−2 x
→
0 x2
е) lim (1 + 3x) . x → 0
Решение. а) lim (sin x + cos x) = lim sin x + x → π x → π
2 2
+ lim cos x = 1 + 0 = 1.
x →
![]()
![]()
x3 − 1 (x − 1) (x2 + x + 1) 2 + x +1) =
в) lim ![]() = lim
= lim ![]() = lim (x x →
1 x − 1 x → 1 x − 1 x → 1
= lim (x x →
1 x − 1 x → 1 x − 1 x → 1
= 12 +1 +1 = 3.
г) При x → −2 переменная u = x + 2 стремится к 0 sin (x + 2) sin u
(u → 0), поэтому lim = lim = 1.
x → −2 x + 2 u → 0 u
![]()
![]() д) lim 1 − cos 2x 2 sin 2 x ⎛
sin x⎞
2 = x →
д) lim 1 − cos 2x 2 sin 2 x ⎛
sin x⎞
2 = x → ![]() =
xlim→
0 x2 = 2 xlim→
0 ⎜⎝ x ⎟⎠
=
xlim→
0 x2 = 2 xlim→
0 ⎜⎝ x ⎟⎠
= 2 ⎛⎜⎝ xlim→ 0 x ⎟⎠ = 2.
1 ⎛ 1 ⎞ 3
е) Так как lim (1 + 3x)x = lim ⎜(1 + 3x)3 x ⎟ и при x → 0 x → 0 x → 0 ⎝ ⎠
1
переменная u = 3x стремится к 0 (u → 0), то lim (1 + 3x)x =
x → 0
⎛ 1 ⎞ 3 ⎛ 1 ⎞ 3
= ulim ⎜⎝(1 + u)u ⎟⎠ = ⎜⎝ulim (→ 0 1 + u)u ⎟⎠ = e3.
→ 0
3 x
2.18. а) Вычислите xlim→ ∞ ⎜⎝⎛1 + x1 ⎞⎟⎠ .
Решение. Положим x ![]() ,
тогда α → 0
при x →
∞ и
,
тогда α → 0
при x →
∞ и
справедливы равенства
xlim ⎜⎝1 + x1 ⎠⎞⎟ 3 x = αlim (→ 0 1 + α)α3 = αlim→ 0 ⎜⎝⎛(1 + α)α1 ⎞⎠⎟ 3 = ⎛
→ ∞
⎛ 1 ⎞ 3
= ⎜⎝ αlim (→ 0 1 + α)α ⎟⎠ = e3.
3x + 7
2.19. а) Вычислите lim
![]() . x → ∞ 2x +
1
. x → ∞ 2x +
1
3x +
7 ![]()
![]() Решение. lim
Решение. lim ![]() = lim= x →
∞ 2x +
1 x →
∞ 2 +
1 x
= lim= x →
∞ 2x +
1 x →
∞ 2 +
1 x
![]() xlim→∞⎜⎝⎛
3 +
7x ⎞⎟⎠
.
xlim→∞⎜⎝⎛
3 +
7x ⎞⎟⎠
.
⎛ 1 ⎞ xlim→∞⎜⎝ 2 + x ⎟⎠
Промежуточный контроль. C—10.
В данном пункте учебника вводятся понятия приращения аргумента и приращения функции, с использованием предела функции объясняется, что такое непрерывность функции в точке и на интервале. Этот материал должны усвоить все учащиеся хотя бы на интуитивном уровне. Вычисление приращений функции в заданной точке x0 и при заданном приращении аргумента Δx готовит учащихся к усвоению понятия производной.
Для обучения на профильном уровне непрерывность функции в точке определяется «на языке ε − δ», вводятся понятия непрерывности справа и непрерывности слева в точке x0, непрерывности на отрезке [a; b].
Решения и комментарии
2.23. а) Вычислите приращение Δf функции y = f (x) в заданной точке x0 и при заданном приращении аргумента Δx, если f (x) = −2x + 1, x0 = 0, Δx = 0,1.
Решение. Δf = f (x0 + Δx) − f (x0) = −2 (x0 + Δx) + 1 −
− (−2x0 + 1) = −2x0 − 2Δx + 1 + 2x0 − 1 = −2Δx = −2 ⋅ 0,1 = −0,2.
2.25. в) Найдите приращение Δf функции y = f (x), соответствующее приращению аргумента Δx, в точке x0, если f (x) = x2. К чему стремится Δf при Δx → 0? Зависит ли ответ на этот вопрос от выбора точки x0?
Решение. Δf = f (x0 + Δx) − f (x0) = (x0 + Δx)2 − (x0)2 =
= (x0)2 + 2x0Δx + (Δx)2 − (x0)2 = 2x0Δx + (Δx)2 = Δx (2x0 + Δx),
Δf → 0 при Δx → 0. Ответ не зависит от выбора точки x0. (Это и означает, что в любой точке x0 своей области определения функция f (x) = x2 непрерывна.)
2.28. Докажите, что в любой точке x0 ∈ (0; +∞) непрерывна функция:
3
−
а) y = log2 x; б) y = x 2.
Доказательство. а) Так как Δf = f (x0
+ Δx)
− f (x0)
= = log2 (x0
+ Δx)
− log2
x0 =
log2 ![]() x0 x+0 Δx = log2 ⎝⎜⎛1 +
xΔx0 ⎟⎞⎠ в любой
точке x0 ∈
(0; +∞),
то при Δx
→ 0
имеем ⎛⎝⎜1
+
xΔx0 ⎞⎟⎠ → 1, а
log2 ⎜⎝⎛1 +
xΔx0 ⎞⎟⎠ → 0, т.
е. Δy → 0 при Δx → 0.
Следовательно, в любой точке x0 ∈ (0; +∞)
функция y = log2
x непрерывна.
x0 x+0 Δx = log2 ⎝⎜⎛1 +
xΔx0 ⎟⎞⎠ в любой
точке x0 ∈
(0; +∞),
то при Δx
→ 0
имеем ⎛⎝⎜1
+
xΔx0 ⎞⎟⎠ → 1, а
log2 ⎜⎝⎛1 +
xΔx0 ⎞⎟⎠ → 0, т.
е. Δy → 0 при Δx → 0.
Следовательно, в любой точке x0 ∈ (0; +∞)
функция y = log2
x непрерывна.
б) Так как ![]()
![]() в любой точке x0
∈ (0;
+∞), то
в любой точке x0
∈ (0;
+∞), то
![]() при Δx
→ 0, т.
е. Δf → 0 при Δx → 0.
при Δx
→ 0, т.
е. Δf → 0 при Δx → 0.
− 3
Следовательно, в любой точке x0 ∈ (0; +∞) функция y = x 2 непрерывна.
В данном пункте учебника перечислены основные элементарные функции, которые являются непрерывными в любой точке своей области определения и на каждом интервале своей области определения.
Для обучения на профильном уровне сформулировано утверждение о непрерывности суперпозиции непрерывных функций, а также теорема о том, что непрерывная на отрезке [a; b] функция принимает все промежуточные значения между ее значениями на концах отрезка [a; b]. Эту теорему можно использовать, например, для доказательства того, что область изменения функции есть отрезок. Доказательство этой теоремы обычно в школе не рассматривается. На рисунке 69, а, б учебника дана геометрическая иллюстрация этого доказательства.
Решения и комментарии
![]() 2.34. а)
Определите все промежутки, на которых непрерывна функция y = 2 sin x .
2.34. а)
Определите все промежутки, на которых непрерывна функция y = 2 sin x .
![]()
![]() Решение.
Область определения D (F) функции F x( ) = 2 sin x состоит
из отрезков [2πn;
π + 2πn], где n
∈ Z.
В любой точке x0, лежащей внутри любого интервала (2πn; π + 2πn), n ∈ Z,
функция u = ϕ
( )x = sin
x непрерывна, а функция f (u) = 2u непрерывна в точке u0
= sin x0
. Поэтому функция F x( ) =
f (ϕ (
))x = 2 sin
x непрерывна в точке x0. Следовательно, функция y
= 2 sin x
непрерывна на каждом из интервалов (2πn;
π + 2πn), где n
∈ Z.
Если добавить, что в левом конце каждого из промежутков функция непрерывна
справа, в правом конце каждого из промежутков функция непрерывна слева, то
получим, что функция y =
2 sin x непрерывна на каждом из отрезков [2πn; π + 2πn], где n
∈ Z.
Решение.
Область определения D (F) функции F x( ) = 2 sin x состоит
из отрезков [2πn;
π + 2πn], где n
∈ Z.
В любой точке x0, лежащей внутри любого интервала (2πn; π + 2πn), n ∈ Z,
функция u = ϕ
( )x = sin
x непрерывна, а функция f (u) = 2u непрерывна в точке u0
= sin x0
. Поэтому функция F x( ) =
f (ϕ (
))x = 2 sin
x непрерывна в точке x0. Следовательно, функция y
= 2 sin x
непрерывна на каждом из интервалов (2πn;
π + 2πn), где n
∈ Z.
Если добавить, что в левом конце каждого из промежутков функция непрерывна
справа, в правом конце каждого из промежутков функция непрерывна слева, то
получим, что функция y =
2 sin x непрерывна на каждом из отрезков [2πn; π + 2πn], где n
∈ Z.
Столь подробное обоснование достаточно провести для одной функции, а для других можно только найти промежутки непрерывности.
2.36. а) Объясните, почему функция f (x) на промежутке [−1; 2] имеет нуль, если f (x) = 5x + 2.
Решение. Так как f (−1) = 5 ⋅ (−1) + 2 = −3 < 0, а f (2) = = 5 ⋅ 2 + 2 = 12 > 0 и функция f (x) непрерывна на отрезке [−1; 2], то по теореме о промежуточных значениях функции существует число x0 ∈ (−1; 2), такое, что f (x0) = 0.
2.37. Докажите, что уравнение x5 − 55 = 0 имеет корень на отрезке [2; 4].
Доказательство. Так как функция f (x) = x5 − 55 на отрезке [2; 4] непрерывна и f (2) = 25 − 55 = −23 < 0, а f (4) = = 45 − 55 = 969 > 0, то по теореме о промежуточных значениях функции существует точка x0 ∈ (2; 4), такая, что f (x0) = 0. Это означает, что уравнение x5 − 55 = 0 имеет корень на отрезке [2; 4].
Замечание. Отметим, что из возрастания функции f (x) = x5 − 55 на отрезке [2; 4] следует, что каждое свое значение она принимает только один раз, поэтому уравнение x5 − 55 = 0 имеет единственный корень на этом отрезке.
А доказать возрастание функции f (x) = x5 − 55 на отрезке [2; 4] можно так. Пусть x1 и x2 — любые числа из отрезка [2; 4], такие, что x1 < x2. Тогда x15 < x25 по свойству числовых неравенств для положительных чисел, поэтому f (x1) − f (x2) = (x15 − 55) − (x25 − 55) = x15 − x25 < 0,
т. е. f (x1) < f (x2), следовательно, функция f (x) = x5 − 55 возрастает на отрезке [2; 4].
В данном пункте учебника напоминается определение функции, непрерывной в точке и на интервале, и дается определение функции, разрывной в точке: функцию, определенную в каждой точке интервала J, называют разрывной в точке x0 ∈ J, если для нее не выполнено условие непрерывности в этой точке. На многочисленных примерах объясняется, что значит, что функция разрывна в некоторой точке интервала.
Например, функцию f x( ) = 1 нельзя назвать разрывной x
в точке x0 = 0, так как 0 ∉ D (f), но, если эту функцию доопределить так, что f (0) = a, где a — любое число, получим, что новая функция будет разрывной в точке x0 = 0.
Отметим, что иногда в вузах дают и другие определения разрывной функции.
Здесь же даны определения устранимого и неустранимого разрывов.
Решения и комментарии
2.40. Имеет ли точки разрыва функция:
а) y =
⎧⎪⎨ | xx | , если x ≠
0, б) y =
⎨⎪⎧ ![]() sinx x , если x ≠ 0,
sinx x , если x ≠ 0,
⎪⎩0, если x = 0; ⎪⎩1, если x = 0?
Решение. а) Если x > 0, то y = 1; если x < 0, то y = −1. Следовательно, функция непрерывна на каждом из промежутков (−∞; 0) и (0; +∞). Так как пределы функции слева и справа при x → 0 не равны, то функция в точке x = 0 не имеет предела, поэтому в точке x = 0 функция имеет неустранимый разрыв.
б) Функция непрерывна на каждом из промежутков (−∞; 0) и (0; +∞). Так как предел функции при x → 0 равен 1 и y (0) = 1, то функция в точке x = 0 непрерывна, следовательно, функция не имеет точек разрыва.
2.41. Можно ли доопределить функцию f (x) в точке x0 (в точках xk) так, чтобы новая функция стала непрерывной на интервале (−∞; +∞)? Если да, то как это сделать?
x2 − 5x + 4
а) f x( ) = ![]() , x0 = 1;
, x0 = 1;
x − 1
д) f (x) = cos x tg x,
xk ![]() k, k ∈ Z.
k, k ∈ Z.
Решение. а) Так как D (f) есть все x, кроме x = 1, x2 − 5x + 4
то для каждого x ∈ D (f) имеем f x( ) = =
x − 1
(x − 1) (x − 4) x2 − 5x + 4
![]() =
= ![]() = x − 4. Поэтому lim = lim (x − 4) = x − 1 x → 1 x − 1 x → 1
= x − 4. Поэтому lim = lim (x − 4) = x − 1 x → 1 x − 1 x → 1
= −3. Доопределив функцию в точке x0 = 1 так, чтобы f (x0) = −3, мы получим новую функцию, непрерывную на интервале (−∞; +∞).
д) Так как D (f) есть все x, кроме xk
![]() k, k ∈ Z, то для каждого x
∈ D (f)
имеем f (x) =
cos x tg x =
sin x. Поэтому lim sin x =
1 для k = 2n
и lim sin x =
−1 для
k, k ∈ Z, то для каждого x
∈ D (f)
имеем f (x) =
cos x tg x =
sin x. Поэтому lim sin x =
1 для k = 2n
и lim sin x =
−1 для
x → xk x → xk
k = 2n + 1, n ∈ Z. Доопределив функцию в каждой точке xk так, чтобы f (xk) = 1 для k = 2n и f (xk) = −1 для k = 2n + 1, n ∈ Z, мы получим новую функцию, непрерывную на интервале (−∞; +∞).
|
§ 3. |
В данном параграфе рассматриваются функции, обратные к данным функциям. Обычно функцию, обратную к функции y = f (x), находят так: сначала выражают x через y, потом заменяют x на y, а y на x. Или наоборот: сначала заменяют x на y, а y на x, потом выражают y через x.
Практика показывает, что учащихся можно научить таким способом находить функцию, обратную к данной (следуя принципу «знаю как»), но при этом они не всегда понимают, что они делают, выполняя шаг «заменим x на y, а y на x». Попытаемся разъяснить это.
В п. 3.1 вводится понятие функции, обратной к данной.
Сначала введем это понятие на простом примере.
Пусть, например, тело движется по прямой по закону
s = 3t, t ∈ [0; 2], (1)
где s (м) — путь, пройденный телом за t (с).
Отсюда следует, что если известно время движения t, то однозначно находится путь s, пройденный телом за это время.
Если же известен путь s, пройденный телом, то однозначно находится и время движения t:
t = s, s ∈ [0; 6]. (2)
3
Функцию (2) принято называть функцией, обратной к функции (1). При этом не возникает желания в формуле (2) «заменить t на s, а s на t».
Однако в отличие от физики в математике принято исходную функцию y = f (x) и обратную к ней функцию записывать как функции одного и того же аргумента x, а это требует шага «заменить x на y, а y на x». Покажем, как это можно сделать в учебнике.
Аналогично разобранному выше примеру для функции y = x2, x ∈ [0; 2] (y ∈ [0; 4]), (3)
найдем обратную к ней функцию
x
![]() = y, y ∈ [0; 4] (x ∈ [0; 2]). (4)
= y, y ∈ [0; 4] (x ∈ [0; 2]). (4)
Но у функции, заданной формулой (4), независимой переменной является y, а зависимой — x. Поскольку более привычно записывать функцию так, чтобы независимой переменной была x, а зависимой — y, то в формуле (4) заменим x на y, а y на x. Получится более привычная запись той же функции:
y
![]() = x, x ∈ [0; 4] (y ∈ [0; 2]). (5)
= x, x ∈ [0; 4] (y ∈ [0; 2]). (5)
Естественно, что функцию (5) также называют функцией, обратной к функции (3), но теперь она записана в привычном виде.
В п. 11 дидактических материалов приведены примеры нахождения функции, обратной к данной функции.
Функцию (5), обратную к функции (3), можно найти и другим способом.
Пусть дана функция (3). Запишем формулу x = y2, y ∈ [0; 2] (x ∈ [0; 4]), (6)
которая получится, если в формуле (3) заменить x на y, а y на x. Выразив в формуле (6) y через x, получим формулу (5).
Ясно, что графики функций (5) и (6) совпадают, поэтому для построения графика функции (5) надо построить график функции (6), откладывая значения y на вертикальной оси в привычной системе координат xOy, а соответствующие значения x на горизонтальной оси (рис. 29).
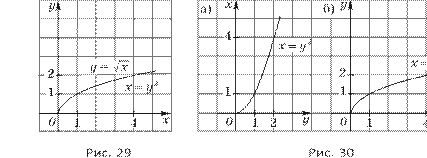
Такое построение вызывает некоторые затруднения у учащихся. Помочь в построении этого графика позволяет такой прием. Изобразим на листе бумаги систему координат так, чтобы ось Oy была горизонтальной, а ось Ox — вертикальной. В этой системе координат легко построить график функции (6) (рис. 30, а).
Чтобы перейти к привычному откладыванию значений x на горизонтальной оси, а значений y на вертикальной оси, выполним последовательно два поворота листа бумаги, на котором изображен график функции (6): первый — на 90° по часовой стрелке вокруг начала координат, а второй — на 180° вокруг нового положения оси Ox. График окажется на невидимой стороне листа, но, посмотрев этот лист на просвет, учащиеся увидят график, изображенный на рисунке 30, б.
Далее в п. 3.1 по аналогии с разобранным примером находится функция, обратная к данной, строго монотонной на заданном промежутке функции.
![]()
![]() Напомним, что в 10 классе
для построения графиков некоторых функций и исследования их свойств применялся
описанный здесь способ. Так, для построения графиков функций y = x, y = n x,
y = loga
x строились графики функций x =
y2, x =
yn, x =
ay. Построение графиков описанным способом дает
доказательство непрерывности и возрастания обратной функции, если данная
функция была непрерывна и возрастала. Аналогичные рассуждения можно провести
для убывающих функций.
Напомним, что в 10 классе
для построения графиков некоторых функций и исследования их свойств применялся
описанный здесь способ. Так, для построения графиков функций y = x, y = n x,
y = loga
x строились графики функций x =
y2, x =
yn, x =
ay. Построение графиков описанным способом дает
доказательство непрерывности и возрастания обратной функции, если данная
функция была непрерывна и возрастала. Аналогичные рассуждения можно провести
для убывающих функций.
В п. 3.2 вводится понятие взаимно обратных функций. Если для функции (4) найти обратную к ней функцию, то получится функция (3). Поэтому функции (3) и (4) — взаимно обратные функции.
![]() Заменив в формуле (4) x на y, а y на x,
получим функцию (5). Функции (3) и (5) также взаимно обратные функции.
Заменив в формуле (4) x на y, а y на x,
получим функцию (5). Функции (3) и (5) также взаимно обратные функции.
В п. 3.2 показывается, что графики взаимно обратных функций y = f (x) и y = ϕ (x) симметричны относительно прямой y = x. Если изобразить в одной системе координат графики взаимно обратных функций
(3) и (5), то получим наглядную илРис. 31 люстрацию этого свойства (рис. 31).
Таким образом, получается еще
один способ построения графика функции y = ϕ (x), обратной к данной функции y = f (x): симметричным отражением относительно прямой y = x графика данной функции.
Практика показывает, что после такого объяснения с демонстрацией графика и его преобразований «таинственный» шаг «заменить x на y, а y на x» становится понятным.
Из проведенных в п. 3.2 рассуждений следует, что достаточным условием существования обратной функции является строгая монотонность данной функции.
Решения и комментарии
3.3. В данной формуле замените x на у, а у на x, затем выразите из полученной формулы y через x:
а) у = 3x + 1; г) y = −x2, x ∈ [0; 3]; ж) y = 3x.
Решение. а) Заменив x на у, а у на
x, получим x =
3у + 1.
Теперь выразим из полученной формулы y чеx − 1 рез x: y = ![]() .
.
3
![]() г)
Из формулы y =
−x2, x ∈
[0; 3] получим, что y ∈
[−9;
0]. В данной формуле, заменив x на у, а у на x,
получим x =
−y2, y ∈
[0; 3], x ∈
[−9;
0]. Теперь выразим из полученной формулы y через x: y = −x, x
∈ [−9; 0].
г)
Из формулы y =
−x2, x ∈
[0; 3] получим, что y ∈
[−9;
0]. В данной формуле, заменив x на у, а у на x,
получим x =
−y2, y ∈
[0; 3], x ∈
[−9;
0]. Теперь выразим из полученной формулы y через x: y = −x, x
∈ [−9; 0].
ж) Заменив x на у, а у на x, получим x = 3y. Отметим, что здесь x > 0. Теперь выразим из полученной формулы y через x: у = log3 x, x ∈ (0; +∞).
![]() 3.8. в) Постройте график данной функции y = f (x).
Найдите функцию y =
ϕ (x), обратную к данной функции, и постройте ее график,
если: y = 1
− 6 , x ∈ (−2; +∞).
3.8. в) Постройте график данной функции y = f (x).
Найдите функцию y =
ϕ (x), обратную к данной функции, и постройте ее график,
если: y = 1
− 6 , x ∈ (−2; +∞).
x + 2
Решение. Найдем функцию x = ϕ (y),
обратную к исходной. Для этого выразим x через y: x ![]()
![]() ,
,
y ∈ (−∞; 1), x ∈ (−2; +∞).
Затем, заменив x на у, а у на x, получим функцию y = ϕ (x), обратную к исходной и записанную в привычном виде
y ![]() Рис.
32
Рис.
32
График обратной функции получим из графика данной функции симметричным отражением его относительно прямой y = x (рис. 32).
3.10. Докажите, что угловые коэффициенты взаимно обратных линейных функций у = k1x + l1 и у = k2x + l2 связаны соотношением k2 = k11 (k1 ≠ 0, k2 ≠ 0).
Доказательство. В первой формуле, заменив x на у, а у на x, получим x = k1у + l1. Теперь, выразив из полученной формулы y через x, найдем обратную функцию:
1 l1
y =
x − ![]() . Отсюда следует, что угловой
коэффициент k2 k1 k1
. Отсюда следует, что угловой
коэффициент k2 k1 k1
функции, обратной к данной, есть k2 = k11 , что и требовалось доказать.
3.11. Приведите пример функции, обратной самой себе.
Решение. Можно привести много примеров таких функций. Они должны быть строго монотонны, а их графики — симметричны относительно прямой у = x. Такими функциями являются, например, следующие функции:
у = x, у = −x, у = −x + 5, у = −x − 2, y = 1 , x ∈ (0; +∞),
x
![]()
![]() y = 2 , x ∈ (−∞; 0), y
= 4 − x2 ,
x ∈ [0;
2], x y = − 9 − x2 ,
x ∈ [−3; 0] и т. д.
y = 2 , x ∈ (−∞; 0), y
= 4 − x2 ,
x ∈ [0;
2], x y = − 9 − x2 ,
x ∈ [−3; 0] и т. д.
Промежуточный контроль. C—11.
В данном пункте учебника изучаются свойства и графики основных обратных тригонометрических функций y = arcsin x, y = arccos x, y = arctg x, y = arcctg x.
Графики обратных тригонометрических функций строят с помощью приемов, описанных выше. Решения и комментарии
3.16. Найдите функцию y = ϕ (x), обратную к функции:
а) y = sin x; x ∈ ⎡⎢⎣− 32π ; − 2π ⎤⎥⎦;
б) y = cos x, x ∈ [π; 2π], — и постройте ее график.
Решение. а) Так как sin x = −sin (x + π) = sin (−x − π), то для
![]() функцию
можно записать в виде y =
sin (−x
− π).
Аргумент α =
−x −
π принадлежит промежутку ⎢⎣⎡−
2π
; 2π
⎤⎥⎦. Из формулы y
= sin α, где α ∈ ⎣⎢⎡−
2π
; 2π
⎤⎥⎦,
функцию
можно записать в виде y =
sin (−x
− π).
Аргумент α =
−x −
π принадлежит промежутку ⎢⎣⎡−
2π
; 2π
⎤⎥⎦. Из формулы y
= sin α, где α ∈ ⎣⎢⎡−
2π
; 2π
⎤⎥⎦,
y ∈ [−1; 1], выразим α через y:
α = arcsin y, где y ∈ [−1; 1],
откуда −x − π = arcsin y, или
x = −π − arcsin y, где y ∈ [−1; 1]. (1) Формула (1) задает функцию x = ϕ (y), обратную к функции y = sin x, x ∈ ⎡⎢⎣− 32π ; − 2π ⎥⎦⎤. Заменим в равенстве (1) x на y и y на x, получим функцию y = −π − arcsin x, где
x ∈ [−1; 1], обратную к функции y = sin x, x ∈ ⎡⎢⎣− 32π ; − 2π ⎦⎤⎥
и записанную в привычном виде. График этой функции
можно построить тремя способами:
1)
![]() график функции y =
sin x,
график функции y =
sin x, ![]() симметрично от-
симметрично от-
разить относительно оси y = x
(рис. 33);
2) построить график функ-
ции x = sin y, y ∈ ⎡⎢⎣− 32π ; − 2π ⎤⎥⎦;
3) график функции y = arcsin x сначала отразить симметрично относительно оси Ox, затем перенести полученный график на π
Рис. 33 единиц вниз.
б) 1-й способ. Так как cos x = − sin ⎛⎜⎝ 32π − x⎠⎟⎞ = sin ⎝⎛⎜x − 32π ⎞⎟⎠,
то для π ≤ x ≤ 2π функцию можно
записать в виде y =
sin ⎛⎜⎝x − 32π
⎞⎟⎠. Аргумент α = x − ![]()
![]() принадлежит промежутку ⎢⎡⎣−
2π
; 2π⎤⎥⎦. Из формулы y
= sin α, где α ∈ ⎣⎢⎡−
2π
; 2π
⎥⎦⎤,
y ∈ [−1; 1], выразим α через y:
принадлежит промежутку ⎢⎡⎣−
2π
; 2π⎤⎥⎦. Из формулы y
= sin α, где α ∈ ⎣⎢⎡−
2π
; 2π
⎥⎦⎤,
y ∈ [−1; 1], выразим α через y:
α = arcsin y, где y ∈ [−1; 1],
откуда x − ![]()
![]() =
arcsin y, или
=
arcsin y, или
x = ![]()
![]() +
arcsin y, где y ∈
[−1;
1]. (2)
+
arcsin y, где y ∈
[−1;
1]. (2)
![]() Формула (2) задает функцию x = ϕ (y),
обратную к функции y =
cos x, x ∈
[π; 2π]. Заменив в
равенстве (2) x на y и y на x, получим функцию y
Формула (2) задает функцию x = ϕ (y),
обратную к функции y =
cos x, x ∈
[π; 2π]. Заменив в
равенстве (2) x на y и y на x, получим функцию y
![]() x, где x ∈ [−1; 1], обратную
к функции y = cos
x, x ∈
[π; 2π] и записанную в
привычном виде. График этой функции можно построить тремя способами:
x, где x ∈ [−1; 1], обратную
к функции y = cos
x, x ∈
[π; 2π] и записанную в
привычном виде. График этой функции можно построить тремя способами:
1) график функции y = cos x, x ∈ [π; 2π] симметрично отразить относительно оси y = x (рис. 34);
2) построить график функции x = cos y, y ∈ [π; 2π];
3)
график функции y =
arcsin x перенести на ![]() единиц вверх.
единиц вверх.
2-й способ. Так как cos x =
|
= cos (x − 2π) = cos (2π − x), то для π ≤ x ≤ 2π функцию можно записать в виде y = cos (2π − x), где |
Рис. 34 |
аргумент α = 2π − x принадлежит промежутку [0; π]. Из формулы y = cos α, где α ∈ [0; π], y ∈ [−1; 1], выразим α через y:
α = arccos y, где y ∈ [−1; 1],
откуда 2π − x = arccos y, или
x = 2π − arccos y, где y ∈ [−1; 1]. (3)
Формула (3) задает функцию x = ϕ (y), обратную к функции y = cos x, x ∈ [π; 2π]. Заменив в равенстве (3) x на y и y на x, получим функцию y = 2π − arccos x, где x ∈ [−1; 1], обратную к функции y = cos x, x ∈ [π; 2π] и записанную в привычном виде.
Так как arcsinx =
![]()
![]() − arccos x,
то полученная формула выражает ту же функцию, что и в первом способе решения.
− arccos x,
то полученная формула выражает ту же функцию, что и в первом способе решения.
3.4*. Примеры использования обратных
В этом пункте учебника даны примеры доказательства некоторых свойств обратных тригонометрических функций, формул для cos (arcsin x), sin (arccos x) и т. п., построены графики функций y = sin (arcsin x), y = cos (arcsin x) и др.
Решения и комментарии
3.18. Докажите, что для любого числа x ∈ R справедливо равенство
arctg x +
arcctg x =
![]()
![]() .
.
Доказательство. Так как 0 < arcctg x < π, то
− 2π < 2π − arcctg x < 2π. Найдем тангенс числа ⎛⎜⎝ 2π − arcctg x⎟⎠⎞,
пользуясь формулой приведения и определением арктангенса:
tg ⎜⎝⎛ 2π − arcctg x⎞⎟⎠ = ctg arcctg( x) = x.
Итак, число ⎜⎝⎛ 2π − arcctg x⎞⎟⎠ принадлежит промежутку ⎛⎜− π ; π⎞⎟⎠, тангенс этого числа равен x, поэтому по опреде-
![]() лению арктангенса имеем − arcctg x = arctg x,
откуда следует, что arctg x +
arcctg x =
, что и требовалось доказать.
лению арктангенса имеем − arcctg x = arctg x,
откуда следует, что arctg x +
arcctg x =
, что и требовалось доказать.
Промежуточный контроль. К—1.
|
§ 4. |
В данном параграфе учебника достаточно традиционно вводится понятие производной, изучаются механический и геометрический смысл производной, производная суммы, разности, произведения и частного, непрерывность функции, имеющей производную. Авторы считают, что для определения производной достаточно использовать понятие предела на интуитивном уровне.
В результате изучения данного параграфа на базовом уровне учащиеся должны знать формулы производных основных элементарных функций. Желательно, чтобы они знали и формулу производной сложной функции. При углубленном изучении математики учащиеся должны уметь доказывать все эти формулы. Производную обратной функции следует рассматривать только при углубленном изучении математики.
В данном пункте учебника рассматриваются физические задачи и задача о касательной, решение которых приводит к выполнению новой операции — дифференцированию функции. Здесь напоминаются определения приращения аргумента и приращения функции, дается определение производной функции. Надо обратить внимание учащихся на то, что производная функции, заданной на интервале, определяется в одной (внутренней) точке этого интервала, что производная функции в данной точке есть число. И только если в каждой точке интервала (a; b) производная существует, то говорят, что производная есть функция аргумента x, определенная на интервале (a; b).
Например, функция y = |x| определена на интервале (−1; 1), она имеет производную в каждой точке интервала, кроме точки x0 = 0, поэтому функция y = | x | не имеет производной — функции, определенной на всем интервале (−1; 1). Но у нее есть производная — функция, определенная на интервале (−1; 0), а также на интервале (0; 1).
В данном пункте с помощью определения вычисляются производные функций y = x, y = С, y = kx + b, y = x2, y = ax2 + bx + c. Теоремы о производной суммы, разности, произведения и частного будут рассмотрены только в следующем пункте, поэтому, например, при отыскании производной функции в заданиях 4.10, 4.11, 4.12 надо для вывода производной пользоваться определением производной функции или опираться на ранее доказанные факты.
Для обучения на профильном уровне вводятся понятия односторонней производной и производной функции, определенной на отрезке [a; b].
Решения и комментарии
4.10. Точка движется прямолинейно по закону s = t2 − 4t.
а) Выразите скорость точки как функцию времени.
б) Вычислите скорость точки в момент времени t = 5.
в) В какой момент времени скорость была равна нулю?
Решение. а) Так как (ax2 + bx + c)′ = 2ax + b, то v (t) = = s′ (t) = (t2 − 4t)′ = 2t − 4.
б) Скорость точки в момент времени t = 5 равна v (5) = = 2 ⋅ 5 − 4 = 6.
в) Скорость точки равна нулю, если 2t − 4 = 0, т. е. в момент времени t = 2.
4.12. С помощью определения найдите производную функции у = x3.
Решение. Пусть f (x) = x3. Для любой точки x приращение функции f равно
Δf = (x + Δx)3 − x3 = (3x2 + 3xΔx + (Δx)2) Δx.
![]() Δf (3x2 +
3x xΔ +
(Δx)2 )Δx 2 2
Δf (3x2 +
3x xΔ +
(Δx)2 )Δx 2 2
Поэтому = = 3x + 3xΔx + (Δx) .
Δx Δx
Поскольку 3x2 + 3xΔx + (Δx)2 стремится к 3x2 при Δx → 0, то f′ (x) = 3x2, т. е. в любой точке х имеем (x3)′ = 3x2.
В данном пункте учебника сначала доказана теорема о производной суммы двух функций, потом теорема о функции, заданной формулой f (x) = Au (x). В качестве следствия двух первых теорем доказана теорема о производной разности двух функций. Теорема 3 обобщает первые теоремы на случай n функций.
Решения и комментарии
4.19. д) Найдите производную функции y = (x − 2)3 в любой точке x ∈ R, используя задание 4.12.
Решение. Пусть f (x) = (x − 2)3. Сначала запишем функцию в виде f (x) = x3 − 6x2 + 12x − 8.
Тогда f′ (x) = (x3)′ − (6x2)′ + (12x)′ − 8′ = 3x2 − 6 (x2)′ + + 12 (x)′ − 0 = 3x2 − 6 ⋅ 2x + 12 ⋅ 1 = 3x2 − 12x + 12.
4.3*. Непрерывность функции, имеющей производную.
В данном пункте учебника доказана теорема о непрерывности в точке функции, имеющей в этой точке производную. Для обучения на профильном уровне вводится понятие дифференциала функции. Здесь надо показать, что дифференциал функции у = х равен Δx, т. е. dх = Δx.
Решения и комментарии
4.26. Найдите дифференциал функции:
а) у = 3х + 5; б) у = х2 + 2х + 4.
Решение. Так как дифференциал функции f (x) в точке x есть f′ (x) Δx, то
а) dу = (3х + 5)′ Δx = 3Δx;
б) dу = (х2 + 2х + 4)′ Δx = (2х + 2) Δx.
4.27. а) Вычислите приближенно приращение Δy функции у = х3 − 4х2 + 2х − 10 в точке x = 1, если Δx = 0,1.
Решение. Так как dу = (х3 − 4х2 + 2х − 10)′ Δx = = (3х2 − 8х + 2) Δx, то в точке x = 1 при Δx = 0,1 находим приращение функции Δy, приближенно равное dy:
Δy ≈ (3 ⋅ 12 − 8 ⋅ 1 + 2) ⋅ 0,1 = −0,3.
В данном пункте учебника доказаны теоремы о производной произведения и производной частного двух функций и на примерах показано их применение.
Решения и комментарии
4.30. а) В любой точке х ∈ R найдите производную функции у = (х2 + 3х) (х − 1).
Решение. Учащиеся могут заметить, что проще всего перед нахождением производной раскрыть скобки, а затем вычислить производную: 1) (х2 + 3х) (х − 1) = х3 + 2х2 − 3х; 2) (х3 + 2х2 − 3х)′ = 3х2 + 4х − 3.
Однако умение находить производную произведения скоро понадобится им в более сложных случаях, поэтому производную надо находить и так:
((х2 + 3х) (х − 1))′ = (х2 + 3х)′ (х − 1) + (х2 + 3х) (х − 1)′ = = (2х + 3) (х − 1) + (х2 + 3х) ⋅ 1 = 3х2 + 4х − 3.
Совпадение результатов покажет, что ответ в этой задаче не зависит от способа ее решения.
Отметим задание 4.31 на нахождение производных функций: а) у = х4; б) у = х5; в) у = х6; г) у = х7. В учебнике имеется у к а з а н и е: представить данную функцию в виде произведения двух функций — и приведен пример нахождения производной:
(х4)′ = (х3 ⋅ х)′ = (х3)′ ⋅ х + х3 ⋅ (х)′ = 3х2 ⋅ х + х3 ⋅ 1 = 4х3.
Доказательство формулы (хn)′ = nхn − 1 в следующем пункте учебника будет опираться именно на этот прием.
−x2 +7 x −
8 4.33. и)
Найдите производную функции y =
![]() x2 − 7 x +
5 в
любой точке ее области определения. Решение.
x2 − 7 x +
5 в
любой точке ее области определения. Решение.
y′
= ⎛⎜⎝ ![]() −xx22−+77xx+−58 ⎞⎟⎠′ =
−xx22−+77xx+−58 ⎞⎟⎠′ =
(−x2 + 7 x − 8)′ (x2 − 7 x + 5) − (−x2 + 7 x − 8)(x2 − 7 x + 5)′
![]()
= (x2 − 7 x + 5)2 =
(−2x + 7)(x2 − 7 x + 5) − (−x2 + 7 x − 8)(2x − 7) 6x − 21
![]() = 2 − 7 x +
5)2 = (x2 −
7 x +
5)2 .
= 2 − 7 x +
5)2 = (x2 −
7 x +
5)2 .
(x
Обратим внимание на необходимость подробной записи в подобных вычислениях, так как поспешность в «сворачивании» вычислений ухудшает результативность обучения.
4.34. а) Вычислите значение производной функции f (x)
в указанной точке х0 =
0, если ![]() .
.
Решение. f′(
)x = ⎛⎜⎝ x25+ 1⎠⎞⎟′
= 5![]() ′
⋅ (x2 +(x1)2 +−
(1x)22 + 1)′
⋅ 5 =
′
⋅ (x2 +(x1)2 +−
(1x)22 + 1)′
⋅ 5 =
= −210+ 1x)2 ; f′ (0) = 0.
(x
4.36. Вычислите значение производной функции у = (х + 1)10 в точке х0 = 0.
Решение. Так как y (x) = х10 + C110х9 + C210х8 + ... +
+ C810х2 + C910х + 1, то y′ (x) = 10х9 + 9C110х8 + 8C210х7 + ... + + 2C810х + C910. Тогда y′ (0) = C910 = C110 = 10.
В данном пункте доказаны формулы производных всех основных элементарных функций, изучаемых в школе. Доказательство формулы
(xn)′ = nxn − 1
для любого натурального n ≥ 2 проведено методом математической индукции (это доказательство, как и некоторые другие, необязательны при обучении на базовом уровне).
Далее доказывается формула (x−n)′ = −nx−n − 1, потом с опоeα − 1
рой на доказанное в п. 2.4 равенство
lim ![]() =
1 доказыα
→ 0 α
=
1 доказыα
→ 0 α
ваются формула
(ax)′ = ax ln a
и ее частный случай (ex)′ = ex.
Формула
(loga x)′ = 1 x ln a
и ее частный случай (lnx)′ = 1 доказываются с опорой на x
1
доказанное в п. 2.4 равенство lim ln (1 + t)t = 1 (без исполь-
t → 0
зования производной обратной функции, которая изучается позже).
Решения и комментарии
4.41. а) Для любого х ≠ 0 найдите производную функ-
ции y = 121 .
x
Решение. Для любого х ≠ 0 имеем у = х−21, поэтому у′ = (х−21)′ = −21х−22.
Укажите, при каких значениях х функция f (x) имеет производную, и найдите эту производную (4.44—4.49):
4.44. а) y = 4xx
; г) f x( ) = ![]() x3x x
; ж) f x( ) =
lg
x3x x
; ж) f x( ) =
lg![]() x.
x.
2 3 + 9 lg e
4x (2x )2 x
Решение. а) Для любого х имеем x
= ![]() x = 2 , поэто-
x = 2 , поэто-
2 2
му функцию можно записать в виде у = 2х. Для любого х ∈ R эта функция имеет производную у′ = (2х)′ = 2х ln 2.
3x 3x 1
![]() г) Для любого х имеем
x x = x
x = x
, 3 +
9 3 (1 +
3 ) 1 +
3
г) Для любого х имеем
x x = x
x = x
, 3 +
9 3 (1 +
3 ) 1 +
3
поэтому функцию можно записать в виде y = 1 x . Для 1 + 3
любого х ∈ R эта функция имеет производную
![]() y′ =
⎛⎜⎝ 1 +13x ⎞⎟⎠′
= 1′
⋅ (1 +
3(1x)+−31x)⋅2(1 + 3x)′ = (−13+x 3lnx)32 .
y′ =
⎛⎜⎝ 1 +13x ⎞⎟⎠′
= 1′
⋅ (1 +
3(1x)+−31x)⋅2(1 + 3x)′ = (−13+x 3lnx)32 .
lg x
ж) Для любого х > 0 имеем ![]() =
ln x, поэтому функlg
e
=
ln x, поэтому функlg
e
цию можно записать в виде у = ln x. Для любого х ∈ (0; +∞) эта функция имеет производную y′ = (ln x)′ = 1 . x
4.45. г) f (x) = 5 log3 х − 6 ln х + 7 lg х.
Решение. Для любого х > 0 эта функция имеет производную f′ (x) = (5 log3 х
− 6 ln х
+ 7 lg х)′ = 5 − 6 + ![]() 7 . x ln 3 x x ln
10
7 . x ln 3 x x ln
10
4.49. а) f (x) = cos 2002х cos 2001х + sin 2001х sin 2002х.
Решение. Для любого х имеем cos 2002х cos 2001х + + sin 2001х sin 2002х = cos (2002х − 2001х) = cos х, поэтому функцию можно записать в виде f (x) = cos х. Для любого х ∈ R эта функция имеет производную f′ (x) = (cos х)′ = = −sin х.
4.50. Найдите значения х, при которых
производная ln x функции
y = ![]() :
:
x
а) равна нулю; б) положительна; в) отрицательна. Решение. Для
любого х > 0
эта функция имеет производ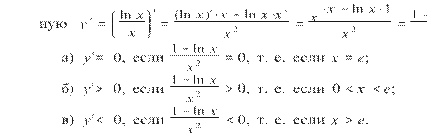 1
1
4.51. Докажите справедливость равенства:
а) (sin 2х)′ = 2 cos 2х; б) (52x)′ = 52x ⋅ ln 25;
г) (ln 17 )x ′ = 1 , x > 0. x
Доказательство. Эти задания выполняются с предварительными преобразованиями, которые станут не нужны после изучения производной сложной функции.
а) (sin 2х)′ = (2 sin х cos х)′ = 2 ((sin х)′ cos х +
+ sin х (cos х)′) = 2 (cos х cos х + sin х (−sin х)) =
= 2 (cos2 х − sin2 х) = 2 cos 2х;
![]() ′ = ′ = =
′ = ′ = =
, x x
где x > 0.
Дополнение. Приведем примеры задач из ЕГЭ на вычисление производной.
A5 (2008). Найдите производную функции y = х6 − 4 sin х.
1) y′ = ![]() х; 2) y′ = 6х5
− 4
cos х; 3) y
х; 2) y′ = 6х5
− 4
cos х; 3) y![]() x; 4) y′ = х5
− 4
cos х.
x; 4) y′ = х5
− 4
cos х.
Решение. Для любого х ∈ R эта функция имеет производную y′ = (х6 − 4sin х)′ = (х6)′ − (4 sin х)′ = 6х5 − 4 cos х.
Ответ. 2.
A5 (2007). Найдите производную функции y = (х − 3)cos х.
1) y′ = cos х + (х − 3) sin х; 2) y′ = (х − 3) sin х − cos х; 3) y′ = cos х − (х − 3) sin х; 4) y′ = −sin х.
Решение. Для любого х ∈ R эта функция имеет производную y′ = (х − 3)′ cos х + (х − 3) (cos х)′ =
= 1 ⋅ cos х + (х − 3) ⋅ (−sin х) = cos х − (х − 3) sin х.
Ответ. 3.
A9 (2004). Вычислите значение производной функции y = sin х − 2х в точке х0 = 0.
1) 1; 2) 0; 3) −3; 4) −1.
Решение. Для любого х ∈ R эта функция имеет производную y′ (х) = (sin х − 2х)′ = cos х − 2.
Тогда значение y′ (0) = cos 0 − 2 = 1 − 2 = −1.
Ответ. 4.
Промежуточный контроль. C—12.
В данном пункте учебника доказывается формула для нахождения производной сложной функции yx′ = yu′ ⋅ ux′ (теорема 1). Примеры на нахождение производной не ограничиваются частным случаем, когда u (x) = kx + l. В теореме 2 для любого х > 0 и любого α ≠ 0 доказана формула
(xα)′ = αxα− 1.
![]() В
примере 6 показано, как для любого х ≠
0 надо находить производную функции y = 5 x2 .
Обратим внимание, что здесь необходимо рассматривать два случая: х > 0 и х < 0.
В
примере 6 показано, как для любого х ≠
0 надо находить производную функции y = 5 x2 .
Обратим внимание, что здесь необходимо рассматривать два случая: х > 0 и х < 0.
Для большей наглядности применения теоремы о производной сложной функции полезно, следуя учебнику, явно использовать замену. Рассмотрим более простые способы решения рассмотренных ранее заданий.
4.51. Докажите справедливость равенства:
а) (sin 2х)′ = 2 cos 2х;
б) (52x)′ = 52x ⋅ ln 25;
г) (ln 17 )x ′ = 1 , x > 0. x
Доказательство. а) (sin 2х)′ = (sin u)′ = cos u ⋅ u′ = = cos 2х ⋅ (2х)′ = 2 cos 2х, где u = 2x.
б) (52x)′ = (5u)′ = (5u) ⋅ ln 5 ⋅ u′ = 52x ⋅ ln 5 (2х)′ = = 52x ⋅ 2 ln 5 = 52x ⋅ ln 52 = 52x ⋅ ln 25, где u = 2x.
г) (ln 17 )x ′ = 1 ⋅ u′ = 1 ⋅ (17 )x ′ = 1 ⋅ 17 = 1 , где u 17 x 17 x x
u = 17x, x > 0.
Решения и комментарии
Укажите, при каких значениях x функция y = f (x) имеет производную, и найдите эту производную, если
(4.54—4.56):
4.54. а) y = ex3; е) y = 9cos x.
Решение. а) Для любого x ∈ R функция имеет производную yx′ = (eu)′ = eu ⋅ u′ = ex3 ⋅ (x3)′ = 3x e2 x3, где u = x3.
е) Для любого x ∈ R функция имеет производную yx′ = (9u)′ = 9u ⋅ ln 9 ⋅ u′ = 9cos x ⋅ ln 9 ⋅ (cos x)′ =
= −9cos x ⋅ ln 9 sin x,
где u = cos x.
4.56. а) у = (cos x)4 − (sin x)4; б) у = 4 cos 17x cos 13x.
Решение. а) Для любого x ∈ R функцию у = (cos x)4 − − (sin x)4 можно записать в виде у = cos 2x, поэтому для любого x ∈ R функция имеет производную yx′ = (cos u)′ = −sin u ⋅ u′ = −sin 2x ⋅ (2x)′ = −2 sin 2x,
где u = 2x.
б) Для любого x ∈ R функцию у = 4 cos 17x cos 13x можно записать в виде у = 2 (cos 30x + cos 4x), поэтому для любого x ∈ R функция имеет производную yx′ = 2 (cos u + cos v)′ = 2 ((cos u)′ + (cos v)′) =
= 2 (−sin u ⋅ u′ − sin v ⋅ v′) = 2 (−sin 30x (30x)′ − sin 4x ⋅ (4x)′) =
= 2 (−30 sin 30x − 4sin 4x) = −60 sin 30x − 8 sin 4x, где u = 30x, v = 4x.
4.68. Для любого x > 0 найдите производную функции:
а) у = xx; б) у = xsin x.
Решение. а) Для любого x > 0 функцию у = xx можно записать в виде у = ex ln x, поэтому для любого x ∈ (0; +∞) эта функция имеет производную yx′ = (eu)′ = eu ⋅ u′ = ex ln x ⋅ (x ln x)′ =
= xx ⋅ (x′ ln x + x (ln x)′) = xx ⎛⎜⎝ln x + x ⋅ x1 ⎟⎞⎠ = xx ⋅ (ln x + 1),
где u = x ln x.
б) Для любого x > 0 функцию у = xsin x можно записать в виде у = esin x ln x, поэтому для любого x ∈ (0; +∞) эта функция имеет производную
yx′ = (eu)′ = eu ⋅ u′ = esin x ln x ⋅ (sin x ln x)′ =
= xsin x ⋅ ((sin x)′ ln x + sin x (ln x)′) =
= x sin x ⋅ ⎛⎜⎝cos x ln x + x1 sin x⎞⎟⎠,
где u = sin x ln x.
4.69. Докажите, что графики функций f (x) = ex и ϕ (x) = xe, x > 0 в точке с абсциссой x = e имеют общую касательную.
Доказательство. Так как f (e) = ee = ϕ (e), то точки графиков данных функций с абсциссой x = e совпадают. Так как f′ (x) = (ex)′ = ex, f′ (e) = ee; ϕ′ (x) = (xe)′ = exe − 1, ϕ′ (e) = eee − 1 = ee, то угловые коэффициенты касательных к графикам функций f (x) и ϕ (x) в точке с абсциссой x = e также совпадают. Это означает, что графики функций f (x) = ex и ϕ (x) = xe, x > 0 в точке с абсциссой x = e имеют общую касательную, что и требовалось доказать.
Промежуточный контроль. C—13, C—14.
В данном пункте учебника доказывается формула для нахождения производной обратной функции. В качестве примеров применения этой формулы находятся производные обратных тригонометрических функций.
Отметим, что для нахождения производной обратной функции надо обратную функцию записывать в виде x = ϕ (y), а не в виде y = ϕ (x).
Решения и комментарии
4.71. Вычислите производную функции у = f (x), используя производную обратной к ней функции x = ϕ (у):
![]() а)
y = x,
x ∈ (0;
+∞) и x = у2,
у ∈ (0;
+∞);
а)
y = x,
x ∈ (0;
+∞) и x = у2,
у ∈ (0;
+∞);
в) у = ln x, x ∈ (0; +∞) и x = ey, у ∈ R.
Решение. В этом задании мы получаем новым методом уже
известные формулы дифференцирования. В п. 4.7 учебника доказано, что если
функции у = f
(x) и x =
ϕ (y) взаимно обратные, то f′( )x![]() , где f′ (x) —
производная по x от f (x), а ϕ′ (y) — производная по y
от ϕ (y).
, где f′ (x) —
производная по x от f (x), а ϕ′ (y) — производная по y
от ϕ (y).
![]() а)
Функции f x( ) = x,
x ∈ (0;
+∞) и ϕ (y) = y2,
у ∈ (0;
+∞) взаимно
обратные, поэтому
а)
Функции f x( ) = x,
x ∈ (0;
+∞) и ϕ (y) = y2,
у ∈ (0;
+∞) взаимно
обратные, поэтому ![]() =
= = .
=
= = .
в) Функции f (x) = ln x, x ∈ (0; +∞) и ϕ (y) = ey, у ∈ R
взаимно обратные, поэтому (ln x)′ = y1 = 1y = 1 .
(e )′y e x Промежуточный контроль. К—2.
|
§ 5. |
Применение производной
Параграф 5 учебника посвящен применению производной. Его содержание довольно близко к традиционному, некоторые пункты и отдельные доказательства выделены как необязательные при обучении на базовом уровне. Дидактические материалы дополняют содержание учебника разбором задач, связанных с геометрией, задач на смеси, в которых требуется находить наибольшее (наименьшее) значение величины.
В данном пункте учебника наибольшее значение функции на отрезке [a; b] названо максимумом функции на отрезке [a; b], а наименьшее значение функции на отрезке [a; b] названо минимумом функции на отрезке [a; b]. Введены соответствующие обозначения max f x( ), min f x( )
[a b; ] [a b; ]
и терминология: точка максимума, точка минимума.
Отметим, что в учебнике точку x0 отрезка [a; b] называют точкой локального максимума (локального минимума) функции у = f (x), если существует отрезок [x0 − δ; x0 + δ] (δ > 0), целиком принадлежащий отрезку [a; b], на котором x0 является точкой максимума (минимума). Следует особое внимание уделить новым терминам, так как учащиеся часто путают точку экстремума (максимума или минимума), т. е. значение x, с экстремумом (максимумом или минимумом) функции, т. е. со значением функции в точке экстремума, или даже с точкой графика функции, которая соответствует точке экстремума.
Такая терминология точнее отражает характер максимума (минимума), но после усвоения этой терминологии по мере приближения экзаменов учащимся нужно привести примеры экзаменационных заданий, в которых слово «локальный» применительно к точкам максимума (минимума) не используется.
В данном пункте вводится также понятие критической точки функции — внутренней точки отрезка, в которой производная функции не существует или равна нулю, и указано, как надо использовать критические точки при отыскании максимума и минимума функции.
Решения и комментарии
5.5. Укажите наибольшее и наименьшее значения функции на отрезке [−2; 2]:
⎧⎪−x при x < −1
а) y = ⎨x + 2 при − 1 ≤ x < 1 в) y = | x − 1 | + | 2x + 1 |. ⎪⎩−3x + 6 при x ≥ 1; Решение. а) В точках x1 = −1 и x2 = 1 производная
Δy
функции f (x) не существует.
Действительно, lim ![]() = −1
= −1
Δx → 0 Δx
Δy
при x <
−1, а lim ![]() = 1 при −1 < x < 1. Следовательно,
= 1 при −1 < x < 1. Следовательно,
Δx → 0 Δx
в точке x1 = −1 не существует производная функции f (x). Аналогично показывается, что производная не существует и в точке x2 = 1. Обе эти точки лежат внутри отрезка [−2; 2], значит, они являются критическими точками функции на этом отрезке. Других критических точек внутри отрезка [−2; 2] нет, так как на каждом из интервалов (−2; −1), (−1; 1) и (1; 2) производная функции не обращается в нуль.
Так как f (−2) = 2, f (−1) = 1, f (1) = 3, f (2) = 0, то max f x( ) = 3, а min f x( ) = 0.
[−2; 2] [−2; 2]
в) В точках x1 = − ![]()
![]() и x2 = 1 производная функции
f (x) не существует (проверьте это). Обе эти точки лежат внутри
отрезка [−2;
2], значит, они являются критическими точками функции на этом отрезке. Других
критических точек внутри отрезка [−2;
2] нет, так как на каждом из интервалов ⎜⎝⎛−2;
−
21⎞⎟⎠, ⎛⎜⎝−
21 ; 1⎞⎟⎠ и (1; 2)
производная функции не обращается в нуль.
и x2 = 1 производная функции
f (x) не существует (проверьте это). Обе эти точки лежат внутри
отрезка [−2;
2], значит, они являются критическими точками функции на этом отрезке. Других
критических точек внутри отрезка [−2;
2] нет, так как на каждом из интервалов ⎜⎝⎛−2;
−
21⎞⎟⎠, ⎛⎜⎝−
21 ; 1⎞⎟⎠ и (1; 2)
производная функции не обращается в нуль.
![]() Так как f (−2) = 6, f ⎛⎜⎝−
21⎞⎟⎠ = 32 , f (1) = 3, f (2) = 6, то max f x(
) = 6, а min f
x( ) =
Так как f (−2) = 6, f ⎛⎜⎝−
21⎞⎟⎠ = 32 , f (1) = 3, f (2) = 6, то max f x(
) = 6, а min f
x( ) = ![]() .
.
[−2; 2] [−2; 2]
Найдите критические точки функции f (х) на указанном отрезке (5.7—5.9):
![]() 5.7. а) f x( )
= 3 x,
[−1; 1].
5.7. а) f x( )
= 3 x,
[−1; 1].
Решение. Найдем производную функции f (х).
![]() Для x > 0 имеем f x(
) = 3 x
= x , поэтому
f′(
)x =
Для x > 0 имеем f x(
) = 3 x
= x , поэтому
f′(
)x = ![]()
![]() x− 32 =
x− 32 =
= 31 ; ни для одного x > 0 производная в нуль не обра-
![]() 3 x2
3 x2
щается.
1
Для x < 0 имеем f x( ) = 3 x = − 3 −x = − −( x)3, поэтому
![]() f′( )x = − 1 (−x)− 23 ⋅ −( x)′ = 3 1 = 31 ; ни для одного
f′( )x = − 1 (−x)− 23 ⋅ −( x)′ = 3 1 = 31 ; ни для одного
3 3 (−x)2 3 x2
x < 0 производная в нуль не обращается.
![]() В
точке x = 0
функция определена, но производная у нее не существует (проверьте это).
Следовательно, x =
0 — единственная критическая точка функции f x( ) = 3 x на
отрезке [−1;
1].
В
точке x = 0
функция определена, но производная у нее не существует (проверьте это).
Следовательно, x =
0 — единственная критическая точка функции f x( ) = 3 x на
отрезке [−1;
1].
5.9. а) f x( ) = ex2 − ex2, [−e; e].
Решение. Найдем производную функции f (х).
Для каждого x ∈ [−e; e] имеем f′( )x = (ex2 − ex2 )′ =
= ex2 (x2)′ − 2ex = 2xex2 − 2ex = 2x (ex2 − e), поэтому функция f (х) имеет производную в каждой точке промежутка [−e; e]. Так как f′ (х) = 0 лишь в точках х1 = 0, х2 = −1, х3 = 1 и эти три точки принадлежат интервалу (−e; e), то на отрезке [−e; e] функция f (х) имеет три критические точки: х1 = 0, х2 = −1, х3 = 1.
5.14. Найдите максимум и минимум функции
y = x4 − 2x2 на:
4
а) отрезке [−2; 2]; б) интервале (−2; 2);
в) полуинтервале (−2; 2]; г) полуинтервале [−2; 2). Решение. Найдем производную данной функции: y′ = x3 − 4x. Так как y′ = 0 в точках х1 = 0, х2 = −2, х3 = 2, то в каждом из случаев а) — г) данная функция на заданном промежутке имеет только одну критическую точку: х1 = 0.
а) Так как y (−2) = y (2) = −4, y (0) = 0, то на отрезке
[−2; 2] максимум функции y = x4 − 2x2 равен 0, а мини-
4
мум равен −4.
б) Так как y (0) = 0, а y = x2 (x2 − 8) < 0 при каждом x,
4
таком, что 0 < | x | < 2, то на интервале (−2; 2) функция имеет максимум 0 в точке x = 0. На интервале (−2; 2)
функция не
имеет минимума, так как y =
x ![]() x − > −
x − > −
4
при каждом x, таком, что | x | < 2 и y = −4 при x = 2 и при x = −2, но 2 ∉ (−2; 2) и −2 ∉ (−2; 2).
в) Так как y (2) = −4, y (0) = 0 и при каждом x ∈ (−2; 2] имеем −4 ≤ x2 (x2 − 8) ≤ 0, то на полуинтервале (−2; 2]
4 4
x 2 максимум функции y = − 2x равен 0, а минимум ра-
4
вен −4.
г) Так как y (−2) = −4, y (0) = 0 и при каждом x ∈ [−2; 2)
x2 2 имеем −4 ≤ (x − 8) ≤ 0, то на полуинтервале [−2; 2) мак-
4 симум функции y = x4 − 2x2 равен 0, а минимум равен −4.
4
5.16. а) При каком значении а наибольшее значение функции y = | x − а | на отрезке [−2; 3] равно 4,5?
Решение. Приведем решение, основанное на использовании очевидных свойств графика функции y = | x − a |. Решение с помощью критических точек предоставляется читателю.
График данной функции y = f (x), где f (x) = | x − a |, изображен на рисунке 35. При a = 0,5 (середина отрезка [−2; 3]) функция f (x) принимает наибольшее значение на отрезке [−2; 3] в концах отрезка, т. е. в двух точках x1 = −2 и x2 = 3, причем f (−2) = f (3) = 2,5 ≠ 4,5.
При a > 0,5 функция принимает наибольшее значение на отрезке [−2; 3] только в левом конце отрезка и оно равно f (−2) = | −2 − a | = a + 2, причем a + 2 = 4,5 при а = 2,5
(рис. 36, а).
При a < 0,5 функция принимает наибольшее значение на отрезке [−2; 3] только в правом конце отрезка и оно равно f (3) = | 3 − a | = 3 − a, причем 3 − a = 4,5 при а = −1,5
(рис. 36, б).
Итак, функция y = | x − а | принимает на отрезке [−2; 3] наибольшее значение, равное 4,5, при а = 2,5 и при а = −1,5.
5.17. а) Последовательность задана формулой общего члена хn = n2 − 30,5n + 205. Найдите наименьший член последовательности.
Решение. Заметим, что члены последовательности {хn}
совпадают со значениями квадратичной функции х (t) = = t2 − 30,5t + 205 в точках t = n, n ∈ N.
Эта функция достигает наименьшего значения в точке t0 = 30 5![]() 2, = 15,25
2, = 15,25
(t0 — абсцисса вершины параболы, ветви которой направлены вверх). Число t0 не натуральное, поэтому наименьший член последовательности совпадает со значением функции х (t) в ближайшей к t0 среди точек t = n, n ∈ N точке t1 = 15 (15,25 − 15 < 16 − 15,25).
Так как х (15) = 152 − 30,5 ⋅ 15 + 205 = −27,5, то наименьший член последовательности {хn} равен х15 = −27,5.
Замечание. Решить задачу можно также с помощью производной функции х (t).
Дополнения
1. Наряду с точками максимума и точками минимума иногда различают точки строгого максимума и точки строгого минимума.
Если функция y = f (x) определена на отрезке [a; b], то точку x0 ∈ [a; b] называют точкой строгого максимума, если для любых других точек x ∈ [a; b] справедливо неравенство f (x0) > f (x).
Если функция y = f (x) определена на отрезке [a; b], то точку x0 ∈ [a; b] называют точкой строгого минимума, если для любых других точек x ∈ [a; b] справедливо неравенство f (x0) < f (x).
У функции, определенной на отрезке [−2; 4], график которой изображен на рисунке 37, нет ни точек строгого максимума, ни точек строгого минимума. Зато любая точка отрезка [1; 2] является точкой максимума, а любая точка отрезка [−2; −1] является точкой минимума.
У функции, определенной на отрезке [−2; 4], график которой изображен на рисунке 38, есть точка строгого максимума x1 = 1 и точка строгого минимума x2 = −2.
У функции, определенной на отрезке [−2; 4], график которой изображен на рисунке 39, нет точки строгого максимума, но есть точка строгого минимума x1 = −2. Зато любая
Рис. 37 Рис. 38 Рис. 39
точка отрезка [2; 4] является точкой максимума этой функ ции.
В определениях в п. 5.1 учебника речь идет о точках максимума и минимума и если такая точка есть точка строгого максимума (строгого минимума), то прилагательное «строгого» опускается для краткости.
2. Приведем примеры задач из ЕГЭ, связанные с вычислением наибольшего или наименьшего значения (максимума или минимума) функции.
В6 (2006). Найдите наибольшее значение функции y = 2 7, ⋅ e3x2 − x3 − 4 на отрезке [1; 3].
Решение. Для любого x ∈ R найдем y′:
y′ = (2 7, ⋅ e3x2 − x3 − 4 )′ = 2 7, ⋅(e3x2 − x3 − 4 )′ = = 2 7, ⋅ e3x2 − x3 − 4 (3x2 − x3 − 4)′ = 2 7, ⋅ e3x2 − x3 − 4 (6x − 3x2) = = 8 1, x ⋅ e3x2 − x3 − 4 (2 − x).
Тогда f′ (х) = 0 в точках х1 = 0 и х2 = 2, из которых только точка х2 принадлежит отрезку [1; 3]. Следовательно, на этом отрезке функция имеет единственную критическую точку х2 = 2.
Сравнив три числа f ( )1 = 2 7![]() ,2 ≈
0 37, , f (2) =
2,7 и
,2 ≈
0 37, , f (2) =
2,7 и
e
f (
)3 = 2 7![]() ,4 ≈
0 05, , найдем, что max[1;
3] f x( ) =
2 7, .
,4 ≈
0 05, , найдем, что max[1;
3] f x( ) =
2 7, .
e
Ответ. 2,7.
![]()
![]() С1 (2008). Найдите
наибольшее значение функции f x( ) =
| 1 − x2
− 2| + 1 − x2 + x3 − 3x2.
С1 (2008). Найдите
наибольшее значение функции f x( ) =
| 1 − x2
− 2| + 1 − x2 + x3 − 3x2.
Решение. Функция определена лишь при x ∈ [−1; 1].
Для каждого x из этого промежутка справедливо неравен-
![]()
![]()
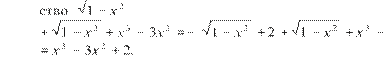 ≤ 1. Поэтому 1 − x2 − 2 ≤ −1 и | 1
− x2
− 2| +
≤ 1. Поэтому 1 − x2 − 2 ≤ −1 и | 1
− x2
− 2| +
Задача свелась к нахождению наибольшего значения функции f (х) = х3 − 3х2 + 2 на отрезке [−1; 1].
Так как f′ (х) = (х3 − 3х2 + 2)′ = 3х2 − 6х = 3х (х − 2), то f′ (х) = 0 в точках х1 = 0 и х2 = 2, из которых только х1 принадлежит отрезку [−1; 1]. Следовательно, на этом отрезке функция имеет единственную критическую точку х1 = 0.
Сравнив три числа f (−1) = −2, f (0) = 2 и f (1) = 0, найдем max f x( ) = 2.
[−1; 1]
Ответ. 2.
Промежуточный контроль. C—15.
В данном пункте учебника выведено уравнение касательной к графику непрерывной на интервале (a; b) функции y = f (х) в точке x0 ∈ (a; b), если функция y = f (х) имеет производную в этой точке. Уравнение касательной имеет вид y − y0 = k (х − х0), где k = f′ (х0), y0 = f (х0). Такая запись удобна для запоминания уравнения, но обычно уравнение записывают в виде y = f′ (х0) (х − х0) + f (х0).
Если требуется провести касательную к графику функции y = f (х), проходящую через точку A (x0; y0), то надо проверить, принадлежит ли эта точка графику функции. Если да, т. е. если y0 = f (х0), то надо написать уравнение касательной, используя приведенное выше уравнение. Если нет, то уравнение касательной находится, как в примере 3 из учебника.
Решения и комментарии
5.30. в) Напишите уравнение касательной к графику функции f x( ) = sin πx + ln (2 − x) в точке с абсциссой x0 = 1. 2
Решение. Функция f (x) определена для каждого x из промежутка (−∞; 2), число x0 принадлежит этому промежутку:
f x![]() f ;
f ;
![]()
![]() f′( )x cos
f′( )x cos ![]() ( x) cos 1 ;
( x) cos 1 ;
2 2 x
f′
![]() x f .
x f .
Поэтому уравнение касательной к графику функции f (x) в точке с абсциссой x0 = 1 имеет вид y = −1 (х − 1) + 1, т. е. y = −х + 2.
5.32. а) Углом пересечения графика функции у = f (x) и прямой l называют угол между прямой l и касательной к графику функции, проведенной в точке пересечения. Под каким углом пересекает ось Ох график функции у = f (x) в каждой из точек пересечения, если f (x) = x2 + x − 2?
Решение. Здесь имеется в виду угол пересечения прямых, он не превосходит прямого угла. Решив уравнение x2 + x − 2 = 0, найдем абсциссы двух точек пересечения графика функции f (x) с осью Ох: x1 = −2 и x2 = 1.
Так как f′ (х) = 2x + 1, то f′ (1) = 3 и f′ (−2) = −3.
![]() В точке (1; 0) касательная пересекает ось Ох под
углом α,
таким, что tg α = f′ (1) = 3, т. е. под углом α = arctg 3. Это
острый угол. Так как f′
(−2)
= −3, то
угол β,
образованный касательной с положительным направлением оси Ox, тупой.
Поэтому угол пересечения графика функции с осью Ох есть угол, смеж ный с
углом β. Его
тангенс равен tg (π
− β) =
−tg β
= 3, а сам угол есть arctg 3 (рис. 40).
В точке (1; 0) касательная пересекает ось Ох под
углом α,
таким, что tg α = f′ (1) = 3, т. е. под углом α = arctg 3. Это
острый угол. Так как f′
(−2)
= −3, то
угол β,
образованный касательной с положительным направлением оси Ox, тупой.
Поэтому угол пересечения графика функции с осью Ох есть угол, смеж ный с
углом β. Его
тангенс равен tg (π
− β) =
−tg β
= 3, а сам угол есть arctg 3 (рис. 40).
5.33. Под каким углом пересекает ось Оу график функции в предыдущем задании?
Решение. Так как f (0) = −2, f′ (х) = 2x + 1, f′ (0) = 1, то касательная к графику функции f (x) образует с осью Ох угол α, такой, что tg α = f′ (0) = 1, т. е. α = 45°. Искомый угол β найдем из прямоугольного треугольника
Рис. 40 (рис. 41), один из углов которого известен: β = 90° − α = 45°.
![]() 5.34. Напишите уравнение касательной к графику
функции: а) f (x) =
xe; б) f (x) = eх в точке с абсциссой
х0 = e.
5.34. Напишите уравнение касательной к графику
функции: а) f (x) =
xe; б) f (x) = eх в точке с абсциссой
х0 = e.
Решение. а) f (e) = ee, f′ (х) = = exe − 1, f′ (e) = ee, поэтому уравнение касательной к графику функции f (x) в точке с абсциссой х0 = e имеет вид y = ee (x − e) + ee,
т. е. y = ee (x − e + 1).
Рис. 41 б) f (e) = ee, f′ (х) = ex, f′ (e) =
= ee, поэтому уравнение каса-
тельной к графику функции f (x) в точке с абсциссой х0 = e имеет вид y = ee (x − e) + ee, т. е. y = ee (x − e + 1).
Отметим, что в пунктах а) и б) получена одна и та же прямая (см. также задание 4.69).
5.35. Напишите уравнение общей касательной к графикам функций у = f (x) и у = ϕ (x), если f (x) = x2 − 2х + 1 и ϕ (x) = −x2 + 4х − 8. Найдите два способа решения задачи. Решение. 1-й способ. Пусть x1 — абсцисса точки касания искомой прямой с графиком функции y = f (x), а x2 — абсцисса точки касания искомой прямой с графиком функции y = ϕ (x). Тогда уравнение касательной имеет вид y = f′ (x1) (x − x1) + f (x1), а также вид y = ϕ′ (x2) (x − x2) + + ϕ (x2). Так как это уравнение одной и той же прямой, то угловые коэффициенты f′ (x1) и ϕ′ (x2), а также свободные члены −f′ (x1) x1 + f (x1) и −ϕ′ (x2) x2 + ϕ (x2) равны. Из этих двух равенств и найдем x1 и x2.
Так как f′ (x1) = 2x1 − 2, ϕ′ (x2) = −2x2 + 4, то из равенства 2x1 − 2 = −2x2 + 4 найдем, что
x1 + x2 = 3. (1)
Так как −f′ (x1) x1 + f (x1) = −2x21 + 2x1 + x21 − 2х1 + 1 =
= −x21 + 1, −ϕ′ (x2) x2 + ϕ (x2) = 2x22 − 4x2 − x22 + 4x2 − 8 = = x22 − 8, то из равенства −x21 + 1 = x22 − 8 найдем, что
x21 + x22 = 9. (2)
Теперь, решив систему уравнений (1) и (2), получим два ее решения: x1 = 0, x2 = 3 и x1 = 3, x2 = 0. Подставив каждое из найденных значений x1 в первое уравнение касательной, получим два уравнения различных прямых: y = −2x + 1 и y = 4x − 8 (подставив каждое из найденных значений x2 во второе уравнение касательной, получим, разумеется, уравнения тех же прямых).
2-й способ. Заметим, что касательной к параболе y = x2 − 2х + 1 или к параболе y = −x2 + 4х − 8 не может быть прямая вида x = a. Это должна быть прямая вида y = kx + b. Тогда если эта прямая имеет единственную точку пересечения с каждой параболой, то каждое из уравнений
x2 − 2х + 1 = kx + b и −x2 + 4х − 8 = kx + b
имеет единственный корень. Но тогда равен нулю дискриминант каждого из квадратных уравнений x2 − (2 + k) х + 1 − b = 0 и −x2 + (4 − k) х − (8 + b) = 0.
Остается найти эти дискриминанты и приравнять их к нулю:
⎧⎩⎨((24 +− kk))22 −− 4 14 8(( −+bb)) == 00. (3)
Затем, решив систему (3) относительно k и b, записать уравнения касательных.
Система (3) имеет два решения: k1 = −2, b1 = 1 и k2 = 4, b2 = −8. Тогда уравнения касательных имеют вид y = −2x + 1 и y = 4x − 8.
5.36. а) При каком значении a прямая y = 7x + a является касательной к графику функции y = x4 + 3x?
Решение. Функция y = x4 + 3x имеет производную y′ = 4x3 + 3. Угловой коэффициент касательной в точке с абсциссой x0 равен y′ (x0) = 4x30 + 3, и он должен быть равен 7. Решив уравнение 4x30 + 3 = 7, найдем абсциссу единственной точки касания: x0 = 1. Тогда уравнение касательной имеет вид y = 7 (x − 1) + 14 + 3, т. е. y = 7x − 3.
Следовательно, прямая y = 7x + a является касательной к графику функции y = x4 + 3x только при a = −3.
Дополнение. Приведем примеры задач из ЕГЭ на применение понятия касательной к графику функции.
B5 (2007). Функция y = f (х) определена на промежутке (−4; 5). На рисунке 42 изображен график ее производной. Найдите число касательных к графику функции y = f (х), которые наклонены под углом 45° к положительному направлению оси абсцисс.
![]() Решение. Касательная к гра фику функции y = f (х) в
точке с абсциссой х0 наклонена под углом 45° к положительному
направлению оси абсцисс, если ее угловой коэффициент, равный f′ (х0),
равен tg 45° = 1.
На рисунке 42 f′
(х) = 1
в трех точках, следовательно, на промежутке (−4;
5) имеются 3 касательные к графику функции y = f (х), ко-
Решение. Касательная к гра фику функции y = f (х) в
точке с абсциссой х0 наклонена под углом 45° к положительному
направлению оси абсцисс, если ее угловой коэффициент, равный f′ (х0),
равен tg 45° = 1.
На рисунке 42 f′
(х) = 1
в трех точках, следовательно, на промежутке (−4;
5) имеются 3 касательные к графику функции y = f (х), ко-
Рис. 42 торые наклонены под углом 45° к положительному направлению оси абсцисс.
Ответ. 3.
А10 (2004). Через точку графика функции f (х) = ex − х2 с абсциссой х0 = 1 проведена касательная. Найдите тангенс угла наклона этой касательной к оси абсцисс.
1) e − 2; 2) −1; 3) e − 1; 4) −2.
Решение. Угловой коэффициент касательной, проведенной к графику функции f (х) в точке с абсциссой х0, равен f′ (х0). Найдем производную функции f (х):
f′ (х) = (ex − х2)′ = ex − 2х.
Так как f′ (1) = e − 2, то искомый тангенс угла наклона этой касательной к оси абсцисс равен e − 2.
Ответ. 1.
А10 (2006). Укажите абсциссу точки графика функции f (х) = 5 + 4х − х2, в которой угловой коэффициент касательной равен нулю.
1) 0; 2) 2; 3) −2; 4) 5.
Решение. Угловой коэффициент касательной, проведенной к графику функции f (х) в точке с абсциссой х0, равен f′ (х0). Найдем производную функции f (х): f′ (х) = (5 + 4х − х2)′ = 4 − 2х.
Так как f′ (х) = 0 лишь в точке х0 = 2, то искомая абсцисса точки графика равна 2.
Ответ. 2.
В5 (2008). Прямая, проходящая через начало координат, касается графика функции y = f (х) в точке А (−7; 14). Найдите f′ (−7).
Решение. 1-й способ. Прямая, проходящая через начало координат, имеет либо уравнение х = 0, либо уравнение y = kх. Так как она проходит через точку А (−7; 14), то она имеет уравнение y = kх и, значит, справедливо равенство 14 = k ⋅ (−7), откуда k = −2.
Угловой коэффициент касательной, проведенной к графику функции y = f (х) в точке с абсциссой −7, равен f′ (−7), следовательно, f′ (−7) = − 2.
2-й способ. Прямая, проходящая через точки (x1; y1) и y1 − y2
(x2; y2), где x1
≠ x2,
имеет угловой коэффициент k = ![]() , x1 −
x2
, x1 −
x2
поэтому прямая, проходящая через начало координат О (0; 0) и через точку А (−7; 14), имеет угловой коэффици-
ент k = ![]()
![]() =
−2. Угловой коэффициент касательной,
=
−2. Угловой коэффициент касательной,
проведенной к графику функции y = f (х) в точке с абсциссой −7, равен f′ (−7), следовательно, f′ (−7) = −2.
Ответ. −2.
Промежуточный контроль. C—16.
В данном пункте учебника приведена формула для приближенного вычисления значений функции и на конкретных примерах показано ее применение для нескольких функций, для положительных и отрицательных значений Δx. Отметим, что первое задание (5.38) для учащихся дано в облегченной формулировке: число x0 и приращение аргумента Δx заданы. В следующем задании учащиеся сами должны определить и x0, и Δx.
Решения и комментарии
5.40. Покажите, как из формулы f (x0 + Δx) ≈ f (x0) + f′ (x0) ⋅ Δx (1)
следует формула для приближенного вычисления квадратного корня из числа, близкого к 1:
. (2)
![]() Вычислите приближенно с помощью этой формулы:
Вычислите приближенно с помощью этой формулы:
б) 1,02; в) 0,99.
![]() Решение.
Рассмотрим функцию f x( ) =
x, тогда для x0 =
1 имеем f (x0) =
f (1) = 1,
f′(
)x =
1 для
x > 0 и
Решение.
Рассмотрим функцию f x( ) =
x, тогда для x0 =
1 имеем f (x0) =
f (1) = 1,
f′(
)x =
1 для
x > 0 и
2 x
f′ ![]() x f . Подставив в формулу (1)
f (x0 +
Δx) =
x f . Подставив в формулу (1)
f (x0 +
Δx) =
= 1 + Δx, f ![]() f x x x,
получим формулу (2).
f x x x,
получим формулу (2).
б) Здесь x0 = 1, Δx = 0,02. По формуле (2) имеем
1
1 02, ≈ 1 + ⋅ 0 02, = 1 01, .
2
в) Здесь x0 = 1, Δx = −0,01. По формуле (2) имеем
![]() 0 99, ≈ 1 + 1 ⋅ −( 0 01, )
= 0,995.
0 99, ≈ 1 + 1 ⋅ −( 0 01, )
= 0,995.
2
Задание 5.41 выполняется, как и предыдущее, но для функции f (x) = xn.
Промежуточный контроль. C—17.
В данном пункте учебника доказаны теоремы Ролля и Лагранжа, на которые опирается доказательство теоремы в следующем пункте учебника. Этот материал рассматривается только при углубленном изучении математики.
Решения и комментарии
5.45. а) Не вычисляя производной, объясните, почему внутри отрезка [−1; 2] функция f (x) = −х3 + 3х имеет точку, в которой производная этой функции равна нулю.
Решение. Так как функция f (x) = −х3 + 3х непрерывна на отрезке [−1; 2], имеет производную на интервале (−1; 2) и принимает на концах отрезка [−1; 2] равные значения f (−1) = f (2) = −2, то по теореме Ролля на интервале (−1; 2) найдется такая точка c, в которой производная равна нулю.
5.47. Дана функция у = f (x). Внутри отрезка [a; b] найдите точку с, для которой справедливо равенство
f b( ) − f a( ) f′( )c =, если:
b − a
![]()
![]() в)
f x( ) = 3
x, a =
0, b = 27; г)
f x( ) = 3
x, a =
−27, b =
0.
в)
f x( ) = 3
x, a =
0, b = 27; г)
f x( ) = 3
x, a =
−27, b =
0.
Решение. в) Функция f x( ) = 3 x непрерывна на отрезке [0; 27] и имеет на интервале (0; 27) производную f′( )x = 31 , тогда по теореме Лагранжа на интервале 3 x2
(0; 27) найдется точка c, такая, что справедливо равенство
![]()
![]() f′( )c = f (27) − f (0) . Следовательно, 1 =
, откуда следу27 −
0 ет, что c = 3 3, так как с > 0.
f′( )c = f (27) − f (0) . Следовательно, 1 =
, откуда следу27 −
0 ет, что c = 3 3, так как с > 0.
![]()
![]() г) Функция f x( ) = 3 x непрерывна
на отрезке [−27;
0] и имеет на интервале (−27;
0) производную f′(
)x =
31 ,
г) Функция f x( ) = 3 x непрерывна
на отрезке [−27;
0] и имеет на интервале (−27;
0) производную f′(
)x =
31 ,
3 x2
тогда по теореме Лагранжа на интервале (−27; 0) найдется точка c, такая, что справедливо равенство
![]()
![]() f′( )c = f (0) − f (−27) . Следовательно, 1 =
, откуда сле0 −
(−27) дует, что c = −3 3, так как с
< 0.
f′( )c = f (0) − f (−27) . Следовательно, 1 =
, откуда сле0 −
(−27) дует, что c = −3 3, так как с
< 0.
5.48. Через две точки A и B графика функции f (x) = х2, имеющие соответственно абсциссы a и b, проведена секущая AB. Существует ли точка С графика функции с абсциссой с ∈ (a; b), через которую можно провести касательную к графику этой функции, параллельную секущей AB?
Решение. Функция f (x) = х2 непрерывна на отрезке [a; b] и имеет на интервале (a; b) производную f′ (x) = 2х, тогда по теореме Лагранжа на интервале (a; b) найдется точка c, такая, что справедливо равенство
f′( )c = ![]() f b( )
−
f a( ) . (1)
f b( )
−
f a( ) . (1)
b − a
f b( ) − f a( )
Угловой коэффициент секущей есть k1 = ![]() b − a ,
b − a ,
а угловой коэффициент касательной к графику этой функции в точке, принадлежащей этому графику, есть k2 = f′ (с). Из равенства (1) следует, что k1 = k2, т. е. секущая и касательная параллельны. Следовательно, такая точка С существует.
Для функции f (x) = х2 равенство (1) перепишется в виде b2 − a2 a + b
![]() 2c =
2c = ![]() , откуда следует, что c = . Итак, точка С b − a 2
, откуда следует, что c = . Итак, точка С b − a 2
a + b (a + b)2
имеет
координаты x0 = ![]() 2 и y 0 = 4 .
2 и y 0 = 4 .
В данном пункте учебника изучается вопрос об определении вида монотонности функции на промежутке по знаку ее производной внутри промежутка. Доказательство теоремы опирается на теорему Лагранжа. Содержание теоретического материала данного пункта играет важную роль в исследовании функции, решении задач на максимум и минимум, поэтому оно должно быть хорошо отработано. Учащиеся должны научиться находить промежутки возрастания (убывания) функции.
Решения и комментарии
5.54. Докажите, что функция f x( ) = 1 убывает на кажx
дом из промежутков (−∞; 0) и (0; +∞).
Доказательство. Так как f′( )x ![]()
![]() для любого x ≠ 0, x
для любого x ≠ 0, x
то функция f (x) убывает на каждом из промежутков (−∞; 0) и (0; +∞).
5.59. Докажите, что функция f x( ) = ![]()
![]() x3 − x2 − 8x +1 на отрезке [−1; 3] имеет
единственный нуль. Сколько нулей на промежутке (−∞;
+∞) имеет
функция f (x)? Определите точки локального экстремума функции f
(x).
x3 − x2 − 8x +1 на отрезке [−1; 3] имеет
единственный нуль. Сколько нулей на промежутке (−∞;
+∞) имеет
функция f (x)? Определите точки локального экстремума функции f
(x).
Доказательство. Напомним, что в учебнике сформулирована теорема о промежуточном значении функции: непрерывная на отрезке [a; b] функция принимает все промежуточные значения между ее значениями на концах отрезка [a; b].
Из этой теоремы следует, что если непрерывная на отрезке [a; b] функция строго монотонна на нем, то она принимает каждое промежуточное значение между ее значениями на концах отрезка [a; b] только один раз.
Область существования функции f (x) есть R. Для любого x ∈ R имеем f′ (x) = x2 − 2x − 8 = (x − 4) (x + 2) и f′ (x) < 0 при −2 < x < 4. Поэтому на промежутке [−2; 4] функция убывает; так как при этом f (−2) > 0, а f (4) < 0 и функция непрерывна на отрезке [−2; 4], то на этом отрезке функция f (x) имеет единственный нуль. Так как f (−1) > 0, а f (3) < 0, то этот нуль принадлежит отрезку [−1; 3], т. е. на отрезке [−1; 3] функция f (x) имеет единственный нуль, что и требовалось доказать.
Так как f′ (x) > 0 при x > 4, то на промежутке [4; +∞) функция f (x) возрастает. Так как f (4) < 0, а f (10) > 0 и функция f (x) непрерывна на отрезке [4; 10], то на интервале (4; 10) функция имеет единственный нуль. Так как функция возрастает на промежутке [10; +∞), то f (x) > > f (10) > 0 для каждого x ∈ [10; +∞), т. е. на этом промежутке функция не имеет нулей. Следовательно, функция f (x) имеет единственный нуль на промежутке (4; +∞).
Аналогично показывается, что на промежутке (−∞; −2) функция f (x) также имеет единственный нуль.
Следовательно, на промежутке (−∞; +∞) функция f (x) имеет три нуля.
Так как в точке x1 = −2 знак производной меняется с «+» на «−», то x1 = −2 — точка локального максимума функции f (x); так как в точке x2 = 4 знак производной меняется с «−» на «+», то x2 = 4 — точка локального минимума функции f (x) (рис. 43).

Рис. 43 Рис. 44
5.60. а) Определите точки локального экстремума функ-
ции f x( ) = 2x . Достигает ли функция f (x) в точках x + 5
локального экстремума своего наибольшего (наименьшего) значения?
![]() Решение.
Так как для любого x ∈
R имеем f′(
)x = ( 5 −
x2
) ( 52 +
x) и f′ (x) = 0 лишь при x1
= −5 и
при
Решение.
Так как для любого x ∈
R имеем f′(
)x = ( 5 −
x2
) ( 52 +
x) и f′ (x) = 0 лишь при x1
= −5 и
при
![]() (x + 5) x2 = 5, то функция f (x) имеет
на R только две критические точки: x1 и x2.
(x + 5) x2 = 5, то функция f (x) имеет
на R только две критические точки: x1 и x2.
![]()
![]()
![]() Определив знак f′ (x) на
интервалах (−∞; −5),
(− 5; 5)
и (5;
+∞)
(рис. 44), получим, что x1 = − 5 — точка локального минимума
функции f (x), а x =
5 — точка локального максимума функции f (x).
Определив знак f′ (x) на
интервалах (−∞; −5),
(− 5; 5)
и (5;
+∞)
(рис. 44), получим, что x1 = − 5 — точка локального минимума
функции f (x), а x =
5 — точка локального максимума функции f (x).
![]()
![]()
![]() Так как f (− 5)
= − 105 , на интервале (−∞; − 5)
функция f (x) убывает, на интервале (− 5; 5)
возрастает, а на промежутке [ 5; +∞)
принимает положительные значения, т. е. значения, большие −
5 ,
то в точке x1 функция f (x)
Так как f (− 5)
= − 105 , на интервале (−∞; − 5)
функция f (x) убывает, на интервале (− 5; 5)
возрастает, а на промежутке [ 5; +∞)
принимает положительные значения, т. е. значения, большие −
5 ,
то в точке x1 функция f (x)
10
достигает своего наименьшего значения.
![]()
![]()
![]() Так как f (
5)
= 105 , на интервале (− 5; 5)
функция f (x) возрастает, на интервале (
5; +∞)
убывает, а на промежутке (−∞; − 5] принимает
отрицательные значения,
Так как f (
5)
= 105 , на интервале (− 5; 5)
функция f (x) возрастает, на интервале (
5; +∞)
убывает, а на промежутке (−∞; − 5] принимает
отрицательные значения,
5
т. е. значения, меньшие , то в точке x2 функция f (x)
10
достигает своего наибольшего значения.
5.61. Докажите, что функция f (x) = x4 + 4x3 + 28 принимает положительные значения на всей своей области определения.
Доказательство. Так как для любого x ∈ R имеем f′ (x) = = 4x3 + 12x2 и f′ (x) = 0 лишь при x1 = −3 и x2 = 0, то функция f (x) имеет только две критические точки: x1 и x2.
![]() Определив знак f′
(x) на интервалах (−∞;
−3), (−3; 0) и (0; +∞) (рис. 45),
получим, что x1 =
−3 — единственная точка локального минимума.
Определив знак f′
(x) на интервалах (−∞;
−3), (−3; 0) и (0; +∞) (рис. 45),
получим, что x1 =
−3 — единственная точка локального минимума.
Так как f (−3) = 1 > 0 и на Рис. 45
промежутке (−∞; −3] функция f (x) убывает, а на промежутке [−3; 0] возрастает, на интервале (0; +∞) принимает положительные значения, то f (x) > 0 для каждого x из области определения, что и требовалось доказать.
В данном пункте учебника введены понятия второй производной и производных высших порядков, разъяснен механический смысл второй производной, разобраны примеры задач, для решения которых применяются новые понятия.
Решения и комментарии
5.65. а) Пусть при прямолинейном движении тела его координата x (в метрах) меняется по закону x (t) =
= 5t + sin 3t − 2 cos t , где t — время (в секундах), t ≥ 0.
2
Найдите начальную скорость и начальное ускорение тела.
Решение. Для любого t имеем x′ (t) = 5 + 3 cos 3t + sin t ,
2
поэтому начальная скорость точки равна x′ (0) = 5 + 3 =
= 8 (м/с). Так как x″ (t) = −9 sin 3t + 1 cos t для любого t,
2 2
то начальное ускорение точки равно x″ (0) = 0 + 0,5 =
= 0,5 (м/с2).
5.67. Найдите производные 1-го, 2-го и 3-го порядков функции f (x) = anxn + an − 1xn − 1 + ... + a1x + a0, где n ≥ 2. Запишите полученный результат для n = 2, n = 3, n = 4. Решение. Для любого x ∈ R имеем f′ (x) = nanxn − 1 + (n − 1) an − 1xn − 2 + ... + 3a3x2 + 2a2x + a1; f″ (x) = n (n − 1) anxn − 2 + (n − 1) (n − 2) an − 1xn − 3 + ... + 6a3x + 2a2;
f″′ (x) = n (n − 1) (n − 2) anxn− 3 +
+ (n − 1) (n − 2) (n − 3) an− 1xn− 4 + ... + 6a3.
Для n = 2 имеем f′ (x) = 2a2x + a1; f″ (x) = 2a2; f″′ (x) = 0. Для n = 3 имеем f′ (x) = 3a3x2 + 2a2x + a1; f″ (x) = 6a3x + 2a2; f″′ (x) = 6a3.
Для n = 4 имеем f′ (x) = 4a4x3 + 3a3x2 + 2a2x + a1; f″ (x) = = 12a4x2 + 6a3x + 2a2; f″′ (x) = 24a4x + 6a3.
5.69. Найдите производные порядков n и (n − 1) функции f (x) = anxn + an − 1xn − 1 + ... + a1x + a0, где n ≥ 2.
Решение. Для любого x ∈ R имеем f (n − 1) (x) = n (n − 1) ⋅ ... ⋅ 2 ⋅ anx + (n − 1) ⋅ ... ⋅ 2 ⋅ 1 ⋅ an − 1 =
= n! ⋅ anx + (n − 1)! an − 1; f (n) (x) = n (n − 1) ⋅ ... ⋅ 2 ⋅ 1 ⋅ an = n! ⋅ an.
В данном пункте учебника рассмотрен вопрос о выпуклости графика функции вверх (вниз) в зависимости от знака второй производной функции, введено понятие точки перегиба для графика функции. На рассмотренных в учебном тексте примерах показано, как новые понятия используются при решении задач.
Решения и комментарии
5.78. а) Определите промежутки выпуклости вверх (вниз) графика функции у = f (x), если f (x) = | x2 − 1 |. Есть ли у графика этой функции точки перегиба?
Решение. а) Рассмотрим функцию f (x) на интервалах (−∞; −1), (−1; 1), (1; +∞).
На интервале (−∞; −1) и на интервале (1; +∞) функцию можно задать формулой y = x2 − 1, тогда y′ = 2x и y″ = 2 > 0 для каждого x ∈ (−∞; −1) ∪ (1; +∞).
На интервале (−1; 1) функцию можно задать формулой y = 1 − x2, тогда y′ = −2x и y″ = −2 < 0 для каждого x ∈ (−1; 1).
Следовательно, график функции имеет выпуклость вниз на интервалах (−∞; −1), (1; +∞) и выпуклость вверх на интервале (−1; 1).
Так как lim ![]() Δf = −2 ≠
lim
Δf = −2 ≠
lim ![]() Δf = 2, то в точке x = −1 x → −1 Δx x → −1 Δx x < −1 x >
−1
Δf = 2, то в точке x = −1 x → −1 Δx x → −1 Δx x < −1 x >
−1
функция f (x) не имеет производной, поэтому в этой точке нельзя провести касательную к графику функции у = f (x). Следовательно, эта точка не является точкой перегиба графика функции f (x).
Аналогично показывается, что точка x = 1 также не является точкой перегиба графика функции f (x). Промежуточный контроль. C—18.
5.8*. Экстремум функции с единственной
В данном пункте учебника рассмотрен вопрос об экстремуме непрерывной на промежутке функции, имеющей на этом промежутке производную и единственную критическую точку.
Решения и комментарии
5.82. а) Найдите наибольшее и наименьшее значения функции f x( ) = x + 4 на промежутке (0; +∞). x
Функция f x( ) = x + 4 определена для каждого x > 0, x
для этих x она
имеет производную f′(
)x = 1 − 42 = ![]() x2 −2
4. x x
x2 −2
4. x x
На интервале (0; +∞) функция f имеет
единственную критическую точку x =
2, в которой производная обращается в нуль. Следовательно, у этой
функции есть единственный экстремум на интервале (0; +∞), достигаемый в точке x = 2. В этой точке
производная меняет знак с «−»
на «+»,
следовательно, x =
2 — точка минимума функции на интервале (0; +∞). Так как на этом интервале точка
экстремума единственная, то в ней функция f достигает наименьшего
значения (имеет минимум) на этом интервале. Итак, ![]() и функция не имеет
наибольшего
и функция не имеет
наибольшего
значения на интервале (0; +∞), так как f
(x) →
+∞ при x ![]() +∞.
+∞.
Замечание. Обучая школьников применению производной, надо не упускать случаев, когда задача может быть решена без использования производной. Это может существенно сэкономить время, что очень важно во время экзамена.
В задании 5.82а возможно такое решение. Так как
![]()
![]() ⎛ 2 ⎞ >
0 верно неравенство
⎛ 2 ⎞ >
0 верно неравенство
xx⎟⎠ и для каждого x
x 2 1
+ ≥ 2 (здесь применяется неравенство a + ≥ 2, спра-
2 x a
ведливое для каждого a > 0), то x + 4 ≥ 4. Равенство x
x + 4 = 4 достигается в точке x = 2, поэтому эта точка явx
ляется точкой минимума функции f (x)
на интервале (0; +∞).
Так как f (x) >
2 при каждом x ∈
(0; 2) ∪ (2;
+∞) и f (x)
→ +∞ при
x ![]() +∞,
то функция не имеет наибольшего значения на интервале (0; +∞).
+∞,
то функция не имеет наибольшего значения на интервале (0; +∞).
Аналогично в задании 5.82б для каждого x < 0 верно
неравенство x + 4 ≤ −4 и
равенство достигается в точке x
x = −2,
поэтому ![]() .
.
В примере 2 из п. 18 дидактических материалов также возможно решение без применения производной. Функция f x( ) = x−216+ 16x в точке x = 0 имеет значение 0, f (x) < 0 для
каждого x > 0 и f (x) > 0 для каждого x < 0. Для x > 0 функцию можно задать формулой f x( ) = −4 . Так как x 4
+ 4 x
для каждого x > 0 верно неравенство x + 4 ≥ 2, то для каж-
4 x
дого x > 0 верно неравенство f (x) ≥ −2, причем f (x) = −2 при x = 4. Поэтому min f x( ) = f ( )4 = −2.
( 0; +∞ )
Аналогично показывается, что ![]() .
.
Итак, для x >
0 имеем f (x) <
0 и ![]() . Для x < 0 имеем f (x) > 0 и
. Для x < 0 имеем f (x) > 0 и ![]() . Для x = 0 имеем
. Для x = 0 имеем
f (x) = 0. Следовательно, min f x( ) = −2 и max f x( ) = 2.
( −∞ +∞; ) ( −∞ +∞; )
5.86. Для каждого значения a найдите наименьшее значение функции f (x) = | x − a | на отрезке [−1; 1].
Решение. Функция f (x) может иметь единственную критическую точку x0 = a, в которой производная не существует.
Если a ≥ 1, то на отрезке [−1; 1] у функции f (x) нет критических точек. Так как f (1) = | 1 − a | = a − 1, f (−1) = | −1 − a | = a + 1, то min f x( ) = a − 1 (рис. 46, а).
[−1; 1]
Если a ≤ −1, то на отрезке [−1; 1] у функции f (x) нет критических точек. Так как f (1) = | 1 − a | = 1 − a, f (−1) = | −1 − a | = −a − 1, то min f x( ) = −a − 1 (рис. 46, б).
[−1; 1]

Если −1 < a < 1, то на отрезке [−1; 1] функция f (x) имеет единственную критическую точку x0 = a. Так как f (a) = 0, f (1) = | 1 − a | = 1 − a, f (−1) = | −1 − a | = a + 1, то
![]() (рис. 46, в).
(рис. 46, в).
Ответ. a − 1, если a ≥ 1; −a − 1, если a ≤ −1; 0, если −1 < a < 1.
5.88. б) Для каждого значения b найдите наибольшее значение функции f (x) = (x − b)2 на отрезке [−1; 1].
Решение. Функция f (x) может иметь единственную критическую точку x0 = b, в которой производная равна нулю.
Вычислим значения функции в точках x = 1 и x = −1:
f (1) = (1 − b)2 = 1 + b2 − 2b,
f (−1) = (−1 − b)2 = (1 + b)2 = 1 + b2 + 2b.
Если b ≤ −1, то на отрезке [−1; 1] у функции f (x) нет критических точек. Так как f (1) > f (−1), то max f x( ) =
= f (1) = (1 − b)2 (рис. 47, а). [−1; 1]
![]() Если −1
< b ≤ 0, то на
отрезке [−1;
1] у функции f (x) имеется единственная критическая точка x = b, и так как f
(1) = (1 − b)2
> f (b)
= 0, то
Если −1
< b ≤ 0, то на
отрезке [−1;
1] у функции f (x) имеется единственная критическая точка x = b, и так как f
(1) = (1 − b)2
> f (b)
= 0, то
(рис. 47, б).
Объединив рассмотренные случаи, имеем: если b ≤ 0, то
![]()
![]() Аналогично показывается, что если b > 0, то = f (−1) = (1 + b)2 (рис.
47, в, г).
Аналогично показывается, что если b > 0, то = f (−1) = (1 + b)2 (рис.
47, в, г).
Ответ. (1 + b)2, если b > 0; (1 − b)2, если b ≤ 0.
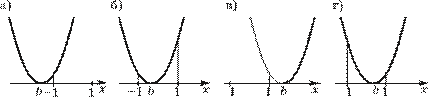
Рис. 47
5.89. Для каждого положительного значения b найдиx + b
![]() те
наибольшее значение функции f x( ) = на
отрез-
те
наибольшее значение функции f x( ) = на
отрез-
ке [1; 2].
Решение. Для каждого х ∈ R имеем ′ . Так
как b > 0, то f′ (x) = 0 лишь при x = 1, т. е. функция имеет b
единственную критическую точку x = 1. Так как f′ (x) > 0 b
при x < 1, f′ (x) < 0 при x > 1, то x = 1 — единственная b b b
точка локального максимума функции на R, в ней достигается максимум на R (наибольшее значение) функции. Остается рассмотреть три случая.
1) Если 0 < 1 ≤ 1, т. е. если b ≥ 1, то точка x = 1 не явb b
ляется внутренней точкой отрезка [1; 2] и на отрезке [1; 2] нет критических точек функции f (x).
1 + b 2 + b 1 + b 2 + b
![]() Так как f (1) = , f (2)
=
Так как f (1) = , f (2)
= ![]() > , то
> , то
max f x( ) = f (1) =
[1; 2]
2) Если 1 < 1 < 2, т. е. если 1 < b < 1, то функция имеет b 2
![]()
![]() единственную
критическую точку на отрезке [1; 2]. Так как f (1) = 1 + b, f ⎛⎜⎝ 1b⎞⎟⎠ = b2
+1, f (2)
=,
единственную
критическую точку на отрезке [1; 2]. Так как f (1) = 1 + b, f ⎛⎜⎝ 1b⎞⎟⎠ = b2
+1, f (2)
=,
 ,
то
,
то ![]() f x f ⎜⎝⎛ 1b⎞⎟⎠
=
f x f ⎜⎝⎛ 1b⎞⎟⎠
=
1 1 1
3) Если ≥ 2, т. е. если 0 < b ≤ , то точка x = не явb 2 b
ляется внутренней точкой отрезка [1; 2] и на отрезке [1; 2] нет критических точек функции f (x).
![]() 1 + b 2 + b 1 + b 2 + b
1 + b 2 + b 1 + b 2 + b
, f
(2) = ![]() и
и ![]() < , то
< , то
Ответ. ![]() ,
если
,
если ![]()
![]() < b < 1;
< b < 1;
1 b
, если b ≥ 1.
Дополнение. Приведем примеры задач из ЕГЭ на отыскание промежутков возрастания (убывания) и точек экстремума функции с помощью производной.
![]() В5 (2006). Функция y = f (х)
определена на промежутке (−3;
7). На рисунке 48 изображен график ее производной. Найдите точку
х0, в которой функция y =
f (х) принимает наибольшее значение.
В5 (2006). Функция y = f (х)
определена на промежутке (−3;
7). На рисунке 48 изображен график ее производной. Найдите точку
х0, в которой функция y =
f (х) принимает наибольшее значение.
Решение. На интервале (−3; 7) производная функции y = f (х) обращается в нуль в единственной точке x = 1. В этой точке производная меняет знак с «+» на «−», следовательно, в точке x = 1 фун- Рис. 48 кция принимает свое наибольшее значение на интервале (−3; 7).
Ответ. 1.
В данном пункте учебника рассмотрены примеры решения задач на максимум и минимум, сводящиеся к отысканию наибольшего (наименьшего) значения функции, заданной на отрезке или интервале. Показывая новый способ решения задач с помощью производной, надо все же не упускать возможности применять более простые способы решения, основанные на отыскании экстремума квадратичной функции, на использовании неравенства a + 1 ≥ 2 a
и других идей. Решения такого рода задач приведены в пп. 19—21 дидактических материалов.
При оформлении решения задач на максимум и минимум с помощью производной можно посоветовать учащимся придерживаться следующего порядка:
1) ввести переменную x, от значения которой зависит та величина, которая согласно условию задачи принимает наибольшее (наименьшее) значение;
2) определить границы изменения переменной x — промежуток X;
3) выразить через x величину, которая согласно условию задачи принимает наибольшее (наименьшее) значение
(получить функцию f (x));
4) рассмотреть функцию f (x), заданную на X, найти ее критические точки, точки локального максимума (минимума);
5) объяснить, почему в точке локального максимума (минимума) функция принимает наибольшее (наименьшее) значение;
6) интерпретировать результаты исследования функции f (x) с точки зрения решаемой задачи.
Решения и комментарии
5.93. Парабола задана уравнением у = 3 − х2. В нее вписан прямоугольник наибольшей площади так, что одна его сторона лежит на оси Ох, а две вершины — на параболе (рис. 49). Определите стороны этого прямоугольника.
![]()
![]() Решение.
Пусть OD = x,
x <3, тогда
DC = 3 − х2,
а площадь прямоугольника ABCD равна
Решение.
Пусть OD = x,
x <3, тогда
DC = 3 − х2,
а площадь прямоугольника ABCD равна
2x (3 − х2) = −2х3 + 6х.
![]() Рассмотрим
функцию f (x) =
= −2х3 +
6х на интервале (0;3).
Рассмотрим
функцию f (x) =
= −2х3 +
6х на интервале (0;3).
В каждой точке этого интервала функция f (x) имеет производную f′ (x) = −6х2 + 6 = −6 (х − 1) (х + 1),
и f′ (x) = 0 в двух точках: x1 = −1 и x2 = 1, из которых только точ-
Рис. 49 ка x2 принадлежит интервалу
![]() (0;3).
Следовательно, на интер-
(0;3).
Следовательно, на интер-
![]()
![]() вале (0;3)
функция имеет единственную критическую точку x2 = 1. Так как в этой
точке производная функции f (x) меняет знак с «+» на «−», то в ней
функция принимает свое наибольшее значение на интервале (0;3).
вале (0;3)
функция имеет единственную критическую точку x2 = 1. Так как в этой
точке производная функции f (x) меняет знак с «+» на «−», то в ней
функция принимает свое наибольшее значение на интервале (0;3).
Итак, прямоугольник имеет наибольшую площадь, если OD = 1, т. е. если AD = CD = 2.
Ответ. Квадрат со стороной 2 см.
5.94. а) Из всех прямоугольных треугольников с данной гипотенузой c найдите тот, площадь которого наибольшая.
![]() Решение.
По условию задачи AB =
c (рис. 50). Пусть CB =
x, 0 < x
< c,
тогда AC = c2
− x2
, а площадь треугольника ABC равна x c2 − x2 = c x2 2 − x4 .
Решение.
По условию задачи AB =
c (рис. 50). Пусть CB =
x, 0 < x
< c,
тогда AC = c2
− x2
, а площадь треугольника ABC равна x c2 − x2 = c x2 2 − x4 .
Рассмотрим функцию f x( ) = c x2 2 − x4 на интервале (0; с). В каждой точке этого интервала функция f (x)
имеет производную f′( )x = (c x2 2 − x4)′ = 2c x2 − 4x3 =
4 c x2 2 − x4 4 c x2 2 − x4
⎛ 2 ⎞ ⎛ 2 ⎞
![]() −x x⎜ − c⎟
⎜ x + c⎟
−x x⎜ − c⎟
⎜ x + c⎟
⎝ 2 ⎠ ⎝ 2 ⎠
= . Так как c x2 2 − x4
![]() f′ (x) = 0 на интервале (0; с)
только в точке x0 = 22 c, то функция Рис.
50 f (x) имеет на этом интервале единственную критическую
точку x0. Так как в этой точке производная функции меняет
знак с «+» на «−», то в ней
функция f (x) достигает наибольшего значения на интервале (0; с).
f′ (x) = 0 на интервале (0; с)
только в точке x0 = 22 c, то функция Рис.
50 f (x) имеет на этом интервале единственную критическую
точку x0. Так как в этой точке производная функции меняет
знак с «+» на «−», то в ней
функция f (x) достигает наибольшего значения на интервале (0; с).
Итак, площадь прямоугольного треугольника с гипоте-
![]() 2 нузой c будет наибольшей, если катет CB равенc.
Тогда
2 нузой c будет наибольшей, если катет CB равенc.
Тогда
2
AC =
![]() c,
т. е. если этот треугольник рав-
c,
т. е. если этот треугольник рав-
нобедренный.
c
![]() Ответ. Равнобедренный треугольник с катетом2.
Ответ. Равнобедренный треугольник с катетом2.
2
Замечания
1. Тот же результат можно получить из геометрических соображений. Заметим, что вершина C прямого угла прямоугольного треугольника ABC лежит на окружности с диаметром c (рис. 51). Поэтому при постоянном основании треугольника его площадь будет наибольшей, если точка D — основание высоты, проведенной к гипотенузе, — является центром этой окружности, т. е. если прямоугольный треугольник является равнобедренным.
2. Там, где это возможно, нужно обращать внимание учащихся на то, что применение производной дает резуль-
таты, подтверждаемые другими методами решения задач на максимум и минимум. В некоторых случаях бывает даже проще не использовать производную. Такие решения нужно обязательно показать учащимся.
![]() 5.97.
Диагональ прямоугольного параллелепипеда, в основании которого лежит
квадрат, равна 33, а высота принимает значения, принадлежащие отрезку [1,5;
3,5]. Найдите параллелепипед, имеющий наибольший объем.
5.97.
Диагональ прямоугольного параллелепипеда, в основании которого лежит
квадрат, равна 33, а высота принимает значения, принадлежащие отрезку [1,5;
3,5]. Найдите параллелепипед, имеющий наибольший объем.
Решение. Пусть высота прямоугольного параллелепипеда DD1 = x (рис. 52), тогда
![]() BD2
= (33)2
− x2
= 27 − x2,
площадь основания прямоугольного параллелепипеда равна
BD2
= (33)2
− x2
= 27 − x2,
площадь основания прямоугольного параллелепипеда равна
S =
![]()
![]() BD2 =
BD2 = ![]()
![]() (27 −
x2),
(27 −
x2),

Рис. 52
а объем равен
![]() V =
V = ![]()
![]() (27 −
x2) x = (27x
− x3).
(27 −
x2) x = (27x
− x3).
Рассмотрим функцию V x( ) = (27x − x3) на отрезке
[1,5; 3,5] и найдем значение x, при котором функция V (x) достигает наибольшего значения на этом отрезке.
Так как для любого x ∈ R функция V (x) имеет производную
V′(
)x = ![]()
![]() (27x − x3)′ =
(27x − x3)′ = ![]()
![]() (3 −
x) (3 + x),
(3 −
x) (3 + x),
то V′ (x) = 0 при x = 3 и при x = −3. Функция V (x) имеет на отрезке [1,5; 3,5] единственную критическую точку x = 3.
Определим значение x, при котором функция V (x) достигает наибольшего значения на отрезке [1,5; 3,5]:
V ![]() ;
;
V ![]() ;
;
V ![]() .
.
Так как ![]() , то в точке x = 3 функция f (x)
достигает наибольшего значения на отрезке [1,5; 3,5].
, то в точке x = 3 функция f (x)
достигает наибольшего значения на отрезке [1,5; 3,5].
Итак, прямоугольный параллелепипед имеет наибольший объем, если его высота равна 3. Так как стороны его основания также равны 3, то этот прямоугольный параллелепипед является кубом.
Ответ. Куб с ребром 3.
5.98. Корабль K стоит в 9 км от ближайшей точки B прямолинейного берега (рис. 53). С корабля нужно послать курьера в лагерь L, находящийся на берегу и расположенный в 15 км (считая по берегу) от точки B. В каком пункте P курьер должен пристать к берегу, чтобы попасть в лагерь за кратчайшее время, если он идет пешком со скоростью 5 км/ч, а на веслах — 4 км/ч?
Решение. Пусть BP = x, 0 < x < 15, тогда PL = 15 − x,
![]()
![]() PK
= 81 + x2 (все
расстояния измеряются в километрах). Тогда время движения курьера по ломаной KPL
равно
PK
= 81 + x2 (все
расстояния измеряются в километрах). Тогда время движения курьера по ломаной KPL
равно
15 − x 81 + x2
+ (ч).
5 4
Рассмотрим функцию
![]() 15 − x 81 + x2
15 − x 81 + x2
f x( ) = + на интер-
Рис. 53 5 4
вале (0; 15). В каждой точке этого интервала функция f (x) имеет производную
![]() f′( )x = x − .
f′( )x = x − .
4 81 + x2
Чтобы найти критические точки функции, решим уравнение f′ (x) = 0. Оно имеет два корня: x1 = −12 и x2 = 12, из которых только x2 принадлежит интервалу (0; 15). Следовательно, на интервале (0; 15) функция имеет единственную критическую точку x2 = 12. Так как в этой точке производная функции f (x) меняет знак с «−» на «+», то в ней функция принимает свое наименьшее значение на интервале (0; 15).
Ответ. Курьер должен пристать к берегу в 12 км от пункта B.
5.100. В некотором царстве, в некотором государстве подорожала жесть, идущая на изготовление консервных банок. Экономный хозяин фабрики рыбных консервов хочет выпускать свою продукцию в банках цилиндрической формы объемом V с наименьшими возможными затратами жести. Вычислите диаметр основания и высоту такой банки.
Решение. Пусть радиус основания цилиндра x, тогда площадь основания цилиндра равна πx2, длина окружности основания цилиндра равна 2πx, а высота цилиндра
V
равна (длины отрезков, площадь и объем вычисляются
πx2
в соответствующих единицах измерения). Площадь полной
![]() 2 +
Vπ⋅
22πx = 2πx2
+ 2xV . поверхности
цилиндра равна 2πx
2 +
Vπ⋅
22πx = 2πx2
+ 2xV . поверхности
цилиндра равна 2πx
x
Рассмотрим функцию f x( ) = 2πx2 + 2V на интервале x
(0; +∞). В каждой точке этого интервала функция f (x) имеет производную f′( )x = 4πx − 2xV2 .
![]() Чтобы
найти критические точки функции, решим уравнение f′ (x) = 0. Оно имеет
единственный корень x1 =
3 2Vπ
.
Чтобы
найти критические точки функции, решим уравнение f′ (x) = 0. Оно имеет
единственный корень x1 =
3 2Vπ
.
Следовательно, на интервале (0; +∞) функция имеет единственную критическую точку x1. Так как в этой точке производная функции f (x) меняет знак с «−» на «+», то в ней функция принимает свое наименьшее значение на интервале (0; +∞).
![]() Итак,
диаметр банки должен быть равен 2x1 = 3 4πV ,
Итак,
диаметр банки должен быть равен 2x1 = 3 4πV ,
![]() а высота равна V2 =
3 4πV .
а высота равна V2 =
3 4πV .
πx1
![]() Ответ. Диаметр и
высота банки равны 3 4V .
Ответ. Диаметр и
высота банки равны 3 4V .
π
![]() 5.101. Статуя высотой а м возвышается на
постаменте высотой b м (рис. 54). На каком расстоянии от основания
постамента должен встать наблюдатель, рост которого до уровня глаз с м, с
< b,
чтобы видеть статую под наибольшим углом?
5.101. Статуя высотой а м возвышается на
постаменте высотой b м (рис. 54). На каком расстоянии от основания
постамента должен встать наблюдатель, рост которого до уровня глаз с м, с
< b,
чтобы видеть статую под наибольшим углом?
Рис. 54
![]() Шириной постамента пренебречь.
Шириной постамента пренебречь.
Решите задачу в общем виде, получите ответ в случае, если: а) а = 3, b = 2,5, с = 1,5;
б) а = 6, b = 3,7, с = 1,7.
Решение. На рисунке 55 статуя изображена отрезком AB, постамент — отрезком BD. Пусть наблюдатель находится на расРис. 55 стоянии х м от постамента: FC = х м.
Требуется найти такое значение х, при котором угол AFB наибольший. Обозначим ∠AFС = α, ∠ВFС = β, тогда ∠AFB = α − β. Из возрастания тангенса угла на интервале (0°; 90°) следует, что угол α − β достигает наибольшего значения при том же значении x, что и tg (α − β).
![]() Так как, tg
α = AC = a + b − c,
Так как, tg
α = AC = a + b − c,
![]()
![]()
![]() FC x a b c+ − b c− b − c −
FC x a b c+ − b c− b − c −
а tg β = = то
x x
= 2 + (a + b − c) (b − c) . x
Рассмотрим функцию f x( ) = ![]() 2 + (a + bax−
c) (b −
c) на инx
2 + (a + bax−
c) (b −
c) на инx
тервале (0; +∞). В каждой точке этого интервала f′( )x = a ((a + b − c b)( − c) − x2).
(x2 + (a + b − c) (b − c))2
![]()
![]() Производная f′ (x)
равна нулю в двух точках: x1 =
(a + b
− c)
(b − c)
и x2 =
− (a +
b − c)
(b − c),
из них только точка х1 принадлежит интервалу (0; +∞).
Следовательно, функция f (x) имеет единственную критическую точку
на интервале (0; +∞).
Так как f′ (x)
> 0 при 0 < x < х1,
а f′ (x)
< 0 при x > х1,
то точка х1 является точкой максимума (локального). Эта точка
единственная на интервале (0; +∞),
в ней функция достигает своего наибольшего значения.
Производная f′ (x)
равна нулю в двух точках: x1 =
(a + b
− c)
(b − c)
и x2 =
− (a +
b − c)
(b − c),
из них только точка х1 принадлежит интервалу (0; +∞).
Следовательно, функция f (x) имеет единственную критическую точку
на интервале (0; +∞).
Так как f′ (x)
> 0 при 0 < x < х1,
а f′ (x)
< 0 при x > х1,
то точка х1 является точкой максимума (локального). Эта точка
единственная на интервале (0; +∞),
в ней функция достигает своего наибольшего значения.
![]() Итак, наблюдатель будет видеть статую под наибольшим
углом, если встанет на расстоянии х1 м от основания
постамента.
Итак, наблюдатель будет видеть статую под наибольшим
углом, если встанет на расстоянии х1 м от основания
постамента.
Рассмотрим другой способ решения задачи 5.101, который предложил И. Ф. Шарыгин.
Построим окружность, проходящую через точки А, В и касающуюся прямой FC. На рисунке 56 наблюдатель находит-
ся от основания постамента на Рис. 56
расстоянии, большем расстояния KC. В этом случае угол AFB, образованный двумя секущими, измеряется полуразностью дуг AB и MN.
Если наблюдатель подойдет к основанию постамента на расстояние, меньшее расстояния KC, то угол обзора статуи опять будет измеряться полуразностью дуг. Угол обзора статуи будет наибольшим, если глаз наблюдателя будет находиться в точке K касания окружности и прямой FC, так как в этом случае угол обзора статуи измеряется только половиной дуги АВ. Вычислим искомое расстояние по теореме Пифагора из треугольника OBE:
OE2 = OB2 − BE2 = OK2 − ⎛⎜⎝ AB2 ⎠⎟⎞ 2 = ⎛⎜⎝b − c + a2 ⎠⎟⎞ 2 − ⎜⎝⎛a2 ⎞⎠⎟ 2 =
= (a + b − c)(b − c).
![]() Тогда
OE = (a
+ b − c) (b
− c),
т. е. наблюдатель должен встать на расстоянии (a + b −
c) (b −
c) м от основания постамента.
Тогда
OE = (a
+ b − c) (b
− c),
т. е. наблюдатель должен встать на расстоянии (a + b −
c) (b −
c) м от основания постамента.
а) Если а = 3, b = 2,5, с = 1,5, то x1 = (3 + 2 5, − 1 5, ) ( ,2 5 − 1 5, ) = 2 (м).
б) Если а = 6, b = 3,7, с = 1,7, то x1 = (6 + 3 7, − 1 7, ) ( ,3 7 − 1 7, ) = 4 (м).
Ответ. а) 2 м; б) 4 м.
Замечание. Задачу 5.101 можно решать не в общем виде, а при указанных значениях букв.
Промежуточный контроль. C—19, C—20, C—21.
В данном пункте дано определение асимптоты, которое фактически уже использовалось ранее при изучении гра-
фика функции y = k, но без соответствующих терминов. x
Здесь приведены формулы для вычисления коэффициентов k и b наклонной асимптоты графика функции y = f (x).
При решении примера 1 из учебника дана запись: − lim ex = −∞. Конечно, это утверждение надо доказыx → +∞ x вать, но здесь оно принято без доказательства.
В качестве примера функции, график которой имеет горизонтальную и вертикальную асимптоты, рассмотрена дробно-линейная функция.
Решения и комментарии
5.104. а) Найдите асимптоты графика функции
2x2
+
1 y = ![]() .
.
x
⎛ 2x2 + 1⎞ ⎛ 2x2 + 1⎞
Решение. Так как xlim→ 0 ⎜⎝ ![]() x ⎟⎠ = +∞, xlim→ 0 ⎜⎝
x ⎟⎠ = +∞, xlim→ 0 ⎜⎝ ![]() x ⎟⎠ = −∞,
x ⎟⎠ = −∞,
x > 0 x < 0
то прямая x = 0 — вертикальная асимптота. Вычислим
2x2 +1
⎛ 2x2 + 1 ⎞
xlim→
+∞ =
2 и xlim→
+∞ ⎜⎝ ![]() x − 2x⎟⎠ = 0, аналогично
x − 2x⎟⎠ = 0, аналогично
x
![]() ⎛ 2x2 +
1 ⎞ xlim→
−∞ x = 2 и xlim→
−∞ ⎜⎝
⎛ 2x2 +
1 ⎞ xlim→
−∞ x = 2 и xlim→
−∞ ⎜⎝ ![]() x −
2x⎟⎠ = 0.
x −
2x⎟⎠ = 0.
Таким образом, k = 2, b = 0 и прямая у = 2x — наклонная асимптота, других асимптот нет.
5.107. а) Найдите асимптоты x − 3
![]() графика функции y =
графика функции y = ![]() и поx + 1
и поx + 1
стройте этот график.
x − 3
Решение. Так как ![]() = x +
1
= x +
1
= 1 − 4 , то график дробно-лиx + 1
x − 3
нейной функции y = ![]() можx + 1
можx + 1
но получить переносом графика
Рис. 57 функции y = − 4 на 1 единицу x
влево и на 1 единицу вверх; по-
этому x = −1 — вертикальная асимптота, у = 1 — горизонтальная асимптота, других асимптот нет. График функции x − 3
y
= ![]() изображен на рисунке 57.
изображен на рисунке 57.
x + 1
Замечание. Уравнения асимптот в задании 5.107 можно получить и с помощью пределов.
−3x − 1
5.112. Дана функция f x(
) = ![]() . Постройте график x + 1
. Постройте график x + 1
функции: а) у = f (x); б) у = | f (x) |; в) у = f (| x |); г) у = | f (| x |) |.

Рис. 58 Рис. 59
−3x − 1 2
![]() Решение. а) Так как = −3 +
, то график x +
1
Решение. а) Так как = −3 +
, то график x +
1
дробно-линейной функции f x( ) = можно получить x + 1
из графика функции y = 2 переносом на 1 единицу влево x
и на 3 единицы вниз; x = −1 — вертикальная асимптота, у = −3 — горизонтальная асимптота, других асимптот нет. График функции у = f (x) изображен на рисунке 58.
![]() б) Для построения графика функции у = | f (x)
| нужно оставить без изменения точки графика функции у = f (x),
расположенные выше оси Ox и на оси Ox, а все точки графика
функции, расположенные ниже оси Ox, нужно симметрично отразить
относительно оси Ox. График функции у = | f (x) | изображен на
рисунке 59.
б) Для построения графика функции у = | f (x)
| нужно оставить без изменения точки графика функции у = f (x),
расположенные выше оси Ox и на оси Ox, а все точки графика
функции, расположенные ниже оси Ox, нужно симметрично отразить
относительно оси Ox. График функции у = | f (x) | изображен на
рисунке 59.
![]() в) Для построения графика функции у
= f (| x |) нужно оставить
без изменения точки графика функции у =
f (x), расположенные правее оси Oy и на оси Oy,
и отразить симметрично эту часть графика относительно оси Oy.
График функции у =
f (| x
|) изоб-
в) Для построения графика функции у
= f (| x |) нужно оставить
без изменения точки графика функции у =
f (x), расположенные правее оси Oy и на оси Oy,
и отразить симметрично эту часть графика относительно оси Oy.
График функции у =
f (| x
|) изоб-
ражен на рисунке 60. Рис. 61
г) Для построения графика функции у = | f (| x |) | нужно оставить без изменения точки графика функции у = f (| x |), расположенные выше оси Ox (здесь таких нет), а все точки графика функции у = f (| x |), расположенные ниже оси Ox, симметрично отразить относительно оси Ox. График функции у = | f (| x |) | изображен на рисунке 61.
5.11. Построение графиков функций с применением
В данном пункте приведены примеры построения графиков функций с применением производных.
Решения и комментарии
5.113. а) Найдите промежутки возрастания, убывания,
точки экстремума функции y =
![]()
![]() x2 (x
− 4)2
и постройте ее график.
x2 (x
− 4)2
и постройте ее график.
![]() Решение. Данную
функцию можно задать формулой y =
4 −2x3
+ 4x2,
она определена для всех x ∈
R, и в каж-
Решение. Данную
функцию можно задать формулой y =
4 −2x3
+ 4x2,
она определена для всех x ∈
R, и в каж-
дой точке этого множества ее производная равна:
y′ = x3 − 6x2 + 8x = x (x − 2) (x − 4).
Функция имеет три критические точки, так как y′ = 0 при Рис. 62 x1 = 0, x2 = 2 и x3 = 4.
![]() Определив знак y′
на интервалах (−∞;
0), (0; 2), (2; 4) и (4; +∞)
(рис. 62), получим, что x1 =
0 и x3 =
4 — точки локального минимума, а x2 = 2 — точка локального
максимума.
Определив знак y′
на интервалах (−∞;
0), (0; 2), (2; 4) и (4; +∞)
(рис. 62), получим, что x1 =
0 и x3 =
4 — точки локального минимума, а x2 = 2 — точка локального
максимума.
Так как y′ > 0 на интервалах (0; 2) и (4; +∞), то на этих интервалах функция возрастает. Так как y′ < 0 на интервалах (−∞; 0) и (2; 4), то на этих интервалах функция убывает.
Определим координаты некоРис. 63 торых точек графика функции:
|
x |
−1 |
0 |
1 |
2 |
3 |
4 |
5 |
|
y |
|
0 |
|
4 |
|
0 |
|
График функции y =
![]()
![]() x2 (x−4)2 изображен
на рисунке 63.
x2 (x−4)2 изображен
на рисунке 63.
5.117. в) Исследуйте функцию y = −x + 4 − 2 и по3 − x
стройте ее график.
Решение. Данная функция у = f (x) определена для всех x ∈ (−∞; 3) ∪ (3; +∞), и в каждой точке этого множества ее производная равна:
f′( )x = − (![]() x − 1) (x 2− 5) .
x − 1) (x 2− 5) .
(x − 3)
Функция имеет две критические точки, так как f′ (x) = 0 при x1 = 1 и x2 = 5.
Определив знак f′ (x) на интервалах (−∞; 1), (1; 3), (3; 5) и (5; +∞) (рис. 64), получим, что x1 = 1 — точка локального минимума, а x2 = 5 — точка локального максимума.
Так как f′ (x) > 0 на интервалах (1; 3) и (3; 5), то на этих интервалах функция возрастает. Так как f′ (x) < 0 на интервалах (−∞; 1) и (5; +∞), то на этих интервалах функция убывает. Так как
|
xlim3 ⎜⎝−x + 3 − x − 2⎟⎠ = +∞, → x < 3 то прямая x = 3 — вертикальная асимптота. |
Рис. 64 |
![]() xlim3 ⎜⎝⎛−x
+ 3 −4 x − 2⎞⎟⎠
= −∞,
xlim3 ⎜⎝⎛−x
+ 3 −4 x − 2⎞⎟⎠
= −∞,
→ x > 3
⎛ 4 ⎞
|
и прямая у = −x − 2 — наклон- |
|
|
ная асимптота. |
Рис. 65 |
![]() Вычислим
Вычислим
f x( )
lim ![]() = x →
+∞ x ⎛⎜ −
+x 4 −2⎞⎟
= x →
+∞ x ⎛⎜ −
+x 4 −2⎞⎟
3 − x
![]() = lim ⎜ ⎟ = −1
и x →
+∞ ⎝ x
⎠
= lim ⎜ ⎟ = −1
и x →
+∞ ⎝ x
⎠
lim (f x( ) − −( 1) x) =
x → +∞ xlim→ +∞ ⎜⎝⎛−x + 3 −4 x − 2 + x⎞⎟⎠ = −2.
f x( )
Аналогично lim ![]() = −1 и x →
−∞ x
= −1 и x →
−∞ x
lim (f x( ) − −( 1) x) = −2. x → −∞
Таким образом, k = −1, b = −2
Определим координаты некоторых точек графика функции:
|
x |
−1 |
0 |
1 |
2 |
4 |
5 |
6 |
7 |
|
y |
0 |
− |
−1 |
0 |
−10 |
−9 |
− 9 |
−10 |
График функции y = −x + 4 − 2 изображен на рисун-
3−x
ке 65.
ln x
5.120. Исследуйте функцию y
= ![]() и постройте ее граx
и постройте ее граx
фик. Сравните числа:
а) 3π и π3; в) eπ и πe.
Решение. Данная функция у = f (x) определена для всех x ∈ (0; +∞), и в каждой точке этого множества ее производная равна:
f′(
)x = 1![]() − ln2 x.
− ln2 x.
x
Функция f (x) имеет единственную критическую точку, так как f′ (x) = 0 лишь при x1 = e.
![]() Определив знак f′
(x) на интервалах (0; е) и (е; +∞), получим, что на интервале (0;
е) функция f (x) возрастает, на интервале (е;
+∞) убывает
(рис. 66), что x1 =
е — единственная точка локального максиму-
Определив знак f′
(x) на интервалах (0; е) и (е; +∞), получим, что на интервале (0;
е) функция f (x) возрастает, на интервале (е;
+∞) убывает
(рис. 66), что x1 =
е — единственная точка локального максиму-
Рис. 66 ма. В этой точке функция достигает своего наибольшего значения.
|
x |
1 e |
1 |
e |
e2 |
|
y |
−e |
0 |
1 e |
2 e2 |
![]() Определим координаты некоторых точек графика функции:
Определим координаты некоторых точек графика функции:
ln x
График функции y = ![]() изображен на рисунке 67. x
изображен на рисунке 67. x
а) Чтобы сравнить два положительных числа 3π и π3, сравним их натуральные логарифмы. Выпишем ряд равно-
сильных сравнений: ln 3![]() .
.
ln x
Так как на интервале (е; +∞) функция f x( ) = ![]() убыx
убыx
![]() вает,
то из справедливости неравенств e <
3 < π следует
справедливость неравенства
вает,
то из справедливости неравенств e <
3 < π следует
справедливость неравенства ![]() >
>
![]() . Но тогда справедливо неравенство 3π > π3.
. Но тогда справедливо неравенство 3π > π3.
в) Сравнение чисел eπ и πe приведено в дидактических
материалах (п. 23).
Промежуточный контроль. C—22, C—23.
В данном пункте рассматриваются формула и ряд Тейлора, приведены примеры применения формулы Тейлора для приближенных вычислений значений некоторых функций.
Решения и комментарии
5.123. г) Напишите формулу Тейлора для функции у = ex при n = 8. Решение. Имеем
f (x) = ex, f′ (x) = ex, f″ (x) = ex, f′′′ (x) = ex, f (4) (x) = ex,
f (5) (x) = ex, f (6) (x) = ex, f (7) (x) = ex; f (0) = 1, f′ (0) = 1, f″ (0) = 1, f′′′ (0) = 1, f (4) (0) = 1,
f (5) (0) = 1, f (6) (0) = 1, f (7) (0) = 1.
Поэтому формула Тейлора при n = 8 имеет вид
ex = 1 + 1x! + x22! + x33! + x44! + x55! + x66! + x77! + R8 ( )x ,
ec 8 (0 < с < x). где R8 ( )x = 8! x
Для х ∈ [0; 1] имеем | R8 (x) | < 10−4.
x x x2 x3 x4 x5 x6 x7 Таким образом, e ≈ 1 + + + + + + +
1! 2! 3! 4! 5! 6! 7 !
с точностью до 10−4.
5.124. г) Вычислите e с точностью до 10−4 с помощью формулы Тейлора.
Решение. Используя результат решения задания 5.123, имеем
e![]() e
e
с точностью до 10−4.
Промежуточный контроль. К—3.
|
§ 6. |
Первообразная и интеграл
В этом пункте приведено определение первообразной для функции, непрерывной на данном интервале, установлен важный факт: если функция F (x) есть какая-либо первообразная для функции f (x) на интервале (a; b), то функция F (x) + C, где C — некоторая постоянная, также есть первообразная для функции f (x) на этом интервале.
Далее определен неопределенный интеграл от непрерывной на интервале (a; b) функции f (x) — это некоторая ее первообразная. Обратим внимание на это определение: неопределенный интеграл понимается как некоторая (любая) первообразная данной функции, т. е. неопределенный интеграл от функции f (x) есть одна функция.
В ряде учебников принято другое определение: неопределенным интегралом от данной функции f (x) называют множество всех первообразных для функции f (x), т. е. неопределенный интеграл от функции f (x) есть множество функций. Полагаем, что наше определение неопределенного интеграла проще для понимания. Например, решая задачи, связанные с неопределенным интегралом, мы каждый раз имеем дело с конкретной функцией, для которой можно определить C, а не с множеством таких функций.
Далее в учебнике доказано основное свойство неопределенного интеграла:
∫ (A f1 1 ( )x + A f2 2 ( ))x dx = A1 ∫ f1 ( )x dx + A2 ∫ f2 ( )x dx + C, из которого как частные случаи получены следующие свойства неопределенного интеграла:
∫(f1 ( )x + f2 ( )x )dx = ∫ f1 ( )x dx + ∫ f2 ( )x dx + C, ∫(f1 ( )x − f2 ( )x )dx = ∫ f1 ( )x dx − ∫ f2 ( )x dx + C,
∫ Af x dx( ) = A∫ f x dx( ) + C.
Решения и комментарии
6.5. в) Докажите, что функция F (x) есть первообразная для функции f (x), если f x( ) = sin ⎛⎜⎝7x − π4⎞⎟⎠, F x( ) = − 71 cos ⎝⎜⎛7x − π4⎞⎟⎠ + C.
Доказательство. Для каждого x ∈ R имеем
F′( )x = ⎛⎜⎝− 71 cos ⎛⎜⎝7x − π4⎟⎠⎞ + C⎟⎞⎠′= 71 sin ⎝⎛⎜7x − π4⎞⎟⎠ ⋅ ⎛⎜⎝7x − π4⎟⎞⎠′+ 0 =
= 71 sin ⎛⎜⎝7x − π4⎞⎟⎠ ⋅ 7 = sin ⎜⎛⎝7x − π4⎞⎟⎠.
Следовательно, функция F (x) есть первообразная для функции f (x) на интервале (−∞; +∞).
6.7. Для функции f (x) = sin x найдите ту первообразную, график которой проходит через точку A ⎜⎝⎛2π ; 2⎞⎟⎠.
Решение. Функция f (x) на интервале (−∞; +∞) имеет
первообразную F (x) =
−cos x +
С, где C — некоторая постоянная. Так как график
первообразной проходит через точку A, то должно выполняться равенство ![]() C,
C,
откуда C ![]() . Поэтому F (x)
= −cos x
+ 2.
. Поэтому F (x)
= −cos x
+ 2.
Найдите неопределенный интеграл (6.15—6.17):
6.15. ![]() .
.
Решение. Применяя основное свойство неопределенного интеграла, имеем
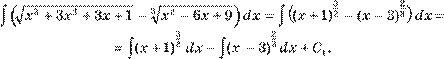
Так как функция ![]() имеет первообразную
имеет первообразную
![]() 3
3
F u( ) =+ C2 , то функция f x( +1) = (x +1)2 имеет перво-
образную F
x( ![]() ) C .
) C .
Так как функция g u( ) = u3 имеет первообразную
2
G ![]()
![]() u(
) =+ C3
, то функция g x( −
3) = (x
− 3)3
имеет перво-
u(
) =+ C3
, то функция g x( −
3) = (x
− 3)3
имеет перво-
3
образную G x( ) C . Следовательно,

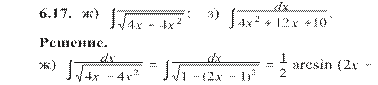 dx
dx
Так как функция f
u( ) = ![]() имеет первообразную
имеет первообразную
F (u) = arcsin u + С, то функция f (2x − 1) = 1
![]() 1 − (2x −
1)2
1 − (2x −
1)2
имеет
первообразную F ![]() x x C.
x x C.
з) ![]() x C.
x C.
Так как функция ![]() имеет первообразную
имеет первообразную
F (u) = arctg u + С, то функция f (2x + 3) = ![]()
![]() имеет первообразную F (2x
+ 3) =
имеет первообразную F (2x
+ 3) = ![]()
![]() arctg (2x + 3) + C.
arctg (2x + 3) + C.
6.18. а) Докажите справедливость равенства
dx
∫ = ln | x | + С (x ≠ 0). x
Решение. Для x >
0 имеем (ln | x | ![]() ;
;
для x < 0 имеем (ln | x | + С)′ = (ln (−x))′ + 0 = 1 ⋅ −( x)′ = 1 ,
−x x
т. е. на каждом из интервалов (−∞; 0) и (0; +∞) справедли-
во равенство (ln | x | + С)′ = 1 . Следовательно, на каждом из x
этих интервалов справедливо равенство![]() ln
| x | + С
(x ≠ 0).
ln
| x | + С
(x ≠ 0).
Замечание. Поскольку неопределенный
интеграл ∫
f x dx( ) определен для функции f (x), непрерывной
на некотором промежутке (a; b), то равенство ![]() ln | x |
+ С (x ≠ 0) следует
понимать как сокращенную форму записи равенств
ln | x |
+ С (x ≠ 0) следует
понимать как сокращенную форму записи равенств
dx
∫ = ln | x | + С, x ∈ (0; +∞) и x dx
∫ = ln | x | + С, x ∈ (−∞; 0). x
Промежуточный контроль. С—24.
В данном пункте на большом числе примеров показаны приемы вычисления неопределенных интегралов с помощью замены переменной и интегрирования по частям. Решения и комментарии
Найдите неопределенный интеграл, используя замену переменной (6.20—6.23):
![]()
![]() 6.20. в) ∫
6.20. в) ∫
![]() Решение.=
∫
⎜⎛− 1 ⎞⎟ dt = − 1 ∫
t−
21dt =
Решение.=
∫
⎜⎛− 1 ⎞⎟ dt = − 1 ∫
t−
21dt =
⎝ 4 t ⎠ 4
= −+ C = − + C (подстановка t = 9 − 4x2, откуда
2 2
dt =
−8xdx, 2xdx ![]() dt
dt
![]() 6.21. в) ∫ x dx.
6.21. в) ∫ x dx.
1 3
Решение. 2 ⋅
2
![]() C (подстановка t = 4 + x2, откуда dt
= 2xdx,
C (подстановка t = 4 + x2, откуда dt
= 2xdx,
xdx ![]() dt
dt
6.22. в) ![]() .
.
Решение. ![]() t C x C
t C x C
(подстановка t = 1 + 9x2, откуда t
> 0, dt
= 18xdx,
xdx ![]() dt
dt
![]() 6.23. в) ∫
1 − 4x2
dx.
6.23. в) ∫
1 − 4x2
dx.
![]() Решение.
Так как x ∈ ⎡⎢⎣−
21 ; 21⎤⎥⎦, то 2x = sin t, где t
∈ ⎡⎢⎣− π2 ; 2π⎤⎥⎦. Следовательно,
t = arcsin
2x, 1 − 4x2
= cos t,
Решение.
Так как x ∈ ⎡⎢⎣−
21 ; 21⎤⎥⎦, то 2x = sin t, где t
∈ ⎡⎢⎣− π2 ; 2π⎤⎥⎦. Следовательно,
t = arcsin
2x, 1 − 4x2
= cos t,
2dx = cos t dt, dx
![]() tdt. Поэтому ∫
1 − 4x2
dx =
tdt. Поэтому ∫
1 − 4x2
dx =
![]()
![]() .
.
![]() Найдите неопределенный интеграл, используя интегрирование
по частям (6.24—6.25): xdx
Найдите неопределенный интеграл, используя интегрирование
по частям (6.24—6.25): xdx
6.24. в).
sin 2 x
Решение. ![]() dx = −x ctg x
+
dx = −x ctg x
+
+ ∫ctg x dx + C1 (здесь u = x, du = dx, dv = dx2 , v = −ctg x). sin x
Так как ∫ ctg x
dx ![]() ln | t | + C2 =
ln | t | + C2 =
= ln | sin x | + C2 (здесь
t = sin x,
dt = cos x
dx), то ![]() C.
C.
6.25. а) ∫ x2ex dx; в) ∫ x2 cos x dx.
Решение. а) ∫ x2exdx = x2ex − ∫ ex2xdx + C1 (здесь u = x2, du = 2xdx, dv = exdx, v = ex).
Так как ∫ exxdx = xex − ∫ exdx + C2 = xex − ex + C3
(здесь u1 = x, du1 = dx, dv1 = exdx, v1 = ex), то
∫ x2exdx = x2ex − 2xex + 2ex + C.
в) ∫ x2 cos xdx = x2 sin x − ∫ sin x 2xdx + C1
(здесь u = x2, du = 2xdx, dv = cos x dx, v = sin x).
Так как ∫ sin x 2xdx = 2 ∫ x sin xdx =
= 2 (−x cos x − ∫ (−cos x) dx) + C2 = −2x cos x + 2 ∫cos xdx + C2 =
= −2x cos x + 2 sin x + C3
(здесь u1 = x, du1 = dx, dv1 = sin x dx, v1 = −cos x dx), то ∫ x2 cos xdx = x2 sin x + 2x cos x − 2 sin x + C.
Промежуточный контроль. С—25.
В данном пункте вводятся понятия криволинейной трапеции и ее площади как предела интегральной суммы. Такой подход не предполагает развития техники вычисления интегральных сумм. Будет достаточно, если учащиеся на примере заданий 6.27—6.28 осознают, что вычисление площади криволинейной трапеции как предела интегральной суммы довольно трудоемкая задача, и выполнят задания, пользуясь имеющимися в них подсказками. В то же время этот подход позволяет обосновать необходимость знака «−» при вычислении интегральной суммы в том случае, когда значения функции на заданном отрезке отрицательны, а также показать, что первоначально вычисление определенных интегралов было сложной задачей и открытие формулы Ньютона — Лейбница существенно упростило вычисления.
Решения и комментарии
6.27. Рассмотрим функцию y = x на отрезке [0; 1]. Разделим отрезок [0; 1] на n равных частей и в качестве интегральной суммы возьмем
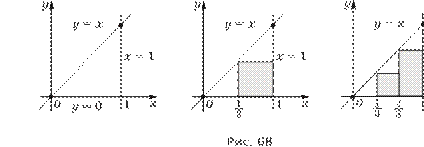
Sn = f (0) ⋅ n1 +
f ⎜⎝⎛n1 ⎟⎠⎞
⋅ n1 + f ⎜⎛⎝n2 ⎟⎠⎞
⋅ n1 + ... +
f ⎛⎝⎜n![]() n− 1⎠⎟⎞
⋅ n1 =
n− 1⎠⎟⎞
⋅ n1 =
![]() = ⎛⎜ 0 + 1 +
2 n − 1 ⎞⎟ ⋅ 1 .
= ⎛⎜ 0 + 1 +
2 n − 1 ⎞⎟ ⋅ 1 .
+ ... +
⎜ n n n ⎟ n ⎝ n слагаемь хi ⎠
а) Вычислите интегральную сумму S1, S2, S3, S4 (рис. 68).
б) Упростите формулу для вычисления Sn.
в) Имеет ли последовательность интегральных сумм S1, S2, S3, ..., Sn, ... предел при n → +∞? Если имеет, то чему он равен?
г) Чему равна площадь фигуры, ограниченной прямы-
ми y = x, y = 0, x = 1?
Решение. а) Вычислим интегральные суммы S1, S2, S3 и S4, пользуясь интегральной суммой Sn:
S![]() f ,
f ,
S![]() f f f f ,
f f f f ,
![]() S3 = f ( )0 ⋅ 31 +
f ⎛⎜⎝
31⎞⎟⎠ ⋅ 31 + f ⎛⎝⎜ 23 ⎞⎟⎠
⋅ 31 = 0 + 31 + 2 ⋅ 31 =
31, S4 = f ( )0 ⋅ 1 +
f ⎛⎜⎝
14⎞⎟⎠
⋅ 14 + f ⎛⎜⎝
24⎞⎠⎟
⋅ 14 + f ⎛⎝⎜
34⎞⎟⎠
⋅ 14 = 0 +
1 +4 2 + 3 ⋅ 14 = 38 . 4
S3 = f ( )0 ⋅ 31 +
f ⎛⎜⎝
31⎞⎟⎠ ⋅ 31 + f ⎛⎝⎜ 23 ⎞⎟⎠
⋅ 31 = 0 + 31 + 2 ⋅ 31 =
31, S4 = f ( )0 ⋅ 1 +
f ⎛⎜⎝
14⎞⎟⎠
⋅ 14 + f ⎛⎜⎝
24⎞⎠⎟
⋅ 14 + f ⎛⎝⎜
34⎞⎟⎠
⋅ 14 = 0 +
1 +4 2 + 3 ⋅ 14 = 38 . 4
Площади закрашенных фигур на рисунке 68 равны соответственно трем первым интегральным суммам.
б) Преобразуем интегральную сумму, воспользовавшись формулой суммы первых n членов арифметической прогрессии:
![]()
![]() Sn = ⎛⎜ 1 2 n − 1 ⎞⎟ ⋅ 1 = 0 +
1 +
2 +
... +
(n −
1) ⋅ 1 =
Sn = ⎛⎜ 1 2 n − 1 ⎞⎟ ⋅ 1 = 0 +
1 +
2 +
... +
(n −
1) ⋅ 1 =
0 + + + ... +
⎜ n n n ⎟ n n n
⎝ n слагаемь хi ⎠
![]() (n −
1) ⋅
n 1 n − 1
(n −
1) ⋅
n 1 n − 1
= ⋅ = .
2n n 2n
![]() в) При n → +∞ интегральная сумма Sn
=
в) При n → +∞ интегральная сумма Sn
= ![]() − 1 имеет
− 1 имеет
2n
предел, равный ![]()
![]() .
.
г) Площадь фигуры, ограниченной прямыми y = x,
y =
0, x = 1,
равна ![]()
![]() .
.
Замечания
1.
Заметим, что результат, полученный новым методом,
подтверждается известным способом вычисления площади треугольника: ![]() .
.
2. В задании 6.28 надо показать, что для функции y = x на отрезке [0; 1] каждое значение функции в интегральной сумме и сама интегральная сумма будут отличаться только знаком от аналогичных значений, полученных в задании 6.27, поэтому площадь криволинейной трапеции (в данном случае треугольника) будет равна пределу интегральной суммы, взятой со знаком «−».
В данном пункте введено понятие определенного интеграла на отрезке [a; b] как предела интегральной суммы, рассмотрен его геометрический смысл, приведены примеры вычисления определенного интеграла с опорой на его геометрический смысл (формула Ньютона — Лейбница будет введена в п. 6.6).
Решения и комментарии
![]() Пользуясь геометрическим смыслом определенного интеграла,
вычислите
Пользуясь геометрическим смыслом определенного интеграла,
вычислите ![]()
6.32.xdx; б) ∫ (−x dx) ; д) ∫ (1 − x dx) .
0 1
Решение. а) Так как функция y = x на отрезке [0; 2] принимает неотрицательные значения, то искомый интеграл равен площади треугольника OAB, взятой со зна-
2
ком «+»
(рис. 69, а). Итак, ∫ xdx ![]() .
.
0
б) Так как функция y = −x на отрезке [0; 2] принимает отрицательные значения, то искомый интеграл равен площади треугольника OAB, взятой со знаком «−» (рис. 69, б).
![]() OB OA⋅ 2 ⋅ 2
OB OA⋅ 2 ⋅ 2
![]() Итак, − = − =
− = −2.
Итак, − = − =
− = −2.
0 2
д) Так как функция y = 1 − x на отрезке [1; 3] принимает отрицательные значения, то искомый интеграл ра-
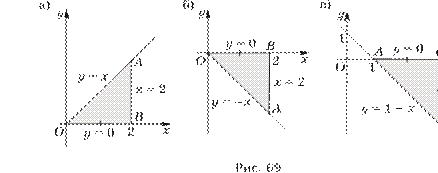
вен площади треугольника ABC (рис. 69, в), взятой со зна-
3 ком «−».
Итак,![]()
![]() .
.
![]()
6.33. а) ∫ (1 − x dx) .
2
Решение. Так как функция y = 1 − x на отрезке [2; 4] принимает отрицательные значения, то искомый интеграл равен площади трапеции ABСD, взятой со знаком «−»
(рис. 70, а).
Итак,![]()
![]() .
.
2
0 π
6.35. а) ∫ sin xdx + ∫ sin xdx.
−π 0
Решение. Функция y = sin x на отрезке [0; π] принимает
положительные значения. Пусть ![]() xdx =
S. Функция y =
sin x на отрезке [−π;
0] принимает отрицатель-
xdx =
S. Функция y =
sin x на отрезке [−π;
0] принимает отрицатель-
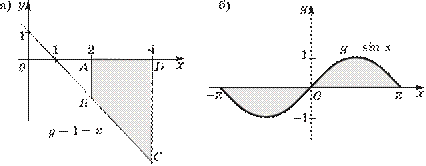
Рис. 70
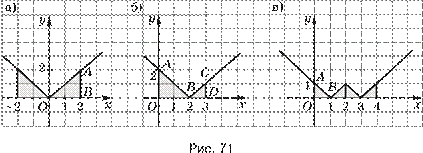
ные значения. Так как функция y = sin x нечетная, то площадь каждой из криволинейных трапеций (над осью Ox и под осью Ox) равна S (рис. 70, б). Поэтому
0 π
∫ sin xdx + ∫ sin xdx = −S + S = 0.
![]() −π
−π
6.36. а) |
x dx| ; б) ![]() | x | dx; в)
| x | dx; в) ![]() .
.
Решение. а) Так как на отрезке [−2; 2] функция y = | x | принимает неотрицательные значения, то искомый интеграл равен площади закрашенной фигуры:
![]() | x
dx|
| x
dx| ![]() (рис. 71, а).
(рис. 71, а).
б) Так как на отрезке [0; 3] функция | x − 2 | принимает неотрицательные значения, то искомый интеграл равен площади закрашенной фигуры:
AO OB⋅ BD CD⋅
![]()
![]() | x − 2| dx = + =
2 5, (рис. 71, б).
| x − 2| dx = + =
2 5, (рис. 71, б).
2 2
в) Так как на отрезке [0; 4] функция | | x − 2 | − 1 | принимает неотрицательные значения, то искомый интеграл равен площади закрашенной фигуры:
![]()
![]() (рис. 71, в).
(рис. 71, в).
0
В данном пункте рассмотрен способ приближенного вычисления определенных интегралов — так называемый способ трапеций, основанный на вычислении среднего арифметического двух интегральных сумм — верхней и нижней. На двух примерах пункта показано, что описанный в учебнике метод (при разбиении отрезка интегрирования на 10 равных частей) дает приближенные зна-
![]() 1
1
чения ∫ x dx2 иxdx с точностью, не превышающей
0
0,5% и 0,2% соответственно.
Решения и комментарии
6.43. б) Вычислите приближенно определенный интег-
1
рал ∫ x dx3 при заданном Δx = 0,2.
−1
Решение. б) Разобьем отрезок [−1; 1] на 10 равных частей точками −0,8 < −0,6 < −0,4 < −0,2 < 0 < 0,2 < 0,4 < < 0,6 < 0,8. Так как на отрезке [−1; 1] функция f (x) = x3 возрастает, то нижнюю интегральную сумму S10 вычислим, используя значения функции f (x) на левых концах
![]()
частичных отрезков, а верхнюю интегральную сумму S10 вычислим, используя значения функции f (x) на правых концах частичных отрезков:
S10 = ((−1)3 + (−0,8)3 + (−0,6)3 + (−0,4)3 + (−0,2)3 + 03 +
+ 0,23 + 0,43 + 0,63 + 0,83) ⋅ 0,2 = −0,2;
![]()
S10 = ((−0,8)3 + (−0,6)3 + (−0,4)3 + (−0,2)3 + 03 + + 0,23 + 0,43 + 0,63 + 0,83 + 13) ⋅ 0,2 = 0,2.
Вычислим приближенно интеграл по формуле
![]() S10 + S10 − 0 2, + 0 2,
S10 + S10 − 0 2, + 0 2,
I ≈ = = 0.
2 2
Промежуточный контроль. С—26.
В данном пункте приведена формула Ньютона — Лейбница, доказательство которой необязательно при обучении на базовом уровне. Оно приведено в конце пункта. На нескольких примерах показано, как с помощью этой формулы можно вычислять площади криволинейных трапеций, а также площади фигур, заключенных между графиками двух функций.
После знакомства с вычислением определенного интеграла как предела интегральной суммы с опорой на геометрический смысл определенного интеграла применение формулы Ньютона — Лейбница воспринимается учащимися как большое упрощение вычислений.
Решения и комментарии
Используя формулу Ньютона — Лейбница, вычислите определенный интеграл (6.46—6.51):
7
6.46. в) ∫ xdx.
3
![]() 77
77
22 2
![]() Решение. ∫ xdx = x3= 7 − 3 =
20.
Решение. ∫ xdx = x3= 7 − 3 =
20.
![]() 22 2
22 2
![]() 6.49. в)xdx.
6.49. в)xdx.
Решение. sinx dx = (−cos x)20π
0
![]() 3
3
dx
6.51. в).
x
1
![]() 33 dx
33 dx
= −cos 2π − (−cos 0) = 0.
Решение. ∫ = ln x= ln 3 − ln 1 = ln 3.
1 x1
Используя формулу Ньютона — Лейбница, вычислите площадь фигуры, ограниченной линиями (6.54—6.58):
6.54. в) y = x2 + 1, y = 3 − x.
![]() Решение. Сначала найдем абсциссы точек пересечения
графиков y = x2
+ 1 и y = 3 − x. Для этого решим уравнение
x2 + 1
= 3 − x. Это уравнение
имеет два корня: x1 =
−2 и x2 =
1.
Решение. Сначала найдем абсциссы точек пересечения
графиков y = x2
+ 1 и y = 3 − x. Для этого решим уравнение
x2 + 1
= 3 − x. Это уравнение
имеет два корня: x1 =
−2 и x2 =
1.
Взаимное расположение графиков функций учащиеся могут обосновать, построив графики этих функций. В каждой точке интервала (−2; 1) график функции y = 3 − x расположен выше графика функции y = x2 + 1, поэтому искомая площадь S равна S1 − S2, где S1 — площадь трапеции ABCD; S2 — площадь кривоРис. 72 линейной трапеции ABKCD
![]() (рис. 72).
(рис. 72).
![]()
![]()
![]()
![]() S1
=
−∫12(3 − x dx) = ⎛⎜⎝3x − x22 ⎠⎟⎞1−2 ⎛3 ⎞
⎛ 6 ⎞
(кв. ед.), S x 1 dx x⎟⎠1−2 = ⎛⎜⎝ 31 +1⎠⎟⎞ −
⎝⎜⎛−38 − 2⎞⎟⎠ = 6
(кв. ед.).
S1
=
−∫12(3 − x dx) = ⎛⎜⎝3x − x22 ⎠⎟⎞1−2 ⎛3 ⎞
⎛ 6 ⎞
(кв. ед.), S x 1 dx x⎟⎠1−2 = ⎛⎜⎝ 31 +1⎠⎟⎞ −
⎝⎜⎛−38 − 2⎞⎟⎠ = 6
(кв. ед.).
⎞
Тогда S = S1 − S2 = 10,5 − 6 = 4,5 (кв. ед.).
Ответ. 4,5.
Замечание. Взаимное расположение графиков функций учащиеся могут обосновать иначе: в каждой точке интервала (−2; 1) график функции y = 3 − x расположен выше графика функции y = x2 + 1, так как для любого x ∈ (−2; 1) справедливо неравенство 3 − x − (x2 + 1) > 0, т. е. неравенство −(x + 2) (x − 1) > 0.
6.58. а) y − x2 = 0 и y2 − x = 0.
![]() Решение. Сначала найдем абсциссы точек пересечения
графиков функций y =
x2 и x =
y2. Для этого решим систему уравнений y = x2 и
x = y2.
Эта система имеет только два решения: (0; 0) и (1; 1). Следовательно, x1
= 0 и x2
= 1 —
абсциссы точек пересечения графиков.
Решение. Сначала найдем абсциссы точек пересечения
графиков функций y =
x2 и x =
y2. Для этого решим систему уравнений y = x2 и
x = y2.
Эта система имеет только два решения: (0; 0) и (1; 1). Следовательно, x1
= 0 и x2
= 1 —
абсциссы точек пересечения графиков.
Так как каждая из формул, которыми заданы графики функций y = x2 и x = y2, может быть получена из другой формулы заменой x на y и y на x, то эти графики симметричны относительно прямой y = x (рис. 73). Тогда площади S1 и S2 фигур ABMO и
ONBC равны: Рис. 73
11
S1 = S2 =
∫
x dx2 = x33 ![]() = 31 − 03 =
31,
= 31 − 03 =
31,
00
а площадь S искомой фигуры равна:
![]() S
= 1 − 2S1
= 1 −
S
= 1 − 2S1
= 1 − ![]() =
= ![]() (кв. ед.).
(кв. ед.).
Ответ. ![]()
![]() .
.
6.59. а) Найдите ту первообразную для функции f (x) = = 2x + 4, график которой касается прямой y = 6x + 3. Вычислите площадь фигуры, ограниченной графиком найденной первообразной и прямыми y = 6x + 3 и y = 0.
Решение. Каждая первообразная для функции f (x) = 2x + 4 имеет вид F (x) = x2 + 4x + С, где С — некоторое число. Пусть график функции y = F (x) касается прямой y = 6x + 3 в точке с абсциссой x0. Тогда F′ (x0) = = 2x0 + 4 = 6, откуда x0 = 1, а ордината точки касания равна y0 = 6x0 + 3 = 9.
Так как график функции F (x) = x2 + 4x + С проходит через точку (1; 9), то верно равенство 9 = 1 + 4 + С, откуда С = 4.
Итак, искомая первообразная задается формулой F (x) = = x2 + 4x + 4.
Теперь вычислим площадь фигуры, ограниченной линиями y = x2 + 4x + 4, y = 6x + 3 и y = 0 (рис. 74).
![]()
![]() Площадь S1
криволинейной трапеции DAC равна
Площадь S1
криволинейной трапеции DAC равна
=
⎛⎜⎝ x33 +2x2 +
4x⎞⎟⎠
![]() 1−2 =
1−2 =
= ⎛⎜⎝ 31 +2 +4⎞⎟⎠ − ⎛⎜⎝ −38 +8 − 8⎞⎟⎠ =
= 9 (кв. ед.).
Площадь S2 треугольника ABC равна
S![]() = =
= =![]() (кв. ед.).
(кв. ед.).
Тогда искомая площадь S равна
S = S1 − S2 =
![]() = 9 − 6
= 9 − 6![]() = 2
= 2 ![]() (кв. ед.).
(кв. ед.).
Ответ. F (x) = x2 + 4x + 4; 2 ![]()
![]() .
.
Промежуточный контроль.
Рис. 74 С—27.
В данном пункте сформулированы основные свойства определенного интеграла и приведены примеры вычисления определенных интегралов с использованием этих свойств. Особое внимание нужно уделить примеру 4, при решении которого конкретно показано, что если графики функций y = f (x) и y = ϕ (x) пересекаются в точках с абсциссами a и b (a < b) и если эти функции непрерывны на отрезке [a; b] и f (x) > ϕ (x) на всем интервале (a; b), то площадь фигуры, ограниченной графиками функций y = f (x) и y = ϕ (x), вычисляется по формуле
b
S = ∫(f x( ) − ϕ ( )x )dx.
a
Решения и комментарии
Примените основные свойства интеграла при вычислении интегралов (6.64—6.65):
1 3
6.64. д) ∫ xdx + ∫ xdx.
0 1 1 3
![]() Решение. ∫ xdx +
∫
xdx =xdx
Решение. ∫ xdx +
∫
xdx =xdx
0 1
3
![]() = x2= 9 − 0 = 4 5, .
= x2= 9 − 0 = 4 5, .
202
|
6.70. а) Вычислите площадь линиями y = x2 − πx и y = sin x. Решение. Сначала построим графики функций y = x2 − πx и |
фигуры, |
ограниченной |
![]() y = sin x. Первый
график — парабола с вершиной ⎜⎝⎛ 2π
; −
π42 ⎞⎟⎠,
y = sin x. Первый
график — парабола с вершиной ⎜⎝⎛ 2π
; −
π42 ⎞⎟⎠,
проходящая через точки (0; 0) и (π; 0). Второй график — синусоида, проходящая через те же точки (0; 0) и (π; 0) (рис. 75).
На интервале (0; π) точки графика функции y = sin x расположены выше точек графика функции y = x2 − πx, поэтому
π π
S = ∫(sin x − (x2 − πx))dx = ∫(sin x − x2 + πx dx) =
0 0
![]() =
⎛⎜⎝− cos x −
x33 +
x2π2 ⎠⎞⎟ π0
=
⎛⎜⎝− cos x −
x33 +
x2π2 ⎠⎞⎟ π0 ![]() ⎞⎟⎠ −
⎞⎟⎠ −
− ⎜⎛⎝− cos 0 − 033 + π ⋅202 ⎞⎟⎠ (кв. ед.).
Ответ. ![]()
![]() + 2.
+ 2.
6.72. а) Вычислите площадь фигуры, ограниченной линией y = 4 + 0,5x2, касательной к ней y = 2x + 2 и прямыми x = 0 и x = 3.
Решение. Решив уравнение 4 + 0,5x2 = 2x + 2, найдем абсциссу x = 2 точки касания параболы и прямой. Для всех x ≠ 2 точки параболы находятся выше точек прямой, так как 4 + 0,5x2 − 2x − 2 = 0,5 (x − 2)2 ≥ 0, поэтому
S ![]() x x dx x x dx
x x dx x x dx
=
⎛⎜⎝ x![]() 3 − x + 2x⎞⎟⎠
3 − x + 2x⎞⎟⎠ ![]() 30=
⎜⎝⎛ 276 − 9 + 6⎞⎠⎟ − 0
= 1,5 (кв. ед.).
30=
⎜⎝⎛ 276 − 9 + 6⎞⎠⎟ − 0
= 1,5 (кв. ед.).
Ответ. 1,5.
6.73. Вычислите определенный интеграл, используя замену переменной:
![]() 1
1
![]() в)
∫
[1] −
x2 dx; д).
в)
∫
[1] −
x2 dx; д).
−1
Решение. в) Так как x ∈ [−1; 1], то заменим переменную в интеграле: x = sin u, u ∈ ⎛⎜⎝− 2π ; 2π ⎠⎞⎟. При этом cos u ≥ 0 и dx = cos u du. Поэтому получим
π π ![]() u
u
![]()
![]() − x dx = udu =
− x dx = udu = ![]() du =
du =
−1 −π −
2 π
![]()
![]() 2⎞⎟⎠
2⎞⎟⎠
=== π.
2 2
−π 2
![]()
![]()
4
![]() 6.74. Вычислите
определенный интеграл: π
6.74. Вычислите
определенный интеграл: π
а) ∫ | sin 2002 |x dx; б)| | | | x| − 4| − 2| − 1| dx.
0
Решение. а) Заменим переменную в интеграле: x = u ,
2002
![]() тогда при возрастании
x от 0 до π переменная
u возрастает от 0 до 2002π,
при этом dx = du . Поэтому получим
тогда при возрастании
x от 0 до π переменная
u возрастает от 0 до 2002π,
при этом dx = du . Поэтому получим
![]() π 2002 π
π 2002 π
![]()
![]() | sin 2002 |x dx |
sin u| | sin u du| =
| sin 2002 |x dx |
sin u| | sin u du| =
0 0
⎛ π 2 π⎞

Рис. 76 Рис. 77
На каждом из 2002 отрезков длины π: [0; π], [π; 2π], ...
... [2001π; 2002π] график функции y = | sin u | ограничивает одну и ту же площадь (рис. 76), поэтому искомый интеграл равен:
⎛ π ⎞ π π
20021 ⎜⎜⎝2002∫0 | sin u du| ⎟⎟⎠ =
∫0 | sin u du| = ∫0 sin udu = − cos u ![]() π0=
π0=
= (−cos π) − (−cos 0) = 1 − (−1) = 2.
б) Построим график функции y = | | | | x | − 4 | − 2 | − 1 |,
последовательно построив графики функций:
1) y = | x |; 2) y = | x | − 4; 3) y = | | x | − 4 |; 4) y = | | x | − 4 | − 2; 5) y = | | | x | − 4 | − 2 |; 6) y = | | | x | − 4 | − 2 | − 1; 7) y = | | | | x | − 4 | − 2 | − 1 |.
Последний, седьмой график изображен на рисунке 77.
Итак, искомый интеграл равен сумме площадей семи равных равнобедренных прямоугольных треугольников с гипотенузой 2, площадь каждого из которых равна
![]() . Поэтому
. Поэтому ![]() | | | | x| − 4| − 2| − 1| dx = 7.
| | | | x| − 4| − 2| − 1| dx = 7.
Промежуточный контроль. С—28.
6.8*. Применение определенных интегралов
В данном пункте учебника рассмотрены задачи, для решения которых используются определенные интегралы: нахождение площади круга, объема тела вращения, работы, совершаемой под действием переменной силы, и т. д.
Решения и комментарии
![]() 6.75. а) Множество точек координатной плоскости xOy,
удовле-
6.75. а) Множество точек координатной плоскости xOy,
удовле-
x2 y2
творяющих
уравнению 2 + ![]() 2 = 1
2 = 1
a b
(a ≠ b), называют эллипсом.
Вычислите площадь фигуры, ограниченной эллипсом
x2 + 9y2 = 9 (рис. 78). Рис. 78
![]() Решение.
Сначала запишем функцию, задающую верхнюю границу эллипса: y = 1 − ⎛⎜⎝ x3 ⎞⎟⎠ 2 . Площадь
S1 фигуры,
Решение.
Сначала запишем функцию, задающую верхнюю границу эллипса: y = 1 − ⎛⎜⎝ x3 ⎞⎟⎠ 2 . Площадь
S1 фигуры,
ограниченной графиком этой функции и осью Ox, равная половине искомой площади, вычисляется по формуле
![]() S1 = ∫3 1 − ⎛⎜⎝ x3 ⎞⎟⎠ 2 dx.
S1 = ∫3 1 − ⎛⎜⎝ x3 ⎞⎟⎠ 2 dx.
−3
Так как x ∈ [−3; 3], то заменим переменную в интеграле: x3 = sin u, u ∈ ⎢⎣⎡− 2π ; 2π⎤⎥⎦, при этом cos u ≥ 0 и dx = 3 cos u du. Поэтому получим
![]() 2
2
− −
Тогда площадь фигуры, ограниченной эллипсом, равна 2S1 = 3π.
Ответ. 3π.
6.77. Используя формулу объема тела вращения, получите формулы для вычисления объемов цилиндра и конуса.
Решение. 1) Пусть дан цилиндр, радиус основания которого R, а высота H. Зададим систему координат xOy так, чтобы центрам оснований цилиндра соответствовали точки оси Ox: x = 0 и x = H (рис. 79, а). Тогда функция y = R задает прямую, вращением которой вокруг оси Ox образуется боковая поверхность цилиндра. Вычислим объем тела
b
вращения по формуле V = π∫ f2 ( )x dx. В нашем примере
a
a = 0 и b = H, f (x) = R, поэтому
H
V =![]() π R dx
= πR
x2
π R dx
= πR
x2 ![]() H0 = πR H2 − 0 = πR H2 .
H0 = πR H2 − 0 = πR H2 .
2) Пусть дан конус, радиус основания которого R, а высота H. Зададим систему координат xOy так, чтобы вершине и центру основания конуса соответствовали точки оси Ox: x = 0 и x = H (рис. 79, б). Тогда функция y = R x
H
задает прямую, вращением которой вокруг оси Ox образуется боковая поверхность конуса. Вычислим объем тела

Рис. 79
b
вращения по формуле V = π∫ f2 ( )x dx. В нашем примере
a
a = 0 и b = H, f x( ) = R x, поэтому H
![]() V = π
V = π![]() H
H ![]() H x dx = πH Hx2 dx =
πHR22 ⎝⎜⎛ x33 ⎞⎟⎠
H x dx = πH Hx2 dx =
πHR22 ⎝⎜⎛ x33 ⎞⎟⎠
![]() 0H =
0H =
![]() R
H2 .
R
H2 .
H2 3 3
6.80. а) К движущейся по прямой точке приложена направленная вдоль этой прямой сила F = 2x − 1, где x — координата движущейся точки. Вычислите работу силы F по перемещению точки от точки x = 0 до точки x = 3. Решение. Работа W по перемещению точки вычисляет-
b
ся по формуле W = ∫ f x dx( ) . В нашем примере a = 0, b = 3,
a
f (x) = 2x − 1, поэтому
3
W =
∫
(2x −
1)dx = (x2
− x)![]() 30=
(9 − 3)
− 0 = 6.
30=
(9 − 3)
− 0 = 6.
0
Ответ. 6.
В данном пункте учебника введены понятия дифференциального уравнения, порядка дифференциального уравнения, рассмотрены дифференциальные уравнения первого и второго порядков, понятия решения дифференциального уравнения, общего, частного решения дифференциального уравнения, приведены примеры применения дифференциальных уравнений.
Решения и комментарии
6.86. Найдите частное решение дифференциального уравнения, удовлетворяющее условию:
а) y′ = 4x3, y (0) = 1; д) y″ = 66x, y (0) = 1, y′ (0) = 3.
Решение. а) Общим решением данного дифференциального уравнения является функция y = ∫ 4x3dx = x4 + C, где C — некоторая постоянная.
Из условия y (0) = 1 имеем 04 + C = 1, откуда C = 1. Искомым частным решением дифференциального уравнения является функция y = x4 + 1.
д) Обозначим у′ = z, тогда исходное дифференциальное уравнение можно переписать в виде z′ = 66x.
Его решение есть функция
z = ∫ 66xdx + C1 = 33x2 + C1,
где C1 — некоторая постоянная. Так как z = у′, то получаем уравнение у′ = 33x2 + C1.
Его решением, а значит, и решением исходного дифференциального уравнения является функция
у = ∫ (33x2 + C1) dx = 11x3 + C1x + C2, где C2 — некоторая постоянная.
Итак, общее решение исходного дифференциального уравнения — это функция у = 11x3 + C1x + C2,
где C1 и C2 — некоторые постоянные.
Из условия y′ (0) = 3 имеем 33 ⋅ 02 + C1 = 3, откуда C1 = 3.
Из условия y (0) = 1 имеем 11 ⋅ 03 + C1 ⋅ 0 + C2 = 1, откуда C2 = 1.
Следовательно, искомое частное решение дифференциального уравнения — это функция у = 11x3 + 3x + 1.
6.10*. Задачи, приводящие к дифференциальным
В данном пункте учебника рассмотрены задачи на нахождение закона движения точки по известной ее скорости, по ее ускорению, на определение зависимости от времени температуры тела по заданной его температуре и температуре окружающей среды, а также задачи на радиоактивный распад, гармонические колебания. Все эти задачи решаются с использованием дифференциальных уравнений.
Решения и комментарии
6.95. Первоначально в баке было 100 л раствора, содержащего 10 кг соли. В бак непрерывно вливается 5 л чистой воды в минуту и столько же воды выливается из бака. Весь процесс происходит при тщательном перемешивании воды. Сколько соли останется в баке через 1 ч?
![]() Решение.
Будем считать, что в каждую минуту из бака вытекает
Решение.
Будем считать, что в каждую минуту из бака вытекает ![]() =
= ![]() имеющейся в
нем соли, т. е. скорость изменения массы соли m пропорциональна этой
массе:
имеющейся в
нем соли, т. е. скорость изменения массы соли m пропорциональна этой
массе:
dm 1
= − m dt 20
(знак «−» означает, что масса соли уменьшается, т. е. функция m (t) убывает).
Этому дифференциальному уравнению удовлетворяет функция − 1 t
m t( ) = Ae 20 ,
где А — некоторая постоянная. Из условия задачи следует, что Т (0) = 10, поэтому A = 10. Определим массу соли в момент времени t = 60: m = 10e−3 ≈ 0,5.
Ответ. Через 1 ч в баке останется 0,5 кг соли.
Замечание. Отметим, что в учебнике и здесь решение уравнения y′ = αy, где α — данное число, записывается в виде y = Aeαt, где А — некоторая постоянная, а решение уравнения y″ + ky2 = 0, где k > 0 — данное число, записывается в виде y = A sin kt + B cos kt,
где А и B — некоторые постоянные. И вопрос о том, есть ли другие решения у этих уравнений, не обсуждается.
Промежуточный контроль. К—4.
Вторая глава учебника посвящена изучению методов решения уравнений, неравенств и систем. В 10 классе учащиеся должны были научиться решать рациональные уравнения, неравенства и системы, простейшие показательные, логарифмические, тригонометрические уравнения и неравенства, а также уравнения и неравенства, сводящиеся к простейшим с помощью замены неизвестного.
В этой главе рассматриваются различные методы решения более сложных уравнений, неравенств и систем. При этом в данной главе нет классификации уравнений, неравенств и систем по их виду (тригонометрические, логарифмические и т. п.). Они классифицируются по методам решения.
Часто уравнение (неравенство, систему) можно решить различными методами. Например, при применении неравносильных преобразований уравнений возможны три основных способа их решения.
Второй способ сводится к решению системы, равносильной исходному уравнению.
Третий способ сводится к решению преобразованного уравнения на том множестве M, на котором оно равносильно исходному уравнению. Этот способ решения уравнений труднее остальных, он рассматривается чаще всего при углубленном изучении математики и позволяет подготовить учащихся к решению сложных задач из ЕГЭ.
Параметры встречались учащимся уже в 7 и 8 классах при обсуждении способов решения линейных и квадратных уравнений и неравенств. В учебниках серии «МГУ — школе», а особенно в дидактических материалах к этим учебникам обсуждается много задач с параметрами. При изучении второй главы эта работа будет продолжена, так как работу с параметрами нельзя откладывать на конец обучения. Заключительный параграф 15 этой главы служит лишь для систематизации способов решения задач с параметрами.
|
§ 7. |
Равносильность уравнений и неравенств
Перед изучением параграфа 7 надо сказать учащимся о том, что имеется много различных способов преобразования уравнений и неравенств. А начинается их изучение с простейших — равносильных преобразований.
В данном пункте учебника вводятся понятия равносильных уравнений и равносильного преобразования уравнений, выделены шесть основных равносильных преобразований уравнений.
При изучении данного пункта сначала повторяются основные способы решения уравнений, в которых используются равносильные преобразования, известные учащимся по предыдущему обучению, а затем усваиваются новые способы.
Стоит подчеркнуть, что если при решении уравнения применялись только равносильные преобразования, то все полученные корни последнего уравнения являются корнями исходного уравнения. Поэтому проверка полученных корней не является обязательным элементом решения уравнения.
Решения и комментарии
7.11. а) Решите уравнение 2x − 1 = 3x.
Решение. Перепишем исходное уравнение в виде
2x − 1 = 2x log2 3.
Это уравнение равносильно уравнению x − 1 = x log2 3,
которое имеет единственный корень x0
= ![]() 1 , поэто1 −
log2 3
1 , поэто1 −
log2 3
му и равносильное ему исходное уравнение имеет единст-
1 венный корень ![]() .
.
1 − log2 3
7.13. При каком значении параметра a уравнение 3x2 − 2 x + a = 9x имеет единственный корень? Решение. Перепишем исходное уравнение в виде
3x2 − 2 x + a = 32x. (1)
При каждом значении параметра a уравнение (1) равносильно уравнению x2 − 2x + a = 2x, которое можно переписать в виде
x2 − 4x + a = 0. (2)
Квадратное уравнение (2) имеет единственный корень только тогда, когда его дискриминант D = 16 − 4a равен нулю, т. е. только при a = 4. Следовательно, и равносильное ему уравнение (1) имеет единственный корень только при a = 4.
Дополнение. При изучении материала данного пункта учащиеся иногда задают вопрос: «Существуют только шесть равносильных преобразований уравнений или есть другие?» Ответить на него можно так: «В основном это все равносильные преобразования, однако есть и неравносильные преобразования уравнений (их мы еще будем изучать), которые в частном случае могут привести к уравнению, равносильному исходному».
Например, при возведении в квадрат уравнения x2 = | x | получим уравнение x4 = x2, равносильное исходному, так как обе части исходного уравнения неотрицательны при каждом x ∈ R. Но надо иметь в виду, что, вообще говоря, это преобразование — возведение уравнения в квадрат — не является равносильным преобразованием. Например, при возведении в квадрат уравнения x2 = x получим уравнение x4 = x2, неравносильное исходному, так как оно имеет корень −1, который не является корнем исходного уравнения.
В качестве дополнительных задач по изучаемой теме учащимся можно предложить задачи из ЕГЭ прошлых лет.
В1 (2005). Решите уравнение 34x + 5 = 81.
Ответ. −0,25.
В2 (2008). Решите уравнение 7x + 1 − 5 ⋅ 7x = 98.
Решение. Так как для каждого x ∈ R справедливы равенства 7x + 1 − 5 ⋅ 7x = 7 ⋅ 7x − 5 ⋅ 7x = (7 − 5) ⋅ 7x = 2 ⋅ 7x, то исходное уравнение равносильно уравнению
2 ⋅ 7x = 98. (3)
Уравнение (3) имеет единственный корень x1 = 2, следовательно, и равносильное ему исходное уравнение имеет тот же корень.
Ответ. 2.
Промежуточный контроль. C—29.
В данном пункте учебника вводятся понятия равносильных неравенств, равносильного преобразования неравенств, выделены шесть основных равносильных преобразований неравенств. Доказательство утверждений о равносильности неравенств проводится аналогично доказательству утверждений о равносильности уравнений в п. 7.1.
При изучении данного пункта сначала повторяются основные способы решения неравенств, в которых используются равносильные преобразования, известные учащимся по предыдущему обучению, а затем усваиваются новые способы.
Стоит подчеркнуть, что если при решении неравенства применялись только равносильные преобразования, то все полученные решения последнего неравенства являются решениями исходного неравенства.
![]() Обратим внимание на то, что в основном все приемы решения
неравенств, рассмотренные в учебнике, обсуждаются для строгих неравенств.
Нестрогое неравенство f (x) ≥
0 рассматривается как совокупность уравнения f (x) = 0 и неравенства f (x)
> 0, т. е. для
решения нестрогого неравенства требуется решить сначала уравнение, затем
строгое неравенство и потом объединить все найденные решения. Это связано с
тем, что иногда учащиеся применяют к нестрогим неравенствам те же приемы
решения, что и к строгим неравенствам, и совершают ошибки.
Обратим внимание на то, что в основном все приемы решения
неравенств, рассмотренные в учебнике, обсуждаются для строгих неравенств.
Нестрогое неравенство f (x) ≥
0 рассматривается как совокупность уравнения f (x) = 0 и неравенства f (x)
> 0, т. е. для
решения нестрогого неравенства требуется решить сначала уравнение, затем
строгое неравенство и потом объединить все найденные решения. Это связано с
тем, что иногда учащиеся применяют к нестрогим неравенствам те же приемы
решения, что и к строгим неравенствам, и совершают ошибки.
Например, строгое неравен-
(x − 1) (x −
2) Рис.
80 ство ![]() <
0 обычно ре-
<
0 обычно ре-
(x − 2) (x − 3) шают так. Это неравенство равносильно неравенству (x − 1) (x − 2)2 (x − 3) < 0. Применяя метод интервалов (рис. 80), находим все его решения: (1; 2) ∪ (2; 3).
Теперь решим нестрогое неравенство
![]() . (1)
. (1)
|
Сначала решим уравнение |
|
|
(x −
1) (x −
2) (x − 2) (x − 3) Оно имеет единственное решение x1 = 1. Затем решим строгое неравенство |
(2) |
|
(x − 1) (x − 2)
|
(3) |
(x − 2) (x − 3)
Множество его решений, как показано выше, есть множество (1; 2) ∪ (2; 3). Объединяя множества решений уравнения (2) и неравенства (3), получаем множество решений неравенства (1): [1; 2) ∪ (2; 3).
Если же учащиеся по ошибке перепишут неравенство (1) в виде
(x − 1) (x − 2)2 (x − 3) ≤ 0,
то получат неравенство, неравносильное неравенству (1). Такой «метод решения» нестрогого неравенства приводит к появлению двух посторонних решений: x1 = 2 и x2 = 3. Поэтому в дальнейшем мы будем придерживаться приведенного в п. 7.2 способа решения нестрогого неравенства.
Решения и комментарии
Решите неравенство (7.20—7.32):
7.20. а) cos 2x + 3 sin2 x + 2 sin x < 4.
Решение. Пользуясь формулами косинуса двойного угла и основным тригонометрическим тождеством, перепишем исходное неравенство в виде
sin2 x + 2 sin x − 3 < 0.
Сделав замену неизвестного t = sin x, получим квадратное
неравенство t2 +
2t −
3 < 0,
все решения которого составляют промежуток −3
< t < 1. Следовательно,
лишь все решения неравенства −3
< sin x < 1 являются
решениями исходного неравенства. Все решения последнего неравенства, а значит,
и исходного неравенства составляют все x ![]() k, k ∈ Z.
k, k ∈ Z.
7.29. а) 5x − 1 > 4x.
Решение. Перепишем исходное неравенство в виде
5x − 1 > 5x log5 4 . (4)
Неравенство (4) равносильно неравенству x − 1 > x log5 4, которое можно переписать в виде
x (1 − log5 4) > 1. (5)
Так как 1 − log5 4 > 0, то все решения неравенства (5),
а значит, и исходного неравенства
составляют x >
![]() 1 . 1 −
log5 4
1 . 1 −
log5 4
7.32. в) 4 ⋅ ⎛⎜⎝ 21⎞⎟⎠ 5x2 ≤ ⎛⎜⎝ 81⎞⎟⎠ −3x.
Решение. Перепишем исходное неравенство в виде
⎛⎜⎝ 21⎞⎟⎠ 5x2 − 2 ≤ ⎛⎜⎝ 21⎞⎟⎠ −9x. (8)
Сначала решим уравнение
⎛⎜⎝ 21⎞⎟⎠ 5x2 − 2 = ⎛⎜⎝ 21⎞⎟⎠ −9x. (9)
Оно равносильно уравнению
5x2 − 2 = −9x. (10)
Уравнение (10), а значит, и равносильное ему уравнение (9)
имеют два корня: x1 =
−2 и x2 =
![]()
![]() .
.
Теперь решим строгое неравенство
|
⎜⎝ 2 ⎟⎠ < ⎜⎝ 2 ⎟⎠ . Оно равносильно неравенству |
(11) |
|
5x2 − 2 > −9x. |
(12) |
⎛ 1⎞ 5x2 − 2 ⎛ 1⎞ −9x
Неравенство (12), а значит, и равносильное ему неравенство (11) имеют одно и то же множество решений:
(−∞; −2) ∪ ⎛⎜⎝ 51 ; + ∞⎞⎟⎠.
Объединяя все решения уравнения (9) и неравенства (11), получаем все решения неравенства (8): (−∞; −2] ∪
∪ ⎡⎢⎣51 ; + ∞⎞⎟⎠.
7.33. При каких значениях параметра a все решения неравенства 2x2 + 2 x − a2 < 4x содержатся в интервале (−1; 1)? Решение. Перепишем исходное неравенство в виде
2x2 + 2 x − a2 < 22 x. (13)
При каждом значении параметра a неравенство (13) равносильно неравенству x2 + 2x − a2 < 2x, которое можно переписать в виде
(x − a) (x + a) < 0. (14)
Если a = 0, то неравенство (14), а значит, и исходное неравенство не имеют решений.
Если a > 0, то неравенство (14), а значит, и исходное неравенство имеют решения: −a < x < a. Все эти решения содержатся в интервале (−1; 1) лишь при a ∈ (0; 1] (рис. 81, а).

Рис. 81
Если a < 0, то неравенство (14), а значит, и исходное неравенство имеют решения: a < x < −a. Все эти решения содержатся в интервале (−1; 1) лишь при a ∈ [−1; 0) (рис. 81, б).
Следовательно, все решения исходного неравенства содержатся в интервале (−1; 1) только при a ∈ [−1; 0) ∪ (0; 1] (см. рис. 81, б).
Дополнение. При изучении материала данного пункта учащиеся иногда задают вопрос: «Существуют только шесть равносильных преобразований неравенств или есть другие?» Ответить на него можно так: «В основном это все равносильные преобразования, однако есть неравносильные преобразования неравенств (их мы еще будем изучать), которые в частном случае могут привести к неравенству, равносильному исходному».
![]()
![]()
![]()
![]()
![]() Например, при приведении
подобных членов неравенства x2 +1
+ x − x2 +1 > 1 получим
неравенство x >
1, равносильное исходному неравенству, так как функция y = x2 +1 определена для
каждого x ∈
R. Но надо иметь в виду, что, вообще говоря, приведение
подобных членов не является равносильным преобразованием. Например, приведя
подобные члены в неравенстве x +
x − x
< 1,
получим неравенство x <
1, неравносильное исходному неравенству, так как оно имеет решения
(например, все x <
0), которые не являются решениями исходного неравенства (для этих
значений x функция y =
x не определена).
Например, при приведении
подобных членов неравенства x2 +1
+ x − x2 +1 > 1 получим
неравенство x >
1, равносильное исходному неравенству, так как функция y = x2 +1 определена для
каждого x ∈
R. Но надо иметь в виду, что, вообще говоря, приведение
подобных членов не является равносильным преобразованием. Например, приведя
подобные члены в неравенстве x +
x − x
< 1,
получим неравенство x <
1, неравносильное исходному неравенству, так как оно имеет решения
(например, все x <
0), которые не являются решениями исходного неравенства (для этих
значений x функция y =
x не определена).
⎛ 1⎞ 3 x − 7 > 0 04, . А9 (2006). Решите неравенство ⎜⎝ 5 ⎟⎠
1) (−∞; 3); 2) ⎛⎜⎝−∞; 53⎞⎟⎠; 3) (3; +∞); 4) ⎛⎜⎝−∞; − 53⎞⎟⎠.
Решение. Перепишем исходное неравенство в виде
⎛⎜ 1⎞⎟ 3 x − 7 > ⎛⎜⎝ 51⎞⎟⎠ 2 . (15)
⎝ 5 ⎠
Неравенство (15) равносильно неравенству
3x − 7 < 2. (16)
Неравенство (16), а значит, и равносильное ему неравенство (15) имеют одно и то же множество решений: (−∞; 3).
Ответ. 1.
Промежуточный контроль. C—30.
|
§ 8. |
Начиная с этого параграфа будут изучаться неравносильные преобразования уравнений.
В данном пункте учебника вводятся понятия уравненияследствия, перехода к уравнению-следствию, корней, посторонних для исходного уравнения. Отмечается, что если в процессе решения уравнения был совершен переход к уравнению-следствию, то проверка полученных корней является обязательным элементом решения исходного уравнения. Выделены четыре основных преобразования, приводящие к уравнению-следствию. Отмечается, что при применении некоторых формул (тригонометрических, логарифмических и др.) также могут получиться уравнения-следствия.
После изучения данного параграфа можно рекомендовать учащимся такой «рецепт»: если при решении уравнения было выполнено либо возведение в квадрат, либо потенцирование логарифмического уравнения, либо освобождение уравнения от знаменателя, либо приведение подобных членов, то обязательным элементом решения является проверка того, какие из найденных чисел являются корнями исходного уравнения.
Решения и комментарии
8.2. Объясните, в результате какого преобразования переход от первого уравнения ко второму приводит к появлению посторонних корней. Подберите корень второго уравнения, посторонний для первого уравнения:
а) x = 2, x2 = 4;
б) log3 x2 = log3 x, x2 = x;
(x − 4) − (2x − 3)
![]() в)= 0, x − 4 − (2x − 3) = 0;
в)= 0, x − 4 − (2x − 3) = 0;
г) x x + 4, x2 + 3x − 4 = 0.
Решение. а) Второе уравнение получено возведением первого уравнения в квадрат. Корень −2 второго уравнения является посторонним для первого уравнения.
б) Второе уравнение получено потенцированием первого логарифмического уравнения. Корень 0 второго уравнения является посторонним для первого уравнения.
в) Второе уравнение получено освобождением первого уравнения от знаменателя. Корень −1 второго уравнения является посторонним для первого уравнения.
г) Второе уравнение получено из первого переносом слагаемых в левую часть с противоположным знаком (это равносильное преобразование) и приведением подобных членов. Корень −4 второго уравнения является посторонним для первого уравнения.
Дополнение. Рассмотрим еще одно преобразование уравнения, приводящее к уравнению-следствию. Уравнения вида
![]() 3 f
x( ) + 3
g x( ) = 3
ϕ ( )x (1)
3 f
x( ) + 3
g x( ) = 3
ϕ ( )x (1)
обычно решают следующим образом. Возведя в куб уравнение (1), получим равносильное ему уравнение f x( ) + 3 3 f x( ) 3 g x( ) (3 f x( ) + 3 g x( )) + g x( ) = ϕ ( )x . (2)
![]() Пользуясь
уравнением (1), заменим в уравнении (2) 3 f x( ) + 3 g x(
) на 3 ϕ
( )x , тогда получим уравнение
Пользуясь
уравнением (1), заменим в уравнении (2) 3 f x( ) + 3 g x(
) на 3 ϕ
( )x , тогда получим уравнение
3 3 f x( ) 3 g x( ) 3 ϕ ( )x = ϕ ( )x − f x( ) − g x( ), (3) которое является следствием уравнения (2), а значит, и уравнения (1). Возведя в куб уравнение (3), получим уравнение, которое равносильно уравнению (3), а значит, является следствием уравнения (1). Решив полученное уравнение, надо проверить, какие из найденных корней удовлетворяют уравнению (1).
Пример. Решим уравнение
3 3 3
![]() x + 2x + 6 = 3x + 24. (4)
x + 2x + 6 = 3x + 24. (4)
Возведя уравнение (4) в куб, получим равносильное ему уравнение x + 3 3 x 3 2x + 6 (3 x + 3 2x + 6) + 2x + 6 = 3x + 24.
![]() Заменив
в этом уравнении 3 x +
3 2x +
6 на 3 3x +
24, получим уравнение
Заменив
в этом уравнении 3 x +
3 2x +
6 на 3 3x +
24, получим уравнение
3 3 3
x 2x + 6 3x + 24 = 6, (5)
являющееся следствием уравнения (4). Возведя в куб уравнение (5), получим равносильное ему уравнение x (2x + 6) (3x + 24) = 63, которое можно переписать в виде x3 + 11x2 + 24x − 36 = 0. (6)
Уравнение (6) имеет два корня: x1 = 1 и x2 = −6. Проверка показывает: x1 является корнем уравнения (4), x2 нет. Ответ. 1.
Покажем, что уравнение (3) действительно есть следствие уравнения (1). Обозначив для краткости 3 f x( ) = 3 f,
![]() 3
g x( ) = 3
g, 3 ϕ
( )x = 3
ϕ,
перепишем уравнение (3) в виде
3
g x( ) = 3
g, 3 ϕ
( )x = 3
ϕ,
перепишем уравнение (3) в виде
![]()
![]() 3
3 f 3 g (3 ϕ − (3
f + 3
g ))
= (3 ϕ)3
− (3
f + 3
g )3
. (7)
3
3 f 3 g (3 ϕ − (3
f + 3
g ))
= (3 ϕ)3
− (3
f + 3
g )3
. (7)
Применив формулу разности кубов, перепишем уравнение (7) в виде
⎛⎛
![]()
![]() (3 f + 3 g − 3 ϕ) ⎜⎜⎜⎝ 3 ϕ + 3 f +2 3 g ⎟⎠⎞
2 + 3 ⎛⎝⎜ 3 f −2 3 g ⎠⎟⎞
2 ⎟⎞⎟⎠ =
0. (8)
(3 f + 3 g − 3 ϕ) ⎜⎜⎜⎝ 3 ϕ + 3 f +2 3 g ⎟⎠⎞
2 + 3 ⎛⎝⎜ 3 f −2 3 g ⎠⎟⎞
2 ⎟⎞⎟⎠ =
0. (8)
⎝
Уравнение (8) равносильно совокупности двух уравнений
3 f + 3 g − 3 ϕ = 0 и
⎛ 3 3 f + 3 g ⎞ 2 ⎛ 3 f − 3 g ⎞ 2
⎜ ϕ + ⎟ + 3 ⎜ ⎟ = 0. (9)
⎝ 2 ⎠ ⎝ 2 ⎠
Уравнение (9) равносильно системе уравнений
![]() 3
f = 3
g = −
3 ϕ. (10)
3
f = 3
g = −
3 ϕ. (10)
Таким образом, множество всех решений уравнения (3) состоит из множества всех решений уравнения (1) и множества всех решений системы уравнений (10), т. е. уравнение (3) действительно является следствием уравнения (1).
Дополнение. Решите уравнение: а) 3 x − 3 + 3 2x = 3 3x +15;
![]() б) 3 x − 4 + 3 2x − 2 = 3 3x +12;
б) 3 x − 4 + 3 2x − 2 = 3 3x +12;
в) 3 x − 1 + 3 2x + 4 = 3 3x + 21;
г) 3 x − 2 + 3 2x + 2 = 3 3x +18. Ответ. а) 4; б) 5; в) 2; г) 3.
В этом пункте учебника приведено утверждение:
Пусть 2m (m ∈ N) — фиксированное четное натуральное число. Тогда следствием уравнения
|
f (x) = g (x) является уравнение |
(1) |
|
(f (x))2m = (g (x))2m. |
(2) |
Доказательство. Пусть число x0 — некоторый корень уравнения (1), т. е. пусть существуют числа f (x0) и g (x0), для которых справедливо числовое равенство f (x0) = g (x0).
Но если равны числа, то равны и любые их степени, т. е. справедливо числовое равенство (f (x0))2m = (g (x0))2m. Следовательно, число x0 есть корень уравнения (2). Такое рассуждение можно провести для любого корня уравнения (1).
Таким образом, любой корень уравнения (1) является корнем уравнения (2), т. е. уравнение (2) является следствием уравнения (1).
Если же уравнение (1) не имеет корней, то тогда, как указано в начале п. 8.1, любое уравнение, а значит, и уравнение (2) есть следствия уравнения (1). Утверждение доказано полностью.
Это утверждение чаще всего применяется при решении иррациональных уравнений. В п. 8.2 учебника и в п. 31 дидактических материалов приведены примеры его применения.
Обратим внимание на то, что это утверждение применяется и при решении уравнений с модулями (пример 3 учебника). Приведем еще один пример из ЕГЭ.
С1 (2005). Решите уравнение | sin x | = sin x cos x.
Решение. Возведя обе части уравнения в квадрат, перейдем к уравнению-следствию sin2 x = sin2 x cos2 x. Очевидно, что sin2 x (1 − cos2 x) = 0 ⇔ sin4 x = 0 ⇔ sin x = 0.
Последнее уравнение имеет серию решений xk = πk, k ∈ Z. Проверка показывает, что все числа xk являются решениями исходного уравнения. Ответ. πk, k ∈ Z.
Решения и комментарии
![]() Решите уравнение (8.10—8.11):
8.10. а) log22 x + 3 =
log2 x −
1;
Решите уравнение (8.10—8.11):
8.10. а) log22 x + 3 =
log2 x −
1;
в) 4x + 1 − 2x + 1 − 3 = 2x +1.
Решение. а) Сделав замену неизвестного t = log2 x, перепишем исходное уравнение в виде
![]() t2
+ 3 = t − 1. (1)
t2
+ 3 = t − 1. (1)
Возведя уравнение (1) в квадрат, получим уравнение t2 + 3 = t2 − 2t +1, (2)
являющееся следствием уравнения (1).
Уравнение (2) имеет единственный корень t0 = −1. Проверка показывает, что число t0 не является корнем уравнения (1), поэтому уравнение (1) не имеет корней. Следовательно, и исходное уравнение не имеет корней.
в) Сделав замену неизвестного t = 2x, перепишем исходное уравнение в виде
![]() 4t2
− 2t
− 3 = t +1. (3)
4t2
− 2t
− 3 = t +1. (3)
Возведя уравнение (3) в квадрат, получим уравнение
4t2 − 2t − 3 = t2 + 2t +1, (4)
являющееся следствием уравнения (3).
Уравнение (4) имеет два корня: t1 = 2 и t2 = − ![]()
![]() . Провер-
. Провер-
ка показывает, что числа t1 и
t2 являются корнями уравнения (3). Следовательно, все корни
исходного уравнения являются корнями двух уравнений 2x = 2 и 2x = − ![]()
![]() . Первое из этих уравнений имеет
единственный корень x0 =
1, а второе уравнение корней не имеет. Поэтому исходное уравнение имеет
единственный корень 1.
. Первое из этих уравнений имеет
единственный корень x0 =
1, а второе уравнение корней не имеет. Поэтому исходное уравнение имеет
единственный корень 1.
8.11. в) | 2 lg x − 3 | = 3 lg x − 2.
Решение. Сделав замену неизвестного t = lg x, перепишем исходное уравнение в виде
| 2t − 3 | = 3t − 2. (5)
Возведя уравнение (5) в квадрат, получим уравнение
4t2 − 12t + 9 = 9t2 − 12t + 4, (6)
являющееся следствием уравнения (5).
Уравнение (6) имеет два корня: t1 = 1 и t2 = −1. Проверка показывает, что лишь число t1 является корнем уравнения (5). Поэтому все корни (и только они) уравнения lg x = 1 являются корнями исходного уравнения.
Уравнение lg x = 1 имеет единственный корень x0 = 10, следовательно, и исходное уравнение имеет единственный корень 10.
![]() 8.12. При каких
значениях параметра a уравнение x2 + 6x − 2a = x + 2 имеет единственный
корень?
8.12. При каких
значениях параметра a уравнение x2 + 6x − 2a = x + 2 имеет единственный
корень?
Решение. Возведя исходное уравнение в квадрат, получим уравнение
x2 + 6x − 2a = x2 + 4x + 4, (7)
являющееся следствием исходного уравнения при каждом значении параметра a.
Для каждого a уравнение (7) имеет единственный корень x0 = a + 2.
![]()
![]() Проверим, является
ли число x0 корнем исходного уравнения при каждом a.
Так как (a + 2)2
+ 6 (a + 2) − 2a = = a2 + 8a +16 = (a + 4)2 = | a + 4|, x + 2 = a + 4, а равенство | a
+ 4 | = a + 4 справедливо лишь
при a ≥
−4, то исходное уравнение имеет единственный корень лишь при a ≥ −4.
Проверим, является
ли число x0 корнем исходного уравнения при каждом a.
Так как (a + 2)2
+ 6 (a + 2) − 2a = = a2 + 8a +16 = (a + 4)2 = | a + 4|, x + 2 = a + 4, а равенство | a
+ 4 | = a + 4 справедливо лишь
при a ≥
−4, то исходное уравнение имеет единственный корень лишь при a ≥ −4.
Дополнение. В качестве дополнительных заданий по изучаемой теме учащимся можно предложить задания из ЕГЭ прошлых лет.
В2 (2006). Решите уравнение 2x + 37 = x +1. Ответ. 6.
![]() В2 (2005). Решите
уравнение x −
2x2 −
9x + 5
= 3. Ответ. 4.
В2 (2005). Решите
уравнение x −
2x2 −
9x + 5
= 3. Ответ. 4.
В3 (2005). Решите уравнение 2x2 − x − 6 = −x. Ответ. −2.
В данном пункте учебника доказано утверждение:
Пусть a > 0, a ≠ 1. Тогда следствием уравнения loga f (x) = loga g (x) является уравнение f (x) = g (x).
Приведены примеры применения этого утверждения при решении уравнений.
Решения и комментарии
Решите уравнение (8.18—8.19):
8.18. а) log2 (4x − 2x + 1 + 2) = x.
Решение. Перепишем исходное уравнение в виде
log2 (4x − 2x + 1 + 2) = log2 2x. (1)
Уравнение 4x − 2x + 1 + 2 = 2x является следствием уравнения (1). Решив его, получим, что оно имеет два корня: x1 = 0 и x2 = 1. Проверка показывает, что числа x1 и x2 являются корнями уравнения (1), следовательно, исходное уравнение имеет два корня: 0 и 1.
8.19. а) log2 cos 2x = log2 cos x.
Решение. Уравнение cos 2x = cos x является
следствием исходного уравнения. Решив его, получим, что оно имеет две серии
решений: xm =
2πm,
m ∈ Z
и xn ![]() n, n ∈ Z.
n, n ∈ Z.
Проверка показывает, что лишь числа xm являются решениями исходного уравнения. Поэтому исходное уравнение имеет единственную серию решений xm = 2πm, m ∈ Z.
8.20. При каких значениях параметра a уравнение lg (x2 + 3x + a) = lg (x + 1)2 не имеет корней?
Решение. Уравнение
x2 + 3x + a = (x + 1)2 (2)
является следствием исходного уравнения при каждом значении параметра a. Для каждого a уравнение (2) имеет единственный корень x0 = 1 − a. Проверим, является ли число x0 корнем исходного уравнения при каждом a.
Так как x20 + 3x0 + a = (a − 2)2 и (x0 + 1)2 = (a − 2)2 и при a = 2 не имеет смысла выражение lg (a − 2)2, то при a = 2 исходное уравнение не имеет корней. При любом a ≠ 2 справедливо равенство lg (x20 + 3x0 + a) = lg (x0 + 1)2, т. е. исходное уравнение имеет корень x0. Следовательно, лишь при a = 2 исходное уравнение не имеет корней.
В данном пункте учебника рассмотрены преобразования, приводящие к уравнению-следствию: 1) приведение подобных членов; 2) освобождение уравнения от знаменателя; 3) применение некоторых формул. Приведены примеры решения уравнений с применением этих неравносильных преобразований уравнений.
Обратим внимание на ошибку, которую иногда допускают учащиеся. Например, при освобождении уравнения
x2 + x − 6
![]() = 0 (1)
= 0 (1)
![]() от
знаменателя учащиеся переходят к уравнению x2 + x − 6 = 0 — следствию
уравнения (1) — и находят два его корня: x1 = 2 и x2 = −3. Дальше
некоторые учащиеся делают «проверку» следующим образом: «Так как x − 1 = 0 только при x = 1, а среди чисел x1
и x2 нет числа 1, то ни одно из чисел x1 и
x2 не обращает в нуль знаменатель в правой части уравнения
(1), поэтому оба эти числа — корни уравнения (1)». При этом они не обращают
внимания на то, что при x =
−3 не имеет смысла этот знаменатель.
от
знаменателя учащиеся переходят к уравнению x2 + x − 6 = 0 — следствию
уравнения (1) — и находят два его корня: x1 = 2 и x2 = −3. Дальше
некоторые учащиеся делают «проверку» следующим образом: «Так как x − 1 = 0 только при x = 1, а среди чисел x1
и x2 нет числа 1, то ни одно из чисел x1 и
x2 не обращает в нуль знаменатель в правой части уравнения
(1), поэтому оба эти числа — корни уравнения (1)». При этом они не обращают
внимания на то, что при x =
−3 не имеет смысла этот знаменатель.
![]()
![]()
![]() На самом деле прежде всего
надо проверить, имеют ли смысл выражения x1 − 1 и x2
− 1,
а потом для того числа xi, для которого имеет смысл выражение
xi −
1, проверить, равно ли это выражение нулю или нет. В нашем примере
выражение x2 −
1 не имеет смысла, а выражение x1 − 1 имеет смысл и
x1 −
1 ≠ 0,
поэтому уравнение (1)
На самом деле прежде всего
надо проверить, имеют ли смысл выражения x1 − 1 и x2
− 1,
а потом для того числа xi, для которого имеет смысл выражение
xi −
1, проверить, равно ли это выражение нулю или нет. В нашем примере
выражение x2 −
1 не имеет смысла, а выражение x1 − 1 имеет смысл и
x1 −
1 ≠ 0,
поэтому уравнение (1)
имеет единственный корень x1 = 2.
Обратим еще внимание на преобразование «применение формул». Этот материал следует рассматривать лишь в классах с углубленным изучением математики.
Решения и комментарии
Решите уравнение (8.27—8.30):
8.27. а) tg 3x = tg 5x.
Решение. Перенеся все члены исходного уравнения в sin kx
правую часть и учитывая, что tg kx = , перепишем
cos kx
![]() sin 5x cos 3x +
sin 3x cos 5x
sin 5x cos 3x +
sin 3x cos 5x
исходное уравнение в виде= 0.
cos 3x cos 5x
Применив формулу синуса разности двух углов, перепишем это уравнение в виде
sin 2x
![]() = 0. (2)
= 0. (2)
cos 3x cos 5x
Освобождаясь от знаменателя в этом уравнении, получаем уравнение
sin 2x = 0, (3)
являющееся следствием уравнения (2). Все решения урав-
нения (3) задаются серией решений xk = πk, k ∈ Z.
2
Проверим, все ли эти числа являются решениями уравнения (2). Так как cos 3xk = cos 3πk и cos 5xk = cos 5πk, то
2 2
при k = 2m + 1, m ∈ Z имеем cos 3xk = 0 и cos 5xk = 0, т. е. числа xk при k = 2m + 1, m ∈ Z не являются решениями уравнения (2). Так как при k = 2m, m ∈ Z имеем cos 3xk ≠ 0 и cos 5xk ≠ 0, то числа xk при k = 2m, m ∈ Z являются решениями уравнения (2).
Следовательно, решениями уравнения (2), а значит, и равносильного ему исходного уравнения являются числа xk = πm, m ∈ Z.
|
8.28. а) 10lg ( x2 + 5 x − 1) = 3x + 2. Решение. Применив формулу |
|
|
10lg ( x2 + 5 x − 1) = x2 + 5x − 1, получим уравнение |
(4) |
|
x2 + 5x − 1 = 3x + 2, |
(5) |
которое является следствием исходного уравнения, так как правая часть формулы (4) определена для каждого x ∈ R, а левая часть — не для каждого x ∈ R.
Решив уравнение (5), получим, что оно имеет два корня: x1 = 1 и x2 = −3. Проверка показывает, что число 1 является корнем исходного уравнения, а число −3 нет. Следовательно, исходное уравнение имеет единственный корень 1.
2
8.29. а) ![]() − log5 x
= 0.
− log5 x
= 0.
(logx 5)2
|
Решение. Применив формулу |
|
|
1
2 = (log5 x) (logx 5) получим уравнение |
(6) |
|
2 (log5 x)2 − log5 x = 0, |
(7) |
![]()
![]()
![]() которое является следствием
исходного уравнения, так как правая часть формулы (6) определена для каждого x
> 0, а
левая часть — для каждого x >
0, но x ≠
1. Решив уравнение (7), получим, что оно имеет два корня: x1
=5 и x2
= 1.
Проверка показывает, что число5 является корнем исходного уравнения, а число 1
нет. Следовательно, исходное уравнение имеет единственный корень5.
которое является следствием
исходного уравнения, так как правая часть формулы (6) определена для каждого x
> 0, а
левая часть — для каждого x >
0, но x ≠
1. Решив уравнение (7), получим, что оно имеет два корня: x1
=5 и x2
= 1.
Проверка показывает, что число5 является корнем исходного уравнения, а число 1
нет. Следовательно, исходное уравнение имеет единственный корень5.
8.30. а) 1![]() − tg22 xx = cos x − sin2 x.
− tg22 xx = cos x − sin2 x.
1 + tg
Решение. Применив формулу
1 − tg2 x
![]() 2 x = cos 2x, (8)
2 x = cos 2x, (8)
1 + tg
получим уравнение
cos 2x = cos x − sin2 x, (9)
которое является следствием исходного уравнения, так как правая часть формулы (8) определена для каждого x ∈ R, а левая часть — не для каждого x ∈ R.
Решив уравнение (9), получим, что оно имеет две серии
решений: xm =
2πm,
m ∈ Z
и xn =
![]()
![]() + πn, n
∈ Z.
Провер-
+ πn, n
∈ Z.
Провер-
ка показывает, что лишь числа xm являются решениями исходного уравнения. Следовательно, оно имеет решения xm = 2πm, m ∈ Z.
8.31. При каких значениях параметра a уравнение: a − 2
![]()
![]() а)
x − a
+ x − a = 2x +1 + x − a; б)
а)
x − a
+ x − a = 2x +1 + x − a; б) ![]() = 1
= 1
ax − 3
имеет единственный корень?
Решение. а) Перенеся все слагаемые в одну часть уравнения (с противоположным знаком) и приведя подобные слагаемые, получим уравнение
x + a + 1 = 0, (10)
![]() которое
является следствием исходного уравнения для каждого a. Решив уравнение
(10) для каждого a, получим, что оно имеет единственный корень x0
= −a
− 1.
Проверим, является ли число x0 корнем исходного уравнения при
каждом а. Так как выражение x −
a имеет смысл лишь при условии x0 − a ≥ 0, т. е. при
условии a
которое
является следствием исходного уравнения для каждого a. Решив уравнение
(10) для каждого a, получим, что оно имеет единственный корень x0
= −a
− 1.
Проверим, является ли число x0 корнем исходного уравнения при
каждом а. Так как выражение x −
a имеет смысл лишь при условии x0 − a ≥ 0, т. е. при
условии a![]() , то исходное уравнение имеет единственный
корень лишь для a
, то исходное уравнение имеет единственный
корень лишь для a ![]() .
.
б) Перенеся число 1 в левую часть уравнения (с противоположным знаком) и приведя дроби к общему знаменателю, перепишем исходное уравнение в виде
a + 1 − ax
![]() = 0. (11)
= 0. (11)
ax − 3
Освобождаясь от знаменателя в этом уравнении, получаем уравнение
a + 1 − ax = 0, (12)
являющееся следствием уравнения (11). Уравнение (12) a + 1
имеет единственный корень x0
= ![]() только для каждого a
только для каждого a
a ≠ 0. Проверим, является ли число x0 корнем исходного уравнения при каждом a ≠ 0. Число x0 является корнем уравнения (11), если ax0 − 3 ≠ 0 (a ≠ 0), т. е. если a ≠ 0 и a ≠ 2.
Итак, исходное уравнение имеет единственный корень для каждого a, такого, что a ≠ 0 и a ≠ 2.
Дополнение. В качестве дополнительного задания по изучаемой теме учащимся можно предложить задание из ЕГЭ.
С1 (2006). Решите уравнение
4 cos x ctg x + 4 ctg x + sin x = 0.
cos x
Решение.
Применив формулу ctg x = ![]() , перепишем
, перепишем
sin x
уравнение в виде
4 cos 2 x + 4 cos x + sin 2 x
![]() = 0. (13)
= 0. (13)
sin x
Освобождаясь от знаменателя в уравнении (13), получаем уравнение
4 cos2 x + 4 cos x + sin2 x = 0, (14)
которое является следствием исходного уравнения. Решив уравнение (14), получим, что оно имеет две серии решений: xm = ±arccos ⎛⎜⎝− 31⎞⎟⎠ + 2πm, m ∈ Z и xn = π + 2πn, n ∈ Z.
Так как sin xm ≠ 0, то все числа xm являются решениями уравнения (13), а значит, и равносильного ему исходного уравнения. Так как sin xn = 0, то ни одно из чисел xn не является решением уравнения (13), а значит и исходного уравнения. Следовательно, исходное уравнение имеет решения xm = ±arccos ⎛⎜⎝− 31⎞⎟⎠ + 2πm, m ∈ Z.
Ответ. ±arccos ⎛⎜⎝− 31⎞⎟⎠ + 2πm, m ∈ Z.
Промежуточный контроль. C—31.
В данном пункте учебника рассмотрены примеры решения уравнений с применением нескольких преобразований, приводящих к уравнению-следствию. Рассмотрим подобные примеры.
Пример 1. Решим уравнение
![]() 3x + 49 + 10x +14 = 3x + 28 + 10x + 35.
3x + 49 + 10x +14 = 3x + 28 + 10x + 35.
Решение. Возведя исходное уравнение в квадрат, получим уравнение
![]() 3x + 49 + 2 3x + 49 10x +14 +10x +14 =
3x + 49 + 2 3x + 49 10x +14 +10x +14 =
= 3x + 28 + 2 3x + 28 10x + 35 +10x + 35, (1)
|
являющееся следствием исходного уравнения. Уравнение (1) можно переписать в виде |
|
|
|
(2) |
Возведя уравнение (2) в квадрат, получим уравнение (3x + 49) (10x + 14) = (3x + 28) (10x + 35) (3)
— следствие уравнения (2).
Уравнение (3) имеет единственный корень x1 = 2. Проверка показывает, что число x1 является корнем исходного уравнения. Следовательно, исходное уравнение имеет единственный корень 2.
Ответ. 2.
Пример 2. Решим уравнение
log3 1 = log3 ⎛⎜⎝ 1![]() +sincosx2x⎞⎟⎠.
(4) tg x
+sincosx2x⎞⎟⎠.
(4) tg x
Потенцируя уравнение (4), получаем уравнение
1 1 + cos 2x
= ![]() , (5) tg x sin x
, (5) tg x sin x
являющееся следствием уравнения (4). Применяя форму-
1 cos x 2
лы =
![]() , 1 +
cos 2x = 2
cos x и перенося все члены tg x sin x
, 1 +
cos 2x = 2
cos x и перенося все члены tg x sin x
уравнения в левую часть, получаем уравнение
cos x − 2 cos 2 x
![]() = 0, (6) sin x
= 0, (6) sin x
являющееся следствием уравнения (5).
Освобождаясь в уравнении (6) от знаменателя, получаем уравнение
cos x − 2 cos2 x = 0, (7)
являющееся следствием уравнения (6), а
значит, и уравнения (4). Множество решений уравнения (7) состоит из объединения
всех решений уравнений cos x =
0 и cos x =
![]()
![]() ,
,
т. е. задается тремя сериями решений: xn
= ![]()
![]() +
πn, n ∈
Z; xk
+
πn, n ∈
Z; xk ![]() k, k ∈ Z и
xm =
−
k, k ∈ Z и
xm =
− ![]()
![]() + 2πm, m ∈ Z.
+ 2πm, m ∈ Z.
Проверка показывает, что все числа серии xk являются решениями уравнения (4), а все числа серий xn и xm нет.
Следовательно, все решения уравнения (4)
задаются серией решений ![]()
![]() + 2πk, k ∈ Z.
+ 2πk, k ∈ Z.
Решения и комментарии
Решите уравнение (8.37—8.41):
![]() 8.37.
а) x −
5 x −
6 = x
− 2.
8.37.
а) x −
5 x −
6 = x
− 2.
Решение. Возведя уравнение в квадрат, получим уравнение-следствие исходного уравнения
(x − 5) (x − 6) = x − 2,
имеющее два корня: x1 = 8 и x2 = 4. Проверка показывает, что число 8 является корнем исходного уравнения, а число 4 нет. Следовательно, исходное уравнение имеет единственный корень 8.
![]() 8.39.
а) log3 x +
log3 x +
8 = 1.
8.39.
а) log3 x +
log3 x +
8 = 1.
![]()
![]()
![]() Решение. Применив
формулу log3 x +
log3 x +
8 = = log3
x x + 8
и заменив число 1 на log3 3, получим уравнение
Решение. Применив
формулу log3 x +
log3 x +
8 = = log3
x x + 8
и заменив число 1 на log3 3, получим уравнение
![]() log3 x x
+ 8 = log3 3, (8)
log3 x x
+ 8 = log3 3, (8)
являющееся следствием исходного уравнения.
Потенцируя уравнение (8), получим уравнение
![]() x x
+ 8 = 3, (9)
x x
+ 8 = 3, (9)
являющееся следствием уравнения (8), а значит, и следствием исходного уравнения.
Возведя уравнение (9) в квадрат, получим уравнение x (x + 8) = 3,
являющееся следствием уравнения (9), а значит, и следствием исходного уравнения. Это уравнение имеет два корня: x1 = 1 и x2 = −9. Проверка показывает, что число 1 является корнем исходного уравнения, а число −9 нет. Следовательно, исходное уравнение имеет единственный корень 1.
8.40. а) log2 (x + 1) = log4 (5x + 1).
Решение. Применив формулу log2 (x + 1) = log4 (x + 1)2, получим уравнение
log4 (x + 1)2 = log4 (5x + 1), (10)
являющееся следствием исходного уравнения.
Потенцируя уравнение (10), получим уравнение
(x + 1)2 = 5x + 1,
являющееся следствием уравнения (10), а значит, и следствием исходного уравнения. Это уравнение имеет два корня: x1 = 0 и x2 = 3. Проверка показывает, что оба эти числа являются корнями исходного уравнения. Следовательно, исходное уравнение имеет два корня: 0 и 3.
![]() 8.41.
а) log (2 x +2)
+log (2 x
+1) = log (2 x
− 2) +log (2 2x
−1).
8.41.
а) log (2 x +2)
+log (2 x
+1) = log (2 x
− 2) +log (2 2x
−1).
Решение. Возведя исходное уравнение в квадрат, получим уравнение log2 (x + 2) + log2 (x + 1) = log2 (x − 2) + log2 (2x − 1), (11) являющееся следствием исходного уравнения. Применив формулы log2 (x + 2) + log2 (x + 1) = log2 (x + 2) (x + 1) и log2 (x − 2) + log2 (2x − 1) = log2 (x − 2) (2x − 1), получим уравнение log2 (x + 2) (x + 1) = log2 (x − 2) (2x − 1), (12) являющееся следствием уравнения (11).
Потенцируя уравнение (12), получим уравнение
(x + 2) (x + 1) = (x − 2) (2x − 1),
являющееся следствием уравнения (12), а значит, и следствием исходного уравнения. Это уравнение имеет два корня: x1 = 8 и x2 = 0. Проверка показывает, что число 8 является корнем исходного уравнения, а число 0 нет. Следовательно, исходное уравнение имеет единственный корень 8.
8.42. Докажите, что при любом значении а уравнение lg x + lg (x − 2a) = lg 4 имеет единственный корень.
Доказательство. Применив формулу lg x + lg (x − 2a) =
= lg x (x − 2a), получим уравнение
lg x (x − 2a) = lg 4, (13)
являющееся следствием исходного уравнения при каждом значении a.
Потенцируя уравнение (13), получим уравнение x (x − 2a) = 4,
являющееся следствием уравнения (13), а значит, и следствием исходного уравнения при каждом значении а.
![]()
![]()
![]()
![]()
![]() Это уравнение имеет два
корня: x1 =
a + a2
+ 4 и x2
= a − a2 + 4. Проверим, является
ли число x1 корнем исходного уравнения при каждом значении a.
Так как для каждого a верны неравенства a2 +4 +a > 0 и a2
+4 − a > 0, то lg x1
(x1 −
2a) = lg
(a
+ a2
+ 4)
+ lg (a
+ a2
+ 4 − 2a)
= = lg (
a2 +4
+a)
+lg (
a2 +4
− a)
= lg (
a2 +4
+a)(
a2 +4
− a)
=
Это уравнение имеет два
корня: x1 =
a + a2
+ 4 и x2
= a − a2 + 4. Проверим, является
ли число x1 корнем исходного уравнения при каждом значении a.
Так как для каждого a верны неравенства a2 +4 +a > 0 и a2
+4 − a > 0, то lg x1
(x1 −
2a) = lg
(a
+ a2
+ 4)
+ lg (a
+ a2
+ 4 − 2a)
= = lg (
a2 +4
+a)
+lg (
a2 +4
− a)
= lg (
a2 +4
+a)(
a2 +4
− a)
=
= lg (a2 + 4 − a2) = lg 4.
Итак, число x1 является корнем исходного уравнения для каждого a. Так как x2 < 0 для каждого a, то выражение lg x2 не имеет смысла и число x2 не является корнем исходного уравнения. Это означает, что при любом значении а исходное уравнение имеет единственный корень, что и требовалось доказать.
Промежуточный контроль. C—32.
|
§ 9. |
Равносильность уравнений и неравенств системам
В данном параграфе будет продолжено изучение неравносильных преобразований уравнений, но будет рассмотрен другой способ решения: переход от исходного уравнения к системе, равносильной этому уравнению. Так как при таком оформлении решения исходное уравнение равносильно системе, то все решения системы являются решениями исходного уравнения, поэтому никакой проверки найденных решений как обязательного элемента решения делать не нужно. В § 9 начинается изучение неравносильных преобразований неравенств; будет рассмотрен способ решения при помощи перехода от неравенства к системе, равносильной этому неравенству.
В данном пункте учебника вводятся понятия системы (составленной из уравнений, неравенств и других условий), решения такой системы, равносильных систем, уравнения (неравенства), равносильного системе, уравнения (неравенства), равносильного совокупности систем. Приведены примеры применения этих понятий.
Поясним еще раз, что подразумевается под словами «система» и «совокупность», под знаками «{» и «[». Слово «система» и знак «{» употребляются в смысле союза «и».
Например, если система содержит несколько условий (уравнений, неравенств и т. п.) с неизвестным x, то имеются в виду все те значения x, каждое из которых удовлетворяет каждому из этих условий.
Слово «совокупность» и знак «[» употребляются в смысле союза «или». Например, если совокупность содержит несколько условий (уравнений, неравенств и т. д.) с неизвестным x, то имеются в виду все те значения x, каждое из которых удовлетворяет хотя бы одному из этих условий.
Решения и комментарии
9.3. а) Запишите систему неравенств, равносильную неравенству | x | < 5.
Решение. По определению модуля числа неравенство | x | < 5 равносильно двойному неравенству −5 < x < 5, которое можно записать в виде системы ⎧⎨⎩xx > −< 5.5
Таким образом, неравенство | x | < 5 равносильно системе ⎧⎨⎩xx > −< 5.5
9.5. а) Запишите совокупность уравнений, равносильную уравнению | x | = 5.
Решение. По определению модуля числа уравнение | x | = 5 справедливо и при x = 5, и при x = −5. Поэтому уравне-
ние | x | = 5 равносильно совокупности уравнений ⎡⎢⎣xx == −55.
9.6. а) Запишите совокупность неравенств, равносильную неравенству | x | > 5.
Решение. По определению модуля числа неравенство | x | > 5 справедливо и при каждом x > 5, и при каждом x < −5. Поэтому неравенство | x | > 5 равносильно совокупности неравенств ⎡⎢⎣xx >< −55.
9.3. Решение уравнений с помощью систем (продолжение)
В пп. 9.2 и 9.3 учебника сформулированы 6 утверждений о равносильности уравнения системе. А в заданиях 9.24 и 9.25 сформулированы еще 4 таких же утверждения, на применение которых стоит обратить внимание сильных учащихся.
Доказательства всех этих утверждений однотипны, поэтому приведем доказательство только утверждения 1. Для любого четного числа 2m (m ∈ N) уравнение
![]() 2m
f x( ) =
g x( ) (1)
2m
f x( ) =
g x( ) (1)
равносильно системе
⎧⎨⎩f xg x( )( ) =≥ (0g x. ( ))2m (2)
![]() Доказательство.
Пусть число х0 — некоторое решение уравнения (1). Это
означает, что существуют числа f (x0) и g (x0),
для которых справедливо числовое равенство 2m f x( 0)
= g x( 0).
Из справедливости этого равенства в силу определения корня четной степени
следует, что g (x0) ≥
0. Но если числа равны, то равны и любые их степени, т. е., в частности,
справедливо числовое равенство f (x0) = (g (x0))2m.
Следовательно, число x0 является решением системы (2).
Доказательство.
Пусть число х0 — некоторое решение уравнения (1). Это
означает, что существуют числа f (x0) и g (x0),
для которых справедливо числовое равенство 2m f x( 0)
= g x( 0).
Из справедливости этого равенства в силу определения корня четной степени
следует, что g (x0) ≥
0. Но если числа равны, то равны и любые их степени, т. е., в частности,
справедливо числовое равенство f (x0) = (g (x0))2m.
Следовательно, число x0 является решением системы (2).
Такое рассуждение можно провести для любого решения уравнения (1), следовательно, любое решение уравнения (1) является решением системы (2).
Докажем теперь, что любое решение системы (2) является решением уравнения (1).
![]() Пусть
число х1 — некоторое решение системы (2). Это означает, что
существуют числа f (x1) и g (x1),
такие, что g (x1) ≥
0 и f (x1) =
(g (x1))2m. Из справедливости
числового равенства f (x1) = (g (x1))2m
следует, что f (x1) ≥ 0. Но если неотрицательные числа
равны, то равны и корни из них любой натуральной степени, т. е., в частности,
справедливо числовое равенство 2m f x( 1) = g x( 1),
означающее, что число x1 является решением уравнения (1).
Пусть
число х1 — некоторое решение системы (2). Это означает, что
существуют числа f (x1) и g (x1),
такие, что g (x1) ≥
0 и f (x1) =
(g (x1))2m. Из справедливости
числового равенства f (x1) = (g (x1))2m
следует, что f (x1) ≥ 0. Но если неотрицательные числа
равны, то равны и корни из них любой натуральной степени, т. е., в частности,
справедливо числовое равенство 2m f x( 1) = g x( 1),
означающее, что число x1 является решением уравнения (1).
Такое рассуждение можно провести для любого решения системы (2), следовательно, любое решение системы (2) является решением уравнения (1).
Методом от противного можно доказать, что если уравнение (1) не имеет решений, то и система (2) не имеет решений, и что если система (2) не имеет решений, то и уравнение (1) не имеет решений.
Итак, утверждение (1) доказано полностью.
Следует отметить, что в § 10 будут приведены и другие утверждения о равносильности уравнения системе. Учащимся можно порекомендовать запомнить следующие наиболее часто употребляемые равносильные переходы (здесь m ∈ N, a > 0, a ≠ 1):
⎧
1. ![]() 2m f x( ) = g x( ) ⇔ ⎨⎩f
xg x(
)( ) =≥ g0.2
( )x
2m f x( ) = g x( ) ⇔ ⎨⎩f
xg x(
)( ) =≥ g0.2
( )x
⎧⎪f x( ) = g x( )
2. 2m f x( ) = 2m g x( ) ⇔ ⎨f x( ) ≥ 0
⎪⎩g x( ) ≥ 0.
⎧⎪f x( ) = g x( )
3. loga f (x) = loga g (x) ⇔ ⎨f x( ) > 0 ⎪⎩g x( ) > 0.
В двух последних утверждениях одно из неравенств (которое окажется сложнее) можно исключить.
В пп. 9.2 и 9.3 учебника и в пп. 33 и 34 дидактических материалов приведено достаточно много примеров, иллюстрирующих сформулированные утверждения.
Надо обратить особое внимание на утверждение 5 из
п. 9.3:
⎡⎧f x1 ( ) = 0
1 2 ⎢⎢⎨⎩x ∈ D (f2) f ( )x ⋅ f ( )x = 0 ⇔
⎢⎧⎨xf2 ( )∈xD=( )f01
⎢⎣⎩
и привести достаточное число примеров на его применение.
Пример 1. Решим уравнение
![]() lg (3 − x) 5
+ 4x − x2 = 0. (3)
lg (3 − x) 5
+ 4x − x2 = 0. (3)
Решение. Уравнение (3) равносильно совокупности двух систем
⎧lg (3 − x) = 0 ⎧5 + 4x − x2 = 0 ⎨⎩5 + 4x − x2 ≥ 0 и ⎨⎩3 − x > 0.
Первая система имеет единственное решение х1 = 2, и вторая также имеет единственное решение х2 = −1. Объединив эти решения, получим все решения уравнения (3): 2 и −1.
Обратим внимание и на правильность применения утверждения 6 из п. 9.3:
f x( ) ⎧f x( ) = 0 ![]() g x( )
= 0 ⇔ ⎨⎩g
x( ) ≠ 0.
g x( )
= 0 ⇔ ⎨⎩g
x( ) ≠ 0.
Надо подчеркнуть, что условию g (x) ≠ 0 удовлетворяют все такие числа x0, каждое из которых удовлетворяет двум условиям:
1) выражение g (x0) определено; 2) число g (x0) не равно нулю.
Поэтому, найдя корни xi уравнения f (x) = 0, надо выбрать те из них, для которых выражение g (xi) определено, а затем из выбранных корней найти такие, для которых не равны нулю числа g (xi). Пример 2. Решим уравнение
x3 − 3x2 + 2x
![]() = 0. (4)
= 0. (4)
Решение. Уравнение (4) равносильно системе
⎧x3 − 3x2 + 2x = 0
⎨
![]() ⎩ x − 1 ≠ 0.
⎩ x − 1 ≠ 0.
![]()
![]() Уравнение системы имеет три
корня: х1 =
0, х2 =
1 и х3 =
2. Так как выражение x1 −
1 не определено, а выражение x2 − 1 определено,
но равно нулю, то числа х1 и х2 не являются
корнями уравнения (4). Так как выражение x3 − 1 определено и
не равно нулю, то число х3 является корнем уравнения (4).
Следовательно, уравнение (4) имеет единственный корень 2.
Уравнение системы имеет три
корня: х1 =
0, х2 =
1 и х3 =
2. Так как выражение x1 −
1 не определено, а выражение x2 − 1 определено,
но равно нулю, то числа х1 и х2 не являются
корнями уравнения (4). Так как выражение x3 − 1 определено и
не равно нулю, то число х3 является корнем уравнения (4).
Следовательно, уравнение (4) имеет единственный корень 2.
Решения и комментарии
Решите уравнение (9.26—9.32):
9.26. а) log2 (x − 2) + log2 (x − 3) = log2 (x2 − 5x + 6).
Решение. Применив утверждение из задания 9.24а, получим, что исходное уравнение равносильно системе
⎧⎨⎩xx −− 23 >> 00. (5)
Система (5), а значит, и равносильное ей исходное уравнение имеют множество решений (3; +∞).
9.28. а) | x2 − 4x + 2 | = −x2 + 6x − 6.
Решение. Применив утверждение из задания 9.25а, получим, что исходное уравнение равносильно совокупности двух систем:
⎧⎨⎩x2 2− 4x + 2 = −x2 + 6x − 6 и ⎧⎨x−2x2−+4x6x+−26=≥x20.− 6x + 6
−x + 6x − 6 ≥ 0 ⎩
![]() Первая
система имеет единственное решение х1 = 4, вторая система также имеет
единственное решение х2 =
2. Следовательно, исходное уравнение имеет два решения: 2 и 4. 9.30. в)
log5 x −
1 + 2x
− 2
= log5 x
+ 2x − 3.
Первая
система имеет единственное решение х1 = 4, вторая система также имеет
единственное решение х2 =
2. Следовательно, исходное уравнение имеет два решения: 2 и 4. 9.30. в)
log5 x −
1 + 2x
− 2
= log5 x
+ 2x − 3.
Решение. Применив утверждение из задания 9.25б, получим, что исходное уравнение равносильно совокупности двух систем
⎧log5 x − 1 = 0 ⎧2x − 2 = 0
⎨⎩2x − 2 ≥ 0 и ⎨⎩log5 x − 1 ≥ 0.
Первая система имеет единственное решение х1 = 5, а вторая система не имеет решений. Следовательно, исходное уравнение имеет единственное решение 5.
9.32. а) logx − 1 (x2 + 2x) = logx − 1 (2x2 − 8x + 16).
Решение. Применив утверждение из задания 9.24б, получим, что исходное уравнение равносильно системе
⎧x2 + 2x = 2x2 − 8x +16
⎪⎪x2 2+ 2x > 0
⎨2x − 8x +16 > 0 (6)
⎪x − 1 > 0
⎪⎩x − 1 ≠ 1.
Решив уравнение системы (6), получим, что оно имеет два корня: х1 = 8 и х2 = 2, из которых только число 8 удовлетворяет другим условиям системы (6). Следовательно, система (6), а значит, и равносильное ей исходное уравнение имеют единственное решение 8.
9.33. а) Сколько корней имеет уравнение
sin πx (lg (x + 5) + lg (400 − x)) = 0?
3
Решение. Применив утверждение 5, получим, что исходное уравнение равносильно совокупности двух систем:
⎧ sin πx = 0
⎪ 3 ⎧lg (x + 5) + lg (400 − x) = 0 ⎨ x + 5 > 0 и ⎨⎩x ∈ R.
⎪⎩ 400 − x > 0
Решениями первой системы являются все числа xk = 3k, k ∈ Z, удовлетворяющие двойному неравенству −5 < xk < 400. Таких чисел 135.
![]() 395 − 164021
395 − 164021
Вторая система имеет два решения: x1 =и
2
![]() 395
+ 164021
395
+ 164021
x2 =. Ни одно из них не содержится среди
2
чисел xk. Следовательно, исходное уравнение имеет 135 + 2 = 137 решений.
9.34. При каких значениях параметра a уравнение
x 1 2 x −
a + x + a = ![]() x2 −
a2 имеет единственный корень?
x2 −
a2 имеет единственный корень?
Решение. Перенеся все члены исходного уравнения в левую часть и сложив дроби, перепишем уравнение в виде x2 + (a + 1) x − (a + 2)
![]() 2 − a2 =
0. (7) x
2 − a2 =
0. (7) x
Уравнение (7) при каждом значении параметра а равносильно системе
⎧⎨⎩xx22 +− (aa2 +≠10).x − (a + 2) = 0 (8)
Уравнение системы (8) имеет два корня: х1 = 1 и х2 = −a − 2. При a = −3 эти корни совпадают, т. е. уравнение системы (8) имеет единственный корень 1, при этом x2 − a2 = −8 ≠ 0. Следовательно, при a = −3 система (8), а значит, и уравнение (7) имеют единственное решение х1 = 1.
При a ≠ −3 корни уравнения системы (8) различны, поэтому это уравнение имеет единственный корень лишь в том случае, если один из этих двух корней удовлетворяет неравенству системы (8), а второй нет. Следовательно, искомые значения a являются решениями совокупности двух систем:
⎧⎨1(a−+a22)= 0 ⎧⎪1 − a2 2≠−0a2 = 0
⎪ 2 − a2 ≠ 0 и ⎨(a + 2) ⎪⎩a ≠ −3 ⎪⎩a ≠ −3.
Так как a = 1 — единственное решение первой системы, а вторая система решений не имеет, то при a = 1 система (8), а значит, и уравнение (7) имеют единственное решение.
Итак, уравнение (7), а значит, и исходное уравнение имеют единственный корень при a = 1 и при a = −3.
Дополнение. В качестве дополнительных задач по изучаемой теме учащимся можно предложить задачи из ЕГЭ прошлых лет.
В2 (2004). Найдите сумму корней уравнения
(32x2 − 29 − 27)
Ответ. 0,4.
![]() В3 (2007). Решите уравнение x x
− 1 = 0.
В3 (2007). Решите уравнение x x
− 1 = 0.
(Если уравнение имеет более одного корня, то в ответе укажите сумму всех его корней.)
Решение. Перепишем исходное уравнение в виде
![]() x
− 1 (x2
− 4) = 0. (9)
x
− 1 (x2
− 4) = 0. (9)
Уравнение (9) равносильно совокупности двух систем:
![]() ⎧⎨⎩xx
− 1 = 0 и ⎧⎨xx2−−14≥=0.0 (10)
⎧⎨⎩xx
− 1 = 0 и ⎧⎨xx2−−14≥=0.0 (10)
∈ R ⎩
Первая система имеет единственное решение х1 = 1, вторая система также имеет единственное решение х2 = 2. Следовательно, совокупность (10) имеет два решения: 1 и 2, а равносильное ей исходное уравнение имеет два корня:
1 и 2, сумма которых равна 3.
Ответ. 3.
Промежуточный контроль. C—33, C—34.
![]() 9.4*. Уравнения вида f ( (x))
= f ( (x))
9.4*. Уравнения вида f ( (x))
= f ( (x))
В данном пункте учебника сформулированы два утверждения, с помощью которых решаются уравнения вида f (α (x)) = f (β (x)).
1. Пусть область существования функции f (u) есть промежуток М и пусть эта функция строго монотонна (т. е. возрастает или убывает) на этом промежутке. Тогда уравнение f (α (x)) = f (β (x)) равносильно системе
⎧⎪α ( )x = β ( )x
⎨α ( )x ∈ M
⎪⎩β ( )x ∈ M.
В этой системе второе или третье условие можно опустить.
2. Пусть R — область существования функции f (u) и пусть эта функция строго монотонна на R, тогда равносильны уравнения f (α (x)) = f (β (x)) и α (x) = β (x).
Решения и комментарии
Решите уравнение (9.38—9.42):
9.38. а) arcsin (x2 − 80,5) = arcsin (x − 8,5).
Решение. Рассмотрим функцию f (u) = arcsin u. Так как D (f) = [−1; 1] и на промежутке [−1; 1] функция f (u) возрастает, то по утверждению 1 исходное уравнение равносильно системе
⎧⎪x2 − 80 5, = x − 8 5,
⎨x − 8 5, ≥ −1 (1)
⎪⎩x − 8 5, ≤ 1.
![]()
![]() Система (1) имеет
единственное решение x1 =
9. Следовательно, равносильное ей исходное уравнение имеет единственный
корень 9. 9.39. а) log 0
5, tg x +
⎛⎜⎝ 31⎞⎟⎠ tg x− 7 tg x = log 0 5, ctg x + ⎝⎛⎜ 31⎟⎞⎠ ctg x− 7 ctg x.
Система (1) имеет
единственное решение x1 =
9. Следовательно, равносильное ей исходное уравнение имеет единственный
корень 9. 9.39. а) log 0
5, tg x +
⎛⎜⎝ 31⎞⎟⎠ tg x− 7 tg x = log 0 5, ctg x + ⎝⎛⎜ 31⎟⎞⎠ ctg x− 7 ctg x.
![]() ⎛ ⎞u
Решение. Рассмотрим функцию
⎛ ⎞u
Решение. Рассмотрим функцию ![]()
![]() − 7 u.
Так как D (f) =
(0; +∞)
и на промежутке (0; +∞)
функция f (u) убывает (как сумма трех убывающих на промежутке (0;
+∞)
функций), то по утверждению 1 исходное уравнение равносильно системе
− 7 u.
Так как D (f) =
(0; +∞)
и на промежутке (0; +∞)
функция f (u) убывает (как сумма трех убывающих на промежутке (0;
+∞)
функций), то по утверждению 1 исходное уравнение равносильно системе
⎧⎨⎩tgtg xx => 0.ctg x (2)
Система (2) имеет единственную серию решений xk = ![]()
![]() +
πk, k ∈
Z, поэтому равносильное ей исходное уравнение имеет ту же
серию решений
+
πk, k ∈
Z, поэтому равносильное ей исходное уравнение имеет ту же
серию решений ![]() k, k ∈ Z.
k, k ∈ Z.
9.42. а) ex ![]() x x x e
x x x x .
x x x e
x x x x .
![]() Решение.
Рассмотрим функцию f u
Решение.
Рассмотрим функцию f u![]() e u. Так как D (f) = R и на
промежутке R функция f (u) возрастает (как сумма
двух возрастающих на промежутке R функций), то по утверждению 2
исходное уравнение равносильно уравнению
e u. Так как D (f) = R и на
промежутке R функция f (u) возрастает (как сумма
двух возрастающих на промежутке R функций), то по утверждению 2
исходное уравнение равносильно уравнению
x2 − 4x + 5 = 2x2 − 3x + 7. (3)
Уравнение (3) не имеет корней, поэтому и равносильное ему исходное уравнение не имеет корней.
Дополнение. Отметим, что существуют уравнения, для решения которых недостаточно утверждений 1 и 2. Они могут быть решены с помощью следующего утверждения:
3. Пусть функция f (u) строго монотонна на промежутке М. Тогда равносильны две системы:
⎧⎪f (α ( ))x = f (β ( ))x ⎧⎪α ( )x = β ( )x
⎨α ( )x ∈ M и ⎨α ( )x ∈ M ⎪⎩β ( )x ∈ M ⎪⎩β ( )x ∈ M.
Пример 1. Решим уравнение
(x2 + 4x − 3)10 + (x2 + 4x − 3)22 = (x + 1)10 + (x + 1)22. (4)
Решение. Если рассмотреть функцию f1 (u) = u10 + u22, то на всей своей области существования R она не является строго монотонной, поэтому для нее неприменимо ни одно из утверждений 1—3. Однако, если обозначить α (x) = (x2 + 4x − 3)2, β (x) = (x + 1)2, f (u) = u5 + u11, то получим, что α (x) ≥ 0 и β (x) ≥ 0 для любого х ∈ R, поэтому уравнение (4) равносильно системе
⎧⎪f (α ( ))x = f (β ( ))x
⎨α ( )x ≥ 0 (5)
⎪⎩β ( )x ≥ 0.
Функция f (u) на промежутке М = [0; +∞) возрастает. Поэтому на основании утверждения 3 система (5) равносильна системе
⎧⎪α ( )x = β ( )x
⎨α ( )x ≥ 0 (6)
⎪⎩β ( )x ≥ 0.
Так как α (x) ≥ 0 и β (x) ≥ 0 для любого х ∈ R, то система (6) равносильна уравнению α (x) = β (x), т. е. уравнению
(x2 + 4x − 3)2 − (x + 1)2 = 0. (7)
Следовательно, исходное уравнение (4) равносильно уравнению (7). Переписав уравнение (7) в виде
(x2 + 3x − 4) (x2 + 5x − 2) = 0,
![]() −5 − 33
−5 − 33
найдем его корни х1 = 1, х2 = −4, x3 =и
2
![]() −5 + 33
−5 + 33
x4 =. Следовательно, исходное уравнение имеет
2
![]() −5 − 33 −5 + 33
−5 − 33 −5 + 33
четыре корня: 1, −4, , .
2 2
Пример 2 (МГУ, биофак, олимпиада, 2006). Решим уравнение
32 arcsin (2 x+ 1) + log (3 2 arcsin (2x +1)) =
= 3arccos 3![]() −42 x + log3 ⎜⎝⎛arccos 3
−42 x + log3 ⎜⎝⎛arccos 3![]() −42x⎞⎟⎠. (8)
−42x⎞⎟⎠. (8)
Решение. Рассмотрим функцию f (u) = 3u + log3 u. Так как D (f) = (0; +∞) и на промежутке (0; +∞) функция f (u) возрастает, то по утверждению 1 уравнение (8) равносильно системе
⎧⎪α ( )x = β ( )x
⎨α ( )x > 0 (9)
⎪⎩β ( )x > 0,
3 − 2x
где α (x) = 2 arcsin (2x + 1), β ( )x = arccos ![]() .
.
4
По определению арксинуса и арккосинуса систему (9) можно переписать в виде ⎧⎪α ( )x = β ( )x
⎨0 < α ( )x ≤ π (10)
⎪⎩0 < β ( )x ≤ π.
Функция g (u) = cos u на промежутке (0; π] убывает, поэтому по утверждению 3 система (10) равносильна системе
⎧⎪cosα ( )x = cosβ ( )x
⎨0 < α ( )x ≤ π (11)
⎪⎩0 < β ( )x ≤ π.
Так как при α (x) ∈ (0; π] и β (x) ∈ (0; π] имеем
x
![]()
![]() ,
, ![]() ,
,
то систему (11) можно переписать в виде
⎧
1 − 2
2( x +1)2
= 3![]() −
2x
−
2x
⎪ 4
⎨ 0 < α ( )x ≤ π (12)
⎪⎩ 0 < β ( )x ≤ π.
Уравнение системы (12) имеет два корня: x1 = − ![]()
![]() и x2 = −
и x2 = − ![]()
![]() . Так как α (x1) = 2 arcsin 0, то число x1
не удовлетворяетнеравенству системы (12). Так как α (x2) = 2 arcsin
. Так как α (x1) = 2 arcsin 0, то число x1
не удовлетворяетнеравенству системы (12). Так как α (x2) = 2 arcsin ![]()
![]() и β
(x2) =
arccos
и β
(x2) =
arccos ![]()
![]() , то число x2
удовлетворяет обоим неравенствам системы (12). Следовательно, система
(12), а значит, и равносильное ей уравнение (8) имеют единственный корень −
, то число x2
удовлетворяет обоим неравенствам системы (12). Следовательно, система
(12), а значит, и равносильное ей уравнение (8) имеют единственный корень − ![]()
![]() .
.
Промежуточный контроль. C—35.
9.6. Решение неравенств с помощью систем (продолжение)
В п. 7.2 изучалось решение неравенств при помощи равносильных преобразований. В пп. 9.5 и 9.6 будет изучаться решение неравенств при помощи неравносильных преобразований. Следует отметить, что в учебнике не рассматривается понятие неравенства-следствия. Поэтому в отличие от уравнений для неравенств нет перехода к следствию.
В § 9 рассматривается решение неравенств при помощи перехода от неравенства к системе, равносильной этому неравенству. Другой способ решения неравенств рассматривается в § 11.
В пп. 9.5 и 9.6 сформулированы семь утверждений о равносильности неравенства системе, а в задании 9.52 — еще три утверждения. Следует отметить, что в § 10 и 12 будут приведены еще и другие утверждения о равносильности неравенства системе.
Можно рекомендовать учащимся запомнить наиболее употребляемые равносильные переходы (m ∈ N):
1. ![]()
2m⎧⎪f x( ) < (g x( ))2m
2. ![]() а) f x( ) < g x( ) ⇔ ⎨f x(
) ≥ 0
а) f x( ) < g x( ) ⇔ ⎨f x(
) ≥ 0
⎪⎩g x( ) > 0;
⎡⎧f x( ) > (g x( ))2m
![]() б) 2m f x( ) > g x( ) ⇔ ⎢⎢⎨⎩g x( ) ≥ 0
б) 2m f x( ) > g x( ) ⇔ ⎢⎢⎨⎩g x( ) ≥ 0
⎢⎧⎨f xg x( )( ) ≥<00.
⎢⎣⎩
3. а) loga f (x) < loga g (x) ⇔ 0 < f (x) < g (x), если а > 1; б) loga f (x) < loga g (x) ⇔ 0 < g (x) < f (x), если 0 < а < 1.
В пп. 9.5 и 9.6 учебника и в пп. 36 и 37 дидактических материалов приведено достаточно много примеров применения этих утверждений.
Решения и комментарии
Решите неравенство (9.47—9.64):
9.47. а) 8 x2 + x ≥ 8 5x − 4 + x.
![]() Решение.
Исходное неравенство равносильно совокупности уравнения
Решение.
Исходное неравенство равносильно совокупности уравнения
8 x2 + x = 8 5x − 4 + x (1)
и неравенства
8 x2 + x > 8 5x − 4 + x. (2)
Уравнение (1) равносильно системе
⎧x2 + x = 5x − 4 + x (3)
⎨ 2
⎩x + x ≥ 0.
Система (3) имеет два решения: x1 = 1 и x2 = 4. Следовательно, и равносильное ей уравнение (1) имеет два корня: x1 = 1 и x2 = 4.
Неравенство (2) равносильно системе
![]()
![]() ⎧⎨x2
+ x > 5x − 4 + x (4)
⎧⎨x2
+ x > 5x − 4 + x (4)
⎩5x − 4 + x ≥ 0.
Все решения первого неравенства системы (4) составляют два промежутка: [0; 1) и (4; +∞). Все решения второго
⎡16 +∞⎞⎟⎠. неравенства системы (4) составляют промежуток ⎢⎣25 ;
Следовательно, множество решений системы (4), а значит,
⎡16 ⎞ ∪ (4; +∞). и равносильного ей неравенства (2) есть ⎢⎣25 ; 1⎟⎠
Объединив все найденные решения, получим множе-
⎡16 ⎤ ∪ [4; +∞). ство решений исходного неравенства: ⎢⎣25 ; 1⎥⎦
9.50. а) ![]() .
.
Решение. Перепишем исходное неравенство в виде
![]() . (5) Неравенство (5) по утверждению
5 учебника равносильно системе
. (5) Неравенство (5) по утверждению
5 учебника равносильно системе
⎧⎪9x − 10 3⋅ x − 1 +1 < 0
⎨⎪⎩ π2x ≠ πk k, ∈ Z. (6)
Все решения первого неравенства системы составляют промежуток (−1; 1). Из этих чисел лишь число 0 не удовлетворяет второму условию системы (6), поэтому все решения системы (6), а значит, и равносильного ей исходного неравенства составляют два промежутка: (−1; 0) и (0; 1).
9.57. а) ![]()
![]() > 0.
> 0.
Решение. Исходное неравенство по утверждению 6 учебника равносильно совокупности двух систем:
⎧log (2 x − 3) > 0 ⎧log (2 x − 3) < 0
⎨⎩log 0,5 (x + 2) > 0 и ⎨⎩log 0,5 (x + 2) < 0. (7)
Первая система совокупности (7) не имеет решений. Все решения второй системы совокупности (7) составляют промежуток (3; 4). Следовательно, совокупность систем и равносильное ей исходное неравенство имеют множество решений (3; 4).
9.58. а) | x + 1 | < x2 − 2x + 1.
Решение. По утверждению из задания 9.52а исходное неравенство равносильно двойному неравенству
−x2 + 2x − 1 < x + 1 < x2 − 2x + 1,
которое можно записать в виде системы
⎧−x2 + 2x − 1 < x +1 ⎨⎩x +1 < x2 − 2x +1. Эта система имеет множество решений (−∞; 0) ∪ (3; +∞). Следовательно, исходное неравенство, равносильное этой системе, имеет то же множество решений (−∞; 0) ∪ (3; +∞).
9.62. а) logx (9x + 1) < logx | 10x − 1 |.
Решение. По утверждению из задания 9.52в исходное неравенство равносильно совокупности двух систем:
⎧⎩⎨0x <> 91x +1 < |10x − 1| и ⎧⎨⎩09x<+x1<>1|.10x − 1| > 0 (8)
Учитывая неравенство x > 1, получим, что первая система совокупности (8) равносильна системе
⎧9x +1 < 10x − 1
⎨⎩x > 1,
имеющей множество решений (2; +∞).
Так как число x = 0,1 не является решением второй системы совокупности (8), то эта система равносильна совокупности двух систем:
⎧⎨⎩9x +1 > −10x +1 и ⎧⎨90 1x, +<1x><101.x − 1 (9)
Первая система совокупности (9) имеет множество решений (0; 0,1). Вторая система совокупности (9) имеет множество решений (0,1; 1). Следовательно, исходное неравенство, равносильное совокупности систем (8), имеет множество решений (0; 0,1) ∪ (0,1; 1) ∪ (2; +∞).
9.64. а) logx ![]() logx
logx
![]() .
.
Решение. По утверждению из задания 9.52в исходное неравенство равносильно совокупности двух систем:
![]()
![]() ⎧⎪⎨ 88xx+−137 ≥ 814xx+−139 > 0 и ⎧⎨⎪0
< 68xx+−117 ≤ 814xx+−139 (10)
⎧⎪⎨ 88xx+−137 ≥ 814xx+−139 > 0 и ⎧⎨⎪0
< 68xx+−117 ≤ 814xx+−139 (10)
⎪⎩x > 1 ⎪⎩0 < x < 1.
Первая система совокупности (10) не имеет решений. Вторая система совокупности (10) имеет множество решений
⎛ 7 ⎞
⎜⎝ 8 ; 1⎟⎠. Следовательно, исходное неравенство, равносильное совокупности систем (10), имеет множество решений ⎜⎝⎛ 78 ; 1⎞⎟⎠.
![]() 9.65.
При каких значениях параметра a все решения неравенства x − 2a > 4 − x содержатся
в интервале (0; 5)? Решение. По утверждению 3 учебника при каждом
значении a это неравенство равносильно двойному неравенству x − 2a > 4 − x ≥ 0, которое
можно переписать в виде
9.65.
При каких значениях параметра a все решения неравенства x − 2a > 4 − x содержатся
в интервале (0; 5)? Решение. По утверждению 3 учебника при каждом
значении a это неравенство равносильно двойному неравенству x − 2a > 4 − x ≥ 0, которое
можно переписать в виде
a + 2 < x ≤ 4. (11)
Двойное неравенство (11), а значит, и исходное неравенство имеют решения, если a + 2 < 4, т. е. при каждом a < 2. Эти решения содержатся в интервале (0; 5), если выполняется условие a + 2 ≥ 0, т. е. при каждом a ∈ [−2; 2). Следовательно, все решения исходного неравенства содержатся в интервале (0; 5) при каждом a ∈ [−2; 2).
Промежуточный контроль. C—36, C—37.
![]() 9.7*. Неравенства вида f ( (x)) f
( (x))
9.7*. Неравенства вида f ( (x)) f
( (x))
В данном пункте учебника сформулированы утверждения, с помощью которых решаются неравенства вида f (α (x)) > f (β (x)). В п. 9.7 учебника и в п. 38 дидактических материалов содержится достаточное число примеров на применение этих утверждений.
Решения и комментарии
Решите неравенство (9.70—9.71):
9.70. а) arcsin (x2 − 2x) < arcsin (x2 + x − 1).
Решение. Рассмотрим функцию f (u) = arcsin u. Так как D (f) = [−1; 1] и на промежутке [−1; 1] функция f (u) возрастает, то исходное неравенство равносильно системе
⎧x2 − 2x < x2 + x − 1
⎪ 2
⎨−1 ≤ x − 2x ≤ 1 (1)
⎪⎩−1 ≤ x2 + x − 1 ≤ 1.
Система (1) имеет множество решений ⎜⎝⎛31 ; 1⎤⎥⎦, следовательно, равносильное ей исходное неравенство имеет то же множество решений ⎜⎝⎛31 ; 1⎤⎥⎦.
![]()
![]() 9.71.
а) log (2 x − 3) +10log2 (x−
3 ) < log (2 x2 − 3x) +10log2 (x2 − 3x).
9.71.
а) log (2 x − 3) +10log2 (x−
3 ) < log (2 x2 − 3x) +10log2 (x2 − 3x).
Решение. Рассмотрим функцию f u( ) = u +10u. Так как
D (f) = [0; +∞) и на промежутке [0; +∞) функция f (u) возрастает (как сумма двух возрастающих на промежутке [0; +∞) функций), то исходное неравенство равносильно системе
⎧⎪log (2 x − 3) < log (2 x2 − 3x)
⎨log (2 x − 3) ≥ 0 (2)
⎪⎩log (2 x2 − 3x) ≥ 0.
Система (2) имеет множество решений [4; +∞), поэтому равносильное ей исходное неравенство имеет то же множество решений [4; +∞).
Промежуточный контроль. C—38.
|
§10. |
Равносильность уравнений на множествах
В данном параграфе будет продолжено рассмотрение неравносильных преобразований уравнений, будет рассмотрен еще один способ решения уравнений — переход к уравнению, равносильному исходному уравнению на некотором множестве М. Этот способ рекомендуется основательно изучать лишь в классах с углубленным изучением математики, так как его применение требует не выполнения заученного алгоритма, а больших логических усилий, так как каждый раз учащимся предстоит осмысленный выбор того множества, на котором будет проводиться преобразование уравнения.
Переход от исходного уравнения к уравнению, равносильному ему на некотором множестве, применяется еще при решении уравнений с модулями в § 12.
В данном пункте учебника вводятся понятия уравнений, равносильных на множестве M, равносильного перехода на множестве M от одного уравнения к другому и равносильного преобразования уравнения на множестве M. Далее указаны пять основных преобразований, приводящих уравнение к равносильному ему на некотором множестве уравнению. В следующих пунктах этого параграфа эти преобразования рассмотрены подробно.
Решения и комментарии
10.2. Определите множество, на котором равносильны уравнения: x x
![]()
![]() а) и
x2 + x
− 2 = 0; б) x
= 1 и x2
= 1;
а) и
x2 + x
− 2 = 0; б) x
= 1 и x2
= 1;
в) x3 + 2x2 − 1 = 0 и x (x3 + 2x2 − 1) = 0;
г) x2 + 5x + x = x − 4 и x2 + 5x + 4 = 0;
д) lg (x2 − 1) = lg x и x2 − 1 = x.
Решение. а) Эти уравнения равносильны при условии x + 2 ≠ 0, т. е. на множестве M = (−∞; −2) ∪ (−2; +∞).
б) Эти уравнения равносильны при условии x ≥ 0, т. е.
на множестве M = [0; +∞).
в) Эти уравнения равносильны при условии x > 0, т. е. на множестве M = (0; +∞).
г) Эти уравнения равносильны при условии x ≥ 0,
т. е. на множестве M = [0; +∞).
д) Эти уравнения равносильны при условиях x2 − 1 > 0
и x > 0, т. е. на множестве M = (1; +∞).
Дополнение. При решении уравнений полезно еще одно определение, не сформулированное в учебнике. Пусть дано уравнение
f (x) = g (x), (1)
совокупность уравнений
⎡f x1 ( ) = g1 ( )x
⎢... (2)
⎢⎣fn ( )x = gn ( )x
и множество M значений неизвестного x. Если любой корень уравнения (1), принадлежащий множеству M, является корнем хотя бы одного из уравнений совокупности (2), а любой корень каждого из уравнений совокупности (2), принадлежащий множеству M, является корнем уравнения (1), то говорят, что уравнение (1) и совокупность (2) равносильны на множестве М.
![]() Например, уравнение x +1 ⋅ lg (2 − x) ⋅ tg x = 0 равно-
Например, уравнение x +1 ⋅ lg (2 − x) ⋅ tg x = 0 равно-
сильно на множестве M = ⎡⎢⎣−1; 2π⎞⎟⎠ ∪ ⎛⎜⎝ 2π ; 2⎞⎟⎠ совокупности трех уравнений
![]() ⎡ x +1 = 0
⎡ x +1 = 0
⎢⎢lg (2 − x) = 0 ⎢⎣tg x = 0.
Этим определением можно воспользоваться при решении ряда уравнений из пп. 10.4 и 10.5.
В этом пункте учебника сформулировано утверждение: уравнения f (x) = g (x) и (f (x))2m = (g (x))2m, где m ∈ N, равносильны на том множестве, где f (x) ≥ 0 и g (x) ≥ 0. Это утверждение применяется прежде всего для решения иррациональных уравнений. В п. 10.2 учебника и в п. 39 дидактических материалов приведены примеры использования этого утверждения. Приведем еще один пример. Пример 1. Решим уравнение
![]() 8
2 − x
= 4 x
− 1. (1)
8
2 − x
= 4 x
− 1. (1)
![]()
![]() Решение. Все корни
уравнения (1) содержатся среди x, удовлетворяющих неравенствам 2 − x ≥ 0 и x − 1 ≥ 0, т. е.
содержатся в множестве M =
[1; 2]. Поэтому надо решить уравнение (1) на этом множестве. На
множестве M обе функции f x( ) =
8 2 −
x и g x( ) =
4 x −
1 определены и неотрицательны, поэтому на этом множестве уравнение (1)
равносильно уравнению
Решение. Все корни
уравнения (1) содержатся среди x, удовлетворяющих неравенствам 2 − x ≥ 0 и x − 1 ≥ 0, т. е.
содержатся в множестве M =
[1; 2]. Поэтому надо решить уравнение (1) на этом множестве. На
множестве M обе функции f x( ) =
8 2 −
x и g x( ) =
4 x −
1 определены и неотрицательны, поэтому на этом множестве уравнение (1)
равносильно уравнению
2 − x = (x − 1)2. (2)
1
![]()
![]() + 5 1 − 5
+ 5 1 − 5
Уравнение (2) имеет два корня: x1 =и x2 =,
2 2
из них множеству M принадлежит только число x1. Поэтому уравнение (2) на множестве M имеет единственный корень x1. Следовательно, и равносильное ему на множестве M уравнение (1) имеет тот же единственный корень
![]() 1 + 5
1 + 5
.
2
Обратим внимание на то, что это утверждение применяется и при решении уравнений с модулями (см. пример 2 из учебника). Приведем еще один пример. Пример 2. Решим уравнение
| 2x2 − 4x − 1 | = | x2 − 3x + 1 |. (3)
Решение. Обе функции f (x) = | 2x2 − 4x − 1 | и g (x) = = | x2 − 3x + 1 | неотрицательны для каждого x ∈ R. Поэтому уравнение (3) равносильно уравнению
(2x2 − 4x − 1)2 = (x2 − 3x + 1)2,
которое можно переписать в виде
(2x2 − 4x − 1)2 − (x2 − 3x + 1)2 = 0
или в виде
(3x2 − 7x) (x2 − 2x − 2) = 0. (4)
Уравнение(4) имеет четыре корня: х1 = −1, х2
= 0, х3
= 2 и x4
= ![]() .
Следовательно, и уравнение (3), равносильное уравнению (4), имеет те же четыре
корня: х1 =
−1, х2 =
0, х3 =
2 и x4
=
.
Следовательно, и уравнение (3), равносильное уравнению (4), имеет те же четыре
корня: х1 =
−1, х2 =
0, х3 =
2 и x4
= ![]() .
.
Решения и комментарии
Решите уравнение (10.8—10.9):
![]() 10.8.
а) −2x
= x +1.
10.8.
а) −2x
= x +1.
![]() Решение.
Все корни исходного уравнения содержатся в множестве M, состоящем из
чисел, удовлетворяющих неравенствам −2x
≥ 0 и x
+ 1 ≥ 0, т. е.
содержатся в множестве M =
[−1;
0]. Поэтому надо решить исходное уравнение на этом множестве. На множестве M
обе функции f x( ) =
−2x и g (x) =
x + 1
определены и неотрицательны, следовательно, на этом множестве исходное
уравнение равносильно уравнению
Решение.
Все корни исходного уравнения содержатся в множестве M, состоящем из
чисел, удовлетворяющих неравенствам −2x
≥ 0 и x
+ 1 ≥ 0, т. е.
содержатся в множестве M =
[−1;
0]. Поэтому надо решить исходное уравнение на этом множестве. На множестве M
обе функции f x( ) =
−2x и g (x) =
x + 1
определены и неотрицательны, следовательно, на этом множестве исходное
уравнение равносильно уравнению
−2x = (x + 1)2. (5)
![]()
![]() Уравнение (5) имеет два
корня: x1 =
−2 +3
и x2 =
−2 −3,
из них множеству M принадлежит только число x1.
Поэтому уравнение (5) на множестве M имеет единственный корень x1.
Следовательно, и равносильное ему на множестве M исходное уравнение
имеет тот же единственный корень −2
+ 3.
Уравнение (5) имеет два
корня: x1 =
−2 +3
и x2 =
−2 −3,
из них множеству M принадлежит только число x1.
Поэтому уравнение (5) на множестве M имеет единственный корень x1.
Следовательно, и равносильное ему на множестве M исходное уравнение
имеет тот же единственный корень −2
+ 3.
![]() 10.9.
а) 2 −
2 sin x = 1.
10.9.
а) 2 −
2 sin x = 1.
2
Решение. Так как для любого x ∈ R число
2 − 2 sin x ≥ 0, то обе части исходного уравнения неотри-
2 цательны для любого x ∈ R, поэтому это уравнение равно-
сильно уравнению 2 − 2 sin x = 1, которое имеет две серии
2
решений: ![]() k и
k и ![]() k,
k ∈ Z.
Следовательно, и равносильное ему исходное уравнение имеет те же две серии
решений:
k,
k ∈ Z.
Следовательно, и равносильное ему исходное уравнение имеет те же две серии
решений: ![]() k, k ∈ Z.
k, k ∈ Z.
В этом пункте учебника сформулировано и доказано утверждение об умножении уравнения на функцию и приведены примеры применения этого утверждения.
Умножение уравнения на функцию весьма «коварное» преобразование. При его применении возможны и потеря корней исходного уравнения, и приобретение посторонних корней, не являющихся корнями исходного уравнения.
Например, уравнение
x2 − 2x − 3 = 0 (1)
имеет два корня: x1 = −1 и x2 = 3, а уравнение
![]() x
− 2 (x2
− 2x
− 3) = 0, (2)
x
− 2 (x2
− 2x
− 3) = 0, (2)
полученное из уравнения (1) умножением его на функцию
![]() ϕ ( )x = x − 2, также имеет
два корня: x3 =
2 и x4 =
3.
ϕ ( )x = x − 2, также имеет
два корня: x3 =
2 и x4 =
3.
Итак, при переходе от уравнения (1) к уравнению (2) был потерян корень x1 = −1 и приобретен посторонний для исходного уравнения корень x3 = 2. Следовательно, необдуманное умножение уравнения на функцию может стать причиной ошибки.
В то же время есть уравнения, которые решаются именно с помощью преобразования — умножения уравнения на функцию. Например, освобождение уравнения от знаменателя, уже рассмотренное выше, есть преобразование умножения уравнения на функцию (на знаменатель). Однако есть уравнения, для решения которых применяют умножение на функцию, хотя сам вид уравнения этого не предусматривает.
Например, для решения уравнения
16 cos x cos 2x cos 4x cos 8x = 1
его надо умножить на функцию ϕ (x) = sin x (пример 3, с. 272 учебника).
Чтобы избежать ошибок, надо обязательно выяснить, не обращается ли в нуль на рассматриваемом множестве функция, на которую умножается уравнение. Пример 1. Решим уравнение
4x + 6 ⋅ 9x = 5 ⋅ 6x. (3)
Решение. Обе части уравнения (3) имеют смысл на
множестве всех x ∈
R. Кроме того, функция ϕ
(x) = 9x
не равна нулю для каждого x ∈
R. Поэтому, разделив уравнение (3) на функцию ϕ (x) (т.
е. умножив ее на функцию ![]()
![]() ), по-
), по-
лучим уравнение ⎛⎜⎝ 23 ⎞⎟⎠ 2 x− 5 ⎛⎜⎝ 23 ⎞⎟⎠ x+ 6 = 0, равносильное уравнению (3).
Так как уравнение у2 − 5у + 6 = 0 имеет два корня: у1 = 2 и у2 = 3, то только все решения двух уравнений
⎛⎜⎝ 23 ⎞⎟⎠ x= 2 и ⎛⎜⎝ 23 ⎠⎞⎟ x= 3 являются решениями уравнения (3). Ре-
шив эти уравнения, получим, что уравнение (3) имеет два корня: x1 = log 2 2 и x2 = log 2 3.
3 3
Решения и комментарии
Решите уравнение (10.14—10.19):
![]() 3 5 1
3 5 1
10.14. а) + = .
(2x + 6)(x − 1) (3x + 5)(x − 1) x − 1
Решение. Все корни исходного уравнения содержатся в
множестве M, состоящем из чисел x, удовлетворяющих условиям x ≠ 1, x ≠ −3 и x![]() .
На этом множестве функ-
.
На этом множестве функ-
ция f x( ) = 6 (x + 3) ⎛⎜⎝x + 53 ⎞⎟⎠ (x − 1) определена и отлична от
нуля, следовательно, умножив на функцию f (x) исходное уравнение, получим, что на множестве M исходное уравнение равносильно уравнению
9 ⎜⎝⎛x + 53 ⎞⎟⎠ +10 (x + 3) = 6 (x + 3) ⎜⎛⎝x + 53 ⎠⎞⎟. (4)
Уравнение (4) имеет два корня: x1 = −2,5 и x2 = 1, из которых только число −2,5 принадлежит множеству M. Следовательно, исходное уравнение, равносильное на множестве М уравнению (4), имеет тот же единственный корень −2,5.
2 4 8 x16 + x2 −5x + 3
10.16. а) (x + 1) (x + 1) (x + 1) (x + 1) = ![]() . x − 1
. x − 1
Решение. Все корни исходного уравнения содержатся в множестве M, состоящем из чисел, удовлетворяющих условию x ≠ 1. На этом множестве функция f (x) = x − 1 определена и отлична от нуля. Следовательно, исходное уравнение равносильно на множестве M уравнению
(x − 1) (x + 1) (x2 + 1) (x4 + 1) (x8 + 1) = x16 + x2 − 5x + 3.
Применив четыре раза формулу разности квадратов и перенеся все члены уравнения в одну часть, перепишем это уравнение в виде
x2 − 5x + 4 = 0. (5)
Уравнение (5) имеет два корня: x1 = 4 и x2 = 1, из которых только число 4 принадлежит множеству M. Следовательно, исходное уравнение, равносильное на множестве М уравнению (5), имеет единственный корень 4.
10.17. а) (x − 1) (x2 + 1) (x4 + 1) = x7.
Решение. Число x = −1 не является корнем исходного уравнения. Поэтому все корни исходного уравнения содержатся в множестве M всех x, кроме x = −1. На этом множестве функция ϕ (x) = x + 1 определена и отлична от нуля. Поэтому исходное уравнение равносильно на множестве M уравнению
(x + 1) (x − 1) (x2 + 1) (x4 + 1) = x7 (x + 1). (6)
Применив три раза формулу разности квадратов, раскрыв скобки в правой части уравнения и перенеся все члены уравнения в одну часть, перепишем уравнение (6) в виде x7 + 1 = 0. (7)
Уравнение (7) имеет единственный корень x1 = −1, который не принадлежит множеству M. Следовательно, исходное уравнение, равносильное на множестве М уравнению (7), не имеет корней.
2 sin x
![]() 10.19. а) = .
10.19. а) = .
−x2 + 4x − 3 −x2 + x −
![]() Решение.
Все корни исходного уравнения содержатся в множестве M, состоящем из
чисел, удовлетворяющих условию −x2
+ 4x − 3 > 0, т. е. в
множестве M = (1;
3). В каждой точке этого множества функция f x( ) = −x2
+ 4x − 3 определена и
отлична от нуля, следовательно, исходное уравнение равносильно на множестве M
уравнению
Решение.
Все корни исходного уравнения содержатся в множестве M, состоящем из
чисел, удовлетворяющих условию −x2
+ 4x − 3 > 0, т. е. в
множестве M = (1;
3). В каждой точке этого множества функция f x( ) = −x2
+ 4x − 3 определена и
отлична от нуля, следовательно, исходное уравнение равносильно на множестве M
уравнению
2 sin x = 1.(8)
Уравнение (8) имеет две серии решений: ![]()
![]() +
2πn,
n ∈ Z
и
+
2πn,
n ∈ Z
и ![]()
![]() + 2πk, k ∈ Z.
Из этих чисел множеству М принадлежит лишь число
+ 2πk, k ∈ Z.
Из этих чисел множеству М принадлежит лишь число ![]()
![]() . Следовательно, исходное
уравнение, равносильное уравнению (8) на множестве М, имеет тот же
единственный корень
. Следовательно, исходное
уравнение, равносильное уравнению (8) на множестве М, имеет тот же
единственный корень ![]()
![]() .
.
В данном пункте учебника сформулированы утверждения о потенцировании и логарифмировании уравнений, о приведении подобных членов и о применении формул. Приведены примеры применения этих утверждений при решении уравнений.
Обратим внимание на утверждение 1 из учебника.
Пусть число a таково, что a > 0 и a ≠ 1, и пусть в каждой точке множества М обе функции f (x) и ϕ (x) определены и положительны. Тогда на множестве М равносильны уравнения
loga f (x) = loga ϕ (x) (1)
и
f (x) = ϕ (x). (2)
Переход от уравнения (1) к уравнению (2) называют потенцированием логарифмического уравнения (1), а переход от уравнения (2) к уравнению (1) называют логарифмированием уравнения (2). Потенцирование уравнения совершают часто, и его можно применять, используя либо переход к уравнению-следствию (п. 8.3), либо переход к системе, равносильной исходному уравнению (п. 9.2), либо переход к уравнению, равносильному исходному на некотором множестве (этот способ и предусматривался в этом пункте). Соответствующие примеры разобраны в п. 10.4 учебника и в п. 40 дидактических материалов.
Логарифмирование уравнения — новый способ решения уравнений. На его усвоение надо затратить достаточно много усилий. В данном пункте учебника разобран пример применения логарифмирования уравнения. Приведем еще один пример.
Пример 1. Решим уравнение
![]() (2 + sin x) 6 + x − x2 = 1. (3)
(2 + sin x) 6 + x − x2 = 1. (3)
Решение. Все корни уравнения (3) содержатся в множестве М, состоящем из чисел, удовлетворяющих условию 6 + x − x2 ≥ 0, т. е. в множестве М = [−2; 3].
![]() В
каждой точке множества М обе функции f (x) = 1 и ϕ ( )x = (2 + sin x) 6 + x − x2 определены
и положительны. Поэтому, логарифмируя уравнение (3), получим, что оно
равносильно на множестве М уравнению
В
каждой точке множества М обе функции f (x) = 1 и ϕ ( )x = (2 + sin x) 6 + x − x2 определены
и положительны. Поэтому, логарифмируя уравнение (3), получим, что оно
равносильно на множестве М уравнению
![]() 6 + x − x2 lg
(2 + sin x)
= 0. (4)
6 + x − x2 lg
(2 + sin x)
= 0. (4)
Уравнение (4) имеет на множестве М три корня: x1
= −2,
x2 = 3
и x3 =
− ![]()
![]() . Следовательно,
и равносильное уравнению (4) уравнение (3) имеет те же три корня: −2, −
. Следовательно,
и равносильное уравнению (4) уравнение (3) имеет те же три корня: −2, − ![]()
![]() и 3.
и 3.
Обратим также внимание и на утверждение 3 из учебника.
Пусть в каждой точке множества М определены обе части некоторой формулы (логарифмической, тригонометрической и т. п.). Тогда, применив эту формулу при решении уравнения, получим уравнение, равносильное на множестве М исходному уравнению.
На применение этого утверждения приведено достаточно много примеров в п. 10.4 учебника и в п. 39 дидактических материалов. Отметим, что утверждение 3 более понятно, чем аналогичное утверждение в п. 8.4 — при переходе к уравнению-следствию. Оно лучше усваивается учащимися. Приведем еще один пример.
Пример 2 (ЕГЭ, 2008, тренировочный вариант). Решим уравнение
2x + 1
x (2x +1) + 2x+1 = 0. (5) x
![]() Решение. Все корни
уравнения (5) содержатся среди x, 2x + 1
Решение. Все корни
уравнения (5) содержатся среди x, 2x + 1
удовлетворяющих неравенству ≥ 0, т. е. содержатся x = ⎛⎜⎝−∞; − 21⎤⎥⎦ ∪ (0; +∞). Поэтому надо рев множестве M
шить уравнение (5) на каждом из множеств M1 = ⎛⎜⎝−∞; − 21⎤⎥⎦
и M2 = (0; +∞).
На множестве M1 определены обе части формулы
2x + 1
![]() −x = x (2x
+1) (положительный
множитель −x
вне-
−x = x (2x
+1) (положительный
множитель −x
вне-
x
![]() сен под знак корня). Поэтому
уравнение (5) равносильно на множестве M1 уравнению x (2x
+1) − 2 x (2x
+1) +1 = 0, которое можно
записать в виде
сен под знак корня). Поэтому
уравнение (5) равносильно на множестве M1 уравнению x (2x
+1) − 2 x (2x
+1) +1 = 0, которое можно
записать в виде
![]() (
x (2x +1)
− 1)2
= 0. (6)
(
x (2x +1)
− 1)2
= 0. (6)
Уравнение (6) равносильно на множестве M1 уравнению
x (2x + 1)
= 1, которое
имеет два корня: x1 =
−1 и x2 =
![]()
![]() . Из этих чисел
лишь число −1
принадлежит множеству M1. Следовательно, на этом множестве
уравнение (5) имеет единственный корень −1.
. Из этих чисел
лишь число −1
принадлежит множеству M1. Следовательно, на этом множестве
уравнение (5) имеет единственный корень −1.
На множестве M2 определены обе части формулы
2x + 1
![]() x = x (2x
+1) (положительный
множитель x внесен x
x = x (2x
+1) (положительный
множитель x внесен x
![]() под знак корня). Поэтому
уравнение (5) равносильно на множестве M2 уравнению x (2x
+1) + 2 x (2x +1) +1 = 0, которое можно
записать в виде
под знак корня). Поэтому
уравнение (5) равносильно на множестве M2 уравнению x (2x
+1) + 2 x (2x +1) +1 = 0, которое можно
записать в виде
![]() (
x (2x +1)
− 1)2
= 0. (7)
(
x (2x +1)
− 1)2
= 0. (7)
![]() Так как
для каждого x ∈
M2 справедливо неравенство x (2x +1) +1 > 0, то уравнение
(7) не имеет корней, принадлежащих множеству M2.
Следовательно, и равносильное ему на множестве M2 уравнение
(5) не имеет корней на этом множестве.
Так как
для каждого x ∈
M2 справедливо неравенство x (2x +1) +1 > 0, то уравнение
(7) не имеет корней, принадлежащих множеству M2.
Следовательно, и равносильное ему на множестве M2 уравнение
(5) не имеет корней на этом множестве.
Итак, уравнение (5) имеет единственный корень −1.
Решения и комментарии
Решите уравнение (10.28—10.30):
10.28. а) 4log4 (2 x + 1) = x2 + 3x − 5.
Решение. Все корни исходного уравнения принадлежат множеству М всех чисел x, удовлетворяющих неравенству 2x + 1 > 0, т. е. множеству М = (−0,5; +∞). Применяя формулу 4log4 (2 x + 1) = 2x +1, обе части которой определены на множестве М, получим, что исходное уравнение равносильно на множестве М уравнению
2x + 1 = x2 + 3x − 5, (8)
имеющему два корня: x1 = −3 и x2 = 2, из которых только число 2 принадлежит множеству M. Следовательно, исходное уравнение, равносильное на множестве М уравнению (8), имеет единственный корень 2.
10.29. а) log3 x = 4 − 3 logx 3.
Решение. Все корни исходного уравнения принадлежат
множеству М всех чисел x, удовлетворяющих условиям x > 0, x ≠ 1, т. е.
множеству М = (0;
1) ∪ (1; +∞). Применяя
формулу logx 3 =
![]() 3 , обе части которой определены log3 x
3 , обе части которой определены log3 x
на множестве М, получим, что исходное уравнение равносильно на множестве М уравнению
log3 x
= 4 − log![]() 33 x.
33 x.
Введя новое неизвестное t = log3 x, перепишем это уравнение в виде
t = 4 − 3 . (9) t
Так как уравнение (9) имеет два корня: t1 = 1 и t2 = 3, то все решения двух уравнений
log3 x = 1 и log3 x = 3,
принадлежащие множеству M, дадут все решения исходного уравнения. Решив эти уравнения на множестве М, получим, что исходное уравнение имеет два корня: x1 = 3 и x2 = 27.
1 − tg2 x
10.30. а) ![]() 2 x = sin x.
2 x = sin x.
1 + tg
Решение. Все корни исходного уравнения принадлежат множеству М всех чисел x, удовлетворяющих условию
x ≠
2π
+
πn, n ∈
Z. Применяя формулу cos 2x = 11![]() −+
tgtg22 xx, обе
−+
tgtg22 xx, обе
части которой определены на множестве М, получим, что исходное уравнение равносильно на множестве М уравнению
cos 2x = sin x. (10)
Применив формулу косинуса двойного угла и основное
тригонометрическое тождество, перепишем уравнение (10) в виде 1 − 2 sin2 x
= sin x,
которое имеет три серии решений: xk ![]() k, k ∈ Z;
xm =
k, k ∈ Z;
xm = ![]()
![]() +
2πm,
m ∈ Z;
xp =
−
+
2πm,
m ∈ Z;
xp =
− ![]()
![]() + 2πp, p ∈ Z.
Все числа xk и xm принадлежат множеству M,
а все числа xp не принадлежат множеству M. Следовательно,
исходное уравнение, равносильное на множестве М уравнению (10), имеет
две серии решений:
+ 2πp, p ∈ Z.
Все числа xk и xm принадлежат множеству M,
а все числа xp не принадлежат множеству M. Следовательно,
исходное уравнение, равносильное на множестве М уравнению (10), имеет
две серии решений:
![]()
![]() + 2πk, k ∈ Z;
+ 2πk, k ∈ Z;
![]() m,
m ∈ Z.
m,
m ∈ Z.
Дополнение. В учебнике (п. 9.3) написано, что уравнение
f1 (x) ⋅ f2 (x) = 0 (11)
равносильно совокупности двух систем:
⎧⎨⎩f1 ( )x = 0 и ⎧⎨xf2 ∈( )xD=( )f01 , x ∈ D (f2) ⎩
где D (f1) — область существования функции f1 (x); D (f2) — область существования функции f2 (x).
Можно дать еще один способ решения уравнения (11).
Все корни уравнения (11) содержатся в множестве M = D (f1) ∩ D (f2). На множестве M уравнение (11) равносильно совокупности уравнений f1 (x) = 0 и f2 (x) = 0. Найдя корни этих уравнений, отберем из них те, которые принадлежат множеству М. Они дадут все корни уравнения (11). Конечно же, здесь использовано не определенное в учебнике, но интуитивно ясное понятие равносильности на множестве уравнения и совокупности двух уравнений, которое сформулировано выше, в дополнении к п. 10.1. Пример 1. Решим уравнение
![]() −x ⋅ lg x = 0. (12)
−x ⋅ lg x = 0. (12)
![]() Решение.
Рассмотрим функции f1 ( )x = −x и f2 (x)
= lg x.
Так как D (f1) =
(−∞;
0], D (f2) =
(0; +∞)
и D (f1) ∩
D (f2) =
∅, то уравнение (12) не имеет корней.
Решение.
Рассмотрим функции f1 ( )x = −x и f2 (x)
= lg x.
Так как D (f1) =
(−∞;
0], D (f2) =
(0; +∞)
и D (f1) ∩
D (f2) =
∅, то уравнение (12) не имеет корней.
Пример 2. Решим уравнение
![]() log (2 3
+ 2x − x2)
⋅ sin x
= 0. (13)
log (2 3
+ 2x − x2)
⋅ sin x
= 0. (13)
![]()
![]() Решение. Рассмотрим
функции f1 (x) =
log2 (3 +
2x −
x2) и f2 ( )x = sin x. Так как
D (f1) =
(−1;
3), D (f2) =
[0; +∞),
M = D (f1)
∩ D (f2)
= [0; 3), то
уравнение (13) равносильно на множестве M совокупности уравнений log2
(3 + 2x − x2)
= 0 и sin x = 0.
Решение. Рассмотрим
функции f1 (x) =
log2 (3 +
2x −
x2) и f2 ( )x = sin x. Так как
D (f1) =
(−1;
3), D (f2) =
[0; +∞),
M = D (f1)
∩ D (f2)
= [0; 3), то
уравнение (13) равносильно на множестве M совокупности уравнений log2
(3 + 2x − x2)
= 0 и sin x = 0.
![]()
![]()
![]() Первое уравнение
совокупности имеет два решения: x1 = 1 +3
и x2 =
1 −3.
Второе уравнение совокупности имеет серию решений xk = (πk)2,
k = 0, 1,
2, ... . Из этих чисел в множество М входят лишь числа x1 = 1 +3 и x0 = 0.
Первое уравнение
совокупности имеет два решения: x1 = 1 +3
и x2 =
1 −3.
Второе уравнение совокупности имеет серию решений xk = (πk)2,
k = 0, 1,
2, ... . Из этих чисел в множество М входят лишь числа x1 = 1 +3 и x0 = 0.
![]() Следовательно,
уравнение (14) имеет два корня: 0 и 1 +3.
Следовательно,
уравнение (14) имеет два корня: 0 и 1 +3.
Промежуточный контроль. C—39.
В этом пункте учебника приведены примеры уравнений, в процессе решения которых приходится выполнять несколько преобразований. Здесь важно обратить внимание учащихся на то, что если найдено множество M, на котором исходное уравнение равносильно новому уравнению, то перед применением нового преобразования необходимо учитывать ограничения, которые могут сузить множество M, и то, что новое преобразование дает уравнение, равносильное исходному уже на множестве M1 ⊂ M, а не на всем множестве М.
![]()
![]() Так, в примере 2 этого
пункта учебника решается уравнение 4 x =
5 + 45 − 4x,
равносильное на множестве M =
[0; 11,25] уравнению
Так, в примере 2 этого
пункта учебника решается уравнение 4 x =
5 + 45 − 4x,
равносильное на множестве M =
[0; 11,25] уравнению
![]() 2x − 7 = 45 − 4x. (1)
2x − 7 = 45 − 4x. (1)
Если теперь возвести в квадрат уравнение (1) без учета условия 2x − 7 ≥ 0, то получится уравнение
4x2 − 28x + 49 = 45 − x, (2)
![]()
![]() имеющее два корня: x1
= 3 + 22 и x2 = 3 − 22,
принадлежащие множеству M, но число x1 является корнем
уравнения (1), а число x2 нет. Чтобы избежать ошибки при
включении числа x2 в ответ, перед вторым возведением
уравнения в квадрат необходимо учесть ограничение 2x − 7 ≥ 0 и то, что
уравнение (2) равносильно уравнению (1) лишь на множестве M1 = [3,5; 11,25], M1
⊂ M.
имеющее два корня: x1
= 3 + 22 и x2 = 3 − 22,
принадлежащие множеству M, но число x1 является корнем
уравнения (1), а число x2 нет. Чтобы избежать ошибки при
включении числа x2 в ответ, перед вторым возведением
уравнения в квадрат необходимо учесть ограничение 2x − 7 ≥ 0 и то, что
уравнение (2) равносильно уравнению (1) лишь на множестве M1 = [3,5; 11,25], M1
⊂ M.
Отметим, что в следующем примере попытки перейти к следствию после возведения в квадрат или к равносильной системе приводят к трудным вычислениям. Гораздо проще это уравнение решается с использованием равносильности на множестве. Пример. Решим уравнение
x + 2
![]() 1 +
x 1 + (x
+1) 1 + (x + 2) (x + 4) = . (3)
1 +
x 1 + (x
+1) 1 + (x + 2) (x + 4) = . (3)
2
Решение. Все корни уравнения (3) содержатся в множестве M, на котором правая часть уравнения неотрицательна, т. е. в множестве M = [−2; +∞). Используя формулу a2 = | a |, определение модуля числа и учитывая, что
x ∈ M, преобразуем левую часть уравнения (3):
1 +x 1 +(x +1) 1 +(x +2)(x +4) = 1 +x 1 +(x +1) (x +3)2 =
= 1 + x 1 + (x +1)| x + 3| = 1 + x 1 + (x +1)(x +3) =
![]() = 1 +
x (x +2)2
= 1 + x x| + 2| = 1 + x x( + 2) = = (x +1)2 = | x +1|.
= 1 +
x (x +2)2
= 1 + x x| + 2| = 1 + x x( + 2) = = (x +1)2 = | x +1|.
Итак, на множестве М уравнение (3) равносильно уравнению
x + 2
|
x +1| = ![]() . (4)
. (4)
2
Обе части уравнения (4) на множестве М неотрицательны, поэтому уравнение (4) равносильно на множестве М уравнению
4 (x + 1)2 = (x + 2)2, (5)
имеющему два корня: x1 = 0 и x2 = − ![]()
![]() . Оба эти числа принадлежат
множеству М. Поэтому и уравнение (3), равносильное на множестве М уравнению
(5), имеет те же два корня: 0 и −
. Оба эти числа принадлежат
множеству М. Поэтому и уравнение (3), равносильное на множестве М уравнению
(5), имеет те же два корня: 0 и −
![]()
![]() .
.
Решения и комментарии
Решите уравнение (10.43—10.46):
![]()
![]() 10.43. а) (x2 +1)
8 x −
x2 − 15 = (2x + 9) 8 x − x2 − 15 .
10.43. а) (x2 +1)
8 x −
x2 − 15 = (2x + 9) 8 x − x2 − 15 .
Решение. Все корни исходного уравнения принадлежат множеству М всех чисел, удовлетворяющих условию 8x − x2 − 15 ≥ 0, т. е. множеству М = [3; 5].
Для каждого x ∈ M обе части исходного уравнения положительны, поэтому, прологарифмировав его, получим, что на множестве М оно равносильно уравнению
![]()
![]() lg (x2 +1) 8 x − x2 − 15 = lg (2x + 9) 8 x − x2 − 15 ,
lg (x2 +1) 8 x − x2 − 15 = lg (2x + 9) 8 x − x2 − 15 ,
которое можно переписать в виде
8x − x2 − 15(lg (x2 +1) − lg (2x + 9)) = 0. (6)
Уравнение (6) равносильно на множестве М совокупности двух уравнений:
![]() 1) 8x
− x2
− 15 = 0 и 2) lg (x2
+ 1) − lg (2x + 9) = 0.
1) 8x
− x2
− 15 = 0 и 2) lg (x2
+ 1) − lg (2x + 9) = 0.
Уравнение 1 имеет два корня: x1 = 3 и x2 = 5, принадлежащие множеству M. Уравнение 2 имеет два корня: x3 = 4 и x4 = −2, из которых множеству M принадлежит лишь число 4. Поэтому уравнение (6), равносильное на множестве М совокупности уравнений 1 и 2, имеет три корня: x1 = 3, x2 = 5 и x3 = 4. Следовательно, исходное уравнение, равносильное на множестве М уравнению (6), также имеет три корня: 3, 4 и 5.
log 1 ( 8 + 2 x − x2 )
1 25 .
![]() 10.44.
а)= (x − 1) x − 1
10.44.
а)= (x − 1) x − 1
Решение. Все корни исходного уравнения принадлежат множеству М всех чисел, удовлетворяющих условиям x − 1 > 0 и 8 + 2x − x2 > 0, т. е. множеству М = (1; 4).
Для каждого x ∈ M обе части исходного уравнения положительны, поэтому, прологарифмировав его, получим, что оно равносильно на множестве М уравнению
1 log 1 ( 8 + 2 x − x2 )
−
lg (x − 1) 2 = lg (x − 1) 25 ,
которое можно переписать в виде
lg (x − 1) ⎜⎛⎝log 1 (8 + 2x − x2) + 21⎞⎟⎠ = 0. (7)
25
![]()
![]() Уравнение (7) равносильно на множестве М совокупности
двух уравнений: 1) lg (x −
1) = 0 и
2) log (8 + 2x
− x2)
+
Уравнение (7) равносильно на множестве М совокупности
двух уравнений: 1) lg (x −
1) = 0 и
2) log (8 + 2x
− x2)
+ ![]()
![]() =
0.
=
0.
Уравнение 1 имеет единственный корень x1 = 2, принадлежащий множеству M. Уравнение 2 имеет два корня: x2 = 3 и x3 = −1, из которых множеству M принадлежит лишь число 3. Следовательно, исходное уравнение, равносильное на множестве М уравнению (7), имеет два корня: 2 и 3. 10.46. а) log| x | (1 + x) = log| x | (x2 − 5).
![]() Решение.
Все корни исходного уравнения принадлежат множеству М всех чисел,
удовлетворяющих условиям 1 +
x > 0,
x2 −
5 > 0, x
≠ 0, x
≠ 1 и x
≠ −1,
т. е. множеству M =
(5;
+ ∞).
Применив формулу перехода к другому основанию, получим, что исходное уравнение
равносильно на множестве М уравнению
Решение.
Все корни исходного уравнения принадлежат множеству М всех чисел,
удовлетворяющих условиям 1 +
x > 0,
x2 −
5 > 0, x
≠ 0, x
≠ 1 и x
≠ −1,
т. е. множеству M =
(5;
+ ∞).
Применив формулу перехода к другому основанию, получим, что исходное уравнение
равносильно на множестве М уравнению
lg (1 + x) lg (x2 − 5)
![]() = . (8) lg | x | lg | x
|
= . (8) lg | x | lg | x
|
В каждой точке множества М функция ϕ (x) = lg | x | определена и отлична от нуля, поэтому уравнение (8) равносильно на множестве М уравнению
lg (1 + x) = lg (x2 − 5). (9)
В каждой точке множества М обе функции f (x) = 1 + x и g (x) = x2 − 5 положительны, поэтому уравнение (9) равносильно на множестве М уравнению
1 + x = x2 − 5, (10)
имеющему два корня: x1 = 3 и x2 = −2, из которых лишь число 3 принадлежит множеству M. Следовательно, исходное уравнение, равносильное на множестве М уравнению (10), имеет единственный корень 3.
10.47. При каких значениях параметра а уравнение
x2 − a2
![]() = 0 имеет единственный
корень?
= 0 имеет единственный
корень?
x − 4
Решение. Все корни исходного уравнения принадлежат множеству М всех чисел x, удовлетворяющих условию x ≠ 4, т. е. множеству М = (−∞; 4) ∪ (4; +∞). Для каждого значения параметра a исходное уравнение равносильно на множестве М уравнению
(x − a) (x − (−a)) = 0. (11)
Если a = 0, то уравнение (11) имеет единственный корень x1 = 0, принадлежащий множеству M.
Если a ≠ 0, то уравнение (11) имеет два корня: x1 = a и x2 = −a, поэтому уравнение (11) имеет единственный корень на множестве М, если один из этих корней есть число 4. Это будет выполняться в двух случаях: при a = 4 или при −a = 4. Следовательно, исходное уравнение, равносильное на множестве М уравнению (11), имеет единственный корень при a = 0, a = −4, a = 4.
Промежуточный контроль. C—40.
В данном пункте учебника приведены примеры решения уравнений при дополнительных условиях, означающих, что уравнение требуется решить на данном множестве. Важно отметить, что эти условия иногда облегчают решение уравнения. Приведем такой пример. Пример 1. Найдем все корни уравнения
sin
2x + sin x
+ cos x = − ![]()
![]() , (1)
, (1)
принадлежащие интервалу ⎜⎝⎛− 2π ; 2π⎞⎟⎠.
Решение. Перенося все члены уравнения (1) в левую часть, применяя формулу синуса двойного угла и умножая обе части уравнения на 2, перепишем уравнение (1) в виде
4 sin x cos x + 2 sin x + 2 cos x + 1 = 0 или в виде
4 ⎜⎝⎛sin x + 21⎞⎟⎠ ⎛⎜⎝cos x + 21⎟⎠⎞ = 0. (2)
Так как ![]() для каждого x, принадлежащего
для каждого x, принадлежащего
множеству M = ⎛⎜⎝− 2π ; 2π⎞⎟⎠, то на этом множестве уравнение (2) равносильно уравнению
sin
x + ![]()
![]() =
0, (3)
=
0, (3)
имеющему на множестве М единственный
корень − ![]()
![]() . Следовательно, и уравнение (1),
равносильное уравнению (3) на множестве М, имеет единственный корень −
. Следовательно, и уравнение (1),
равносильное уравнению (3) на множестве М, имеет единственный корень − ![]()
![]() .
.
Часто дополнительное условие не облегчает решение уравнения. В таких случаях обычно сначала решают уравнение, а потом решают дополнительную задачу — отбирают из найденных корней те, которые удовлетворяют условию.
Решения и комментарии
Найдите все решения уравнения, принадлежащие указанному промежутку (10.50—10.53):
10.50. а) | x2 − 3x + 2 | = 2x − 2, [3; 5].
Решение. Для каждого x ∈ [3; 5] справедливо неравенство x2 − 3x + 2 > 0, поэтому на множестве М = [3; 5] исходное уравнение равносильно уравнению
x2 − 3x + 2 = 2x − 2. (4)
Уравнение (4) имеет два корня: x1 = 1 и x2 = 4, из которых лишь число 4 принадлежит множеству M. Следовательно, исходное уравнение, равносильное на множестве М уравнению (4), имеет единственный корень 3, принадлежащий отрезку [3; 5].
10.51. а) x4 + x3 + x2 − 3x = 0, [−2; 0].
Решение. Исходное уравнение имеет очевидные корни x1 = 0 и x2 = 1, поэтому его можно переписать в виде
x (x − 1) (x2 + 2x + 3) = 0. (5)
Так как для каждого x ∈ [−2; 0] справедливы неравенства x2 + 2x + 3 > 0 и x − 1 < 0, то уравнение (5) равносильно на множестве [−2; 0] уравнению
x = 0, (6)
имеющему единственный корень x1 = 0, принадлежащий множеству М = [−2; 0]. Следовательно, исходное уравнение, равносильное на множестве М уравнению (5), имеет единственный корень 0, принадлежащий отрезку [−2; 0].
10.53. а) 3tg2 ⎜⎝⎛πx − 8π ⎞⎟⎠ = 1, ⎜⎛⎝ 23 ; 3⎞⎟⎠.
Решение. Исходное уравнение равносильно совокупности двух систем:
|
⎪tg ⎜⎝ 8 ⎨ ⎪ 3 < x < 3 ⎩ 2 |
и |
⎪tg ⎜⎝ 8 ⎨ ⎪ 3 < x < 3. ⎩ 2 |
(7) |
Уравнение первой системы имеет единственную серию решений xk
= ![]()
![]() +
k, k ∈
Z. Из этих чисел двойному неравенству этой системы
удовлетворяет лишь число x1 =
2
+
k, k ∈
Z. Из этих чисел двойному неравенству этой системы
удовлетворяет лишь число x1 =
2![]()
![]() , т. е. первая
система имеет лишь одно решение, принадлежащее множеству M = ⎛⎜⎝ 32 ; 3⎞⎟⎠: число x1
= 2
, т. е. первая
система имеет лишь одно решение, принадлежащее множеству M = ⎛⎜⎝ 32 ; 3⎞⎟⎠: число x1
= 2![]()
![]() .
.
Уравнение второй системы имеет единственную серию решений xn
= − ![]()
![]() +
n, n ∈
Z. Из этих чисел двойному неравенству этой системы
удовлетворяют лишь числа x2 =
1
+
n, n ∈
Z. Из этих чисел двойному неравенству этой системы
удовлетворяют лишь числа x2 =
1![]()
![]() и x3
= 2
и x3
= 2![]()
![]() , т. е. вторая система имеет лишь
два решения, принадлежащие множеству M =
⎛⎜⎝ 32 ;3⎞⎟⎠: числа x2
=1
, т. е. вторая система имеет лишь
два решения, принадлежащие множеству M =
⎛⎜⎝ 32 ;3⎞⎟⎠: числа x2
=1![]()
![]() и x3 = 2
и x3 = 2![]()
![]() .
.
![]() Следовательно,
исходное уравнение, равносильное на множестве М совокупности (7), имеет
на этом множестве лишь три корня: 1
Следовательно,
исходное уравнение, равносильное на множестве М совокупности (7), имеет
на этом множестве лишь три корня: 1![]() , 2
, 2![]() , 2
, 2![]() .
.
Дополнение. В этом параграфе рассматривался метод решения уравнений — замена уравнения на преобразованное уравнение, равносильное исходному на некотором множестве М. При этом множество М каждый раз выписывалось в явном виде.
Однако иногда удобно не выписывать это множество в явном виде, а лишь записывать это множество М в виде условий (обычно задающихся неравенствами) и рассматривать преобразованное уравнение вместе с этими условиями в виде системы, равносильной исходному уравнению. Приведем пример.
Пример 2. Решим уравнение
![]() sin x = . (8)
sin x = . (8)
Решение. Все корни уравнения (8) содержатся в множестве М всех тех x, для каждого из которых
sin x ≥ 0 (9)
и
![]() . (10)
. (10)
Можно решить неравенства (9) и (10), выписать в явном виде множество М, а затем решить на нем уравнение (8).
Но можно рассуждать иначе. На множестве М при выполнении условий (9) и (10) уравнение (8) равносильно уравнению
sin2
x = cos
x + ![]()
![]() . (11)
. (11)
Итак, множество корней уравнения (8) совпадает с множеством тех корней уравнения (11), которые удовлетворяют условиям (9) и (10), т. е. уравнение (8) равносильно системе
⎧⎪⎪sin2 x = cos x + 14
⎨sin x ≥ 0 (12)
⎪⎪⎩cos![]() .
.
Таким образом, рассуждая о равносильности на множестве уравнений (8) и (11), мы пришли к выводу: уравнение (8) равносильно системе (12).
Итак,
⎧⎪
(8) ⇔ (12) ⇔ ⎨sin2 x = cos x + 14 ⇔
⎪⎩sin x ≥ 0
⎧⎛
⇔ ⎨⎪⎝⎜cos x − 21⎞⎟⎠ ⎛⎜⎝cos x + 23 ⎠⎟⎞ = 0 ⇔ ⎧⎪⎨cos x = 21
⎪⎩sin x ≥ 0 ⎪⎩sin x ≥ 0.
Решив последнюю систему, получим, что множество ее решений, а значит, и решений уравнения (8) есть серия
xk = ![]()
![]() +
2πk,
k ∈ Z.
+
2πk,
k ∈ Z.
Отметим, что в данном примере нахождение множества М в явном виде довольно трудоемкая работа, содержащая, в частности, ненужные вычисления, связанные с решением неравенства (10). Поэтому рассмотренный пример лучше решать переходом к системе, равносильной исходному уравнению.
Во многих примерах, рассмотренных в § 10, также можно не выписывать в явном виде множество М, а, рассуждая, как в приведенном выше примере, показать, что исходное уравнение равносильно некоторой системе, и затем решить эту систему.
Таким образом, метод решения уравнений, рассмотренный в § 10, позволяет заменить исходное уравнение равносильной ему системой не только в случаях, отмеченных в § 9, но и во многих других. При этом такие преобразования, как в § 9, можно просто запомнить, а преобразования, рассмотренные в § 10, приводят исходное уравнение к равносильной ему системе лишь после некоторых рассуждений.
Конечно, при оформлении учащимися перехода от уравнения (8) к системе (12) обычно не пишут длинные рассуждения, а просто пишут, что уравнение (8) равносильно системе (12). Однако если от учащегося потребуется обоснование этого факта, то ему придется повторить все эти рассуждения.
Промежуточный контроль. К—5.
|
§11. |
Равносильность неравенств на множествах
В данном параграфе будет продолжено рассмотрение неравносильных преобразований неравенств, будет рассмотрен способ решения неравенств: переход к неравенству, равносильному исходному неравенству на некотором множестве чисел М. Его рекомендуется основательно изучать лишь в классах с углубленным изучением математики, так как его применение требует не формального выполнения заученного алгоритма, а осмысленного выбора учащимися того множества, на котором будет проводиться преобразование неравенства.
Переход от исходного неравенства к неравенству, равносильному ему на некотором множестве, применяется еще и при решении неравенств с несколькими модулями.
Такие неравенства будут рассмотрены в § 12.
В этом пункте учебника введены понятия неравенств, равносильных на некотором множестве М, равносильного перехода на множестве М от одного неравенства к другому или равносильного преобразования неравенства на множестве М; перечислены пять основных преобразований неравенств, приводящих исходное неравенство к неравенству, равносильному ему на некотором множестве. В следующих пунктах § 11 эти преобразования рассматриваются подробно.
Решения и комментарии
11.5. Объясните, в результате какого преобразования из первого неравенства получено второе:
а) sin x > соs x, sin2 x > соs2 x;
![]()
![]()
![]() в) log3 tg
x > log33,
tg x >3;
x2 −
5x −6 , x2 − 5x > −6.
в) log3 tg
x > log33,
tg x >3;
x2 −
5x −6 , x2 − 5x > −6.
е) >
lg x lg x
В каждом случае выясните, на каком множестве равносильны первое и второе неравенства.
Решение. а) Второе неравенство получено из первого возведением в квадрат. Неравенства равносильны на множестве М чисел x, удовлетворяющих условиям sin x ≥ 0 и cos x ≥ 0, т. е. на множестве M = ⎡⎢⎣2πm; 2π + 2πm⎤⎥⎦, m ∈ Z.
в) Второе неравенство получено потенцированием первого неравенства. Эти неравенства равносильны на множестве М тех чисел x, которые удовлетворяют условию tg x > 0, т. е. на множестве M = ⎛⎜⎝πm; 2π + πm⎞⎟⎠, m ∈ Z.
е) Второе неравенство получено из первого неравенства умножением обеих частей на функцию y = lg x. Неравенства равносильны на множестве М тех чисел x, которые удовлетворяют условию lg x > 0, т. е. на множестве М = (1; +∞).
В этом пункте учебника сформулировано следующее утверждение: неравенства f (x) > g (x) и (f (x))2m > (g (x))2m, где m ∈ N, равносильны на том множестве М, где f (x) ≥ 0 и g (x) ≥ 0. В п. 11.2 учебника и в п. 41 дидактических материалов приведены примеры применения этого утверждения при решении неравенств. Обратим внимание на то, что это утверждение применяется при решении не только иррациональных неравенств, но и неравенств с модулями (пример 3 из учебника). Приведем еще один пример. Пример. Решим неравенство
| 1 + 2 sin x | < | 1 − 3 sin x |. (1)
Решение. Обе функции f (x) = | 1 + 2 sin x | и ϕ (x) = = | 1 − 3 sin x | неотрицательны для каждого x ∈ R. Поэтому неравенство (1) равносильно неравенству
(1 + 2 sin x)2 < (1 − 3 sin x)2. (2)
Неравенство (2) можно переписать в виде
5 sin x (2 − sin x) < 0. (3)
Так как 2 − sin x > 0 для каждого x ∈ R, то неравен-
ство (3) равносильно неравенству
sin x < 0. (4)
Множество решений неравенства (4), а значит, и равносильного ему неравенства (1) составляет серию промежутков (π + 2πk; 2π + 2πk), k ∈ Z.
Решения и комментарии
Решите неравенство (11.8—11.16):
![]() 11.8.
а) x +1
< x − 1.
11.8.
а) x +1
< x − 1.
![]() Решение.
Все решения исходного неравенства принадлежат множеству М чисел х,
удовлетворяющих условиям x +
1 ≥ 0,
x − 1
> 0, т. е.
множеству М = (1;
+∞). Для
каждого x ∈
M обе функции f x( ) =
x +1
и ϕ (x)
= x − 1
неотрицательны, поэтому исходное неравенство равносильно на множестве М неравенству
Решение.
Все решения исходного неравенства принадлежат множеству М чисел х,
удовлетворяющих условиям x +
1 ≥ 0,
x − 1
> 0, т. е.
множеству М = (1;
+∞). Для
каждого x ∈
M обе функции f x( ) =
x +1
и ϕ (x)
= x − 1
неотрицательны, поэтому исходное неравенство равносильно на множестве М неравенству
x + 1 < (x − 1)2. (5)
Все решения неравенства (5) составляют два промежутка: (−∞; 0) и (3; +∞), из них множеству M принадлежат все x из промежутка (3; +∞). Следовательно, все решения неравенства (5) на множестве М составляют промежуток (3; +∞). Поэтому и равносильное ему на множестве М исходное неравенство имеет те же решения: промежуток (3; +∞).
![]() 11.9.
а) x +1
> x − 1.
11.9.
а) x +1
> x − 1.
Решение. Все решения исходного неравенства принадлежат множеству М чисел х, удовлетворяющих условию x + 1 ≥ 0, т. е. множеству М = [−1; +∞).
1) Очевидно, что все x ∈ M, для которых x − 1 < 0, являются решениями исходного неравенства, т. е. все x ∈ [−1; 1) являются решениями исходного неравенства.
2) ![]() В каждой точке множества M1
= [1; +∞) обе функции f
x( ) = x +1 и g (x)
= x − 1
неотрицательны, поэтому исходное неравенство равносильно на множестве M1
неравенству x +
1 > (x
− 1)2. (6)
В каждой точке множества M1
= [1; +∞) обе функции f
x( ) = x +1 и g (x)
= x − 1
неотрицательны, поэтому исходное неравенство равносильно на множестве M1
неравенству x +
1 > (x
− 1)2. (6)
Все решения неравенства (6) составляют промежуток (0; 3), из них множеству M1 принадлежит промежуток [1; 3). Следовательно, все решения неравенства (6) на множестве M1 составляют промежуток [1; 3). Поэтому и равносильное ему на множестве М исходное неравенство имеет те же решения на множестве M1.
Объединив решения, найденные в пп. 1 и 2, получим, что множество решений исходного неравенства составляет промежуток [−1; 3).
11.16. а) 1 + sin x > | cos x |.
Решение. В каждой точке множества R обе функции f (x) = 1 + sin x и g (x) = | cos x | неотрицательны, поэтому исходное неравенство равносильно неравенству
(1 + sin x)2 > cos2 x. (7)
Применив формулу квадрата суммы, перенеся все слагаемые в одну часть и применив основное тригонометрическое тождество, перепишем неравенство (7) в виде
2 sin x (1 + sin x) > 0. (8)
Так как неравенство t (1 + t) > 0 имеет решения: все t < −1 и все t > 0, то решения неравенства (8) найдем, объединив все решения неравенств sin x < −1 и sin x > 0. Первое из этих неравенств не имеет решений, а множество решений второго неравенства есть серия промежутков (2πk; π + 2πk), k ∈ Z.
Следовательно, исходное неравенство имеет то же множество решений: серию промежутков (2πk; π + 2πk), k ∈ Z.
В этом пункте учебника сформулировано утверждение: неравенства f (x) > g (x) и f (x) ϕ (x) > g (x) ϕ (x) равносильны на том множестве М, на котором определена и положительна функция ϕ (x). В п. 11.3 учебника и в п. 41 дидактических материалов приведены примеры применения этого утверждения при решении неравенств. Приведем еще пример.
Пример. Решим неравенство
18 x2 + 3x
> . (1)
![]() sin x sin x
sin x sin x
![]() Решение.
Все решения неравенства (1) содержатся в множестве М всех тех x,
для каждого из которых sin x >
0, т. е. содержатся в множестве М — серии интервалов (2πk; π + 2πk), k ∈ Z.
В каждой точке множества М функция ϕ
( )x = sin
x определена и положительна, поэтому, умножив неравенство (1) на функцию
ϕ (x),
получим, что оно равносильно на множестве M неравенству
Решение.
Все решения неравенства (1) содержатся в множестве М всех тех x,
для каждого из которых sin x >
0, т. е. содержатся в множестве М — серии интервалов (2πk; π + 2πk), k ∈ Z.
В каждой точке множества М функция ϕ
( )x = sin
x определена и положительна, поэтому, умножив неравенство (1) на функцию
ϕ (x),
получим, что оно равносильно на множестве M неравенству
18 > x2 + 3x. (2)
Множество решений неравенства (2) составляет интервал (−6; 3). Из них множеству M принадлежат лишь x из двух интервалов: (−6; −π) и (0; 3).
Следовательно, все решения неравенства (2) на множестве М составляют множество (−6; −π) ∪ (0; 3). Поэтому и равносильное ему на множестве M неравенство (1) имеет те же решения: (−6; −π) ∪ (0; 3).
Решения и комментарии
x2 x + 2
![]() 11.20.
а) Решите неравенство < .
11.20.
а) Решите неравенство < .
1 − cos x 1 − cos x
Решение. Все решения исходного неравенства содержатся в множестве М всех тех x, для каждого из которых cos x ≠ 1, т. е. содержатся в множестве всех x ≠ 2πk, k ∈ Z. В каждой точке множества М функция ϕ (x) = 1 − cos x определена и положительна, поэтому, умножив исходное неравенство на функцию ϕ (x), получим, что оно равносильно на множестве M неравенству
x2 < x + 2. (3)
Множество решений неравенства (3) составляет интервал (−1; 2). Из них множеству M принадлежат лишь x из двух интервалов: (−1; 0) и (0; 2).
Следовательно, все решения неравенства (3) на множестве М составляют множество (−1; 0) ∪ (0; 2). Поэтому и равносильное ему на множестве M исходное неравенство имеет те же решения: (−1; 0) ∪ (0; 2).
В этом пункте учебника сформулированы утверждения о потенцировании логарифмических неравенств, о приведении подобных членов и применении формул при решении неравенств. В п. 11.4 учебника и в пп. 41 и 42 дидактических материалов приведены примеры применения этих утверждений при решении неравенств. Обратим внимание на утверждение 3 из учебника.
Пусть в каждой точке множества М определены обе части некоторой формулы. Тогда, применив эту формулу при решении неравенства, получим неравенство того же знака, равносильное на множестве М исходному неравенству.
Приведем пример на применение этого утверждения. Пример. Решим неравенство
3log3 (2 x − 5 ) > x2 − 4x +1. (1)
Решение. Обе части формулы 3log3 (2 x − 5 ) > 2x − 5 определены для всех x, удовлетворяющих условию 2x − 5 > 0, т. е. на множестве M = (2,5; +∞). Поэтому по утверждению 3 неравенство (1) равносильно на множестве M неравенству
2x − 5 > x2 − 4x + 1. (2)
Все решения неравенства (2) составляют промежуток
![]()
![]()
![]() (3 − 3; 3 + 3).
Из них множеству М принадлежат лишь x из промежутка (2,5;
3 +3).
Следовательно, все решения неравенства (1) составляют промежуток (2,5;
3 +3).
(3 − 3; 3 + 3).
Из них множеству М принадлежат лишь x из промежутка (2,5;
3 +3).
Следовательно, все решения неравенства (1) составляют промежуток (2,5;
3 +3).
Следует отметить, что утверждение 3 — единственное утверждение в учебнике, позволяющее применять формулы при решении неравенств.
Решения и комментарии
11.29. а) Решите неравенство tg x + x2 < tg x + 2x + 3.
Решение. Все решения исходного неравенства содержатся
в множестве М всех чисел x, удовлетворяющих условию x![]() n,
n ∈ Z.
Так как в каждой точке множества М определена функция ϕ (x) = tg x, то,
приведя подобные члены, получим, что исходное неравенство равносильно на
множестве M неравенству
n,
n ∈ Z.
Так как в каждой точке множества М определена функция ϕ (x) = tg x, то,
приведя подобные члены, получим, что исходное неравенство равносильно на
множестве M неравенству
x2 < 2x + 3, (3)
имеющему множество решений (−1; 3). Из этих чисел множеству М принадлежат лишь x из двух промежутков:
⎛⎜−1; π⎞⎟⎠ и ⎛⎜⎝ 2π ; 3⎞⎟⎠. Поэтому исходное неравенство, равносиль-
⎝ 2
ное на множестве М неравенству (3), имеет то же множество решений: ⎜⎝⎛−1; 2π⎞⎟⎠ ∪ ⎛⎜⎝ 2π ; 3⎞⎟⎠.
В данном пункте учебника приведены примеры применения нескольких преобразований при решении неравенств.
Решения и комментарии
![]() Решите
неравенство ( ):
Решите
неравенство ( ):
11.37. а) .
| x − 2|
Решение. Все решения исходного неравенства содержатся в множестве М всех тех x, для каждого из которых x ≠ 2, 13x + 25 ≥ 0 и 11x + 23 ≥ 0, т. е. в множестве
M ![]() ). В каждой точке множества М
). В каждой точке множества М
функция ϕ (x) = | x − 2 | определена и положительна, поэтому, умножив исходное неравенство на функцию ϕ (x), получим, что оно равносильно на множестве M неравенству
13x + 25 > 11x + 23. (1)
![]()
![]() В каждой точке множества М
обе функции f x( ) =
= 13x + 25
и g x( ) = 11x
+ 23 определены
и неотрицательны, поэтому неравенство (1) равносильно на множестве M неравенству
В каждой точке множества М
обе функции f x( ) =
= 13x + 25
и g x( ) = 11x
+ 23 определены
и неотрицательны, поэтому неравенство (1) равносильно на множестве M неравенству
13x + 25 > 11x + 23. (2)
Неравенство (2) имеет множество решений (−1; +∞). Из этих чисел множеству М принадлежат лишь x из двух промежутков: (−1; 2) и (2; +∞). Поэтому исходное неравенство, равносильное на множестве М неравенству (2), имеет то же множество решений: (−1; 2) ∪ (2; +∞).
x2 + 1 − | cos x | 2x − | cos x |
![]() 11.43. а) > .
11.43. а) > .
2x + | cos x | x2 + 1 + | cos x |
![]()
![]() Решение. Все решения
исходного неравенства содержатся в множестве М всех тех x, для
каждого из которых x ≥
0. В каждой точке множества М функция ϕ ( )x = ( 2x + | cos x| )(
x2 +1
+ | cos x|
)
определена и положительна, поэтому, умножив исходное неравенство на
функцию ϕ (x),
получим, что оно равносильно на множестве M неравенству
Решение. Все решения
исходного неравенства содержатся в множестве М всех тех x, для
каждого из которых x ≥
0. В каждой точке множества М функция ϕ ( )x = ( 2x + | cos x| )(
x2 +1
+ | cos x|
)
определена и положительна, поэтому, умножив исходное неравенство на
функцию ϕ (x),
получим, что оно равносильно на множестве M неравенству
![]()
![]() (
x2 +1)2
− |
cos x|2 >
(
2x)2 − | cos x|2 . (3)
(
x2 +1)2
− |
cos x|2 >
(
2x)2 − | cos x|2 . (3)
Неравенство (3) равносильно на множестве M неравенству
x2 − 2x + 1 > 0. (4)
Неравенство (4) имеет множество решений (−∞; 1) ∪ ∪ (1; +∞). Из этих чисел множеству М принадлежат лишь x из двух промежутков: [0; 1) и (1; +∞). Поэтому исходное неравенство, равносильное на множестве М неравенству (4), имеет то же множество решений: [0; 1) ∪ (1; +∞).
![]() 11.45.
а) 2 + log x2 − 2 x −
3 ⎛⎜⎝ xx ++
14⎠⎟⎞ > logx2 −
2 x − 3 (x2 − 2x − 2) .2
11.45.
а) 2 + log x2 − 2 x −
3 ⎛⎜⎝ xx ++
14⎠⎟⎞ > logx2 −
2 x − 3 (x2 − 2x − 2) .2
Решение. Все решения исходного неравенства содержатся в множестве М всех тех x, для каждого из которых
2 2 x + 4 2
x − 2x − 3 >
0, x − 2x − 3 ≠ 1, ![]() > 0, x −
2x −
2 ≠ 0,
x +
1
> 0, x −
2x −
2 ≠ 0,
x +
1
![]()
![]() т. е. в множестве М,
состоящем из трех промежутков: (−∞;
−4), (3;
1 +5)
и (1
+5; +∞).
В каждой точке множества М определены все части формул
т. е. в множестве М,
состоящем из трех промежутков: (−∞;
−4), (3;
1 +5)
и (1
+5; +∞).
В каждой точке множества М определены все части формул
![]() ⎠
⎠
x − 2 x −
=
Поэтому исходное неравенство равносильно на множестве М неравенству
lg (x2 + x − 12) lg (x2 − 2x − 2)
> . (5) lg x2 − 2x − 3 lg x2 − 2x − 3
1)
![]()
![]() В каждой точке множества М1
= (−∞; −4) ∪ ∪ (1
+5; +∞)
функция ϕ (
)x = lg x2
− 2x
− 3 определена
и положительна, поэтому, умножив неравенство (5) на функцию ϕ (x),
получим, что оно равносильно на множестве М1 неравенству lg (x2
+ x − 12) > lg (x2
− 2x
− 2).
В каждой точке множества М1
= (−∞; −4) ∪ ∪ (1
+5; +∞)
функция ϕ (
)x = lg x2
− 2x
− 3 определена
и положительна, поэтому, умножив неравенство (5) на функцию ϕ (x),
получим, что оно равносильно на множестве М1 неравенству lg (x2
+ x − 12) > lg (x2
− 2x
− 2).
Потенцируя это неравенство, получим, что оно равносильно на множестве М1 неравенству
x2 + x − 12 > x2 − 2x − 2. (6)
Неравенство (6) имеет решения: x > ![]()
![]() , все они принадлежат множеству М1.
Следовательно, неравенство (5) на
, все они принадлежат множеству М1.
Следовательно, неравенство (5) на
1 ∈ ⎛⎜⎝ 103 ; +∞⎞⎟⎠. множестве М имеет решения: x
2) ![]()
![]() В каждой точке множества М2
= (3;
1 +5)
функция ϕ (
)x = lg x2
− 2x
− 3 определена
и отрицательна, поэтому, умножив неравенство (5) на функцию ϕ (x),
получим, что оно равносильно на множестве М2 неравенству
В каждой точке множества М2
= (3;
1 +5)
функция ϕ (
)x = lg x2
− 2x
− 3 определена
и отрицательна, поэтому, умножив неравенство (5) на функцию ϕ (x),
получим, что оно равносильно на множестве М2 неравенству
lg (x2 + x − 12) < lg (x2 − 2x − 2).
Потенцируя это неравенство, получим, что оно равносильно на множестве М2 неравенству
x2 + x − 12 < x2 − 2x − 2. (7)
Неравенство (7) имеет решения: x < ![]()
![]() . Из этих чисел множеству М2
принадлежат лишь x из промежутка
. Из этих чисел множеству М2
принадлежат лишь x из промежутка
![]()
![]() (3; 1 + 5).
Следовательно, неравенство (5) на множестве М2 имеет решения:
x ∈
(3; 1 + 5).
(3; 1 + 5).
Следовательно, неравенство (5) на множестве М2 имеет решения:
x ∈
(3; 1 + 5).
![]() Объединяя
найденные решения, получим, что исходное неравенство имеет множество решений: (3;
1 + 5)
∪
Объединяя
найденные решения, получим, что исходное неравенство имеет множество решений: (3;
1 + 5)
∪
∪ ⎛⎜⎝ 103 ; +∞⎞⎟⎠.
1
![]() 11.46.
а) (4 − x)x2 − 9 −
sin2 10° < (4 − x) logcos 10° 4 − x .
11.46.
а) (4 − x)x2 − 9 −
sin2 10° < (4 − x) logcos 10° 4 − x .
Решение. Все решения исходного неравенства содержатся в множестве М всех тех x, для каждого из которых 4 − x > 0, 4 − x ≠ 1, т. е. в множестве М = (−∞; 3) ∪ (3; 4). В каждой точке множества М определены все части формул
1
![]()
![]() (4 − x) logcos 10 ° 4 − x = (4 −
x)log 4 − x cos 10 °
= (4 − x)log4 − x cos2 10 °
=
(4 − x) logcos 10 ° 4 − x = (4 −
x)log 4 − x cos 10 °
= (4 − x)log4 − x cos2 10 °
=
= cos2 10°,
поэтому исходное неравенство равносильно на множестве М неравенству
(4 − x)x2 − 9 − sin2 10° < cos2 10°,
которое можно переписать в виде
(4 − x)x2 − 9 < 1. (8)
В каждой точке множества М определены все части формул
(4 − x)x2 − 9 = 10lg (4 − x )x2 − 9 = 10( x2 − 9 ) lg (4 − x ) ,
поэтому неравенство (8) равносильно на множестве М неравенству
10( x2 − 9 ) lg (4 − x ) < 100 . (9)
Логарифмируя показательное неравенство (9), получаем, что оно равносильно неравенству
(x2 − 9) lg (4 − x) < 0. (10)
Итак, исходное неравенство равносильно на множестве М неравенству (10).
1) В каждой точке множества М1 = (−∞; 3) справедливо неравенство 4 − x > 1, а значит, справедливо неравенство lg (4 − x) > 0. Поэтому на множестве М1 неравенство (10) равносильно неравенству x2 − 9 < 0, все решения которого составляют промежуток (−3; 3). Все эти числа принадлежат множеству М1. Следовательно, неравенство (10) имеет на множестве М1 решения: x ∈ (−3; 3).
2) В каждой точке множества М2 = (3; 4) справедливо двойное неравенство 0 < 4 − x < 1, а значит, справедливо неравенство lg (4 − x) < 0. Поэтому на множестве М2 неравенство (10) равносильно неравенству x2 − 9 > 0, все решения которого составляют два промежутка: (−∞; −3) и (3; +∞). Из этих чисел множеству М2 принадлежат лишь x ∈ (3; 4). Следовательно, неравенство (10) имеет на множестве М2 решения x ∈ (3; 4).
Объединяя все найденные решения, получим, что исходное неравенство имеет множество решений: (−3; 3) ∪ (3; 4).
11.47. При каких значениях параметра а все решения неравенства loga (x − 2) > loga (8 − x) содержатся в интервале (1; 5)?
Решение. По определению логарифма при a = 1 и при каждом a ≤ 0 не имеют смысла обе части исходного неравенства, поэтому при каждом из этих значений a исходное неравенство не имеет решений. Остается рассмотреть значения параметра из двух промежутков: 0 < a < 1 и a > 1. Все решения исходного неравенства содержатся в множестве М всех тех x, для каждого из которых x − 2 > 0 и 8 − x > 0, т. е. содержатся в множестве М = (2; 8).
1) При каждом a ∈ (0; 1) исходное неравенство равносильно на множестве М неравенству x − 2 < 8 − x, все решения которого составляют промежуток (−∞; 5). Из этих чисел лишь x ∈ (2; 5) принадлежат множеству М и содержатся в интервале (1; 5).
2) При каждом a > 1 исходное неравенство равносильно на множестве М неравенству x − 2 > 8 − x, все решения которого составляют промежуток (5; +∞). Из этих чисел лишь x ∈ (5; 8) принадлежат множеству М, но не содержатся в интервале (1; 5).
Итак, только при каждом a ∈ (0; 1) все решения исходного неравенства содержатся в интервале (1; 5).
Промежуточный контроль. C—41, C—42.
В данном пункте учебника приведены примеры решения неравенств при дополнительных условиях, которые фактически означают, что неравенство нужно решить на заданном множестве. В некоторых случаях, используя заданное множество, можно существенно упростить решение задачи.
Решения и комментарии
Найдите все решения неравенства, принадлежащие указанному промежутку (11.48—11.53):
![]() 11.48. а) ⎜⎝⎛sin x −
21⎞⎟⎠ ⎛⎜⎝sin x +
22 ⎟⎠⎞ > 0,
(0; π).
11.48. а) ⎜⎝⎛sin x −
21⎞⎟⎠ ⎛⎜⎝sin x +
22 ⎟⎠⎞ > 0,
(0; π).
Решение. Так как для каждого x ∈ (0; π) справедливо
![]() неравенство sin x + 2 > 0, то исходное неравенство равно-
неравенство sin x + 2 > 0, то исходное неравенство равно-
2
сильно на промежутке (0; π) неравенству
sin
x − ![]()
![]() >
0. (1)
>
0. (1)
Промежутку (0; π) принадлежат лишь решения неравенства (1), составляющие промежуток ⎜⎝⎛ 6π ; 56π ⎞⎟⎠. Следовательно, все решения исходного неравенства из промежутка (0; π) составляют промежуток ⎛⎜⎝π6 ; 56π ⎞⎟⎠.
11.50. а) x4 + x3 + x2 − 3x > 0, [−2; 2].
Решение. Очевидно, что многочлен, записанный в левой части исходного неравенства, имеет корни x1 = 0 и x2 = 1, поэтому это неравенство можно переписать в виде
x (x − 1) (x2 + 2x + 3) > 0. (2)
Так как x2 + 2x + 3 > 0 для каждого x ∈ R, то неравенство (2) равносильно неравенству
x (x − 1) > 0,
все решения которого составляют два промежутка: (−∞; 0) и (1; +∞). Из этих чисел заданному промежутку принадлежат лишь все x из промежутков [−2; 0) и (1; 2]. Следовательно, все решения исходного неравенства из промежутка [−2; 2] составляют множество [−2; 0) ∪ (1; 2].
![]()
![]() 11.52.
а) sin πx +3 cos πx + sin πx + 3 > 0, [−1; 5].
11.52.
а) sin πx +3 cos πx + sin πx + 3 > 0, [−1; 5].
24 4 2
Решение. Применив формулу синуса двойного угла, можно переписать исходное неравенство в виде
![]() 2
⎜⎝⎛sin
π4x + 23 ⎞⎟⎠ ⎛⎜⎝cos
π4x + 21⎞⎟⎠ > 0.
2
⎜⎝⎛sin
π4x + 23 ⎞⎟⎠ ⎛⎜⎝cos
π4x + 21⎞⎟⎠ > 0.
Так как для каждого x ∈ [−1; 5] верны неравенства
![]() и sin πx ≥ − 2 , то для каждого x ∈ [−1; 5]
и sin πx ≥ − 2 , то для каждого x ∈ [−1; 5]
4 2
справедливо неравенство sin πx + 3 > 0, поэтому исходное
4 2
неравенство равносильно на промежутке [−1; 5] неравенству cos πx + 1 > 0. (3) 4 2
Все решения неравенства (3), принадлежащие промежутку [−1; 5], составляют промежуток ⎡⎢⎣−1 2; 23⎞⎟⎠.
![]() 11.53.
а) sin2 x +
sin2x −
3cos2 x >
cos x −
sin x, ⎝⎜⎛π4 ; 54π⎞⎟⎠.
11.53.
а) sin2 x +
sin2x −
3cos2 x >
cos x −
sin x, ⎝⎜⎛π4 ; 54π⎞⎟⎠.
Решение. Заметим, что для каждого x ∈ ⎛⎜⎝π4 ; 54π⎞⎟⎠ спра-
ведливо неравенство cos x − sin x < 0. Поэтому все решения исходного неравенства, принадлежащие множеству M = ⎛⎜⎝π4 ; 54π⎞⎟⎠, совпадают со всеми решениями неравенства
sin2 x + sin 2x − 3 cos2 x ≥ 0,
которое, применив формулу синуса двойного угла, можно переписать в виде
sin2 x + 2 sin x cos x − 3 cos2 x ≥ 0. (4)
Неравенство (4) можно переписать в виде
(sin x + 3 cos x) (sin x − cos x) ≥ 0. (5)
Для каждого x ∈ M справедливо неравенство sin x − cos x > 0, поэтому неравенство (5) равносильно на множестве M неравенству
sin x + 3 cos x ≥ 0. (6)
![]() Введя
вспомогательный угол α
= arcsin 3 ,
перепишем
Введя
вспомогательный угол α
= arcsin 3 ,
перепишем
10
неравенство (6) в виде
sin (x + α) ≥ 0. (7)
![]() Все
решения неравенства (7) составляют серию промежутков 2πk − α ≤ x ≤ π − α
+ 2πk,
k ∈ Z.
Из этих чисел x в промежуток ⎜⎝⎛π4 ; 54π⎞⎟⎠ попадают лишь x
из промежутка ⎛⎜⎝
π4 ; π − α⎤⎥⎦.
Следовательно, условиям задачи удовлетворяют лишь x ∈ ⎜⎝⎛ π4 ; π − arcsin 310⎤⎥⎦.
Все
решения неравенства (7) составляют серию промежутков 2πk − α ≤ x ≤ π − α
+ 2πk,
k ∈ Z.
Из этих чисел x в промежуток ⎜⎝⎛π4 ; 54π⎞⎟⎠ попадают лишь x
из промежутка ⎛⎜⎝
π4 ; π − α⎤⎥⎦.
Следовательно, условиям задачи удовлетворяют лишь x ∈ ⎜⎝⎛ π4 ; π − arcsin 310⎤⎥⎦.
Замечания
1. ![]() Утверждение, что cos x − sin x < 0 на множестве ⎛⎜⎝π4 ; 54π⎞⎟⎠, можно доказать
следующим образом. Так как cos x −
sin x =
− 2 sin ⎛⎜⎝x − π4⎞⎟⎠ и для каждого x
∈ ⎝⎛⎜π4 ; 54π⎞⎟⎠ верно
неравенство 0 < x
−
Утверждение, что cos x − sin x < 0 на множестве ⎛⎜⎝π4 ; 54π⎞⎟⎠, можно доказать
следующим образом. Так как cos x −
sin x =
− 2 sin ⎛⎜⎝x − π4⎞⎟⎠ и для каждого x
∈ ⎝⎛⎜π4 ; 54π⎞⎟⎠ верно
неравенство 0 < x
− ![]()
![]() <
π, то sin ⎝⎛⎜x
− π4⎞⎟⎠ > 0.
Следовательно, cos x −
sin x <
0 для каждого x ∈ ⎛⎜⎝π4 ; 54π⎞⎟⎠, что и
требовалось доказать.
<
π, то sin ⎝⎛⎜x
− π4⎞⎟⎠ > 0.
Следовательно, cos x −
sin x <
0 для каждого x ∈ ⎛⎜⎝π4 ; 54π⎞⎟⎠, что и
требовалось доказать.
2.
Неравенство (4) учащиеся чаще всего решают по аналогии с
уравнением sin2 x +
2sin x cos x −
3 cos2 x =
0, но не проверяют, выполняется ли неравенство (4) при условии cos2
x = 0.
Они делят неравенство на cos2 x и допускают ошибку, теряя в
ответе решение ![]()
![]() .
.
Нестрогие неравенства уже рассматривались ранее в п. 7.2. В этом пункте сформулирован общий метод решения нестрогих неравенств, сводящийся к решению совокупности уравнения и строгого неравенства. Этим общим приемом лучше пользоваться всякий раз, когда решается сложное нестрогое неравенство, среди решений которого могут оказаться «изолированные» точки. Применение этого приема основано на умении рассуждать, а не на механическом следовании однажды усвоенному алгоритму. Решение нестрогих неравенств разобрано в примерах 1 и 2 учебника.
Решения и комментарии
Решите неравенство (11.57—11.62):
![]() 12 − x − x2 12 − x − x2
12 − x − x2 12 − x − x2
11.57. а) ≤ .
2x + 7 x − 5
Решение. Перенеся все члены исходного неравенства в правую часть, перепишем его в виде
![]() . (1)
. (1)
Неравенство (1) равносильно совокупности уравнения (2) и неравенства (3):
⎡(x + 12) 12 − x − x2
⎢= 0 ( )2
![]() ⎢ (2x +
7) (x −
5)
⎢ (2x +
7) (x −
5)
⎢(x + 12) 12 − x − x2
⎢⎣ (2x + 7) (x − 5) > 0. ( )3
![]() Уравнение
(2) имеет два корня: x1 =
−4 и x2 =
3. Так как числа x1 =
−4 и x2 =
3 не являются решениями неравенства (3), то все решения неравенства (3)
принадлежат множеству М =
(−4;
3). В каждой точке этого множества справедливы неравенства x + 12 > 0, 12 − x − x2 > 0 и x − 5 < 0, поэтому
неравенство (3) равносильно на множестве М неравенству 2x + 7 < 0, множество
решений которого есть промежуток (−∞;
−3,5). Из
этих чисел в множество М входят лишь x из промежутка (−4; −3,5).
Следовательно, неравенство (3) имеет множество решений: (−4; −3,5).
Уравнение
(2) имеет два корня: x1 =
−4 и x2 =
3. Так как числа x1 =
−4 и x2 =
3 не являются решениями неравенства (3), то все решения неравенства (3)
принадлежат множеству М =
(−4;
3). В каждой точке этого множества справедливы неравенства x + 12 > 0, 12 − x − x2 > 0 и x − 5 < 0, поэтому
неравенство (3) равносильно на множестве М неравенству 2x + 7 < 0, множество
решений которого есть промежуток (−∞;
−3,5). Из
этих чисел в множество М входят лишь x из промежутка (−4; −3,5).
Следовательно, неравенство (3) имеет множество решений: (−4; −3,5).
Объединив найденные решения, получим множество решений совокупности уравнения (2) и неравенства (3):
[−4; −3,5) ∪ {3}. Следовательно, исходное неравенство име ет то же множество решений: [−4; −3,5) ∪ {3}.
Дополнения
1. В § 11 приведен ряд утверждений о равносильности строгих неравенств при некоторых преобразованиях, а в § 10 приведен ряд аналогичных утверждений о равносильности уравнений. Поэтому при решении строгих неравенств переходом к совокупности строгого неравенства и уравнения к каждому из них применяется соответствующее утверждение.
Однако в некоторых случаях объем таких решений можно сократить, если воспользоваться следующими утверждениями, объединяющими соответствующие утверждения из § 10 и 11:
1. Пусть 2m — четное натуральное число (m ∈ N) и пусть в каждой точке множества М обе функции f (x) и g (x) неотрицательны. Тогда на этом множестве равносильны неравенства f (x) ≥ g (x) и (f (x))2m ≥ (g (x))2m.
2. Пусть в каждой точке множества М функция ϕ (x) определена и положительна. Тогда на этом множестве равносильны неравенства f (x) ≥ g (x) и f (x) ϕ (x) ≥ g (x) ϕ (x).
3. Пусть в каждой точке множества М обе функции f (x) и g (x) положительны, тогда на этом множестве равносильны неравенства
а) loga f (x) ≥ loga g (x) и f (x) ≥ g (x), если a > 1;
б) loga f (x) ≥ loga g (x) и f (x) ≤ g (x), если 0 < a < 1.
4. Пусть в каждой точке множества М определена функция ϕ (x), тогда на этом множестве равносильны неравенства f (x) + ϕ (x) − ϕ (x) ≥ 0 и f (x) ≥ 0.
5. Пусть в каждой точке множества М справедливы обе части некоторой формулы, тогда, применив эту формулу при решении нестрогого неравенства, получим нестрогое неравенство того же знака, равносильное на этом множестве исходному неравенству.
Приведем пример решения нестрогого неравенства с применением этих утверждений.
![]() 11x + 5 10x +
13
11x + 5 10x +
13
11.62. а) ≥ .
| x − 20| | x − 20|
Решение. Все решения исходного неравенства удовлетворяют условиям x ≠ 20, 11x + 5 ≥ 0, 10x + 13 ≥ 0, т. е. принадлежат множеству M = ⎡⎢⎣− 115 ; 20⎞⎟⎠ ∪ (20; +∞). В каж-
дой точке множества M функция ϕ (x) = | x − 20 | определена и положительна, поэтому, умножив исходное неравенство на эту функцию, получим, что оно равносильно на множестве M неравенству
![]() 11x + 5 ≥ 10x +13. (4)
11x + 5 ≥ 10x +13. (4)
Так как в каждой точке множества M обе функции f (x) = 11x + 5 и g (x) = 10x + 13 неотрицательны, то на этом множестве неравенство (4) равносильно неравенству
11x + 5 ≥ 10x + 13. (5)
Решениями неравенства (5) являются все x ≥ 8. Из этих чисел множеству M принадлежат только числа из двух промежутков: [8; 20) и (20; +∞). Все эти числа и составляют множество решений исходного неравенства. Следовательно, исходное неравенство имеет множество решений: [8; 20) ∪ (20; +∞).
2. В этом параграфе рассматривается следующий метод решения неравенств — замена неравенства на преобразованное неравенство, равносильное исходному на некотором множестве. При этом множество М выписывается в явном виде.
Однако иногда удобно не выписывать множество M в явном виде, а лишь записывать это множество в виде условий (обычно задающихся неравенствами) и рассматривать преобразованное неравенство вместе с этими условиями в виде системы, равносильной исходному неравенству.
Пример. Решим неравенство
4x2 − 8x + lg sin x < 1 + lg sin x. (6)
Решение. Все решения неравенства (6) содержатся в множестве М всех тех x, для каждого из которых
sin x > 0. (7)
На множестве М при выполнении условия (7) неравенство (6) равносильно неравенству
4x2 − 8x < 1. (8)
Итак, множество решений неравенства (6) совпадает с множеством тех решений неравенства (8), которые удовлетворяют условию (7), т. е. неравенство (6) равносильно системе
⎧⎨⎩4sinx2 x− >8x0.< 1 (9)
Таким образом, рассуждая о равносильности на множестве неравенств (6) и (8), мы пришли к выводу: неравенство (6) равносильно системе (9).
Решив систему (9), получим, что множество ее решений, а значит, и решений исходного неравенства составляет про-
![]() ⎛ 2 + 5 ⎞
межуток ⎜0;⎟.
⎛ 2 + 5 ⎞
межуток ⎜0;⎟.
⎝ 2 ⎠
Отметим, что практически во всех примерах, рассмотренных в § 11, также можно не выписывать в явном виде множество М, а рассуждая, как в приведенном выше примере, показать, что исходное неравенство равносильно некоторой системе, а затем решить эту систему.
Таким образом, метод решения неравенств, рассмотрен ный в § 11, позволяет заменить исходное неравенство равносильной ему системой не только в случаях, отмеченных в § 9, но и во многих других случаях. При этом такие преобразования, как в § 9, можно просто запомнить, а преобразования, рассмотренные в § 10, приводят исходное неравенство к равносильной ему системе лишь после некоторых рассуждений.
Конечно, при оформлении перехода от неравенства (6) к системе (9) учащиеся обычно не приводят длинные рассуждения, а просто пишут, что неравенство (6) равносильно системе (9). Однако если от учащегося потребуется обоснование этого факта, то ему придется повторить все эти рассуждения.
|
§12. |
Метод промежутков для уравнений и неравенств
В этом параграфе для решения уравнений (неравенств) с модулями применяется введенное ранее понятие равносильности уравнений (неравенств) на множестве.
В этом пункте учебника подробно разобран общий метод решения уравнений с модулями. Он проиллюстрирован различными примерами в п. 12.1 учебника и в п. 43 дидактических материалов.
Напомним, что уравнения вида
| f (x) | = | g (x) | (1)
можно также решать возведением в квадрат и переходом к уравнению f2 (x) = g2 (x), равносильному уравнению (1) на том множестве, на котором определены обе функции f (x) и g (x).
Уравнения вида
| f (x) | = g (x) (2)
можно также решать возведением в квадрат и переходом к уравнению f2 (x) = g2 (x), являющемуся следствием уравнения (2).
В данном пункте учебника рассмотрены уравнения с модулями специального вида, приведено утверждение
| f (x) | + | g (x) | = f (x) + g (x) ⇔ ⎩⎨⎧g xf x( )( ) ≥≥ 00.
Очевидно, что использование этой равносильности существенно упрощает решение уравнений такого вида.
Решения и комментарии
Решите уравнение (12.3—12.9):
12.3. а) | x2 + 4x + 2 | = x + 2.
Решение. Следствием исходного уравнения является уравнение
(x2 + 4x + 2)2 = (x + 2)2. (3)
Перенеся все слагаемые уравнения (3) в одну часть уравнения, перепишем его в виде
(x2 + 4x + 2)2 − (x + 2)2 = 0. (4)
Применив формулу разности квадратов, перепишем уравнение (4) в виде
(x2 + 3x) (x2 + 5x + 4) = 0. (5)
Уравнение (5) имеет четыре корня: x1 = −4, x2 = −3, x3 = −1 и x4 = 0. Из них исходному уравнению удовлетворяют лишь числа x3 и x4. Следовательно, исходное уравнение имеет два корня: −1 и 0.
12.4. а) | x2 − x − 1 | = x2 + 2x + 1.
Решение. Так как для каждого x ∈ R обе части уравнения неотрицательны, то исходное уравнение равносильно уравнению
(x2 − x − 1)2 = (x2 + 2x + 1)2. (6)
Перенеся все слагаемые уравнения (6) в одну часть уравнения, перепишем его в виде
(x2 − x − 1)2 − (x2 + 2x + 1)2 = 0. (7)
Применив формулу разности квадратов, перепишем уравнение (7) в виде
(−3x − 2) (2x2 + x) = 0. (8)
![]() Уравнение
(8) имеет три корня: x1 =
−
Уравнение
(8) имеет три корня: x1 =
− ![]()
![]() , x2 = −
, x2 = − ![]()
![]() и x3 = 0. Следовательно, и
равносильное ему исходное уравнение имеет те же три корня: −
и x3 = 0. Следовательно, и
равносильное ему исходное уравнение имеет те же три корня: − ![]() , −
, − ![]() и 0.
и 0.
| 2x − 4| + | x − 5|
12.5. а) ![]() = 1.
= 1.
| x − 1| + x − 1
Решение. Так как при каждом x ≤ 1 знаменатель
дроби в левой части уравнения равен нулю, то все корни исходного уравнения
принадлежат промежутку (1; +∞).
Исходное ![]() уравнение равносильно на мно-
уравнение равносильно на мно-
жестве М = (1; +∞) уравнению Рис. 82 | 2x − 4 | + | x − 5 | = 2x − 2.
Сначала решим уравнения 2x − 4 = 0 и x − 5 = 0 и отметим на координатной оси корни этих уравнений — числа 2 и 5 (рис. 82).
Числа 2 и 5 разбивают промежуток (1; +∞) на три промежутка: (1; 2), [2; 5] и (5; +∞).
1) На промежутке (1; 2) исходное уравнение равносиль но уравнению
−2x + 4 − x + 5 = 2x − 2. (9)
Уравнение (9) имеет единственный корень x1 = 2,2, не принадлежащий промежутку (1; 2). Следовательно, на этом промежутке исходное уравнение не имеет корней.
2) На промежутке [2; 5] исходное уравнение равносильно уравнению
2x − 4 − x + 5 = 2x − 2. (10)
Уравнение (10) имеет единственный корень x2 = 3, принадлежащий промежутку [2; 5]. Следовательно, на этом промежутке исходное уравнение имеет тот же единственный корень.
3) На промежутке (5; +∞) исходное уравнение равносильно уравнению
2x − 4 + x − 5 = 2x − 2. (11)
Уравнение (11) имеет единственный корень x3 = 7, принадлежащий промежутку (5; +∞). Следовательно, на этом промежутке исходное уравнение имеет тот же единственный корень.
Итак, исходное уравнение имеет два корня: 3 и 7.
| x + 1| | x + 3|
![]() 12.6.
а) + =
0.
12.6.
а) + =
0.
x + 1 x + 3
Решение. Все корни исходного уравнения принадлежат множеству тех x, для которых x + 1 ≠ 0 и x + 3 ≠ 0, т. е. множеству М всех чисел x, таких, что x ≠ −1, x ≠ −3. Теперь отметим на координатной оси числа −3 и −1 (рис. 83).
Числа −3
и −1
разбивают множество М на три промежут![]() ка: (−∞; −3), (−3; −1) и (−1; +∞). 1) Для
каждого x из проме-
ка: (−∞; −3), (−3; −1) и (−1; +∞). 1) Для
каждого x из проме-
Рис. 83 жутка (−∞; −3) левая часть
уравнения равна −2, поэтому
уравнение не имеет корней на этом промежутке.
2) Для каждого x ∈ (−3; −1) справедливы равенства | x + 1| | x + 3|
![]() + =
−1 +1
= 0, поэтому
каждое число из проме-
+ =
−1 +1
= 0, поэтому
каждое число из проме-
x + 1 x + 3 жутка (−3; −1) является корнем исходного уравнения.
3) Для каждого x из промежутка (−1; +∞) левая часть уравнения равна 2, поэтому уравнение не имеет корней на этом промежутке.
Итак, исходное уравнение имеет бесконечно много корней: каждое число x ∈ (−3; −1) является корнем исходного уравнения.
12.7. а) | 9 − 3x | + | x − 6 | = 3x − x + 9.
Решение. Сначала решим уравнения 9 − 3x = 0 и x − 6 = 0 и отметим на координатной оси корни этих уравнений — числа 2 и 6 (рис. 84).
Числа 2 и 6 разбивают координатную ось на три промежут- ![]() ка: (−∞;
2), [2; 6] и (6; +∞).
ка: (−∞;
2), [2; 6] и (6; +∞).
1) На промежутке (−∞; 2) исходное уравнение равносильно Рис. 84 уравнению
9 − 3x − x + 6 = 3x − x + 9. (12)
Уравнение (12) имеет единственный корень x1 = 1, принадлежащий промежутку (−∞; 2). Следовательно, на этом промежутке исходное уравнение имеет тот же единственный корень 1.
2) На промежутке [2; 6] исходное уравнение равносильно уравнению
−9 + 3x − x + 6 = 3x − x + 9. (13)
Уравнение (13) не имеет корней. Следовательно, на этом промежутке исходное уравнение также не имеет корней.
3) На промежутке (6; +∞) исходное уравнение равносильно уравнению
−9 + 3x + x − 6 = 3x − x + 9. (14)
Уравнение (14) имеет единственный корень x2 = 12, принадлежащий промежутку (6; +∞). Следовательно, на этом промежутке исходное уравнение имеет тот же единственный корень 12.
Итак, исходное уравнение имеет два корня: 1 и 12.
![]()
![]()
![]()
![]() 12.9. а)sin x
− 1 + cos x − 3 = sin x + cos x − 1 + 3 .
12.9. а)sin x
− 1 + cos x − 3 = sin x + cos x − 1 + 3 .
22 2
Решение. Исходное уравнение имеет вид | f (x) | + | g (x) | =
= f (x) + g (x), где f x( ) = sin x −, g x( ) = cos x − 3 . Оно
2
равносильно системе
⎧sin x − 1 ≥ 0
⎪ 2
![]() ⎨ 3
⎨ 3
⎪cos x −≥ 0,
⎩ 2
которую можно переписать в виде системы неравенств:
⎧⎪sin x ≥ 21 (15)
![]() ⎨ 3
⎨ 3
⎪cos x ≥. (16)
⎩ 2
Все решения неравенства (15) составляют серию отрезков ⎡⎢⎣ 6π + 2πk; 56π + 2πk⎤⎥⎦, k ∈ Z, а все решения неравенства (16) составляют серию отрезков ⎡⎢⎣− 6π + 2πn; 6π + 2πn⎤⎥⎦,

Рис. 85
n ∈
Z. В обе эти серии входит лишь одна серия решений ![]() k,
k ∈ Z
(рис. 85).
k,
k ∈ Z
(рис. 85).
Следовательно, система неравенств (15) и (16), а значит, и
равносильное ей исходное уравнение имеют одну серию решений ![]()
![]() +
2πk,
k ∈ Z.
+
2πk,
k ∈ Z.
В этом пункте учебника подробно разобран общий метод решения неравенств с модулями, он проиллюстрирован на различных примерах в п. 12.2 учебника и в п. 43 дидактических материалов.
Напомним, что неравенства вида
| f (x) | > | g (x) | (1)
можно также решать возведением в квадрат и переходом к неравенству (f (x))2 > (g (x))2, равносильному неравенству (1) на том множестве, на котором определены обе функции f (x) и g (x).
Решения и комментарии
Решите неравенство (12.15—12.16):
12.15. а) 2 | x | (x2 − 4x + 3) + x | x2 − 4x + 3 | > 0.
Решение. Сначала решим уравнения x = 0 и x2 − 4x + 3 = 0 и отметим на координатной оси корни этих уравнений — числа 0, 1 и 3. Эти три числа не являются решениями исходного неравенства. В этом примере полезно рассмотреть функции f (x) = x и g (x) = x2 − 4x + 3, определить промежутки их знакопостоянства (рис. 86).
1) ![]() На
интервале (−∞;
0) исходное неравенство равносильно неравенству −x
(x2 −
4x + 3)
> 0, которое
справедливо в каждой точке этого промежутка. Следовательно, каждое число x
из промежутка (−∞;
0) является решением исходного Рис. 86 неравенства.
На
интервале (−∞;
0) исходное неравенство равносильно неравенству −x
(x2 −
4x + 3)
> 0, которое
справедливо в каждой точке этого промежутка. Следовательно, каждое число x
из промежутка (−∞;
0) является решением исходного Рис. 86 неравенства.
2) На каждом из промежутков (0; 1) и (3; +∞) исходное неравенство равносильно неравенству 3x (x2 − 4x + 3) > 0, и оно справедливо для каждого числа x из этих двух промежутков. Следовательно, каждое число x из промежутков (0; 1) и (3; +∞) является решением исходного неравенства.
3) На промежутке (1; 3) исходное неравенство равносильно неравенству x (x2 − 4x + 3) > 0,
которое не имеет решений на этом промежутке.
Итак, все решения исходного неравенства составляют три промежутка: (−∞; 0), (0; 1) и (3; +∞).
12.16. а) (x + 2) ⋅ 22 − | x − 2 | − x < (x + 1) ⋅ | 2x − 1 | + 2x + 1.
Решение. Сначала решим уравнения x − 2 = 0 и 2x − 1 = 0 и отметим на координатной оси корни этих уравнений — числа 0 и 2 (рис. 87).
1)
На промежутке (−∞;
0) исходное неравенство равносильно ![]() неравенству
неравенству
(x + 1) (2x − 1) < 0. (2) Рис. 87
Так как 2x − 1 < 0 в любой
точке промежутка (−∞; 0), то, умножив
неравенство (2) на функцию ![]() , получим, что неравенство (2) равно-
, получим, что неравенство (2) равно-
сильно на этом промежутке неравенству x + 1 > 0, все решения которого составляют промежуток (−1; +∞). Из этих чисел промежутку (−∞; 0) принадлежат лишь все x из промежутка (−1; 0). Все эти числа являются решениями исходного неравенства на промежутке (−∞; 0).
2) На промежутке [0; 2] исходное неравенство равносильно неравенству (x + 2) 2x < (x + 2) 2x, которое не имеет решений. Следовательно, и равносильное ему на этом промежутке исходное неравенство также не имеет решений, принадлежащих промежутку [0; 2].
3) На промежутке (2; +∞) исходное неравенство равносильно неравенству
(x + 2) (24 − x − 2x) < 0. (3)
Так как x + 2 > 0 и 24 − x − 2x < 0 в любой точке промежутка (2; +∞), то неравенство (3) справедливо в любой точке промежутка (2; +∞), т. е. все эти числа являются решениями исходного неравенства на промежутке (2; +∞).
Итак, все решения исходного неравенства составляют два промежутка: (−1; 0) и (2; +∞).
Дополнения
1. Для неравенств с модулями специального вида справедливо утверждение
| f (x) | + | g (x) | ≤ f (x) + g (x) ⇔ ⎩⎨⎧g xf x( )( ) ≥≥ 00.
Пример 1. Решим неравенство
| x2 − 4x + 3 | + | x − 4 | − x2 + 5x − 7 ≤ 0. (4)
Решение. Перепишем неравенство в виде
| x2 − 4x + 3 | + | 4 − x | ≤ (x2 − 4x + 3) + (4 − x). (5)
По приведенному утверждению неравенство (5) равносильно системе
⎧⎨⎩4x3−−x4≥x 0+.3 ≥ 0 (6)
Все решения системы (6) составляют два промежутка: (−∞; 1] и [3; 4]. Следовательно, множество решений неравенства (4), равносильного системе (6), есть множество (−∞; 1] ∪ [3; 4].
Дополнительное задание. Решите неравенство: а) | x2 − 7x + 10 | + | x − 3 | − x2 + 8x − 13 ≤ 0;
б) | 2x − 8 | + | x − 4 | − 2x + x + 4 ≤ 0;
в) | 3x + 1 − 9 | + | lg x − 1 | − 3x + 1 + lg x + 8 ≤ 0. Ответ. а) (−∞; 2]; б) [3; 4]; в) [1; 10].
2. В тех случаях, когда при освобождении неравенства от знака модуля координатная ось разбивается на бесконечное множество промежутков, бывает полезно перейти к совокупности систем, равносильной исходному неравенству. Проиллюстрируем это на примере.
Пример 2. Решим неравенство
| sin x | + sin x (x2 − 7x + 11) < 0. (7)
![]() Решение. Ни одно из чисел x, для которого
верно равенство sin x =
0, не является решением неравенства (7). Следовательно, неравенство (7)
равносильно совокупности двух систем:
Решение. Ни одно из чисел x, для которого
верно равенство sin x =
0, не является решением неравенства (7). Следовательно, неравенство (7)
равносильно совокупности двух систем:
⎧sin x > 0
⎨⎩1 + x2 − 7x +11 < 0 (8) и
⎧sin x < 0
⎨⎩−1 + x2 − 7x +11 > 0. (9)
Рис. 88 Второе неравенство системы (8) имеет множество решений (3; 4).
Из них первому неравенству
этой системы удовлетворяют лишь x из промежутка (3; π) (рис. 88). Следовательно, система (8) имеет множество решений (3; π).
Второе неравенство системы (9) имеет множество решений (−∞; 2) ∪ (5; +∞), а первое неравенство этой системы — серию промежутков (π + 2πn; 2π + 2πn), n ∈ Z. Следовательно, система (9) имеет множество решений: интер-
вал (5; 2π) и серию интервалов (π + 2πn; 2π + 2πn), n ∈ Z, n ≠ 0 (рис. 89).
Итак, множество решений неравенства (7) состоит из интервалов (3; π) и (5; 2π) и серии интервалов (π + 2πn; 2π + 2πn), n ∈ Z, n ≠ 0.
Дополнительное задание. Решите неравенство: а) | cos x | − cos x (x2 − 5x + 5) ≥ 0;
б) 2 | sin x | + sin x (x2 − x − 4) ≤ 0;
в) 2 | cos x | − cos x (x2 + x − 4) ≥ 0.
Ответ. а) ⎢⎣⎡ 2π + 2πn; 32π + 2πn⎦⎤⎥, n ∈ Z, n ≠ 0; ⎡⎢⎣ 2π ; 2⎦⎥⎤; ⎣⎢⎡3; 32π ⎥⎦⎤;
б) [−π + 2πn; 2πn], n ∈ Z, n ≠ 0; [−π; −2]; [0; 2];
в) ⎢⎣⎡− 32π + 2πn; − 2π + 2πn⎦⎤⎥, n ∈ Z, n ≠ 0; ⎡⎢⎣− 32π ; − 2⎤⎥⎦; ⎡⎣⎢− 2π ; 2π ⎥⎤⎦.
Промежуточный контроль. С—43.
В этом пункте учебника разобран метод интервалов решения неравенств. Обратим внимание на то, что до сих пор метод интервалов применялся для решения тех неравенств, левая часть которых — алгебраическая дробь (напомним, что многочлен — частный случай алгебраической дроби), а правая часть неравенства — нуль. При этом метод решения неравенств существенно опирался на свойство двучлена сохранять знак на промежутках правее и левее числа, обращающего этот двучлен в нуль. Непрерывность функции при этом явно не использовалась.
Для решения произвольных неравенств вида f (x) ∨ 0, где ∨ — один из четырех знаков неравенства (>, <, ≥, ≤), применяется метод решения, который подробно рассмотрен в учебнике, кратко описан ниже и демонстрируется на примерах. Он опирается на свойство функции, непрерывной на каждом интервале своей области определения, не содержащем нулей этой функции, сохранять на нем знак.
Метод интервалов решения неравенства
f (x) ∨ 0, (1)
где ∨ — один из четырех знаков неравенства (>, <, ≥, ≤), должен содержать следующие шаги:
1) Найти область существования D (f) функции f (x).
2) Проверить, являются ли концы промежутков, составляющих множество D (f), решениями неравенства (1).
3) Найти нули функции f (x) и проверить, являются ли они решениями неравенства (1).
4) Исключив концы промежутков и нули функции f (x) из D (f), решить неравенство (1) на полученном множестве, состоящем из интервалов.
5) Объединить все решения, найденные в пп. 2—4.
Полученное множество и будет множеством всех решений неравенства (1).
Пример 1. Решим неравенство
![]() 10 16 − x2 (x2 − 4)
10 16 − x2 (x2 − 4)
2 + x − 6 > 0. (2)
x
![]() 10 16 − x2 (x2 − 4)
10 16 − x2 (x2 − 4)
Решение. Рассмотрим функцию f x( ) = 2 + x − 6 .
x
1) Ее область существования D (f) определяется условиями 16 − x2 ≥ 0, x2 + x − 6 ≠ 0, т. е. D (f) = [−4; −3) ∪
∪ (−3; 2) ∪ (2; 4].
2) Проверим, являются ли концы промежутков, входящих в D (f), — числа −4 и 4 — решениями неравенства (2).
Так как и f (−4) =
![]()
![]() = 2 > 0, и f ( )
= 2 > 0, и f ( )![]()
=
![]()
![]() > 0, то числа −4 и 4 являются
решениями неравенства (2).
> 0, то числа −4 и 4 являются
решениями неравенства (2).
3) Функция f (x) имеет единственный нуль при x1 = −2, это число не является решением неравенства (2).
4) Исключив −4 и 4 (концы промежутков) и −2 (нуль функции f (x)) из D (f), решим неравенство (2) на полученном множестве, состоящем из интервалов. Для этого определим знак функции f (x) на каждом из интервалов:
(−4; −3), (−3; −2), (−2; 2), (2; 4), заполнив таблицу.
|
Функция |
(−4; −3) |
(−3; −2) |
(−2; 2) |
(2; 4) |
|
|
+ |
+ |
+ |
+ |
|
x2 − 4 |
+ |
+ |
− |
+ |
|
x2 + x − 6 |
+ |
− |
− |
+ |
|
f (x) |
+ |
− |
+ |
+ |
Решения неравенства (2) составляют три интервала: (−4; −3), (−2; 2) и (2; 4).
5) Объединив найденные решения, найдем, что множество всех решений неравенства (2) состоит из трех промежутков: [−4; −3) ∪ (−2; 2) ∪ (2; 4].
Пример 2. Решим неравенство
![]() 10 16 − x2 (x2 − 4)
10 16 − x2 (x2 − 4)
2 + x − 6 ≥ 0. (3) x
Решение. Все решения неравенства (2) являются решениями неравенства (3), кроме них, неравенство (3) имеет еще одно решение: нуль функции f (x) — число −2. Следовательно, множество всех решений неравенства (3) состоит из трех промежутков: [−4; −3) ∪ [−2; 2) ∪ (2; 4].
Решения и комментарии
Решите неравенство (12.19—12.22):
(2x − 8) (lg x − 1)
12.19. а)> 0.
![]() (log x +
1)
12 −
x
(log x +
1)
12 −
x
(2x − 8) (lg x − 1)
Решение. Рассмотрим функцию f x( ) =.
![]() x x
x x
Ее область существования D (f) определяется условиями x > 0, log 1 x ≠ −1, 12 − x > 0, т. е. D (f) = (0; 2) ∪ (2; 12).
2
Функция f (x) имеет два нуля: x1 = 3 и x2 = 10, но эти числа не являются решениями исходного неравенства.
Исключив числа x1 и x2 из D (f), решим исходное неравенство на полученном множестве М, состоящем из интервалов (0; 2), (2; 3), (3; 10), (10; 12). Для этого определим знак функции f (x) на каждом из интервалов, заполнив таблицу.
|
Функция |
(0; 2) |
(2; 3) |
(3; 10) |
(10; 12) |
|
2x − 8 |
− |
− |
+ |
+ |
|
lg x − 1 |
− |
− |
− |
+ |
|
|
+ |
− |
− |
− |
|
|
+ |
+ |
+ |
+ |
|
f (x) |
+ |
− |
+ |
− |
Решения исходного неравенства на множестве М составляют два интервала: (0; 2), (3; 10). Так как других решений исходное неравенство не имеет, то эти два промежутка и составляют множество решений исходного неравенства:
(0; 2) ∪ (3; 10).
12.22. а) ![]() .
.
Решение. Перенеся все слагаемые в левую часть уравнения, сложив полученные дроби и разложив на множители числитель и знаменатель полученной дроби, получим неравенство
2 (2x + 1 5, ) (2x − 2)
![]() ≥ 0, (4)
≥ 0, (4)
3 (2x − 4) ⎛⎜⎝ 2x + 73 ⎞⎟⎠
равносильное исходному неравенству.
3 ⎜⎝⎛ 2x + 73 ⎞⎟⎠
Так как
функция ϕ (
)x = ![]() x определена
и поло-
x определена
и поло-
2 (2 + 1 5, )
жительна для каждого x ∈ R, то, умножив неравенство (4) на функцию ϕ (x), получим, что неравенство (4) равносильно неравенству
![]() . (5)
. (5)
Рассмотрим функцию ![]() .
.
Ее область существования D (f) определяется условием 2x − 4 ≠ 0, т. е. D (f) = (−∞; 2) ∪ (2; +∞).
Функция f (x) имеет единственный нуль — число x1 = 1, это число является решением неравенства (5).
Исключив нуль функции f (x) из D (f), решим неравенство
![]()
![]() >
0 (6)
>
0 (6)
на полученном множестве М, состоящем из интервалов (−∞; 1), (1; 2), (2; +∞). Для этого определим знак функции f (x) на каждом из интервалов, заполнив таблицу.
|
Функция |
(−∞; 1) |
(1; 2) |
(2; +∞) |
|
2x − 2 |
− |
+ |
+ |
|
2x − 4 |
− |
− |
+ |
|
f (x) |
+ |
− |
+ |
Решения неравенства (6) на множестве М составляют два интервала: (−∞; 1) и (2; +∞).
Объединив полученные решения, найдем, что множество всех решений неравенства (5), а значит, и равносильного ему исходного неравенства состоит из двух промежутков: (−∞; 1] ∪ (2; +∞).
Промежуточный контроль. С—45. К—6.
|
§13* |
Использование свойств функций при решении уравнений и неравенств
В этом параграфе рассмотрены приемы решения уравнений (неравенств) с использованием свойств функций, входящих в уравнение (неравенство).
![]() Следует
отметить, что ранее при решении уравнений (неравенств) уже использовались
свойства функций: например, монотонность функции при решении уравнений и
неравенств вида f x( ) ∨
g x( ), loga f (x) ∨ loga g
(x), f (α
(x)) ∨
f (β (x)),
где ∨ —
один из знаков =,
>, <, ≥, ≤.
Следует
отметить, что ранее при решении уравнений (неравенств) уже использовались
свойства функций: например, монотонность функции при решении уравнений и
неравенств вида f x( ) ∨
g x( ), loga f (x) ∨ loga g
(x), f (α
(x)) ∨
f (β (x)),
где ∨ —
один из знаков =,
>, <, ≥, ≤.
В § 13 последовательно рассмотрены способы решения уравнений и неравенств с использованием: 1) областей существования функций; 2) неотрицательности функций; 3) ограниченности функций; 4) монотонности функций и др. Кроме того, в этом параграфе рассмотрено использование числовых неравенств при решении уравнений и неравенств, а в дидактических материалах — решение уравнений вида ϕ (ϕ (x)) = x (п. 44). Освоение описанных приемов решения уравнений (неравенств) является обязательным при подготовке к решению сложных заданий конкурсных экзаменов в вузы и ЕГЭ.
Если при рассмотрении уравнения (неравенства) выясняется, что обе его части определены на множестве М, состоящем из одного или нескольких чисел, то нет необходимости проводить какие-либо преобразования уравнения (неравенства); достаточно проверить, является или нет каждое из этих чисел решением этого уравнения (неравенства).
Прежде чем разбирать громоздкие с виду задания из п. 13.1 учебника, можно предложить учащимся решить следующий пример:
Пример 1. Решим уравнение 3x − 6 + 8 − 4x = 5x − 10.
![]() Можно
ожидать, что учащиеся предложат возвести уравнение в квадрат и перейти к
уравнению-следствию. Однако если заметить, что функция f x( ) = 3x − 6 + 8 − 4x определена
лишь в точке x = 2,
тогда, если исходное уравнение имеет корень, то им может быть лишь число 2.
Остается проверить, что число 2 действительно является корнем исходного
уравнения.
Можно
ожидать, что учащиеся предложат возвести уравнение в квадрат и перейти к
уравнению-следствию. Однако если заметить, что функция f x( ) = 3x − 6 + 8 − 4x определена
лишь в точке x = 2,
тогда, если исходное уравнение имеет корень, то им может быть лишь число 2.
Остается проверить, что число 2 действительно является корнем исходного
уравнения.
![]() Чтобы
закрепить понимание необходимости проверки в таких заданиях, можно предложить
следующий пример: Пример 2. Решим уравнение 3x − 6 + 8 − 4x = 5x +10.
Чтобы
закрепить понимание необходимости проверки в таких заданиях, можно предложить
следующий пример: Пример 2. Решим уравнение 3x − 6 + 8 − 4x = 5x +10.
Здесь, как и в примере 1, функция f x( ) = 3x − 6 + 8 − 4x определена лишь в точке x = 2. Поэтому существует единственное число x = 2, которое могло бы быть корнем уравнения. Проверка показывает, что число x = 2 не является корнем исходного уравнения. Следовательно, исходное уравнение не имеет корней.
Решения и комментарии
Решите уравнение (13.1—13.2):
13.1. а) ![]() .
.
Решение. Обе части уравнения определены при выполнении двух условий: −x2 + 9x − 14 ≥ 0 и x2 − 5x − 14 ≥ 0. Этим условиям удовлетворяет единственное число x1 = 7. Проверка показывает, что число 7 является решением исходного уравнения. Следовательно, оно имеет единственный корень 7.
![]()
![]() 13.2.
а) 5 16 −
x2 +
3 = lg (1
+ x2
− 16)
+ x.
13.2.
а) 5 16 −
x2 +
3 = lg (1
+ x2
− 16)
+ x.
Решение. Обе части уравнения определены при выполнении двух условий: 16 − x2 ≥ 0 и x2 − 16 ≥ 0. Этим условиям удовлетворяют лишь два числа: x1 = 4 и x2 = −4. Проверка показывает, что число 4 является решением исходного уравнения, а число −4 нет. Следовательно, оно имеет единственный корень 4.
Решите неравенство (13.3—13.5):
![]() 13.3.
а) e 1 −
x2 + x2
− 7x
− 8 ≥ −6.
13.3.
а) e 1 −
x2 + x2
− 7x
− 8 ≥ −6.
Решение. Обе части неравенства определены при выполнении двух условий: 1 − x2 ≥ 0 и x2 − 7x − 8 ≥ 0. Этим условиям удовлетворяет единственное число x1 = −1. Проверка показывает, что число −1 является решением исходного неравенства. Следовательно, оно имеет единственное решение
![]()
![]() 13.4. а) (
x2 −
81 + 2)
log |3 x| + (
81 − x2
+1)
> 4. x
13.4. а) (
x2 −
81 + 2)
log |3 x| + (
81 − x2
+1)
> 4. x
Решение. Обе части неравенства определены при выполнении трех условий: x2 − 81 ≥ 0, 81 − x2 ≥ 0 и x ≠ 0. Этим условиям удовлетворяют лишь два числа: x1 = 9 и x2 = −9. Проверка показывает, что число 9 является решением исходного уравнения, а число −9 нет. Следовательно, оно имеет единственное решение 9.
![]() 13.5. а) 3 sin x
− 1
+ log3
(x2 +
3) > cos
x + 2.
13.5. а) 3 sin x
− 1
+ log3
(x2 +
3) > cos
x + 2.
Решение. Обе части неравенства определены при выполнении
условия sin x = 1,
т. е. только для xn ![]() n, n ∈ Z.
Проверка показывает, что для каждого xn, n ∈ Z
n, n ∈ Z.
Проверка показывает, что для каждого xn, n ∈ Z
![]() 3 sin xn − 1 + log3 ⎜⎜⎝⎛⎜⎝ 2π
+ 2πn⎟⎠⎞ 2 + 3⎟⎞⎟⎠ =
1 + log3
⎜⎝⎜⎛⎝⎜⎛
2π
+ 2πn⎟⎠⎞ 2 + 3⎞⎠⎟⎟
> 2 и ⎛
3 sin xn − 1 + log3 ⎜⎜⎝⎛⎜⎝ 2π
+ 2πn⎟⎠⎞ 2 + 3⎟⎞⎟⎠ =
1 + log3
⎜⎝⎜⎛⎝⎜⎛
2π
+ 2πn⎟⎠⎞ 2 + 3⎞⎠⎟⎟
> 2 и ⎛
cos xn + 2 = 2.
Поэтому каждое число xn = ![]()
![]() +
2πn,
n ∈ Z
является решением исходного неравенства.
+
2πn,
n ∈ Z
является решением исходного неравенства.
В этом пункте учебника сформулировано утверждение: Если каждая из функций f1 (x), f2 (x), ..., fn (x) неотрицательна для каждого x из области ее существования, то уравнение f1 (x) + f2 (x) + ... + fn (x) = 0 и неравенство f1 (x) + f2 (x) + ... + fn (x) ≤ 0 равносильны системе уравнений
⎧f x1 ( ) = 0
⎪⎨...f2 ( )x = 0 ⎪ ⎩fn ( )x = 0.
В п. 13.2 учебника и в п. 46 дидактических материалов приведены примеры применения этого утверждения при решении уравнений и неравенств.
Решения и комментарии
Решите уравнение (13.7—13.9):
13.7. а) 9x − 2 ⋅ 6x + 2 ⋅ 4x − 2 ⋅ 2x + 1 = 0.
Решение. Перепишем исходное уравнение в виде
(3x − 2x)2 + (2x − 1)2 = 0. (1)
Так как левая часть уравнения (1) есть сумма функций, неотрицательных для каждого x ∈ R, то уравнение (1) равносильно системе уравнений
⎧3x − 2x = 0 (2)
⎨⎩2x − 1 = 0. (3)
Так как уравнение (3) имеет единственный корень x1 = 0, который является также корнем уравнения (2), то эта система и равносильное ей исходное уравнение имеют единственное решение 0.
13.9. а) log2 (x2 + 2x + 2) + log3 (x6 + 2x5 + x4 + 1) = 0.
Решение. Перепишем исходное уравнение в виде log2 ((x + 1)2 + 1) + log3 ((x3 + x2)2 + 1) = 0. (4)
Так как левая часть уравнения (4) есть сумма функций, неотрицательных для каждого x ∈ R, то уравнение (4) равносильно системе уравнений
⎧log ((2 x +1)2 +1) = 0 (5)
⎨⎩log ((3 x3 + x2)2 +1) = 0. (6)
Так как уравнение (5) имеет единственный корень x1 = −1, который является также корнем уравнения (6), то эта система и равносильное ей исходное уравнение имеют единственное решение −1.
13.10. а) Решите неравенство
(x2 + 4x − 21)2 + lg (x2 − 6x + 10) ≤ 0.
Решение. Перепишем исходное неравенство в виде
(x2 + 4x − 21)2 + lg ((x − 3)2 + 1) ≤ 0. (7)
Так как левая часть неравенства (7) есть сумма функций, неотрицательных для каждого x ∈ R, то неравенство (7) равносильно системе уравнений
⎧x2 + 4x − 21 = 0 (8)
⎨⎩log ((3 x − 3)2 +1) = 0. (9)
Так как уравнение (9) имеет единственный корень x1 = 3, который является также корнем уравнения (8), то эта система и равносильное ей исходное неравенство имеют единственное решение 3.
Дополнения. Разберем решения заданий из ЕГЭ.
1. В7 (2008). Решите уравнение
![]()
![]() 25x2 − 20x + 6 =
⎛⎜⎝2 −
cos 5π4x⎞⎠⎟
⎛⎝⎜2 +
cos 5π4x⎞⎟⎠. (10)
25x2 − 20x + 6 =
⎛⎜⎝2 −
cos 5π4x⎞⎠⎟
⎛⎝⎜2 +
cos 5π4x⎞⎟⎠. (10)
Решение. Применив формулу разности квадратов и перенеся все слагаемые в левую часть, перепишем уравнение (10) в виде
(5x − 2)2 + cos2 5πx = 0. (11)
4
Так как левая часть уравнения (11) есть сумма функций, неотрицательных для каждого x ∈ R, то это уравнение равносильно системе уравнений
⎧⎪5x − 2 = 0 (12)
⎨⎪⎩cos2 5π4x = 0. (13)
Так как уравнение (12) имеет единственный корень x1
= ![]()
![]() , который является также корнем
уравнения (13), то эта система и равносильное ей уравнение (10) имеют
единственное решение
, который является также корнем
уравнения (13), то эта система и равносильное ей уравнение (10) имеют
единственное решение ![]()
![]() .
.
2. С2 (2005). Найдите нули функции y = ln2 (x2 − 3x − 9) + x3 − 8x − 8.
![]() Решение.
Для нахождения нулей функции надо решить уравнение
Решение.
Для нахождения нулей функции надо решить уравнение
ln2 (x2 − 3x − 9) + x3 − 8x − 8 = 0. (14)
Так как левая часть уравнения (14) есть сумма функций, каждая из которых неотрицательна для любого x из области ее существования, то уравнение (14) равносильно системе уравнений
⎧x2 − 3x − 9 = 1 (15)
⎨⎩x3 − 8x − 8 = 0. (16)
Уравнение (15) имеет два корня: x1 = −2 и x2 = 5. Число x1 удовлетворяет уравнению (16), а число x2 нет. Поэтому эта система уравнений, а значит, и равносильное ей уравнение (14) имеют единственное решение x2. Следовательно, исходная функция имеет один нуль, равный −2.
В этом пункте учебника сформулировано утверждение:
Если f (x) ≥ А и g (x) ≤ А для любого x ∈ D (f) ∩ D (g), где А — некоторое число, то уравнение f (x) = g (x) и неравенство f (x) ≤ g (x) равносильны системе уравнений
⎧f x( ) = A
⎨⎩g x( ) = A.
Здесь же приведены многочисленные примеры применения этого утверждения при решении уравнений и неравенств. Кроме того, в этом пункте при решении уравнений и неравенств используются неравенства a + 1 ≥ 2 (a > 0) и a
a + b
![]() ≥ ab (a
≥ 0, b
≥ 0).
≥ ab (a
≥ 0, b
≥ 0).
2
Решения и комментарии
Решите уравнение (13.14—13.17):
13.14. а) x2 − πx + π2 = sin x − 1.
4
Решение. Перепишем исходное уравнение в виде
⎛⎜⎝ − 2π ⎞⎟⎠ 2 = sin x − 1. (1) x
Так как обе части уравнения определены для каждого x ∈ R и для каждого x справедливы неравенства ⎛⎜⎝x − 2π ⎞⎟⎠ 2 ≥ 0 и sin x − 1 ≤ 0, то уравнение (1) равносильно системе уравнений
⎧⎪⎛⎜x − π ⎞⎟⎠ 2 = 0 (2)
⎨⎝ 2
⎪⎩sin x − 1 = 0. (3)
Так как уравнение (2) имеет единственный корень x1
= ![]()
![]() , который является также корнем
уравнения (3), то эта система и равносильное ей исходное уравнение имеют
единственное решение
, который является также корнем
уравнения (3), то эта система и равносильное ей исходное уравнение имеют
единственное решение ![]() .
.
13.17. а) 2 cos2 (x sin x) = 2 + | log2 (x2 − 4x + 1) |.
![]()
![]() Решение. Обе части
уравнения определены на множестве M всех x, таких, что x2
− 4x
+ 1 > 0, т. е. на
множестве M = (−∞; 2 −3)
(∪ 2
+3; +∞).
Так как для каждого x ∈
М справедливы неравенства 2 cos2 (x sin πx) ≤ 2 и 2 + | log2 (x2
− 4x
+ 1) | ≥ 2, то исходное
уравнение равносильно системе уравнений
Решение. Обе части
уравнения определены на множестве M всех x, таких, что x2
− 4x
+ 1 > 0, т. е. на
множестве M = (−∞; 2 −3)
(∪ 2
+3; +∞).
Так как для каждого x ∈
М справедливы неравенства 2 cos2 (x sin πx) ≤ 2 и 2 + | log2 (x2
− 4x
+ 1) | ≥ 2, то исходное
уравнение равносильно системе уравнений
⎧2 cos (2 x sin πx) = 2 (4)
⎨⎩2 + log (2 x2 − 4x +1) = 2. (5)
Уравнение (5) имеет два корня: x1 = 0 и x2 = 4, из которых лишь число 0 является корнем уравнения (4), поэтому эта система и равносильное ей исходное уравнение имеют единственное решение 0.
Ограниченность функций на том или ином множестве можно использовать при решении неравенств.
13.19. а) Решите неравенство log2 (x + 2) > 1 − x.
Решение. Обе части неравенства определены на множестве M всех x, таких, что x + 2 > 0, т. е. на множестве M = (−2; +∞). Для x = 0 справедливы равенства log2 (x + 2) = 1 − x = 1, для каждого x ∈ (−2; 0) справедливы неравенства log2 (x + 2) < 1 и 1 − x > 1, поэтому исходное неравенство не имеет решений на промежутке (−2; 0]. Так как для каждого x ∈ (0; +∞) справедливы неравенства log2 (x + 2) > 1 и 1 − x < 1, то каждое x ∈ (0; +∞) является решением исходного неравенства.
13.22. Решите уравнение
sin 2 x + 5 + cos 2 x + 4 4 2 2
= (sin x + 5) (cos x + 4).
2
![]() Решение.
Так как для каждого x справедливы неравенства sin2 x + 5 > 0 и cos2
x + 4
> 0, то из неравенства
Решение.
Так как для каждого x справедливы неравенства sin2 x + 5 > 0 и cos2
x + 4
> 0, то из неравенства
a b
ab (a ≥ 0, b ≥ 0) следует, что для каждого x спра-
ведливо неравенство
sin 2 x cos 2 x
.
a + b
Так как равенство = ab возможно лишь при а = b
2
(a > 0), то исходное уравнение равносильно уравнению
sin2 x + 5 = cos2 x + 4. (6)
Уравнение (6) равносильно уравнению sin2 x + 5 = = cos2 x + 4 или уравнению cos 2x = 1, все решения которого составляют серию решений xn = πn, n ∈ Z.
Следовательно, исходное уравнение, равносильное уравнению (6), имеет ту же серию решений πn, n ∈ Z.
Дополнения. Разберем решения заданий из конкурсных экзаменов и ЕГЭ.
1. (Мехмат МГУ, 2006). Решите уравнение
| 1 − 2 sin x + cos x | + 2sin x + 1 = cos 2x. (7)
Решение. Перепишем уравнение (7) в виде
| 1 − 2 sin x + cos x | − (1 − 2 sin x + cos x) =
= cos 2x − 2 − cos x. (8)
Применяя формулу косинуса двойного угла, перепишем уравнение (8) в виде
| 1 − 2 sin x + cos x | − (1 − 2 sin x + cos x) =
|
= −2 ⎜⎝ 2 − cos x⎟⎠ (1 + cos x). Так как для каждого x ∈ R имеем | 1 − 2 sin x + cos x | − (1 − 2 sin x + cos x) ≥ 0 и −2 ⎛⎜⎝ 32 − cos x⎞⎟⎠ (1 + cos x) ≤ 0, то уравнение (9) равносильно системе уравнений |
(9) |
|
⎧|1 − 2 sin x + cos x| − (1 − 2 sin x + cos x) = 0 ⎪ ⎨⎛ 3 − cos x⎞⎟ (1 + cos x) = 0. ⎜ |
(10) (11) |
⎛ 3 ⎞
⎪⎩⎝ 2 ⎠
Уравнение (11) имеет единственную серию решений xk = π + 2πk, k ∈ Z. Каждое из чисел xk удовлетворяет уравнению (10). Следовательно, эта система, а значит, и равносильное ей уравнение (7) имеют единственную серию решений π + 2πk, k ∈ Z.
2. В7 (ЕГЭ, 2008, тренировочный вариант). Решите уравнение
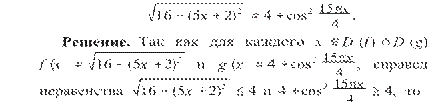
нение (12) равносильно системе уравнений
|
⎨ 2 15πx = 4. ⎪4 + cos |
(13) (14) |
⎩ 4
Так как уравнение (13) имеет единственный корень x1
= − ![]()
![]() , который является также корнем
уравнения (14), то эта система, а значит, и равносильное ей уравнение (12)
имеют единственное решение −
, который является также корнем
уравнения (14), то эта система, а значит, и равносильное ей уравнение (12)
имеют единственное решение −
![]()
![]() .
.
В этом пункте учебника сформулировано утверждение:
Если функция f (x) возрастает, а функция g (x) убывает на множестве D (f) ∩ D (g), то уравнение f (x) = g (x) имеет не более одного корня.
В п. 13.4 приведены примеры применения этого утверждения при решении уравнений. Приведем еще примеры. Пример 1. Решим уравнение
![]() 2x + cos x = 1 − 3 x. (1)
2x + cos x = 1 − 3 x. (1)
![]() Решение.
Рассмотрим функции f (x) =
2x + cos
x и g x( ) =
1 − 3
x.
Решение.
Рассмотрим функции f (x) =
2x + cos
x и g x( ) =
1 − 3
x.
![]() Так
как f′ (x)
= 2 − sin x > 0 для любого x ∈ R,
то функция f (x) возрастает на множестве R. Так как
функция 3 x возрастает на множестве R и функция
g (x) убывает на множестве R, то это означает, что
если уравнение (1) имеет корень, то он единственный. Подбором убеждаемся, что
число x1 =
0 является корнем уравнения (1), других корней уравнение (1) не имеет.
Так
как f′ (x)
= 2 − sin x > 0 для любого x ∈ R,
то функция f (x) возрастает на множестве R. Так как
функция 3 x возрастает на множестве R и функция
g (x) убывает на множестве R, то это означает, что
если уравнение (1) имеет корень, то он единственный. Подбором убеждаемся, что
число x1 =
0 является корнем уравнения (1), других корней уравнение (1) не имеет.
Следовательно, уравнение (1) имеет единственный корень 0.
Пример 2. Решим уравнение
![]() 2x
= 1 − x − 1. (2)
2x
= 1 − x − 1. (2)
![]() Рассмотрим
функции f (x) =
2x и g x( ) =
1 − x
− 1.
Обе части уравнения (2) определены на множестве М = D (f) ∩ ∩ D (g)
= [1; +∞). На множестве
M функция f (x) возрастает, а функция g (x)
убывает. Поэтому если уравнение (2) имеет корень, то он единственный. Но в
отличие от уравнения (1) уравнение (2) не имеет корней. Это следует из того,
что на множестве М функция f (x) возрастает, поэтому для
каждого x ∈
М имеем f (x) ≥
f (1) = 2.
На множестве М функция g (x) убывает, поэтому для каждого x
∈ М имеем
g (x) ≤
g (1) = 1.
Следовательно, для каждого x ∈
М имеем f (x) >
g (x), т. е. нет ни одного числа x0,
такого, чтобы выполнялось равенство f (x0) = g (x0).
А это означает, что уравнение (2) не имеет корней.
Рассмотрим
функции f (x) =
2x и g x( ) =
1 − x
− 1.
Обе части уравнения (2) определены на множестве М = D (f) ∩ ∩ D (g)
= [1; +∞). На множестве
M функция f (x) возрастает, а функция g (x)
убывает. Поэтому если уравнение (2) имеет корень, то он единственный. Но в
отличие от уравнения (1) уравнение (2) не имеет корней. Это следует из того,
что на множестве М функция f (x) возрастает, поэтому для
каждого x ∈
М имеем f (x) ≥
f (1) = 2.
На множестве М функция g (x) убывает, поэтому для каждого x
∈ М имеем
g (x) ≤
g (1) = 1.
Следовательно, для каждого x ∈
М имеем f (x) >
g (x), т. е. нет ни одного числа x0,
такого, чтобы выполнялось равенство f (x0) = g (x0).
А это означает, что уравнение (2) не имеет корней.
В этом пункте учебника рассматривается вопрос об использовании экстремумов функции при решении уравнений. Приведем пример.
Пример 3. Решим уравнение
x2 = 2 ln x + 1. (3)
Решение. Рассмотрим функцию f (x) = x2 − 2 ln x − 1. Область ее существования — множество М = (0; +∞). Функ-
ция f (x) имеет производную f′( )x =
2![]() (x2 − 1) . Производная
(x2 − 1) . Производная
x
обращается в нуль в единственной точке x1 = 1, принадлежащей множеству М. Это точка локального экстремума функции f (x). Так как f′ (x) > 0 для каждого x ∈ (1; +∞), f′ (x) < 0 для каждого x ∈ (0; 1) и f′ (1) = 0, то точка x1 = 1 — единственная точка минимума функции f (x). Поэтому f (x) > f (1) для каждого x ∈ М и x ≠ 1. Так как f (1) = 0, то f (x) = 0 только для x1 = 1. Следовательно, уравнение (3) имеет единственный корень 1. Пример 4. Решим неравенство
⎛ 1 ⎞ 3x
log
(2 x +10)
> ⎜⎝![]() ⎟⎠ . (4)
⎟⎠ . (4)
Решение. Сначала решим уравнение
⎛ 1 ⎞ 3x
![]() log (2 x
+10) = ⎜⎟ . (5)
log (2 x
+10) = ⎜⎟ . (5)
⎝⎠
Обе части уравнения (5) определены на множестве М = (−10; +∞). Поэтому если уравнение (5) имеет корни, то они принадлежат множеству М. На множестве M функ-
x
⎛ 1 ⎞ 3
![]() ция f (x)
= log2 (x
+ 10)
возрастает, а функция g x( ) =
⎜⎝⎟⎠
ция f (x)
= log2 (x
+ 10)
возрастает, а функция g x( ) =
⎜⎝⎟⎠
убывает. Проверка показывает, что число x0 = −6, принадлежащее множеству М, удовлетворяет уравнению (5) и в силу доказанного утверждения этот корень единственный.
Теперь перейдем к решению неравенства (4). Так как на множестве M функция f (x) возрастает, а функция g (x) убывает, то для каждого x1 ∈ M и x1 > x0 имеем f (x1) > > f (x0) = g (x0) > g (x1), откуда следует, что f (x1) > g (x1) для каждого x1 ∈ M и x1 > x0. Это означает, что любое такое число x1 является решением неравенства (4).
Для каждого x1 ∈ M и x1 < x0 имеем f (x1) < f (x0) = = g (x0) < g (x1). Отсюда следует, что f (x1) < g (x1) для каждого x1 ∈ M и x1 > x0. Это означает, что ни одно из таких чисел x1 не является решением неравенства (4).
Если же x1 = x0, то f (x1) = g (x1), т. е. число x0 также не является решением неравенства (4). Следовательно, все решения неравенства (4) составляют промежуток (−6; +∞).
Рассмотрим второй способ решения задания из п. 13.3 с явной опорой на монотонность функции.
13.19. а) Решите неравенство log2 (x + 2) > 1 − x.
![]() Решение. Обе части неравенства определены на
множестве M = (−2; +∞). Функция f
(x) = log2
(x + 2)
возрастает на множестве M. Функция g (x) = 1 − x убывает
на множестве M. Так как 0 ∈
М и f (0) =
g (0) = 1,
то для каждого x ∈
(−2;
0) справедливо неравенство f (x) <
1 < g
(x), а для каждого x ∈
(0; +∞)
справедливо неравенство f (x) >
1 > g
(x), поэтому только каждое x ∈
(0; +∞)
является решением исходного неравенства. Это решение иллюстрирует рисунок 90.
Решение. Обе части неравенства определены на
множестве M = (−2; +∞). Функция f
(x) = log2
(x + 2)
возрастает на множестве M. Функция g (x) = 1 − x убывает
на множестве M. Так как 0 ∈
М и f (0) =
g (0) = 1,
то для каждого x ∈
(−2;
0) справедливо неравенство f (x) <
1 < g
(x), а для каждого x ∈
(0; +∞)
справедливо неравенство f (x) >
1 > g
(x), поэтому только каждое x ∈
(0; +∞)
является решением исходного неравенства. Это решение иллюстрирует рисунок 90.
Решения и комментарии
![]() 13.30. а) Решите
уравнение x5 +
x3 +1
− 10 − x = 0.
13.30. а) Решите
уравнение x5 +
x3 +1
− 10 − x = 0.
Решение. Перепишем исходное уравнение в виде
![]() Рис. 90 x5 + x3 +1
= 10 − x. (6)
Рис. 90 x5 + x3 +1
= 10 − x. (6)
Общая часть областей суще-
ствования функций f (x) = x5 + x3 + 1 и g x( ) = 10 − x есть промежуток M = (−∞; 10]. На этом промежутке функция f (x) возрастает (как сумма возрастающих функций), а функция g (x) убывает. Так как 1 ∈ М и f (1) = g (1), то уравнение (6) имеет единственный корень 1. Следовательно, и равносильное ему на множестве M исходное уравнение имеет единственный корень 1.
13.32. а) Решите неравенство
12x5 + 10x3 + 35x − 17 sin 2x > 0.
Решение. Рассмотрим функцию f (x) = 12x5 + 10x3 + + 35x − 17 sin 2x. Область существования этой функции — множество R. Так как f′ (x) = 60x4 + 30x2 + 35 − 34 cos 2x, то для каждого x ∈ R справедливо неравенство f′ (x) > 0, поэтому функция f (x) возрастает на R. Так как f (0) = 0, то для каждого x ∈ (0; +∞) справедливо неравенство f (x) > f (0) = 0, а для каждого x ∈ (−∞; 0) справедливо неравенство f (x) < f (0) = 0. Следовательно, только каждое x ∈ (0; +∞) является решением исходного неравенства.
13.34. а) Сколько действительных корней имеет уравнение 2x4 − 4x2 + 1 = 0?
Решение. Рассмотрим функцию f (x) = 2x4 − 4x2 + 1. Область существования этой функции − множество R. Так как f (0) ≠ 0, то число 0 не является корнем исходного уравнения. Так как функция f (x) четная, то если исходное уравнение имеет положительный корень x0, то оно имеет и отрицательный корень −x0. Поэтому исследуем функцию f (x) на промежутке
(0; +∞).
![]() Для каждого x ∈ [0; +∞) имеем f′ (x) = 8x3 − 8x = 8x (x − 1) (x + 1).
Для каждого x ∈ [0; +∞) имеем f′ (x) = 8x3 − 8x = 8x (x − 1) (x + 1).
Внутри промежутка [0; +∞) имеРис. 91 ется единственная критическая точка x0 = 1. Определим знак f′ (x) на интервалах (0; 1) и (1; +∞) (рис. 91).
На промежутке (0; 1) функция убывает, f (0) = 1 > 0, f (1) = −1 < 0. Следовательно, по теореме о промежуточных значениях непрерывной функции (с. 66 учебника) на промежутке (0; 1) функция имеет единственный нуль.
На промежутке (1; +∞) функция возрастает, f (1) = = −1 < 0, f (2) = 17 > 0. Следовательно, по теореме о промежуточных значениях непрерывной функции на промежутке (1; 2) функция также имеет единственный нуль. На промежутке [2; +∞) функция возрастает, поэтому f (x) > f (2) = = 17 > 0 для каждого x ∈ (2; +∞). Следовательно, на промежутке [2; +∞) функция не имеет нулей.
Итак, если на промежутке (0; +∞) функция f (x) имеет два нуля и так как она четная, то на промежутке (−∞; 0) она также имеет два нуля. Поэтому исходное уравнение имеет четыре корня.
Дополнение. Разберем решения заданий из ЕГЭ.
1. В6 (2006). Решите уравнение
(0,2)x + 1 = 35 + 5x. (7)
![]() Решение.
Общая часть областей существования функций f (x) = (0,2)x + 1 и g x(
) = 35 + 5x есть
промежуток M = [−7; +∞). На этом
промежутке функция f (x) убывает, а функция g (x)
возрастает. Так как f (−2)
= g (−2), то уравнение
(7) имеет единственный корень −2.
Решение.
Общая часть областей существования функций f (x) = (0,2)x + 1 и g x(
) = 35 + 5x есть
промежуток M = [−7; +∞). На этом
промежутке функция f (x) убывает, а функция g (x)
возрастает. Так как f (−2)
= g (−2), то уравнение
(7) имеет единственный корень −2.
2. С5 (2008). Решите уравнение f (g (x)) + (g (3 + f (x)) = 30,
если известно, что
4 ⎧⎪25, x ≥ 4
f (x) = 0,5x − 4x + 5 и g x( ) = ⎨2x + 9 , x < 4.
⎪⎩ 5 − x
![]()
![]() Решение. Исследуем
сначала функцию f (x). Область ее определения — множество R.
Так как f′ (x)
= 2x3
− 4,
то f′ (x)
= 0 лишь в одной
точке x0 =
3 2. Так как f′
(x) > 0
для x > 32
и f′ (x)
< 0 для x < 3 2, то
x0 = 3
2 — единственная точка минимума функции f (x). Тогда для
каждого x ∈
R имеем f . Но тогда для каждого x ∈ R имеем
3 + f (x)
> 4.
Следовательно, g (3 +
f (x)) =
25 и исходное уравнение можно записать в виде f (g (x))
+ 25 = 30, или в виде 0,5 (g
(x))4 −
4g (x) =
0, или в виде
Решение. Исследуем
сначала функцию f (x). Область ее определения — множество R.
Так как f′ (x)
= 2x3
− 4,
то f′ (x)
= 0 лишь в одной
точке x0 =
3 2. Так как f′
(x) > 0
для x > 32
и f′ (x)
< 0 для x < 3 2, то
x0 = 3
2 — единственная точка минимума функции f (x). Тогда для
каждого x ∈
R имеем f . Но тогда для каждого x ∈ R имеем
3 + f (x)
> 4.
Следовательно, g (3 +
f (x)) =
25 и исходное уравнение можно записать в виде f (g (x))
+ 25 = 30, или в виде 0,5 (g
(x))4 −
4g (x) =
0, или в виде
g (x) ((g (x))3 − 8) = 0. (8)
Если x ≥ 4, то уравнение (8) не имеет корней, так как в этом случае g (x) = 25.
Если x < 4, то уравнение (8) равносильно на множестве М = (−∞; 4) совокупности двух уравнений: g (x) = 0 и g (x) = 2, которые перепишем в виде
2x = 9 (9) x − 5
и
2x = 9 + 2. (10) x − 5
Для каждого x ∈ М имеем 2х > 0 и 9 < 0, поэтому x − 5
уравнение (9) не имеет корней на множестве М.
Так как на множестве М функция g (x) = 2х возрастает, а функция ϕ ( )x = 9 убывает, то уравнение (10) имеет x − 5
не более одного корня. Проверка показывает, что число x1 = −1 является корнем уравнения (10). Поэтому число x1 = −1 является единственным корнем уравнения (10) на множестве М. Следовательно, совокупность уравнений (9) и (10) имеет на множестве М единственный корень −1. Поэтому уравнение (8) имеет единственный корень −1.
Итак, исходное уравнение имеет единственный корень −1.
Промежуточный контроль. С—44.
В этом пункте при решении уравнений и неравенств продолжается использование ограниченности функций, но применительно к функциям sin αx и cos βx. Следует обратить внимание на применение способа «рассуждения с числовыми значениями», который уже знаком учащимся по доказательствам равносильности уравнений и неравенств. Он будет применяться в дальнейшем еще и при решении систем уравнений.
Решения и комментарии
13.36. а) Решите уравнение 2 sin8 2x − 5 cos7 4x = 7.
Решение. Если число x0 — корень
исходного уравнения, то справедливо числовое равенство 2 sin8 2x0
− − 5
cos7 4x0 =
7, откуда следует, что sin8 2x0 = 1, так как в
противном случае cos7 4x0 = ![]()
![]() <
−1, что невозможно. Но тогда cos7 4x0 = −1.
Следовательно, число x0 является решением системы уравнений
<
−1, что невозможно. Но тогда cos7 4x0 = −1.
Следовательно, число x0 является решением системы уравнений
⎧sin 8 2x = 1
⎨⎩cos7 4x = −1.
Очевидно также, что любое решение этой системы является решением исходного уравнения. Следовательно, исходное уравнение равносильно этой системе уравнений.
Все решения первого уравнения системы составляют серию xn = π + πn, n ∈ Z. Так как cos7 4xn = −1 для каждо-
4 2 го xn, то все числа xn являются решениями системы и равносильного ей исходного уравнения. Поэтому исходное
уравнение имеет решения: π + πn, n ∈ Z.
4 2
Промежуточный контроль. С—46, С—47.
|
§14. |
Системы уравнений с несколькими неизвестными
В этом параграфе рассматриваются системы уравнений с несколькими неизвестными. Отличие от ранее изученного материала заключается в том, что к системам рациональных уравнений добавляются системы, содержащие корни, степени, логарифмы, тригонометрические функции.
В этом пункте напоминаются основные понятия, связанные с системами уравнений с несколькими неизвестными, сформулированы 6 утверждений о равносильности систем. Подробно разобраны метод подстановки и метод линейного преобразования систем уравнений.
Решения и комментарии
Решите систему уравнений (14.9—14.17):
14.9.
а) ⎧⎨⎩xy22 −− 42xx −+ 62yy +−141 ==00.
Решение. Заменив второе уравнение системы суммой двух ее уравнений, получим систему уравнений
⎧x2 − 4x − 2y − 1 = 0 (1)
⎨⎩x2 − 6x + y2 + 4y +13 = 0, (2)
равносильную исходной системе.
Уравнение (2) можно переписать в виде (x − 3)2 + + (y + 2)2 = 0, оно имеет единственное решение: x1 = 3, y1 = −2. Проверка показывает, что эта пара чисел является также решением уравнения (1). Следовательно, система уравнений (1) и (2), а значит, и исходная система имеют единственное решение (3; −2).
14.10. а) ⎧⎨⎩3yy−+logx =3 x10= 2.
Решение. Выразив y из второго уравнения системы через х и подставив 2 + log3 х вместо y в первое уравнение, получим систему уравнений
⎧⎨⎩y3log=3logx + 23 +xx+ =2,10 ( )( )43
равносильную исходной системе.
Уравнение (3) имеет единственный корень x1 = 1. Подставляя число 1 вместо x в уравнение (4), находим соответствующее ему значение y1 = 2. Следовательно, исходная система имеет единственное решение (1; 2).
а) ⎧⎩⎨35xx22 ++ 22xyxy −− 129xx−−44yy= −= −64.
14.15.
Решение. Заменив второе уравнение системы разностью ее второго и первого уравнений, получим систему уравнений
⎧3x2 + 2xy − 9x − 4y = −6 (5)
⎨⎩2x2 − 3x = 2, (6)
равносильную исходной системе.
Уравнение (6) имеет два корня: x1
= − ![]()
![]() и x2 = 2.
и x2 = 2.
Подставив число − ![]()
![]() вместо х в уравнение (5),
найдем соответствующее ему значение y1 =
вместо х в уравнение (5),
найдем соответствующее ему значение y1 =
![]()
![]() . Пара чисел ⎛⎜⎝ 21 ; 94⎞⎟⎠
. Пара чисел ⎛⎜⎝ 21 ; 94⎞⎟⎠
является решением исходной системы.
Подставив число 2 вместо х в уравнение (5), получим уравнение
12 + 4y − 18 − 4y = −6,
имеющее бесконечное множество корней, — любое число t ∈ R является его корнем. Следовательно, любая пара чисел (2; t), t ∈ R, также является решением исходной системы. Итак, исходная система имеет решения: ⎜⎝⎛21; 94⎞⎟⎠; (2; t), t ∈ R.
⎧⎪x − y = 5π
14.16. а) ⎨ 3
⎪⎩sin x = 2 sin y.
Решение. Исходная система равносильна системе уравнений
⎧⎪x = y + 5π (7)
⎨⎪⎩sin
⎛⎜⎝y + ![]()
![]() 3 ⎞⎟⎠ = 2 sin y. (8)
3 ⎞⎟⎠ = 2 sin y. (8)
![]() Применив
формулу синуса суммы двух углов, перенеся все слагаемые в левую часть уравнения
(8) и разделив обе части полученного уравнения на −3, получим, что уравнение (8)
равносильно уравнению
Применив
формулу синуса суммы двух углов, перенеся все слагаемые в левую часть уравнения
(8) и разделив обе части полученного уравнения на −3, получим, что уравнение (8)
равносильно уравнению
![]()
![]() 3
3
sin y +
![]() cos y = 0,
cos y = 0,
2
которое перепишем в виде
sin ⎜⎝⎛y + 6π ⎞⎟⎠ = 0. (9)
Уравнение (9) имеет единственную серию решений yk = − ![]()
![]() +
πk, k ∈
Z. Каждому числу yk найдем
соответствующее число хk из уравнения (7): xk =
+
πk, k ∈
Z. Каждому числу yk найдем
соответствующее число хk из уравнения (7): xk = ![]()
![]() +
πk, k ∈
Z.
+
πk, k ∈
Z.
Следовательно, исходная система имеет решения:
⎛⎜⎝ 32π + πk; − 6π + πk⎟⎠⎞, k ∈ Z.
⎧x + log2 y = y log2 3 + log2 x 14.17. ⎨⎩x log2 72 + log2 x = 2y + log2 y.
Решение. Заменив второе уравнение системы суммой двух ее уравнений, получим систему, равносильную исходной системе:
⎧x + log2 y = y log2 3 + log2 x (10)
⎨⎩x + x log2 72 = 2y + y log2 3.
Так как второе уравнение системы (10) можно переписать в виде
(2 + log2 3) (2x − y) = 0
и так как 2 + log2 3 ≠ 0, то система (10) равносильна системе
⎧⎨⎩xy +=log2x.2 y = y log2 3 + log2 x (11)
Подставив 2х вместо y в первое уравнение системы (11), получим систему уравнений
⎧⎨⎩xy +=log2x,2 2x = 2x log2 3 + log2 x (12)
равносильную системе (11). Первое уравнение системы (12) имеет единственный корень x1 = log4,5 2. Соответствующее ему значение y1 найдем из второго уравнения системы (12): y1 = log4,5 4.
Следовательно, исходная система имеет единственное решение (log4,5 2; log4,5 4).
Дополнения
1. Решите систему
⎧⎪⎨xy22 ++ yz22 == 22zxyz (13)
⎪⎩z2 + x2 = 2xy.
Решение. Заменив третье уравнение системы (13) суммой трех уравнений этой системы, получим равносильную ей систему
⎧
⎪⎨xy22 ++ yz22 == 22zxyz (14)
⎪⎩x2 + y2 + z2 + x2 + y2 + z2 = 2xy + 2yz + 2zx.
Перенеся все члены третьего уравнения системы (14) в левую часть и применив формулу квадрата разности, получим систему, равносильную системе (13)
⎧⎪⎨xy22 ++ yz22 == 22zxyz (15)
⎪⎩(x − y)2 + (y − z)2 + (z − x)2 = 0.
Третье уравнение системы (15) означает, что x = y = z, поэтому его решениями являются лишь тройки чисел (t, t, t), где t — любое число. Так как каждая такая тройка чисел является и решением других уравнений системы (15), то все такие тройки являются решениями системы (15), а значит, и равносильной ей системы (13).
Итак, исходная система имеет решения: (t, t, t), t ∈ R.
2. В4 (ЕГЭ, 2007). Найдите значение выражения 2x − y, если (x; y) является решением системы уравнений
⎧⎨⎩7 22x⋅ + 1x −+36yy == 432 . (16)
Решение. Заменив второе уравнение системы (16) суммой первого уравнения и второго уравнения, умноженного на 2, получим систему
⎧⎨⎩7 22 2⋅⋅ xx ++16+y7 2=⋅ 2x = 88, (17)
равносильную системе (16).
Второе уравнение системы (17) можно переписать в виде 2x = 8, откуда x = 3.
Подставляя вместо 2x число 8 в первое уравнение системы (17), получаем, что y = −9. Следовательно, система (17), а значит, и равносильная ей система (16) имеют единственное решение (x; y), где x = 3, y = −9.
Теперь находим, что значение выражения 2x − y равно 23 − (−9) = 17.
Ответ. 17.
3. С5 (ЕГЭ, 2007). Найдите количество всех решений системы уравнений
⎧⎪y (1 − x)2 + x3 = 0
⎨⎪⎩2x
− ![]() 10y = 5 log32 (0125, y2) − 7. (18) x log 2
10y = 5 log32 (0125, y2) − 7. (18) x log 2
Решение. Так как ни при каком y0 ∈ R пара чисел
(1; y0) не удовлетворяет первому уравнению системы (18), то из первого уравнения системы (18) выражаем y через x:
![]() y =
(1−−xx3 2 .
y =
(1−−xx3 2 .
)
![]() −x3
−x3
Подставляя вместо y во второе уравнение систе-
(1 − x)2
мы (18), получаем, что система (18) равносильна системе
![]() ⎧⎪y = (1−−xx3 )2
⎧⎪y = (1−−xx3 )2
![]()
![]()
![]() ⎪⎨⎪⎪ x log −x 2 ⎛ ⎛ −x3 ⎞⎟
2 ⎟⎠⎞⎟
− 7. (19)
⎪⎨⎪⎪ x log −x 2 ⎛ ⎛ −x3 ⎞⎟
2 ⎟⎠⎞⎟
− 7. (19)
2x − 10 = 5 log32 ⎜⎜0125, ⋅ ⎝⎜ (1 − x)2 ⎠
⎝
⎩
Второе уравнение системы (19) есть уравнение с одним неизвестным x. Количество решений этого уравнения и будет количеством решений системы (19), так как для каждого решения x второго уравнения системы (19) соответствующее число y однозначно определяется из первого уравнения системы (19).
Все решения второго уравнения системы (19) принадлежат
множеству M всех x, одновременно удовлетворяющих условиям x ≠ 0, ![]() .
На множестве M
.
На множестве M
второе уравнение системы (19) равносильно уравнениям
 2
(x + 5) − 2 log = 0,
2
(x + 5) − 2 log = 0,
x ⎝ 2 (1 − x)2 ⎠
Уравнение (20) на множестве М равносильно совокупности уравнений
![]() x + 5 = 0 и x − log2 −x3 2 = 0. (21)
x + 5 = 0 и x − log2 −x3 2 = 0. (21)
Итак, второе уравнение системы (19) равносильно на множестве M совокупности двух уравнений (21). Первое из уравнений совокупности (21) имеет решение x0 = −5, принадлежащее множеству M, а второе равносильно на множестве M уравнению
![]() 2x = −x3 2 . (22)
2x = −x3 2 . (22)
(1 − x)
![]() Выясним количество решений уравнения (22). При каждом x
≥ 0
левая часть уравнения (22) положительна, а правая неположительна,
следовательно, на множестве x ≥ 0 уравнение
(22) не имеет корней. На множестве x < 0 функция f (x)
= 2x возрастает, а функ-
Выясним количество решений уравнения (22). При каждом x
≥ 0
левая часть уравнения (22) положительна, а правая неположительна,
следовательно, на множестве x ≥ 0 уравнение
(22) не имеет корней. На множестве x < 0 функция f (x)
= 2x возрастает, а функ-
![]() ция
g x( ) = −x3 2 убывает, так
ция
g x( ) = −x3 2 убывает, так
как она имеет производную g′( )x = − ![]() x2 (−3 − x3 )
, отрицатель-
x2 (−3 − x3 )
, отрицатель-
(1 x) ную на этом множестве. Следовательно, на множестве x < 0 урав-
Рис. 92 нение (22) имеет не более одного решения.
![]() Так
как f (−1)
=
Так
как f (−1)
= ![]() >
> ![]() = g (−1)
= g (−1)
![]() и
f (−3)
=
и
f (−3)
= ![]() <
< ![]() = g (−3) и обе функции
непрерывны на промежутке (−3;
−1), то на
этом промежутке есть единственная точка x1, такая, что f (x1)
= g (x1)
(рис. 92).
= g (−3) и обе функции
непрерывны на промежутке (−3;
−1), то на
этом промежутке есть единственная точка x1, такая, что f (x1)
= g (x1)
(рис. 92).
Следовательно, уравнение (22) имеет единственное решение — число x1 ∈ (−3; −1), причем число x1 не совпадает с числом x0 = −5.
Проверим, принадлежит ли число x1 множеству M.
![]() −x13
−x13
Очевидно, что x1
≠ 0 и ![]() 2 >
0. Так как (
2 >
0. Так как (![]() 1 − x1)2 =
1 − x1)2 =
=
2x1 <
2−1
< 1, то ![]() .
Поэтому x1 ∈
M.
.
Поэтому x1 ∈
M.
Итак, второе уравнение совокупности (21) имеет единственное решение, принадлежащее множеству M. Следовательно, совокупность (21) имеет два различных решения, принадлежащих множеству M. Поэтому и система (18) имеет два различных решения. Ответ. 2 решения.
В этом пункте вводится новое понятие «система-следствие» и перечисляются основные способы получения систем-следствий. Для каждого из них разобраны примеры решения систем с использованием этого способа.
Решения и комментарии
Решите систему уравнений (14.22—14.24):
![]() ⎧ y + 7x + y + 2x = 5
⎧ y + 7x + y + 2x = 5
14.22. а) ⎨
⎩ y + 2x − y + x = 1.
Решение. Заменив первое уравнение исходной системы разностью первого и второго ее уравнений, получим систему
![]() ⎧ y + 7x + y − x = 4
⎧ y + 7x + y − x = 4
⎨
⎩ y + 2x − y + x = 1,
равносильную исходной системе.
Перенеся слагаемые, не содержащие корней, в правые части уравнений и возведя каждое уравнение в квадрат, получим систему
⎧⎨⎩yy ++ 72xx == xx22 ++yy22 ++116−−2xy2xy+−2y8y− +2x8,x (1)
являющуюся следствием исходной системы.
Заменив первое уравнение системы (1) разностью первого и второго ее уравнений, получим систему
⎧5x = 15 − 10y +10x
⎨⎩y + 2x = x2 + y2 +1 − 2xy + 2y − 2x, (2)
равносильную системе (1).
Выразив из первого уравнения системы (2) x через y и подставив во второе уравнение 2y − 3 вместо x, получим систему
⎧x = 2y − 3
⎨⎩y2 − 13y + 22 = 0, (3)
равносильную системе (2) и являющуюся следствием исходной системы.
Второе уравнение системы (3) имеет два корня: y1 = 2 и y2 = 11. Соответствующие им значения x найдем из первого уравнения системы (3): x1 = 1 и x2 = 19. Таким образом, система (3) имеет два решения: (1; 2) и (19; 11). Проверка показывает, что лишь пара чисел (1; 2) является решением исходной системы. Следовательно, она имеет единственное решение (1; 2).
14.24. а) ⎧⎨⎩3log (log33 ( 2x x− y−) y=)1+ log3 y = 1.
Решение. Применив формулу 3log3 ( x − y ) = x − y в первом уравнении исходной системы и формулу log3 (2x − y) + log3 y = = log3 (2xy − y2) во втором уравнении, получим систему
⎧x − y = 1
⎨⎩log (3 2xy − y2) = 1, (4)
являющуюся следствием исходной системы.
Потенцируя второе уравнение системы, получаем систему
⎧x − y = 1
⎨⎩2xy − y2 = 3, (5)
являющуюся следствием системы (4), а значит, и исходной системы.
Выразив из первого уравнения системы (5) x через y и подставив во второе уравнение y + 1 вместо x, получим систему
⎧x = y +1
⎨⎩2y y( +1) − y2 = 3, (6)
равносильную системе (5) и являющуюся следствием исходной системы.
Второе уравнение системы (6) имеет два корня: y1 = 1 и y2 = −3. Соответствующие им значения x найдем из первого уравнения системы (6): x1 = 2 и x2 = −2. Таким образом, система (6) имеет два решения: (2; 1) и (−2; −3). Проверка показывает, что лишь пара чисел (2; 1) является решением исходной системы. Следовательно, она имеет единственное решение (2; 1).
В этом пункте сформулировано утверждение о способе решения систем при помощи замены неизвестных. Отметим, что этот прием решения систем использовался ранее при решении систем, составленных из рациональных уравнений. Теперь этот прием применяется для более широкого класса уравнений.
Решения и комментарии
Решите систему уравнений (14.30—14.37):
![]() ⎧ 2x − 1 + y + 3 = 3
⎧ 2x − 1 + y + 3 = 3
14.30. а) ⎨
⎩2xy − y + 6x − 3 = 4.
Решение. Разложив на множители левую часть второго уравнения исходной системы, получим систему
![]() ⎧ 2x − 1 + y + 3 = 3
⎧ 2x − 1 + y + 3 = 3
⎨
⎩(2x − 1) (y + 3) = 4,
равносильную исходной системе.
![]()
![]() Сделав замену
неизвестных u = 2x
− 1 и v
= y + 3, перепишем систему
в виде
Сделав замену
неизвестных u = 2x
− 1 и v
= y + 3, перепишем систему
в виде
⎧u + v = 3
⎨⎩u v2 2 = 4. (1)
Решив систему (1) методом подстановки, получим, что она имеет четыре решения: u1 = 2, v1 = 1; u2 = 1, v2 = 2;
![]()
![]()
![]()
![]() 3 − 17 3 + 17 3 + 17 3 − 17
3 − 17 3 + 17 3 + 17 3 − 17
u3 =, v3 =; u4 =, v4 =. Поэто-
2 2 2 2
му исходная система равносильна совокупности четырех систем:
![]()
![]() ⎧ 2x − 1 = 2 ⎧ 2x − 1 = 1
⎧ 2x − 1 = 2 ⎧ 2x − 1 = 1
⎨⎨
⎩ y + 3 = 1, ⎩ y + 3 = 2,
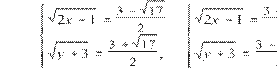
Первая система совокупности имеет единственное решение (2,5; −2), вторая — единственное решение (1; 1), а третья и четвертая системы не имеют решений. Следовательно, исходная система, равносильная совокупности четырех систем, имеет два решения: (2,5; −2) и (1; 1).
⎧ xy x − 2y 14
⎪x + 2y + xy = 15
![]() 14.34. а)
⎨⎪ xy + x + 2y = 14.
14.34. а)
⎨⎪ xy + x + 2y = 14.
⎩x − 2y xy 3
xy
Решение. Сделав замену неизвестных u
= ![]() и x + 2y
и x + 2y
x − 2y
v = ![]() , перепишем исходную систему в виде
, перепишем исходную систему в виде
xy
⎧⎪⎨u1 + v1 = 151414 (2)
⎪⎩u + v = 3 .
Выразив из первого уравнения системы (2) u через v и
подставив во второе уравнение этой системы ![]()
![]() −
v
−
v
|
вместо u, получим систему |
|
|
⎧u = 14 − v ⎪⎪ 15 ⎨ ⎪⎩ 15 равносильную системе (2). |
(3) |
Так как система (3) имеет два решения: u1 = ![]()
![]() , v1 =
, v1 = ![]()
![]() ; u2 =
; u2 = ![]()
![]() , v2 =
, v2 = ![]()
![]() — и она равносильна системе (2),
то исход-
— и она равносильна системе (2),
то исход-
ная система равносильна совокупности двух систем:
⎧ xy 1 ⎧ xy 3
⎪x + 2y = 3 ⎪x + 2y = 5
![]()
![]() ⎨⎪ xy = 5 и ⎨⎪ xy = 3. (4) ⎩x − 2y 3 ⎩x − 2y
⎨⎪ xy = 5 и ⎨⎪ xy = 3. (4) ⎩x − 2y 3 ⎩x − 2y
Перваяиз систем (4) имеет единственное решение x1
= ![]()
![]() , y1 =
, y1 = ![]()
![]() , а вторая из систем (4) имеет
единственное решение x2 =
3, y2 =
1. Поэтому исходная система, равносильная совокупности двух систем (4),
имеет два решения:
, а вторая из систем (4) имеет
единственное решение x2 =
3, y2 =
1. Поэтому исходная система, равносильная совокупности двух систем (4),
имеет два решения:
⎛ 5 5 ⎞
⎜⎝ 3 ; 9 ⎟⎠ и (3; 1).
![]() ⎧4 x + y − 4 x
− y = 2
⎧4 x + y − 4 x
− y = 2
14.35. а) ⎨
⎪⎩ x + y − x − y = 8.
![]()
![]() Решение. Сделав
замену неизвестных u =
4 x +
y и v =
4 x −
y, перепишем исходную систему в виде
Решение. Сделав
замену неизвестных u =
4 x +
y и v =
4 x −
y, перепишем исходную систему в виде
⎧u − v = 2
⎨⎩u2 − v2 = 8. (5)
Так как система (5) имеет единственное решение u1 = 3, v1 = 1, то исходная система равносильна системе
⎧4 x + y = 3
![]() ⎨4(6)
⎨4(6)
⎪⎩ x − y = 1.
Система (6) имеет единственное решение x1 = 41, y1 = 40. Следовательно, равносильная ей исходная система имеет единственное решение (41; 40).
⎧ x + y + 4 x − y = 8
![]() 14.37. ⎨4 3 2 2 3
14.37. ⎨4 3 2 2 3
⎪⎩ x + x y − xy − y = 12.
![]()
![]() Решение. Так
как x3 +
x2y −
xy2 −
y3 =
(x −
y) (x +
y)2, то, сделав замену неизвестных u = x + y и v = 4 x − y,
перепишем исходную систему в виде
Решение. Так
как x3 +
x2y −
xy2 −
y3 =
(x −
y) (x +
y)2, то, сделав замену неизвестных u = x + y и v = 4 x − y,
перепишем исходную систему в виде
⎧u + v = 8
⎨4 4 4 (7)
![]() ⎩ u v = 12.
⎩ u v = 12.
Так как система (7) имеет два решения: u1 = 6, v1 = 2; u2 = 2, v2 = 6, то исходная система равносильна совокупности двух систем:
⎧ x + y = 6 ⎧ x + y = 2
![]()
![]() ⎨4и ⎨4(8)
⎨4и ⎨4(8)
⎪⎩ x − y = 2 ⎪⎩ x − y = 6.
Первая из систем (8) имеет единственное решение x1 = 26, y1 = 10, а вторая из систем (8) имеет единственное решение x2 = 650, y2 = −646.
Так как исходная система равносильна совокупности двух систем (8), то она имеет только эти два решения:
(26; 10) и (650; −646).
Дополнение
С3 (ЕГЭ, 2005). Решите систему уравнений
⎧ −y + 10x + 11
⎪⎨ ![]() −2y −
5x = −5y − 15x + 22 (9)
−2y −
5x = −5y − 15x + 22 (9)
⎪⎩25−2 y − 5 x + 25 = 26 5⋅ −2 y ⋅ 5−5 x.
Решение. Сделав замену неизвестных t = 5−2y − 5x, перепишем второе уравнение системы (9) в виде
t2 − 26t + 25 = 0. (10)
Уравнение (10) имеет два корня: t1 = 25, t2 = 1. Поэтому система (9) равносильна совокупности двух систем
⎧ −y + 10x + 11
⎪⎨ ![]() −2y −
5x = −5y − 15x + 22 (11)
−2y −
5x = −5y − 15x + 22 (11)
⎪⎩5−2 y − 5 x = 25
и
⎧ −y + 10x + 11
⎪⎨ ![]() −2y −
5x = −5y − 15x + 22 (12)
−2y −
5x = −5y − 15x + 22 (12)
⎪⎩5−2 y − 5 x = 1.
Решим каждую из этих систем. Второе уравнение системы (11)
равносильно уравнению x =
− ![]()
![]() (1 + y). Подставляя
−
(1 + y). Подставляя
− ![]()
![]() (1 +
y) вместо x в первое уравнение системы (11), получаем
систему
(1 +
y) вместо x в первое уравнение системы (11), получаем
систему
⎧ −y + 10x + 11
⎪ ![]() −2y −
5x = −5y − 15x + 22 (13)
−2y −
5x = −5y − 15x + 22 (13)
⎨
⎪x = − 2 (1 + y),
⎩ 5
равносильную системе (11). Система (13) имеет единственное решение (2,4; −7). Следовательно, и равносильная ей система (11) имеет то же единственное решение. Второе уравнение системы (12) равносильно уравнению −2y − 5x = 0.
Поэтому система (12) равносильна системе
⎧ −y + 10x + 11
⎪⎨ ![]() −2y −
5x = −5y − 15x + 22
−2y −
5x = −5y − 15x + 22
⎪⎩−2y − 5x = 0,
которая не имеет решений.
Следовательно, система (9) имеет единственное решение (2,4; −7).
Ответ. (2,4; −7).
Промежуточный контроль. С—48.
В этом пункте приведены примеры решения систем уравнений при помощи метода, называемого «рассуждения с числовыми значениями». Используется этот метод тогда, когда перечисленные в пп. 14.1—14.3 методы решения оказываются неприменимыми. Суть его заключается в том, что сначала предполагается, что система, например, с двумя неизвестными x и y имеет решение (x0; y0), затем, подставляя x0 и y0 вместо x и y в уравнения системы, получают верные числовые равенства, из которых находят ограничения на x0 и y0 или выражают одно из этих чисел через другое. Тем самым получают более простую систему, решением которой является эта пара. Таким образом, если пара чисел (x0; y0) — решение исходной системы, то эта пара является решением новой, более простой системы.
Обратим внимание на важный шаг: такое рассуждение должно заканчиваться проверкой всех найденных решений подстановкой в исходную систему, так как исходной системе могут удовлетворять не все найденные пары. Пары, удовлетворяющие исходной системе, дают все ее решения.
Решения и комментарии
Решите систему уравнений (14.38—14.45):
14.38. а) ⎧⎨⎩2tgx22x++1y=2 y= −1.| sin x|
Решение. Пусть пара чисел (x0; y0) является решением исходной системы, тогда справедливы числовые равенства
2x20 + 1 = y0 − | sin x0 |, tg2 x0 + y02 = 1.
Из первого равенства следует, что y0 = | sin x0 |
+ 2x20
+ 1, т. е. y0
≥ 1.
Из второго равенства следует, что y![]() , т. е. y
, т. е. y![]() 1. Это означает, что y0 =
1. Подставив в оба равенства вместо y0 число 1,
получим, что справедливы числовые равенства
1. Это означает, что y0 =
1. Подставив в оба равенства вместо y0 число 1,
получим, что справедливы числовые равенства
2x20 = − | sin x0 | и tg2 x0 = 0,
откуда следует, что x0 = 0.
Итак, если исходная система имеет решение (x0; y0), то это может быть только пара (0; 1). Проверка показывает, что пара (0; 1) действительно является решением исходной системы. Следовательно, исходная система имеет единственное решение (0; 1).
⎧(x2 + xy + y2) x2 + y2 = 185
![]() 14.40.
а) ⎨⎪⎩(x2 −
xy + y2) x2 +
y2 = 65.
14.40.
а) ⎨⎪⎩(x2 −
xy + y2) x2 +
y2 = 65.
Решение. Пусть пара чисел (x0; y0) является решением исходной системы, тогда справедливы числовые равенства
![]() (x20 + x y0 0 +
y20 )
x20 + y20 = 185, (1)
(x20 + x y0 0 +
y20 )
x20 + y20 = 185, (1)
(x20 + x y0 0 + y20 ) x20 + y20 = 65. (2)
![]() Обе
части каждого из равенств (1) и (2) имеют смысл и положительны, поэтому
справедливо числовое равенство (x20 +x y0 0 +y20 ) x20 +y20
Обе
части каждого из равенств (1) и (2) имеют смысл и положительны, поэтому
справедливо числовое равенство (x20 +x y0 0 +y20 ) x20 +y20
= ,
(x20 −x y0 0 +y20 ) x20 +y20
которое перепишем в виде
![]() 0. (3)
0. (3)
Так как x0 ≠ 0 (в противном случае из равенства (3) следует, что и y0 = 0, но тогда оба равенства (1) и (2) неверны), то равенство (3) можно переписать в виде
x20 x0
![]() 12 − 25 +12
= 0, y20 y0
12 − 25 +12
= 0, y20 y0
откуда следует, что или x0 = 34 y 0 или x0 = 34 y 0 .
Это означает, что пара чисел (x0; y0) является решением совокупности двух систем:
![]()
![]() ⎧⎪(x2 − xy +y2) x2
+y2
= 65 ⎧⎪(x2
− xy
+y2) x2
+y2
= 65
⎧⎪(x2 − xy +y2) x2
+y2
= 65 ⎧⎪(x2
− xy
+y2) x2
+y2
= 65
⎨ 3 и ⎨ 4 (4)
⎪⎩x = 4 y ⎪⎩x = 3 y.
Первая система совокупности (4) имеет два решения: (3; 4) и (−3; −4). Вторая система совокупности (4) имеет два решения: (4; 3) и (−4; −3). Итак, показано, что если исходная система имеет решения, то они содержатся среди четырех пар чисел: (3; 4), (−3; −4), (4; 3) и (−4; −3). Проверка показывает, что все эти пары действительно являются решениями исходной системы. Следовательно, исходная система имеет четыре решения: (3; 4), (−3; −4), (4; 3) и (−4; −3).
⎧x − y + x2 − 4y2 = 2
![]() 14.41. ⎨⎪⎩x5 x2 − 4y2 =
0.
14.41. ⎨⎪⎩x5 x2 − 4y2 =
0.
Решение. Пусть пара чисел (x0; y0) является решением исходной системы, тогда справедливы числовые равенства
![]() x0 − y 0
+ x20
− 4y20
= 2, (5) x50 x20 − 4y20 =
0. (6)
x0 − y 0
+ x20
− 4y20
= 2, (5) x50 x20 − 4y20 =
0. (6)
Обе части каждого из равенств имеют смысл, поэтому
справедливо числовое неравенство x![]() 0. Заметим,
что если x0 =
0, то и y0 =
0, но тогда равенство (5) неверно, следовательно, x0 ≠ 0. Тогда из
равенства (6) следует, что x
0. Заметим,
что если x0 =
0, то и y0 =
0, но тогда равенство (5) неверно, следовательно, x0 ≠ 0. Тогда из
равенства (6) следует, что x![]() 0, т. е. или x0 = 2y0,
или x0 =
−2y0. А это означает, что пара чисел (x0;
y0) является решением совокупно-
0, т. е. или x0 = 2y0,
или x0 =
−2y0. А это означает, что пара чисел (x0;
y0) является решением совокупно-
сти двух систем:
![]() ⎧⎨x
− y + x2 − 4y2
= 2 и
⎧⎨x
− y + x2 − 4y2
= 2 и
⎩x = 2y
![]() ⎧⎨x − y + x2 − 4y2
= 2 (7)
⎧⎨x − y + x2 − 4y2
= 2 (7)
⎩x = −2 .y
Первая система совокупности (7) имеет единственное решение (4; 2). Вторая система совокупности (7) имеет единственное решение ⎜⎝⎛ 34; − 23 ⎞⎟⎠ . Итак, показано, что если исходная система имеет решения, то они содержатся среди двух пар чисел: (4; 2) и ⎜⎝⎛ 34; − 23 ⎞⎟⎠ . Проверка показывает,
что обе эти пары являются решениями исходной системы. Следовательно, исходная система имеет два решения:
(4; 2) и ⎜⎝⎛ 34; − 23 ⎞⎟⎠ .
⎧2 log1− x (−xy − 2x +y +2) + log2 + y (x2 − 2x +1) = 6
14.42. а) ⎨⎩log1− x (y +5) − log2 + y (x +4) = 1.
Решение. Пусть пара чисел (x0; y0) является решением исходной системы, тогда справедливы числовые равенства
2 log1− x0 (−x y0 0 − 2x0 +y 0 +2) + log2 + y0 (x20 − 2x0 +1) = 6, (8) log1− x0 (y 0 + 5) − log2 + y0 (x0 +4) = 1. (9)
Обе части каждого из равенств имеют смысл, поэтому справедливы числовые неравенства
1 − x0 > 0, 1 − x0 ≠ 0, 2 + y0 > 0,
(10)
2 + y0 ≠ 1, y0 + 5 > 0, y0 + 4 > 0.
Учитывая эти неравенства, левую часть равенства (8) можно переписать так:
2 log1− x0 (1 − x0)(2 + y 0) + log2 + y0 (1 − x0)2 =
= 2 log1− x0 (1 − x0)(2 + y 0) + 2 log2 + y0 (1 − x0) = = 2 (log1− x0 (1 − x0) + log1− x0 (2 + y 0) + log2 + y0 (1 − x0)) =
= 2 1⎜⎜⎝⎛ +
log1−
x0 (2 + y 0) +
log![]() 1− x01(2
+
y0) ⎟⎟⎠⎞.
1− x01(2
+
y0) ⎟⎟⎠⎞.
Тогда равенство (8)
перепишется в виде log1−
x0 (2 + y 0) +
log![]() 1− x 1(2 + y0)
= 2. (11)
1− x 1(2 + y0)
= 2. (11)
0
Из справедливости равенства (11) следует, что число log1− x0 (2 + y 0) положительное (в противном случае равенство (11) или не имеет смысла, или неверно). Так как для
каждого числа a > 0 справедливо неравенство a + 1 ≥ 2, a
причем a + 1 = 2 лишь при a = 1, то равенство (11) спра-
a
ведливо лишь при условии log1− x0 (2 + y 0) = 1, т. е. если y0 = −x0 − 1.
Подставив в равенство (9) −x0 − 1 вместо y0, получим, что справедливо равенство log1− x0 (4 − x0) − log1− x0 (x0 + 4) = log1− x0 (1 − x0).
Теперь очевидно, что число x0 является корнем уравнения log1 − x (4 − x) − log1 − x (x + 4) = log1 − x (1 − x).
Так как это уравнение имеет единственный корень x0 = −2, то решением исходной системы может быть лишь пара чисел x0 = −2, y0 = 2 − 1 = 1.
Проверка показывает, что пара (−2; 1) действительно является решением исходной системы. Следовательно, исходная система имеет единственное решение (−2; 1).
⎧⎪ 1− 25 logx y = x y
![]() 14.43. а) ⎨ ⎛ 3y⎞
14.43. а) ⎨ ⎛ 3y⎞
⎪⎩1 + logx ⎜⎝1 − x ⎟⎠ = logx 4.
Решение. Пусть пара чисел (x0; y0) является решением исходной системы, тогда справедливы числовые равенства
1 − 25 logx0 y0 ![]()
![]()
y 0 = x0 , (12)
⎛ 3y0 ⎞
1
+ logx0 ⎜⎝1 −
![]() x0 ⎟⎠ = logx0 4. (13)
x0 ⎟⎠ = logx0 4. (13)
Обе части каждого из равенств имеют смысл, поэтому справедливы числовые неравенства
3y0 x0
> 0, x0
≠ 1, y0
> 0, 1 − ![]() > 0. (14) x0
> 0. (14) x0
Учитывая эти неравенства, преобразуем левую часть равенства (13):
⎛ 3y0 ⎞ ⎛ 3y0 ⎞
1 +
logx0 ⎜⎝1 −
![]() x0 ⎠⎟ = logx0 x0 + logx0 ⎜⎝1
−
x0 ⎠⎟ = logx0 x0 + logx0 ⎜⎝1
−
![]() x0 ⎠⎟ = logx0 (x0 − 3y 0).
x0 ⎠⎟ = logx0 (x0 − 3y 0).
Поэтому равенство (13) можно записать в виде logx0 (x0 − 3y 0) = logx0 4, откуда, учитывая неравенства (14), получаем, что x0 − 3y0 = 4 и обе части равенства (12) положительны. Поэтому, прологарифмировав равенство (12) по основанию x0 (x0 > 0 и x0 ≠ 1) и умножив обе части полученного равенства на 5, получим, что справедливо числовое равенство (5 − 2 logx0 y 0) logx0 y 0 = 2.
![]() Так
как уравнение (5 −
2t) t =
2 имеет два корня: t1 =
2, t2
=
Так
как уравнение (5 −
2t) t =
2 имеет два корня: t1 =
2, t2
= ![]()
![]() , то получим, что справедливо или
равенство logx0 y 0 =
2, или равенство logx0 y 0 =
, то получим, что справедливо или
равенство logx0 y 0 =
2, или равенство logx0 y 0 = ![]()
![]() , т. е. получим, что или y0
= x20,
или y 0 =
x0 . Это означает, что пара чисел (x0;
y0) является решением совокупности двух систем:
, т. е. получим, что или y0
= x20,
или y 0 =
x0 . Это означает, что пара чисел (x0;
y0) является решением совокупности двух систем:
![]() ⎧⎨⎩y
= x2 и ⎧⎨y −= 3yx= 4. (15)
⎧⎨⎩y
= x2 и ⎧⎨y −= 3yx= 4. (15)
x − 3y = 4 ⎩x
Первая система совокупности (15) не имеет решений. Вторая система совокупности (15) имеет единственное решение (16; 4). Итак, показано, что решением исходной системы может быть лишь пара чисел (16; 4).
Проверка показывает, что пара чисел (16; 4) является решением исходной системы. Следовательно, исходная система имеет единственное решение (16; 4).
а) ⎧⎨⎩sintg22xy++ctgcos22xz == 21.sin2 y
14.44.
Решение. Пусть тройка чисел (x0; y0; z0) является решением исходной системы, тогда справедливы числовые равенства:
tg2 x0 + ctg2 x0 = 2sin2 y0, (16) sin2 y0 + cos2 z0 = 1. (17)
Числа x0, y0 и z0 таковы, что обе части равенств (16) и (17) определены, но тогда tg2 x0 > 0. Так как для каж-
дого числа a > 0 справедливо неравенство a + 1 ≥ 2, то a
tg2 x0 + ctg2 x0 ≥ 2. Для любого числа y0 имеем 2 sin2 y0 ≤ 2, следовательно, из справедливости равенства (16) следует, что справедливы равенства
tg2 x0 + ctg2 x0 = 2 (18)
и
sin2 y0 = 1. (19)
Из равенства (18) получим, что tg2 x0 = 1, т. е. x0 = π4 + π2k,
k ∈
Z, из равенства (19) получим, что y ![]() l .
l .
Но тогда из равенства (17) получим, что cos2
z0 =
0, т. е. z0 =
![]()
![]() + πm, m
∈ Z.
+ πm, m
∈ Z.
Итак, показано, что если исходная система имеет решение, то оно содержится среди троек чисел
⎛⎝⎜ π4 + π2k; 2π + πl; 2π + πm⎟⎞⎠, k ∈ Z, l ∈ Z, m ∈ Z.
Проверка показывает, что все эти тройки чисел являются решениями исходной системы. Следовательно, исходная система имеет решения ⎜⎝⎛ π4 + π2k; 2π + πl; 2π + πm⎞⎟⎠, k ∈ Z, l ∈ Z, m ∈ Z.
![]() 14.45. ⎧⎪⎨ 3 + 2 cos (2 x −
y) = 3 +
2x − x2 ⎪⎩z2 + 2x2 − 2z − 1 = 4(x − 1).
14.45. ⎧⎪⎨ 3 + 2 cos (2 x −
y) = 3 +
2x − x2 ⎪⎩z2 + 2x2 − 2z − 1 = 4(x − 1).
![]() 2 x − y +
sin2 x −
y cos
2 x − y +
sin2 x −
y cos
2 2
Решение. Пусть тройка чисел (x0; y0; z0) является решением исходной системы, тогда справедливы числовые равенства:
3
![]()
![]() +
2 cos (x0 −y0) = + − 2 cos2 x0 −
y0 +
sin2 x0 − y0 , (20)
+
2 cos (x0 −y0) = + − 2 cos2 x0 −
y0 +
sin2 x0 − y0 , (20)
2 3 2x0 x0 2 2
z20 + 2x20 − 2z0 − 1 = 4 (x0 − 1). (21)
Равенство (21) можно переписать в виде (z0 − 1)2 + + 2 (x0 − 1)2 = 0, поэтому x0 = 1, z0 = 1. Подставив в равенство (20) вместо x0 число 1, получим верное числовое равенство
![]()
![]()
![]()
![]()
![]()
![]() + −
y = 2 −
y + sin2 −
y . (22)
+ −
y = 2 −
y + sin2 −
y . (22)
2 cos
Применив формулы для синуса и косинуса половинного угла, перепишем равенство (22) в виде
![]()
![]() + cos ( −
y ) −
cos ( −
y )
+ cos ( −
y ) −
cos ( −
y )
![]() = 1 + cos (1 − y 0)
+
= 1 + cos (1 − y 0)
+ ![]() ,
,
откуда получим, что cos (1Последнее равенство справедливо, если− y0) = 0 или cosy(0y0=−11)+ 2π=+0.πm, m ∈ Z.
Проверка показывает, что для каждого m ∈ Z тройка чисел ⎜⎝⎛1 1; + 2π + πm; 1⎞⎟⎠ является решением исходной системы. Следовательно, исходная система имеет серию решений ⎜⎝⎛1 1; + 2π + πm; 1⎞⎟⎠, m ∈ Z.
Дополнения
1. Отметим, что существуют системы уравнений, в которых число уравнений меньше числа неизвестных. В таких случаях обычно в уравнениях скрыты какие-либо дополнительные ограничения на неизвестные, которые и позволяют решить систему. Рассуждения с числовыми значениями позволяют решать некоторые системы двух уравнений с тремя неизвестными (задания 14.44 и 14.45) и даже одно уравнение с двумя или тремя неизвестными. Приведем примеры.
Пример 1. Решим уравнение
(x2 − 4x + 7) (y2 + 6y + 14) = 15. (23)
Решение. Пусть пара чисел (x0; y0) есть решение уравнения (23), т. е. пусть справедливо числовое равенство
(x20 − 4x0 + 7) (y20 + 6y0 + 14) = 15,
которое перепишем в виде
((x0 − 2)2 + 3) ((y0 + 3)2 + 5) = 15. (24)
Равенству (24) удовлетворяет единственная пара чисел x0 = 2, y0 = −3. Поэтому если уравнение (23) имеет решение, то это может быть только пара чисел (2; −3). Проверка показывает, что эта пара чисел удовлетворяет уравнению (23). Следовательно, уравнение (23) имеет единственное решение (2; −3).
Пример 2. Решим уравнение
![]()
![]() arcsin ⎛⎜⎜x ⎛ 1 ⎞ 2 − x 4y2 |⎞⎟⎟⎠ +
arcsin ⎛⎜⎜x ⎛ 1 ⎞ 2 − x 4y2 |⎞⎟⎟⎠ +
2 − x + ⎜
⎝ ⎝ 2 ⎟⎠ + arccos π + | tg (x + z − π − 1)
+ 2x2 − x − 1 = x − x2 + arctg (2 − x). (25)
![]() Решение.
Предположим, что тройка чисел (x0; y0; z0)
есть решение уравнения (25), т. е. предположим, что справедливо числовое
равенство arcsin ⎛⎜⎜⎝x20
− x0
+
⎛⎝⎜ 12 ⎞⎠⎟ 2 − x0 +
arccos 4yπ0 + | tg (x0 + z − π − 1)2 |⎞⎠⎟⎟ +
Решение.
Предположим, что тройка чисел (x0; y0; z0)
есть решение уравнения (25), т. е. предположим, что справедливо числовое
равенство arcsin ⎛⎜⎜⎝x20
− x0
+
⎛⎝⎜ 12 ⎞⎠⎟ 2 − x0 +
arccos 4yπ0 + | tg (x0 + z − π − 1)2 |⎞⎠⎟⎟ +
0
+ 2x20 − x0 − 1 = x0 − x20 + arctg (2 − x0). (26)
![]() Из
справедливости равенства (26) следует, в частности, что выражения и определены,
а это означает, что число x0 удовлетворяет одновременно двум
неравенствам: 2x
Из
справедливости равенства (26) следует, в частности, что выражения и определены,
а это означает, что число x0 удовлетворяет одновременно двум
неравенствам: 2x![]() 0 и x
0 и x![]() 0.
Легко проверить, что существует только одно такое число: x0 = 1. Но если x0
= 1, то
равенство (26) можно переписать в виде
0.
Легко проверить, что существует только одно такое число: x0 = 1. Но если x0
= 1, то
равенство (26) можно переписать в виде
⎛ 1 4y0 ⎞
![]() arcsin ⎜⎝ + arccos
arcsin ⎜⎝ + arccos
![]() π + | tg z0 |⎟⎠ = arctg
1. (27) Так как arctg 1 =
и arcsin a =
π + | tg z0 |⎟⎠ = arctg
1. (27) Так как arctg 1 =
и arcsin a =
![]()
![]() только для a =
только для a = ![]() ,
то
,
то
|
равенство (27) означает справедливость равенства |
|
|
4y0 arccos |
(28) |
π
4y0
Так как существуют числа arccos ![]() и | tg z0 | и
оба π
и | tg z0 | и
оба π
они неотрицательны, то равенство (28) справедливо лишь тогда, когда каждое из этих чисел равно нулю, т. е.
4y0 лишь
тогда, когда arccos ![]() = 0 и tg z0
= 0. Первое
из этих π
= 0 и tg z0
= 0. Первое
из этих π
равенств справедливо лишь для y 0
= ![]()
![]() , а второе лишь для z0 = πk, k ∈ Z.
, а второе лишь для z0 = πk, k ∈ Z.
Итак, если уравнение (25) имеет решения, то все они содержатся среди троек чисел ⎜⎝⎛1; π4 ; πk⎞⎟⎠, k ∈ Z. Проверка
показывает, что такая тройка удовлетворяет уравнению (25) только при k ∈ N. Следовательно, все решения уравнения (25) есть тройки чисел ⎜⎝⎛1; π4 ; πk⎞⎟⎠, k ∈ N.
2. Разберем решение задания из ЕГЭ.
С5 (2008). Докажите, что система уравнений
⎧⎪8x3 +18x2 +15x +14 = 0 (29)
![]() ⎨⎪⎩(10 +4x)y − 2 = y ⎛⎜⎝5+ 7x⎞⎟⎠ +7x
y+ 16x
x( +1)2 +40x2 +89x +49
⎨⎪⎩(10 +4x)y − 2 = y ⎛⎜⎝5+ 7x⎞⎟⎠ +7x
y+ 16x
x( +1)2 +40x2 +89x +49
имеет хотя бы два различных решения.
Доказательство. Пусть пара чисел (x0; y0) есть решение системы уравнений (29), т. е. пусть справедливы числовые равенства
8x30 +18x20 +15x0 +14 = 0, (30)
(10 + 4x0)y0 − 2 =
![]() = y 0 ⎜⎝⎛5 +
x70 ⎞⎟⎠ + 7x0 0+ y 16x x +1 + 40x + 89x + 49. (31)
= y 0 ⎜⎝⎛5 +
x70 ⎞⎟⎠ + 7x0 0+ y 16x x +1 + 40x + 89x + 49. (31)
Но если справедливо числовое равенство (31), то, в частности, справедливо числовое неравенство
![]() 0. (32)
0. (32)
Так как 16x0 (x0 + 1)2 + 40x20 + 89x0 + 49 = 16x0 (x0 + 1)2 +
+ 40 (x2 + 2x + 1) + 9 (x + 1) = (x + 1) (16x2 + 56x + 49) =
![]() , то неравенство (32) можно записать
, то неравенство (32) можно записать
в виде
(x0 + 1) (4x0 + 7)2 ≥ 0. (33)
Неравенство (33) справедливо для числа x0
= − ![]()
![]() и каждого из чисел x0 ≥ −1.
Функция f (x) =
8x3 +
18x2 +
15x + 14
возрастает на множестве R, так как имеет производную f′ (x) = 24x2 + 36x + 15 = 24 ⎜⎝⎛x
+
34⎟⎠⎞ 2 +
32 > 0 для каждого
и каждого из чисел x0 ≥ −1.
Функция f (x) =
8x3 +
18x2 +
15x + 14
возрастает на множестве R, так как имеет производную f′ (x) = 24x2 + 36x + 15 = 24 ⎜⎝⎛x
+
34⎟⎠⎞ 2 +
32 > 0 для каждого
x ∈ R. Так как f (−1) = −8 + 18 − 15 + 14 > 0, то для каждого числа x0 ≥ −1 имеем f (x0) ≥ f (−1) > 0. Поэтому ни одно из чисел x0 ≥ −1 не удовлетворяет равенству (30). Число
x0 = − ![]()
![]() удовлетворяет равенству (30).
удовлетворяет равенству (30).
Итак, если система (29) имеет решения, то они содержатся среди пар ⎜⎝⎛− 74 ; y⎞⎟⎠. Каждая такая пара удовлетворяет первому уравнению системы (29), а второе уравнение этой системы принимает вид
3y − 2 = y. (34)
Очевидно, что уравнение (34) имеет корень y1 = 1. Покажем, что это
уравнение имеет еще хотя бы один корень y2 ≠ 1. Рассмотрим
функцию g (y)=
3y −
2 − y
на отрезке [−2;
0]. Так как g (−2)
= 3−2 − 2 + 2 = ![]()
![]() >
0, а g (0) =
30 −
2 − 0
=
>
0, а g (0) =
30 −
2 − 0
=
= −1 < 0 и функция g (y) на отрезке [−2; 0] непрерывна, то по теореме о промежуточном значении функции на этом отрезке существует точка y2, такая, что g (y2) = 0, причем y2 ≠ 1, так как 1 ∉ [−2; 0].
Итак, показано, что уравнение (34) имеет хотя бы два различных корня. Это означает, что система (29) имеет хотя бы два различных решения, что и требовалось доказать.
Замечание. Если заметить, что первое уравнение системы (29) может иметь лишь отрицательные корни (в противном случае f (x) = 8x3 + 18x2 + 15x + 14 > 0), то по теореме о рациональных корнях многочлена степени n с целыми коэффициентами эти корни содержатся среди чисел
![]() −1,
− 2, − 7, − 14, −
−1,
− 2, − 7, − 14, − ![]() , −
, − ![]() , −
, − ![]() , −
, − ![]() , −
, − ![]() , −
, − ![]() . (35)
. (35)
Так как f (−1) = 9 > 0, а f (−2) = −8 < 0, то между числами
−2 и −1 находится единственное из чисел множества (35) —
![]() 0 = −. Так как f
x( ) = ⎛⎜⎝x +
74⎞⎟⎠ (8x2
+ 4x + 8) и диск-
0 = −. Так как f
x( ) = ⎛⎜⎝x +
74⎞⎟⎠ (8x2
+ 4x + 8) и диск-
число x
риминант квадратного трехчлена 8x2
+ 4x + 8 отрицателен, то
первое уравнение системы (29) имеет единственный корень x0 = − ![]()
![]() .
.
Итак, в приведенном выше доказательстве можно дать другое доказательство того, что все решения системы (29) содержатся среди пар чисел ⎜⎝⎛− 74 ; y⎞⎟⎠.
Промежуточный контроль. С—49. К—7.
|
§15*. |
Уравнения, неравенства и системы с параметрами
Этот параграф завершает главу II, посвященную методам решения уравнений, неравенств и систем. Следует отметить, что работа с параметрами велась на протяжении нескольких лет, начиная с 7 класса, не только в учебниках, но и в дидактических материалах, где, начиная с 8 класса, имеются отдельные самостоятельные работы и специальные подготовительные работы, посвященные параметрам. Использование четности функции при решении уравнений с параметром рассмотрено в п. 5 дидактических материалов для 11 класса. В данном параграфе учебника лишь систематизируются способы решения задач с параметром, приводятся примеры решения таких задач.
Работа с задачами этого параграфа позволяет в конце 11 класса не только повторить некоторые общие приемы решения уравнений, неравенств и систем в процессе решения задач с параметрами, но и подготовиться к решению сложных задач с параметрами, которые встречаются на конкурсных экзаменах в вузы и на ЕГЭ.
В этом пункте учебника объяснено, что значит решить уравнение с параметром, в чем заключен основной принцип решения уравнения, как должен быть записан ответ в таких задачах. Приведены примеры решения уравнений с параметром, показано применение свойств функций при определении числа корней рационального уравнения с параметром.
Решения и комментарии
Для каждого значения параметра а решите уравнение
(15.2—15.5):
x2 − 1
15.2. а) ![]() = a.
= a.
x − 1
Решение. При каждом значении параметра а корни исходного уравнения удовлетворяют условию x − 1 ≠ 0, т. е. принадлежат множеству М = (−∞; 1) ∪ (1; +∞).
Так как x − 1 ≠ 0 на множестве М, то исходное уравнение равносильно на множестве М уравнению
x + 1 = а. (1)
Уравнение (1) при каждом значении параметра а имеет единственный корень x1 = а − 1. Этот корень принадлежит множеству М при условии x1 ≠ 1, т. е. при а ≠ 2. Следовательно, при каждом а ≠ 2 исходное уравнение имеет единственный корень а − 1, при а = 2 исходное уравнение не имеет корней.
15.5. а) | x − 1 | − а | x + 1 | = 2.
Решение. Для освобождения от знаков модулей рассмотрим три случая.
1) Если x ∈ (−∞; −1), то исходное уравнение можно переписать в виде
(а − 1) x = − (а − 1). (2)
При а = 1 корнем уравнения (2), а значит, и исходного уравнения на промежутке (−∞; −1) является любое число x ∈ (−∞; −1).
При а ≠ 1 уравнение (2), а значит, и исходное уравнение имеют единственный корень −1, не принадлежащий промежутку (−∞; −1). Следовательно, при а ≠ 1 уравнение (2), а значит, и исходное уравнение не имеют корней на промежутке (−∞; −1).
2) Если x ∈ [−1; 1], то исходное уравнение можно переписать в виде
(а + 1) x = − (а + 1). (3)
При а = −1 корнем уравнения (3), а значит, и исходного уравнения на промежутке [−1; 1] является любое число x ∈ [−1; 1].
При а ≠ −1 уравнение (3) имеет единственный корень x = −1, принадлежащий промежутку [−1; 1]. Следовательно, при а ≠ −1 уравнение (3), а значит, и исходное уравнение имеют единственный корень x = −1 на промежутке [−1; 1].
3) Если x ∈ (1; +∞), то исходное уравнение можно переписать в виде
(1 − а) x = а + 3. (4)
При а = 1 уравнение (4), а значит, и исходное уравнение не имеют корней на промежутке (1; +∞).
При а ≠ 1 уравнение (4) имеет единственный корень a + 3
x = ![]() на промежутке (1; +∞), но это число
принадлежит
на промежутке (1; +∞), но это число
принадлежит
1 − a
a + 3
промежутку (1; +∞) лишь при
условии ![]() >
1, т. е. при 1 −
a
>
1, т. е. при 1 −
a
−1 < a < 1. Следовательно, уравнение (4), а значит, и исходное уравнение на промежутке (1; +∞) имеют единственa + 3
ный корень
x = ![]() при −1
< a < 1.
при −1
< a < 1.
1 − a
Итак, для каждого a ∈ (−∞; −1) ∪ (1; +∞) исходное уравнение имеет единственный корень x0 = −1; для каждоa + 3
го a ∈ (−1;
1) — два корня: x1 =
−1 и x2 =
![]() ; для a = −1 1 − a
; для a = −1 1 − a
любое число x ∈ [−1; 1] — корень; для a = 1 любое число x ∈ (−∞; −1] — корень.
В этом пункте учебника объяснено, что значит решить неравенство с параметром, приведены примеры решения рациональных и логарифмического неравенств с параметром.
Решения и комментарии
Для каждого значения параметра а решите неравенство (15.10—15.18):
15.10. а) (a − 1) x > a2 − 1.
Решение. 1) При a = 1 исходное неравенство имеет вид
0 ⋅ x > 0. (1)
Так как неравенство (1) не имеет решений, то и исходное неравенство при a = 1 не имеет решений.
2) При каждом a > 1 исходное неравенство имеет решения: все x > a + 1.
3) При каждом a < 1 исходное неравенство имеет решения: все x < a + 1.
Итак, при a = 1 исходное неравенство не имеет решений; при каждом a > 1 любое x > a + 1; при каждом a < 1 любое x < a + 1.
x − 1
15.16. а) ![]() > 0.
> 0.
x − a
Решение. 1) При a = 1 исходное неравенство имеет вид x − 1
![]() > 0. (2) x − 1
> 0. (2) x − 1
Так как неравенство (2) имеет множество решений (−∞; 1) ∪ (1; +∞), то и исходное неравенство при a = 1 имеет то же множество решений.
2) При каждом a > 1 исходное неравенство имеет решения: все x < 1 и все x > a.
3) При каждом a < 1 исходное неравенство имеет решения: все x < a и все x > 1.
Итак, исходное неравенство при a = 1 имеет множество решений (−∞; 1) ∪ (1; +∞); при каждом a > 1 любое x ∈ (−∞; 1) ∪ (а; +∞); при каждом a < 1 (−∞; a) ∪ (1; +∞).
x2 − a2
15.17. а) ![]() > 0.
> 0.
x − 1
Решение. Каждое решение исходного неравенства удовлетворяет условию x ≠ 1, т. е. принадлежит множеству
(−∞; 1) ∪ (1; +∞). Исходное неравенство можно переписать
(x − a) (x + a)
в виде ![]() > 0.
> 0.
x − 1
1)
![]() При a =
0 исходное неравенство можно переписать в виде
При a =
0 исходное неравенство можно переписать в виде
x2
> 0. (3) x − 1
Неравенство (3) имеет решения: все x > 1 (рис. 93, а).
2) При a = 1 и при a = −1 исходное неравенство можно переписать в виде
(x − 1) (x + 1)
![]() >
0. (4)
>
0. (4)
x − 1
Неравенство (4) имеет решения x > 1 и −1 < x < 1 (рис. 93, б).
3) При каждом a > 1 исходное неравенство имеет решения
x > а и −a < x < 1 (рис. 93, в). Рис. 93
4) При каждом 0 < a < 1 исходное неравенство имеет решения x > 1 и −а < x < a (рис. 93, г).
5) При каждом a ∈ (−1; 0) исходное неравенство имеет решения x > 1 и а < x < −a (рис. 93, д).
6) При каждом a < −1 исходное неравенство имеет решения x > −а и a < x < 1 (рис. 93, е).
Итак, исходное неравенство имеет решения −1 < x < 1 и x > 1 при a = ±1; −а < x < 1 и x > а при a > 1; −а < x < a и x > 1 при 0 < a < 1; а < x < −a и x > 1 при −1 < a < 0; x > 1 при a = 0; x > −a и a < x < 1 при a < −1.
![]() 15.18.
а) (x −
a) x −
1 ≥ 0.
15.18.
а) (x −
a) x −
1 ≥ 0.
Решение. Исходное неравенство равносильно совокупности уравнения
![]() (x − a) x
− 1 = 0 (5)
(x − a) x
− 1 = 0 (5)
и неравенства
(x − a) x − 1 > 0. (6)
При каждом a > 1 уравнение (5) имеет два корня: x = 1 и x = a.
При a = 1 уравнение (5) имеет единственный корень x = 1.
При каждом a < 1 уравнение (5) имеет единственный корень x = 1.
При каждом a > 1 неравенство (6) имеет множество решений: все x > a.
При a = 1 неравенство (6) имеет множество решений: все x > 1.
При каждом a < 1 неравенство (6) имеет множество решений: все x > 1.
Объединив решения уравнения (5) и неравенства (6), получим все решения исходного неравенства: x ≥ а и x = 1 при a > 1; x ≥ 1 при a ≤ 1.
В этом пункте учебника напоминается, что решить систему уравнений с параметром — значит для каждого значения параметра найти множество всех решений данной системы. Далее приведены примеры решения систем уравнений с параметром.
Решения и комментарии
Для каждого значения параметра а решите систему уравнений (15.24—15.29):
а) ⎧⎨⎩x(a+−y1)=ya.= a +1
15.24.
Решение. При a = 1 первое уравнение исходной системы не имеет решений, поэтому и система не имеет решений.
При каждом a ≠ 1 первое уравнение исходной системы a + 1
имеет
единственное решение y = ![]() . Из второго уравнения
. Из второго уравнения
a − 1
a2 − 2a − 1
системы найдем соответствующее
значение x = ![]() . a − 1
. a − 1
Следовательно, при каждом a ≠ 1 исходная система имеет
a + 1 a2 − 2a − 1
![]() единственное решение y = , x = .
единственное решение y = , x = .
a − 1 a − 1
Итак, исходная система уравнений не имеет решений
a2 − 2a − 1 a + 1
![]() при a = 1; x = , y
= при
каждом a ≠ 1.
при a = 1; x = , y
= при
каждом a ≠ 1.
a − 1 a − 1
⎧(a − 1) y = a2 − 1
15.25. а) ⎨⎩x + y = a.
Решение. При a = 1 решением первого уравнения исходной системы является любое число y = t, где t ∈ R. Из второго уравнения системы находим, что x = 1 − t, где t ∈ R. Поэтому при a = 1 система имеет решения x = 1 − t, y = t, где t ∈ R.
При каждом a ≠ 1 из первого уравнения исходной системы находим, что y = a + 1. Из второго уравнения системы находим, что x = −1.
Итак, исходная система уравнений имеет решения x = 1 − t, y = t, где t ∈ R при a = 1; x = −1, y = a + 1 при a ≠ 1.
⎧x2 + y2 = a
15.26. а) ⎨⎩x + y = 1.
Решение. Выразив из второго уравнения исходной системы y через x и подставив 1 − x вместо y в первое уравнение этой системы, получим систему уравнений
⎧⎨⎩y2x=2 1− −2xx,+1 − a = 0 (1)
равносильную исходной системе.
Так как дискриминант первого уравнения системы (1) равен D = 8a − 4, то надо рассмотреть три случая: a < 0,5, a = 0,5 и a > 0,5.
1) При каждом a < 0,5 имеем D < 0, поэтому первое уравнение системы (1) не имеет решений, следовательно, и исходная система не имеет решений.
2) При a = 0,5 первое уравнение системы (1) имеет единственное решение x = 0,5. Из второго уравнения системы находим, что y = 0,5, т. е. при a = 0,5 система уравнений (1), а значит, и исходная система имеют единственное решение (0,5; 0,5).
3) При каждом a > 0,5 первое уравнение системы (1)
имеет два решения: x1 = ![]() и
x2 =
и
x2 =
![]()
![]() второго уравнения
системы находим, что y1 = и
y2 = ,
т. е. при a > 0,5
система уравнений (1), а значит, и исходная система имеют два решения:
второго уравнения
системы находим, что y1 = и
y2 = ,
т. е. при a > 0,5
система уравнений (1), а значит, и исходная система имеют два решения:
⎛ 1 + 2a − 1 1 − 2a − 1 ⎞ ⎛ 1 − 2a − 1 1 + 2a − 1 ⎞
⎜ ; ⎟ и ⎜ ; ⎟.
⎝ 2 2 ⎠ ⎝ 2 2 ⎠
Итак, исходная система не имеет решений при a < 0,5;
![]() ⎛ 1 + 2a −
1 1 − 2a −
1 ⎞
⎛ 1 + 2a −
1 1 − 2a −
1 ⎞
имеет два решения: ⎜ ; ⎟ и
⎝ 2 2 ⎠
![]() ⎛ 1 − 2a −
1 1 + 2a −
1 ⎞
⎛ 1 − 2a −
1 1 + 2a −
1 ⎞
⎜ ; ⎟ при a > 0,5; имеет единственное
⎝ 2 2 ⎠
решение (0,5; 0,5) при a = 0,5.
⎧(a2 − a) sin x + 2 cos y = a + 5
⎪
15.29. а) ⎨ x 2
⎪⎩3 sin 2 + cos y = 4.
Решение. Если пара чисел (x0; y0) есть решение исходной системы, то, в частности, справедливо числовое равенx0 x0
ство 3 sin ![]() + cos y 0 =
4, откуда следует, что sin
+ cos y 0 =
4, откуда следует, что sin ![]() = 1 и
= 1 и
2 2 cos y0 = 1 (в противном случае левая часть этого равенства будет меньше 4). Таким образом, второе уравнение систе-
мы равносильно системе уравнений ⎧⎪⎨sin x2 = 1 имеющей
⎪⎩cos y = 1,
решения (xn; yk), где xn = π + 4πn, n ∈ Z, yk = 2πk, k ∈ Z. Пары чисел (xn; yk) являются также решениями первого уравнения исходной системы, если выполняется условие a2 − a + 2 = a + 5, т. е. при a = −1 и при a = 3. Значит, исходная система имеет решения (xn; yk), где xn = π + 4πn, n ∈ Z, yk = 2πk, k ∈ Z при a = −1 и a = 3.
При каждом a, отличном от −1 и 3, пары чисел (xn; yk) не являются решениями первого уравнения исходной системы, в этом случае система не имеет решений.
Итак, система имеет решения (π + 4πn; 2πk), n ∈ Z, k ∈ Z при a = −1 и при a = 3; система не имеет решений при каждом a, отличном от −1 и 3.
Замечание. Обратим внимание, что в задании 5.29 нельзя решения (xn; yk) выражать с помощью одной буквы n, так как каждому значению xn соответствует не одно, а бесконечно много значений yk.
В этом пункте учебника рассматриваются задачи, в которых требуется найти все значения параметра, при каждом из которых выполняется некоторое условие, и разобраны соответствующие примеры. Приведем решения еще некоторых таких задач.
Пример 1. Найдем все значения параметра a, при каждом из которых уравнение
![]() (3x2 − (5a + 3) x + 2a2 + 2 )a −x2 − 4x − 3 = 0 (1) имеет ровно три
различных корня.
(3x2 − (5a + 3) x + 2a2 + 2 )a −x2 − 4x − 3 = 0 (1) имеет ровно три
различных корня.
Решение. Для каждого значения параметра a уравнение (1) равносильно совокупности двух систем:
⎧⎨⎩3−xx22 −−(45xa −+ 33)≥x0+ 2a2 + 2a = 0 (2)
и
![]() ⎧⎨ −x2
− 4x
− 3 = 0 (3)
⎧⎨ −x2
− 4x
− 3 = 0 (3)
⎩x ∈ R.
Система (3) имеет два решения: x1 = −3 и x2
= −1,
а уравнение системы (2) при каждом значении параметра a имеет два корня:
x3 = a
+ 1 и x4
= ![]()
![]() a. Решением системы (2)
a. Решением системы (2)
окажется то из чисел x3 и x4, которое удовлетворяет неравенству системы, т. е. то, которое принадлежит множеству М = [−3; −1].
Число x3 принадлежит множеству М,
если −3 ≤ a + 1 ≤ ≤ −1,
т. е. если −4
≤ a ≤ −2. Число
x4 принадлежит множеству М, если![]() , т. е. если
−4,5 ≤ a ≤ −1,5.
, т. е. если
−4,5 ≤ a ≤ −1,5.
Уравнение (1) имеет ровно три различных корня только в двух случаях:
1) если корни x3 и x4 совпадают и принадлежат множеству (−3; −1);
2) если эти корни различны и один из них принадлежит множеству (−3; −1), а другой нет.
Первый случай возможен, лишь если a есть решение системы
⎧x3 = x4 ⎨⎩−3 < x3 < −1,
т. е. при a = −3.
Второй случай возможен, лишь если a есть решение совокупности четырех систем:
⎧−3 < x3 < −1 ⎧−3 < x3 < −1 ⎧−3 < x4 < −1 ⎧−3 < x4 < −1 ⎨⎩x4 ≥ −1, ⎨⎩x4 ≤ −3, ⎨⎩x3 ≥ −1, ⎩⎨x3 ≤ −3,
т. е. при условии, что a ∈ (−4,5; −4] ∪ [−2; −1,5).
Следовательно, уравнение (1) имеет ровно три различных корня, если a ∈ (−4,5; −4] ∪ [−2; −1,5) ∪ {−3}.
Пример 2. Найдем все значения параметра a, при каждом из которых все x > 3 являются решениями неравенства
(a − 2) x2 − 2x − a > 0. (4)
Решение. При a = 2 неравенство имеет вид −2x − 2 > 0, множество его решений есть все x < −1. Поэтому a = 2 не удовлетворяет условию задачи.
При a ≠ 2 дискриминант квадратного неравенства (4) D = 4 (a − 1)2 ≥ 0.
При a = 1 неравенство (4) имеет вид −x2 − 2x − 1 > 0, оно не имеет решений, поэтому a = 1 также не удовлетворяет условию задачи.
При a, отличном от 1 и 2, квадратный трехчлен имеет
два различных корня: x1 = −1 и x2 = a , поэтому неравенa − 2
ство (4) можно переписать в виде
(a − 2) (x − x1) (x − x2) > 0. (5)
При каждом a > 2 имеем x1 < x2, поэтому решения нера-
венства (5) есть все x < −1 и все x > a . Если a > 3, a − 2 a − 2
т. е. если a < 3, то не все x > 3 содержатся среди
x ![]() .
.
Следовательно, ни одно a из промежутка 2 < a < 3 не удовлетворяет условию задачи.
Если ![]() , т. е. если a ≥ 3, то все x > 3 содержатся
, т. е. если a ≥ 3, то все x > 3 содержатся
среди x > x2. Следовательно, каждое a ≥ 3 удовлетворяет условию задачи.
При a < 2, но a ≠ 1 все решения неравенства (5) составляют промежуток (x1; x2) при x1 < x2 или промежуток (x2; x1) при x2 < x1 и поэтому не все x > 3 содержатся в этом промежутке. Следовательно, ни одно из этих значений a не удовлетворяет условию задачи.
Итак, условию задачи удовлетворяет лишь каждое a ≥ 3.
Решения и комментарии
15.31. а) При каких значениях параметра a уравнение x + 2 = a | x − 1 | имеет единственное решение?
Решение. 1-й способ. Для освобождения от знака модуля рассмотрим два случая.
1) Если x ≥ 1, т. е. если x ∈ [1; +∞), то исходное уравнение можно переписать в виде
(a − 1) x = a + 2. (6)
При a = 1 уравнение (6) не имеет корней.
![]() При a ≠ 1 уравнение (6)
имеет единственный корень a +
2 a
При a ≠ 1 уравнение (6)
имеет единственный корень a +
2 a
x1 = ![]() . Так как
. Так как ![]() лишь
при a > 1,
то x1 ∈
[1; +∞)
a −
1 a лишь
при a > 1.
лишь
при a > 1,
то x1 ∈
[1; +∞)
a −
1 a лишь
при a > 1.
2) Если x < 1, т. е. если x ∈ (−∞; 1), то исходное уравнение можно переписать в виде
(a + 1) x = a − 2. (7)
При a = −1 уравнение (7) не имеет корней.
![]() При a ≠ −1
уравнение (7) имеет единственный корень a − 2 a
При a ≠ −1
уравнение (7) имеет единственный корень a − 2 a
x2 =
![]() a + 1. Так как
a + 1. Так как ![]() a лишь при a > −1, то x2
∈ (−∞; 1) лишь
при a >
−1.
a лишь при a > −1, то x2
∈ (−∞; 1) лишь
при a >
−1.
Итак, при каждом a ≤ −1 исходное уравнение не имеет корней, при каждом a ∈ (−1; 1] исходное уравнение имеет a − 2
единственный корень x2 =
![]() a + 1, при каждом a > 1 исход-
a + 1, при каждом a > 1 исход-
ное уравнение имеет два корня: x1 и x2. Остается выяснить, нет ли среди чисел a > 1 такого значения, при котором корни x1 и x2 равны. Так как x2 ∈ (−∞; 1), а x1 ∈ [1; +∞), то x1 ≠ x2 ни для каких a. Поэтому исходa − 2
ное уравнение имеет единственный
корень x = ![]() лишь a + 1
лишь a + 1
при каждом a ∈ (−1; 1].
Заметим, что описанная выше процедура решения уравнения на каждом из двух промежутков значений x с рассмотрением всех случаев для значений параметра a
достаточно трудоемкая. Ту же задачу можно решить, используя свойства функций. Рассмотрим такой способ.
2-й способ. Так как для каждого значения параметра a число x = 1 не является корнем исходного уравнения, то для каждого значения параметра a это уравнение равносильно уравнению
![]() x +
2 a = .
x +
2 a = .
| x − 1|
Построим графики функций
(рис. 94).
3
x + 2
f x(
) = ![]() и ϕ (x) = a
и ϕ (x) = a
| x − 1|
Если x > 1, то f x( ) = +1. На промежутке (1; +∞) x − 1
функция f (x) убывает, принимая все значения из промежутка (1; +∞).
Если x < 1, то f x( ) = −3 − 1. На промежутке (−∞; 1) x − 1
функция f (x) возрастает, принимая все значения из промежутка (−1; +∞).
График функции y = a — прямая, параллельная оси Ox. Эта прямая пересекает график функции f (x) в единственной точке лишь при a ∈ (−1; 1], поэтому исходное уравнение имеет единственный корень при a ∈ (−1; 1].
15.32. а) Сколько решений в зависимости от параметра a имеет уравнение
| x + 2 | = ax + 1? (8)
Решение. При каждом значении параметра a следствием исходного уравнения является уравнение (x + 2)2 = (ax + 1)2, которое можно переписать в виде
(a2 − 1) x2 + 2 (a − 2) x − 3 = 0. (9)
1)
При a =
1 уравнение (9) имеет единственный корень ![]() , который не
удовлетворяет исходному уравнению.
, который не
удовлетворяет исходному уравнению.
2)
При a =
−1 уравнение (9) имеет единственный корень ![]() , который
удовлетворяет исходному уравнению.
, который
удовлетворяет исходному уравнению.
3)
При a2 ≠
1 уравнение (9) квадратное, его дискриминант D = 4 (2a − 1)2.
При a = ![]()
![]() уравнение (9) имеет единственный
корень −2,
который удовлетворяет исходному уравнению.
уравнение (9) имеет единственный
корень −2,
который удовлетворяет исходному уравнению.
4)
При каждом а, таком, что a2 ≠ 1 и a![]() ,
уравне-
,
уравне-
![]() ние (9) имеет два
корня: x1 = 1 и x.
Проверка a −
1
ние (9) имеет два
корня: x1 = 1 и x.
Проверка a −
1
показывает, что число x1 удовлетворяет уравнению (8),
![]() 2a −
1
2a −
1
если ![]() > 0, т. е. если или
a < ,
но a ≠
−1, или a >
1, a −
1
> 0, т. е. если или
a < ,
но a ≠
−1, или a >
1, a −
1
2a − 1
а число x2 удовлетворяет
уравнению (8), если ![]() <
0, a +
1
<
0, a +
1
т. е. если![]() .
.
Итак, уравнение (8) не имеет корней при каждом
a ∈ ⎛⎜⎝ 21 ; 1⎤⎥⎦; имеет единственный корень a 1− 1 при каждом
a ≤
−1, при a =
![]()
![]() и при каждом a
> 1; имеет
два корня:
и при каждом a
> 1; имеет
два корня:
a 1− 1 и a−+31 — при каждом a ∈ ⎛⎜⎝−1; 21⎞⎟⎠.
Задания, аналогичные заданиям 15.33 и 15.35, разобраны соответственно в пп. 5 и 50 дидактических материалов.
15.37. а) При каких значениях параметра b уравнение log2x + 1 (3x2 − bx − 0,25b) = 2 (10)
имеет два различных корня?
Решение. Уравнение (10) равносильно системе
⎧⎪3x2 − bx − 0 25, b = (2x +1)2
⎨2x +1 > 0
⎪⎩2x +1 ≠ 1.
Перепишем эту систему в виде
⎧⎪x2 + (4 + b x) + (1 + 0 25, b) = 0
⎨x > −0 5, (11)
⎪⎩x ≠ 0.
Если система (11) имеет два различных решения, то и уравнение (10) имеет два различных корня.
Уравнение системы (11) имеет два различных корня х1 и х2, если D = (4 + b)2 − 4 − b = (b + 3) (b + 4) > 0, т. е. если b ∈ (−∞; −4) ∪ (−3; +∞). Так как для этих значений b имеем 1 + 0,25b ≠ 0, то х1 ≠ 0 и х2 ≠ 0.
При каждом значении параметра b ∈ (−∞; −4) ∪ (−3; +∞)
![]() −4 − b + D −4 − b − D
−4 − b + D −4 − b − D
![]() имеем x1 => x2 = .
Поэтому остается
имеем x1 => x2 = .
Поэтому остается
2 2
выяснить, при каких значениях b число х2 > −0,5, т. е.
−4 − b − D
надо решить неравенство > −0 5, . Перепишем его
2
в виде
− (3 + b) > (b + 3) (b + 4). (12)
При b > −3 имеем −(3 + b) < 0, т. е. среди этих b нет решений неравенства (12). При b < −4 обе части неравенства (12) положительны, поэтому неравенство (12) равносильно неравенству (3 + b)2 > (b + 3) (b + 4), множество решений которого b < −3. Поэтому условию х2 > −0,5 удовлетворяют лишь b < −4.
Следовательно, система (11) имеет два различных решения только для b < −4, т. е. условию задачи удовлетворяет лишь каждое b ∈ (−∞; −4).
15.39. а) При каких значениях параметра a неравенство
2 2a2 − 4a − 3
![]() x − 10x + 26 ≥ 2 (13)
x − 10x + 26 ≥ 2 (13)
a − 2a − 8
выполняется для всех x?
Решение. Так как для каждого x верно неравенство x2 − 10x + 26 ≥ 1, то неравенство (13) выполняется для всех x при тех значениях а, для каждого из которых
2a2 − 4a − 3
![]() 2 ≤ 1. (14) a − 2a −
8
2 ≤ 1. (14) a − 2a −
8
Решив неравенство (14), получим, что все его решения образуют промежуток (−2; 4). Следовательно, для каждого a ∈ (−2; 4) неравенство (13) выполняется для всех x.
15.40. а) Найдите все значения параметра a, при каждом из которых неравенство
a2 + a − sin2 x − 2a cos x > 1 (15)
выполняется для любого значения x.
Решение. Используя основное тригонометрическое тождество и сделав замену переменной t = cos x, перепишем неравенство (15) в виде
t2 − 2at + a2 + a − 2 > 0. (16)
Чтобы найти искомые значения параметра, найдем все значения параметра a, для каждого из которых функция f (t) = t2 − 2at + a2 + a − 2 принимает положительные значения для любого t ∈ [−1; 1].
1) Если D = 4 (a2 − a2 − a + 2) = 4 (2 − a) < 0, т. е. если a > 2, то неравенство (16) справедливо для каждого t ∈ R, а значит, и для каждого t ∈ [−1; 1].
2) Если D = 4 (2 − a) = 0, т. е. если a = 2, то неравенство (16) справедливо для каждого t ∈ [−1; 1], так как f (t) = t2 − 4t + 4 = (t − 2)2 > 0 для каждого t ≠ 2.
3)
![]() Если D =
4 (2 − a)
> 0, т. е.
если a < 2,
то неравенство (16) справедливо для каждого t ∈ [−1;
1] лишь для тех значений a, для которых абсцисса вершины параболы t = a — графика
функции y = f
(t) — не принадлежит промежутку [−1;
1] и для которых еще справедливо одно из
Если D =
4 (2 − a)
> 0, т. е.
если a < 2,
то неравенство (16) справедливо для каждого t ∈ [−1;
1] лишь для тех значений a, для которых абсцисса вершины параболы t = a — графика
функции y = f
(t) — не принадлежит промежутку [−1;
1] и для которых еще справедливо одно из
Рис. 95 неравенств f (−1) > 0 и f (1) > 0
(рис. 95).
Итак, искомые значения a являются решениями совокупности двух систем:
⎧a < −1 ⎧1 < a < 2
⎨⎩1 + 2a + a2 + a − 2 > 0 и ⎨⎩1 − 2a + a2 + a − 2 > 0.
Решив каждую из двух систем и объединив все найденные решения, получим решения этой совокупности:
−3 − 13 1 + 5
![]() a < , < a < 2.
a < , < a < 2.
2 2
Итак, условиям задачи удовлетворяют каждое
![]() −3 − 13 1 +
5 a < и каждое a >.
−3 − 13 1 +
5 a < и каждое a >.
2 2
15.42. Найдите все значения параметра a, при каждом 7a2 − a − 2
из которых неравенство x + ![]() < −7a не имеет решеx − 2
< −7a не имеет решеx − 2
ний, больших 1.
Решение. Перепишем исходное неравенство в виде x2 + (7a − 2) x + 7a2 − 15a − 2
![]() < 0. (17)
< 0. (17)
x − 2
Все решения неравенства (17) принадлежат множеству всех x, таких, что x ≠ 2.
Если при некотором значении параметра а найдутся решения неравенства (17), удовлетворяющие условию x > 2, то все они удовлетворяют условию x > 1, поэтому такие значения параметра а не удовлетворяют условию задачи. Рассмотрим решение неравенства (17) на множестве М = (−∞; 2).
Для каждого x ∈ М справедливо неравенство x − 2 < 0, поэтому для каждого значения параметра a неравенство (17), а значит, и исходное неравенство равносильны на множестве М неравенству
x2 + (7а − 2) x + 7а2 − 15а − 2 > 0. (18)
Для каждого значения параметра a рассмотрим функцию
f (x) = x2 + (7а − 2) x + 7а2 − 15а − 2.
Так как D = (7а − 2)2 − 4 (7а2 − 15а − 2) = 21 ⎝⎜⎛a + 76 ⎠⎟⎞ ⎛⎝⎜a + 23 ⎞⎟⎠,
то при![]() справедливо
неравенство D ≤
0, поэтому для каждого x ∈
М справедливо неравенство f (x) ≥ 0.
Следовательно, при этих значениях а найдутся решения неравенства (18), а
значит, и исходного неравенства, большие 1. Поэтому все значения a ∈ ⎡⎢⎣−
76 ; −
23 ⎤⎥⎦ не
удовлетворяют условию задачи.
справедливо
неравенство D ≤
0, поэтому для каждого x ∈
М справедливо неравенство f (x) ≥ 0.
Следовательно, при этих значениях а найдутся решения неравенства (18), а
значит, и исходного неравенства, большие 1. Поэтому все значения a ∈ ⎡⎢⎣−
76 ; −
23 ⎤⎥⎦ не
удовлетворяют условию задачи.
Если a ∈ ⎛⎜⎝−∞; − 76 ⎞⎟⎠ ∪ −⎛⎜⎝ 23 ; +∞⎞⎟⎠, то D > 0 и решения не-
![]() равенства (18)
составляют два промежутка: (−∞;
x1) и (x2; +∞),
где x1 и x2 — нули функции f (x).
Среди этих решений нет решений, больших 1 и принадлежащих множеству М,
только в том случае, когда справедливы неравенства x1 ≤ 1 и 2 ≤ x2 (рис.
96), т. е. когда справедливы неравенства f (1) ≤ 0 и f (2) ≤ 0. Решив
систему
равенства (18)
составляют два промежутка: (−∞;
x1) и (x2; +∞),
где x1 и x2 — нули функции f (x).
Среди этих решений нет решений, больших 1 и принадлежащих множеству М,
только в том случае, когда справедливы неравенства x1 ≤ 1 и 2 ≤ x2 (рис.
96), т. е. когда справедливы неравенства f (1) ≤ 0 и f (2) ≤ 0. Решив
систему
⎧1 + (7a − 2) + 7a2 − 15a − 2 ≤ 0 Рис. 96
⎨⎩4 + 2 7( a − 2) + 7a2 − 15a − 2 ≤ 0,
![]() ⎡4 − 37 1 + 56⎤
⎡4 − 37 1 + 56⎤
найдем все ее решения: a ∈ ⎢⎣ 7 ; 14 ⎥⎦. Так как все
эти числа принадлежат промежутку ⎜⎝⎛− 23 ; +∞⎞⎟⎠, то все они
удовлетворяют условию задачи.
Следовательно, исходное неравенство не имеет реше-
![]() ⎡4 − 37 1 + 56⎤
⎡4 − 37 1 + 56⎤
ний, больших 1, лишь при a ∈ ⎢⎣ 7 ; 14 ⎥⎦.
15.43. Найдите все значения параметра a, при каждом из которых множество решений неравенства 2x2 − 3x + а + 12 ≤ 0 не пусто и содержится среди решений неравенства x2 + 10x + а ≤ 0.
Решение. Рассмотрим неравенства
|
и |
2x2 − 3x + а + 12 ≤ 0 |
(19) |
|
|
x2 + 10x + а ≤ 0. |
(20) |
Множество решений неравенства (19) не пусто, если его
дискриминант D1 =
9 − 8
(а + 12) = −8а − 87 ≥ 0, т. е. при a
![]() . Для каждого такого а дискриминант
неравенства (20) D2 =
100 − 4а
> 0, т. е.
для каждого a
. Для каждого такого а дискриминант
неравенства (20) D2 =
100 − 4а
> 0, т. е.
для каждого a![]() неравенство (20) имеет решения.
неравенство (20) имеет решения.
При a![]() решения неравенства (19) составляют про-
решения неравенства (19) составляют про-
межуток x1 ≤ x ≤ x2,
где x1 =
![]() ,
x2 =
,
x2 = ![]()
(при a ![]() неравенство (19)
имеет единственное решение — число
неравенство (19)
имеет единственное решение — число ![]()
![]()
![]() При a
При a![]() решения неравенства (20) составляют промежуток x3 < x < x4,
где x3 =
−5 − 25
− a,
x4 =
−5 + 25
− a.
решения неравенства (20) составляют промежуток x3 < x < x4,
где x3 =
−5 − 25
− a,
x4 =
−5 + 25
− a.
Все решения неравенства (19) содержатся среди решений
неравенства (20) лишь при выполнении трех условий: x3 ≤ x1, x2 ≤ x4 и a![]() ,
т. е. являются решениями
,
т. е. являются решениями
системы неравенств
⎧ 3 − −8a − 87
![]() ⎪−5 − 25 − a ≤ 4
⎪−5 − 25 − a ≤ 4
⎪⎪ 3 + −8a − 87
⎨ ≤ −5 + 25 − a (21)
![]() ⎪ 4
⎪ 4
⎪a.
⎪⎩
Решив систему (21), найдем все ее решения:
![]() ⎡ ⎤
⎡ ⎤
а ⎣ ⎥⎦. Итак, условию задачи удов-
![]() ⎡ ⎤
⎡ ⎤
летворяет лишь каждое а ⎣ ⎥⎦.
15.44. а) При каких значениях параметра a система уравнений
![]() ⎧⎨x2+ y2 − a − 2 =
0 (22)
⎧⎨x2+ y2 − a − 2 =
0 (22)
⎩y − x = a (2x + a)
имеет два различных решения?
Решение. Перепишем эту систему в виде
![]() ⎧⎨x2+ y
− a −2 2 = 0 (23)
⎧⎨x2+ y
− a −2 2 = 0 (23)
⎩y = (x + a) .
При каждом значении параметра a система (23) равносильна совокупности двух систем:
![]()
![]() ⎧⎨x + y − a − 2 = 0 и ⎧⎨x + y − a − 2 = 0
⎧⎨x + y − a − 2 = 0 и ⎧⎨x + y − a − 2 = 0
⎩y = x + a ⎩y = −x − a.
Эти системы равносильны соответственно системам
![]() ⎧⎨⎩xy += xx+−a2 = 0 (24)
⎧⎨⎩xy += xx+−a2 = 0 (24)
и
⎧⎨⎩xy += −−xx−−a2.a − 2 = 0 (25)
Первое уравнение системы (24) не имеет решений, следовательно, эта система не имеет решений.
Так как все решения системы (25) являются решениями системы (22), то система (22) имеет два различных решения, если первое уравнение системы (25) имеет два различных корня.
Перепишем первое уравнение системы (25) в виде
![]() −x − 2a − 2 = −x. (26)
−x − 2a − 2 = −x. (26)
Ясно, что это уравнение имеет решения лишь на множестве всех x ≤ 0. На этом множестве уравнение (26) равносильно уравнению
x2 + x + 2a + 2 = 0. (27)
Так как D = 1 − 8а − 8 = −8а − 7, то уравнение (27) име-
ет два корня: x![]() и x
и x![]() ,
толь-
,
толь-
![]() ко
если −8а
− 7 > 0, т. е. если a
ко
если −8а
− 7 > 0, т. е. если a
![]() . При этом оба эти корня удовлетворяют
условию x ≤
0, только если −1 + 2−8a − 7 ≤
0, т. е. если a ∈ ⎡⎢⎣−1; − 78 ⎤⎥⎦.
. При этом оба эти корня удовлетворяют
условию x ≤
0, только если −1 + 2−8a − 7 ≤
0, т. е. если a ∈ ⎡⎢⎣−1; − 78 ⎤⎥⎦.
Итак, условию задачи удовлетворяет лишь каждое a ∈ ⎡⎢⎣−![]() − ⎤⎥⎦.
− ⎤⎥⎦.
15.45. а) При каких значениях параметра a система уравнений
⎧⎪y = ![]() 2x2
2x2
⎨ x + | x | (28)
⎪⎩(x − 2 (a + 2))2 + (y − a)2 = 8
имеет хотя бы одно решение?
Решение. При любом значении a система (28) равносильна системе
⎧⎪⎪y
= ![]() x2+x|2x | (29)
x2+x|2x | (29)
⎨⎪(x − 2 (a + 2))2 + ⎛⎜ ![]() 2x2 − a⎞⎟ 2 =
8. (30)
2x2 − a⎞⎟ 2 =
8. (30)
⎪⎩ ⎝ x + | x | ⎠
Уравнение (30) есть уравнение с одним неизвестным x. Ясно, что при любом значении a все его решения содержатся в множестве M всех положительных x, так как для всех x ∈ (−∞; 0] имеем x + | x | = 0, а делить на нуль нельзя. На множестве M уравнение (30) равносильно уравнению
2x2 − 2 (3a + 4) x + 5a2 + 16a + 8 = 0. (31)
Квадратное уравнение (31) имеет хотя бы один корень,
принадлежащий множеству M, если выполнены два условия: D = 4 ((3а + 4)2 − 10а2
− 32а
− 16) = −4а (а
+ 8) ≥ 0 — и больший
из корней этого уравнения x ![]() положительный. Решив систему неравенств
положительный. Решив систему неравенств
⎧−4a a( + 8) ≥ 0
![]() ⎨⎩3a + 4 + −4a a( + 8) > 0,
⎨⎩3a + 4 + −4a a( + 8) > 0,
найдем все ее решения а ∈ (−4; 0]. Следовательно, уравнение (31) имеет хотя бы один корень только при каждом а ∈ (−4; 0]. Поэтому система уравнений (29) и (30), а значит, и система (28) имеют хотя бы одно решение только при каждом а ∈ (−4; 0].
Дополнение. Приведем решение задания из ЕГЭ.
С3 (2008). Найдите все значения a, для которых при каждом x из промежутка (−3; −1] значение выражения x4 − 8x2 − 2 не равно значению выражения ax2.
Решение. Задачу можно переформулировать так: найдите все значения a, при каждом из которых уравнение
|
x4 − 8x2 − 2 = ax2 не имеет корней на промежутке (−3; −1]. Перепишем уравнение (32) в виде |
(32) |
|
x4 − (8 + a) x2 − 2 = 0. |
(33) |
Сначала выясним, при каких значениях a уравнение (33) имеет хотя бы один корень, принадлежащий промежутку (−3; −1].
Биквадратное уравнение (33) при каждом значении a имеет два корня:
x1 =
− ![]() и x2
=
и x2
= ![]()
Так как x2 > 0 при каждом значении a, то x2 ∉ (−3; −1]. Корень x1 ∈ (−3; −1] только для тех a, для каждого из которых выполнено двойное неравенство −3 < x1 ≤ −1, т. е. для тех a, которые удовлетворяют двойному неравенству
1
≤ ![]() (34)
(34)
Решениями двойного неравенства (34) являются все a ∈ −⎡⎢⎣ 9; 79⎞⎟⎠.
Итак, уравнение (32) имеет корень на промежутке (−3; −1] только при a ∈ −⎡⎢⎣ 9; 79⎞⎟⎠. Следовательно, все значения a, удовлетворяющие условию задачи, есть a ∈ (−∞; −9) ∪ ⎡⎢⎣ 79; +∞⎞⎟⎠.
Ответ. (−∞; −9) ∪ ⎡⎢⎣79 ; +∞⎞⎟⎠.
Промежуточный контроль. С—50.
|
§16*. |
Алгебраическая форма и геометрическая интерпретация комплексных чисел
В этом пункте учебника приведено формальное определение комплексных чисел, введены арифметические операции над комплексными числами, понятия мнимой единицы и мнимого числа, действительной и мнимой частей комплексного числа, понятия противоположного и обратного числа для данного комплексного числа, понятие алгебраической формы комплексного числа.
Решения и комментарии
16.22. а) Разложите на множители x2 + 1.
Решение. x2 + 1 = x2 − (−1) = x2 − i2 = (x − i) (x + i).
16.26. Для какого действительного числа x выражение
(3 + xi)2 − (4x + 2) i
(3 + xi)2 − (4x + 2) i = 9 + 6xi − x2 − 4xi − 2i = (9 − x2) + (2x − 2) i.
а) Данное выражение является действительным числом, если его мнимая часть равна нулю: 2x − 2 = 0, т. е. при x = 1.
б) Данное выражение является мнимым числом, если его действительная часть равна нулю: 9 − x2 = 0, т. е. при x = −3 и при x = 3.
16.30. а) Найдите все комплексные числа z, удовлетворяющие двум условиям: z2 = −15 + 8i и Im z > 0.
Решение. Пусть z = a + bi. Тогда z2 = a2 − b2 + 2abi. По условию задачи числа a2 − b2 + 2abi и −15 + 8i равны и b > 0. Следовательно, пара чисел a и b является решением системы
⎧⎪a2 − b2 = −15
⎨2ab = 8 (1)
⎪⎩b > 0.
Решив систему (1), получим, что a = 1, b = 4. Следовательно, z = 1 + 4i.
В этом пункте учебника введены понятия числа, сопряженного с данным комплексным числом, взаимно сопряженных комплексных чисел, сформулированы основные свойства, связанные с сопряженными числами. Здесь нужно обратить внимание на то, что деление на комплексное число, отличное от нуля, можно заменить умножением на комплексное число, сопряженное с делителем.
Решения и комментарии
16.40. а) Найдите все комплексные числа z, удовлетворяющие условию z Re z + z¯ Im z = 3 − 2i.
Решение. Пусть z = a + bi. Тогда z Re z + z¯ Im z = = (a + bi) a + (a − bi) b = a2 + ab + (ab − b2) i. По условию задачи a2 + ab + (ab − b2) i = 3 − 2i. Следовательно, пара чисел a и b является решением системы
⎧⎨⎩aab2 +− abb2 = −= 32. (1)
Решив систему (1), получим, что она имеет четыре ре-
![]()
![]() 3 2 2 шения: a = 1, b = 2; a = −1, b = −2; a =, b = −;
3 2 2 шения: a = 1, b = 2; a = −1, b = −2; a =, b = −;
2 2
![]() a
= − ,
b = .
Следовательно, условию задачи удовлет-
a
= − ,
b = .
Следовательно, условию задачи удовлет-
2 2
3
![]() 2 2 воряют четыре числа: z1
= 1 + 2i; z2
= 1 − 2i; z3
= − i;
2 2 воряют четыре числа: z1
= 1 + 2i; z2
= 1 − 2i; z3
= − i;
2 2
3
![]() 2 2
2 2
z4 = − + i.
2 2
В этом пункте учебника введены понятия геометрической интерпретации комплексных чисел с помощью точек комплексной плоскости и модуля комплексного числа, дано геометрическое истолкование суммы и модуля разности комплексных чисел, приведены примеры использования новых понятий при решении задач.
Решения и комментарии
16.49. а) Найдите множество точек z комплексной плоскости, удовлетворяющих условию | z − 4 | = | z + 4i |.
Решение. Пусть z = x + yi. Тогда условие задачи означает, что верно равенство
![]() (x − 4)2 + y2 = x2 + (y − 4)2 . (1)
(x − 4)2 + y2 = x2 + (y − 4)2 . (1)
Решив уравнение (1), получим, что y = x. Это означает, что исходному условию удовлетворяют лишь точки прямой y = x комплексной плоскости xOy (рис. 97).
![]() Тот же результат можно получить из геометрических
соображений. Выражения | z −
4 | и | z +
4i | задают расстояние от точки (x; y) комплексной
плоскости, соответствующей комплексному числу z = x +
yi, до точек (4; 0) и (0; 4), соответствующих комплексным числам z1
= 4 + 0i и z2
= 4 + 0i. Поэтому
множество всех точек (x; y) комплексной плоскости, одинаково уда-
Тот же результат можно получить из геометрических
соображений. Выражения | z −
4 | и | z +
4i | задают расстояние от точки (x; y) комплексной
плоскости, соответствующей комплексному числу z = x +
yi, до точек (4; 0) и (0; 4), соответствующих комплексным числам z1
= 4 + 0i и z2
= 4 + 0i. Поэтому
множество всех точек (x; y) комплексной плоскости, одинаково уда-
Рис. 97 ленных от точек (4; 0) и (0; 4), есть
серединный перпендикуляр к отрез-
ку, соединяющему эти точки, т. е. прямая y = x.
16.51. а) Найдите комплексное число z, удовлетворяющее условию zi = 5 − 2i, и соответствующую ему точку комплексной плоскости.
Решение. Пусть z = x + yi. Тогда из условия задачи следует, что верно равенство −y + xi = 5 − 2i. Это равенство справедливо при условии x = −2, y = −5, т. е. z = −2 − 5i. Числу z соответствует точка (−2; −5) комплексной плоскости.
|
§17*. |
Тригонометрическая форма комплексных чисел
В этом пункте учебника вводится понятие главного аргумента комплексного числа z, аргумента комплексного числа z, тригонометрической формы комплексного числа. Доказана теорема о умножении и делении комплексных чисел, записанных в тригонометрической форме, формула Муавра о возведении в целую степень комплексного числа, записанного в тригонометрической форме. Приведены примеры использования новых понятий при решении задач.
Решения и комментарии
Запишите в тригонометрической форме комплексное число z, укажите его главный аргумент (17.3—17.6):
17.3. а) z = cos ⎛⎜⎝− π4⎞⎟⎠ + i sin ⎜⎝⎛ 34π ⎞⎟⎠;
б) z = −3 ⎛⎜⎝cos π4 + i sin π4⎞⎟⎠.
Решение. а) z = cos ⎛⎜⎝− π4⎞⎟⎠ + i sin ⎜⎝⎛ 34π
⎞⎠⎟ = cos π4 + i sin π4; arg z = ![]()
![]() .
.
б) z = −3 ⎛⎜⎝cos π4 + i sin π4⎟⎞⎠ = −3 ⎛⎜⎝− cos 54π − i sin 54π ⎟⎠⎞ =
= 3 ⎛⎜⎝cos 54π + i sin 54π ⎞⎟⎠; arg z = 54π.
![]() 17.5.
а) z = 3
+ i; б)
z = 3 − i.
17.5.
а) z = 3
+ i; б)
z = 3 − i.
![]()
![]() Решение. а) Так как |
z | = (
3)2
+12 = 2, то z = 2 ⎜⎝⎛ 23 + 21 i⎞⎟⎠
= 2 ⎜⎝⎛cos
6π
+ i
sin 6π
⎞⎠⎟;
arg z = 6π.
Решение. а) Так как |
z | = (
3)2
+12 = 2, то z = 2 ⎜⎝⎛ 23 + 21 i⎞⎟⎠
= 2 ⎜⎝⎛cos
6π
+ i
sin 6π
⎞⎠⎟;
arg z = 6π.
![]() б) Так как | z | = (
3)2
+ −(
1)2 = 2,
то
б) Так как | z | = (
3)2
+ −(
1)2 = 2,
то
![]() z
= 2 ⎜⎝⎛ 23 − 21 i⎞⎟⎠
= 2 ⎜⎝⎛cos
116π + i sin 116π ⎟⎠⎞; arg
z = 116π.
z
= 2 ⎜⎝⎛ 23 − 21 i⎞⎟⎠
= 2 ⎜⎝⎛cos
116π + i sin 116π ⎟⎠⎞; arg
z = 116π.
17.6. а) z = 3 + 4i; б) z = 3 − 4i.
![]() Решение.
а) Так как | z | = 32
+ 42 = 5, то z = 5 ⎝⎛⎜ 53 + 54 i⎞⎟⎠ =
Решение.
а) Так как | z | = 32
+ 42 = 5, то z = 5 ⎝⎛⎜ 53 + 54 i⎞⎟⎠ =
= 5 (cos arccos 0,6 + i sin arccos 0,6); arg z = arccos 0,6.
б) Так как | z | = 32 + −( 4)2 = 5, то z = 5 ⎝⎜⎛ 53 − 54 i⎠⎞⎟ =
= 5 (cos (2π − arccos 0,6) + i sin (2π − arccos 0,6)); arg z = 2π − arccos 0,6.
17.7. а) Выполните умножение комплексных чисел
⎛⎜⎝ 53π + i sin 53π ⎞⎟⎠ ⎛⎜⎝cos 3π + i sin 3π ⎟⎠⎞.
cos
Решение. Каждое из чисел z1
= cos ![]() π
+ i
sin
π
+ i
sin ![]() π и
π и
z2 = cos π + i sin π записано в тригонометрической форме,
3 3
имеет модуль 1, поэтому ⎜⎝⎛cos 53π + i sin 53π ⎞⎟⎠ ⎛⎜⎝cos 3π + i sin 3π ⎞⎟⎠ =
![]()
![]()
![]()
![]()
![]()
![]() π π π
+ π π + i sin π
= 1.
π π π
+ π π + i sin π
= 1.
= cos+ i sin= cos
Замечание. Тот же ответ получится, если в данном выражении раскрыть скобки с помощью распределительного закона умножения и применить формулы косинуса суммы двух углов и синуса суммы двух углов.
17.15. а) Возведите в степень с показателем n = 1, 2, 3,
![]() 4, 5, 6, 7 комплексное число
z = 3 + 1 i и найдите на ком-
4, 5, 6, 7 комплексное число
z = 3 + 1 i и найдите на ком-
2 2
плексной плоскости точки, соответствующие полученным числам.
![]() Решение. Так как z1
= z = 3 + 1 i =
cos π + i sin π и
Решение. Так как z1
= z = 3 + 1 i =
cos π + i sin π и
2 2 6 6
| z | = 1, то по формуле Муавра имеем
![]()
![]()
![]() z2
= cos π
+ i
sin 2π
= cos
π
+
z2
= cos π
+ i
sin 2π
= cos
π
+
6 3
+ i sin + i;
2
z3 = cos π + i sin 3π = cos π +
6 2
![]() + i sin
+ i sin ![]()
![]() =
i; z4 =
cos π + i sin
=
i; z4 =
cos π + i sin ![]() π
= cos
π
= cos
![]() π
+
π
+
+ i sin = − i;
2
![]()
![]() Рис. 98 z5 = cos 5π + i sin 5π = − 3 +
Рис. 98 z5 = cos 5π + i sin 5π = − 3 + ![]() i;
i;
6 6 2
z6 = cos ![]() π
+ i
sin
π
+ i
sin ![]() π = cos π + i sin π = −1;
π = cos π + i sin π = −1;
![]()
![]()
![]() z7 = cos π + i sin π
=
−cos π − i sin π
=
−i (рис. 98).
z7 = cos π + i sin π
=
−cos π − i sin π
=
−i (рис. 98).
6 6 2
17.17. а) Выразите sin 4x и cos 4x через sin x и cos x. Решение. По формуле Муавра имеем
(cos x + i sin x)4 = cos 4x + i sin 4x.
Применяя формулу бинома Ньютона и основное тригонометрическое тождество, имеем
(cos x + i sin x)4 = cos4 x + 4 cos3 x (i sin x) +
+ 6 cos2 x (i sin x)2 + 4 cos x (i sin x)3 + (i sin x)4 =
= (cos4 x − 6 cos2 x sin2 x + sin4 x) +
+ i (4 cos3 x sin x − 4 cos x sin 3x) =
= (cos4 x − 6 cos2 x (1 − cos2 x) + (1 − cos2 x)2) +
+ i (4 cos3 x sin x − 4 cos x sin 3x) =
= (8 cos4 x − 8 cos2 x + 1) + i (4 cos3 x sin x − 4 cos x sin 3x).
По правилу равенства комплексных чисел имеем cos 4x = 8 cos4 x − 8 cos2 x + 1;
sin 4x = 4 cos3 x sin x − 4 cos x sin3 x.
16i ⎜⎝⎛ sin 3π − i cos 3π ⎞⎟⎠ 2
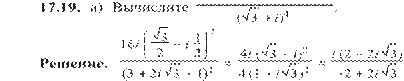
17.20. а) Пусть z — комплексное число: | z | = 2, arg z =
=
![]()
![]() . Найдите модуль
и один из аргументов числа z3 −
8i.
. Найдите модуль
и один из аргументов числа z3 −
8i.
Решение. Так как z = 2 ⎛⎜⎝cos 3π + i sin 3π ⎞⎟⎠, то z1 = z3 − 8i =
![]() = 8 (cos π
+ i sin π)
− 8i = −8 − 8i; |
z1 | =
8 2;
= 8 (cos π
+ i sin π)
− 8i = −8 − 8i; |
z1 | =
8 2;
![]()
![]() z1 = 8 2 ⎛⎜⎝−
22 − 22 i⎞⎟⎠ = 8 2 ⎛⎜⎝cos
54π
+ i
sin 54π
⎟⎠⎞; arg z1
=
54π.
z1 = 8 2 ⎛⎜⎝−
22 − 22 i⎞⎟⎠ = 8 2 ⎛⎜⎝cos
54π
+ i
sin 54π
⎟⎠⎞; arg z1
=
54π.
![]() Итак, один из аргументов числа z1
равен
Итак, один из аргументов числа z1
равен ![]()
![]() ; | z1
| = 8 2.
; | z1
| = 8 2.
17.21. а) Найдите множество точек z комплексной
плоскости, удовлетворяющих условию z ![]() .
.
Среди этих точек найдите такие, для которых
выполняется равенство | z | =
| z −
2i |, и запишите числа, соответствующие этим точкам, в
тригонометрической форме. Решение. Пусть z = x + yi. Тогда z
![]()
=
x2 +
y2; (2 +
i)2 + 17 = 4 + 4i − 1 + ![]() = 3 + 4i
+
= 3 + 4i
+
1 + 4i (1 + 4i) (1 − 4i)
.
![]() Итак, условию задачи удовлетворяют точки (x;
y) комплексной плоскости, для которых верно равенство x2
+ y2
= 4, т. е.
точки окружности с центром O (0; 0) и радиусом 2.
Итак, условию задачи удовлетворяют точки (x;
y) комплексной плоскости, для которых верно равенство x2
+ y2
= 4, т. е.
точки окружности с центром O (0; 0) и радиусом 2.
Найдем среди этих точек такие, для которых выполняется равенство | z | = | z − 2i |, т. е. равенство x2 + y2 = x2 + (y − 2)2 .
Возведя в квадрат последнее равенство, получим, что y = 1, т. е.
равенство | z | = | z − 2i | выполня- Рис. 99 ется для всех чисел z = x + i, изображаемых точками прямой
![]()
![]() y = 1. Тогда существуют
только две точки ( 3; 1) и (−
3 1; ), принадлежащие окружности x2 + y2 = 4 и прямой y = 1 (рис. 99). Они
соответствуют комплексным числам:
y = 1. Тогда существуют
только две точки ( 3; 1) и (−
3 1; ), принадлежащие окружности x2 + y2 = 4 и прямой y = 1 (рис. 99). Они
соответствуют комплексным числам:
![]() z1 = 2 ⎛⎜⎝+ 21 i⎞⎟⎠ = 2
⎛⎜⎝cos
6π
+ i
sin 6π
⎞⎟⎠
и z2 = 2 ⎜⎝⎛− 2 + 21 i⎞⎟⎠
= 2 ⎜⎛⎝cos
56π + i sin 56π ⎞⎟⎠.
z1 = 2 ⎛⎜⎝+ 21 i⎞⎟⎠ = 2
⎛⎜⎝cos
6π
+ i
sin 6π
⎞⎟⎠
и z2 = 2 ⎜⎝⎛− 2 + 21 i⎞⎟⎠
= 2 ⎜⎛⎝cos
56π + i sin 56π ⎞⎟⎠.
Замечание. Числа z1 и z2 можно найти и из геометрических соображений. Запишем равенство | z | = | z − 2i | в виде | z − (0 + 0i) | = | z − (0 + 2i) |. Тогда искомые точки z одинаково удалены от точек (0; 0) и (0; 2), соответствующих комплексным числам 0 + 0i и 0 + 2i. Такие точки лежат на серединном перпендикуляре к отрезку, соединяющему точки (0; 0) и (0; 2), т. е. на прямой y = 1.
В этом пункте доказывается теорема о существовании n различных корней степени n из любого комплексного числа, отличного от нуля, приведены примеры вычисления корней степени n из комплексных чисел.
Решения и комментарии 17.23. а) Найдите корни степени 2 из комплексного
числа 4 ⎜⎝⎛cos 43π + i sin 43π ⎞⎟⎠.
Решение. Для числа z = 4 ⎛⎜⎝cos 43π + i sin 43π ⎠⎞⎟ имеем r = 4,
ϕ
= ![]()
![]() , поэтому αk =
, поэтому αk =
⎛ 4π + 2πk 4π + 2πk⎞⎟
⎜ 3 3
![]() 4 ⎜⎜⎝cos
4 ⎜⎜⎝cos ![]() 2 +
i sin
2 +
i sin ![]() 2 ⎟⎟⎠, где
2 ⎟⎟⎠, где
Рис. 100
![]() ⎛⎜ π
+ 2πk
⎛⎜ π
+ 2πk
k = 0, 1, т. е.
α 0 = 2 ⎛⎜⎝cos 23π + i sin 23π ⎞⎟⎠, α 1 = 2 ⎛⎜⎝cos 53π + i sin 53π ⎞⎟⎠.
17.25. д) Найдите корни степени 3 из комплексного числа 1 + i и найдите на комплексной плоскости точки, их изображающие. Решение. Для числа
![]() z
= 1 + i = 2 ⎛⎜⎝cos π4 + i sin π4⎠⎞⎟
z
= 1 + i = 2 ⎛⎜⎝cos π4 + i sin π4⎠⎞⎟
имеем r
= 2,
ϕ = ![]()
![]() , поэтому
, поэтому
π + 2πk⎞⎟
![]()
![]() αk
=⎜⎜⎝cos
4 3 + i sin 4 3 ⎟⎟⎠, где k
= 0, 1, 2, т.
е.
αk
=⎜⎜⎝cos
4 3 + i sin 4 3 ⎟⎟⎠, где k
= 0, 1, 2, т.
е.
α 0 = 2 ⎜⎝⎛cos 12π + i sin 12π ⎞⎟⎠, α 1 = 2 ⎜⎝⎛cos 34π + i sin 34π ⎞⎟⎠, α 2 = 2 ⎜⎝⎛cos 1127π + i sin 1127π ⎟⎠⎞ (рис. 100).
|
§18*. |
Корни многочленов.
Показательная форма комплексных чисел
В этом пункте обобщается понятие корня многочлена степени n (n ∈ N, n ≥ 1) относительно x:
Pn (x) = anxn + an − 1xn − 1 + ... + a1x + a0 (1)
с действительными коэффициентами an, an−1, ... , a1, a0 (an ≠ 0). Если ранее корень многочлена был действительным числом, то теперь корень многочлена (1) может быть комплексным числом.
Далее сформулирована основная теорема алгебры и другие теоремы, выражающие свойства корней многочлена степени n.
Решения и комментарии
Найдите все корни уравнения (18.2—18.4):
18.2. в) x2 + 3x + 6,25 = 0.
Решение. Так как D = 9 −
25 = −16,
то x1 =
− ![]()
![]() − 2i, x2
= −
− 2i, x2
= − ![]()
![]() +
2i.
+
2i.
|
18.3. а) 2x2 + 2x + 1 = 0. |
|
|
|
D Решение. Так как = 1 − 2 = −1, 4 |
то |
x1 = − 21 − 21 i, |
![]() x2 = −
x2 = − ![]() +
+ ![]() i.
i.
18.4. г) x3 + 1 = 0.
Решение. Применив формулу суммы кубов, перепишем исходное уравнение в виде
(x + 1) (x2 − x + 1) = 0. (2)
Уравнение (2) имеет три корня: x1
= −1,
x2
= ![]() 2 ,
2 ,
x3 = ![]() 2 .
2 .
В этом пункте приведена формула Эйлера eiϕ = cos ϕ + i sin ϕ, используя которую число z можно записать в более компактной форме
z = r ⋅ eiϕ,
называемой показательной формой комплексного числа z.
Здесь же приведены правила умножения и деления комплексных чисел, записанных в показательной форме.
Решения и комментарии
18.5. а) Представьте в показательной форме комплексное число 3 − 4i.
Решение. Найдем модуль числа z = 3 − 4i:
![]() | z |
= 32 + −( 4)2 = 5.
| z |
= 32 + −( 4)2 = 5.
Следовательно, z = 5 ⎛⎜⎝ 35 − 54 i⎞⎟⎠. При этом среди углов α,
удовлетворяющих двойному неравенству 0 ≤ α < 2π, существует, и притом единственный, такой угол α, что
![]()
![]() = cosα, −
= cosα, − ![]()
![]() =
sinα,
и поэтому z = 5
(cos α + i
sin α) = 5e−iα,
=
sinα,
и поэтому z = 5
(cos α + i
sin α) = 5e−iα,
где α
= − arcsin ![]()
![]() , т. е. z = 5e
, т. е. z = 5e![]() .
.
18.7. Запишите в алгебраической форме комплексное число:
iπ iπ
а) e 4 ; б) 2e 3 .
4 4
3 3 ⎝ 2
18.9. Вычислите:
iπ 4iπ iπ iπ
а) e 5 ⋅ 2e 5 ; б) 3e 4 ⋅ 4e 3 .
Решение. а) e 5 ⋅ 2e 5 = 2e 5 5 = 2eiπ = 2 (cos π + i sin π) = = −2.
π π π + π 7 π
б) 3ei4 ⋅ 4ei3 = 12ei4 i3 = 12e 12i = 12 ⎝⎜⎛cos 712π + i sin 712π ⎟⎠⎞.
Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
О пособии для учителей . . . . . . . . . . . . . . . . . . . . . . . . —
Концепция учебников серии «МГУ — школе» . . . . . . . . . . 4
О работе по учебнику и дидактическим материалам . . . . . . 5
Примерное тематическое планирование . . . . . . . . . . . . . . 8
Глава I. Функции. Производные. Интегралы . . . . . . . . . . 13
§ 1. Функции и их графики . . . . . . . . . . . . . . . . . . . . . . . —
1.1. Элементарные функции . . . . . . . . . . . . . . . . . . . . — 1.2. Область определения и область изменения функции.
Ограниченность функции . . . . . . . . . . . . . . . . . . . 14
1.3. Четность, нечетность, периодичность функций . . . . . 20
1.4. Промежутки возрастания, убывания, знакопостоянства
и нули функции. . . . . . . . . . . . . . . . . . . . . . . . . . 29
1.5. Исследование функций и построение их графиков
элементарными методами . . . . . . . . . . . . . . . . . . . 31
1.6. Основные способы преобразования графиков. . . . . . . 33
1.7*. Графики функций, содержащих модули . . . . . . . . . 38
1.8*. Графики сложных функций . . . . . . . . . . . . . . . . . —
§ 2. Предел функции и непрерывность . . . . . . . . . . . . . . . 43
2.1. Понятие предела функции . . . . . . . . . . . . . . . . . . —
2.2. Односторонние пределы . . . . . . . . . . . . . . . . . . . . 44
2.3. Свойства пределов функций . . . . . . . . . . . . . . . . . 48
2.4. Понятие непрерывности функции. . . . . . . . . . . . . . 50
2.5. Непрерывность элементарных функций . . . . . . . . . . 51
2.6*. Разрывные функции . . . . . . . . . . . . . . . . . . . . . . 52
§ 3. Обратные функции . . . . . . . . . . . . . . . . . . . . . . . . . . 54
3.1. Понятие обратной функции. . . . . . . . . . . . . . . . . . —
3.2*. Взаимно обратные функции . . . . . . . . . . . . . . . . . —
3.3*. Обратные тригонометрические функции. . . . . . . . . . 58
3.4*. Примеры использования обратных
тригонометрических функций . . . . . . . . . . . . . . . . 60
§ 4. Производная. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . —
4.1. Понятие производной. . . . . . . . . . . . . . . . . . . . . . 61
4.2. Производная суммы. Производная разности . . . . . . . 62 4.3*. Непрерывность функции, имеющей производную.
Дифференциал . . . . . . . . . . . . . . . . . . . . . . . . . . —
4.4. Производная произведения. Производная частного . . 63
4.5. Производные элементарных функций . . . . . . . . . . . 64
4.6. Производная сложной функции . . . . . . . . . . . . . . . 66
4.7*. Производная обратной функции. . . . . . . . . . . . . . . 68
§ 5. Применение производной. . . . . . . . . . . . . . . . . . . . . . 69
5.1. Максимум и минимум функции. . . . . . . . . . . . . . . —
5.2. Уравнение касательной. . . . . . . . . . . . . . . . . . . . . 75
5.3. Приближенные вычисления. . . . . . . . . . . . . . . . . . 79
5.4*. Теоремы о среднем . . . . . . . . . . . . . . . . . . . . . . . 80
5.5. Возрастание и убывание функции. . . . . . . . . . . . . . 81
5.6. Производные высших порядков . . . . . . . . . . . . . . . 83
5.7*. Выпуклость графика функции . . . . . . . . . . . . . . . . 84
5.8*. Экстремум функции с единственной критической
точкой . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85
5.9. Задачи на максимум и минимум . . . . . . . . . . . . . . 89
5.10*. Асимптоты. Дробно-линейная функция . . . . . . . . . . 95
5.11. Построение графиков функций с применением
производных . . . . . . . . . . . . . . . . . . . . . . . . . . . 98
5.12*. Формула и ряд Тейлора . . . . . . . . . . . . . . . . . . . . 101
§ 6. Первообразная и интеграл . . . . . . . . . . . . . . . . . . . . . 102
6.1. Понятие первообразной . . . . . . . . . . . . . . . . . . . . —
6.2*. Замена переменной. Интегрирование по частям. . . . . 104
6.3. Площадь криволинейной трапеции . . . . . . . . . . . . . 106
6.4. Определенный интеграл . . . . . . . . . . . . . . . . . . . . 108
6.5*. Приближенное вычисление определенного интеграла 110
6.6. Формула Ньютона — Лейбница . . . . . . . . . . . . . . . 111
6.7. Свойства определенного интеграла . . . . . . . . . . . . . 114
6.8*. Применение определенных интегралов в геометрических и физических задачах . . . . . . . . . 117
6.9*. Понятие дифференциального уравнения. . . . . . . . . . 119
6.10*. Задачи, приводящие к дифференциальным уравнениям . . . . . . . . . . . . . . . . . . . . . . . . . . . . 120
Глава II. Уравнения. Неравенства. Системы . . . . . . . . . . 122
§ 7. Равносильность уравнений и неравенств. . . . . . . . . . . 123
7.1. Равносильные преобразования уравнений. . . . . . . . . — 7.2. Равносильные преобразования неравенств . . . . . . . . 124
§ 8. Уравнения-следствия. . . . . . . . . . . . . . . . . . . . . . . . . 128
8.2. Возведение уравнения в четную степень . . . . . . . . . 130
8.3. Потенцирование логарифмических уравнений. . . . . . 133
8.4. Другие преобразования, приводящие к уравнению-следствию . . . . . . . . . . . . . . . . . . . . 134
8.5. Применение нескольких преобразований, приводящих к уравнению-следствию . . . . . . . . . . . . . . . . . . . . 137
§ 9. Равносильность уравнений и неравенств системам . . . 141
9.1. Основные понятия. . . . . . . . . . . . . . . . . . . . . . . . —
9.2. Решение уравнений с помощью систем . . . . . . . . . . 142
9.3. Решение уравнений с помощью систем (продолжение) — 9.4*. Уравнения вида f (α (x)) = f (β (x)) . . . . . . . . . . . . . 147
9.5. Решение неравенств с помощью систем . . . . . . . . . . 150
9.6. Решение неравенств с помощью систем (продолжение) — 9.7*. Неравенства вида f (α (x)) > f (β (x)) . . . . . . . . . . . . 153
§ 10. Равносильность уравнений на множествах . . . . . . . . . 154
10.1. Основные понятия. . . . . . . . . . . . . . . . . . . . . . . . 155 10.2. Возведение уравнения в четную степень . . . . . . . . . 156
10.3*. Умножение уравнения на функцию . . . . . . . . . . . . 158
10.4*. Другие преобразования уравнений . . . . . . . . . . . . . 160 10.5*. Применение нескольких преобразований . . . . . . . . . 165
10.6*. Уравнения с дополнительными условиями . . . . . . . . 168
[1] ⎜
= 2002 ⎜⎝∫0 | sin u du| + ∫π | sin u du| + ... + 2001∫ π| sin u du| ⎠⎟⎟.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.