

УДК 372.8:51 16+
ББК 74.262.21
П64
Серия «МГУ — школе» основана в 1999 году
Потапов М. К.
П64 Математика. Методические рекомендации. 5 класс : учеб. пособие для общеобразоват. организаций / М. К. Потапов, А. В. Шевкин. — М. : Просвещение, 2017. — 127 с. : ил. — (МГУ — школе.) — ISBN978-5-09-042966-5.
Эта книга адресована учителям, работающим по учебнику серии «МГУ — школе» «Математика, 5» (авторы: С. М. Никольский, М. К. Потапов, Н. Н. Реш етн иков, А. В. Шевкин). В ней дана характеристика курса математики 5—6 классов, приведено примерное тематическое планирование для 5 класса, методические рекомендации по всем темам и решения наиболее трудных задач.
УДК 372.8:51
ББК 74.262.21
ISBN978-5-09-042966-5 © Издательство «Просвещение», 2012 © Художественное оформление.
Издательство «Просвещение», 2012
Все права защищены
О книге для учителя
Данная книга предназначена учителям, работающим по учебнику «Математика, 5» (авторы: С. М. Никольский, М. К. Потапов, Н. Н. Решет ни ков, А. В. Шевкин). Этот учебник является частью учебного комплекта для 5—6 классов, рекомендованного Министерством образования и науки Российской Федерации. Учебники для 5 и 6 классов начинают серию учебников «МГУ — школе» тех же авторов для 5—11 классов и нацелены на развитие и поддержку интереса к ма-
тематике.
В учебный комплект для 5—6 классов входят:
Математика. 5 класс: учебник для общеобразоват. организаций / С. М. Ник ольс кий, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. — М.: Просвещение, 2016;
Математика. Дидактические материалы. 5 класс / М. К. Потапов, А. В. Шев кин. — М.: Просвещение, 2014—2016;
Математика. Рабочая тетрадь. 5 класс. В 2 ч. / М. К. Пот а пов,
А. В. Шевкин. — М.: Просвещение, 2012—2016;
Математика. Тематические тесты. 5 класс / П. В. Чулков, Е. Ф. Шерш нев, О. Ф. Зарапина. — М.: Просвещение, 2009—2016;
Математика. 6 класс: учебник для общеобразоват. организаций / С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. — М.: Просвещение, 2016;
Математика. Дидактические материалы. 6 класс / М. К. Потапов, А. В. Шев кин. — М.: Просвещение, 2014—2016;
Математика. Рабочая тетрадь. 6 класс / М. К. Потапов, А. В. Шевкин. — М.: Просвещение, 2007—2016;
Математика. Тематические тесты. 6 класс / П. В. Чулков, Е. Ф. Шерш нев, О. Ф. Зарапина. — М.: Просвещение, 2010—2016;
Задачи на смекалку. 5—6 классы / И. Ф. Шарыгин, А. В. Шев кин. — М.: Просвещение, 2014—2016;
Математика. Методические рекомендации. 5 класс / М. К. Пот а пов, А. В. Шевкин. — М.: Просвещение, 2016;
Математика. Методические рекомендации. 6 класс / М. К. Пот а пов, А. В. Шев кин. — М.: Просвещение, 2016.
В данной книге рассмотрены концепция учебников математики серии «МГУ — школе» и структура учебников для 5—6 классов, приведено примерное тематическое планирование, даны методические рекомендации по изучению основных тем курса 5 класса и комментарии к решению некоторых трудных задач. Комментарии к учебнику приводятся по переработанному изданию 2012 г. Иногда комментарии к близким по содержанию пунктам объединены. При этом не обсуждается время, отводимое на изучение пункта, — оно отражено в планировании. В комментариях для учителя не выделяется обязательный и необязательный материал, так как в учебнике есть соответствующие обозначения. Во многих пунктах методические комментарии даны в расчёте на возможно более глубокое изучение вопроса, поэтому при подготовке к уроку учитель должен отобрать главное, что будет изложено учащимся на уроке, решить, каким будет закрепление материала в классе и дома, каким и когда будет контроль изученного. При этом не надо стремиться донести до учащихся все подробности и тонкости изучаемого материала, если учащиеся существенно ограничены во времени изучения темы. В книге также даны рекомендации по использованию дидактических материалов (ДМ) и рабочей тетради (РТ).
Практически для всех пунктов учебника в книге для учителя имеются рубрики Решения и комментарии и Промежуточный контроль. В первой из них приведены условия многих задач и их решения или даны рекомендации, как найти решение. При этом даны пояснения, помогающие обучению школьников. Во второй рубрике даны номера самостоятельных работ по дидактическим материалам.
Об учебниках математики серии «МГУ — школе»
В серии «МГУ — школе» издательство «Просвещение» выпускает учебники «Математика» для 5 и 6 классов, «Алгебра» для 7, 8 и 9 классов, «Алгебра и начала математического анализа» для 10 и 11 классов (авторы: С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шев кин).
Эти учебники рекомендованы министерством в качестве учебников для любых типов общеобразовательных организаций и входят в перечень учебников, рекомендованных к использованию в средних школах. Их издание является составной частью программы «МГУ — школе», разработанной по инициативе ректора Московского университета академика В. А. Садовничего и нацеленной на сохранение и развитие лучших традиций отечественного математического образования.
Авторами учебников разработана концепция многоуровневых учебников математики. Приведём основные положения этой концепции.
![]() Математика едина и
может быть изложена в одном учебнике для работы по разным программам.
Содержание учебника должно соответствовать научной точке зрения на изучаемые
вопросы.
Математика едина и
может быть изложена в одном учебнике для работы по разным программам.
Содержание учебника должно соответствовать научной точке зрения на изучаемые
вопросы.
Учебник должен сочетать в себе научность, стройность, экономность и логичность изложения материала с доступностью для учащихся его учебных текстов.
Учебник не должен ограничиваться интересами среднего ученика, он должен удовлетворять интересам всех учащихся — от слабых до сильных.
Учебник должен быть пригоден для организации дифференцированного обучения и обеспечивать любой желаемый уровень глубины изучения материала.
Способ изложения материала в учебнике, организация учебных текстов и системы упражнений должны обеспечивать достижение разных целей обучения при работе по разным программам.
Структура учебников серии «МГУ — школе» и их методический аппарат отвечают основным положениям этой концепции.
Авторы учебников уверены, что не следует упрощать обучение за счёт сокращения числа изучаемых вопросов и необходимо сохранить фундаментальность изложения теории в учебниках, оставляя за учителем право более или менее глубокого изложения теоретического материала на уроке в зависимости от уровня подготовки класса и целей обучения. В учебниках коротко, ясно и доступно, без долгих введений излагается суть вопроса. Мотивировать появление тех или иных понятий, определений при необходимости должен учитель, так как в разных классах это надо делать по-разному.
Учебники серии «МГУ — школе» имеют высокий научный и методический потенциал. Они различаются расположением учебного материала в естественной логической последовательности, позволяющей излагать материал более глубоко, экономно и строго. Учебники нацелены не только на формирование навыков, но и учат действовать осознанно. Обычно обучение больше ориентировано на вопрос «как?», на действия по образцу, требует многократных повторений для поддержания навыков. В учебниках серии «МГУ — школе» уделяется достаточно внимания вопросу «почему?», имеющему большой развивающий потенциал. Учебники позволяют интенсифицировать процесс обучения, что в условиях уменьшения числа учебных часов особенно важно. Они полностью обеспечивают обучение тех школьников, которые хотят и могут обучаться основам наук.
Главный методический принцип, положенный в основу изложения теоретического материала и организации системы упражнений, заключается в том, что ученик за один раз должен преодолевать не более одной трудности. Поэтому каждое новое понятие формируется, каждое новое умение отрабатывается сначала в «чистом» виде, затем трудности совмещаются. Так происходит, например, при изучении арифметических действий с обыкновенными дробями: сначала изучаются обыкновенные дроби, только потом вводится понятие смешанной дроби и изучаются арифметические действия со смешанными дробями.
Важную роль в формировании первоначальных представлений о зарождении и развитии математики играют исторические сведения, завершающие каждую главу учебников. Работа со старинными задачами — одна из сильных сторон учебников, она может много дать в воспитании уважения к традициям и истории.
О структуре учебников математики для 5 и 6 классов
Авторы считают, что основное содержание курса математики 5—6 классов должна составлять арифметика. Именно поэтому первые издания учебников для 5—6 классов назывались «Арифметика». Этим подчёркивалась значимость основательного изучения арифметики до изучения систематических курсов алгебры и геометрии, а также уважение к традициям отечественного математического образования.
Арифметика — стержень курса математики 5—6 классов и фундамент всей школьной математики и смежных дисциплин. Это важнейшая основная логическая наука. Правильное её изучение приводит к формированию не только умения вычислять, но и умения логически мыслить. Поэтому необходимо основательное изучение арифметики каждым учеником независимо от профиля школы, в которой он учится, и образования, которое будет получать в дальнейшем.
Внутренняя логика арифметики диктует порядок изложения основного учебного материала. Существенной особенностью учебников является расположение материала в естественной логической последовательности, позволяющей сделать его изучение более глубоким, экономным и строгим. Из всех возможных схем изложения материала в учебниках выбрана та, которая отвечает научным представлениям о расширении понятия числа и в то же время учитывает возрастные особенности учащихся 5—6 классов, количество учебных часов, отведённых программой на курс математики в этих классах. Так, в частности, обыкновенные дроби изучаются в 5 классе в полном объёме до десятичных дробей, которые рассматриваются в 6 классе; целые числа изучаются отдельно до отрицательных дробей, что позволяет учащимся освоиться с идеей знака числа в более простой ситуации, после чего вводятся рациональные числа; наконец, изучается запись некоторых рациональных чисел в виде десятичных дробей и показывается, как действовать с ними. Такая схема изложения материала позволяет интенсифицировать процесс обучения.
Принципиальной особенностью учебников является то, что они не «натаскивают» ученика, они не только ориентированы на формирование навыка, но и учат действовать осознанно.
Учебники серии «МГУ — школе» ориентированы на более высокие, чем формирование вычислительных навыков, цели: на формирование теоретического мышления и простейших доказательных умений, вычислительных умений, опирающихся на понимание смысла выполняемых действий, а не на схожесть алгоритмов вычислений, на развитие мышления и речи учащихся в процессе изучения арифметики, на формирование и развитие универсальных учебных действий.
Известно, что спорам о необходимости обоснованного изложения арифметического материала не одна сотня лет. Ещё Л. Эйлер писал: «Если арифметика без оснований и доказательств показываться будет, то оная не довольна ни к разрешению всех случаев, ни к поощрению человеческого разума, о чём наипаче надлежало бы стараться». По его мнению, в арифметике надо учеников «приучать праведное основание и причину видеть», благодаря чему они «приобвыкнут к основательному размышлению».
В учебниках вводятся элементы доказательств некоторых утверждений, при этом доказательства часто проводятся на конкретных примерах.
Для решения текстовых задач в основном используются арифметические способы, применение уравнений к решению таких задач отнесено на вторую половину 6 класса. Основной целью решения текстовых задач арифметическими способами является развитие мышления, умения делать логически правильные выводы на основе анализа имею щихся данных задачи и использовать эти данные для её решения. Авторы считают, что это пока наиболее эффективный способ развития логического мышления и речи учащихся, что в конечном счёте повышает эффективность обучения. Следует отметить, что отказ от решения текстовых задач арифметическими способами в рамках реформы математического образования конца 60-х гг. XX в. привёл к заметному ухудшению речи учащихся и их логического мышления.
Академик С. М. Никольский писал: «При обучении арифметике в 5—6 классах большое внимание должно быть уделено «физике» и логике изучаемых вопросов. Так, при изучении обыкновенных дробей необходимо привести примеры, подводящие к пониманию дроби. Это такие важнейшие «физические» примеры, как:
1) три одинаковых яблока разделить между пятью мальчиками поровну;
2) убедиться в том, что две третьих части торта и четыре шестых его части — это физически одно и то же.
Первая задача приводит не только к дроби ![]() , но и к
тому, что её надо рассматривать как частное 3 5. Вторая задача приводит к
естествен- ности формального равенства
, но и к
тому, что её надо рассматривать как частное 3 5. Вторая задача приводит к
естествен- ности формального равенства ![]() =
= ![]() . Перед
авторами учебников стоит задача все эти вещи формализовать, изложить компактно
и доступно, но так, чтобы было видно, где в них логическое начало и где конец,
где здесь «физика» и где логика. Арифметика — логическая наука, на ней можно и
нужно учиться логически мыслить. Счастливым образом формализм арифметики имеет
прикладное значение, потому что он даёт правила вычислений. Но прикладной части
тоже надо уделить внимание. Умножить
. Перед
авторами учебников стоит задача все эти вещи формализовать, изложить компактно
и доступно, но так, чтобы было видно, где в них логическое начало и где конец,
где здесь «физика» и где логика. Арифметика — логическая наука, на ней можно и
нужно учиться логически мыслить. Счастливым образом формализм арифметики имеет
прикладное значение, потому что он даёт правила вычислений. Но прикладной части
тоже надо уделить внимание. Умножить ![]() на
на ![]() — это значит
вычислить дробь
— это значит
вычислить дробь ![]() . Это надо твёрдо знать. Но также
необходимо знать, что при этом мы реши- ли и «физическую» задачу — взяли две
третьих части от пяти седьмых (например, яблока) или вычислили площадь
прямоугольника со сто ронами
. Это надо твёрдо знать. Но также
необходимо знать, что при этом мы реши- ли и «физическую» задачу — взяли две
третьих части от пяти седьмых (например, яблока) или вычислили площадь
прямоугольника со сто ронами ![]() и
и ![]() ».
».
В учебниках «Математика, 5», «Математика, 6» учтены эти выска зывания С. М. Никольского. Авторы стремились в изложении теоретического материала для младших школьников избегать ставших уже традиционными логических подмен, когда факты для чисел получаются не из определений операций, а из физических действий над предметами. Так, например, упомянутое деление поровну трёх одинаковых яблок между пятью мальчиками действительно приводит к равенству
![]() = 3 5, но не
доказывает это равенство. Сравнение дробей вводится иногда с помощью никак не
определённого сложения равных долей, а правило умножения отрицательных чисел
«доказывается». Такого рода «доказательства» должны считаться неприемлемыми и
опасными не только для логического развития школьников, но и для квалификации
учителя математики.
= 3 5, но не
доказывает это равенство. Сравнение дробей вводится иногда с помощью никак не
определённого сложения равных долей, а правило умножения отрицательных чисел
«доказывается». Такого рода «доказательства» должны считаться неприемлемыми и
опасными не только для логического развития школьников, но и для квалификации
учителя математики.
Авторы учебников считают, что изучение чисел в средней школе должно проводиться по следующей схеме:
1. Сначала основательно изучаются натуральные числа.
2. Затем изучаются обыкновенные дроби. При этом очень важным моментом здесь является понимание того, что арифметические действия с обыкновенными дробями происходят по правилам:
a c a d b c +
+ = (b 0, d 0),
b d b d
a c a d b c -
– = (b 0, d 0),
b
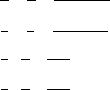 d b d (*)
d b d (*)
a c a c
= (b 0, d 0),
b d b d a c a d
= (b 0, c 0, d 0),
b d b c
т. е. действия с обыкновенными дробями представляют собой несколько действий с натуральными числами. Следовательно, если усвоены действия с натуральными числами, то в работе с обыкновенными дробями возникает только одна трудность — запоминание правил (*), которые учащиеся усваивают в соответствующих формулировках и на конкретных примерах. Заметим, что экономное выполнение сложения и вычитания дробей требует приведения дробей к наименьшему общему знаменателю.
3. Потом изучаются целые числа. Здесь также одна трудность — работа со знаками. А работа с абсолютными величинами — натуральными числами — должна быть усвоена ранее.
4. Наконец, изучаются рациональные числа. Здесь основной трудностью является понимание того, что арифметические действия с рациональными числами производятся по тем же правилам (*). Только теперь числа a, b, c, d не натуральные, а целые.
Важность правил (*) заключается ещё и в том, что в курсе алгебры 7 класса по этим правилам будут выполняться действия с алгебраическими дробями.
Только после изучения всех рациональных чисел можно переходить к изучению конечных десятичных дробей (сначала положительных), так как они:
1) являются частным случаем обыкновенных дробей;
2) позволяют проводить приближённые вычисления;
3) естественным образом подводят к бесконечным десятичным дробям, т. е. к изучению действительных чисел.
Действительные числа можно изучать в конце 6 класса и/или в начале 7 класса, используя учебники «Математика, 6» и «Алгебра, 7» серии «МГУ — школе».
Ведущей идеей учебников для 5—6 классов является идея формирования понятия числа как длины отрезка, а точнее, как координаты точки на координатной оси.
В учебниках уделено достаточно внимания алгебраическому и геометрическому материалу, который принято изучать в 5—6 классах. Но этот материал расположен так, чтобы не мешать развитию арифметических идей. В учебнике употребляются буквы, но очень осторожно — только тогда, когда кажется, что буквы легче проясняют вопрос, чем пример с числами. В большей части рассуждений доказательства ведутся на характерных числовых примерах, из которых при замене чисел буквами можно получить общее доказательство. Всё же примеров, когда можно использовать буквы, достаточно много, и, таким образом, учебники вносят определённый алгебраический элемент в образование учащихся.
В учебниках имеются нестандартные развивающие задачи, старинные задачи. Это позволяет значительно расширить возможности для развития мышления и речи учащихся, их представления о способах решения задач в далёкие времена, разнообразить приёмы решения задач, может способствовать развитию школьников, формированию у них интереса к решению задач и к самой математике.
Особенности построения системы упражнений в учебниках математики
Главная особенность построения системы упражнений в учебниках заключается в учёте важного методического принципа: «Ученик должен преодолевать за один раз не более одной трудности». Другими словами, сложность заданий в каждом пункте должна нарастать линейно. При этом в учебниках имеется достаточное число действительно сложных задач — учитель сам должен определить, на какой ступени лестницы сложности он остановится со своим классом или с конкретным учеником.
Кроме того, для каждого нового действия, приёма решения задач в учебнике имеется достаточное число упражнений, которые не перебиваются упражнениями на другие темы.
Ещё одна особенность системы упражнений в учебниках заключается в том, что к наиболее трудным видам деятельности учащиеся готовятся заранее. Так происходит с упомянутыми задачами на совместную работу, с введением понятия дроби, с подготовкой к использованию уравнений при решении задач. К некоторым трудным задачам учащиеся возвращаются многократно, но обязательно поднимаясь на новую ступень в освоении материала. Так, в 6 классе сначала изучаются простейшие задачи на проценты, потом, после изучения десятичных дробей, учащиеся осваивают решение тех же задач с использованием умножения и деления на дробь. Далее введён необязательный пункт «Сложные задачи на проценты», в котором приведены задачи на так называемые сложные проценты, и через некоторое время показано применение калькулятора для ведения процентных расчётов. Все указанные меры помогут учащимся освоить проценты на более высоком, чем это удавалось до сих пор, уровне.
Четвёртая особенность системы упражнений в учебниках заключается в регулярном использовании старинных задач — это связано с необходимостью демонстрации учащимся разнообразных, в том числе и не применяемых сейчас, способов решения задач. Тем самым учащиеся получают не только весьма полезный опыт мыслительной деятельности при решении задач, но и важное воспитательное воздействие от знакомства с древнейшим пластом человеческой культуры.
Наконец, пятая особенность построения системы упражнений в учебниках заключается в систематическом использовании занимательных задач как в упражнениях по отдельным темам, так и в специальных пунктах в конце глав. Трудная для данного возраста учебная деятельность школьников должна стимулироваться интересными заданиями, иногда даже не связанными напрямую с изучаемым материалом. Это необходимо делать для повышения интереса учащихся сначала к урокам математики, а потом и к изучению самого предмета.
Разделы «Занимательные задачи», расположенные после каждой главы, содержат задачи, главное назначение которых заключается в том, чтобы заинтересовать учащихся решением нестандартных и сложных задач. Некоторые учащиеся к началу 5 класса ещё не успели почувствовать себя способными к успешному изучению математики. Это может происходить по разным причинам (медленное письмо, ошибки по невнимательности, накопившиеся пробелы в знаниях и т. п.). Поэтому их успехи в работе с задачами, решение которых мало зависит от предыдущего обучения, а больше от сообразительности, могут вернуть им веру в свои силы.
В отдельные пункты разделов «Занимательные задачи» часто помещаются задачи, завершающие некоторые задачные линии учебников и не являющиеся обязательными для всех учащихся. Их можно использовать как в классной работе с сильным классом, так и для индивидуальной работы с сильными учащимися или для внеклассной работы.
 В учебниках
использованы некоторые задачи из сборника «Задачи для умственного счёта» С. А.
Рачинского, который окончил естественно-исторический факультет Московского
университета, блестяще начал карьеру молодого профессора, затем переехал в село
Татево Бельского уезда Смоленской губернии и там работал учителем.
В учебниках
использованы некоторые задачи из сборника «Задачи для умственного счёта» С. А.
Рачинского, который окончил естественно-исторический факультет Московского
университета, блестяще начал карьеру молодого профессора, затем переехал в село
Татево Бельского уезда Смоленской губернии и там работал учителем.
При доработке учебников для 5 и 6 классов в соответствии с требованиями Федерального государственного стандарта общего образования авторы учебника выделили некоторые из заданий учебника в отдельные рубрики. Отметим, что большая часть заданий для рубрик «Доказываем», «Исследуем» содержалась в учебниках предыдущих изданий, но выделение рубрик акцентирует внимание учителя и уче- ника на тех видах учебной деятельности, которые предполагается применять и развивать, выполняя именно эти задания. Для рубрик «Исследуем», «Ищем информацию», «Придумываем задачи» С. А. Рачинский (1838—1902) были составлены новые задания.
Таким образом, в учебниках и других книгах серии «МГУ — школе» имеются задания для осмысления теоретического материала, на воспроизведение и действия по образцу, для самостоятельного поиска решения и исследования, для проведения мысленного эксперимента и доказательства, для проявления творческого подхода к учению и собственных личностных качеств, для самоконтроля, что отвечает требованиям стандартов второго поколения.
О работе по учебникам «Математика, 5», «Математика, 6»
В учебниках параграфы без звёздочки соответствуют стандарту по математике. Параграфы со звёздочкой и специально выделенный в параграфах без звёздочек материал предназначены для учащихся, заинтересованных в изучении математики. Этот материал можно использовать при наличии достаточного учебного времени.
Каждая глава учебников завершается разделом, содержащим дополнительный материал, исторические сведения и занимательные задачи. В конце учебников помещены разделы «Задания для повторения».
В обычных классах дополнительные материалы и сложные задачи, специально выделенные в учебниках, можно не рассматривать. Пропуск необязательных пунктов и задач не нарушает целостности курса. Уменьшается лишь уровень погружения учащихся в теоретические тонкости, а также число доказываемых фактов, технически или идейно сложных задач. Однако учебники позволяют заинтересованному ученику изучить необходимый материал по учебнику самостоятельно или под руководством учителя.
Работать по учебнику для 5 класса можно после обучения в 4 классе по любому из учебников, рекомендованных Министерством образования и науки РФ, так как в начале учебника повторяются основные вопросы программы начальной школы, что позволяет систематизировать имеющиеся знания и подготовиться к изучению нового материала.
При организации повторения курса математики 5 или 6 класса необходимо обратить особое внимание на наиболее трудные темы для данного класса, постараться учесть индивидуальные пробелы учащихся.
При повторении необходимо выделять основные теоретические факты, изученные за год, давая иллюстрации их применения на наиболее характерных примерах.
«Математика, 5»
Учебник «Математика, 5» содержит четыре главы:
1. Натуральные числа и нуль.
2. Измерение величин.
3. Делимость натуральных чисел.
4. Обыкновенные дроби.
В учебнике излагаются вопросы, связанные с натуральными числами и обыкновенными дробями. Особое внимание уделяется использованию законов арифметических действий для обоснования вычислений столбиком и для рационализации вычислений, для доказательства ряда фактов на конкретных примерах.
Основная цель — научить осознанному владению арифметическими действиями с натуральными числами и обыкновенными дробями.
Рассматривая решение текстовых задач арифметическими способами, надо стараться развивать у учащихся умение логически мыслить и точно выражать свою мысль. Для этого нужно уметь формулировать вопросы, давать на них ответы, проверять правильность полученного ответа и т. п.
Рассматривая элементы доказательств некоторых утверждений, надо постараться сформировать у учащихся представление о том, что они могут быть как истинными, так и ложными. Учащиеся должны понимать, что некоторые истинные утверждения можно доказать.
При работе по учебнику предполагается использование рабочей тетради, дидактических материалов и сборника «Задачи на смекалку».
Рабочая тетрадь чаще используется на этапе начального усвоения понятия или умения. Здесь заполнение пропусков и наличие подсказок позволяют увеличить темп продвижения по материалу.
Дидактические материалы используются для промежуточного контроля по теме (самостоятельные работы) и итогового контроля (контрольные работы). Следует учесть, что провести все самостоятельные работы с выставлением отметки со всем классом, скорее всего, не удастся, да это и не требуется. Некоторые из них можно использовать как домашние задания или как дополнительные задания на отметку заинтересованным учащимся. Самостоятельные работы отнесены к соответствующим темам, но могут использоваться и при изучении других тем (например, для организации повторения).
Задачи из сборника «Задачи на смекалку» и разделов «Занимательные задачи» можно включать в уроки по мере необходимости разнообразить изучаемый материал. Эта работа развивает сообразительность у детей, интерес к математике и вкус к решению задач.
К данному курсу существует Электронная форма учебника (ЭФУ) — соответствующая по структуре, содержанию и художественному оформлению печатной форме учебника и включающая в себя интерактивные ссылки, расширяющие и дополняющие материал печатного учебника.
Функциональными особенностями ЭФУ является:
— удобный и понятный интерфейс и навигация по ЭФУ;
— работа в онлайн- и офлайн-режимах;
— тестовые задания к каждой теме, разделу учебника;
— возможность добавления материалов, созданных учителем;
— инструменты изменения размера шрифта, создания заметок и закладок.
Использование ЭФУ предоставляет учителю следующие возможности:
— организовать контроль и самоконтроль по результатам изучения темы;
— реализовать технологии мобильного, дистанционного или смешанного обучения;
— реализовать требования ФГОС по формированию информационно-образовательной среды системой электронных образовательных ресурсов и др.
Примерное тематическое планирование работы по учебнику
«Математика, 5»
Из приведённых двух вариантов примерного тематического планирования вариант I (5 ч в неделю, всего 170 ч) предназначен для классов, работающих по обычной программе, а вариант II (6 ч в неделю, всего 204 ч) — для классов, работающих по расширенной программе. Справа от пункта учебника указано число часов, отведённых на его изучение для каждого варианта планирования.
|
Глава 1. Натуральные числа и нуль 1.1. Ряд натуральных чисел 1.2. Десятичная система записи натуральных чисел 1.3. Сравнение натуральных чисел 1.4. Сложение. Законы сложения 1.5. Вычитание 1.6. Решение текстовых задач с помощью сложения и вычитания 1.7. Умножение. Законы умножения 1.8. Распределительный закон 1.9. Сложение и вычитание чисел столбиком К о н т р о л ь н а я р а б о т а № 1 1.10. Умножение чисел столбиком 1.11. Степень с натуральным показателем 1.12. Деление нацело 1.13. Решение текстовых задач с помощью умножения и деления 1.14. Задачи «на части» 1.15. Деление с остатком 1.16. Числовые выражения К о н т р о л ь н а я р а б о т а № 2 1.17. Задачи на нахождение двух чисел по их сумме и разности Дополнения к главе 1 1. Вычисления с помощью калькулятора 2. Исторические сведения 3. Занимательные задачи Глава 2. Измерение величин 2.1. Прямая. Луч. Отрезок 2.2. Измерение отрезков 2.3. Метрические единицы длины 2.4. Представление натуральных чисел на координатном луче К о н т р о л ь н а я р а б о т а № 3 2.5. Окружность и круг. Сфера и шар 2.6. Углы. Измерение углов |
I 46 1 2 2 3 3 2 3 2 3 1 3 2 3 2 3 3 2 1 3 — — 2 30 2 2 2 2 1 1 2 |
II 52 1 2 2 3 3 2 3 2 3 1 3 2 3 2 5 3 2 1 5 1 — 3 38 2 2 2 2 1 1 3 |
|
2.7. Треугольники 2.8. Четырёхугольники 2.9. Площадь прямоугольника. Единицы площади 2.10. Прямоугольный параллелепипед 2.11. Объём прямоугольного параллелепипеда. Единицы объёма 2.12. Единицы массы 2.13. Единицы времени 2.14. Задачи на движение К о н т р о л ь н а я р а б о т а № 4 Дополнения к главе 2 1. Многоугольники 2. Исторические сведения 3. Занимательные задачи Глава 3. Делимость натуральных чисел 3.1. Свойства делимости 3.2. Признаки делимости 3.3. Простые и составные числа 3.4. Делители натурального числа 3.5. Наибольший общий делитель 3.6. Наименьшее общее кратное К о н т р о л ь н а я р а б о т а № 5 Дополнения к главе 3 1. Использование чётности при решении задач 2. Исторические сведения 3. Занимательные задачи Глава 4. Обыкновенные дроби 4.1. Понятие дроби 4.2. Равенство дробей 4.3. Задачи на дроби 4.4. Приведение дробей к общему знаменателю 4.5. Сравнение дробей 4.6. Сложение дробей 4.7. Законы сложения 4.8. Вычитание дробей К о н т р о л ь н а я р а б о т а № 6 4.9. Умножение дробей 4.10. Законы умножения. Распределительный закон 4.11. Деление дробей 4.12. Нахождение части целого и целого по его части К о н т р о л ь н а я р а б о т а № 7 4.13. Задачи на совместную работу 4.14. Понятие смешанной дроби 4.15. Сложение смешанных дробей 4.16. Вычитание смешанных дробей |
2 2 2 2 2 1 1 3 1 1 — 1 19 2 3 2 3 3 3 1 — — 2 65 1 3 4 4 3 3 4 4 1 4 2 4 2 1 3 3 3 3 |
3 3 3 2 3 1 1 4 1 2 — 2 25 3 4 2 3 4 4 1 2 — 2 75 1 3 5 4 3 3 4 4 1 4 2 4 2 1 5 3 3 4 |
|
4.17. Умножение и деление смешанных дробей К о н т р о л ь н а я р а б о т а № 8 4.18. Представление дробей на координатном луче 4.19. Площадь прямоугольника. Объём прямоугольного параллелепипеда Дополнения к главе 4 1. Сложные задачи на движение по реке 2. Исторические сведения 3. Занимательные задачи Повторение Повторение И т о г о в а я к о н т р о л ь н а я р а б о т а № 9 |
5 1 3 2 — — 2 10 9 1 |
5 1 4 3 2 — 4 14 13 1 |
ГЛАВА 1
В этой главе проводится систематизация полученных в начальной школе сведений о натуральных числах. В ней содержится не просто повторение изученного ранее материала, а его развитие, нацеленное на осознанное овладение способами выполнения арифметических действий. Учащиеся приучаются к определённому порядку изучения чисел: запись чисел, их сравнение, арифметические действия с ними, законы арифметических действий, применение этих законов, степень числа с натуральным показателем, изображение чисел на координатной прямой (для натуральных чисел этот вопрос рассмотрен в главе 2).
Особое внимание уделено решению текстовых задач арифметическими способами. Ученик должен научиться осознанно решать такие задачи, сначала формулируя вопросы, а затем делая выкладки. Решение задач таким способом содействует развитию речи и мышления учащихся, учит умению рассуждать.
![]() Цели изучения главы:
научить осознанному выполнению арифметических действий над
Цели изучения главы:
научить осознанному выполнению арифметических действий над
натуральными числами и применению законов для упрощения вычислений;
развить язык и логическое мышление при помощи решения текстовых задач арифметическими методами.
Эта глава — фундамент всего изучения математики. Поэтому не надо жалеть времени на её изучение, надо добиться действительно осмысленного и уверенного владения четырьмя арифметическими действиями над натуральными числами.
В пункте 1.1 вводятся основные понятия: натуральные числа, ряд натуральных чисел. Говорится, что в ряду натуральных чисел есть первое, но нет последнего числа.
Отметим, что в США и ряде других стран принято считать нуль натуральным числом. Однако в курсе математики, изучаемом в средней школе России, нуль не считается натуральным числом.
В первом пункте учебника заданий немного, так как на первом уроке с новым классом учитель должен объяснить устройство учебника, назначение учебного текста, устных вопросов после учебного текста. Учащиеся должны знать, что для успешного обучения математике следует начинать подготовку домашнего задания с чтения учебного текста, так как в нём содержатся ответы на все вопросы, задаваемые сразу после учебного текста. Учитель должен задавать их на следующем уроке, чтобы стимулировать чтение учебника и научить учащихся правильно им пользоваться. Приучение школьников к работе с учебным текстом потребует определённых усилий учителя ещё и потому, что в начальной школе учащиеся не имели учебных текстов по математике и в последние годы заметно падает желание детей читать что-либо. Задания 5 и 6 нацелены на развитие речи учащихся и умения различать ситуации «от числа a до числа b» (включительно) и «между числами a и b».
В пункте 1.2 объясняется, что известную учащимся систему записи натуральных чисел называют десятичной системой счисления. Надо заметить, что это не единственная система записи натуральных чисел. О других системах записи натуральных чисел говорится в дополнении к главе 1. В пункте 1.2 определяются основные понятия: цифра, однозначные и многозначные натуральные числа, разряды и классы, отрабатывается чтение и запись многозначных натуральных чисел. Имеются задачи (21 и 22) на перебор всех возможных вариантов. Их использование помогает воспитывать привычку при решении задачи рассматривать все возможные случаи.
В пункте 1.3 говорится о том, что натуральные числа можно сравнивать как при помощи натурального ряда, так и по их десятичной записи. Здесь вводятся знаки сравнения: =, и , понятие положительного и неотрицательного чисел. В этом пункте впервые используются буквы латинского алфавита для обозначения натуральных чисел.
Задания 37—41 нацелены на развитие умения правильно понимать и применять слова: больше — меньше, старше — моложе, выше — ниже и т. п.
РТ. Лучшему усвоению материала пунктов 1.1—1.3 учебника будет способствовать использование заданий 1—25.
5. Сколько чисел в натуральном ряду: а) от 1 до 29; в) от 30 до 38?
Решение. а) От числа 1 до числа 29 имеется 29 чисел: 1, 2, 3, 4, ..., 28, 29.
в) От числа 1 до числа 38 имеется 38 чисел: 1, 2, 3, 4, ..., 37, 38,
но первые 29 не входят в требуемый перечень чисел. Поэтому от числа 30 до числа 38 имеется 38 – 29 = 9 чисел (их можно пересчитать: 30, 31, 32, 33, 34, 35, 36, 37, 38).
6. Сколько чисел в натуральном ряду между числами: а) 1 и 29; в) 30 и 38?
Решение. а) Между числами 1 и 29 находятся числа 2, 3, 4, ..., 28 — всего 28 – 1 = 27 чисел.
в) Между числами 30 и 38 находятся числа 31, 32, 33, 34, 35, 36, 37 — всего 37 – 30 = 7 чисел.
21. б) Запишите все трёхзначные числа без повторения одинаковых цифр, в записи которых используются цифры 0, 1, 2.
Решение. Запись трёхзначного числа может начинаться или с 1, или с 2. В каждом из этих двух случаев имеется по 2 числа: 102, 120 и 201, 210 — всего 4 числа.
22. б) Запишите все трёхзначные числа, в записи которых исполь-зуются цифры 0, 1, 2, если разрешается повторять одинаковые цифры в записи одного числа.
Решение. Запись трёхзначного числа может начинаться или с 1, или с 2. В каждом из этих двух случаев вторая цифра может быть или 0, или 1, или 2 и каждая третья цифра может быть или 0, или 1, или 2. Следовательно, всего случаев 2 3 3 = 18, т. е. существует 18 чисел, удовлетворяющих условию задачи:
100, 101, 102, 200, 201, 202,
110, 111, 112, 210, 211, 212, 120, 121, 122, 220, 221, 222.
23. а) В книге 120 страниц. Сколько цифр напечатали для нумера-ции страниц начиная с третьей страницы?
б) Для нумерации страниц начиная с третьей использовано 169
цифр. Сколько страниц в книге?
Решение. а) Для нумерации страниц с 3-й по 9-ю использовано
7 цифр. Для нумерации страниц с 10-й по 99-ю использовано 2 (99 – 9) = = 180 цифр. Для нумерации страниц с 100-й по 120-ю использовано 3 (120 – 99) = 63 цифры. Всего 7 + 180 + 63 = 250 цифр.
б) Для нумерации страниц с 3-й по 9-ю использовано 7 цифр. Для нумерации страниц начиная с 10-й осталось 169 – 7 = 162 цифры. Их хватит для нумерации 162 2 = 81 страницы, т. е. последняя страница 90-я (9 + 81 = 90). В книге 90 страниц.
24. Сколько раз используется каждая из цифр от 1 до 9 в записи первых 99 натуральных чисел?
Решение. В записи 1, 2, 3, ..., 99 цифра 1 используется 20 раз (10 раз в разряде единиц и 10 раз в разряде десятков). Цифры 2, 3, ..., 8, 9 используются тоже по 20 раз.
38. Саша моложе Даши, а Даша моложе Коли. Кто моложе: Саша или Коля?
Решение. Запишем коротко условие задачи: С Д, Д К (буквами С, Д, К обозначен возраст Саши, Даши и Коли соответственно). По свойству неравенств заключаем, что С К, т. е. Саша моложе Коли.
40. Арбуз тяжелее яблока, и дыня тяжелее яблока. Можно ли по этим данным определить, что тяжелее: арбуз или дыня?
Решение. Обозначим буквами а, я, д вес арбуза, яблока и дыни соответственно. Запишем коротко условие задачи: а я, д я. Здесь нельзя определить, что тяжелее: арбуз или дыня (можно привести примеры, подтверждающие этот вывод).
Промежуточный контроль. C–1.
В данном пункте с помощью числового ряда на небольших числах показывается, как можно сложить два натуральных числа. На примерах подтверждается, что верны переместительный и сочетательный законы сложения для неотрицательных чисел.
Важно подчеркнуть, что приведённые рассуждения можно провести для любой пары натуральных чисел (не только пары чисел 3 и 5), поэтому переместительный закон верен для любых натуральных чисел a и b, что записывают в виде равенства
a + b = b + a.
Обратим внимание на то, что введение переместительного закона сложения можно мотивировать с опорой на опыт школьника. Например, можно показать 3 красных карандаша и 5 синих и подсчитать их общее число, начиная сперва с синих карандашей, потом с красных.
Очевидно, что общее число карандашей будет одно и то же.
Аналогичная работа проводится для сочетательного закона сложения.
Все вычисления до введения вычислений в столбик проводятся устно с записью действий в строчку, законы сложения используются для рационализации вычислений (задания 48—50). При этом учащиеся должны научиться находить слагаемые, дающие «круглую» сумму, оканчивающуюся нулями.
РТ. Лучшему усвоению материала пункта 1.4 учебника будет способствовать использование заданий 28—33. При выполнении заданий 30 и 31 надо обратить внимание на разные способы записи вычислений сумм, содержащих более двух слагаемых (по действиям и «цепочкой»). Задание 32 выполняется подбором, оно готовит учащихся к изучению вычитания на следующем уроке.
51. а) Выполните сложение «цепочкой»: 8 + 9 + 13 + 22. Решение. 8 + 9 + 13 + 22 = 17 + 13 + 22 = 30 + 22 = 52.
Следует учесть весьма распространённую ошибку учащихся, возникающую ввиду того, что они не осознают значение знака «=» и понимают его как знак перехода к следующему этапу вычисления. Вместо приведённого решения они ошибочно пишут:
8 + 9 + 13 + 22 = 17 + 13 = 30 + 22 = 52.
Если возникнет такая ошибка, то надо показать, что в этой записи знак «=» два раза поставлен неверно.
В данном пункте вводится понятие разности двух чисел. Его введение можно мотивировать с опорой на опыт детей, разобрав конкретный пример. В начальной школе они уже изучали вычитание и знают, что 9 – 6 = 3. Здесь нужно спросить: как проверить правильность вычисления? Учащиеся должны ответить: с помощью сложения (3 + 6 = 9).
Вот теперь можно дать определение разности для любых натуральных чисел a и b. Из данного определения следует, что для неотрицательных чисел a и b вычитание выполнимо лишь в случае a b.
Обратим внимание на то, что уравнения будут изучаться в 6 классе, поэтому задание 61 выполняется с помощью правил нахождения неизвестных компонентов. Эти правила полезны для развития математической речи учащихся, так как и в других случаях они должны уметь говорить: «Чтобы ..., надо ...». Если учащиеся в начальной школе достаточно легко решали уравнения, то им можно предъявлять и более сложные задания, содержащие несколько действий:
(x + 12) – 20 = 50.
Польза от заданий такого вида двойная: это — обучение применению сформированного умения в усложнённой ситуации и приу чение воспринимать (x + 12) как уменьшаемое. Но увлекаться такой работой, требовать от каждого ученика умения выполнять подобные задания всё же не следует, так как в дальнейшем это «неперспективное» умение вытеснится умением раскрывать скобки, приводить подобные слагаемые, переносить слагаемые в другую часть уравнения.
РТ. Лучшему усвоению материала пункта 1.5 учебника будет способствовать использование заданий 34—43. Обратим внимание на задания 41 и 42. Они помогают учащимся лучше уяснить взаимосвязь операций сложения и вычитания, а также готовят к решению задач «обратным ходом» (например, задания 48 и 49 рабочей тетради, 66 учебника).
63. Докажите, что от прибавления к уменьшаемому и вычитаемому одного и того же числа разность не изменяется. То есть если a – b = c, то (a + n) – (b + n) = c.
Доказательство. К числу c прибавим число (b + n) и преобразуем сумму c + (b + n), применяя сочетательный закон сложения: c + (b + n) = = (c + b) + n.
Так как a – b = c, то c + b = a, поэтому (c + b) + n = a + n. Это означает, что справедливо равенство (a + n) – (b + n) = c, что и требовалось доказать.
66. а) Задумали число, увеличили его на 45 и получили 66. Каким действием можно найти задуманное число? Найдите его.
Решение. Задуманное число можно найти вычитанием: 66 – 45 = 21.
Если это задание выполнить после задания 42 рабочей тетради, то учащиеся нарисуют аналогичную схему (рис. 1, а) и найдут искомое число «обратным ходом» (рис. 1, б).
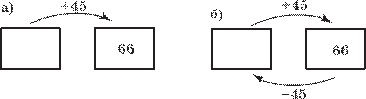
Рис. 1
В этом пункте начинается обучение решению текстовых задач арифметическими способами. На первом этапе задачи решаются с вопросами: перед каждым действием формулируется вопрос, затем выполняется действие, дающее ответ на поставленный вопрос (см. задачу 1 в учебном тексте). Если учащийся затрудняется с формулировкой первого вопроса в задаче, решаемой в несколько действий, то начинать надо с главного вопроса задачи. Такой анализ задачи знаком учащимся из начальной школы.
Покажем, как это можно сделать, при решении задачи 1 из учебного текста.
Задача 1. У покупателя было 50 р. Из них он отдал 30 р. за купленный товар и получил 2 р. сдачи. Сколько денег осталось у покупателя?
Запишем диалог, который может возникнуть при поиске решения задачи.
— Каков главный вопрос задачи, т. е. что требуется найти?
— Требуется найти, сколько денег осталось у покупателя.
— А что нужно знать, чтобы ответить на этот вопрос?
— Сколько денег было у покупателя и сколько денег он потратил?
— Знаем ли мы, сколько денег было у покупателя?
— Да, у него было 50 р.
— Знаем ли мы, сколько денег он потратил?
— Нет, но можем определить, так как знаем, что он отдал за покупку 30 р. и получил 2 р. сдачи.
— Что же мы узнаем первым действием?
— Сколько рублей стоил купленный товар.
30 – 2 = 28 (р.).
— Что теперь можно узнать?
— Сколько денег осталось у покупателя.
50 – 28 = 22 (р.).
Ответ. 22 р.
На первом уроке надо закрепить этот способ решения задач, разобрав решение с вопросами задачи 44 рабочей тетради. В решении задачи 45 записаны действия и требуется сформулировать к ним вопросы, а в задаче 46 сформулирован только первый вопрос. Наконец, решить задачу 47, для которой нет никаких подсказок. Дальше можно решить несколько задач из учебника. Скорость продвижения по материалу в разных классах может быть разной, но сначала надо отработать первый способ записи решения.
Отметим, что задачи, аналогичные задаче 2 из учебного текста, вызывают затруднения у многих учащихся, для которых слово «больше», встреченное в условии задачи, всегда означает, что нужно сложить. На примере решения этой задачи в учебнике показан второй способ оформления решения задачи — с пояснениями: после каждого действия даётся пояснение, показывающее, что именно найдено этим действием.
Если в отведённое время будут решены не все задачи из учебника, то оставшиеся задачи надо использовать на следующих уроках как задачи на повторение.
Особо отметим вопрос, который обычно задают пятиклассники учителю математики: «Надо ли делать краткую запись условия задачи?» На наш взгляд, отвечать на него следует так: «Если краткая запись условия задачи вам помогает, то делайте; если можете без неё обойтись, то не делайте».
РТ. Использование заданий 44—47 на первом уроке описано выше. После освоения учащимися способа решения задачи с пояснениями можно разобрать задания 51—53. Особо отметим задания 56—65 на нахождение неизвестных: слагаемого (56, 57), слагаемых и суммы (58, 59), вычитаемого (60, 61), уменьшаемого, вычитаемого и разности (62, 65).
69. Торговец купил некий товар за 7 р., продал его за 8 р., потом вновь купил за 9 р. и опять продал его за 10 р. Какую прибыль он
получил?
Здесь учащиеся часто по ошибке считают, что, покупая товар второй раз, торговец имеет 1 р. убытка. А это не так. Можно переформулировать задачу, сказав, что торговец купил сразу два товара — один за 7 р., а другой за 9 р., потом продал их за 8 и 10 р. соответственно. Торговец получил 2 р. прибыли:
(8 – 7) + (10 – 9) = 2 (р.),
или
(8 + 10) – (7 + 9) = 2 (р.).
79. а) Маша сказала, что у неё сестёр на две больше, чем братьев. На сколько в семье Маши сестёр больше, чем братьев?
б) Миша сказал, что у него сестёр на две больше, чем братьев. На сколько в семье Миши сестёр больше, чем братьев?
Решение. а) У Маши сестёр на две больше, чем братьев, а вместе с Машей сестёр на 2 + 1 = 3 больше, чем братьев. Если задача вызовет затруднения, то можно попросить учащихся представить, что Маша строит своих братьев и сестёр парами так, чтобы каждый брат был в паре с одной из сестёр Маши. Сколько сестёр останется без пары?
(Маша и ещё две сестры.)
б) Сестёр в семье на 2 – 1 = 1 больше, чем братьев. Ответ. а) На 3; б) на 1.
81. На первой полке стояло 12 книг, на второй — на 3 книги больше, а на третьей полке — на a книг меньше, чем на двух первых полках вместе. Сколько книг на третьей полке?
а) Выберите такое число a, чтобы задача имела решение. Решите
задачу с выбранным числом a.
б) Какое самое большое число a можно взять, чтобы задача имела
решение, если на третьей полке была хотя бы одна книга?
Решение. Сначала определим, сколько книг было на второй полке:
12 + 3 = 15 (книг).
Теперь определим, сколько книг было на первых двух полках:
12 + 15 = 27 (книг).
а) Теперь при различных значениях a будут получаться различные ответы. Например, если a = 10, то на третьей полке было
27 – 10 = 17 книг,
если a = 12, то на третьей полке было
27 – 12 = 15 книг.
Мы видим, что с увеличением a число книг на третьей полке уменьшается.
б) Самое большое значение a должно быть таким, чтобы на третьей
полке была хотя бы одна книга.
Если a = 26, то на третьей полке было
27 – 26 = 1 (книга).
26 — это наибольшее число a, удовлетворяющее условиям задачи.
Следующая задача имеет большое воспитательное значение: учащиеся не должны, условно говоря, к землекопам прибавлять лопаты. В любом случае они не должны бездумно складывать и вычитать числа, не имеющие друг к другу никакого отношения.
Задача-шутка. Ира одолжила у мамы 100 р., но потеряла их. Потом одолжила у подруги 50 р. На 20 р. купила пирожков, а оставшиеся 30 р. вернула маме. Получается, что маме она должна 70 р. плюс 50 р. подруге, всего 120 р., плюс 20 р., которые потратила на пирожки. Итого 140 р., но всего она должна вернуть 150 р. Вопрос: где ещё 10 р.?
Решение. Ира потеряла и потратила 100 + 20 = 120 р. И должна именно эти деньги вернуть: маме 100 – 30 = 70 р. и подруге 50 р. А все остальные расчёты от лукавого.
В пункте 1.7 вводится понятие произведения двух чисел на примере произведения чисел 3 и 4. Обратим внимание, что это произведение есть сумма трёх слагаемых, каждое из которых равно 4, т. е. 3 4 = 4 + 4 + 4. Это необходимо, чтобы в дальнейшем под 3 a понимать сумму a + a + a. Для любого числа a считается верным равенство 1 a = a. Такой подход к определению произведения кажется неудобным, так как в начальной школе говорят, что 3 4 — это 3 + 3 + 3 + 3 (3 взять 4 раза). Но это кажущееся неудобство устраняется на первом же уроке, как только будет показано, что справедлив переместительный закон умножения.
Переместительный и сочетательный законы умножения разъясняются при подсчёте числа квадратов и числа кубиков.
Для любого числа a считаются верными равенства 0 a = 0, a 0 = 0. Кроме того, верно равенство 0 0 = 0.
В пункте 1.8 распределительный закон разъясняется при подсчёте числа квадратов, показывается применение распределительного закона для раскрытия скобок и вынесения общего множителя за скобки.
При изучении всех трёх законов следует приучать школьников к записи законов с помощью букв, обозначающих произвольные числа, и к заучиванию формулировок законов. Это помогает развитию чёткой математической речи, даёт учащимся «речевые заготовки» для устных ответов.
Здесь и далее следует обращать внимание учащихся на те преимущества в скорости вычислений, которые имеет тот, кто владеет изученными законами. Тем самым учитель создаёт внутрипредметную, идущую от предмета (а не извне) мотивацию к учению.
РТ. Использование заданий 66—70 на первом уроке позволит повторить таблицу умножения, обратить внимание учащихся на пары множителей, дающие при умножении 10, 100, 1000 и т. д. Задания 71—76 нацелены на отработку применения изученных законов.
90. а) Число 12 сначала увеличили в 2 раза, полученный результат увеличили ещё в 3 раза. Какой получился результат?
б) Задумали число, увеличили его в 3 раза, полученный результат
увеличили ещё в 4 раза. Во сколько раз увеличилось число в итоге?
Решение. а) 12 2 = 24, 24 3 = 72, получился результат 72.
Здесь желательно спросить учащихся: во сколько раз увеличилось число 12 за 2 раза? Ответ можно получить, используя сочетательный закон умножения:
(12 2) 3 = 12 (2 3) = 12 6.
Число 12 за 2 раза увеличилось в 6 раз. Этот ответ подготовит учащихся к самостоятельному решению задачи 90 б.
б) Сначала задачу можно решить для конкретного задуманного числа, например 2 или 3. Окажется, что и в том и в другом случае задуманное число увеличилось в 12 раз. Чтобы показать, что ответ в этом задании действительно не зависит от выбора задуманного числа, обозначим задуманное число буквой a. Тогда
(a 3) 4 = a (3 4) = a 12. Число a за 2 раза увеличилось в 12 раз.
91. Какие законы использованы при следующих вычислениях:
20 30 = (2 10) (3 10) = (2 3) (10 10) = 6 100 = 600?
а) Вычислите: 20 50.
Решение. Были использованы оба закона умножения: переместительный и сочетательный. Заметим, что выше применение этих законов не показано подробно, например, так:
20 30 = (2 10) (3 10) = ((2 10) 3) 10 = (2 (10 3)) 10 =
= 2 (3 10) 10 = ((2 3) 10) 10 = (2 3) (10 10) = 6 100 = 600, так как учащиеся ещё не имеют мотивации к точности в преобразованиях числовых выражений. Однако при выполнении следующих заданий можно не требовать и такой неполной записи решений, которая приведена выше. Решение можно записать кратко: а) 20 50 = 1000.
118. г) Вычислите: 356 73 + 644 27 + 73 644 + 27 356.
Решение. 356 73 + 644 27 + 73 644 + 27 356 = 356 (73 + 27) + + 644 (27 + 73) = 356 100 + 644 100 = (356 + 644) 100 = 1000 100 = = 100000.
Промежуточный контроль. C–2.
Назначение данных пунктов заключается в демонстрации учащимся того, как законы сложения и умножения, распределительный закон используются при сложении, вычитании и умножении многозначных чисел столбиком. При этом не предполагается, что учащиеся должны сами делать аналогичные обоснования, но было бы полез но, чтобы они обратили внимание на то, что правильность вычислений в столбик следует из справедливости законов сложения и умножения.
Особое внимание надо уделить правильности подписывания друг под другом множителей, запись которых оканчивается нулями.
С этого момента в вычислительную практику пятиклассников входят вычисления в столбик, но надо обратить внимание учащихся, что иногда вычисления с многозначными числами бывает проще выполнить без столбика, если заметить пары чисел, дающих «круглые» суммы (задание 135), или если заметить, что можно общий множитель вынести за скобки (задание 144). Надо всемерно развивать и поддерживать стремление школьников вычислять экономно, а для этого, как мы уже отмечали, от них требуется наблюдательность и владение изучаемой теорией.
В дальнейшем желание сэкономить время в вычислениях должно стать побудительным мотивом для развития наблюдательности, а также для формирования представления о том, что знание многих теоретических сведений может упростить решение задачи.
РТ. Использование заданий 77, 78 на первом уроке, посвящённом сложению и вычитанию столбиком, позволит интенсифицировать процесс обучения, так как учащимся нужно лишь вписывать ответы в уже записанные столбики. Задание 79 готовит их к выполнению задания 80 и заданий 133 и 134 учебника. Задание 81 выполняется в начале изучения умножения столбиком, при этом надо обратить внимание учащихся на запись множителей. Задание 82 посвящено разгадыванию ребусов.
133.На доске были записаны верно выполненные примеры на сло-жение и вычитание, потом некоторые цифры стёрли и заменили их буквами. Перепишите примеры, заменяя буквы цифрами так, чтобы опять получились верные записи:
а) 72и б) д52 в) 5ин г) ну56
+[1]р3 –6в4 +д79 – 5л8
![]()
![]()
т98 28а о381 88ь
Здесь и далее учащиеся могут получать ответы подбором подходящей цифры и проверкой правильности полученного ответа, но будет лучше, если у доски будут даны образцы рассуждения: чтобы получить 8, к 3 надо прибавить 5 (пример «а») и т. п.
Ответ. а) 725 + 173 = 898; б) 952 – 664 = 288; в) 502 + 879 = 1381;
г) 1456 – 568 = 888.
134.Восстановите примеры, считая, что одинаковые буквы обозна-чают одинаковые цифры, а разные буквы — разные цифры:
в) удар г) деталь +удар +деталь
![]()
![]()
драка изделие
Решение. в) Это задание более простое, при его выполнении реализуется линейный алгоритм поиска ответа. На каждом шаге он даёт единственное значение для буквы.
1) Сумма двух четырёхзначных чисел — пятизначное число. Следовательно, д = 1, т. е.
у1ар
+у1ар
2) Сумма р + р — число, оканчивающееся на чётную цифру,
т. е. а — чётное число, но тогда (см. разряд сотен суммы) а = 2, т. е.
у12р +у12р
![]()
1р2к2
3) Сумма р + р — число, оканчивающееся на 2, это возможно толь- ко в двух случаях: р = 1 и р = 6. Но цифра 1 уже есть (разным буквам соответствуют разные цифры), следовательно, р = 6, т. е.
у126
+у126
![]()
162к2
4) Тогда к = 5, у = 8, т. е.
8126
+8126
![]()
16252
Пример «в» восстановлен, причём все цифры найдены однозначно.
г) Это задание более сложное, при его выполнении реализуется ветвящийся алгоритм поиска ответа. Он на некотором шаге даёт не единственное значение для буквы. Сложность заключается в том, чтобы не забыть довести до конца рассуждение по каждой ветви алгоритма.
1) Сумма двух шестизначных чисел — семизначное число, следовательно, и = 1, т. е.
деталь
+деталь
![]()
1здел1е
2) Сумма ь + ь оканчивается на чётную цифру, т. е. е — чётное число. В разряде десятков л + л — число, оканчивающееся на чётную цифру. Чтобы получить в разряде десятков суммы число 1, надо, чтобы было ь 5 и л = 0 или л = 5.
3) Если л = 0, т. е.
дета0ь
+дета0ь
![]()
1зде01е,
то а = 5, т. е.
дет50ь +дет50ь
![]()
1зде01е
Но тогда в разряде тысяч сумма т + т + 1 оканчивается на нечётное число, т. е. е — нечётное число, а выше было установлено, что е — чётное число. Полученное противоречие означает, что л 0. Значит, л = 5.
4) Так как л = 5, т. е. дета5ь
+дета5ь
![]()
1зде51е,
то в разряде сотен сумма а + а + 1 оканчивается на 5. Это возможно в двух случаях: а = 2 и а = 7. Но при а = 7 в разряде тысяч число е нечётное, что невозможно, так как выше установлено, что е — число чётное. Следовательно, а 7. Значит, а = 2.
5) Так как а = 2, т. е.
дет25ь
+дет25ь
![]()
1зде51е,
и так как е — чётное число, то оно не может быть нулём (если е = 0, то ь = 0 или ь = 5, что невозможно, так как уже установлено, что ь 5, и цифра 5 уже есть). Число 2 уже есть, поэтому е 2. Таким образом, осталось рассмотреть три возможных случая: е = 4, е = 6, е = 8.
6) Если е = 4, то ь = 7, тогда (см. разряд тысяч) т = 2 или т = 7, что невозможно, так как цифры 2 и 7 уже есть.
7) Если е = 6, то в разряде десятков тысяч суммы д = 3 (так как число 2 уже есть), но тогда сумма не будет семизначным числом, что невозможно. Значит, е = 8.
8) Так как е = 8, то ь = 9, т = 4, д = 6, з = 3, т. е.
684259
+684259
![]()
1368518
Пример «г» восстановлен, причём все цифры найдены однозначно.
Показывать решения примеров «в» и «г» на доске проще, чем публиковать в книге, так как в случае линейного алгоритма с помощью тряпки и мела можно постепенно заменять буквы числами и из данного примера с буквами получить искомый пример с числами. А в случае ветвящегося алгоритма надо оставлять на доске все не до конца рассмотренные варианты. Схему алгоритма, реализованного при выполнении задания «г», можно изобразить так:
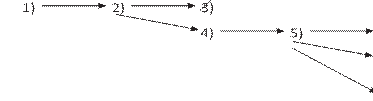
Разумеется, учащиеся могут просто подобрать нужные цифры, но тогда не будет уверенности, что найденное решение единственное.
135. а) Выполните действия: (5486 + 3578) + 1422.
Решение. Здесь хотелось бы, чтобы, кроме умения применить 2 раза вычисления в столбик, кто-то из учащихся заметил, что сумма второго и третьего чисел «круглая», поэтому вычисление легко выполнить в строчку:
(5486 + 3578) + 1422 = 5486 + (3578 + 1422) = 5486 + 5000 = 10486.
146. Произведение четырёх последовательных натуральных чисел равно 3024. Найдите эти числа.
Решение. Заметим, что среди искомых четырёх чисел нет числа 10 и числа 5, так как если бы был хотя бы один из этих множителей, то произведение оканчивалось бы на нуль. Осталось проверить: 1 2 3 4 = 24, 6 7 8 9 = 3024.
Ответ. 6, 7, 8, 9.
В данном пункте вводится понятие степени с натуральным показателем для случаев n 1 и n = 1. Учащиеся должны овладеть терминологией: степень, основание степени (число, которое возводим в степень), показатель степени (показывает, в какую степень возводим основание степени), квадрат числа, куб числа, а также научиться вычислять степени.
РТ. Задания 83—86 желательно использовать на начальном этапе изучения материала. При изучении данного пункта можно использовать задания 87—90.
171. Среди первых пяти натуральных чисел имеются два неравных числа m и n, такие, что nm= mn. Найдите эти числа.
Решение. Эти числа 2 и 4. Действительно, 24 = 2 2 2 2 = 16, 42 = 4 4 = 16, т. е. 24 = 42. Ответ. 2 и 4.
В данном пункте вводится понятие деления нацело и соответствующая терминология, объясняется, почему нельзя делить на нуль любое натуральное число или нуль. Приведены примеры упрощения деления в некоторых случаях. Следует обратить внимание на свойство частного, которое иногда помогает упростить вычисления (задания 186, 187). Например, при делении числа на 5 можно делимое и делитель умножить на 2 и разделить новое делимое на 10: 320 5 = 640 10 = 64.
Доказательство этого свойства частного в учебнике не проведено. На уроке достаточно привести его на таком примере: «Докажем, что если 320 5 = c, то (320 2) (5 2) = c, где c — натуральное число».
Для этого умножим c на 5 2 и проверим, получится ли в результате 320 2. При этом учтём, что так как 320 5 = c, то верно равенство c 5 = 320. c (5 2) = (c 5) 2 = 320 2.
Тем самым свойство частного доказано для частного 320 5 и натурального числа c.
Заметим, что если вместо чисел 320 и 5 взять любые натуральные числа a и b, такие, что верно равенство a b = c, а вместо числа 2 взять любое натуральное число d, то, рассуждая аналогично, мы получим доказательство того же утверждения в общем виде:
a b = (a c) (b c).
В данном пункте задания подобраны так, чтобы при их выполнении не требовалось деление в столбик, которое будет ещё изучаться в пункте 1.15.
РТ. Задания 91—93 желательно использовать на начальном этапе изучения деления. Они проверяют понимание правила (определения) деления. Задания 94—97 на вычисления без столбика. Задание 98 на отыскание неизвестных компонентов при умножении и делении. Задания 99—107 на проверку понимания взаимосвязи компонентов при умножении и делении.
188. Докажите, что если каждое из натуральных чисел a и b делится на натуральное число c, то верно равенство
(a + b) c = a c + b c.
Решение. Приведём доказательство в общем виде. Так как каждое из натуральных чисел a и b делится на натуральное число c, то существуют натуральные числа a c и b c. Умножим их сумму на c и преобразуем полученное произведение с помощью распределительного закона и определения частного (a c — это такое число, которое при умножении на c даёт a, поэтому (a c) c = a):
(a c + b c) c = (a c) c + (b c) c = a + b,
следовательно, равенство (a + b) c = a c + b c верно.
Если учитель считает, что в его классе приведённое общее доказательство (на буквах) учащиеся ещё не готовы воспринимать, то лучше провести его для конкретного случая, например такого:
(15 + 35) 5 = 15 5 + 35 5.
Однако не следует проводить доказательство с помощью вычислений — убеждаться, что слева и справа получится один и тот же ответ (на буквах такое «доказательство» не получится). Надо, пусть и на конкретных числах, проводить те же рассуждения, что и при доказательстве в общем случае, это позволит постепенно приучать учащихся к доказательствам утверждений.
Промежуточный контроль. C–3.
В данном пункте продолжается начатая ранее работа по приучению школьников к решению задач арифметическими способами. В учебном тексте задачи решены с пояснениями, но время от времени надо давать учащимся указание: «А эту задачу надо решить с вопросами». Особое внимание следует обратить на то, что у некоторых учащихся с начальной школы закрепились неправильные представления о выборе действия для решения задачи. Если они встречают в тексте задачи вопрос «на сколько?», то говорят, что надо вычитать и т. п. Поэтому задачу 193 надо выполнить в классе и проследить, чтобы действия для получения ответа были выбраны правильно.
РТ. Задачи 108—117 можно использовать на первых уроках по теме, решив задачи 108—112 с вопросами, а задачи 113—117 с пояснениями. Решение задач 118—137 предполагает использование всех изученных действий.
193.а) На каждую телегу нагрузили по 8 мешков картофеля. На сколько телег погрузили 72 мешка?
б) В некоторые из 40 пакетов насыпали сахарный песок. Осталось 10 пустых пакетов. Во сколько пакетов насыпали сахарный песок?
в) В швейной мастерской осталось 2 куска материи по 60 м. Сколь-
ко метров материи осталось?
Решение. а) 72 8 = 9 — на 9 телег погрузили картофель.
б) 40 – 10 = 30 — в 30 пакетов насыпали сахарный песок.
в) 2 60 = 120 (м) — материи осталось.
194.а) У Алёши, Бори и Васи вместе 120 марок. У Алёши марок столько, сколько у Бори и Васи вместе. Сколько марок у Алёши?
б) Коля, Миша и папа поймали 24 карася. Папа поймал столько, сколько его сыновья вместе, а они поймали карасей поровну. Сколько карасей поймал Коля?
Решение. а) 120 2 = 60 (марок) — было у Алёши.
б) 1) 24 2 = 12 (карасей) — поймали Коля и Миша вместе; 2) 12 2 = 6 (карасей) — поймал Коля.
195.Старинная задача. Родник в 24 мин даёт бочку воды. Сколько бочек воды даёт родник в сутки?
Решение. Так как 1 ч в 60 раз больше 1 мин, то за 24 ч родник даст в 60 раз больше воды, чем за 24 мин. Следовательно, в сутки родник даст 60 бочек воды.
206. Некто работает 24 дня в месяц, тратит в каждый из тридцати дней по 50 р. и откладывает за месяц 900 р. Сколько он получает за рабочий день?
Решение.
1) Сколько рублей он тратит за 30 дней?
50 30 = 1500 (р.).
2) Сколько рублей он зарабатывает за месяц?
1500 + 900 = 2400 (р.).
3) Сколько рублей он зарабатывает за 1 день?
2400 24 = 100 (р.). Ответ. 100 р.
208. а) Первая машинистка печатает 10 страниц в час, а вторая за 5 ч печатает столько же страниц, сколько первая за 4 ч. Сколько страниц отпечатают обе машинистки за 3 ч совместной работы?
Такие многошаговые задачи сложны тем, что при их решении учащиеся не всегда умеют определить, что требуется знать для ответа на вопрос задачи и как можно найти требуемое. На примере таких задач можно обучать их поиску решения.
Анализ условия и составление плана решения задачи 208 а можно провести в таком диалоге:
— Сформулируйте главный вопрос задачи.
— Сколько страниц отпечатают обе машинистки за 3 ч совместной работы? (I и II за 3 ч?)
— Что нужно знать, чтобы ответить на этот вопрос?
— Сколько страниц печатают две машинистки за 1 ч. (I и II за
1 ч.)
— Всё ли мы знаем для этого? Что ещё нужно узнать?
— Нет, не всё. Нужно узнать, сколько страниц печатала вторая машинистка за 1 ч. (II за 1 ч.)
— Что известно о работе второй машинистки?
— Она за 5 ч печатает столько же страниц, сколько первая за 4 ч.
— А мы знаем, сколько страниц печатает первая машинистка за 4 ч? (I за 4 ч?)
— Нет, но можем узнать, умножив 10 на 4.
В скобках мы привели записи, которые учитель может делать на доске по ходу обсуждения. Стрелки, поставленные учителем от последней записи к первой, дают план решения:
I за 4 ч
II
![]() за 1 ч
за 1 ч
I и II за 1 ч
I и II за 3 ч
Решение.
1) 10 4 = 40 (страниц) — отпечатает первая машинистка за 4 ч;
2) 40 5 = 8 (страниц) — отпечатает вторая машинистка за 1 ч; 3) 10 + 8 = 18 (страниц) — отпечатают обе машинистки за 1 ч; 4) 18 3 = 54 (страницы) — отпечатают обе машинистки за 3 ч. Ответ. 54 страницы.
Для повышения эффективности обучения решению задач, а также для приучения школьников к планированию своей деятельности советуем обучать их делать краткую запись условия задачи и намечать по ней план решения. Разумеется, этот совет нельзя превращать в обязательное требование. Учащиеся могут делать краткую запись условия задачи в произвольной, удобной для них форме тогда, когда она действительно помогает им в работе.
212. а) В двух комнатах было 56 человек. Когда в первую пришли ещё 12 человек, а во вторую — 8 человек, то в комнатах людей стало поровну. Сколько человек было в каждой комнате первоначально?
Решение.
1) 56 + 12 + 8 = 76 (чел.) — стало в двух комнатах вместе;
2) 76 2 = 38 (чел.) — стало в каждой комнате;
3) 38 – 12 = 26 (чел.) — было первоначально в первой комнате;4) 38 – 8 = 30 (чел.) — было первоначально во второй комнате. Ответ. 26 и 30 человек.
213. а) В магазин привезли 420 мужских и женских часов. Когда продали 150 мужских и 140 женских часов, то тех и других осталось поровну. Сколько мужских часов привезли в магазин?
Решение.
1) 150 + 140 = 290 (часов) — продали всего;
2) 420 – 290 = 130 (часов) — осталось в магазине;
3) 130 2 = 65 (часов) — каждого вида осталось;
4) 65 + 150 = 215 (часов) — столько мужских часов привезли в магазин.
Ответ. 215 часов.
214. На четырёх полках стояло 164 книги. Когда с первой полки сняли 16, со второй переставили на третью 15, а на четвёртую поставили 12 новых книг, то на всех полках книг оказалось поровну.
Сколько книг было на каждой полке первоначально?
Решение.
1) 164 – 16 + 12 = 160 (книг) — стало после всех перестановок;
2) 160 4 = 40 (книг) — стало на каждой полке после всех перестановок;
3) 40 + 16 = 56 (книг) — было первоначально на первой полке;
4) 40 + 15 = 55 (книг) — было первоначально на второй полке;5) 40 – 15 = 25 (книг) — было первоначально на третьей полке; 6) 40 – 12 = 28 (книг) — было первоначально на четвёртой полке.
Ответ. 56, 55, 25 и 28 книг.
216. На лугу паслось несколько коров. У них ног на 54 больше, чем голов. Сколько коров паслось на лугу?
Решение. У одной коровы разность числа ног и числа голов составляет 4 – 1 = 3. Поэтому на лугу паслось 54 3 = 18 коров.
Записать это решение по действиям можно так:
1) 4 – 1 = 3 — на 3 число ног у коровы больше числа голов; 2) 54 3 = 18 (коров) — паслось на лугу. Ответ. 18 коров.
В первых задачах речь о частях идёт в явном виде. При их решении создаётся основа для решения задач 225—229 на нахождение двух чисел по их отношению и сумме (разности). Учащиеся должны научиться принимать подходящую величину за 1 часть, определять, сколько таких частей приходится на другую величину, на их сумму (разность). Здесь впервые в учебнике даются рекомендации по записи условия задачи с помощью схематического рисунка. Обратим внимание на то, что выполнение такого рисунка не является обязательным требованием, но если школьник его делает, то процесс осмысления условия задачи и соотношений между данными величинами становится более продуктивным. Сначала можно рисовать пачки тетрадей (рис. 2), затем изображать величины отрезками (как при решении задач 1 и 2 в учебном тексте).
Заметим, что схематические рисунки позволяют иногда находить нетрадиционные решения задач. Такие примеры мы приведём дальше.
Закрепляя тему «Решение текстовых задач» на следующих уроках, надо добиться, чтобы учащиеся понимали отношения «больше на», «меньше на», «больше в», «меньше в» и правильно выбирали арифметические операции для нахождения неизвестного числа.
РТ. Задачи 138—144 можно использовать на первых уроках по теме, так как в некоторых из них уже имеются схематические рисунки и поставлены вопросы.
225. Купили 60 тетрадей, причём тетрадей в клетку было в 2 раза больше, чем тетрадей в линейку. Пользуясь рисунком 2, определите, сколько частей приходится на тетради в линейку; на тетра-
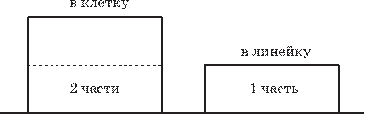
Рис. 2
ди в клетку; на все тетради. Сколько купили тетрадей в линейку?
Сколько — в клетку?
Решение.
1) 1 + 2 = 3 (части) — приходится на все тетради;
2) 60 3 = 20 (тетр.) — приходится на 1 часть (тетради в линейку); 3) 20 2 = 40 (тетр.) — приходится на 2 части (тетради в клетку). Ответ. 20 и 40 тетрадей.
226. а) За рубашку и галстук папа заплатил 200 р. Рубашка дороже галстука в 4 раза. Сколько стоит галстук?
С целью развития мышления и речи школьников советуем иногда давать им задание решить задачу с вопросами.
Решение.
1) Сколько частей приходится на рубашку и галстук?
1 + 4 = 5 (частей).
2) Сколько рублей приходится на 1 часть (стоимость галстука)?
200 5 = 40 (р.). Ответ. 40 р.
227. б) Мальчик и девочка рвали в лесу орехи. Всего они сорвали 120 штук. Девочка сорвала в 2 раза меньше мальчика. Сколько орехов было у мальчика и девочки в отдельности?
Эта задача взята из повести Николая Носова «Витя Малеев в школе и дома», где дано довольно точное описание характерных ошибок, допускаемых учащимися при её решении, и самой процедуры поиска решения.
«Прочитал я задачу, и даже смех разобрал. „Вот так задача! — думаю. — Чего тут не понимать? Ясно, 120 надо поделить на 2, получится 60. Значит, девочка сорвала 60 орехов. Теперь нужно узнать, сколько [орехов сорвал] мальчик: 120 отнять 60, тоже будет 60... Только как же это так? Получается, что они сорвали поровну, а в задачни ке сказано, что девочка сорвала в два раза меньше орехов. Ага! — думаю. — Значит, 60 надо поделить на 2, получится 30. Значит, мальчик сорвал 60, а девочка 30 орехов“. Посмотрел в ответ; а там: мальчик 80, а девочка 40».
(Заметим, что Витя смог решить задачу лишь тогда, когда нарисовал девочку в переднике с одним карманом, а мальчика в курточке с двумя карманами.)
«Все 120 орехов теперь лежали у них в трёх карманах: в двух карманах у мальчика и в одном кармане у девочки, а всего, значит, в трёх.
И вдруг у меня в голове, будто молния, блеснула мысль: „Все
120 орехов надо делить на три части!“»
Надо сказать, что первое действие, к которому с таким трудом пришёл Витя, вызывает большие трудности у учащихся, этот шаг решения задач «на части» требует специальной отработки, которая будет тем успешнее, чем активнее учащиеся опираются на наглядные образы.
230. Задача С. А. Рачинского. Я провёл год в деревне, в Москве и в дороге — и притом в Москве в 8 раз более времени, чем в дороге, а в деревне в 8 раз более, чем в Москве. Сколько дней провёл я в дороге, в Москве и в деревне?
Решение. Пусть дни, которые автор задачи провёл в дороге, в Москве и в деревне, составляют 1 часть, 8 частей и 64 части соответственно. Всего 73 части. Здесь подразумевается, что в году 365 дней, поэтому в дороге он провёл 365 73 = 5 дней, в Москве 5 8 = 40 дней, в деревне 40 8 = 320 дней.
Ответ. 5, 40 и 320 дней.
Промежуточный контроль. C–4.
В данном пункте объясняется правило деления натуральных чисел нацело и с остатком, вводятся понятия неполного частного и остатка. На деление уголком стоит обратить особое внимание, так как в начальной школе это действие бывает хуже отработано, чем другие действия с натуральными числами.
РТ. Задания 145 и 146 на деление уголком без остатка, т. е. с остатком 0. Их желательно использовать на начальном этапе изучения деления. Задания 147 и 148 на деление с остатком.
247. Ученик выполнил деление: 148 15 = 8 (ост. 28). В чём заключается ошибка? Выполните деление правильно.
Решение. Остаток не может быть больше делителя, неполное частное надо увеличить: 148 15 = 9 (ост. 13).
Задания 248—250 вызывают затруднения у учащихся, которые лучше преодолеваются, если сначала написать верное равенство, например 14 5 = 2 (ост. 4), а затем по очереди заменять буквой делимое, неполное частное, делитель и в каждом случае находить число (значение этой буквы).
248. а) На доске написано несколько примеров на деление с остат-ком. В каждом примере делимое стёрли и заменили буквой. Найдите делимое: a 12 = 3 (ост. 2).
Решение. a = 12 3 + 2 = 38.
249. а) Определите неполное частное: 76 12 = a (ост. 4). Решение. a = (76 – 4) 12 = 6.
250. а) Определите делитель: 56 a = 11 (ост. 1). Решение. a = (56 – 1) 11 = 5.
251. Какой остаток получится от деления числа
1 2 3 4 5 6 7 8 9 10 + 1
на: а) 2; б) 3; в) 4; г) 5; д) 6; е) 7; ж) 8; з) 9; и) 10; к) 100?
Решение. Так как произведение 1 2 3 4 5 6 7 8 9 10 делится на 2, на 3, на 4, на 5, на 6, на 7, на 8, на 9, на 10 и на 100, то остаток от деления числа 1 2 3 4 5 6 7 8 9 10 + 1 на каждое из перечисленных чисел равен 1.
255. В подъезде семнадцатиэтажного дома расположены квартиры с 1-й по 68-ю. На каком этаже расположена квартира 63?
Решение.
1) 68 17 = 4 (квартиры) — на каждом этаже; 2) 63 4 = 15 (ост. 3).
Полученный результат означает, что ниже квартиры 63 имеется 15 этажей по 4 квартиры на каждом этаже, а квартира 63 находится на следующем — 16-м этаже. Ответ. На 16-м этаже.
256.Семь девочек играли в прятки. Они решили, что водить будет та из них, которая окажется 25-й при счёте по кругу. Вера начала счёт с себя: 1, 2, 3, ... . Катя, не дожидаясь окончания счёта, сказала: «Водить буду я». Какой номер был у Кати в начале счёта?
Решение. При счёте по кругу Вера была сначала 1-й, потом 8-й, 15-й, 22-й. Поскольку Катя сказала, что она будет водить, то её последний номер будет 25. Значит, Катя была 4-й в начале счёта.
Число 4 можно получить как остаток от деления числа 25 на 7:
25 7 = 3 (ост. 4).
257.Какое наименьшее число при делении и на 3, и на 5, и на 7 даёт в остатке: а) 0; б) 1; в) 2?
Решение. а) Произведение 3 5 7 = 105 делится и на 3, и на 5, и на 7 без остатка. Это наименьшее число, удовлетворяющее условию задачи, так как произведение 3 5 7 содержит каждый из множителей 3, 5, 7 по одному разу и 5 не делится на 3, а 7 не делится ни на 3, ни на 5.
б) 3 5 7 + 1 = 106 — наименьшее число, удовлетворяющее усло-
вию задачи.
в) 3 5 7 + 2 = 107 — наименьшее число, удовлетворяющее усло-
вию задачи.
Промежуточный контроль. C–5.
В данном пункте рассматриваются числовые выражения и правила порядка действий, применяемые при нахождении значения числового выражения.
Отметим, что учащиеся не понимают, почему первыми выполняются умножение и деление по порядку слева направо. К заданию 261 имеется замечание, на которое следует обратить внимание. Учащимся можно сказать, что первоначально действия в числовых выражениях выполняли по порядку слева направо, а при необходимости изменить порядок действий использовали скобки, например, в выражении a + (b c) сначала выполняют умножение чисел b и c, а потом к числу a прибавляют полученное произведение. Далее для таких случаев договорились скобки не писать, но первыми выполнять умножение и деление по порядку слева направо.
Среди заданий к данному пункту имеются задания, нацеленные на обучение правильному чтению числовых и буквенных выражений (под буквой понимается число). Нужно посоветовать учащимся определять последнее действие в данном числовом выражении. Например, в задании 273 встречаются (5 + 2)2 и 52 + 22 — соответственно квадрат суммы и сумма квадратов. Задание 279 нацелено на закрепление правильного выбора операции в задаче, где используются отношения «больше на» и др.
РТ. На начальном этапе освоения материала учащимся будет полезно выполнить задания 154—156, в которых требуется только определить порядок действий, а позднее задания 157, 158. Задание 159 имеет творческий характер, его можно дать для домашней работы, а на следующем уроке обсудить полученные результаты.
279. а) Решите задачу, составив числовое выражение:
Сейчас брату 5 лет, а через 3 года ему будет в 2 раза меньше лет, чем сестре сейчас. Сколько лет сестре сейчас?
Решение. (5 + 3) 2 = 16 (лет) — сестре сейчас. Ответ. 16 лет.
280. а) В автобусе было 25 пассажиров. На первой остановке вы-шло 8 и вошло 12 пассажиров, на второй — вышло 7 и вошло 5 пассажиров. Сколько пассажиров стало в автобусе после второй остановки?
б) В автобусе было несколько пассажиров. На первой остановке вышло 7 и вошло 4, а на второй вышло 6 и вошло 13 пассажиров. Сколько пассажиров было в автобусе до первой остановки, если после второй остановки автобусa их стало 38?
Решение. Задачи «а» и «б» легко решить, составив числовые выражения.
а) 25 – 8 + 12 – 7 + 5 = 27.
б) Решая задачу «обратным ходом», получим 38 – 13 + 6 – 4 + 7 = 34. Ответ. а) 27 пассажиров; б) 34 пассажира.
Похожие задачи уже рассматривались в рабочей тетради (задания 48, 49). Там же рассмотрено решение «обратным ходом» задачи, аналогичной задаче 280 б.
В данном пункте продолжается обучение школьников решению задач арифметическим способом. Первые задачи предполагают мысленные эксперименты с величинами. Например: «Уменьшим число тет радей в первой пачке на 20, тогда в обеих пачках тетрадей станет поровну...» или «Если 5 мальчиков выйдут из класса, то девочек и мальчиков в классе станет поровну...».
Начать можно с формулировки задачи 160 из рабочей тетради с одновременной демонстрацией двух пачек тетрадей. Решение задачи надо обсудить устно, фиксируя все действия на доске, а когда будет найдено верное решение, то записать его в рабочей тетради.
160 (РТ). В двух пачках 70 тетрадей. В первой на 20 тетрадей больше, чем во второй. Сколько тетрадей в каждой пачке?
Учащиеся иногда предлагают неверное решение этой задачи, например такое:
1) 70 2 = 35 (тетр.) — во второй пачке; 2) 35 + 20 = 55 (тетр.) — в первой пачке.
Желая научить школьников проверять найденное решение, нужно обязательно учить их определять, удовлетворяет ли оно условию задачи. Специально придумывать ситуации для такого обучения не приходится, учащиеся создают их довольно часто. Ими нужно только умело пользоваться.
В приведённом «решении» нарушено условие «в двух пачках 70 тетрадей».
Если же учащиеся верно решат задачу, то обучение исправлению ошибок надо отложить до того момента, когда ошибка будет допущена.
Рассмотрим первый способ решения задачи 160.
Решение.
I способ.
1) 70 – 20 = 50 (тетр.) — удвоенное число тетрадей во второй пачке;
2) 50 2 = 25 (тетр.) — во второй пачке; 3) 70 – 25 = 45 (тетр.) — в первой пачке.
После решения задач 281—283 из учебника нужно отметить то общее, что имеется в условии и в способе их решения: известны сумма и разность двух неизвестных чисел; чтобы их найти, нужно из суммы этих чисел вычесть их разность — получится удвоенное меньшее число.
Если же сложить сумму и разность двух чисел, то получится удвоенное большее число (такой вывод можно сделать, решив задачу 160 из рабочей тетради вторым способом: добавить разность (20) тетрадей во вторую пачку, тогда в двух пачках тетрадей окажется в 2 раза больше, чем в первой пачке).
Решение.
II способ.
1) 70 + 20 = 90 (тетр.) — удвоенное число тетрадей в первой пачке;
2) 90 2 = 45 (тетр.) — в первой пачке; 3) 70 – 45 = 25 (тетр.) — во второй пачке.
Позднее приведённые выше утверждения для любых чисел можно обосновать ещё и алгебраически, а пока можно ограничиться обоснованием их с помощью рисунка 3.

Рис. 3
Задачи на нахождение чисел по их сумме и разности можно решить ещё и составлением числового выражения: из суммы чисел вычесть их разность и полученный результат разделить на 2; сложить сумму и разность чисел и полученный результат разделить на 2.
Упростим решения задачи 160 для каждого из приведённых выше способов.
I способ.
1) (70 – 20) 2 = 25 (тетр.) — во второй пачке; 2) 70 – 25 = 45 (тетр.) — в первой пачке.
II способ.
1) (70 + 20) 2 = 45 (тетр.) — в первой пачке; 2) 70 – 45 = 25 (тетр.) — во второй пачке.
Задачу 160 можно решить третьим способом. Уравняем число тетрадей в пачках, переложив половину разности, т. е. 10 тетрадей, из первой пачки во вторую. Тогда тетрадей в пачках станет поров ну — по 70 2 = 35. Возьмём 10 тетрадей из второй пачки и переложим в первую пачку.
III способ.
1) 20 2 = 10 (тетр.) — половина разности тетрадей в двух пачках;
2) 70 2 = 35 (тетр.) — половина всех тетрадей; 3) 35 – 10 = 25 (тетр.) — во второй пачке; 4) 35 + 10 = 45 (тетр.) — в первой пачке.
К этому способу решения можно подвести учащихся, решив подготовительные задачи 288. Но делать это лучше только тогда, когда будет хорошо освоен первый способ решения задач такого типа, так как разнообразие методов решения, полезное для сильного ученика, может окончательно запутать слабого.
РТ. К данному пункту учебника относятся задачи 160—164.
288. а) На двух полках книг было поровну. С первой полки пере-ставили 10 книг на вторую полку. На сколько книг на второй полке стало больше, чем на первой?
Решение. На двух полках книг было поровну. После перестановки на первой полке стало книг на 10 меньше, а на второй — на 10 боль-
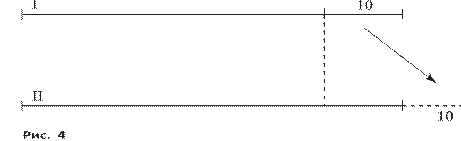
ше, чем было первоначально на каждой полке. На второй полке стало на 20 книг больше, чем на первой.
Ответ. На 20 книг.
Решение задачи 288 можно проиллюстрировать рисунком 4.
289. Бутылка масла весит 900 г. Масло на 100 г тяжелее бутылки.
Сколько весит пустая бутылка?
Решение.
1) 900 – 100 = 800 (г) — удвоенный вес пустой бутылки; 2) 800 2 = 400 (г) — вес пустой бутылки. Ответ. 400 г.
290. На вопрос учеников о дне своего рождения учитель математики ответил загадкой: «Если сложить день и номер месяца моего рождения, то получится 20; если из дня рождения вычесть номер месяца рождения, то получится 14; если к произведению дня и номера месяца моего рождения прибавить 1900, то получится год моего рождения». Когда родился учитель математики?
Решение. Сначала найдём день и номер месяца рождения по их сумме 20 и разности 14. Это 17 и 3. Затем найдём год рождения:
17 3 + 1900 = 1951.
Ответ. 17 марта 1951 г.
Промежуточный контроль. C–6.
В данном пункте учебника приведено описание применения калькулятора к вычислениям с натуральными числами. Однако авторы учебника считают, что чем меньше пятиклассники пользуются калькулятором, тем лучше для их умственного развития. Дело в том, что вычисления в столбик требуют запоминания промежуточных результатов и использования их в вычислениях. Это несложное упражнение развивает память, тренирует способность выполнять манипуляции с числами, удерживаемыми в памяти. Опытные учителя замечают, что учащиеся, слишком рано перекладывающие на калькулятор вычислительную работу, начинают отставать от своих сверстников в развитии. У таких учащихся притупляется и самоконтроль. Они настолько доверяют калькулятору, что забывают, что ошибка в вычислениях может быть вызвана неправильным введением в него чисел или неправильным нажатием клавиш.
Единственной причиной, по которой можно рекомендовать применение калькулятора учащимся, является быстрота проверки вычислений, выполненных в столбик (когда нет другого способа быстро проверить вычисления).
Этот раздел способствует общему развитию учащихся. Они должны понять, что существуют разные системы счисления и, возможно, с некоторыми из них (например, с двоичной) им придётся иметь дело в дальнейшем.
В задачах 301, 302 рассматриваются магические квадраты. Квадрат n n называют магическим, если n2 первых натуральных чисел (от 1 до n2) расставлены в клетках этого квадрата так, что сумма чисел в каждой строке, в каждом столбце и на каждой диагонали равна одному и тому же числу. В задаче 302 квадрат не назван магическим, так как, кроме нескольких первых натуральных чисел, содержит число 0.
303. Докажите, что сумма всех чисел любого магического квадрата 3 3 делится на 3.
Решение. I способ. Сумма чисел магического квадрата 3 3 равна 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45 — эта сумма делится на 3.
II способ. Так как суммы чисел в трёх строках равны, а их сумма составляет сумму всех чисел магического квадрата, то она делится на 3.
Утверждение задачи 303 можно обобщить сначала на магический квадрат 4 4 (сумма всех чисел любого магического квадрата 4 4 делится на 4), а потом и на магический квадрат n n (сумма всех чисел любого магического квадрата n n делится на n). На примере этих дополнительных задач можно учить не только важной логической операции — обобщению утверждения, но и соответствующей терминологии. Можно спросить: «Будет ли верно похожее утверждение для магического квадрата 4 4?» После получения верного ответа и доказательства утверждения можно сказать: «Мы обобщили задачу о магическом квадрате 3 3 для магического квадрата 4 4».
Этот раздел содержит в основном задачи о записях чисел, текстовые задачи и т. п.
309. а) К двузначному числу приписали цифру 5 сначала слева, а потом справа — получили два трёхзначных числа, сумма которых равна 912. Найдите двузначное число.
Решение. Имея небольшой опыт решения числовых ребусов, кто-то из учащихся догадается заменить цифры неизвестного числа буквами ab, тогда два трёхзначных числа будут иметь вид 5ab и ab5. Теперь, записав сумму этих чисел столбиком, учащиеся получат обыкновенный числовой ребус, решение которого показано по этапам:
1) 5ab 2) 5a7
+ +
ab5 a75
![]()
912 912
3) 537
+
375
![]()
912 Ответ. 37.
311. а)
Автотурист отправился в путешествие на четырёхколёсном автомобиле с одним
запасным колесом. По дороге он менял колёса с таким расчётом, чтобы каждое
колесо проехало один и тот же путь. Определите, сколько километров проехало
каждое колесо, если автомобиль проехал 4000 км.
а)
Автотурист отправился в путешествие на четырёхколёсном автомобиле с одним
запасным колесом. По дороге он менял колёса с таким расчётом, чтобы каждое
колесо проехало один и тот же путь. Определите, сколько километров проехало
каждое колесо, если автомобиль проехал 4000 км.
Решение. Если бы колёса не меняли, то каждое из четырёх колёс проехало бы 4000 км, а суммарный пробег колёс составил бы 16000 км. Так как 5 колёс изнашивались равномерно, то каждое из них проехало 16000 5 = 3200 км.
312.На столе лежат девять спичек (рис. 5). Рас-положите их так, чтобы в каждом горизонтальном ряду было: а) по 4; б) по 6; в) по 9; г) по 11.
Это задача-шутка, но на ней проверяется знание римской нумерации.
Решение. Спички надо расположить так:
а) IV б) VI
IV VI
IV VI в) IX г) XI
IX XI
IX XI
313.Из спичек сложили шесть неверных ра-венств (рис. 6).
Переложите в каждом равенстве по одной спичке так, чтобы равенства стали верными. Рис. 5
 |
Решение.
а) XII – IX = III;
б) V – IV = I;
 |
д) VI + V = XI;
е) IV = I + V – II.
315. а) Гости спросили: сколько лет исполнилось каждой из трёх сестёр? Вера ответила, что ей и Наде вместе 28 лет, Наде и Любе вместе 23 года, а всем троим 38 лет. Сколько лет каждой из сестёр?
Решение. Основная идея решения задачи заключается в том, что если из суммы возрастов трёх девочек вычесть сумму возрастов двух из них, то получится возраст третьей девочки.
Так как Вере, Наде и Любе вместе 38 лет, а Вере и Наде вместе 28 лет, то Любе 38 – 28 = 10 лет. Так как Наде и Любе вместе 23 года, а Любе 10 лет, то Наде 23 – 10 = 13 лет. Так как Вере и Наде вместе 28 лет, а Наде 13 лет, то Вере 28 – 13 = 15 лет.
Для сравнения можно привести ещё одно решение.
Обозначим количество лет Веры, Нади и Любы соответственно В, Н и Л. Тогда условия задачи можно записать в виде трёх верных равенств:
В + Н + Л = 38,
В + Н = 28, Н + Л = 23.
Вычитая из первого равенства второе, а потом третье, получаем, что Л = 10, В = 15. Теперь легко вычислить возраст Нади:
Н = 38 – 10 – 15 = 13.
Ответ. Вере 15 лет, Наде 13 лет, Любе 10 лет.
Заметим, что здесь нет ещё решения уравнения или системы уравнений, но действия, выполняемые при решении этой задачи, готовят учащихся к работе с этими абстракциями.
В задании 316 учащиеся могут предложить несколько способов решения, что нужно всячески поощрять, так как обсуждение различных
а) б)
способов решения одной и той же задачи, кроме прочего, способствует развитию речи школьников. Для анализа условия и выбора плана решения этих задач полезно использовать круги Эйлера. В задаче 316 а есть наводящие вопросы.
316. а) В нашем классе коллекционируют только марки и монеты. Mарки коллекционируют 8 человек, монеты — 5 человек. Всего коллекционеров 11. Объясните, как это может быть. Сколько человек коллекционируют только марки? Сколько — только монеты?
Решение. Объяснение простое: некоторые учащиеся коллекционируют и марки, и монеты.
1) 11 – 5 = 6 (чел.) — коллекционируют только марки; 2) 11 – 8 = 3 (чел.) — коллекционируют только монеты.
Решать задачу 316 а помогает наглядное представление условия задачи с помощью кругов Эйлера (рис. 7, а).
Рассмотрим дополнительную задачу:
Миша и Коля за лето прочитали 15 книг. Из них Миша прочитал 10 книг, а Коля — 12. Поставьте различные вопросы и ответьте на них.
По ходу решения получаемые ответы удобно отмечать на рисунке 7, б. Например:
1) Сколько книг прочитал Миша, но не прочитал Коля?
15 – 12 = 3 (книги).
2) Сколько книг прочитали оба мальчика?
10 – 3 = 7 (книг).
3) ...
323. Коля написал два раза своё имя (рис. 8, а). Его сосед по парте заметил, что Коля может прочитать своё имя более чем 10 способами, и показал один из них (рис. 8, б). Сколькими способами Коля может прочитать своё имя?
а) б)
Решение. I способ. Читая слово «КОЛЯ», к каждой букве О можно прийти двумя способами (от верхней буквы К и от нижней), к каждой букве Л — четырьмя способами (два способа через верхнюю букву О и два — через нижнюю), к каждой букве Я — восемью (четыре способа через верхнюю букву Л и четыре — через нижнюю), а всего прочитать слово можно шестнадцатью способами (8 + 8 = 16).
К О2 Л4 Я8
К О2 Л4 Я8
II способ. Можно рассуждать иначе. Букву К можно выбрать двумя способами, в каждом из них букву О можно выбрать двумя способами, т. е. прочитать КО можно четырьмя способами (2 2 = 4). В каждом из этих четырёх случаев букву Л можно выбрать двумя способами, т. е. прочитать КОЛ можно восемью способами (4 2 = 8). В каждом из этих восьми случаев букву Я можно выбрать двумя способами, т. е. прочитать слово «КОЛЯ» можно шестнадцатью способами (8 2 = 16). Вычисления можно записать коротко: 2 2 2 2 = 16.
324. На рисунке 9 показано, как можно прочитать слово «МАРШРУТ». Подсчитайте число всех способов, которыми можно прочитать это слово.
Решение. Если считать, что переходить от буквы к букве можно только в соседнюю клетку следующего столбца, то, рассуждая, как и в задаче 323, придём к таблице:
 М Р2 Р6 Т18 А2 Ш6 У18
М Р2 Р6 Т18 А2 Ш6 У18
М Р4 Р12 Т36 А2 Ш6 У18
М Р2 Р6 Т18
Остаётся сложить числа: 18 + 36 + + 18 = 72. Существует 72 способа, чтобы прочитать слово «МАРШРУТ».
Однако если считать, что можно переходить в клетку следующего столбца
Рис. 9 (необязательно соседнюю), то имеется 648 способов, чтобы прочитать слово «МАРШРУТ»: 3 2 3 2 3 2 3 = 648.
325. Учащиеся выполняли задание, в котором требуется найти пропущенные числа (рис. 10).

У них получились разные ответы (рис. 11).
1) 2)
2)  3)
3) 
Найдите правила, по которым ребята заполнили клетки, и придумайте ещё одно решение.
Решение. 1) Сумма двух первых чисел в строке равна третьему; 2) разность чисел в столбце равна 8; 3) сумма трёх чисел в строке равна 80.
Другие решения (рис. 12):
4) произведение двух первых чисел в строке равно третьему; 5) сумма трёх чисел в строке равна 81; 6) сумма трёх чисел в строке равна 82.
 4) 5)
4) 5)  6)
6) 
326.Докажите, что предыдущая задача имеет бесконечно много решений.
Решение. В предыдущем задании показано, как образовать суммы трёх чисел в строке, равные 80, 81, 82, ... . Этот ряд чисел можно продолжать бесконечно, поэтому задача имеет бесконечно много решений.
327.б) Имеются два сосуда вместимостью 8 л и 5 л. Как с помощью этих сосудов налить из водопроводного крана 7 л воды?
Решение задачи показано в таблице:
|
Ходы |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
8 л |
— |
5 |
5 |
8 |
— |
2 |
2 |
7 |
|
5 л |
5 |
— |
5 |
2 |
2 |
— |
5 |
— |
328.Из нескольких монет только одна фальшивая — она легче остальных. Как с помощью чашечных весов без гирь определить фальшивую монету:
а) за одно взвешивание, если монет 3;
б) за два взвешивания, если монет 9;
в) за три взвешивания, если монет 27?
Решение. а) Положим по одной монете на каждую чашку весов, одна монета останется на столе. Если весы придут в равновесие, то фальшивая монета на столе, если нет — фальшивая монета та, что легче. Итак, за одно взвешивание можно определить одну фальшивую монету из трёх.
б) Положим по 3 монеты на каждую чашку весов, 3 монеты останутся на столе. Первое взвешивание позволяет определить тройку монет, среди которых одна фальшивая. Вторым взвешиванием из трёх монет определим одну фальшивую (см. выше).
в) Положим по 9 монет на каждую чашку весов, 9 монет останется на столе. Первое взвешивание позволяет определить 9 монет, среди которых одна фальшивая. Далее за два взвешивания из девяти монет определим одну фальшивую (см. выше).
336. Однажды Чёрт предложил Бездельнику заработать.
— Как только ты перейдёшь через этот мост, — сказал он, — так твои деньги удвоятся. Можешь переходить по нему сколько хочешь раз, но после каждого перехода отдавай мне за это 24 копейки.
Бездельник согласился и... после третьего перехода остался без гроша. Сколько денег было у него сначала?
Решение. Задачу можно решить «обратным ходом», изобразив изменения исходной суммы схематически (рис. 13).

Рис. 13
Остаётся выполнить вычисления «обратным ходом» (рис. 14).
Ответ. 21 копейка.
337. Три брата получили 24 яблока, причём младшему досталось меньше всех. Видя это, младший брат предложил такой обмен яблоками: «Я оставлю себе половину имеющихся у меня яблок, а остальные разделю между вами поровну. После этого пусть средний брат, а за ним старший поступят так же». Братья согласились. В результате у всех яблок стало поровну. Сколько яблок было у каждого первоначально?
Решение. И эту задачу можно решить «обратным ходом», изобразив изменения количества яблок каждого брата схематически (рис. 15).
Так как в конечном итоге яблок стало поровну, то их стало по 8. При последнем изменении старший брат оставил себе половину, значит, у него до того было 16 яблок. Младшим он отдал другую половину — 8 яблок, разделив их поровну между братьями, значит, до этого младший и средний братья имели по 4 яблока. Эти данные внесены в третий столбец схемы. Далее надо рассуждать аналогично.
Средний брат отдал своим братьям половину того, что имел сам, т. е. до этого момента он имел 8 яблок, младший брат имел 2 яблока, старший — 14 яблок. Эти данные приведены во втором столбце.
Рис. 15
Младший брат отдал своим братьям половину того, что имел сам, т. е. до этого момента он имел 4 яблока, средний брат имел 7 яблок, старший — 13 яблок. Эти данные приведены в первом столбце. Ответ. 4, 7 и 13 яблок.
338. Старинная задача. Однажды умный бедняк попросил у скупого богача приюта на две недели, причём сказал: «За это я тебе в первый день заплачу 1 р., во второй день — 2 р., в третий день — 3 р. и т. д. Словом, каждый день я буду прибавлять тебе по одному рублю, так что за один только четырнадцатый (последний) день я заплачу 14 р. Ты же будешь мне подавать милостыню: в первый день копейку, во второй — 2 к., в третий день — 4 к. и т. д., увеличивая каждый день свою милостыню вдвое». Богач с радостью согласился на такие условия, которые ему показались выгодными. Какой барыш принесла эта сделка богачу?
Решение. Бедняк уплатил 1 + 2 + 3 + 4 + ... + 14 = 105 (р.).
Богач заплатил 1 + 2 + 4 + 8 + ... + 8192 = 16383 (к.).
Вычислению первой суммы помогает следующее наблюдение: суммы первого и последнего, второго и предпоследнего чисел и т. д. рав- ны 15, таких пар слагаемых 14 2 = 7, поэтому сумма равна 15 7 = 105.
Вычислению второй суммы помогает следующее наблюдение: сумма двух первых чисел равна третьему, уменьшенному на 1; сумма трёх первых чисел равна четвёртому, уменьшенному на 1, и т. д. Вся сумма равна 8192 2 – 1 = 16383 (к.), или 163 р. 83 к.
Богач потерял на этой сделке 58 р. 83 к.
ГЛАВА 2
В этой главе повторяются и систематизируются изученные ранее элементы геометрии. Здесь же рассматривается измерение отрезков и представление натуральных чисел на координатном луче. У учащихся должны быть сформированы первые понятия о числе как о длине отрезка и об изображении чисел на координатном луче, т. е. понятие о числе как о координате точки на координатной оси.
Кроме того, здесь вводятся понятия пути, времени, скорости и продолжается решение текстовых задач арифметическими способами (задачи на движение).
Цели изучения главы: систематизировать сведения о геометрических фигурах; сформировать первые представления о числе как о длине отрезка и об изображении чисел на координатном луче;
продолжить развитие математического языка и логического мышления учащихся при помощи решения текстовых задач арифметическими методами.
В данном пункте вводятся понятия прямой, параллельных прямых, луча, отрезка, равных отрезков, вводятся буквенные обозначения перечисленных фигур.
РТ. При изучении данного пункта можно использовать задания 165— 171. Задания 165, 166 лучше выполнить после выполнения заданий 350, 351 из учебника.
358.Назовите все отрезки с концами в точках M, N и K (рис. 16).
Сколько отрезков получилось?
Решение. Образовалось три отрезка: MN, NK, MK.
Трудность решения данной задачи и похожих на неё задач заключается в том, что учащиеся не видят фигуру, составленную из других фигур, а видят только её части. Такие задачи важны для развития способности ребёнка решать задачу полным перебором всех случаев, они включены в самостоятельные работы.
359.На прямой отметили четыре точки. Образовалось 6 отрезков с концами в этих точках. Проверьте.
![]()
Рис. 16
![]()
Рис. 17
Решение. Если на прямой последовательно отметили четыре точки: A, B, M и N (рис. 17), то образовалось три «маленьких» отрезка: AB, BM, MN; два отрезка, содержащие по два «маленьких» отрезка: AM и BN; один отрезок, содержащий три «маленьких» отрезка: AN. Всего 3 + 2 + 1 = 6 отрезков.
2.2. Измерение отрезков
В пункте 2.2 учебника вводятся понятия единицы длины отрезков, приближённой длины отрезка с недостатком, с избытком, с округлением.
В пункте 2.3 учебника вводятся метрические (производные от метра) единицы длины и объясняются соотношения между ними.
В задании 381 приведена часть таблицы, помещённой на втором форзаце учебника. Учащиеся должны хорошо усвоить, что при переходе в соседнюю клетку таблицы вправо получаем единицу длины, большую в 10 раз, а при переходе в соседнюю клетку таблицы влево получаем единицу длины, меньшую в 10 раз: 1 см = 10 мм, ... . При переходе в таблице через клетку единица длины изменяется в 100 раз: 1 м = 100 см, ..., при переходе через две клетки — в 1000 раз: 1 км = 1000 м, ... .
Для двух единиц длины из таблицы — 10 м и 100 м — нет общепринятых названий, но они нужны для лучшего понимания описанной выше взаимосвязи единиц длины. Кроме того, 10 м и 100 м будут сторонами квадратов, площади которых получат специальные названия — ар и гектар (см. таблицу на форзаце учебника).
После устного разбора задания 381 из учебника можно предложить учащимся задание 172 из рабочей тетради.
РТ. Задания 172—175 посвящены единицам длины, приближённому измерению длины отрезка, откладыванию отрезка данной длины на прямой от заданной точки.
377. Рейка длиной 147 см разрезана на 4 равные части. Какую длину имеет каждая часть с точностью до 1 см: а) с недостатком; б) с избытком; в) с округлением?
Решение. 147 4 = 36 (ост. 3), поэтому длина каждой части равна:
а) 36 см с недостатком; б) 37 см с избытком; в) 37 см с округле-
нием.
389. Туристы прошли 70 км за 4 дня. Определите, какое расстояние они проходили в день, если считать, что каждый день они проходили одно и то же расстояние. Ответ выразите приближённо с точностью до 1 км: а) с недостатком; б) с избытком; в) с округлением.
Решение. 70 4 = 17 (ост. 2), поэтому каждый день туристы проходили: а) 17 км с недостатком; б) 18 км с избытком; в) 18 км с округлением.
Если выразить расстояние в метрах, то 70000 4 = 17500 (м). 17500 м = 17 км 500 м 18 км (с округлением).
Промежуточный контроль. C–7.
В данном пункте учебника вводятся понятия координатного луча, единичного отрезка, даётся правило сравнения натуральных чисел по их расположению на координатном луче (имеется в виду расположение точек, соответствующих натуральным числам на координатном луче).
РТ. Задания 176, 177 посвящены изображению натуральных чисел на координатном луче.
401. Кузнечик прыгает вдоль координатного луча попеременно: на 5 единичных отрезков вправо и на 3 единичных отрезка влево. Сможет ли он за несколько прыжков из точки 0 попасть: а) в точку 6; б) в точку 7?
Решение. а) После первой пары прыжков — на 5 единичных отрезков вправо и на 3 единичных отрезка влево — кузнечик попадёт в точку 2, после второй — в точку 4, после третьей — в точку 6.
б) Так как каждая пара прыжков (вправо и влево) перемещает куз-
нечика на 2 единицы вправо, то из точки 0 кузнечик может попасть в точки 2, 4, 6, 8, ..., но не может попасть в точки 1, 3, 5, 7, ... . Ответ. а) Да; б) нет.
Дополнительное задание. Как надо изменить условие задания 401, чтобы кузнечик мог попасть в точку 7?
Ответ. Можно убрать слово «попеременно». Тогда, совершив подряд 2 прыжка вправо на 5 + 5 = 10 единичных отрезков и один прыжок влево на 3 единичных отрезка, кузнечик попадёт в точку 7.
 В данном пункте
учебника вводятся понятия окружности, её центра, радиуса, хорды, диаметра, дуги
окружности, понятия круга, сферы и шара. Материал данного пункта не только даёт
учащимся возможность продемонстрировать усвоение основных понятий, но и
позволяет проявить аккуратность и художественный вкус при решении задач
творческого характера (задания 410, 411). Здесь же имеются задачи
пропедевтического характера, которые не являются обязательными для всех
учащихся.
В данном пункте
учебника вводятся понятия окружности, её центра, радиуса, хорды, диаметра, дуги
окружности, понятия круга, сферы и шара. Материал данного пункта не только даёт
учащимся возможность продемонстрировать усвоение основных понятий, но и
позволяет проявить аккуратность и художественный вкус при решении задач
творческого характера (задания 410, 411). Здесь же имеются задачи
пропедевтического характера, которые не являются обязательными для всех
учащихся.
РТ. Задания 178—183 можно использовать для отработки понятий «окружность» и «круг» при решении задач по готовому чертежу или по чертежу, который дополняется по ходу решения задачи.
418. Постройте две окружности с центрами A и B и радиусами 3 см и 5 см, касающие ся внешним образом. Постройте третью окружность, центр которой лежит на отрезке AB и которая касается двух первых окружностей внутренним образом.
Рис. 18 Решение. Для решения задачи надо на прямой отметить точки A
и B так, чтобы AB = 3 см + 5 см = 8 см. Построить две окружности — с центром A радиусом 3 см и с центром B радиусом 5 см. Они пересекут прямую AB в точках M и N (рис. 18). Затем построить окружность с центром O (середина отрезка MN) радиусом 8 см.
В данном пункте учебника вводится понятие угла. Равенство углов определяется через их совпадение при наложении. Здесь же введены понятия вершины, сторон угла, введена единица величины углов — градус — и её доли: минута и секунда. Рассмотрены виды углов — развёрнутый, прямой, острый и тупой. Введено понятие перпендикулярных прямых и соответствующее обозначение.
Понятия «смежные углы» (задания 433—436) и «вертикальные углы» (задания 438, 439) не являются обязательными для усвоения всеми учащимися.
Задачи 434, 435, 439 — типовые арифметические задачи на нахождение двух чисел по их сумме и разности, «на части».
При работе с материалом данного пункта надо обратить внимание на развитие умения учащихся формулировать определения. Эта работа не только окажется полезной для развития мышления и ре- чи учащихся, но и поможет им при дальнейшем изучении математики.
РТ. В начале изучения темы можно использовать задания 184, 185 для отработки понятия «угол». Задания 186—188 нацелены на использование понятия «угол» в более сложной ситуации.
 Решения и комментарии
Решения и комментарии426. Определите угол между направлениями (рис. 19):
а) север и восток;
б) север и юг;
д) северо-восток и восток;
з) северо-запад и восток.
Решение. Здесь считается известным, что, например, направление восток (В) делит угол между направлениями север (С) и юг (Ю) на две равные части, образуя углы по 90 , направление северо-восток (С–В) делит угол между направлениями сев ер (С) и восток (В) на две
|
равные части, образуя углы по 45 . Поэтому угол между направления- |
Рис. 19 |
ми: а) север и восток равен 90 ; б) север и юг равен 180 ; д) северо-восток и восток равен 45 ; з) северо-запад и восток равен 135 .
427. а) Какой угол образуют часовая и минутная стрелки в: 6 ч; 3 ч; 1 ч; 5 ч?
б) На какой угол повернётся часовая стрелка за: 6 ч; 3 ч; 1 ч; 4 ч?
в) На какой угол повернётся минутная стрелка за: 30 мин; 15 мин; 10 мин; 1 мин?
Решение. а) Часовая и минутная стрелки образуют:
в 6 ч развёрнутый угол, т. е. угол в 180 ;
в 3 ч — угол, в 2 раза меньший развёрнутого, т. е. угол, рав-
ный 90 ; в 1 ч — угол, в 3 раза меньший, чем в 3 ч, т. е. угол, равный 30 ; в 5 ч — угол, в 5 раз больший, чем в 1 ч, т. е. угол, равный 150 . б) Часовая стрелка повернётся:
за 6 ч на угол 180 ;
за 3 ч на угол, в 2 раза меньший, чем за 6 ч, т. е. на угол, рав-
ный 90 ; за 1 ч на угол, в 3 раза меньший, чем за 3 ч, т. е. на угол, рав-
ный 30 ; за 4 ч на угол, в 4 раза больший, чем за 1 ч, т. е. на угол, рав-
ный 120 .
в) Минутная стрелка повернётся:
за 30 мин на угол 180 ;
за 15 мин на угол, в 2 раза меньший, чем за 30 мин, т. е. на угол,
равный 90 ; за 10 мин на угол, в 3 раза меньший, чем за 30 мин, т. е. на угол, равный 60 ;
за 1 мин на угол, в 10 раз меньший, чем за 10 мин, т. е. на угол,
равный 6 .
Задания 428—431 предназначены для ознакомления учащихся с долями градуса — минутами и секундами. Здесь полезно подчеркнуть, что названия долей градуса и часа совпадают не случайно. В Древнем Вавилоне меру веса и денег — талант — делили на 60 равных частей, которые назывались минами, а каждую мину делили ещё на 60 частей. Такая шестидесятеричная система записи чисел в настоящее время используется только при измерении времени и углов.
Надо обратить внимание на правильное чтение величин углов, например: 4 719 — 4 градуса 7 минут 19 секунд.
При выполнении заданий 430, 431 учащиеся не должны забывать, что 60 = 1 , а 60 = 1.
Вычисления надо производить подробно, следуя образцам, приведённым в учебнике. Владение такими вычислениями не является обязательным для всех учащихся. Эти вычисления в 5 классе имеют, скорее, мировоззренческую нагрузку: ученик должен понимать, что общеупотребимая и привычная десятичная система записи чисел не является единственной. И ещё: знакомство с долями градуса и действия с ними готовят учащихся к введению обыкновенных дробей в 5 классе и десятичных дробей в 6 классе.
432. б) Постройте острый угол AOB, проведите внутри этого угла два луча OD и OE. Сколько острых углов получилось?
Решение. Здесь учащиеся должны увидеть все шесть острых углов: AOD, AOE, AOB, DOE, DOB, EOB (рис. 20).
434. Луч OC делит развёрнутый угол AOB на два смежных угла AOC и BOC так, что угол AOC на 30 больше угла BOC. Найдите AOC и BOC.
Решение. Здесь нужно решить задачу на нахождение двух чисел по их сумме (180 ) и разности (30 ).
![]() 1) 180 – 30 = 150 —
удвоенная величина меньшего угла BOC; 2) 150 2 = 75 — величина
меньшего угла BOC;
1) 180 – 30 = 150 —
удвоенная величина меньшего угла BOC; 2) 150 2 = 75 — величина
меньшего угла BOC;
3) 75 + 30 = 105 — величина большего угла AOC.
Ответ. 105 и 75 .
435. Луч OC делит развёрнутый угол AOB на два смежных угла AOC и BOC так, что угол AOC в 3 раза больше угла BOC. Найдите AOC и BOC.
Решение. Здесь нужно решить задачу «на части».
1) 1 + 3 = 4 (части) — приходится на два угла AOC и BOC;
2) 180 4 = 45 — величина меньше-
Рис. 20 го угла BOC;
3) 45 3 = 135 — величина большего угла AOC. Ответ. 135 и 45 .
Дополнение. Для более сильных учащихся можно уточнить понятия угла и его градусной меры. В учебнике сказано, что два луча с общим началом делят плоскость на две части, называемые углами, но обычно рассматривают лишь один из этих углов. Поясним, какой из них обычно рассматривают.
Возможны только три различных случая взаимного расположения двух лучей с общим началом (рис. 21).
На рисунке 21, а лучи BA и BC различны и лежат на одной прямой. Они делят плоскость на две части. Чаще всего рассматривают верхнюю (закрашенную) часть плоскости, именно её называют развёрнутым углом и считают, что градусная мера развёрнутого угла равна 180 .
На рисунке 21, б лучи BA и BC совпадают. Они делят плоскость на две части. Одну из них, задаваемую лучом BA (BC), считают углом, градусная мера которого равна 0 .
На рисунке 21, в лучи BA и BC не лежат на одной прямой. Они делят плоскость на две части. Чаще всего рассматривают «меньшую» (закрашенную) часть плоскости (не стоит пытаться в 5 классе определить «меньшую» и «большую» части плоскости, обычно из условия рассматриваемой задачи интуитивно ясно, о какой из этих частей идёт речь). Градусная мера такого угла заключена между 0 и 180 .
Дальше в основном будут использоваться углы, градусная мера a которых такова, что 0 a 180 , т. е. те углы, градусную меру которых можно измерить с помощью транспортира.
Впрочем, из этого правила будут делаться исключения, так как иногда требуется рассматривать углы, большие развёрнутого. Рассмотрим задачи, где такие углы возникают.
1. На какой угол повернётся часовая стрелка за: 9 ч; 12 ч?
Решение. Часовая стрелка повернётся за 6 ч на 180 , потом за 3 ч ещё на 90 , а всего за 9 ч она повернётся на 270 . За 12 ч часовая стрелка повернётся на угол 180 + 180 = 360 .
в)
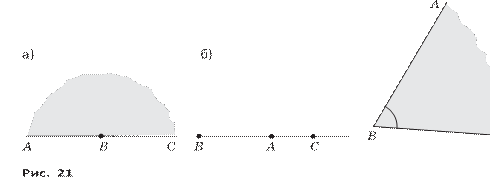
2. ![]() Из
квадрата MBCD вырезали прямоугольник MAFE (рис. 22). Найдите угол
F полученного шестиугольника ABCDEF.
Из
квадрата MBCD вырезали прямоугольник MAFE (рис. 22). Найдите угол
F полученного шестиугольника ABCDEF.
Решение. В задаче речь идёт о внутренних углах шестиугольника ABCDEF. Ясно, что угол AFE (в прямоугольнике MAFE) равен 90 , а внутренний угол F шестиугольника ABCDEF равен 270 .
Обратим внимание на следующую задачу.
3. Какой угол образуют часовая и минутная стрелки в: 9 ч; 12 ч?
Решение. Часовая и минутная стрелки образуют: в 9 ч угол в 90 ; в 12 ч угол в 0 . Однако (учитывая задачу 1) часть учащихся может дать и такой ответ: они образуют Рис. 22 в 9 ч угол, равный 270 , и в 12 ч
угол, равный 360 .
В данном пункте учебника введены понятия треугольника, вершин, сторон и углов треугольника, периметра треугольника, равенства треугольников, рассмотрены виды треугольников (классификация по углам, по сторонам). В учебном тексте говорится о боковых сторонах и основании равнобедренного треугольника — желательно, чтобы учащиеся усвоили и эти термины.
РТ. При изучении данного пункта можно использовать задания 189—192. Задание 190 нацелено на тренировку в измерении угла с помощью транспортира и экспериментальное установление факта «сумма углов треугольника равна 180 ».
451.В равнобедренном треугольнике даны длины двух сторон: 5 см и 6 см. Каким может быть периметр треугольника?
Решение. Если стороны треугольника 5, 5 и 6 см, то периметр равен 16 см; если стороны треугольника 5, 6 и 6 см, то периметр равен 17 см. Ответ. 16 см или 17 см.
452.Периметр равнобедренного треугольника ABC равен 30 см, а одн а из сторон на 3 см больше другой. Какими могут быть стороны треугольника ABC?
Решение. Если основание равнобедренного треугольника ABC на 3 см больше каждой из его боковых сторон, то каждая из них равна (30 – 3) 3 = 9 (см), а основание равно 9 + 3 = 12 (см).
![]() Если
основание равнобедренного треугольника ABC на 3 см меньше каждой из его
боковых сторон, то каждая из них равна (30 + 3) 3 = 11 (см), а основание равно
11 – 3 = 8 (см).
Если
основание равнобедренного треугольника ABC на 3 см меньше каждой из его
боковых сторон, то каждая из них равна (30 + 3) 3 = 11 (см), а основание равно
11 – 3 = 8 (см).
Ответ. 9, 9 и 12 см или 11, 11 и 8 см.
453.а) Верно ли, что если два тре-угольника равны, то их периметр ы равны?
б) Верно ли, что если периметры двух треугольников равны, то и сами треугольники равны?
Решение. а) Так как у равных треугольников стороны попарно равны (они совмещаются при наложении), Рис. 23 то периметры равных треугольников равны.
б) Утверждение неверно, так как у треугольника со сторонами 10, 10 и 10 см периметр равен 30 см, у треугольника со сторонами 9, 10 и 11 см такой же периметр, но эти треугольники не равны. Ответ. а) Да; б) нет.
Замечание. Рассмотренное задание позволяет разъяснить, что если мы считаем утверждение верным, то должны его обосновать, доказать. Если мы считаем утверждение неверным, то достаточно привести один пример (контрпример), показывающий, что утверждение неверно.
191 (РТ). Сколько треугольников изображено на рисунке 23?
Решение. На рисунке 23 изображено 9 маленьких треугольников, 3 средних треугольника, каждый из которых содержит по 4 маленьких, и один большой треугольник, содержащий 9 маленьких. Всего 9 + 3 + 1 = 13 треугольников.
На это задание надо обратить особое внимание, так как похожие задания содержатся в следующей самостоятельной работе.
В данном пункте учебника введены понятия четырёхугольника, вершин, сторон и углов четырёхугольника, периметра четырёхугольника и равенства четырёхугольников, а также понятия прямоугольника и квадрата. Понятие ромба (задание 474) не является обязательным для всех учащихся.
При изучении данного пункта можно использовать материал пункта 1 из Дополнений к главе 2, так как каждый учащийся должен владеть понятиями «пятиугольник», «шестиугольник», ..., «многоугольник».
РТ. Задания 195, 196 нацелены на отработку понятий «прямоугольник», «периметр прямоугольника», на подсчёт числа квадратов и прямоугольников на сложном рисунке.
467. Периметр прямоугольника равен 56 см, одна из его сторон равна 17 см. Найдите его другую сторону.
Решение. I способ. Сумма длин двух сторон прямоугольника равна 17 2 = 34 см. Поэтому сумма длин двух других его сторон равна 56 – 34 = 22 см. Тогда неизвестная сторона прямоугольника равна 22 2 = 11 см.
II способ. Сумма двух соседних сторон прямоугольника равна 56 2 = 28 см. Поэтому неизвестная сторона прямоугольника равна 28 – 17 = 11 см.
Ответ. 11 см.
468. а) Периметр прямоугольника равен 48 см, основание на 4 см больше высоты. Найдите высоту прямоугольника.
Решение. Сумма основания и высоты равна 48 2 = 24 см, а разность равна 4 см. Решив задачу на нахождение двух чисел по их сумме и разности, найдём меньшую сторону, она равна 10 см. Ответ. 10 см.
472.а) Как изменится периметр квадрата, если его сторону увели-чить в 2 раза?
Решение. Если у квадрата сторона равна a см, то он имеет периметр P = 4a см. Если множитель a увеличить в 2 раза, то и произведение увеличится в 2 раза. Следовательно, периметр квадрата увеличится в 2 раза.
473.Убедитесь, что на рисунке 24, а изображено 18 прямоугольников. Учтите, что квад рат является прямоугольником. Сколько пря- моугольников изобр ажено на рисунке 24, б?
|
|
|
![]()
![]() Решение. На рисунке 24, а
изображено 6 маленьких квадратов, 7 прямоугольников, каждый из которых
составлен из двух маленьких квадратов, 2 прямоугольника, каждый из которых
составлен из трёх маленьких квадратов, 2 прямоугольника, каждый из которых
составлен из четырёх маленьких квадратов, и один большой прямоугольник,
составленный из шести маленьких квадратов. Всего 6 + 7 + 2 + 2 + 1 =
Решение. На рисунке 24, а
изображено 6 маленьких квадратов, 7 прямоугольников, каждый из которых
составлен из двух маленьких квадратов, 2 прямоугольника, каждый из которых
составлен из трёх маленьких квадратов, 2 прямоугольника, каждый из которых
составлен из четырёх маленьких квадратов, и один большой прямоугольник,
составленный из шести маленьких квадратов. Всего 6 + 7 + 2 + 2 + 1 =
Рис. 24 = 18 прямоугольников.
Рассуждая аналогично, получим, что на рисунке 24, б изображено
8 + 10 + 4 + 5 + 2 + 1 = 30 прямоугольников.
Ответ. 30 прямоугольников.
477. Периметр треугольника ABD равен 12 см, периметр треугольника BDC — 30 см, а периметр четырёхугольника ABCD — 32 см (рис. 25). Определите длину отрезка BD.
Решение. Сумма периметров треугольников ABD и BDC равна 12 + 30 = 42 см. Она равна сумме периметра четырёхугольника ABCD и удвоенной длины отрезка BD. Поэтому длина отрезка BD равна (42 – 32) 2 = 5 см. Ответ. 5 см.
Промежуточный контроль. C–8.
В данном пункте учебника вводится понятие единичного квадрата, на конкретном примере обосновывается формула для вычисления площади прямоугольника: если длины сторон прямоугольника выражаются натуральными числами a и b, то площадь S прямоугольника равна a b (S = a b).
Далее объясняются соотношения между квадратными единицами. Усвоению этих соотношений будет способствовать работа с таблицей в задании 481.
РТ. В начале изучения темы можно использовать задания 205—210.
492. Как изменится площадь прямоугольника, если: а) его длину увеличить в 2 раза;
б) его длину и ширину увеличить в 2 раза?
Решение. Пусть длина прямоугольника a см, а ширина b см, тогда его площадь равна ab см2.
а) Если длину прямоугольника увеличить в 2 раза, то площадь но-
вого прямоугольника будет равна 2a b см2 = 2 ab см2 — она в 2 раза больше площади данного прямоугольника.
б) Если длину и ширину прямоугольника увеличить в 2 раза, то площадь нового прямоугольника будет равна 2a 2b см2 = 4 ab см2 — она в 4 раза больше площади данного прямоугольника.
Ответ. а) Увеличится в 2 раза; б) увеличится в 4 раза.
В данном пункте учебника вводятся понятие прямоугольного параллелепипеда и вся соответствующая терминология, понятия куба, развёртки прямоугольного параллелепипеда. Изучаемый материал позволяет дать возможность учащимся поработать с бумагой, вырезая развёртку прямоугольного параллелепипеда (задание 499). Здесь имеются задачи развивающего характера, связанные с необходимостью представления пространственного объекта — куба, чисел, изображённых на его гранях (задания 501—503). В задании 504 требуется определить, какая из предложенных фигур является развёрткой куба. РТ. К изучаемой теме относятся задания 214, 215.
501. На гранях куба (рис. 26) написали числа 1, 2, 3, 4, 5, 6 так, что сумма чисел на двух противоположных гранях равна семи. Рядом с кубиком изображены его развёртки, на которых указано одно из этих чисел. Укажите остальные числа.
Решение. Для решения задачи учащимся надо представить, что они мысленно складывают развёртку, чтобы получить куб. Тогда на каждой развёртке сначала определяется положение чисел 1, 2 и 3 (на рисунке 27 они изображены с учётом их взаимного расположения на гранях куба, но это не обязательное требование). Затем определяется

Рис. 27
![]() положение чисел 4, 5
и 6. Для проверки своего решения учащиеся могут сделать развёртку куба.
положение чисел 4, 5
и 6. Для проверки своего решения учащиеся могут сделать развёртку куба.
507.На рисунке 28 изобр ажён куб, сложенный из восьми одинаковых кубиков с ребром 1 см. Сколько прямоугольных параллелепипедов на этом рисунке?
![]() Решение. На
рисунке 28 изоб ражено 8 маленьких кубиков (не все они, конечно, видны). Есть
12 прямоугольных параллелепипедов, составленных из двух маленьких кубиков, 6
прямоугольных параллелепипедов, составленных из четырёх маленьких кубиков, и 1
большой куб, составленный из восьми маленьких кубиков. Всего 8 + 12 + 6 + 1 =
27 прямоугольных параллелепипедов. Ответ. 27.
Решение. На
рисунке 28 изоб ражено 8 маленьких кубиков (не все они, конечно, видны). Есть
12 прямоугольных параллелепипедов, составленных из двух маленьких кубиков, 6
прямоугольных параллелепипедов, составленных из четырёх маленьких кубиков, и 1
большой куб, составленный из восьми маленьких кубиков. Всего 8 + 12 + 6 + 1 =
27 прямоугольных параллелепипедов. Ответ. 27.
508.Окрашенный куб распилили на 27 одинаковых кубиков с ребр ом 1 см (рис. 29). У скольких маленьких кубиков окрашена только одна грань; только две грани; три грани?
Решение. Окрашена только одна грань у 6 маленьких кубиков (в центре Рис. 29 каждой грани большого куба); окраше- но только две грани у 12 кубиков (в середине каждого ребра большого куба); окрашено три грани у 8 кубиков (в каждой вершине большого куба). (И нет кубиков, у которых окрашено более трёх граней.)
В данном пункте учебника вводится понятие единичного куба, поясняется, что значит измерить объём прямоугольного параллелепипеда при помощи единичных кубов, обосновывается на конкретном примере формула для вычисления объёма прямоугольного параллелепипеда: если измерения прямоугольного параллелепипеда выражаются натуральными числами a, b и c, то объём прямоугольного параллелепипеда равен: V = a b c.
Далее объясняются соотношения между кубическими единицами. Усвоению этих соотношений будет способствовать работа с таблицей в задании 510.
РТ. В начале изучения темы можно использовать задания 211—213.
515. Аквариум имеет форму прямоугольного параллелепипеда, длина которого 45 см, ширина 30 см, а высота 25 см. Сколько раз придётся наполнить водой трёхлитровую банку, чтобы уровень воды в аквариуме был равен 20 см?
Решение. Надо налить 45 30 20 = 27000 см3 воды. Это 27 дм3, или 27 л. Трёхлитровую банку придётся наполнить водой 27 3 = 9 раз. Ответ. 9 раз.
516. Как изменится объём прямоугольного параллелепипеда, если:а) его длину увеличить в 2 раза;
б) увеличить его длину в 2 раза, а ширину — в 3 раза?
Решение. Пусть a см — длина, b см — ширина, c см — высота прямоугольного параллелепипеда, тогда его объём равен abc см3.
а) Если длину прямоугольного параллелепипеда увеличить в 2 раза, то его объём будет равен 2a b c см3 = 2 abc см3 — он в 2 раза больше объёма данного прямоугольного параллелепипеда.
б) Если длину увеличить в 2 раза, а ширину — в 3 раза, то объём нового прямоугольного параллелепипеда будет равен 2a 3b c см3 = = 6 abc см3 — он в 6 раз больше объёма данного прямоугольного параллелепипеда.
Ответ. а) Увеличится в 2 раза; б) увеличится в 6 раз.
2.12. Единицы массы
В пункте 2.12 вводятся единицы массы: грамм, килограмм, центнер, тонна — и соотношения между ними. В пункте 2.13 вводятся единицы времени: сутки, час, минута, секунда — и соотношения между ними. Знание этих единиц необходимо не только в обиходе, но и для решения задач на движение, а в дальнейшем для осмысленного перевода одних единиц скорости в другие, а также при изучении физики.
525. Данные величины запишите с точностью до 1 кг: а) с недостатком; б) с избытком; в) с округлением.
1) 5 кг 768 г; 2) 9 кг 326 г; 3) 4 ц 36 кг 125 г; 4) 5 т 7 ц. Решение.
1) а) 5 кг 768 г 5 кг с недостатком;
б) 5 кг 768 г 6 кг с избытком;
в) 5 кг 768 г 6 кг с округлением;
2) а) 9 кг 326 г 9 кг с недостатком;
б) 9 кг 326 г 10 кг с избытком;
в) 9 кг 326 г 9 кг с округлением;
3) а) 4 ц 36 кг 125 г 436 кг с недостатком;
б) 4 ц 36 кг 125 г 437 кг с избытком;
в) 4 ц 36 кг 125 г 436 кг с округлением;
4) а) 5 т 7 ц 5700 кг с недостатком;
б) 5 т 7 ц 5700 кг с избытком;
в) 5 т 7 ц 5700 кг с округлением.
535. Увеличьте: а) 3 ч 15 мин в 3 раза; б) 1 ч 20 мин в 4 раза.
Решение.
а) 3 ч 15 мин 3 = 9 ч 45 мин;
б) 1 ч 20 мин 4 = 4 ч 80 мин = 5 ч 20 мин.
В данном пункте учебника рассмотрены задачи на равномерное движение, движение по реке и движение двух участников навстречу друг другу или в одном направлении. Здесь вводятся понятия скоростей: собственной, течения, по течению, против течения, сближения и удаления. Такого рода задачи будут встречаться и далее, поэтому способы их решения желательно усвоить уже сейчас.
РТ. В начале изучения задач каждого типа полезно рассмотреть задания 216—225. К части из них приведены иллюстрации, на которых скорости изображены отрезками. При этом важно обратить внимание на оба способа решения задач 218, 220, 222 и 224. Задания 226—229 предназначены сильным учащимся, этими заданиями можно завершить изучение темы, рассмотрев их решения после выполнения заданий 561 и 564 учебника.
545. Определите, какая скорость получится следующим действием:а) vс. + vт.; б) vс. – vт.; в) vпр. т. + vт.;
г) vпр. т. + 2vт.; д) vпо т. – vт.; е) vпо т. – vпр. т..
Решение. Решение этой задачи должно опираться на опыт решения задачи 544 (и аналогичных задач из рабочей тетради).
а) vс. + vт. = vпо т.; б) vс. – vт. = vпр. т.; в) vпр. т. + vт. = vс.;
г) vпр. т. + 2vт. = vпо т.; д) vпо т. – vт. = vс.; е) vпо т. – vпр. т. = 2vт..
546. а) По течению моторная лодка проплыла 48 км за 3 ч, а про-тив течения — за 4 ч. Найдите скорость течения.
Решение.
1) 48 3 = 16 (км/ч) — скорость лодки по течению реки;
2) 48 4 = 12 (км/ч) — скорость лодки против течения реки; 3) 16 – 12 = 4 (км/ч) — удвоенная скорость течения; 4) 4 2 = 2 (км/ч) — скорость течения.
Ответ. 2 км/ч.
548. 15 июля 1923 года из Москвы в Нижний Новгород вылетел аэроплан «Ультиматум». Так была открыта первая трасса Аэрофлота длиной 420 км. Аэроплан шёл на высоте 250 м и преодолел всё расстояние за 3 ч 30 мин. Найдите скорость аэроплана. Какие условия в задаче являются лишними?
Решение. Предварительно выразим время в минутах: 3 ч 30 мин = = 210 мин. Тогда 420 210 = 2 (км/мин) — скорость аэроплана. Запишем её в других единицах: 2 60 = 120 (км/ч).
Лишние условия в задаче (от которых не зависит ответ) — высота и дата полёта.
552. а) Расстояние между двумя городами 900 км. Два поезда вышли из этих городов навстречу друг другу со скоростями 60 км/ч и 80 км/ч. На каком расстоянии друг от друга были поезда за 1 ч до встречи? Есть ли в задаче лишнее условие?
б) Расстояние от села до города 45 км. Из села в город вышел пешеход со скоростью 5 км/ч. Через час из города в село выехал велосипедист со скоростью 15 км/ч. Кто из них в момент встречи будет ближе к селу?
Решение. Это задачи-шутки. Иногда, прочитав условие задачи, учащиеся сразу начинают вычислять. Эти задачи показывают, что довольно часто бывает полезно сначала поразмышлять над условиями задачи.
а) 1) 60 + 80 = 140 (км/мин) — скорость сближения;
2) 140 1 = 140 (км) — расстояние, на котором были поезда друг от друга за 1 ч до встречи.
Лишнее условие в задаче — 900 км.
б) В момент встречи они будут на одинаковом расстоянии от села.
556. Старинная задача. Из Москвы в Тверь вышли одновременно 2 поезда. Первый проходил в час 39 вёрст и прибыл в Тверь двумя часами раньше второго, который проходил в час 26 вёрст. Сколько вёрст от Москвы до Твери?
Решение. 1) 39 – 26 = 13 (вёрст) — на столько отставал второй поезд от первого за каждый час;
2) 26 2 = 52 (версты) — на столько отстал второй поезд за всё время движения;
3) 52 13 = 4 (ч) — время движения первого поезда; 4) 39 4 = 156 (вёрст) — от Москвы до Твери.
560. Пассажир метро, стоящий на ступеньке эскалатора, поднимается вверх за 3 мин. Если он идёт вверх, то поднимается за 2 мин.
С какой скоростью идёт пассажир метро, если длина эскалатора 150 м? Решение. 1) 150 3 = 50 (м/мин) — скорость эскалатора;
2) 150 2 = 75 (м/мин) — скорость пассажира, идущего по движущемуся вверх эскалатору;
3) 75 – 50 = 25 (м/мин) — скорость пассажира, идущего по стоящему эскалатору.
Ответ. 25 м/мин.
561. Папа и сын плывут на лодке против течения. В какой-то момент сын уронил за борт папину шляпу. Только через 15 мин папа заметил пропажу. Как далеко друг от друга в этот момент находились лодка и шляпа, если собственная скорость лодки 8 км/ч, а скорость течения 3 км/ч? Нет ли в задаче лишних данных?
Решение. Для ответа на вопрос «Как далеко...?» выражать 8 км/ч в метрах в секунду не следует, так как 8000 «плохо делится» на 60. Можно рассуждать так. За 60 мин они удалились бы на 8 км, а за время, в 4 раза меньшее (60 15 = 4), — на расстояние, в 4 раза меньшее, — на 8 4 = 2 (км). Лишнее условие — скорость течения.
Дополнительное задание. Папа и сын плывут на лодке против течения. В какой-то момент сын уронил за борт папину шляпу. Только через 15 мин папа заметил пропажу. Через сколько минут они догонят шляпу, если сразу повернут лодку и поплывут по течению?
(Собственная скорость лодки постоянна.)
Решение. Так как скорость удаления лодки и шляпы равна
(vс. – vт.) + vт. = vс.,
а скорость сближения лодки и шляпы равна
(vс. + vт.) – vт. = vс.,
то удаление и сближение лодки и шляпы происходило на одно и то же расстояние и с одной и той же скоростью. Поэтому они догонят шляпу за то же время, за которое они удалялись от неё, т. е. за 15 мин.
562.Два поезда движутся навстречу друг другу по параллельным путям — один со скоростью 100 км/ч, другой со скоростью 80 км/ч. Пассажир, сидящий во втором поезде, заметил, что первый поезд шёл мимо него 12 с. Какова длина первого поезда?
Решение. Поезда сближались со скоростью 100 + 80 = 180 (км/ч), или 180000 60 = 3000 (м/мин). Это означает, что за 1 мин (60 с) мимо пассажира мог бы пройти поезд длиной 3000 м. Так как 12 с в 5 раз меньше, чем 60 с, то длина поезда равна 3000 5 = 600 (м).
563.Железнодорожный состав длиной 1 км проходит мимо кило-метрового столба за 1 мин, а через туннель при той же скорости за 3 мин. Какова длина туннеля?
Решение. Чтобы пройти мимо столба, состав должен пройти путь, равный длине состава. На это уходит 1 мин, значит, за 1 мин поезд проходит 1 км. Чтобы пройти туннель, состав должен пройти путь, равный сумме длин туннеля и состава. За 3 мин поезд проходит 3 км, значит, длина туннеля равна 3 – 1 = 2 (км). Ответ. 2 км.
564.а) Из пункта A в пункт B вышел пешеход со скоростью 5 км/ч. Одновременно с ним из A в B выехал велосипедист со скоростью 10 км/ч. Велосипедист доехал до B, повернул назад и поехал с той же скоростью навстречу пешеходу. Через сколько часов после начала движения они встретятся, если расстояние между A и B 30 км?
Решение. Приведём «длинное» решение задачи без пояснений:
|
1) 30 10 = 3 (ч); 3) 30 – 15 = 15 (км); 5) 15 15 = 1 (ч); |
2) 5 3 = 15 (км); 4) 10 + 5 = 15 (км/ч); 6) 3 + 1 = 4 (ч). |
Его можно упростить, заметив, что в задаче речь идёт, по сути дела, о движении навстречу друг другу с удвоенным расстоянием (рис. 30). Тот же ответ получится, если переформулировать условие задачи так:
Расстояние между пунктами A и B равно 60 км. Из пункта A в пункт B вышел пешеход со скоростью 5 км/ч. Одновременно с ним из B в A выехал велосипедист со скоростью 10 км/ч. Через сколько часов после начала движения они встретятся?
Это редкий пример удачной переформулировки задачи, приводящей к упрощению её решения:
1) 30 2 = 60 (км); 2) 10 + 5 = 15 (км/ч); 3) 60 15 = 4 (ч).
Промежуточный контроль. C–10, C–11.
Материал данного пункта может рассматриваться после изучения главы 2, а может включаться в изучаемые пункты этой главы.
В данном пункте вводятся понятия ломаной линии, многоугольника, равенства многоугольников, выпуклого многоугольника со всей необходимой терминологией.
В задании 577 написано: «Считают, что если многоугольники равны, то их площади равны; если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей составляющих его многоугольников». Это пока единственная основа для рассуждений о площадях многоугольников и их вычислений. А устанавливать равенство фигур можно наложением фигур — сначала реальным: вырезать прямоугольник из бумаги, разрезать его по

диагонали и объяснить, почему два полученных треугольника совпадают (прямые углы совпадут, так как они равны друг другу; стороны треугольников совпадут, так как они являются противоположными сторонами прямоугольника, которые равны), а потом воображаемым наложением фигур.
Замечание. Обратите внимание: надо не убедиться, что два треугольника совпадут (то ли совпадут, то ли нет, а при воображаемом наложении фигур вообще ни в чём убедиться нельзя), а объяснить, почему два полученных треугольника совпадают.
РТ. При изучения материала данного пункта можно использовать задания 193, 194, 197—204. Они нацелены на отработку понятия «равенство многоугольников» и развитие творческих способностей и пространственного воображения.
576. Периметры треугольников BCD, BDE и ABE равны соответственно 20 см, 21 см и 22 см, а периметр пятиугольника ABCDE равен 31 см (рис. 31). Определите длины диагоналей BD и BE, если известно, что они равны.
Решение. Сумма периметров треугольников BCD, BDE и ABE равна 20 + 21 + 22 = 63 см. Она равна сумме периметра пятиугольника ABCDE и удвоенных длин равных отрезков BD и BE. Так как 2BD + 2BE = 4BD, то BD = BE = (63 – 31) 4 = 8 см.
Ответ. 8 и 8 см.
578. В прямоугольнике KLMN диагонали KM и LN пересекаются в точке O (рис. 32). Докажите, что площади треугольников KLO и NMO равны.
Решение. Так как площадь каждого из треугольников KLM и NMK составляет половину площади одного и того же прямоугольника, то
площади этих треугольников равны. Если из этих равных площадей вычесть поровну — вычесть площадь треугольника KNO, то площади оставшихся треугольников KLO и NMO будут равны.
202 (РТ). Изобразите прямоугольник ABMF, имеющий такой же периметр, как шестиугольник ABCDEF. Вычислите периметр шестиугольника ABCDEF (рис. 33, а).
Решение. Идея решения задачи, подсказанная в условии, проста: надо данную фигуру заменить прямоугольником с тем же периметром (рис. 33, б):
P = 2 (3 + 5) = 16 (ед.).
Замечание. Та же идея применяется при выполнении заданий 203 и 204.
В этом пункте учебника рассказывается о старинных мерах длины в России и об истории введения метрической системы мер.
Рис. 33
586.Прямоугольник 4 9 разрежьте на две части так, чтобы из них можно было сложить квадрат.
Решение. Из частей данного прямоугольника требуется сложить квадрат, площадь которого равна 4 9 = 36. Следовательно, сторона квадрата должна быть 6 (62 = 36). На рисунке 34 показано, как это можно сделать.
|
|
|
Рис. 34
587.Из прямоугольника 10 7 вырезали прямоугольник 1 6 (рис. 35). Разрежьте полученную фигуру на две части так, чтобы из них можно было сложить квадрат.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 35
Решение. Из частей данного прямоугольника требуется сложить квадрат, площадь которого равна 10 7 – 1 6 = 64. Следовательно, сторона квадрата должна быть 8 (82 = 64).
На рисунке 36 показано, как это можно сделать.

Работа с заданиями 588—592 подробно описана в книге «Задачи на смекалку» (авторы И. Ф. Шарыгин, А. В. Шевкин).
593. Пол в классе имеет форму прямоугольника со сторонами 5 м и 6 м. Если изобразить класс на плане с уменьшением сторон в 10 раз, то во сколько раз площадь класса на этом плане будет меньше настоящей площади класса?
Решение. I способ. Очевидно, что план класса в длину и в ширину в 10 раз меньше реальных размеров класса, т. е. «длина на плане» 10 раз укладывается в длине класса. А «ширина на плане» 10 раз укладывается в ширине класса. Значит, на пол класса можно уложить 100 планов класса. Это означает, что площадь класса на плане в 100 раз меньше реальной площади класса.
II способ. Длина и ширина класса на плане равны 50 см и 60 см, а площадь равна 50 60 = 3000 (см2). Реальная площадь класса равна 500 600 = 300000 (см2), что в 300000 3000 = 100 (раз) больше.
ГЛАВА 3
В данной главе изучаются делимость натуральных чисел, признаки делимости, вводятся понятия простого числа, составного числа, разложения числа на простые множители. Этой главой завершается изучение натуральных чисел и закладываются основы вычислений с обыкновенными дробями.
Здесь продолжается работа по формированию умений проводить доказательства. Особое внимание следует обратить на мотивацию доказательств, так как этот вид деятельности ещё мало знаком учащимся.
Доказательство утверждений проводится на числовых примерах, но таким способом, что если заменить числа буквами, то получится общее доказательство утверждений. Цели изучения главы:
сформировать у учащихся умение проводить простые доказательные рассуждения и подготовить их к изучению обыкновенных дробей; продолжить развитие математического языка и логического мышле-
ния учащихся в процессе доказательства несложных утверждений.
В данном пункте учебника вводятся четыре свойства делимости, доказательство которых проводится на конкретных числовых примерах. На понимание этих свойств учащимися надо обратить особое внимание, так как они будут применяться в доказательствах признаков делимости. Обратите внимание на задания 601—605 учебника, которые пока что являются сложными для учащихся, так как требуют выполнения деления для получения ответа на поставленный вопрос. После изучения признаков делимости в пункте 3.2 эти задачи станут простыми.
601. в) Объясните, почему сумма 13 a + 13 c делится на 13, где a и c — натуральные числа.
Решение. I способ. Так как 13 делится на 13, то и каждое из произведений 13 a и 13 c делится на 13 (по свойству 1). Так как числа 13 a и 13 c делятся на 13, то и их сумма делится на 13 (по свойству 3), что и требовалось доказать.
II способ. Применив распределительный закон, перепишем сум- му 13 a + 13 c в виде произведения: 13 a + 13 c = 13 (a + c). Так как 13 делится на 13, то и произведение 13 (a + c) делится на 13 (по свойству 1). Тогда и равная ему сумма 13 a + 13 c делится на 13, что и требовалось доказать.
602. а) Докажите, что если a, b и c — натуральные числа, то (3 a + 3 b) 3 = a + b.
Решение. Так как произведение частного a + b и делителя 3 равно
3 (a + b) и равно делимому (3 a + 3 b), то равенство
(3 a + 3 b) 3 = a + b
верно.
В данном пункте учебника на конкретных числовых примерах доказываются признаки делимости на 10, на 5, на 2, на 9 и на 3. Признаки делимости на 10, на 5 и на 2 лучше изучать отдельно от признаков делимости на 9 и на 3, чтобы не запутать слабых учащихся. В формулировках признаков используется оборот «число оканчивается цифрой...», заменяющий более сложный оборот «десятичная запись числа заканчивается цифрой...» (речь идёт о цифре разряда единиц в десятичной записи числа).
В тексте учебника имеются краткие ссылки на свойства 1—4 из
п. 3.1, однако при обсуждении доказательств с классом нужно делать содержательные ссылки, говоря не «по свойству 1», а «так как один из множителей делится на 10, то и произведение делится на 10». Это надо делать по двум причинам. Во-первых, для лучшего понимания учащимися сути доказательства, во-вторых, для развития речи учащихся и обучения их доказательствам. Отметим, что некоторые учащиеся обычно быстро запоминают, в чём заключаются свойства 1—4, но не стоит торопить более слабых учащихся, которые могут стать ещё слабее, если не будут понимать того, о чём говорят в классе.
РТ. В начале изучения темы можно использовать задания 230—239, выбирая сначала задания на признаки делимости на 10, на 5 и на 2.
616. Докажите, что произведение чётного числа и любого натурального числа есть число чётное.
Доказательство. Так как чётное число делится на 2, то произведение его и любого натурального числа делится на 2, т. е. произведение — число чётное, что и требовалось доказать.
624. Саша купил в магазине 20 тетрадей, 2 альбома для рисования, авторучку за 6 р., несколько карандашей по 60 к. и несколько обложек для книг по 1 р. 20 к. Продавец сказал, что нужно заплатить в кассу 34 р. 25 к. Саша попросил пересчитать стоимость покупки, и ошибка была исправлена. Как он определил, что продавец ошибся в подсчётах?
Решение. Так как или число купленных предметов чётное, или цена одного предмета чётная, то стоимость каждой покупки чётная. Поэтому и сумма стоимостей этих покупок должна быть чётной. А продавец сказал, что нужно уплатить нечётную сумму. Эту ошибку и определил Саша.
629. б) Докажите, что нельзя подобрать пять нечётных чисел, сумма которых равна 100.
Доказательство. Так как сумма двух нечётных чисел чётная, то сумма первой пары нечётных чисел чётная, сумма второй пары нечётных чисел тоже чётная. Тогда сумма первых четырёх нечётных чисел чётная (при любом выборе этих чисел). Если к этой чётной сумме прибавить пятое нечётное число, то в результате получим нечётное число, которое не может быть равным чётному числу 100.
В данном пункте учебника вводятся понятия простого и составного чисел, подчёркивается, что число 1 не относится ни к простым, ни к составным числам. Утверждение «Каждое натуральное число p делится на 1 и само на себя:
p 1 = p, p p = 1»
сформулировано для любого натурального числа p, большего 1 (если p = 1, то равенства повторяют друг друга).
Утверждение о том, что простых чисел бесконечно много, можно не доказывать, так как оно будет доказано в 7 классе.
РТ. В начале изучения темы можно использовать задание 242.
640.Докажите, что, кроме числа 2, не существует других чётных простых чисел.
Доказательство. Так как любое чётное число, кроме числа 2, делится на 1, на 2 и на себя, то оно не является простым. Следовательно, кроме числа 2, не существует других чётных простых чисел.
641.Можно ли простое число записать в виде суммы: а) двух чёт-ных чисел; б) двух нечётных чисел; в) чётного и нечётного чисел?
Решение. а) Простое число нельзя записать в виде суммы двух чётных чисел, так как эта сумма чётная и больше 2 и поэтому не равна простому числу.
б) Только одно простое число можно записать в виде суммы двух
нечётных чисел: 2 = 1 + 1. Сумма любых других нечётных чисел чётная и больше 2 и поэтому не равна простому числу.
в) Любое простое число, большее 2, — это нечётное число, его мож-
но представить в виде суммы чётного и нечётного чисел. Например, 5 = 4 + 1, 37 = 34 + 3, а простое число 2 нельзя записать в виде суммы чётного и нечётного чисел.
642.а) Может ли сумма двух простых чисел быть простым числом?
б) Верно ли, что сумма любых двух простых чисел является про-
стым числом?
Решение. а) Да, например 2 + 3 = 5. Числа 2, 3 и 5 простые.
б) Нет, например 3 + 5 = 8. Числа 3 и 5 простые, а число 8 составное.
В данном пункте учебника вводятся понятия делителя натурального числа, простого делителя, разложения составного числа на простые множители. Обратим внимание на то, что учащиеся должны овладеть разложением составного числа на простые множители с помощью вертикальной черты, однако увлекаться этой работой для больших чисел не нужно, так как после изучения следующих тем (НОД и НОК) это умение будет применяться редко.
РТ. В начале изучения темы можно использовать задания 240, 241, 250, 251. В задании 250 показан другой приём разложения натурального числа на простые множители. Задача 252 не является обязательной. Это пример задачи на математические игры, здесь для поиска выигрышной стратегии используется понятие делимости.
Дополнение. В пункте 3.4 определено, что значит разложить составное число на простые множители. Можно добавить, что составное число можно записать в виде произведения степеней различных его простых делителей (в том числе и степеней с показателем 1).
Каждое простое число можно записать в виде степени с показателем 1. Например, 3 = 31, 11 = 111, 47 = 471. Правые части этих равенств также называют разложением простого числа на простые множители.
После этих замечаний можно сформулировать основную теорему арифметики: каждое отличное от 1 натуральное число можно разложить на простые множители, и такое разложение единственно. Любые два разложения данного натурального числа на простые множители содержат одинаковые простые множители в одинаковых степенях, следовательно, они могут различаться только порядком множителей.
655. а) Запишите число 32 в виде произведения двух множителей всеми возможными способами.
Решение. 32 = 1 32 = 2 16 = 4 8 = 8 4 = 16 2 = 32 1.
Не будет ошибкой и такое решение: 32 = 1 32 = 2 16 = 4 8, если указать, что изменение порядка множителей не учитывается.
659.а) Подберите такие натуральные числа a и b, чтобы выполнялось равенство: 3 a + 6 b = 1998.
б) Почему нельзя подобрать такие натуральные числа a и b, чтобы
выполнялось равенство: 3 a + 6 b = 1999?
в) Можно ли подобрать такие натуральные числа a и b, чтобы вы-
полнялось равенство: 18 a + 81 b = 996?
Решение. а) Перепишем данное равенство в виде
3 (a + 2 b) = 3 666.
Подберём числа a и b, такие, чтобы выполнялось равенство a + 2 b = = 666. Например, возьмём самое маленькое b = 1, тогда a = 664, или возьмём самое маленькое a = 2, тогда b = 332.
б) При любых натуральных числах a и b левая часть равенства 3 a + + 6 b = 1999 делится на 3, а правая нет, поэтому нельзя подобрать такие натуральные числа a и b, чтобы выполнялось это равенство.
в) При любых натуральных числах a и b левая часть равенства 18 a + 81 b = 996 делится на 9, а правая нет, поэтому нельзя подобрать такие натуральные числа a и b, чтобы выполнялось это равенство.
660.а) Представьте число 8 в виде произведения нескольких мно-жителей так, чтобы сумма этих множителей была равна 8.
Решение. Так как 8 = 4 2, а 4 + 2 меньше числа 8 на две единицы, то добавим в произведение два множителя 1 (произведение не изменится, а сумма станет равной 8): 8 = 4 2 1 1, 4 + 2 + 1 + 1 = 8. Но можно и так: 8 = 2 2 2 1 1, 2 + 2 + 2 + 1 + 1 = 8.
252 (РТ). Имеется куча, сложенная из k камней. Двое игроков по очереди берут из неё камни. Выигрывает тот, кто берёт последний камень. Определите, может ли выиграть первый игрок при правильной игре второго по каждому из трёх правил игры. П р а в и л о 1. За один ход берут по одному камню.
а) k = 6; б) k = 7; в) k = 19;
г) k = 20; д) k = 2n; е) k = 2n + 1.
П р а в и л о 2. За один ход берут один или два камня.
а) k = 6; б) k = 7; в) k = 8;
г) k = 3n; д) k = 3n + 1; е) k = 3n + 2.
П р а в и л о 3. За один ход берут один, два или три камня.
а) k = 8; б) k = 9; в) k = 10; г) k = 11;
д) k = 4n; е) k = 4n + 1; ж) k = 4n + 2; з) k = 4n + 3.
Решение. П р а в и л о 1. При игре по этому правилу у каждого из игроков нет выбора — они каждый раз берут по одному камню. Исход игры здесь зависит не от ходов игроков, а только от того, кто из них первым делает ход.
Если камней 6, 20, 2n (n — натуральное число), то после каждого хода первого игрока остаётся нечётное число камней, поэтому завершающим ходом второй выиграет партию. В этих случаях первый игрок не сможет выиграть партию.
Если же камней 7, 19, 2n + 1 (n — натуральное число), то после каждого хода первого игрока остаётся чётное число камней, поэтому завершающим ходом он выиграет партию. В этих случаях первый игрок выиграет партию.
П р а в и л о 2. Если камней 6, 3n (n — натуральное число), то первый игрок не может выиграть при правильной игре второго. Сколько бы камней (1 или 2) ни брал первый игрок, второй всегда может своим ходом оставить число камней, делящееся на 3. Поэтому перед последним ходом первого игрока второй может оставить 3 камня и закончить игру после любого хода первого игрока.
Во всех остальных случаях первый игрок первым ходом должен оставить число камней, делящееся на 3. А дальше после каждого хода второго игрока он может оставлять число камней, делящееся на 3. После того как останется 3 камня, второй возьмёт 1 или 2 камня, а первый закончит игру. В этих случаях первый игрок может выиграть при любой игре второго. В таких случаях говорят, что у первого игрока имеется выигрышная стратегия.
П р а в и л о 3. Если камней 8, 4n (n — натуральное число), то первый игрок не может выиграть при правильной игре второго. Сколько бы камней (1, 2 или 3) ни брал первый игрок, второй всегда может своим ходом оставить число камней, делящееся на 4. Поэтому перед последним ходом первого игрока второй может оставить 4 камня и закончить игру после любого хода первого игрока.
Во всех остальных случаях первый игрок первым ходом должен оставить число камней, делящееся на 4. А дальше после каждого хода второго игрока он может оставлять число камней, делящееся на 4. После того как останется 4 камня, второй возьмёт 1, 2 или 3 камня, а первый закончит игру. В этих случаях первый игрок может выиграть при любой игре второго. В таких случаях говорят, что у первого игрока имеется выигрышная стратегия.
В данном пункте учебника вводятся понятия общего делителя двух натуральных чисел, наибольшего общего делителя двух натуральных чисел, взаимно простых чисел. Учащиеся лучше усвоят сложение и вычитание дробей с разными знаменателями, если уже сейчас научатся устанавливать, какие два натуральных числа являются взаимно простыми. В учебнике утверждается, что два различных простых числа, а также два соседних натуральных числа взаимно простые. Можно добавить, что если из двух натуральных чисел одно простое, а другое на него не делится, то эти числа взаимно простые. Доказательства этих утверждений просты. Приведём их.
У любых двух простых чисел имеется только один общий делитель — число 1. Поэтому эти числа взаимно простые. (Это решение задачи 670.)
Разность двух соседних натуральных чисел равна 1. Если предположить, что эти числа имеют общий делитель, отличный от 1, то на него должно делиться число 1. Но 1 не делится ни на одно натуральное число, отличное от 1. Поэтому два соседних натуральных числа взаимно простые. (Это решение задачи 671.)
Если из двух натуральных чисел одно простое, а другое на него не делится, то у этих чисел есть только один общий делитель — число 1.
Поэтому эти числа взаимно простые.
Отметим, что увлекаться решением сложных задач на нахождение НОД двух (и более) чисел не следует, так как это умение будет применяться редко. Но учащиеся должны хорошо усвоить, что:
если натуральные числа a и b взаимно простые, то НОД (a, b) = 1; если натуральное число a делится на b, то НОД (a, b) = b.
РТ. При изучении этой темы можно использовать задания 253—259.
676. а) Даны разложения чисел a и b на простые множители. Найдите НОД (a, b): a = 23 34 5 72, b = 22 35 52 7.
Решение. НОД (a, b) должен содержать все общие делители чисел a и b, поэтому НОД (a, b) = 22 34 5 7 (вычислять это произведение не нужно).
678. Для участия в эстафете нужно разделить 36 девочек и 24 мальчика на команды с одинаковым числом участников, состоящие только из мальчиков или только из девочек. Какое наибольшее число участников может быть в каждой команде? Сколько команд получится?
Решение. НОД (36, 24) = 12, поэтому 12 — наибольшее число участников в каждой команде. Получится 36 12 + 24 12 = 5 команд с наибольшим числом участников.
В данном пункте учебника вводятся понятия общего кратного двух натуральных чисел, наименьшего общего кратного двух натуральных чисел.
Отметим, что увлекаться решением сложных задач на нахождение НОК двух (и более) чисел не следует, так как это умение будет применяться редко. Но учащиеся должны хорошо усвоить, что:
если натуральные числа a и b взаимно простые, то НОК (a, b) = ab; если натуральное число a делится на b, то НОК (a, b) = a.
РТ. При изучении этой темы можно использовать задания 260—268.
694. а) Даны разложения чисел a и b на простые множители. Найдите НОД (a, b) и НОК (a, b): a = 23 34 5, b = 24 35 52.
Решение. НОД (a, b) = 23 34 5; НОК (a, b) = 24 35 52.
699. Из двух сцепленных шестерёнок одна имеет 16 зубцов, а другая — 28 зубцов. До начала вращения шестерёнок соприкасающиеся зубцы пометили мелом. Через какое наименьшее число оборотов каждой шестерёнки метки будут совпадать?
Решение. Так как НОК (16, 28) = 112, то первая шестерёнка должна сделать 112 16 = 7 оборотов, а вторая шестерёнка — 112 28 = 4 оборота.
Ответ. 7 оборотов и 4 оборота.
Промежуточный контроль. C–12.
В данном пункте учебника рассмотрены решения задач, в которых используется идея чётности чисел. Здесь рассмотрена задача о рисовании так называемых уникурсальных фигур (которые рисуются без отрыва карандаша от бумаги).
701.Некто утверждает, что знает 4 натуральных числа, произведе-ние и сумма которых — нечётные числа. Не ошибается ли он?
Решение. Ошибается, так как если произведение натуральных чисел нечётное, то все эти четыре числа нечётные, тогда их сумма должна быть чётной.
702.Имеется 9 листов бумаги. Некоторые из них разорвали или на 7, или на 9 частей. Некоторые из образовавшихся частей разорвали или на 7, или на 9 частей, и так несколько раз. Можно ли после нескольких таких операций получить 100 частей?
Решение. Если рвать лист на 7 или 9 частей, то число кусков бумаги будет увеличиваться на 6 или на 8, т. е. на чётное число. Если к нечётному числу 9 прибавить несколько раз чётное число, то получится нечётное число. Число 100 получить невозможно. Поэтому, имея 9 кусков (листов) бумаги и увеличивая их число на 6 или на 8, невозможно получить 100 кусков бумаги.
703.Записано четыре числа: 0, 0, 0, 1. За один ход разрешается прибавить 1 к любым двум из этих чисел. Можно ли за несколько ходов получить 4 равных числа?
Решение. Прибавляя по 1 сразу к двум числам, мы на 2 увеличиваем первоначальную нечётную сумму 0 + 0 + 0 + 1 = 1. В результате каждой такой операции получится нечётное число. Четыре одинаковых числа (т. е. чётную сумму) получить невозможно.
711. Экскурсоводу нужно выбрать маршрут по залам музея так, чтобы обойти все залы, не проходя ни через одну дверь дважды. Где нужно начать и где закончить осмотр? Найдите один из возможных маршрутов (рис. 37).
Решение. Среди залов музея есть только два — 5-й и 8-й, имеющие нечётное число дверей. Следовательно, начать экскурсию в соответст-
вии с условиями задачи можно в одном из них, а закончить в другом. В остальных залах чётное число дверей — они будут пройдены по одному разу, а 6-й и 7-й залы (в которых по 4 двери) — два раза. Возможный маршрут: 5, 1, 2, 6, 5, 9, 10, 6, 7, 11, 12, 8, 4, 3, 7, 8.
В данном пункте учебника приведены сведения о простых числах, о решете Эратосфена, «формула» простых чисел Л. Эйлера, сформулированы некоторые решённые и нерешённые задачи, связанные с простыми числами.
714. а) Почему после «просеивания» чисел, кратных 2, 3, 5, 7, в таблице натуральных чисел от 1 до 100 остались только простые числа?
б) На каком числе следует остановить «просеивание», если в таб-
лице будет 150; 10000 первых натуральных чисел?
Решение. а) Когда среди первых 100 натуральных чисел вычеркнули те, которые кратны простым числам 2, 3, 5, 7, вычеркнуты ми оказались числа, кратные натуральным числам от 2 до 10. При этом в таблице будут вычеркнуты все составные числа, так как наименьшее составное число, не делящееся ни на одно из натуральных чисел от 2 до 10, есть 11 11 = 121, но оно больше 100, и в таблице его нет.
б) Если чисел будет 150, то «просеивание» надо остановить на про-
стом числе 11, так как при этом все числа, кратные натуральным числам от 2 до 12, окажутся вычеркнутыми. В этом случае в таблице будут вычеркнуты все составные числа, так как наименьшее составное число, не делящееся ни на одно из натуральных чисел от 2 до 12, есть 13 13 = 169, но оно больше 150, и в таблице его нет.
Если же чисел будет 10000, то «просеивание» надо остановить на простом числе 97, так как при этом все числа, кратные натуральным числам от 2 до 100, окажутся вычеркнутыми. В этом случае в таблице будут вычеркнуты все составные числа, так как наименьшее составное число, не делящееся ни на одно из натуральных чисел от 2 до 100, есть 101 101 = 10201, но оно больше 10000, и в таблице его нет.
715. а) Петя придумал новую формулу для нахождения простых чисел: P = n2 + n + 41. Для любых ли натуральных n число P простое?
Решение. Нет. Для простого числа 41 число P = 412 + 41 + 41 делится на 1, на 41 и на P, т. е. число P составное.
718. Я предлагаю товарищу записать (так, чтобы я не видел) любое трёхзначное число, состоящее из различных цифр (без нуля). Пусть он теперь переставит цифры этого числа в любом порядке и получит новое число. Пусть меньшее из этих двух чисел он вычтет из большего числа, зачеркнёт одну цифру в полученной разности и назовёт мне сумму незачёркнутых цифр. Тогда я могу легко определить, какую цифру зачеркнул мой товарищ. Объясните с помощью признака делимости на 9 этот фокус.
![]() Решение. Сначала надо
убедиться, что получаемая разность всегда будет делиться на 9. Пусть дано
трёхзначное число abc = 100a +
10b + c. Переставим цифры этого числа, например, так: bca = 100b + 10c + a.
Решение. Сначала надо
убедиться, что получаемая разность всегда будет делиться на 9. Пусть дано
трёхзначное число abc = 100a +
10b + c. Переставим цифры этого числа, например, так: bca = 100b + 10c + a.
Если первое число больше второго, то их разность abc – bca = 100a + + 10b + c – 100b – 10c – a = 99a – 90b – 9c — натуральное число, оно делится на 9. При других перестановках цифр разности 100a – a, 100a – 10a, 10a – a и др. делятся на 9, поэтому получаемая разность всегда будет делиться на 9.
Теперь зачёркнутую цифру легко определить, так как сумма цифр разности должна делиться на 9.
Например, если задумали число 347, после перестановки цифр получили 473, тогда разность 473 – 347 = 126. Сумма цифр 1 + 2 + 6 делится на 9, а если зачеркнуть, например, 1, то сумма незачёркнутых цифр 2 + 6 = 8. Так как до ближайшего числа, кратного 9, не хвата- ет 1, то зачёркнутая цифра 1.
721. Старший брат выписал из справочника число 15! (см. задачу 719), а Вася случайно поставил в его тетради кляксу на одну цифру. Вот что из этого получилось (рис. 38).
Определите пропавшую цифру без справочника и не вычисляя произведение 1 2 3 ... 15.
Решение. Число 15! делится на 9, так как содержит множитель 9. Сумма оставшихся без кляксы цифр равна
1 + 3 + 0 + 6 + 7 + 4 + 3 + 6 + 8 + 0 + 0 + 0 = 38.
Если под кляксой оказалась одна из цифр: 0, 1, 2, 3, 4, 5, 6, 8, 9, то сумма всех цифр числа 15! окажется равной 38 + 0 = 38, 38 + 1 = 39,
..., 38 + 9 = 47 соответственно. Только одна из этих сумм (38 + 7=45) делится на 9. Следовательно, под кляксой оказалась цифра 7. Ответ. 15! = 1307674368000.
727. Головоломка. Имеется 3 штырька, на один из которых насажены 3 кольца (рис. 39). За сколько ходов можно перенести пирамиду из этих трёх колец на другой штырёк, если за один ход разрешается переносить только одно кольцо; при этом нельзя большее кольцо класть на меньшее? Решите задачу: а) для четырёх колец; б) для пяти колец.
Решение. Это пример задачи, имеющей большой воспитательный потенциал. На её примере можно показать, как математики решение следующей задачи умеют сводить к уже решённой.
Сначала решим задачу для двух колец. Очевидно, что пирамиду из двух колец можно перенести за три хода.
Чтобы перенести пирамиду из трёх колец, сначала перенесём на свободный штырёк пирамиду из двух колец. Для этого требуется 3 хода. Перенесём нижнее кольцо на свободный штырёк. Наконец, опять за 3 хода перенесём пирамиду из двух колец на тот штырёк, где уже находится большее кольцо. Пирамиду из трёх колец можно перенести за 3 + 1 + 3 = 7 ходов.
а) Рассуждая аналогично, пирамиду из четырёх колец перенесём
за 7 + 1 + 7 = 15 ходов.
б) Пирамиду из пяти колец перенесём за 15 + 1 + 15 = 31 ход.
ГЛАВА 4
В этой главе изучаются в полном объёме обыкновенные дроби по плану, намеченному в главе 1. Важно, чтобы каждый учащийся понял, что действия с обыкновенными дробями сводятся к нескольким действиям с натуральными числами. Здесь снова вводятся элемен ты доказательных рассуждений при изучении теоретического материала, а также решение текстовых задач арифметическими способами.
Цели изучения главы:
![]() сформировать у
учащихся осознанные умения выполнять арифметические действия над обыкновенными
дробями;
сформировать у
учащихся осознанные умения выполнять арифметические действия над обыкновенными
дробями;
продолжить развитие математического языка и логического мышления учащихся при изучении теоретического материала и при решении текстовых задач арифметическими методами.
В данном пункте учебника вводятся понятия обыкновенной дроби (коротко: дроби), её числителя и знаменателя, рационального числа. Отмечается, что любое натуральное число считается дробью со знаменателем 1. Первый пункт нацелен на формирование понятия дроби и подготовку учащихся к изучению сравнения дробей и арифметических действий с ними. Здесь решаются простейшие задачи на дроби, ведётся подготовка к решению задач на совместную работу. Поэтому надо особенно внимательно отнестись ко всем заданиям пункта, даже если они кажутся простыми. Однако подводить учащихся к формулировкам правил решения таких задач рано, это можно будет сделать при изучении пункта 4.3. А пока главным объектом изучения является дробь, задачи лишь помогают лучше понять, что показывают её числитель и знаменатель.
РТ. При изучении данного пункта можно использовать задания 269— 281.
745. Из пакета с картофелем, вес которого 3 кг, отсыпали 1 кг. Какая часть картофеля осталась в пакете?
Решение. В пакете осталось 3 – 1 = 2 кг
картофеля, 2 кг составля ют ![]() от 3 кг.
от 3 кг.
747.а) Работу выполнили за 4 ч. Какую часть работы выполняли за каждый час?
Решение. За каждый час
выполняли ![]() часть работы.
часть работы.
748.а)
Путник проходит в час ![]() пути. За сколько часов он пройдёт весь
путь?
пути. За сколько часов он пройдёт весь
путь?
Решение. Путник пройдёт весь путь за 5 ч.
749.а) Два путника вышли одновременно навстречу друг другу и встретились через 3 ч. На какую часть первоначального расстояния они сближались каждый час?
Решение. Путники сближались каждый час на ![]() первоначального
расстояния.
первоначального
расстояния.
Замечание. Задания, аналогичные заданиям 747—749, должны присутствовать в устной работе на ближайших уроках, ответы на них получаются с помощью рассуждений. Лишь после изучения всех действий с дробями эти ответы можно будет получить в результате действий с дробями.
В данном пункте учебника вводится понятие равенства
дробей, на конкретных примерах разъясняется, почему, например, ![]() =
= ![]() .
Вводят ся понятия сокращения дроби и несократимой дроби.
.
Вводят ся понятия сокращения дроби и несократимой дроби.
Обратим внимание, что эти разъяснения, данные для длин
отрезков (можно было бы дать их для кругов, тортов и т. п.), не доказывают
основное свойство дроби, а только иллюстрируют его. Тот факт, что дробь есть
частное её числителя и знаменателя, устанавливает ся пока для того случая,
когда числитель дроби делится нацело на знаменатель. Учащимся можно сказать,
что позднее (после изучения деления дробей) будет доказано, например, что ![]() = 2
3, поэтому дробь
= 2
3, поэтому дробь ![]() иногда читают «2, делённое на 3».
Пытаться проиллюстриро- вать этот факт, например, с помощью двух яблок, которые
хотят раз делить на 3 равные части, сейчас не стоит, так как в данный момент
ещё не известно, что есть результат деления натурального числа 2 на натуральное
число 3. Рассуждения с яблоками можно рассматривать лишь как мотивацию
предстоящего доказательства равенства
иногда читают «2, делённое на 3».
Пытаться проиллюстриро- вать этот факт, например, с помощью двух яблок, которые
хотят раз делить на 3 равные части, сейчас не стоит, так как в данный момент
ещё не известно, что есть результат деления натурального числа 2 на натуральное
число 3. Рассуждения с яблоками можно рассматривать лишь как мотивацию
предстоящего доказательства равенства
2 3 = ![]() .
.
Заметим, что при сокращении дробей на первых порах лучше за- писывать числитель и знаменатель в виде произведения двух чисел (см. решение задачи 775), затем делить числитель и знаменатель на их общий множитель. Такая запись позволяет донести до ученика суть выполняемого действия. Торопить переход ученика к свёрнутой записи сокращения дроби не следует, он сам её освоит, как только во всём разберётся. При этом не надо стремиться к поиску наибольшего общего делителя числителя и знаменателя, пусть ученик сокращает дробь поэтапно. Желание экономить время в конце концов заставит его сокращать числитель и знаменатель дроби на возможно больший множитель.
РТ. При изучении данного пункта можно использовать задания 282— 289.
775. а) Сократите дробь ![]() .
.
Решение. ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
По способам действия задачи, решаемые в данном пункте учебника, знакомы учащимся. Они уже решали такие задачи, знакомясь с понятием дроби. Но в данном пункте они воспринимаются учащимися уже как объект изучения. Для однотипных задач (найти часть целого..., найти целое по его части...) рассматриваются общие способы их решения, формулируются правила решения.
Задачи расположены по нарастанию сложности. Если в задачах 776 и 777 требуется найти часть числа, то для решения следующих задач необходимо выпольнить дополнительные действия (чтобы узнать, сколько всего, сколько осталось и т. п.).
Если учащиеся испытывают затруднения в решении задач, то можно посоветовать им рисовать схематические рисунки, чтобы понять условие задачи и наметить свои действия для её решения. Здесь они могут опираться на умения рисовать отрезок, его часть, выраженную данной дробью, и т. п.
Задания 788—790 на увеличение (уменьшение) данного числа на указанную его часть готовят учащихся к решению аналогичных задач на проценты (6 класс).
РТ. При изучении данного пункта можно использовать задания 296— 303.
777. а) На ветке сидели 12 птиц; ![]() из них
улетели. Сколько птиц
из них
улетели. Сколько птиц
улетело?
Решение. На примере этой задачи покажем применение
схемати- ческого рисунка. Находим ![]() от 12 птиц. Эту величину изобразим от
резком (рис. 40).
от 12 птиц. Эту величину изобразим от
резком (рис. 40).
1) Сколько
птиц приходится на ![]() от числа всех птиц?
от числа всех птиц?
12 3 = 4 (птицы).
2)
Сколько птиц приходится на ![]() от числа всех птиц
(они улетели)?
от числа всех птиц
(они улетели)?
4 2 = 8 (птиц).
Можно объединить эти два действия, записав решение задачи с помощью числового выражения:
12 3 2 = 8 (птиц) — улетели. Ответ. 8 птиц.
780. б) В коллекции 45 юбилейных рублёвых монет.
Число трёх- и пятирублёвых монет составляет ![]() числа рублёвых монет.
Сколько всего юбилейных монет достоинством в один, три и пять рублей в кол
лекции?
числа рублёвых монет.
Сколько всего юбилейных монет достоинством в один, три и пять рублей в кол
лекции?
Решение. Здесь учащихся будет сбивать тот факт, что нельзя определить число трёх- и пятирублёвых монет в отдельности.
1) 45 9 2 = 10 (монет) — число трёх- и пятирублёвых монет; 2) 45 + 10 = 55 (монет) — в один, три и пять рублей. Ответ. 55 монет.
781. а) 12 р. составляют ![]() имеющейся суммы
денег. Какова эта сумма?
имеющейся суммы
денег. Какова эта сумма?
Решение. Находим ![]() от всей суммы (она
неизвестна). Эту величину изобразим отрезком (рис. 41).
от всей суммы (она
неизвестна). Эту величину изобразим отрезком (рис. 41).
Рис. 41
1) Сколько рублей приходится на ![]() от
всей суммы?
от
всей суммы?
12 3 = 4 (р.). 2) Какова вся сумма?
4 4 = 16 (р.).
Можно объединить эти два действия, записав решение задачи с помощью числового выражения:
12 3 4 = 16 (р.). Ответ. 16 р.
784. Из «Арифметики» Л. Ф. Магницкого.
Некто оставил в наследство жене, дочери и трём сыновьям 48000 рублей и завещал
жене ![]() всей суммы, а каждому из сыновей вдвое
больше, чем дочери. Сколь -
всей суммы, а каждому из сыновей вдвое
больше, чем дочери. Сколь -
ко досталось каждому из наследников?
Решение.
1) 48000 8 = 6000 (р.) — жене;
2) 48000 – 6000 = 42000 (р.) — детям;
3) 2 + 2 + 2 + 1 = 7 (частей) — приходится на 42000 р.;
4) 42000 7 = 6000 (р.) — дочери;
5) 6000 2 = 12000 (р.) — каждому сыну.
Ответ. 6000 р., 6000 р., 12000 р., 12000 р., 12000 р.
791. Из папируса Ахмеса (Египет, ок. 2000 лет до н. э.). Приходит пастух с 70 быками. Его спрашивают:
— Сколько приводишь ты из своего многочисленного стада?
Пастух отвечает:
— Я привожу две трети от трети скота.
Сколько быков в стаде?
Решение. Начнём с замечания, что в те давние
годы египтяне ещё не знали дробей, кроме аликвотных (имеющих в числителе
единицу) и дроби ![]() . Только для таких дробей у них были
соответствующие обо значения в виде иероглифов. Поэтому дробь
. Только для таких дробей у них были
соответствующие обо значения в виде иероглифов. Поэтому дробь ![]() выражена в
задаче как
выражена в
задаче как
«две трети от трети».
1) 70 2 3 = 105 (быков) — в трети стада; 2) 105 3 = 315 (быков) — в стаде. Ответ. 315 быков.
Задачи 302, 303 (РТ) по усмотрению учителя можно решить до изучения вычитания дробей (см. I способ) или после изучения вычитания дробей (см. II способ).
302 (РТ). Бригада заасфальтировала
![]() дороги,
и ей осталось заас- фальтировать 25 км. Какова длина дороги?
дороги,
и ей осталось заас- фальтировать 25 км. Какова длина дороги?
I способ. Представим, что длину дороги разбили на 11 равных участков и 6 из них заасфальтировали. Тогда осталось заасфальтировать 11 – 6 = 5 таких участков — их длина 25 км. Отсюда длина дороги равна 25 5 11 = 55 (км).
II способ.
1) 1 – ![]() =
= ![]() (длины дороги) —
осталось заасфальтировать;
(длины дороги) —
осталось заасфальтировать;
2) 25 5 11 = 55 (км) — длина дороги. Ответ. 55 км.
303 (РТ). Туристы проплыли на
байдарках 125 км, и им осталось проплыть ![]() длины всего маршрута.
Какова длина маршрута?
длины всего маршрута.
Какова длина маршрута?
I способ. Представим, что длину маршрута разбили на 32 равных участка, из которых осталось проплыть 7 участков. Тогда уже проплыли 32 – 7 = 25 таких участков — их длина 125 км. Отсюда длина маршрута равна 125 25 32 = 160 (км).
II способ.
1) 1 – ![]() =
= ![]() (длины маршрута) —
проплыли;
(длины маршрута) —
проплыли;
2) 125 25 32 = 160 (км) — длина маршрута. Ответ. 160 км.
Промежуточный контроль. C–13.
В данном пункте учебника вводятся понятия: общий знаменатель, приведение к общему знаменателю, дополнительный множитель. Умение приводить дроби к общему знаменателю лежит в основе сравнения, сложения и вычитания дробей с разными знаменателями. Поэтому это умение должно быть надёжно сформировано.
Прежде всего отметим, что приведение дробей к
наименьшему общему знаменателю не является обязательным требованием, поэтому
отыскание НОК числителя и знаменателя не является обязательным элементом
решения этой задачи. Другое дело, что решение без приведения дробей к
наименьшему общему знаменателю может оказаться неэкономным и потребует
сокращения полученных дробей. В приме- ре 1 показано приведение дробей ![]() и
и ![]() к
знаменателю 8 12 = 96. По- лученные дроби можно сократить. Дальше показано
приведение тех же дробей к знаменателю 24 = НОК (8, 12).
к
знаменателю 8 12 = 96. По- лученные дроби можно сократить. Дальше показано
приведение тех же дробей к знаменателю 24 = НОК (8, 12).
Для поиска наименьших дополнительных множителей двух дробей можно предложить учащимся такое решение (вычисления в простых случаях выполняются устно, а в сложных — на черновике). Разделим знаменатели 8 и 12 на их общий делитель 4, получим 2 и 3 соответственно. Так как 2 и 3 — взаимно простые числа, то 2 — дополнительный множитель второй дроби, а 3 — дополнительный множитель первой дроби.
При записи приведения дробей к общему знаменателю рекомендуем преобразование каждой дроби писать в отдельной строке:
3/
![]() =
= ![]() ,
,
2/
![]() =
= ![]() .
.
Иначе в дальнейшем будет трудно отучать учащихся от неправиль-
3/ 2/
ных записей вида ![]() и
и ![]() =
= ![]() и
и ![]() .
Здесь учащиеся ставят знак «=» как знак перехода к следующему этапу
рассуждения, что в даль- нейшем будет приводить к ошибочным записям решений при
сравнении дробей. Образец правильной записи решения приведён в задании 290
(РТ).
.
Здесь учащиеся ставят знак «=» как знак перехода к следующему этапу
рассуждения, что в даль- нейшем будет приводить к ошибочным записям решений при
сравнении дробей. Образец правильной записи решения приведён в задании 290
(РТ).
В простых случаях наименьший общий знаменатель двух дробей можно искать так. Разделить больший знаменатель на меньший. Если деление выполняется нацело, то делимое и есть наименьший общий знаменатель двух дробей. Если нет, то больший знаменатель умножают на 2, 3, 4, 5, ..., проверяя каждый раз, делится ли произведение на второй знаменатель. Как только произведение разделится на второй знаменатель, то оно и есть наименьший общий знаменатель двух дробей.
В приведённом выше примере 12 не делится на 8, а 12 2 = 24 делится на 8, 24 8 = 3 — дополнительный множитель первой дроби, а 2 — дополнительный множитель второй дроби.
РТ. При изучении данного пункта можно использовать задание 290.
803. Определите, равны ли дроби. Результат запишите с помощью знаков = и .
б) ![]() и
и ![]() ; г)
; г) ![]() и
и ![]() .
.
Решение. б) ![]() =
= ![]() ,
, ![]() =
= ![]() ,
поэтому
,
поэтому ![]() =
= ![]() ;
;
2 3 12 15
![]()
![]()
![]()
![]()
![]() г) = ,
= , так как
г) = ,
= , так как ![]() , то .
, то .
5 5 30 25
Замечание. Надо обращать внимание учащихся, что если дробь сократима, то часто бывает полезно сначала сократить её, а потом выполнять предложенное задание.
Промежуточный контроль. C–14.
В данном пункте учебника вводится правило сравнения дробей. Это определение, с помощью которого сравнивают дроби с общим знаменателем. Как всякое определение, оно не нуждается в доказательстве, но необходимо привести примеры, как в учебнике, чтобы мотивировать появление именно такого определения.
Обратим внимание на то, что в данном пункте в общем виде (на буквах) доказывается, что если первая дробь меньше второй, а вторая дробь меньше третьей, то первая дробь меньше третьей (транзитивность неравенств).
Далее введены понятия правильной и неправильной дробей.
Следует уделить внимание правильной записи при
сравнении дро бей. Например, сравним дроби ![]() и
и ![]() . Сначала
приведём их к общему знаменателю:
. Сначала
приведём их к общему знаменателю:
3/ 2/
3 99 10 3 5
![]()
![]()
![]()
![]() = ,
=. Так как , то .
= ,
=. Так как , то .
8 2424 24 8 12
РТ. Начать работу на закрепление нового материала можно с заданий 291—295, где показан другой вариант записи выполнения таких заданий:
3/ 2/
3 5 3 99 10
![]()
![]()
![]()
![]()
![]() ,
так как = , = и .
,
так как = , = и .
8 12 8 2424 24
При выполнении задания 812 на сравнение дробей с одинаковыми числителями надо подвести учащихся к выводу, который сформулирован в следующей задаче.
813. Докажите, что из двух дробей с равными числителями больше та дробь, у которой знаменатель меньше.
Доказательство. Пусть m n, где m и n — натуральные числа.
n/
1 1 1 n
![]()
![]() Докажем, что m n.
Приведём дроби к общему знаменателю m = mn,
Докажем, что m n.
Приведём дроби к общему знаменателю m = mn,
m/
1 m n m
![]()
![]() n = mn. Из
двух дробей mn
и mn
с общим знаменателем больше та
n = mn. Из
двух дробей mn
и mn
с общим знаменателем больше та
![]() n m дробь, у которой числитель
больше. Так как m n, то mn mn, тогда
n m дробь, у которой числитель
больше. Так как m n, то mn mn, тогда
1 1
![]() m n, что и требовалось доказать.
m n, что и требовалось доказать.
Замечание. Можно ограничиться доказательством для дробей с одинаковым числителем 1 (если обе дроби имеют одинаковые числители k, то из неравенства m n следует неравенство mk nk, но это свойство неравенств в учебнике не доказано). Если учащиеся класса ещё не готовы к восприятию доказательства в общем виде, то можно отметить, что та дробь, у которой знаменатель меньше, получит больший дополнительный множитель, поэтому после приведения дробей к общему знаменателю из неё получится большая дробь.
816.В
некоторых случаях бывает удобно сравнивать не сами дроби, а их «дополнения» до
единицы. Например, сравним дроби ![]() и
и ![]() . Что бы из первой
дроби получить 1, надо добавить
. Что бы из первой
дроби получить 1, надо добавить ![]() , а чтобы из второй дроби получить 1, надо
добавить меньше:
, а чтобы из второй дроби получить 1, надо
добавить меньше: ![]() . Следовательно, вторая
. Следовательно, вторая
7
8 дробь
больше: ![]() .
.
8 9
При выполнении этого задания неявно используется сложение дробей. Опыт учащихся в действиях с долями отрезков, кругов и т. п. позволяет надеяться, что интуитивно учащиеся понимают, о чём идёт речь, и с заданием справятся.
Если есть сомнение, что учащиеся поймут такое решение, то к этому заданию лучше вернуться после изучения сложения дробей.
817.а) Алёша с папой стреляли в тире. Алёша из 10 выстрелов имел 5 попаданий, а папа из 5 выстрелов имел 3 попадания. Чей результат
лучше?
Решение. Попадания Алёши составляют ![]() от всех его
выстрелов,
от всех его
выстрелов,
![]()
![]()
![]() 6 5 а попадания
папы — . Так как = и
6 5 а попадания
папы — . Так как = и ![]() , то
результат папы
, то
результат папы
10 10
лучше.
818.а)
Найдите все дроби со знаменателем 10, которые больше ![]() ,
,
но меньше ![]() .
.
Решение. Учащиеся могут решить эту задачу,
перебирая подряд дро- би со знаменателем 10, начиная с дроби ![]() , которая
меньше дроби
, которая
меньше дроби ![]() , и кончая дробью
, и кончая дробью ![]() , которая больше дроби
, которая больше дроби
![]() .
Затем, убедившись, что
.
Затем, убедившись, что
5 5 6 7 7 8
![]() ,
,
10 9 10 10 9 10
найти, что таких дробей две: ![]() и
и ![]() .
.
А могут привести данные дроби к знаменателю 90: ![]() =
= ![]() ,
, ![]() =
= ![]() —
и из дробей со знаменателем 90, заключённых между
—
и из дробей со знаменателем 90, заключённых между ![]() и
и ![]() , т. е. из
дробей
, т. е. из
дробей ![]() ,
, ![]() , ...,
, ..., ![]() ,
, ![]() ,
выбрать те, числитель которых делится на 9. Таких дробей всего две:
,
выбрать те, числитель которых делится на 9. Таких дробей всего две: ![]() и
и ![]() .
Сократив каждую из этих дробей на 9, получим две искомые дроби:
.
Сократив каждую из этих дробей на 9, получим две искомые дроби: ![]() и
и ![]() .
.
Ответ. ![]() и
и ![]() .
.
Промежуточный контроль. C–15.
В данном пункте учебника вводятся правила сложения для дробей с общим знаменателем и дробей с разными знаменателями.
Обратим внимание на то, что если знаменатели двух дробей — взаимно простые числа, то общим знаменателем этих дробей будет произведение их знаменателей и сложение дробей выполняется по формуле
p r p s r q +
q
![]() +
s = q s .
(1)
+
s = q s .
(1)
Если знаменатели двух дробей не являются взаимно простыми числами (имеют общий делитель, отличный от 1), то по формуле (1) также можно получить верный ответ, но полученная дробь обязательно будет сократимой.
Мы не считаем необходимым требовать от слабого ученика приведения дробей к наименьшему общему знаменателю, но если он вычисляет сумму по формуле (1), то должен не забывать сокращать полученную дробь.
Если знаменатели двух дробей не являются взаимно простыми числами, то при отыскании общего знаменателя этих дробей можно поступать разными способами. Покажем это на примерах.
8/4/ 5/
1) ![]() +
+ ![]() =
= ![]() +
+ ![]() =
= ![]() .
2)
.
2) ![]() +
+ ![]() =
= ![]() +
+ ![]() =
= ![]() .
.
В первом случае один знаменатель делится на другой и является общим знаменателем этих дробей, дополнительный множитель первой дроби находим делением: 24 3 = 8.
Во втором случае для нахождения общего знаменателя данных дробей можно убедиться, что 30 не делится на 24, 30 2 = 60 не делится на 24, 30 3 = 90 не делится на 24, а 30 4 = 120 делится на 24 и 120 24 = 5 — дополнительный множитель второй дроби, а 120 30 = 4 — дополнительный множитель первой дроби.
![]() Но можно начать с
отыскания дополнительных множителей дробей. Разделим знаменатели дробей 30 и 24
на их общий делитель 2, получим числа 15 и 12. Теперь разделим числа 15 и 12 на
их общий делитель 3, получим 5 и 4 — взаимно простые числа. Они и являются
дополнительными множителями данных дробей. Если ученик сразу заметит, что 30 и
24 имеют общий делитель 6, то он быстрее придёт к нужному результату. Чтобы
этим вычислениям добавить опору на зрительное восприятие, можно в сторонке или
под знаменателями данных дробей делать запись, необходимость в которой после
достаточной тренировки отпадёт. Числа 15, 12, 5 и 4 удобно писать на черновике,
приложенном под знаменатели написанных дробей (рис. 42). Рис. 42
Но можно начать с
отыскания дополнительных множителей дробей. Разделим знаменатели дробей 30 и 24
на их общий делитель 2, получим числа 15 и 12. Теперь разделим числа 15 и 12 на
их общий делитель 3, получим 5 и 4 — взаимно простые числа. Они и являются
дополнительными множителями данных дробей. Если ученик сразу заметит, что 30 и
24 имеют общий делитель 6, то он быстрее придёт к нужному результату. Чтобы
этим вычислениям добавить опору на зрительное восприятие, можно в сторонке или
под знаменателями данных дробей делать запись, необходимость в которой после
достаточной тренировки отпадёт. Числа 15, 12, 5 и 4 удобно писать на черновике,
приложенном под знаменатели написанных дробей (рис. 42). Рис. 42
В упражнениях к данному пункту приведены текстовые зада чи, решение которых сводится к сложению обыкновенных дробей. Задание 843 готовит учащихся к решению задач на совместную работу.
РТ. При изучении данного пункта можно использовать задания 304— 307.
840. Девочка прочитала ![]() книги, потом ещё
книги, потом ещё ![]() .
Какую часть книги она прочитала?
.
Какую часть книги она прочитала?
Решение. ![]() +
+ ![]() =
= ![]() (книги)
— прочитала девочка.
(книги)
— прочитала девочка.
ж
Дополнительный вопрос. Всю ли книгу прочитала девочка? зОтвет.
и
3 ц
Нет,
так как ![]() 1ч.
1ч.
5 ш
843. в) Легковая машина в час проезжает ![]() расстояния
между городами, а грузовая —
расстояния
между городами, а грузовая — ![]() этого расстояния. На какую часть этого
расстояния в час будут сближаться машины при движении навстречу друг другу?
этого расстояния. На какую часть этого
расстояния в час будут сближаться машины при движении навстречу друг другу?
Решение. ![]() +
+ ![]() =
= ![]() +
+ ![]() =
= ![]() (расстояния)
— на такую часть рас стояния в час будут сближаться машины при движении
навстречу друг другу.
(расстояния)
— на такую часть рас стояния в час будут сближаться машины при движении
навстречу друг другу.
В данном пункте учебника вводятся переместительный и сочетательный законы сложения для дробей. Обратим внимание на то, что эти законы доказываются для конкретных дробей (с одинаковыми знаменателями), но так, что если вместо чисел в числителях и знаменателях поставить буквы, то получится их полное доказательство со ссылкой на соответствующие законы для натуральных чисел.
Если на уроке провести доказательство закона для одной пары дробей, затем для другой пары дробей (с одинаковыми знаменателями), то сильный ученик должен повторить это доказательство для дробей, числитель и знаменатель которых обозначены буквами. При этом полезно выяснить, на что делается ссылка при доказательстве (на правило (определение) сложения дробей и на соответствующий закон для натуральных чисел).
Задание 859 готовит учащихся к решению задач на совместную работу.
858.
а) Вычислите: ![]() +
+ ![]() +
+ ![]() +
+ ![]() .
.
1 3 1 1 ж1 1ц ж3 1ц 2 2 5 7
![]()
![]() Решение. + + + =
з + ч + з + ч = +
1 = + = .
Решение. + + + =
з + ч + з + ч = +
1 = + = .
5 4 5 4 и5 5ш и4 4ш 5 5 5 5
859.
Старинные задачи. б) Для постройки купальни наняты три
плотника. Первый сделал в день ![]() всей работы, второй —
всей работы, второй — ![]() , тре тий —
, тре тий — ![]() .
Какую часть всей работы сделали все они за день?
.
Какую часть всей работы сделали все они за день?
в) Для переписки сочинения наняты 4 писца. Первый мог бы один переписать сочинение за 24 дня, второй — за 36 дней, третий — за 20 дней и четвёртый — за 18 дней. Какую часть сочинения перепишут они за один день, если будут работать вместе?
Решение. б) ![]() +
+ ![]() +
+ ![]() =
= ![]() +
+ ![]() +
+ ![]() =
= ![]() (работы)
— такую часть всей работы сделали все они за день.
(работы)
— такую часть всей работы сделали все они за день.
в) Сначала определим, что первый мог бы в день
переписать ![]() со чинения, второй —
со чинения, второй — ![]() , третий —
, третий — ![]() и
четвёртый —
и
четвёртый — ![]() . Тогда за один день совместной работы они
перепишут
. Тогда за один день совместной работы они
перепишут
![]() +
+ ![]() +
+ ![]() +
+ ![]() =
=
ж 1 1 ц ж 1 1 ц
![]() =
з + ч + з + ч =
и24
20ш и36 18ш
=
з + ч + з + ч =
и24
20ш и36 18ш
ж 5 6 ц ж 1 2 ц
= з + ч + з + ч = и120 120ш и36 36ш
= ![]() +
+ ![]() =
= ![]() +
+ ![]() =
= ![]() +
+ ![]() =
= ![]() =
= ![]() .
.
Обратим внимание, что применение законов сложения и сокращения дробей позволило приводить дроби к знаменателю 120, а не 360.
860. Отпили полчашки чёрного кофе и долили её
молоком. Потом отпили ![]() чашки и долили её молоком. Потом отпили
чашки и долили её молоком. Потом отпили ![]() чашки
и до- лили её молоком. Наконец, допили содержимое чашки до конца. Чего выпили
больше: кофе или молока?
чашки
и до- лили её молоком. Наконец, допили содержимое чашки до конца. Чего выпили
больше: кофе или молока?
Решение. При решении этой задачи учащиеся часто путаются в ненужных промежуточных подсчётах. Надо посоветовать им подсчитать,
![]() ж1 1 1ц сколько молока долили в кофе за 3 раза з + + ч, и сравнить это
коли-
ж1 1 1ц сколько молока долили в кофе за 3 раза з + + ч, и сравнить это
коли-
и2 3 6ш
чество с первоначальным количеством чёрного кофе. Получится, что кофе и молока выпили поровну — по одной чашке.
В данном пункте учебника вычитание дробей определяется как операция, обратная сложению. При вычитании равных дробей получается нуль, но из меньшей дроби нельзя вычесть большую и получить положительную дробь.
Обратим внимание на то, что если знаменатели двух дробей — взаимно простые числа, то общим знаменателем этих дробей будет произведение знаменателей и вычитание дробей выполняется по формуле
p r p s r q –
q
![]() –
s = q s .
(1)
–
s = q s .
(1)
Если знаменатели двух дробей не являются взаимно простыми числами (имеют общий делитель, отличный от 1), то по формуле (1) также можно получить верный ответ, но полученная дробь обязательно будет сократимой.
Мы не считаем необходимым требовать от слабого ученика приведения дробей к наименьшему общему знаменателю, но если он вычисляет разность по формуле (1), то он должен не забывать сокращать полученную дробь.
Рекомендации по поиску общего знаменателя дробей или дополнительных множителей при вычитании дробей те же, что и при сложении.
Обратим внимание на задание 870, где требуется найти число x, для которого верно равенство. В учебнике такие задания не формулируются как задания на решение уравнений, так как уравнения будут изучаться позже, но если учащиеся класса владеют терминами «корень уравнения», «решить уравнение», если они решали в начальной школе многоходовые задания по поиску корня уравнения (например, такого: 98 – (49 – x) = 50), то аналогичные задачи можно давать сильным учащимся и для дробей. Только следует иметь в виду, что использовать шесть правил нахождения компонентов арифметических действий (неизвестного слагаемого, ...) имеет смысл лишь для развития речи учащихся, а с точки зрения решения уравнений эти правила находят применение на короткое время — до изучения правил раскрытия скобок, правила переноса слагаемого в другую часть уравнения с противоположным знаком. Поэтому увлекаться заданиями такого рода и перегружать ими слабых учащихся не следует.
Что касается текстовых задач, то они усложняются: в одних случаях для решения задачи придётся из единицы вычитать дробь, в дру гих — к единице прибавлять дробь. Часто лучшему восприятию условий задачи помогают схематические рисунки. Делать их полезно, но не обязательно, если ученик и без рисунка справляется с задачей.
Задание 881 готовит учащихся к решению задач на совместную работу.
РТ. При изучении данного пункта можно использовать задания 308— 311.
878. в) В первый день туристы прошли ![]() намеченного
маршрута, а во второй день — оставшиеся 15 км. Какова длина маршрута?
намеченного
маршрута, а во второй день — оставшиеся 15 км. Какова длина маршрута?
г) Сейчас у Васи в коллекции 200 марок. Известно, что за послед-
ний год число марок в коллекции
увеличилось на ![]() . Сколько марок было в коллекции год
назад?
. Сколько марок было в коллекции год
назад?
Решение. в) 1) 1 – ![]() =
= ![]() (маршрута)
— осталось пройти во второй день;
(маршрута)
— осталось пройти во второй день;
2) 15 3 5 = 25 (км) — длина маршрута.
г) Заметим, что за последний год число
марок в коллекции увели- чилось на ![]() , т. е. было
, т. е. было ![]() , стало
, стало ![]() +
+ ![]() =
= ![]() (рис.
43).
(рис.
43).
1) 1
+ ![]() =
= ![]() (часть марок) — такую
часть от старого числа марок со-
(часть марок) — такую
часть от старого числа марок со-
ставляют 200 марок;
2) 200 5 4 = 160 (марок) — было год назад. Ответ. в) 25 км; г) 160 марок.
879. б) За ![]() м тесьмы заплатили на
6 р. больше, чем за
м тесьмы заплатили на
6 р. больше, чем за ![]() м такой же тесьмы. Сколько стоит 1 м
тесьмы?
м такой же тесьмы. Сколько стоит 1 м
тесьмы?
Решение. 1) ![]() –
– ![]() =
= ![]() (м)
— за столько тесьмы заплатили 6 р.;
(м)
— за столько тесьмы заплатили 6 р.;
2) 6 3 10 = 20 (р.) — стоит 1 м тесьмы. Ответ. 20 р.
882. Машинистка перепечатала третью часть рукописи, потом ещё 10 страниц. В результате она перепечатала половину всей рукописи.
Сколько страниц в рукописи?

Рис. 43
Решение. 1) ![]() –
– ![]() =
= ![]() (часть
рукописи) — составляют 10 страниц
(часть
рукописи) — составляют 10 страниц
(рис. 44);
2) 10 6 = 60 (страниц) — всего в рукописи. Ответ. 60 страниц.
Промежуточный контроль. C–16.
В данном пункте учебника вводятся операции умножения дробей, умножения натурального числа на дробь, понятия обратной дроби и взаимно обратных дробей.
Определение произведения двух дробей, разумеется, не
требует доказательства. Но учащиеся нуждаются в мотивации введения нового
понятия. Только не надо пытаться объяснить умножение дробей с помощью площади
прямоугольника, длины сторон которого выражаются дробями. Как вычислять площадь
прямоугольника в этом случае, мы ещё не знаем. Можно, например, попросить учащихся
перемножить числа 2 и 3 — получится 6. Если же те же числа записать в виде дро
би, то получим 2 = ![]() , 3 =
, 3 = ![]() и 6 =
и 6 = ![]() . Возникает
естественный вопрос: каким бы могло быть правило умножения дробей, чтобы было
верно
. Возникает
естественный вопрос: каким бы могло быть правило умножения дробей, чтобы было
верно
![]()
![]() 2 3 равенство =?
Скорее всего, сами учащиеся предложат правило:
2 3 равенство =?
Скорее всего, сами учащиеся предложат правило:
1 1
надо произведение числителей записать в числитель дроби, а произве дение знаменателей — в знаменатель. Теперь учащиеся будут готовы к восприятию правила умножения дробей.
Обратим внимание, что правило умножения дробей (определение) не доказывается, а правило умножения натурального числа на дробь можно доказать, используя правило умножения дробей. И сильный ученик должен уметь это делать на буквах.
Сначала учащиеся должны научиться умножать дроби в случае, когда сокращение не требуется, потом следует повторить с ними сокращение дробей и показать, как надо выполнять умножение дробей с сокращением, чтобы не делать лишних вычислений. Примеры такого рода есть в рабочей тетради.
Задания 913, 914 учебника готовят учащихся к решению задач на совместную работу.
РТ. При изучении данного пункта можно использовать задания 312—315.
907. Могут ли взаимно обратные числа быть одновременно: а) меньше 1; в) равны 1?
p p
Решение. а) Если ![]() q 1, то
q 1, то ![]() q —
правильная дробь и p q. Тогда так
q —
правильная дробь и p q. Тогда так
q
![]() p p q q как p p, а p = 1, то
для обратной дроби
p p q q как p p, а p = 1, то
для обратной дроби ![]() p верно
неравенство
p верно
неравенство ![]() p 1.
p 1.
Следовательно, взаимно обратные числа не могут быть одновременно меньше 1.
в) Взаимно обратные числа могут быть одновременно равны 1, если
оба эти числа равны 1.
914. б) За минуту через первую трубу наполняется
![]() бассейна,
а че- рез вторую трубу —
бассейна,
а че- рез вторую трубу — ![]() бассейна. Какую часть бассейна наполнят
обе трубы за 6 мин?
бассейна. Какую часть бассейна наполнят
обе трубы за 6 мин?
Решение. 1) ![]() +
+ ![]() =
= ![]() (бассейна)
— наполнят две трубы за 1 мин совместной работы;
(бассейна)
— наполнят две трубы за 1 мин совместной работы;
![]()
![]() 3 6
3 6 ![]()
![]() 2) 6 = = = =
(бассейна) — наполнят две трубы за
2) 6 = = = =
(бассейна) — наполнят две трубы за
6 мин совместной работы.
Ответ. ![]() часть
бассейна.
часть
бассейна.
В данном пункте учебника вводятся переместительный и сочетательный законы умножения и распределительный закон для дробей. Обратим внимание на то, что два первых закона доказываются для конкретных дробей, но так, что если вместо чисел в числителях и знаменателях поставить буквы, то получится их полное доказательство со ссылкой на соответствующие законы для натуральных чисел и правило (определение) умножения дробей. Распределительный закон доказан в общем виде для дробей, приведённых к общему знаменателю. Первые два закона сильные учащиеся также могут доказать в общем виде.
В учебном тексте не упоминается терминология, применяемая при использовании распределительного закона: «раскроем скобки, применяя распределительный закон», «вынесем общий множитель за скобки», но при выполнении заданий учитель должен её активно использовать и просить учащихся комментировать свои действия при выполнении заданий, применяя эту терминологию.
Отметим, что изучение законов умножения для дробей даёт учителю дополнительные возможности для усиления мотивации учения, так как на нескольких выигрышных примерах можно показать, что, не владея этими законами, ученик обречён на долгие и, возможно, ошибочные вычисления, а применение законов позволяет ему в ряде случаев проводить вычисления устно (задание 919 и др.). Однако начинать вычисления с использованием законов надо с подробной записи всех шагов, чтобы исключить их непонимание.
Вычислите, используя законы умножения (918, 919).
ж12 14ц ж17 13ц
918.
![]() в)
зи13
17чш зи14 24чш.
в)
зи13
17чш зи14 24чш.
Решение. Применим два раза сочетательный закон умножения:
ж12 14ц ж17 13ц
з ч зи14 24чш = и13 17ш
жж12 14ц 17ц 13 ж12 ж14 17цц 13
![]() =
зизи чш чш 24 = зи13 из17
14шччш 24 =
=
зизи чш чш 24 = зи13 из17
14шччш 24 =
13 17 14
ж12 ц 13 12 1
=
зи13
1чш ![]() = = = =
2.
= = = =
2.
Такое решение имеет смысл показать для демонстрации сочетательного закона умножения дробей. Но более короткое решение могут предложить сами учащиеся:
ж12 14ц ж17 13ц
![]() з ч зи14
24чш = и13 17ш
з ч зи14
24чш = и13 17ш
= ![]() =
= ![]() .
.
22 5 20 5
919.
![]() д)
+ .
д)
+ .
21 14 21 14
Решение. Вынесем общий
множитель ![]() слагаемых за скобки:
слагаемых за скобки:
22 5 20 5 5 ж22 20ц
![]() 21 14 + 21 14 = 14 зи21
+ 21чш =
21 14 + 21 14 = 14 зи21
+ 21чш =
![]()
![]() 5 42 5
5 42 5
= = = = =.
15 a 15 3
![]() 921. Дано выражение 17 13 – 17 13.
921. Дано выражение 17 13 – 17 13.
а) Каким натуральным числом надо заменить букву a, чтобы мож -
но было устно найти значение этого выражения?
б) Какое натуральное число a можно взять, чтобы значение данно-
го выражения было дробью со знаменателем 13? со знаменателем 17? натуральным числом? нулём?
Решение. Очевидно, что если вместо a
подставить любое число, то значение выражения не всегда можно вычислить устно.
Вынесем об- щий множитель ![]() за скобки:
за скобки:
15 a 15 3
– =
![]() 17 13 17 13 15 ж a 3 ц 15 a -3
17 13 17 13 15 ж a 3 ц 15 a -3
= з – ч = .
17 и13 13ш 17 13
Теперь видно, что для некоторых значений a действительно ответ можно получить устно.
а) Найти устно значение выражения можно, если, например, бук-
ву a заменить числом 16. Тогда
второй множитель равен 1 и значение выражения равно ![]() .
.
б) Чтобы значение данного выражения было дробью со знаменате- лем 13, надо сделать так, чтобы множитель 17 в знаменателе можно было сократить. Для этого число a – 3 должно быть равно 17, 34,
51, ... . Если взять a = 20, то
значение данного выражения равно ![]() — дробь со знаменателем 13.
— дробь со знаменателем 13.
Чтобы значение данного выражения было дробью со
знаменателем 17, надо сделать так, чтобы множитель 13 в знаменателе можно было
сократить. Если взять a = 16, то значение данного выражения равно ![]() —
дробь со знаменателем 17.
—
дробь со знаменателем 17.
Чтобы значение данного выражения было нулём, надо сделать так, чтобы число a – 3 было равно 0. Если взять a = 3, то значение данного выражения равно 0.
В данном пункте учебника деление дробей определяется как операция, обратная умножению. Здесь формулируется и доказывается на конкретном примере утверждение:
Частное любых двух натуральных чисел равно дроби, числитель которой равен делимому, а знаменатель — делителю.
Это утверждение, которое часто «доказывают» с помощью деления яблок, сосисок и т. п. на равные части, можно доказать только после введения деления дробей. Доказательство проведено для конкретных дробей, но сильные ученики смогут провести его для любых натуральных чисел p и q:
![]() p q p 1 p p q
= 1 1 = 1 q = q.
p q p 1 p p q
= 1 1 = 1 q = q.
С этого момента есть все основания считать черту дроби другим знаком деления и использовать её при записи числовых выражений (такие примеры приведены в учебнике).
Далее в учебнике приведены правило деления дроби на натуральное число, утверждение «делить на нуль нельзя», напоминаются правила порядка действий.
Обратим внимание на задание 927, где требуется найти число x, для которого верно равенство. Такого рода задания, как и ранее, можно использовать для развития речи учащихся, но увлекаться ими не следует.
РТ. При изучении данного пункта можно использовать задания 316— 318.
Обратим внимание на то, что некоторые задания на вычисление значений числового выражения допускают не только вычисления по действиям, но и применение законов арифметических действий для упрощения вычислений. Однако чтобы воспользоваться более простым способом вычисления, надо проявить наблюдательность и знание теории. Использование таких примеров при обучении математике и контроле знаний учащихся помогает учителю формировать положительную мотивацию к изучен ию теоретического материала. Кроме того, такая работа готовит учащихся к преобразованиям числовых и буквенных выражений в алгебре.
Отметим, что развитая наблюдательность подводит учащихся и к первым «научным» результатам. Например, учащиеся иногда спраши-
![]() 35 5 35
35 5 35 ![]() вают:
а можно ли частное дробей вычислить так:
вают:
а можно ли частное дробей вычислить так: ![]() = =
36 6
= =
36 6 ![]()
= ![]() ? Это очень хороший
повод для обсуждения и проверки понимания усвоенного теоретического материала.
? Это очень хороший
повод для обсуждения и проверки понимания усвоенного теоретического материала.
Можно спросить учащихся, верный ли ответ получился в
результате. Как это проверить? Учащиеся обычно предлагают перемножить частное и
делитель — дроби ![]() и
и ![]() . В результате
получится
. В результате
получится ![]() . Уча- щихся можно спросить, во всех ли
случаях удобно пользоваться таким приёмом вычисления. А в каких удобно? Дети
ответят: в тех случаях, когда числитель первой дроби делится на числитель вто
рой и знаменатель первой дроби делится на знаменатель второй. Очевидно, что
такие обсуждения улучшают понимание теоретического материала и развивают
мышление учащихся. Рассмотрим примеры.
. Уча- щихся можно спросить, во всех ли
случаях удобно пользоваться таким приёмом вычисления. А в каких удобно? Дети
ответят: в тех случаях, когда числитель первой дроби делится на числитель вто
рой и знаменатель первой дроби делится на знаменатель второй. Очевидно, что
такие обсуждения улучшают понимание теоретического материала и развивают
мышление учащихся. Рассмотрим примеры.
3 9 3 8
937. ![]() г) Вычислите: – .
г) Вычислите: – .
5 10 5 9
Решение. Заменим деление на ![]() умножением
на обратную дробь
умножением
на обратную дробь ![]() и применим распределительный закон:
и применим распределительный закон:
3 9 3 8 3 10 3 8 3 ж10 8ц 3 2
![]() = = =
= = = ![]() .
.
5 10 5 9 5 9 5 9 5 9 9 15
4 5 4 24
938. г) Вычислите: – + .
5 8 5 25 25 4
Решение.
4 5 4 24 1 5 4 8 4 24 1 4 4 ж8 24 1 ц
![]() ч =
ч =
ш
4 ж40 24
= з – + ч = = .
5 и25 25 25ш 5 25 125
Замечание. В рассмотренных примерах большого упрощения вычислений не получилось, но польза для учащихся от такой работы несомненна.
Промежуточный контроль. C–17.
В данном пункте учебника вводится новый способ решения задач на дроби, связанный с умножением (делением) на дробь. При решении задач можно использовать схематические рисунки, чтобы наглядно показать величину, от которой находят часть, саму эту часть, что известно и что требуется найти. Использование рисунков особенно эффективно при решении более сложных задач, в которых требуется находить часть не только от данного числа, но и от остатка.
Для успешного решения задач, в которых дана часть неизвестного числа, полезно показать, почему то число, часть которого выражена дробью, удобно принимать за единицу (см. решение задачи 944).
944. а) Уменьшите 900 р. на ![]() этой
суммы.
этой
суммы.
б) Увеличьте 150 р. на ![]() этой суммы.
этой суммы.
Решение.
а) 1) ![]() 900 = 300 (р.) — на
такую сумму уменьшили 900 р.; 2) 900 – 300 = 600 (р.) — стало после уменьшения
суммы (рис. 45, а). б) 1)
900 = 300 (р.) — на
такую сумму уменьшили 900 р.; 2) 900 – 300 = 600 (р.) — стало после уменьшения
суммы (рис. 45, а). б) 1) ![]() 150 = 60 (р.) — на такую сумму увеличили
150 р.;
150 = 60 (р.) — на такую сумму увеличили
150 р.;
2) 150 + 60 = 210 (р.) — стало после увеличения суммы (рис. 45, б).
Ответ. а) 600 р.; б) 210 р.
Запишем решение задачи 944 а с помощью числового выражения:
900 – ![]() 900 = 600 (р.).
900 = 600 (р.).
Вынесем общий множитель за скобки:
1 ж 1ц
900
– ![]() 900 = з1 –
900 = з1 – ![]() ч 900.
ч 900.
3 и 3ш
ж
Теперь видно, что если принять данное число за 1 зоно составляет
и
3 3 ц ![]() самого
себя, а
самого
себя, а ![]() =
1ч, то решение можно записать так:
=
1ч, то решение можно записать так:
3 3 ш
1) 1 – ![]() =
= ![]() (суммы)
— осталось;
(суммы)
— осталось;
2) ![]() 900
= 600 (р.) — осталось после уменьшения суммы.
900
= 600 (р.) — осталось после уменьшения суммы.
Аналогично решение задачи 944 б можно записать так:
1) 1 + ![]() =
= ![]() (суммы)
— стало;
(суммы)
— стало;
2) ![]() 150
= 210 (р.) — стало после увеличения суммы.
150
= 210 (р.) — стало после увеличения суммы.
948. а) Число уменьшили на ![]() этого
числа, получилось 210. Най дите число.
этого
числа, получилось 210. Най дите число.
б) Задумали число, увеличили его на ![]() этого числа
и получили 56. Какое число задумали?
этого числа
и получили 56. Какое число задумали?
Решение. а) 1) 1 – ![]() =
= ![]() (числа)
— осталось после его уменьшения;
(числа)
— осталось после его уменьшения;
2) 210 ![]() = 300 — неизвестное
число (рис. 46, а).
= 300 — неизвестное
число (рис. 46, а).
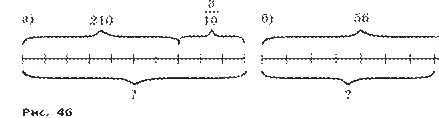
б) 1) 1 + ![]() =
= ![]() (числа) —
стало после его увеличения;
(числа) —
стало после его увеличения;
2) 56 ![]() = 49 — задуманное
число (рис. 46, б).
= 49 — задуманное
число (рис. 46, б).
Ответ. а) 300; б) 49.
Промежуточный контроль. C–18, C–19.
В данном пункте учебника вводится новый тип текстовых задач, традиционных для курса арифметики. В этих задачах зависимость между известными величинами и неизвестной величиной выражается
![]() 1 1 1 формулой a + b = c. Умение
их решать необходимо в старших классах при формировании умения решения задач на
совместную работу с помощью уравнения с неизвестным в знаменателе.
1 1 1 формулой a + b = c. Умение
их решать необходимо в старших классах при формировании умения решения задач на
совместную работу с помощью уравнения с неизвестным в знаменателе.
В предыдущих пунктах учебника уделено достаточно внимания подготовке учащихся к решению задач данного типа.
В учебнике приведены способы решения задач на совместную работу с помощью дробей — это должен быть основной способ решения задач такого типа. Однако для развития мышления учащихся полезно рассматривать и другие способы. Поэтому для задачи про кадь пития в учебнике приведён ещё и старинный способ решения — без дробей. В сильном классе можно показать третий способ решения той же задачи.
Старинная задача. Муж выпьет кадь пития в 14 дней, а с женою выпьет ту же кадь в 10 дней. Спрашивается, за сколько дней жена его отдельно выпьет ту же кадь.
Решение. «Работая» с мужем, жена выпивает за 10
дней столько пития, сколько муж выпивает за 14 – 10 = 4 дня, значит, жена в
день выпивает в 10 4 = ![]() раза меньше, чем муж, поэтому на всю кадь
она затратит времени в
раза меньше, чем муж, поэтому на всю кадь
она затратит времени в ![]() раза больше, чем муж, т. е. 14
раза больше, чем муж, т. е. 14 ![]() =
35 дней.
=
35 дней.
РТ. При изучении данного пункта можно использовать задания 319— 323.
962. Из пунктов A и B одновременно вышли два пешехода. Они встретились через 40 мин после своего выхода, а через 32 мин после встречи первый пришёл в B. Через сколько минут после своего выхода из B второй пришёл в A?
Решение.
Из условия задачи можно узнать, что первый пешеход был в пути 40 + 32 = 72 мин.
1)
1 72 = ![]() (расстояния AB) — проходит первый
пешеход за 1 мин;
(расстояния AB) — проходит первый
пешеход за 1 мин;
2)
1 40 = ![]() (расстояния AB) — проходят
пешеходы вместе за 1 мин;
(расстояния AB) — проходят
пешеходы вместе за 1 мин;
3)
![]() –
– ![]() =
= ![]() (расстояния
AB) — проходит второй пешеход за 1 мин;
(расстояния
AB) — проходит второй пешеход за 1 мин;
4)
1 ![]() = 90 (мин) — через 90 мин после выхода из
B второй пеше- ход пришёл в пункт A.
= 90 (мин) — через 90 мин после выхода из
B второй пеше- ход пришёл в пункт A.
Ответ. Через 90 мин.
964. а) Старинная задача. Лошадь съедает воз сена за месяц, коза — за два месяца, овца — за три месяца. За какое время лошадь, коза и овца вместе съедят такой же воз сена?
Решение. Из условия задачи можно узнать, что за
6 месяцев лошадь съест 6 возов сена, коза — 3 воза, овца — 2 воза, а вместе они
за 6 месяцев съедят 6 + 3 + 2 = 11 возов сена. Поэтому 1 воз сена они съедят
вместе за 6 11 = ![]() месяца.
месяца.
Но можно решить эту задачу с помощью дробей: все вместе за 1 ме-
сяц они съедают 1 + ![]() +
+ ![]() =
= ![]() возов.
Поэтому 1 воз сена они съедят вместе за 1
возов.
Поэтому 1 воз сена они съедят вместе за 1 ![]() =
= ![]() месяца.
месяца.
Ответ. За ![]() месяца.
месяца.
Промежуточный контроль. C–20.
В данном пункте учебника вводятся понятия смешанной дроби, целой части и дробной части смешанной дроби. При изучении данного пункта учащиеся должны научиться записывать неправильную дробь, числитель которой не делится нацело на знаменатель, в виде смешанной дроби и выполнять обратное преобразование.
РТ. Освоению учащимися записи дроби в виде смешанной дроби и обратному преобразованию помогут задания 324, 325.
Решения и комментарии 979. Сравните числа:
а) ![]() и
и ![]() ; г) 1
; г) 1![]() и 1
и 1![]() ;
ж) 2
;
ж) 2![]() и 1
и 1![]() ; к) 1
; к) 1![]() и 2
и 2![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]() 3 2 1
1
3 2 1
1
![]() Решение. а) = , = ,
Решение. а) = , = ,
![]() ,
поэтому ;
,
поэтому ;
2 3
1
г) 1
1 , так как 1 = 1, а ![]() ;
;
2 3
ж) 2![]() 1
1![]() , так как 2 1;
, так как 2 1;
к) 1![]() 2
2![]() , так как 1 2.
, так как 1 2.
Промежуточный контроль. C–21.
В данном пункте учебника рассматривается операция сложения смешанных дробей, сводящаяся к отдельному сложению целых и дробных частей. При этом подразумевается, что результат сложения должен быть записан в виде смешанной дроби или целого числа.
Отметим, что любое натуральное число и любую правильную
дробь обычно не называют смешанными дробями. Однако при сложении (а в
дальнейшем и при вычитании) удобно считать, что у каждого натурального числа
целая часть есть само это число, а дробная часть есть нуль, а у каждой
правильной дроби целая часть есть нуль, а дробная часть есть сама эта дробь.
Тогда складывать натуральные числа и правильные дроби со смешанными дробями
можно по правилу сложения смешанных дробей: 1 + 1![]() = 2
= 2![]() ; 2
; 2![]() +
+ ![]() = 2
= 2![]() .
.
Сначала можно рассмотреть лишь случаи сложения смешанной дро- би с целым числом, затем с дробью и, наконец, со смешанной дробью с общим знаменателем. Только когда учащиеся освоят эти действия, задания можно усложнить, рассматривая дроби с разными знаменателями.
При сложении смешанных дробей могут получаться суммы целого числа и неправильной дроби, которые учащиеся должны уметь записать в виде смешанной дроби. Такие задания есть в учебнике (задание 987), сначала их нужно выполнить с более подробной записью.
Дополнительное задание. Запишите в виде смешанной дроби:
а) 1 + ![]() ; б) 2 +
; б) 2 + ![]() ;
в) 3 +
;
в) 3 + ![]() ; г) 4 +
; г) 4 + ![]() .
.
Решение. а) 1 + ![]() = 1 + 1
= 1 + 1![]() = 2
= 2![]() ;
б) 2 +
;
б) 2 + ![]() = 2 + 2
= 2 + 2![]() = 4
= 4![]() ;
;
в) 3 + ![]() = 3 + 1
= 3 + 1![]() = 4
= 4![]() ;
г) 4 +
;
г) 4 + ![]() = 4 + 1
= 4 + 1![]() = 5
= 5![]() .
.
При сложении дробных частей двух смешанных дробей может по- лучиться неправильная дробь. В этом случае в учебнике принята запись, как в следующем примере:
1![]() + 2
+ 2![]() = 3 +
= 3 + ![]() = 3 + 1
= 3 + 1![]() = 4
= 4![]() .
.
Запись 3![]() не используется и не называется смешанной
дробью, так как может возникнуть путаница: ученики могут считать, что 3 и
не используется и не называется смешанной
дробью, так как может возникнуть путаница: ученики могут считать, что 3 и ![]() соответственно
целая и дробная части числа 3
соответственно
целая и дробная части числа 3![]() и смешанная дробь — это сумма целого
числа и неправильной дроби. Но если учи- тель проведёт соответствующую
разъяснительную работу, то записи такого вида можно использовать, они окажутся
полезными при вычитании смешанных дробей (с заниманием единицы).
и смешанная дробь — это сумма целого
числа и неправильной дроби. Но если учи- тель проведёт соответствующую
разъяснительную работу, то записи такого вида можно использовать, они окажутся
полезными при вычитании смешанных дробей (с заниманием единицы).
РТ. Освоению учащимися сложения смешанных дробей помогут задания 326, 327.
999. На отрезке AB отметили точку C
так, что CB = 7![]() м и CB на 2
м и CB на 2![]() м меньше AC.
Найдите длину отрезка AB.
м меньше AC.
Найдите длину отрезка AB.
Решение. CB на 2![]() м
меньше AC, значит, AC на 2
м
меньше AC, значит, AC на 2![]() м больше CB
м больше CB
(рис. 47).
1) 7![]() + 2
+ 2![]() = 7
= 7![]() +
2
+
2![]() = 9
= 9![]() (м) — длина отрезка AC;
2) 7
(м) — длина отрезка AC;
2) 7![]() + 9
+ 9![]() = 7
= 7![]() + 9
+ 9![]() =
16
=
16![]() (м) — длина отрезка AB.
(м) — длина отрезка AB.
Ответ. 16![]() м.
м.
1000. Даны три числа. Первое 4![]() ,
второе на 5 больше, чем первое,
,
второе на 5 больше, чем первое,
а третье на 3![]() больше второго.
Какова сумма трёх чисел?
больше второго.
Какова сумма трёх чисел?
Решение. 1) 4![]() + 5 = 9
+ 5 = 9![]() —
второе число;
—
второе число;
2) 9![]() + 3
+ 3![]() = 12
= 12![]() —
третье число; 3) 4
—
третье число; 3) 4![]() + 9
+ 9![]() + 12
+ 12![]() = 25
= 25![]() —
сумма трёх чисел.
—
сумма трёх чисел.
Ответ. 25![]() .
.
![]()
Рис. 47
В данном пункте учебника рассматривается операция вычитания смешанных дробей, сводящаяся к отдельному вычитанию целых и дробных частей. Сначала можно рассмотреть лишь случаи вычитания из смешанной дроби целого числа, затем дроби, потом смешанной дроби (с общим знаменателем). Только когда учащиеся освоят эти действия, задания можно усложнить, рассматривая дроби с разными знаменателями.
Если дробная часть уменьшаемого меньше дробной части вычитаемого, то вычисления усложняются. В этом случае в учебнике принята запись, как в следующем примере:
4![]() – 2
– 2![]() = 4 +
= 4 + ![]() – 2
– 2![]() = 3
+
= 3
+ ![]() – 2
– 2![]() = 1
= 1![]() .
.
Если учитель провёл описанную в комментариях к пункту 4.15 разъяснительную работу, то запись вычислений можно сделать короче:
4![]() – 2
– 2![]() = 3
= 3![]() – 2
– 2![]() = 1
= 1![]() .
.
Возможна и другая запись вычитания:
4![]() – 2
– 2![]() = 2
= 2![]() –
– ![]() = 1
+
= 1
+ ![]() –
– ![]() = 1
= 1![]() .
.
РТ. Освоению учащимися вычитания смешанных дробей помогут задания 328—330.
Если числовое выражение содержит более двух чисел, то вычисления можно провести по действиям, а можно преобразовывать всё выражение. Начинать нужно с освоения первого способа, но в простых случаях можно применять и второй так, как показано ниже.
1014. Вычислите: а) 3![]() – 2
– 2![]() +
+ ![]() ;
в) 3
;
в) 3![]() – 2
– 2![]() +
+ ![]() .
.
Решение. а) 1) 3![]() – 2
– 2![]() = 3
= 3![]() –
2
–
2![]() = 2 +
= 2 + ![]() – 2
– 2![]() =
= ![]() ;
;
2) ![]() +
+ ![]() =
= ![]() +
+ ![]() =
= ![]() =
= ![]() .
.
в) 3![]() – 2
– 2![]() +
+ ![]() = 3
= 3![]() – 2
– 2![]() +
+ ![]() = 1
= 1![]() +
+ ![]() = 1
= 1![]() .
.
Ответ. а) ![]() ; в) 1
; в) 1![]() .
.
Промежуточный контроль. C–22.
В данном пункте учебника вводятся операции умножения и деления смешанных дробей, выполняемые с помощью записи каждой смешанной дроби в виде неправильной дроби (основной приём вычисления). Вместе с тем в учебнике рассмотрены примеры упрощения вычислений с помощью распределительного закона в особых случаях. Для всех таких случаев в учебнике проведены подробная и краткая записи вычислений.
Добавим ещё один пример применения распределительного закона.
7 11 7 11
![]() Найдём значение
числового выражения: 13 9 – 12 9 .
Найдём значение
числового выражения: 13 9 – 12 9 .
8 24 8 24
Если выполнять вычисления, применяя основной приём, то
эта работа потребует много сил и времени. Если же заметить, что общий множитель
9![]() можно вынести за скобки, а разность в
скобках ока- жется равной единице, то вычисления можно выполнить устно. В от -
можно вынести за скобки, а разность в
скобках ока- жется равной единице, то вычисления можно выполнить устно. В от -
вете получится 9![]() .
.
Такого рода примеры надо использовать для укрепления мотивации школьников к изучению теории, которая даёт простые приёмы вычисления для особых случаев.
Закончив изучение четырёх действий со смешанными дробями, учащиеся могут теперь выполнять любые вычислительные задания с натуральными числами, обыкновенными и смешанными дробями, в том числе и с использованием черты дроби в качестве знака деления (задание 1029). Выполнение таких заданий учит планированию действий, тренирует наблюдательность, «вычислительную выносливость», умение предвидеть, в какой форме надо оставить результат выполненного действия, чтобы им было удобно воспользоваться в последующих вычислениях, в каком случае удобно объединить запись нескольких действий и т. п.
РТ. Освоению учащимися умножения и деления смешанных дробей помогут задания 331—335.
ж 3 ц
![]() 5 зи2
1– 20чш 48
5 зи2
1– 20чш 48
5 40
![]()
![]()
![]()
![]()
![]()
![]()
![]() 1029.
Вычислите: е) + .
1029.
Вычислите: е) + .
![]()
![]() 17
17 ![]()
5)
48 = ![]() = = =
= = = ![]() ;
;
6)
![]() 20 =
20 = ![]() =
= ![]() =
= ![]() =
5;
=
5;
7)
1 10 = ![]() ;
;
8)
5 + ![]() = 5
= 5![]() =
= ![]() ;
;
9)
![]()
![]()
![]() = = =
= = = ![]() =
= ![]() = 8;
= 8;
10)
1![]() + 8 = 9
+ 8 = 9![]() .
.
Ответ. 9![]() .
.
Промежуточный контроль. C–23.
В данном пункте учебника вводятся понятия точки координатного
p
луча с координатой ![]() q,
положительных рациональных чисел, положи- тельных рациональных точек, среднего
арифметического нескольких чисел, определяется расстояние между точками,
координата середины отрезка, показано, что между любыми двумя рациональными
точками находится ещё хотя бы одна точка.
q,
положительных рациональных чисел, положи- тельных рациональных точек, среднего
арифметического нескольких чисел, определяется расстояние между точками,
координата середины отрезка, показано, что между любыми двумя рациональными
точками находится ещё хотя бы одна точка.
Заметим, что для изображения на координатном луче неправильной дроби лучше выделить её целую часть.
1036. а) Найдите координаты точек, делящих отрезок AB на три
ж 1ц
равные части: A(5), Bзи9![]() 2чш.
2чш.
Решение. Пусть точки M(a) и N(b) делят отрезок AB на три равные части, а точка O(0) — начало отсчёта (рис. 48).
![]()
![]()
![]()
![]()
![]()
![]()
![]() 1 9 Так как AB =
9– 5 = 4=, то AM = MN =AB = == 1.
1 9 Так как AB =
9– 5 = 4=, то AM = MN =AB = == 1.
3 2 Так как OM =
OA + AM, то a = 5 + 1![]() = 6
= 6![]() .
.
Так как ON = OM + MN,
то b = 6![]() + 1
+ 1![]() = 8.
= 8.
![]()
Рис. 48
1038. На рисунке 49 указаны координаты точек A и B, найдите координаты точек C и D.
Решение. Пусть точки C и D имеют координаты c и d соответственно, а точка O(0) — начало отсчёта (на рисунке 49 точка O не изображена).
в) Точка B — середина отрезка AC, поэтому c = b.
a b+ a b+
Так
как AB = BC = CD = ![]() – a, то OD = OC +
CD = b +
– a, то OD = OC +
CD = b + ![]() – a. От-
– a. От-
2 2
куда получим, что
a b+ d = b + ![]() – a.
– a.
2 3b a–
Сильные
учащиеся могут привести этот ответ к виду d = ![]() (но
(но
2
это не обязательное требование).
г) Точки C и D делят отрезок AB на три равные части. Так как
b a–
AB = b – a, то AC = CD = .
3
b a– b a–
Так
как OC = OA + AC = a + , то c
= a + ![]() .
.
3 3 b a– b a–
![]() Так как OD =
OC + CD = a + + , то
Так как OD =
OC + CD = a + + , то
3 3
b a– b a– d = a + + .
3 3
2a b+
![]() Сильные
учащиеся могут привести эти ответы к виду c = ,
Сильные
учащиеся могут привести эти ответы к виду c = ,
3
a+2b
![]() d =
(но это не обязательное требование).
d =
(но это не обязательное требование).
3
1041.
Средний возраст одиннадцати игроков футбольной команды 21
год. Во время матча один из игроков получил травму и ушёл с по ля. Средний
возраст оставшихся игроков оказался равным 20![]() года.
года.
Сколько лет игроку, получившему травму?
Решение. Сумма возрастов всех игроков команды равна 21 11 = 231 год.
Сумма возрастов оставшихся на поле игроков равна
20![]() 10 = 208 лет.
10 = 208 лет.
Значит, возраст игрока, получившего травму, равен
231 – 208 = 23 года.
Ответ. 23 года.
1042. Дети спросили своего учителя математики:
— Сколько вам лет?
— Если подсчитать средний возраст 32 учеников нашего
класса, то получится 10![]() года. Если же при подсчётах учесть и мой
возраст, то получится 11 лет.
года. Если же при подсчётах учесть и мой
возраст, то получится 11 лет.
Сколько лет учителю математики?
Решение. Сумма возрастов всех
учащихся класса равна 32 10![]() =
=
= 336 лет. Сумма возрастов всех учащихся и их учителя математики равна 11 33 = 363 года. Значит, возраст учителя математики равен 363 – 336 = 27 лет.
Ответ. 27 лет.
В данном пункте учебника на конкретных примерах показывается, что площадь прямоугольника вычисляется по формуле a b, где a и b — длина и ширина прямоугольника, выраженные рациональными числами, а объём прямоугольного параллелепипеда вычисляется по формуле a b c, где a, b и c — измерения прямоугольного параллелепипеда, выраженные рациональными числами.
1048. Сколько банок краски потребуется для покраски железной крыши дома, если содержимого одной банки хватает на покраску 10 м2 поверхности? (Размеры крыши указаны на рисунке 50.)
Рис. 50
Решение. 1) 2
3 7 = 42 (м2) — площадь поверхности крыши; 2) 42 10 = 4![]() (банки) — пойдёт на покраску.
(банки) — пойдёт на покраску.
Следовательно, потребуется 5 банок краски. Ответ. 5 банок.
1049. Необходимо покрыть кафельной плиткой пол, имеющий фор-му прямоугольника со сторонами 4 м 50 см и 2 м 40 см. Плитки имеют форму квадрата со стороной 15 см. Сколько ящиков плитки потребуется, если в каждом ящике 50 плиток?
Решение. 4 м 50 см = 450 см, 2 м 40 см = 240 см.
1) 450 15 = 30 (плиток) — укладывается в один ряд в длину;
2) 240
15 = 16 (рядов) — укладывается в ширину; 3) 30 16 = 480 (плиток) —
потребуется всего; 4) 480 50 = 9![]() (ящиков) — плитки потребуется.
(ящиков) — плитки потребуется.
Следовательно, потребуется 10 ящиков плитки. Ответ. 10 ящиков.
В данном пункте учебника рассмотрены задачи на движение по реке, при решении которых удобно весь путь принимать за единицу, а скорость катера (моторной лодки) по течению реки, против течения и скорость течения реки выражать как часть пути, пройденного за единицу времени. В тексте учебника приведены решения двух таких задач.
Заметим, что решения всех задач рассматриваемого пункта можно оформить иначе, обозначив всё расстояние через x км. При этом решение остаётся арифметическим по сути, так как уравнение не составляется и x не находится (его и нельзя найти), но содержит элементы алгебры — вычисления с буквенными выражениями. Получается выигрыш в большей простоте пояснений каждого действия и в обозначениях единиц измерения величин.
Рассмотрим такое оформление решения на примере задачи 1 из учебного текста.
Задача 1. Расстояние между пристанями A и B на реке плот проплывает за 12 ч. Такое же расстояние теплоход проплывает по озеру за 4 ч. За сколько часов теплоход проплывёт расстояние между пристанями A и B:
а) по течению реки; б) против течения реки?
Решение. Пусть расстояние между пристанями A и B равно x км.
Тогда
x
1) x 4 = (км/ч) — собственная скорость теплохода;
4 x
2) x 12 = (км/ч) — скорость течения реки;
12 x x x
3) + = (км/ч) — скорость теплохода по течению реки;
4 ![]() 12 3 x x x
12 3 x x x
4) – = (км/ч) — скорость теплохода против течения реки;
4 12 6 x
5) x = 3 (ч) — время движения теплохода по течению реки;
3 x
6) x = 6 (ч) — время движения теплохода против течения реки. 6
Ответ. а) За 3 ч; б) за 6 ч.
Разумеется, в этом решении применяются, по сути дела, действия с алгебраическими дробями, которые изучаются в курсе 7 класса. Но учащиеся понимают суть выполняемых действий, так как для них это ещё не алгебраические дроби, а обыкновенные дроби, в которых числителем служит известное, но не названное число (расстояние между пунктами A и B, выраженное в указанных единицах). Поэтому такое «забегание» вперёд можно считать оправданным, оно готовит учащихся к изучению алгебры.
РТ. При изучении данного пункта можно использовать задания 344— 348.
1062. Расстояние между пристанями A и B на реке плот проплывает за 15 мин, а катер проплывает расстояние AB против течения реки за 30 мин. За сколько минут катер проплывёт расстояние AB: а) по озеру; б) по течению реки?
Решение. 1) 1 15 = ![]() (расстояния) —
проплывает плот за 1 мин по течению реки;
(расстояния) —
проплывает плот за 1 мин по течению реки;
2)
1 30 = ![]() (расстояния) — проплывает катер за 1 мин
против те чения реки;
(расстояния) — проплывает катер за 1 мин
против те чения реки;
3)
![]() +
+ ![]() =
= ![]() (расстояния)
— проходит катер за 1 мин по озеру;
(расстояния)
— проходит катер за 1 мин по озеру;
4)
![]() +
+ ![]() =
= ![]() (расстояния)
— проходит катер за 1 мин по течению реки;
(расстояния)
— проходит катер за 1 мин по течению реки;
5)
1 ![]() = 10 (мин) — за это время катер проплывёт
расстояние AB по озеру;
= 10 (мин) — за это время катер проплывёт
расстояние AB по озеру;
6)
1 ![]() = 6 (мин) — за это время катер проплывёт
расстояние AB по течению реки.
= 6 (мин) — за это время катер проплывёт
расстояние AB по течению реки.
Ответ. а) За 10 мин; б) за 6 мин.
1066. а) Теплоход от Киева до Херсона идёт трое суток, а от Херсона до Киева четверо суток (без остановок). Сколько времени будут плыть плоты от Киева до Херсона? Решение. I способ.
1) 1 3 = ![]() (пути)
— проходит теплоход в сутки по течению реки;
(пути)
— проходит теплоход в сутки по течению реки;
2) 1 4 = ![]() (пути)
— проходит теплоход в сутки против течения реки;
(пути)
— проходит теплоход в сутки против течения реки;
3) ![]() –
– ![]() =
= ![]() (пути)
— на столько больше теплоход проплывает в сут-
(пути)
— на столько больше теплоход проплывает в сут-
ки по течению, чем против течения (на столько течение относит теп лоход или плоты за двое суток);
4) ![]() 2
=
2
= ![]() (пути) — на столько течение за сутки
относит плоты;
(пути) — на столько течение за сутки
относит плоты;
5) 1 ![]() =
24 (дня) — время движения плотов от Киева до Херсона.
=
24 (дня) — время движения плотов от Киева до Херсона.
II способ. Пусть x км — расстояние от Киева до Херсона, тогда ско -
x рость теплохода по течению равна км в сутки (км/сут.), против те-
3
x чения — км/сут.
4 x
1) x 3 = (км/сут.) — скорость теплохода по течению реки;
3 x
2) x 4 = (км/сут.) — скорость теплохода против течения реки;
4
x x x
3) – = (км/сут.) — удвоенная скорость течения;
3 4 12 x x
4) 2 = (км/сут.) — скорость течения реки;
![]() 12 24
12 24
x
5) x = 24 (дня) — время движения плотов.
24
Ответ. 24 дня.
Замечание. Использование «вспомогательного неизвестного x» упрощает пояснения к выполняемым действиям в решении задач рассматриваемого типа и готовит учащихся к изучению алгебры.
Промежуточный контроль. C–24.
В данном пункте приведена информация о древнем вавилонском способе записи дробей без знаменателя, об индийском способе записи дробей и смешанных чисел, об использовании сложения дробей в нотной записи.
Задачи 1068—1070 в разделе «Занимательные задачи» также связаны со старинными способами записи и чтения дробей.
С помощью задач из данного пункта можно продолжить работу по развитию у учащихся интереса к решению задач.
1070. Ананий из Ширака (Армения, VII в.). В городе Афины был водоём, в который проведены три трубы. Одна из труб может наполнить водоём за один час, другая, более тонкая, — за два часа, третья, ещё более тонкая, — за три часа. Итак, узнай, за какую часть часа все три трубы вместе наполняют водоём.
П р и м е ч а н и е. Ананий дал такой ответ: ![]() .
Используйте его для проверки своего решения.
.
Используйте его для проверки своего решения.
Решение. Время наполнения водоёма равно
ж 1 1ц 6
![]() 1 з1
+ + ч = (ч). и 2 3ш 11
1 з1
+ + ч = (ч). и 2 3ш 11
Этот результат Ананий записывал с помощью дробей с числите лем 1 и без знака сложения так:
![]() ,
,
что означало сумму
![]() +
+ ![]() +
+ ![]() +
+ ![]() ,
,
равную ![]() .
.
1082.
У Саши на дне рождения было 5 друзей. Первому он отрезал ![]() часть
пирога, второму —
часть
пирога, второму — ![]() остатка, третьему —
остатка, третьему — ![]() того, что
осталось, четвёртому —
того, что
осталось, четвёртому — ![]() нового остатка. Последний кусок Саша
разделил по ровну с пятым другом. Кому достался самый большой кусок?
нового остатка. Последний кусок Саша
разделил по ровну с пятым другом. Кому достался самый большой кусок?
Решение. Пусть пирог разделён на 6 равных
частей. Первому да- ли ![]() пирога — 1 кусок, 5 кусков осталось;
второму дали
пирога — 1 кусок, 5 кусков осталось;
второму дали ![]() от этих 5 кусков, т. е. такой же кусок
... В результате все получили поровну.
от этих 5 кусков, т. е. такой же кусок
... В результате все получили поровну.
1083.
а) В нашем классе есть певцы и танцоры: ![]() всех певцов
ещё и танцует, а
всех певцов
ещё и танцует, а ![]() танцоров ещё и поёт. Кого у нас в классе
больше: пев- цов или танцоров?
танцоров ещё и поёт. Кого у нас в классе
больше: пев- цов или танцоров?
в) В делегации иностранных гостей ![]() англичан
знала немецкий язык, а
англичан
знала немецкий язык, а ![]() немцев знала английский язык. Кого в
делегации больше: немцев или англичан? Можно ли ответить на вопрос задачи?
немцев знала английский язык. Кого в
делегации больше: немцев или англичан? Можно ли ответить на вопрос задачи?
Решение. а) Как видно из рисунка 51, одна и та
же группа уча щихся класса составляет ![]() от всех поющих и
от всех поющих и ![]() от всех танцующих,
следовательно, поющих в классе было больше.
от всех танцующих,
следовательно, поющих в классе было больше.
в) Здесь ![]() англичан и
англичан и ![]() немцев
— это не одна и та же группа лю-
немцев
— это не одна и та же группа лю-
дей. Поэтому ответить на вопрос нельзя. Ответы будут разными при разных количествах англичан и немцев. Так, условию задачи удовлетворяют и 1) 8 англичан и 7 немцев, и 2) 8 англичан и 14 немцев, и 3) 16 англичан и 7 немцев.
1085. Задача Метродора. Корона весит 60
мин (греческая мера веса и денег) и состоит из сплава золота, меди, олова и
железа. Золото и медь составляют ![]() , золото и олово —
, золото и олово — ![]() , золото и железо —
, золото и железо — ![]() общего
веса. Определите вес каждого металла в отдельности. Решение.
общего
веса. Определите вес каждого металла в отдельности. Решение.
2
1) 60 = 40 (мин) — вес золота и меди;
![]() 3
3
3
2) 60 = 45 (мин) — вес золота и олова;
3) 60 ![]() =
36 (мин) — вес золота и железа;
=
36 (мин) — вес золота и железа;
4) 40 + 45 + 36 = 121 (мина) — вес сплава и удвоенного веса золота;
5) (121 –
60) 2 = 30![]() (мин) — вес золота;
(мин) — вес золота;
6) 40 – 30![]() = 9
= 9![]() (мин) — вес меди;
(мин) — вес меди;
7) 45 – 30![]() =
14
=
14![]() (мин) — вес олова;
(мин) — вес олова;
8) 36 – 30![]() = 5
= 5![]() (мин) — вес железа.
(мин) — вес железа.
Ответ. 30![]() мин золота, 9
мин золота, 9![]() мин
меди, 14
мин
меди, 14![]() мин олова, 5
мин олова, 5![]() мин же леза.
мин же леза.
1086.
а) Вася сказал, что у них в классе 35 учащихся, причём ![]() всех
учащихся — девочки. Папа сказал, что такого не может быть.
всех
учащихся — девочки. Папа сказал, что такого не может быть.
Почему?
б) Известно, что ![]() класса учится на «4» и «5». Сколько
учащихся
класса учится на «4» и «5». Сколько
учащихся
может быть в классе?
г) Известно, что ![]() класса — девочки,
класса — девочки, ![]() из них — отличницы.
Сколь -
из них — отличницы.
Сколь -
ко учащихся может быть в классе?
Решение. а) 35 не делится на 3. Поэтому Вася ошибся.
б) Число учащихся делится на 15 — это 15 или 30 учащихся (мож-
но считать, что классов по 45 учащихся не бывает).
г) Число учащихся делится на 5 и на 7. Наименьшее такое число — 35 (классов по 70 учащихся уж точно не бывает).
1087. а) В классе послушных девочек столько же, сколько непо-слушных мальчиков. Кого в классе больше: послушных детей или мальчиков?
Решение. В классе имеются послушные девочки (ПД) и непослушные девочки (НД), послушные мальчики (ПМ) и непослушные мальчики (НМ). Требуется сравнить число послушных детей и число мальчиков:
ПМ + ПД и ПМ + НМ.
По условию задачи послушных девочек (ПД) столько же,
сколько непослушных мальчиков (НМ), поэтому в классе послушных детей (ПМ + ПД)
столько же, сколько мальчиков (ПМ + НМ).
В этом разделе имеются задачи для повторения изученного в начальной школе и в 5 классе. Учитель может использовать приведённые задания для организации повторения в случае обнаружения пробелов по какой-либо теме, а также для текущего и итогового повторения.
1139. Задачи С. А. Рачинского. а) Я дал одному ученику 3 ореха, а всем остальным по 5. Если бы я всем дал по 4 ореха, у меня осталось бы 15. Сколько было орехов?
б) В школе равное число девочек и мальчиков. Я принёс 234 ореха, и каждому мальчику досталось по 5 орехов, каждой девочке — по 4 ореха. Но девочки обиделись, и в другой раз я принёс столько орехов, что всем досталось по 6. Сколько орехов я принёс?
Решение. а) I способ. Чтобы каждому ученику досталось по 4 ореха и 15 орехов осталось, можно забрать по 1 ореху у 15 учащихся, у которых по 5 орехов, ещё 1 орех взять у 16-го ученика, у которого также было 5 орехов, и отдать 17-му, у которого было 3 ореха. Следовательно, у 16 учащихся было по 5 орехов и у одного — 3. Всего орехов было
1 3 + 16 5 = 83.
II способ. Представим, что сначала раздали всем учащимся по 4 ореха и 15 орехов осталось. Раздадим по 1 ореху 15 учащимся, ещё 1 орех возьмём у 16-го ученика и отдадим 17-му. У 16 учащихся станет по 5 орехов и у одного — 3. Орехов было 1 3 + 16 5 = 83.
б) 1) 234 (5 + 4) = 26 (пар) — мальчиков и девочек; 2) 26 (2 6) = 312 (орехов) — я принёс во второй раз. Ответ. а) 83 ореха; б) 312 орехов.
1140. Из «Азбуки» Л. Н. Толстого. Пять братьев разделили после отца наследство поровну. В наследстве было три дома. Три дома нельзя было делить, их взяли старшие три брата. А меньшим за то выделили деньги. Каждый из старших заплатил по 800 р. меньшим. Меньшие разделили эти деньги между собою, и тогда у всех братьев стало поровну. Много ли стоили дома?
Решение. 1) 3 800 = 2400 (р.) — дали старшие братья; 2) 2400 2 = 1200 (р.) — получил каждый младший брат.
Здесь учащиеся часто ошибаются, считая, что они нашли стоимость каждого дома. Это стоимость дома без 800 р.
3) 800 + 1200 = 2000 (р.) — стоил каждый дом.
Если возникнут сомнения в правильности решения, можно сделать проверку: 2000 3 5 = 1200 (р.) — доля наследства каждого. Младшие братья её получили, старшие тоже:
2000 – 800 = 1200 (р.).
Ответ. По 2000 р.
1143. а) Мама раздала детям по четыре конфеты, и три конфеты остались лишними. Чтобы дать детям по пять конфет, двух конфет не хватит. Сколько детей?
Решение. Представьте, что мама раздала детям по 4 конфеты. Сколько конфет у неё осталось? (3.) Скольким детям хватит ещё по одной (пятой) конфете? (Троим.) Скольким детям не хватит ещё по одной конфете? (Двоим.) Сколько всего детей? (3 + 2 = 5.) Ответ. 5 детей.
1145. Из «Всеобщей арифметики» И. Ньютона. Некто желает распределить между бедными деньги. Если бы у него было на восемь динаров больше, то он мог бы дать каждому по три, но он раздаёт лишь по два, и у него ещё остаётся три. Сколько бедных?
Решение. Пусть сначала некто раздавал по 2 динара, и у него осталось 3 динара. Если бы у него было ещё 8 динаров, то он смог бы дать ещё по 1 динару 11 бедным (3 + 8 = 11). Итак, было 11 бедных. Ответ. 11 бедных.
1146. а) Для детского сада купили 20 пирамид: больших и малень-ких — по 7 и по 5 колец. У всех пирамид 128 колец. Сколько больших пирамид?
Решение. Если бы все 20 пирамид имели по 5 колец, то всех колец было бы
20 5 = 100,
а по условию их 128. Лишние
128 – 100 = 28 колец —
это кольца (сверх пяти) от больших пирамид, которых было
28 2 = 14. Ответ. 14 больших пирамид.
1148. Древнекитайская задача. В клетке сидят фазаны и кролики. У них вместе 35 голов и 94 ноги. Сколько фазанов и сколько кроликов в клетке?
Решение. Задачу можно решить аналогично задаче 1146. Если бы в клетке сидели одни фазаны, то ног было бы
2 35 = 70,
но их на 94 – 70 = 24 больше. Разница образовалась за счёт того, что у каждого кролика на 2 лапы больше, чем у фазана. Кроликов
24 2 = 12,
а фазанов
35 – 12 = 23.
Не менее интересно рассуждение, найденное нами у старых мастеров методики математики и вызывающее у детей живейшее участие в решении задачи. Опишем примерный диалог учителя с классом (в скобках показаны действия, с помощью которых получен результат). — Представим, что на верх клетки, в которой сидят фазаны и кролики, мы положили морковку. Все кролики встанут на задние лапы, чтобы дотянуться до морковки. Сколько лап в этот момент будет стоять на земле?
— 70 лап (35 2 = 70).
— Но в условии задачи даны 94 лапы, где же остальные?
— Остальные не посчитаны — это передние лапы кроликов.
— Сколько их?
— 24 (94 – 70 = 24).
— Сколько же кроликов?
— 12 (24 2 = 12).
— А фазанов?
— 23 (35 – 12 = 23).
После завершения диалога можно предложить учащимся записать решение задачи в тетрадях «с пояснениями». Разумеется, здесь трудно кратко и точно пояснить первое действие. Ответ. 23 фазана и 12 кроликов.
1150. Старинная задача. а) Крестьянин хочет купить лошадь и для этого продаёт рожь. Если он продаст 15 ц ржи, то ему не хватит для покупки лошади 80 рублей, а если он продаст 20 ц ржи, то после покупки у него останется 110 рублей. Сколько стоит лошадь?
Решение. Продав 20 – 15 = 5 (ц) ржи, крестьянин заплатит недостающие 80 р. и у него останется 110 р., т. е. 1 ц ржи стоит
(80 + 110) 5 = 38 (р.).
Тогда лошадь стоит 15 38 + 80 = 650 (р.). Ответ. 650 р.
1151. а) Старинная задача. За 1000 р. я купил 44 коровы — по 18 р. и по 26 р. Сколько тех и других?
Решение. Если бы купили 44 коровы по 18 р., то заплатили бы 792 р., на самом деле заплатили на 1000 – 792 = 208 (р.) больше, так как за каждую более дорогую корову платили на 26 – 18 = 8 (р.) больше. Дорогих коров было
208 8 = 26,
дешёвых —
44 – 26 = 18.
Ответ. 18 коров по 18 р. и 26 коров по 26 р.
1153. Из «Арифметики» Л. Ф. Магницкого. Некто купил 112 баранов, старых и молодых, дал 49 рублей и 20 алтын. За старого он платил по 15 алтын и по 2 деньги, а за молодого — по 10 алтын; узнайте, сколько старых и сколько молодых баранов купил он.
Решение. После перевода всех сумм в копейки решение задачи можно объяснить так. Пусть сначала за всех баранов заплатили как за молодых — по 30 к. Это составило 112 30 = 3360 (к.). По условию задачи заплатили больше на 4960 – 3360 = 1600 (к.). Эта разность образовалась за счёт того, что за каждого старого барана платили на 46 – 30 = 16 (к.) больше, чем за молодого. Тогда старых баранов было 1600 16 = 100, а молодых — 112 – 100 = 12.
В тетрадях учащиеся это решение могут записать так:
1) 112 30 = 3360 (к.) — стоят 112 молодых баранов;
2) 4960 – 3360 = 1600 (к.) — надо доплатить за старых баранов;
3) 46 – 30 = 16 (к.) — на столько старый баран дороже молодого;
4) 1600 16 = 100 (бар.) — купили старых баранов; 5) 112 – 100 = 12 (бар.) — купили молодых баранов. Ответ. 100 старых и 12 молодых баранов.
1154. Старинная задача. Купец купил 110 фунтов табака. 50 фунтов оказались подмоченными, и купец продал их на 2 р. дешевле за 1 фунт, чем заплатил сам. Остальной табак он продал на 3 р. дороже за 1 фунт, чем уплатил сам. Подсчитайте прибыль купца.
Решение. На 50 фунтах подмоченного табака купец имел убытка
2 50 = 100 (р.),
на оставшихся 110 – 50 = 60 (фунтах) он имел прибыли
3 60 = 180 (р.).
Итого вся прибыль составила
180 – 100 = 80 (р.). Ответ. 80 р.
1156. а) За краски и две кисти заплатили 32 р. 19 к., за краски и кисть — 21 р. 72 к. Сколько стоят краски? Сколько стоит кисть?
б) За две тетради и ручку заплатили 6 р. 66 к., а за тетрадь и две ручки заплатили 9 р. 93 к. Сколько стоит тетрадь? Сколько стоит ручка?
Решение. а) В первом случае за лишнюю кисть заплатили
3219 – 2172 = 1047 (к.).
Краски стоят
2172 – 1047 = 1125 (к.). 1047 к. = 10 р. 47 к., 1125 к. = 11 р. 25 к.
б) За два раза купили 3 тетради и 3 ручки за 666 + 993 = 1659 (к.), тогда тетрадь и ручка стоят 1659 3 = 553 (к.), тетрадь стоит 666 – 553 = 113 (к.), а ручка стоит 553 – 113 = 440 (к.).
113 к. = 1 р. 13 к., 440 к. = 4 р. 40 к.
Ответ. а) 11 р. 25 к., 10 р. 47 к.; б) 1 р. 13 к., 4 р. 40 к.
1160. Алёша и Боря вместе весят 82 кг, Алёша и Вова весят 83 кг, Боря и Вова весят 85 кг. Сколько весят вместе Алёша, Боря и Вова?
Решение. I способ. Сравнение двух первых условий показывает, что Боря легче Вовы на 1 кг, а вместе они весят 85 кг, т. е. Боря весит
(85 – 1) 2 = 42 (кг),
а втроём они весят
42 + 83 = 125 (кг).
II способ. Если записать краткое условие задачи так:
А + Б = 82
А + В = 83
В + Б = 85
и сложить левые и правые части равенств, то получим
2(А + Б + В) = 250,
откуда получим, что
А + Б + В = 125,
т. е. втроём они весят 125 кг. Здесь А, Б, В — вес Алёши, Бори и Вовы соответственно.
1161. а) Старинная задача. Четверо купцов имеют некоторую сумму денег. Известно, что, сложившись без первого, они соберут 90 р.; сложившись без второго — 85 р.; сложившись без третьего — 80 р.; сложившись без четвёртого — 75 р. Сколько у кого денег?
Решение. I способ. Из двух первых условий следует, что у второго купца было на 5 р. больше, чем у первого. Из второго и третьего условий следует, что у третьего купца было на 5 р. больше, чем у второго. Если бы третий купец дал первому 5 р., то у первых трёх купцов денег стало бы поровну — по 75 3 = 25 (р.). Значит, у первого купца было 25 – 5 = 20 (р.), у второго — 25 р., у третьего — 25 + 5 = 30 (р.), а у четвёртого — 90 – 25 – 30 = 35 (р.).
II способ. Запишем коротко условие, обозначив через I, II, III, IV суммы первого, второго, третьего и четвёртого купцов соответственно:
IV + I + II = 80
I + II + III = 75.
Сложим левые и правые части равенств, получим
3(I + II + III + IV) = 330, I + II + III + IV = 110.
Тогда у первого купца было 110 – 90 = 20 (р.), у второго купца было 110 – 85 = 25 (р.), у третьего — 110 – 80 = 30 (р.), а у четвёртого — 110–75=35 (р.).
Ответ. 20 р., 25 р., 30 р., 35 р.
1162. Спортсмен плыл против течения реки. Проплывая под мо-стом, он потерял флягу. Через 10 мин пловец заметил пропажу и повернул обратно. Он догнал флягу у второго моста. Найдите скорость течения реки, если известно, что расстояние между мостами 1 км.
Решение. Эта задача развивает идею задачи 561. Самое трудное для учащихся — понять, что пловец сближался с флягой столько же времени, сколько удалялся от неё, так как удаление и сближение происходили на одно и то же расстояние и скорости удаления и сближения равны. В самом деле, обозначим собственную скорость пловца x км/ч, а скорость фляги y км/ч. Тогда их скорость удаления равна (x – y) + y = x (км/ч), а скорость сближения (x + y) – y = x (км/ч). Итак, за 20 мин фляга проплыла 1 км, за 60 мин она проплывёт в 3 раза больше — 3 км. Следовательно, скорость течения реки 3 км/ч. Ответ. 3 км/ч.
1163. Три соседки готовили обед на общей плите в коммуналь-ной квартире. Первая принесла 10 поленьев, вторая — 8 поленьев, а у треть ей дров не было — она угостила своих соседок, дав им 9 яблок. Как соседки должны поделить яблоки по справедливости?
Решение. При решении этой задачи учащиеся чаще всего не обращают внимания на то, что яблоки были даны лишь за 6 поленьев.
1) (10 + 8) 3 = 6 (поленьев) — израсходовала третья соседка; 2) 10 – 6 = 4 (полена) — первая соседка дала третьей; 3) 8 – 6 = 2 (полена) — вторая соседка дала третьей.
Первая соседка должна получить яблок в 2 раза больше, чем вторая. Первая — 6 яблок, вторая — 3. Ответ. 6 яблок и 3 яблока.
1165. Несколько торговцев продавали бананы по 24 р. за 1 кг, а один — по 21 р. 60 к. за 1 кг. Когда контролёры проверили его весы, то оказалось, что при весе 800 г они показывали ровно 1 кг. По какой цене на самом деле продавал бананы этот торговец?
Решение. Так как 800 г = ![]() кг, то торговец
продавал бананы по це не 2160
кг, то торговец
продавал бананы по це не 2160 ![]() = 2700 (к.) за 1 кг. 2700 к. = 27 р.
= 2700 (к.) за 1 кг. 2700 к. = 27 р.
Ответ. По 27 р.
Замечание. В задаче 1165 есть лишнее условие — 24 р., от него ответ не зависит.
1176. Расстояние между двумя пристанями по течению реки катер проходит за 8 ч, а плот — за 72 ч. Сколько времени потратит катер на тот же путь по озеру?
Решение. 1) 1 8 = ![]() (расст.) — проходит
катер за 1 ч по течению реки;
(расст.) — проходит
катер за 1 ч по течению реки;
2) 1 72 = ![]() (расст.)
— проплывает плот за 1 ч;
(расст.)
— проплывает плот за 1 ч;
3) ![]() –
– ![]() =
= ![]() (расст.)
— проходит катер за 1 ч по озеру;
(расст.)
— проходит катер за 1 ч по озеру;
4) 1 ![]() = 9
(ч) — потратит катер на тот же путь по озеру.
= 9
(ч) — потратит катер на тот же путь по озеру.
Ответ. 9 ч.
1177. а) Моторная лодка проходит расстояние между двумя пунктами A и B по течению реки за 2 ч, а плот — за 8 ч. Какое время затратит моторная лодка на обратный путь?
Решение. 1) 1 2 = ![]() (расст.) — проходит
лодка за 1 ч по течению реки;
(расст.) — проходит
лодка за 1 ч по течению реки;
2)
1 8 = ![]() (расст.) — проплывает плот за 1 ч;
(расст.) — проплывает плот за 1 ч;
3)
![]() –
– ![]() =
= ![]() (расст.) —
проходит лодка за 1 ч в стоячей воде;
(расст.) —
проходит лодка за 1 ч в стоячей воде;
4)
![]() –
– ![]() =
= ![]() (расст.) —
проходит лодка за 1 ч против течения реки;
(расст.) —
проходит лодка за 1 ч против течения реки;
5)
1 ![]() = 4 (ч) — время движения моторной лодки
против течения реки.
= 4 (ч) — время движения моторной лодки
против течения реки.
Ответ. 4 ч.
1181. Из «Всеобщей арифметики» И. Ньютона. Трое рабочих могут выполнить некоторую работу, при этом A может выполнить её один раз за 3 недели, B — три раза за 8 недель, C — пять раз за 12 недель. Спрашивается, за какое время они смогут выполнить эту работу все вместе. (Считайте, что в неделе 6 рабочих дней по 12 ч.)
Решение. Рабочий A выполняет в неделю 1 3
= ![]() (работы), рабо чий B — 3 8 =
(работы), рабо чий B — 3 8 = ![]() (работы),
а рабочий C — 5 12 =
(работы),
а рабочий C — 5 12 = ![]() (работы). Вместе они могут выполнить в
неделю
(работы). Вместе они могут выполнить в
неделю
![]() +
+ ![]() +
+ ![]() =
= ![]() (работы).
(работы).
Тогда на выполнение всей работы при совместной работе им потре буется
1 ![]() =
= ![]() (недели).
(недели).
В соответствии с условиями задачи это составит 5 дней и 4 ч.
Ответ. 5 дней и 4 ч.
Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
Примерное тематическое планирование работы по учебнику «Ма-
тематика, 5». . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
Глава 1. Натуральные числа и нуль . . . . . . . . . . . . . . . . . . . . . . . . 16
Глава 2. Измерение величин . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
Глава 3. Делимость натуральных чисел. . . . . . . . . . . . . . . . . . . . . . 73
Глава 4. Обыкновенные дроби. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84
Повторение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 120
У ч е б н о е и з д а н и е
Серия «МГУ — школе»
Потапов Михаил Константинович
Шевкин Александр Владимирович
Методические рекомендации
5 класс
Учебное пособие для общеобразовательных организаций
Центр естественно-математического образования
Редакция математики и информатики
Зав. редакцией Т. А. Бурмистрова
Редактор Т. Г. Войлокова
Младший редактор Е. А. Андреенкова
Художественные редакторы О. П. Богомолова, Т. В. Глушкова
Компьютерная графика Е. В. Бугаевой
Техническое редактирование и компьютерная вёрстка Н. В. Кондратьевой Корректор Н. В. Бурдина
Налоговая льгота — Общероссийский классификатор продукции ОК 005-93—953000.
Изд. лиц. Серия ИД № 05824 от 12.09.01. Подписано в печать 02.03.16. Формат
7090 1/16. Бумага офсетная. Гарнитура SchoolBookCSanPin. Уч.изд. л. 7,97. Тираж 50 экз. Заказ № .
Акционерное общество «Издательство «Просвещение». 127521, Москва, 3-й проезд Марьиной рощи, 41.
Отпечатано в типографии «Onebook» ООО «Сам Полиграфист».
129090, Москва, Протопоповский пер., 6. Тел.: +7(495)545-37-10. E-mail: indo@onebook.ru Сайт: www.onebook.ru
[1] рака
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.