
МИНИСТЕРСТВО ОБРАЗОВАНИЯ ОРЕНБУРГСКОЙ ОБЛАСТИ
Государственное автономное профессиональное образовательное учреждение
«Бузулукский строительный колледж» г. Бузулука Оренбургской области
|
РАССМОТРЕНО И ОДОБРЕНО на заседании ПЦК Протокол №_1 от «___»___2019г Руководитель ПЦК __________/Корочкина Е.Ю.
|
УТВЕРЖДАЮ Зам. директора по УР ________Е.Н. Индерейкина «___» ________ 2019г.
|
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ДЛЯ ОБУЧАЮЩИХСЯ ПО ВЫПОЛНЕНИЮ
ПРАКТИЧЕСКИХ РАБОТ
по дисциплине ЕН.01 «Математика»
по специальности: 08.02.01 Строительство и эксплуатация зданий и сооружений.
Разработал: преподаватель
Попович Марина Алексеевна
Бузулук , 2019
Разработчик: Попович Марина Алексеевна, преподаватель ГАПОУ «БСК», высшей квалификационной категории
Методические рекомендации для обучающихся по выполнению практических работ по дисциплине ЕН.01 «Математика» являются частью программы подготовки специалистов среднего звена ГАПОУ «БСК» по специальности: 08.02.01 Строительство и эксплуатация зданий и сооружений.
Методические рекомендации адресованы студентам очной формы обучения.
Рекомендовано к использованию предметно-цикловой комиссией колледжа.
Содержание
Введение
Пояснительная записка
Перечень практических занятий
Практическое занятие №1
Практическое занятие №2
Практическое занятие № 3
Практическое занятие № 4
Практическое занятие № 5
Практическое занятие №6
Практическое занятие № 7
Практическое занятие № 8
Практическое занятие №9
Практическое занятие № 10
Практическое занятие №11
Практическое занятие № 12
Литература
Учебная дисциплина «Математика» изучается студентами на втором курсе. По окончании учебного курса (76ч) студенты сдают устный экзамен. Методические рекомендации по выполнению практических работ обеспечивают реализацию рабочей программы по дисциплине ЕН 01. «Математика».
Реализация программы обеспечит компетентность будущих специалистов в области математики как неотъемлемой части их профессионализма в период вступления в самостоятельную жизнь.
Ведущей дидактической целью практических занятий является формирование практических умений, необходимых в последующей учебной деятельности и жизни.
В соответствии с ведущей дидактической целью содержанием практических занятий является решение разного рода задач, в том числе профессиональных (анализ проблемных ситуаций, решение ситуационных задач, работа с инструктивными материалами, справочниками).
На практических занятиях студенты овладевают первоначальными умениями и навыками, которые будут использовать в профессиональной деятельности и жизненных ситуациях.
Наряду с формированием умений и навыков в процессе практических занятий обобщаются, систематизируются, углубляются и конкретизируются теоретические знания, вырабатывается способность и готовность использовать теоретические знания на практике, развиваются интеллектуальные умения.
В результате обучения студент в области математики должен:
Уметь:
- выполнять необходимые измерения и связанные с ними расчеты;
- вычислять площади и объемы деталей строительных конструкций, объемы земляных работ;
- применять математические методы для решения профессиональных задач;
Знать:
- основные понятия о математическом синтезе и анализе, дискретной математики, теории вероятностей и математической статистики;
- основные формулы для вычисления площадей фигур и объемов тел, используемых в строительстве;
|
№ п/п |
№ урока |
Тема практических занятий |
Количество часов |
|
1 |
3 |
ПЗ № 1. Вычисление скалярного произведения векторов, модуля вектора и угла между векторами. Определение расстояния между точками и координат середины отрезка |
2 |
|
2 |
4 |
ПЗ № 2. Применение векторов для решения геометрических и практических задач |
2 |
|
3 |
7 |
ПЗ № 3. Определение взаимного расположения прямых и угла между ними, расстояние от точки до прямой |
2 |
|
4 |
13 |
ПЗ № 4. Расчет площадей строительных конструкций |
2 |
|
5 |
15 |
ПЗ №5. Вычисление объемов деталей строительных конструкций, определение объема земляных работ |
2 |
|
6 |
19 |
ПЗ № 6. Вычисление пределов последовательностей и функций с применением различных методов. Исследование функций на непрерывность, определение точек разрыва |
2 |
|
7 |
21 |
ПЗ № 7. Составление уравнения касательной и нормали. Определение экстремумов функций. Вычисление наибольшего и наименьшего значений функций на заданном отрезке |
2 |
|
8 |
22 |
ПЗ № 8. Применение производной к исследованию функции и для нахождения наилучшего решения в прикладных задачах |
2 |
|
9 |
24 |
ПЗ № 9. Вычисление неопределенных интегралов методом замены переменных и с помощью интегрирования по частям |
2 |
|
10 |
27 |
ПЗ № 10. Построение криволинейной трапеции. Применение определенного интеграла к вычислению площадей плоских фигур и к вычислению объемов |
2 |
|
11 |
31 |
ПЗ № 11. Вычисление вероятностей сложных событий. Теоремы сложения и умножения вероятностей. Формула полной вероятности и формула Бернулли |
2 |
|
12 |
33 |
ПЗ № 12. Составление статистического распределения выборки, построение полигона и гистограммы |
2 |
Тема: Вычисление скалярного произведения векторов, модуля вектора и угла между векторами. Определение расстояния между точками и координат середины отрезка
Цель работы: закрепить умения выполнять действия над векторами
Содержание работы.
Основные понятия.
1
Вектором называется отрезок, у
которого указано, какой из концов является началом, а какой – концом
(направленный отрезок), обозначается ![]() ,
, ![]() , где
, где ![]() - начало вектора,
- начало вектора, ![]() - конец.
- конец.
2 Векторы называются коллинеарными, если они расположены на одной или параллельных прямых.
3
Векторы называются ортогональными, если угол между ними ![]() .
.
4
Векторы можно складывать ( по правилам треугольника и параллелограмма), можно
умножать на число: ![]()
![]()
![]() ;
;
![]() .
.
5
Необходимое и достаточное условие коллинеарности векторов: 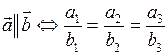
6
Модуль вектора ![]() равен
равен ![]()
7
Если заданы начало ![]() и
конец
и
конец ![]() вектора
вектора ![]() ,
то его координаты и длина находятся следующим образом:
,
то его координаты и длина находятся следующим образом:
![]() ;
;
![]() .
.
8 Скалярным произведением векторов называется число, равное произведению длин этих векторов на косинус угла между ними
![]()
![]()
9
Косинус угла между векторами 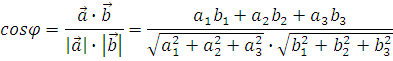
10
Необходимое и достаточное условие ортогональности векторов: ![]() .
.
11
Проекция вектора на направление: 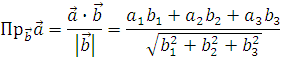
Задание
1 Найти линейную комбинацию векторов ![]()
2 Найти длины векторов ![]()
3 Найти косинусы углов между векторами ![]()
4 Найти ф![]()
5 Найти ![]()
6 Выяснить, коллинеарны ли векторы ![]() и
и ![]()
7 Выяснить, ортогональны ли векторы ![]() и
и ![]()
Исходные данные:
Даны точки ![]() .
.
Задание 1
Решение:
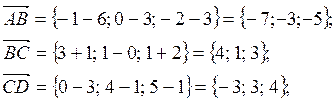
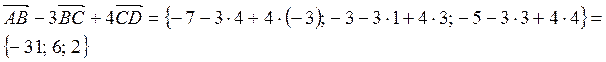
Задание 2
Решение:
![]()
![]()
![]()
Задание 3
Решение:
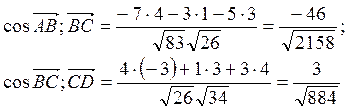
Задание 4
Решение:
Даны точки ![]() .
.
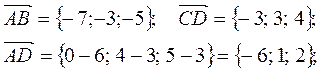
![]()
![]()
Задание 5
Решение:
![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
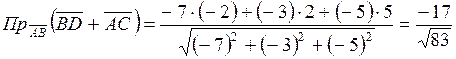 .
.
Задание 6
Решение:
![]() ,
, ![]()
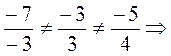 векторы не являются коллинеарными.
векторы не являются коллинеарными.
Задание 7
Решение:
![]() ,
, ![]()
![]() , следовательно, векторы не являются
ортогональными.
, следовательно, векторы не являются
ортогональными.
Задания к практической работе.
1 A (2; 3; -1); B (0; 1; 2); C (4; -1; -1); D (2; -3; 1)
2 A (3; -1; 1); B (1; 3; 2); C (1; -1; -1); D (4; 0; 3)
3 A (4; 1; 2); B (1; 0; 1); C (-1; 2; -1); D (3; 1; 0)
4 A (3; -2; 1); B (2; -1; 1); C (4; 0; 2); D (1; 1; -1)
5 A (-2; 2; 1); B (3; 0; 4); C (7; 1; 0); D (3; 0; 5)
6 A (1; -1; -1); B (2; 5; 7); C (-3; 1; -1); D (2; 2; 3)
7 A (-3; 1; 4); B (1; -2; -3); C (2; 2; 3); D (5; 3; 1)
8 A (2; -5; 1); B (4; 3; 5); C (-1; 0; 1); D (2; 1; 0)
9 A (-2; 2; 1); B (3; -1; 0); C (4; 4; 0); D (1; -1; 1)
10 A (4; 2; 5); B (0; 1; 3); C (-1; -1; 1); D (2; -2; 1)
11 A (1; 0; 1); B (7; 4; 3); C (3; -5; 1); D (-2; 2; 2)
12 A (5; 1; 0); B (-1; -1; -1); C (2; 4; 7); D (1; 0; 1)
13 A (10; 1; 1); B (-2; -1; 1); C (4; 3; 2); D (1; 0; -1)
14 A (2; -7; 4); B (2; -1; 3); C (1; 0; -1); D (2; 1; 3)
15 A (6; 3; 3); B (-1; 0; -2); C (3; 1; 1); D (0; 4; 5)
16 A (3; 2; 0); B (2; -1; 7); C (4; 0; 5); D (1; -2; -1)
17 A (4; -1; 2); B (1; 0; 3); C (-2; 1; 5); D (3; 8; -1)
18 A (1; 1; -3); B (-7; 5; 2); C (2; 1; 0); D (3; -3; 1)
19 A (5; 0; 1); B (2; -1; -1); C (-6; -1; 1); D (3; 1; 3)
20 A (3; 5; 1); B (7; -4; 3); C (2; 1; 1); D (0; -1; 3)
21 A (1; -2; 1); B (-1; 8; -3); C (3; 2; 1); D (5; 3; 1)
22 A (-3; -1; 1); B (2; -3; 0); C (1; 4; 5); D (2; 3; 4)
23 A (3; -1; 2); B (4; 0; 4); C (-1; 9; -1); D (3; -2; -2)
24 A (3; -2; 1); B (4; 2; 1); C (-1; -1; 1); D (3; 0; 1)
25 A (-2; 0; 1); B (4; -1; 3); C (-3; 2; 1); D (4; 1; 1)
26 A (2; -2; 1); B (2; 5; 7); C (1; 3; 5); D (7; 0; 3)
27 A (2; 3; 3); B (-2; 4; 1); C (3; 5; 2); D (3; 8; -1)
28 A (1; 1; -3); B (-3; 2; -1); C (4; 1; 2); D (7; -3; 0)
29 A (7; 6; 1); B (2; -1; -1); C (1; 0; 1); D (-2; 1; -1)
30 A (-7; 2; -1); B (2; 5; 1); C (2; 1; 1); D (0; 1; 3)
Критерии оценки
|
«2» |
«3» |
«4» |
«5» |
|
0-2 |
3-4 |
5-6 |
7 |
Тема работы: Применение векторов для решения геометрических и практических задач
Цель работы: закрепить умения выполнять действия над векторами
Содержание работы
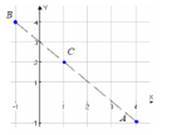
Пример 1. Найти (геометрически и аналитически) цент масс С системы двух точек А(4;-1), В(-1;4), имеющих соответственно массы m1=, m2=3.
Решение: Координаты цента масс системы двух точек: ![]()
![]() ,
, ![]()
![]() . Центр масс С(1;2) делит отрезок
АВ в отношении
. Центр масс С(1;2) делит отрезок
АВ в отношении ![]() , считая от точки А.
, считая от точки А.
![]()
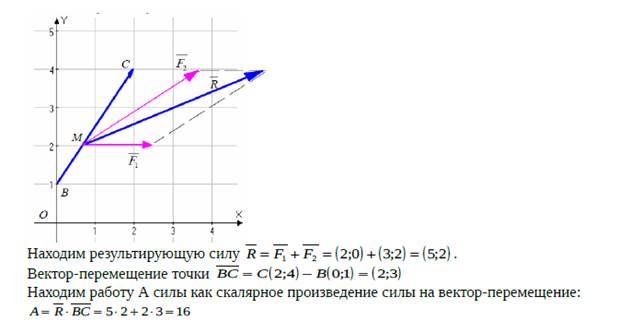
Пример 2. Найти равнодействующую сил ![]() ,
, ![]() , приложенных к точке А(1;1), где
, приложенных к точке А(1;1), где ![]() ,
, ![]() .
.
Решение: Запишем силы в проекциях ![]() ,
, ![]()
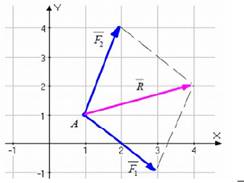
При построении силы, например ![]() , смещаемся из точки А
горизонтально на 1 единицу вправо и на три единицы вверх. Равнодействующая
равна сумме сил:
, смещаемся из точки А
горизонтально на 1 единицу вправо и на три единицы вверх. Равнодействующая
равна сумме сил: ![]()
Пример 3. Определить угол α и силу ![]() , приложенную к середине С отрезка
АВ, такую, что система сил, изображенных на чертеже, уравновешенная.
, приложенную к середине С отрезка
АВ, такую, что система сил, изображенных на чертеже, уравновешенная.
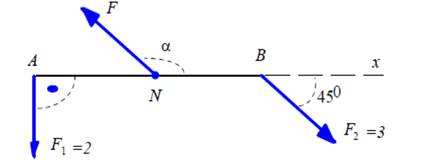
Решение: Введем систему координат. Направим ось ОХ вдоль
АВ, точку А примем за начало отсчета. Обозначим ![]() . Система уравновешена, если их
векторная сумма равна нулю. Находим проекции сил на координатные оси:
. Система уравновешена, если их
векторная сумма равна нулю. Находим проекции сил на координатные оси:
![]()
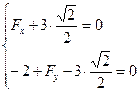 =>
=>  , модуль
, модуль ![]()
![]() , α≈1170.
, α≈1170.
Пример 4. Точка движется с ускорением ![]() по дуге АВ. Разложить
геометрически ускорение
по дуге АВ. Разложить
геометрически ускорение ![]() в сумму нормального и касательного ускорений
в сумму нормального и касательного ускорений ![]() .
.
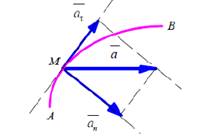
Решение: Проводим через точку касания М касательную к траектории АВ. Далее
проводим нормаль траектории, т.е. перпендикуляр к касательной, проходящий через точку
М. Построим прямоугольник на этих прямых с диагональю, равной вектору а .
Получаем разложение ускорения ![]() .
.
Пример 5.
Найти силу, растягивающую стержень СВ кронштейна, к
которому подвешен груз Р. ![]() .
.
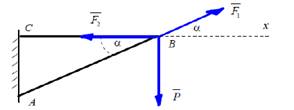
Решение: Укажем на чертеже силы, приложенные к точке В:
вес груза - ![]() , реакция
, реакция ![]() стержня АВ, реакция
стержня АВ, реакция ![]() стержня СВ. Составим уравнение
равновесия точки В:
стержня СВ. Составим уравнение
равновесия точки В:
![]()
Решаем систему уравнений
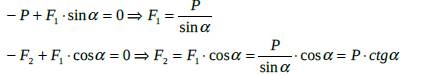
Ответ: ![]() ,
, ![]() .
.
Пример 6. 
Пример 7. 
Задания для самостоятельной работы

Критерии оценки
|
«2» |
«3» |
«4» |
«5» |
|
0-2 |
3-4 |
5-6 |
7 |
Тема: Определение взаимного расположения прямых и угла между ними, расстояние от точки до прямой
Цель работы: закрепить умения составления уравнения прямой различными способами и вычисления расстояния от точки до прямой
Содержание работы:
Прямая на плоскости. Различные способы задания прямой.
Уравнение прямой с угловым коэффициентом
![]() – это уравнение прямой
с угловым коэффициентом (1)
– это уравнение прямой
с угловым коэффициентом (1)
Если
прямая проходит через начало координат, то ![]() и уравнение
и уравнение ![]() .
.
Если
прямая параллельна оси ![]() , то
, то ![]() и уравнение
и уравнение ![]() .
.
Уравнение
прямой, параллельной оси ![]() , получается особо. Ясно, что
оно:
, получается особо. Ясно, что
оно: ![]() .
.
Общее
уравнение прямой ![]() (2)
(2)
Геометрический смысл коэффициентов А и В общего уравнения прямой: упорядоченная пара (-В,А) является координатами направляющего вектора прямой, упорядоченная пара (А,В) является координатами вектора нормали.
Уравнение прямой, проходящей через две заданные точки.
Уравнение
прямой, проходящей через точки ![]() и
и ![]() имеет вид
имеет вид ![]() (3)
(3)
Уравнение
прямой в отрезках ![]() – это уравнение прямой в отрезках. (4)
– это уравнение прямой в отрезках. (4)
Уравнение прямой, проходящей через точку в заданном направлении
Найдем
уравнение прямой, не параллельной оси ![]() , проходящей через данную точку
, проходящей через данную точку ![]() и имеющей заданное
направление. Направление прямой можно задать ее угловым коэффициентом
и имеющей заданное
направление. Направление прямой можно задать ее угловым коэффициентом ![]() .
.
![]() . (5)
. (5)
Пример: через точку ![]() провести прямую перпендикулярную к
прямой
провести прямую перпендикулярную к
прямой ![]() .
.
Решение:
из условия перпендикулярности ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]() .
.
Уравнение прямой, заданной точкой и вектором нормали.
Точка М0(х0,у0) и ненулевой вектор n(A,B).
A(x-x0)+B(y-y0)=0 – уравнение прямой заданной точкой и вектором нормали. (6)
Каноническое уравнение прямой.
Точка М0(х0,у0)
и ненулевой вектор а(а1,а2) – параллелен прямой
(называется направляющий вектор). ![]() (7)
(7)
Параметрические уравнения прямой
М(х,у) – произвольная точка прямой, М0(х0,у0) – данная точка прямой, ненулевой вектор а(а1,а2) – направляющий вектор этой прямой, t – вещественное число (параметр).
![]()
Пусть
даны две пересекающиеся прямые ![]() ;
; ![]() .
.
Требуется
найти острый угол ![]() между ними.
между ними. 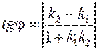 .
.
Если
прямые 1 и 2 заданы их общими уравнениями ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
. 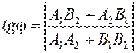
Если
прямые - параллельны, то углы ![]() и
и ![]() равны между собой, то есть
равны между собой, то есть ![]() .
.
Равенство угловых коэффициентов – условие параллельности прямых.
Условие
перпендикулярности двух прямых имеет вид: ![]() или
или ![]() .
.
В случае,
когда прямые заданы общими уравнениями, условие параллельности ![]() ; условие перпендикулярности:
; условие перпендикулярности: ![]() .
.
Расстояние от точки до прямой
Пусть на
плоскости ![]() задана
прямая
задана
прямая ![]() своим
общим уравнением
своим
общим уравнением ![]() и точка
и точка ![]() . Требуется найти расстояние
. Требуется найти расстояние ![]() от точки
от точки ![]() до прямой
до прямой ![]() .
.
![]() :
: 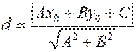 .
.
Пример: определить расстояние от точки ![]() до прямой
до прямой ![]() .
.
Решение: 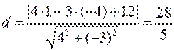 .
.
Задание (сделать рисунок)
1. Составить каноническое, общее и параметрическое уравнения прямых, задающих стороны треугольника
2. Составить общие уравнения прямых, проходящих через вершины треугольника, параллельно его сторонам
3. Составить уравнения медиан треугольника
4. Найти координаты центра тяжести треугольника ( точка пересечения медиан)
5. Найти длины высот треугольника
6. Составить уравнения высот
7. Найти углы треугольника
1 A (2; 3); B (-2; 1); C (-4; -1)
2 A (3; -1); B (1; 3) C (-1; -1)
3 A (-4; 1); B (1; 0); C (-1; -5);
4 A (3; -2); B (-2; -1); C (4; 4)
5 A (-2; 5); B (3; 0); C (7; 5)
Критерии оценки
|
«2» |
«3» |
«4» |
«5» |
|
0-1 |
2-3 |
4-5 |
6-7 |
Тема: Расчет площадей строительных конструкций
Цель Занятия: Рассмотреть практическое применение формул площадей геометрических тел при решении задач.
Теоретические сведения к практической работе
1. Площадь поверхности многогранника находится как сумма площадей всех его граней.
2. Площадь поверхности призмы равна: Sп.п = Sбок + 2Sосн
Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту. Sбок = Ph
3. Площадь поверхности цилиндра равна: Sбок= 2πrh, Sосн=πr2,
Sцил п.п = Sбок + 2Sосн=2πrh + 2πr2= 2πr(r + h),
где r - радиус цилиндра, h -высота цилиндра
4. Площадь поверхности конуса равна: Sбок= πrl , Sосн=πr2, Sкон п.п = Sбок + Sосн=πrl + πr2= πr(r + l)
где r - радиус конуса, l -образуюущая конуса
5. Площадь поверности усеченного конуса: Sбок= πl(r1 + r2), Sус кон п.п = Sбок + Sосн1 + Sосн2,
где r - радиус конуса, l -образуюущая конуса
6. Площадь поверхности пирамиды равна: Sпир= Sбок + Sосн
7. Площадь поверхности шара (сферы): Sсф= 4πr2
Примеры и последовательность выполнения заданий.
Необходимо оштукатурить стены и потолок гаража, размеры которого 3 ´ 4,3 ´ 2,3м толщиной 15мм. Ворота гаража имеют размеры 2,5´2,2м. Найти объем необходимого материала.
Решение: 15мм = 0, 015м
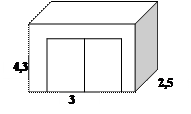 1.
Площадь боковой поверхности:
1.
Площадь боковой поверхности:
Sбок.=
2 (a + b) ![]() h = 2
h = 2![]() (3 +
4,3)
(3 +
4,3) ![]() 2,5=36,5м2;
2,5=36,5м2;
2. Площадь потолка: Sп.= ab
= 3 ![]() 4,3
=12,9м2;
4,3
=12,9м2;
3. Площадь ворот: Sв. = ab =2,5 ![]() 2,2
= 5,5 м2;
2,2
= 5,5 м2;
4. Рабочая поверхность: Sраб. = Sбок. +Sп. - Sв. = 36,5 + 12,9 – 5,5 = 43,9м2
5. Объём материала: V
= Sраб![]() h = 43,9
h = 43,9 ![]() 0,015
= 0, 6585 » 0,66м3
0,015
= 0, 6585 » 0,66м3
Ответ: Потребуется 0,66м3 материала.
Задания для практической работы
Задание 1. Крыша имеет форму пирамиды, основание которой – прямоугольник со сторонами a и b, боковые ребра равнонаклонены к основанию под углом β. Сколько листов железа размером 0,70×1,4 м нужно для покрытия крыши, если на отходы нужно добавить 10% площади крыши?
|
Вариант |
a |
b |
β |
|
1 |
5 |
17 |
300 |
|
2 |
9 |
13 |
450 |
|
3 |
8 |
55 |
600 |
Задание 2. Во что обойдется окраска конического шпиля здания, диаметр окружности основания которого d Угол между образующими в осевом сечении β, окраска 1 м2 по ЕНИР стоит 55 руб.
|
Вариант |
1 |
2 |
3 |
|
d, м |
6,6 |
4 |
4 |
|
β |
600 |
900 |
1200 |
Задание 3. Рабочий оштукатуривает вручную колонну улучшенной штукатуркой. Сколько времени ему понадобится, чтобы оштукатурить колонну высотой 6 м, диаметром 1 м, соблюдая норму времени k=0,79ч на 1 м2?
|
Вариант |
1 |
2 |
3 |
|
h, м |
5 |
4 |
6 |
|
d, м |
1 |
1,5 |
0,5 |
Задача 4. Сколько олифы потребуется для окраски внешней поверхности n ведер, имеющих форму усеченного конуса с диаметром оснований 25см и 30см и образующей 27,5см, если на 1м2 требуется k=150 гр. олифы?
|
Вариант |
d1,см |
d2,см |
L,см |
n |
|
1 |
20 |
35 |
27 |
50 |
|
2 |
15 |
20 |
260 |
100 |
|
3 |
25 |
30 |
280 |
90 |
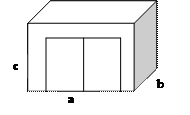 Задача
5. Необходимо оштукатурить стены и потолок гаража, размеры которого a´b´c (м)
толщиной h мм. Ворота гаража имеют размеры d´f(м). Найти объем необходимого
материала.
Задача
5. Необходимо оштукатурить стены и потолок гаража, размеры которого a´b´c (м)
толщиной h мм. Ворота гаража имеют размеры d´f(м). Найти объем необходимого
материала.
|
Вариант |
Размер гаража, a´b´c, м |
Размер ворот, d´f , м |
Толщина,h- мм |
|
1 |
5´3´2,5 |
2´2,5 |
15 |
|
2 |
4,5´3´3 |
2,5´2,3 |
16 |
|
3 |
4,8´2,8´2,6 |
2,7´2,5 |
18 |
Критерии оценки
|
«2» |
«3» |
«4» |
«5» |
|
0-2 |
3 |
4 |
5 |
Тема: Вычисление объемов деталей строительных конструкций, определение объема земляных работ
Цель работы: Научить решать профессиональные задачи по нахождению объемов тел.
Теоретические сведения к практической работе
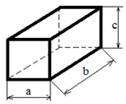 Кирпичи-
параллелепипед
Кирпичи-
параллелепипед
250×120×65 мм - пустотелый ,
250×120×88 мм - утолщенный
Объем параллелепипеда равен произведению трех его измерений: V = а∙b∙с,
где а – ширина, b – длина, с – высота параллелепипеда.
Пример 1. Найти объем 10 кирпичей в мм3, см3 , м3.
а) пустотелого; б) утолщенного.
Решение:
а) объем пустотелого кирпича: V1 = 250 · 120 · 65 = 1950000мм 3
объем 10 кирпичей: 1950000мм 3 ·10 = 195 · 10 5мм3; 1950см3 ·10 = 19500см3; 0,00195м3 ·10 = 0,0195м3
б) объем пустотелого кирпича: V2 = 250 ·120 ·88 = 2640000мм 3
объем 10 кирпичей: 2640000мм 3 ·10 = 264 ·105мм3; 2640см3 ·10 = 26400см 3; 0,00264м3 ·10 = 0,0264м3.
Пример 2. Определить расход уплотненного кирпича и количество раствора для кладки стены длинной 20м, высотой 5,2м, толщиной в 2,5 кирпича и площадью проема 4м 2.
Решение:
Пример 3.
Вычислить необходимое количество кирпичей, для кладки стены площадью 1м2 толщиной:
а) в один кирпич; 1 кв.м. кладки в 1 кирпич (толщина кладки в 25 см.)
б) в два кирпича; 1 кв.м. кладки в 2 кирпича (толщина кладки 51 см.)
 в) в два с половиной
кирпича; 1 кв.м. кладки в 2,5 кирпича (толщина кладки 64
см)
в) в два с половиной
кирпича; 1 кв.м. кладки в 2,5 кирпича (толщина кладки 64
см)
Решение:
а) 1. 1 ·1 · 0,25 = 0,25м 3 – объем кладки в один кирпич;
2. 0,25м 3 : 0,00195м 3 = 128,2шт., т.е.129 кирпичей;
б) 1. 1 · 1 · 0,51 = 0,51м 3 – объем кладки в два кирпича;
2. 0,51м 3 : 0,00195м 3 = 261,5шт., т.е. 262 кирпичей;
в) 1. 1 · 1 · 0,64 = 0,64м 3 – объем кладки в два с половиной кирпича;
2. 0,64м 3 : 0,00195м 3 = 328,2шт., т.е. 329 кирпичей.
Пример 4. На строительных площадках песок хранят в штабелях. После приемки влажный песок уложили в штабель конической формы, размеры которого оказались следующими: длина окружности основания L 32 м, длина по откосу a7 м. Определите объем принимаемого песка, учитывая скидку на влажность воздуха 15 %. (Ответ: 111,1м3)
S Дано: конус Решение:
![]()



![]() L = 32м V =
0,85·Vк = =
0,85·1/3·pR2 ·H
L = 32м V =
0,85·Vк = =
0,85·1/3·pR2 ·H
7 a = 7м L = 2pR = 32 м
n = 15 % R = 32/2p = 16/p » 5,09м
Найти: V D ASO – прямоугольный, по т. Пифагора
![]()
V = 0,85·1/3·3,14·5,092·4,8 » 110,64 (м3 )
![]()
![]() A
O B
A
O B
16/p
Задания для практической работы.
Задание №1. Определите расход кирпича, для кладки колонны, имеющей форму параллелепипеда с размерами а×b×с м: а) пустотелый кирпич; б) уплотненный кирпич.
|
Размеры комнаты |
Вариант 1. |
Вариант 2. |
Вариант 3. |
|
Длина - a |
3 м |
2м |
1,5 м |
|
Ширина - b |
2 |
0,5м |
1 |
|
Высота - с |
5 м |
4м |
4,5 м |
Задание №2. Определить расход кирпича для кладки в один кирпич двух емкостей для песка, если они имеют цилиндрическую форму радиусом основания R м, высотой H м.
|
Размеры емкости |
Вариант 1. |
Вариант 2. |
Вариант 3. |
|
Радиус основания - R |
1,5 м |
1,5 м |
1,5 м |
|
Высота - с |
6 м |
4м |
5 м |
Задание №3. Рассчитать необходимое количество кирпича для кладки шарообразного купольного свода радиусом R м, шириной кирпича 0,12м
|
Размеры купола |
Вариант 1. |
Вариант 2. |
Вариант 3. |
|
Радиус купола - R |
5 м |
2 м |
4 м |
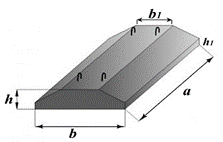 Задание №4. Определить объем бетона (м3)
фундаментального блока, подушки ленточного фундамента для блока изображенного
на рисунке.
Задание №4. Определить объем бетона (м3)
фундаментального блока, подушки ленточного фундамента для блока изображенного
на рисунке.
|
Вариант |
Размеры, мм |
||||
|
a |
b |
b1 |
h |
h1 |
|
|
1 |
2380 |
1000 |
600 |
300 |
100 |
|
2 |
1180 |
2000 |
900 |
400 |
150 |
|
3 |
2380 |
2400 |
900 |
500 |
1050 |
Задание №5. Определить расход стандартного кирпича и количество раствора для кладки стены длиной a (м), высотой b (м), толщиной в два кирпича и проемом площадью Sпроем (м2).
|
Вариант |
Размеры, мм |
||
|
a |
b |
Sпроем |
|
|
1 |
25 |
5,2 |
4 |
|
2 |
30 |
4 |
3 |
|
3 |
15 |
2,5 |
3,5 |
Задание №6. Вычислить необходимое количество кирпичей, для кладки стены площадью Sм2 толщиной:
а) в пол кирпича - 1 кв.м. кладки в 0,5 кирпича (толщина кладки 12 см.);
б) в полтора кирпича - 1 кв.м. кладки в 1,5 кирпича (толщина кладки в 38 см.);
в) в два с половиной кирпича - 1 кв.м. кладки в 2 кирпича (толщина кладки 51 см.).
|
Площадь стены |
Вариант 1. |
Вариант 2. |
Вариант 3. |
|
Sм2 |
1,5 |
2 |
3 |
Задание №7. На строительных площадках песок хранят в штабелях. После приемки влажный песок уложили в штабель конической формы, размеры которого оказались следующими: длина окружности основания L м, длина по откосу a м. Определите объем принимаемого песка, учитывая скидку на влажность воздуха 15 %. (Ответ: 111,1м3)
|
Вариант |
Размеры, |
||
|
L, м |
a, м |
n% |
|
|
1 |
25 |
8 |
15 |
|
2 |
30 |
9 |
16 |
|
3 |
33 |
6 |
17 |
Критерии оценки
|
«2» |
«3» |
«4» |
«5» |
|
0-2 |
3-4 |
5-6 |
7 |
Тема: Вычисление пределов последовательностей и функций с применением различных методов. Исследование функции на непрерывность, определение точек разрыва
Цель работы: освоение знаний алгоритма раскрытия неопределённостей для вычисления пределов,
Освоение умений применения пределов функций для исследования функций на непрерывность и определение точек разрыва
Краткие теоретические сведения
Типы неопределенностей и методы их раскрытия
Часто при вычислении пределов какой-либо функции, непосредственное применение теорем о пределах не приводит к желаемой цели. Так, например, нельзя применять теорему о пределе дроби, если ее знаменатель стремится к нулю. Поэтому часто прежде, чем применять эти теоремы, необходимо тождественно преобразовать функцию, предел которой мы ищем. Рассмотрим некоторые приемы раскрытия неопределенностей.
I.
Неопределенность вида ![]()
Пример 1. Вычислить предел ![]()
![]()
Решение: При подстановке вместо переменной х числа
5 видим, что получается неопределенность вида ![]() . Для ее раскрытия нужно
разложить знаменатель на множители: х2 -25 = (х-5)*(х+5), получили общий множитель
(х-5), на который можно сократить дробь. Заданный предел примет вид:
. Для ее раскрытия нужно
разложить знаменатель на множители: х2 -25 = (х-5)*(х+5), получили общий множитель
(х-5), на который можно сократить дробь. Заданный предел примет вид: ![]()
![]() . Подставив х=5, получим результат:
. Подставив х=5, получим результат: ![]()
![]() =
=![]()
![]() =
=![]()
![]() =
= ![]()
Пример 2. Вычислить предел ![]()
![]()
Решение: При подстановке вместо переменной х числа
3 видим, что получается неопределенность вида ![]() . Для ее раскрытия разложим числитель
и знаменатель на множители и сократим на общий множитель х-3. В результате получим новый
предел, знаменатель которого при подстановке вместо переменной х числа 3 не равен нулю. Этот
предел легко вычисляется по теоремам. Таким образом, неопределенность будет
раскрыта.
. Для ее раскрытия разложим числитель
и знаменатель на множители и сократим на общий множитель х-3. В результате получим новый
предел, знаменатель которого при подстановке вместо переменной х числа 3 не равен нулю. Этот
предел легко вычисляется по теоремам. Таким образом, неопределенность будет
раскрыта.
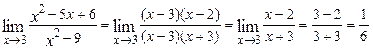
Пример 3. Вычислить предел ![]()
![]()
Решение: При подстановке вместо переменной х числа 0 видим, что
получается неопределенность
вида ![]() . Для ее раскрытия воспользуемся
первым замечательным пределом
. Для ее раскрытия воспользуемся
первым замечательным пределом ![]()
![]() и
его следствием
и
его следствием ![]()
![]() . После чего предел легко вычисляется по теоремам. Таким образом, неопределенность будет раскрыта.
. После чего предел легко вычисляется по теоремам. Таким образом, неопределенность будет раскрыта.
![]()
![]()
I
I. Неопределенность вида ![]()
Пример
4. Вычислить
предел ![]()
![]()
Решение:
При подстановке вместо переменной х бесконечности (![]() ) видим, что получается неопределенность вида
) видим, что получается неопределенность вида ![]() . Для ее раскрытия нужно числитель и знаменатель
разделить на наивысшую степень, в данном случае на х. Получим:
. Для ее раскрытия нужно числитель и знаменатель
разделить на наивысшую степень, в данном случае на х. Получим:
![]()
![]() =
=![]()
![]() =
=![]()
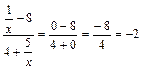 ,
т.к. величины
,
т.к. величины ![]() являются бесконечно
малыми и их пределы равны 0.
являются бесконечно
малыми и их пределы равны 0.
Определение непрерывности функции
Определение
Пусть функция ![]() определена на
некотором интервале
определена на
некотором интервале ![]() , для которого
, для которого ![]() -- внутренняя точка.
Функция
-- внутренняя точка.
Функция ![]() называется непрерывной в точке
называется непрерывной в точке ![]() , если существует предел
, если существует предел ![]() при
при ![]() и
этот предел равен значению
и
этот предел равен значению ![]() , то есть
, то есть ![]()
Пусть функция ![]() определена на
некотором полуинтервале
определена на
некотором полуинтервале ![]() , для которого
, для которого ![]() --
левый конец. Функция
--
левый конец. Функция![]() называется непрерывной справа в точке
называется непрерывной справа в точке ![]() , если существует
предел
, если существует
предел![]() при
при
![]() и
этот предел равен значению
и
этот предел равен значению ![]() , то есть
, то есть ![]()
Пусть, наконец, функция ![]() определена
на некотором полуинтервале
определена
на некотором полуинтервале ![]() , для которого
, для которого ![]() --
правый конец. Функция
--
правый конец. Функция![]() называется непрерывной
слева в точке
называется непрерывной
слева в точке ![]() , если существует предел
, если существует предел ![]() при
при ![]() и этот предел равен
значению
и этот предел равен
значению ![]() , то есть
, то есть ![]()
Из теоремы о связи двустороннего предела с односторонними (теорема 2.1) сразу следует, как уже отмечалось в главе 2, что имеет место следующее предложение.
Предложение
: Функция![]() тогда и только
тогда непрерывна в точке
тогда и только
тогда непрерывна в точке ![]() , когда она непрерывна в
точке
, когда она непрерывна в
точке ![]() справа и слева, то есть когда выполнены следующие условия:
справа и слева, то есть когда выполнены следующие условия:
1) функция ![]() определена в точке
определена в точке ![]() и в
некоторой окрестности этой точки;
и в
некоторой окрестности этой точки;
2) существует предел
значений функции слева: ![]() ;
;
3) существует предел
значений функции справа: ![]() ;
;
4) эти два предела
совпадают между собой и со значением функции в точке ![]() :
: ![]()
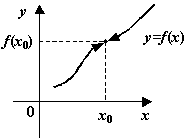
Рис.Функция непрерывна:
пределы слева и справа совпадают с ![]()
Точка ![]() , в которой функция
непрерывна, называется точкой непрерывности функции
, в которой функция
непрерывна, называется точкой непрерывности функции ![]() ; так же
определяются точки непрерывности слева и справа.
; так же
определяются точки непрерывности слева и справа.
Пример 5. Пусть ![]() и
и ![]() . Тогда
. Тогда ![]() и
и ![]() . Эти значения совпадают, значит, функция
. Эти значения совпадают, значит, функция ![]() непрерывна в
точке
непрерывна в
точке ![]() .
.
(Функция ![]() -- элементарная
функция;
-- элементарная
функция; ![]() -- точка её области определения
-- точка её области определения ![]() . Все
элементарные функции непрерывны во всех внутренних точках своих областей определения,
в том числе и эта. Так что в этом примере можно было бы заменить
. Все
элементарные функции непрерывны во всех внутренних точках своих областей определения,
в том числе и эта. Так что в этом примере можно было бы заменить ![]() любой элементарной
функцией, а
любой элементарной
функцией, а ![]() -- любой внутренней точкой области
-- любой внутренней точкой области ![]() , и
вывод остался бы тем же.)
, и
вывод остался бы тем же.)
Пример 6. Рассмотрим
функцию 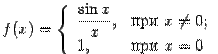 и
точку
и
точку ![]() . При
. При ![]() функция задаётся формулой
функция задаётся формулой
![]() , при этом имеем
, при этом имеем ![]() (первый
замечательный предел). Это значение совпадает с тем, которое задано при
(первый
замечательный предел). Это значение совпадает с тем, которое задано при ![]() :
: ![]() . Итак,
. Итак,
![]() , что означает непрерывность функции
, что означает непрерывность функции ![]() при
при ![]() .
.
Тем, кто внимательно изучил данное в главе 2 общее понятие базы предела, можно предложить продумать и доказать следующее утверждение:
Определение точек разрыва
Дадим теперь определение точек разрыва функции.
Определение
Точка ![]() называется точкой разрыва
функции
называется точкой разрыва
функции ![]() , если она определена в некоторой проколотой окрестности точки
, если она определена в некоторой проколотой окрестности точки ![]() (то есть
определена на некотором интервале, для которого
(то есть
определена на некотором интервале, для которого ![]() служит внутренней точкой, но
в самой точке
служит внутренней точкой, но
в самой точке ![]() , возможно, не определена) и выполняется хотя бы одно из следующих
условий:
, возможно, не определена) и выполняется хотя бы одно из следующих
условий:
1) не существует предела
слева ![]() ;
;
2) не существует предела
справа ![]() ;
;
3) пределы слева ![]() и справа
и справа ![]() существуют, но не равны друг
другу:
существуют, но не равны друг
другу: ![]() ;
;
4) пределы слева ![]() и справа
и справа ![]() существуют и равны друг другу:
существуют и равны друг другу: ![]() , но не совпадают со значением функции в точке
, но не совпадают со значением функции в точке ![]() :
: ![]() , или функция
, или функция ![]() не определена в точке
не определена в точке ![]() .
.
Если имеет место либо случай
3, либо случай 4, то точка разрыва ![]() называется точкой разрыва
первого рода, а поведение функции в окрестности точки
называется точкой разрыва
первого рода, а поведение функции в окрестности точки ![]() называется разрывом
первого рода в точке
называется разрывом
первого рода в точке ![]() ; в случае 4 точка разрыва
первого рода называется устранимой точкой разрыва, а разрыв функции в
этой точке -- устранимым разрывом.
; в случае 4 точка разрыва
первого рода называется устранимой точкой разрыва, а разрыв функции в
этой точке -- устранимым разрывом.
Если же имеет место либо
случай 1, либо случай 2 (либо и тот и другой сразу), то точка разрыва ![]() называется
точкой разрыва второго рода, а поведение функции в окрестности этой
точки -- разрывом второго рода в точке
называется
точкой разрыва второго рода, а поведение функции в окрестности этой
точки -- разрывом второго рода в точке ![]() .
.
Итак, если функция ![]() имеет
разрыв первого рода в точке
имеет
разрыв первого рода в точке ![]() , то существуют, как часто
говорят, значения функции "на берегах разрыва":
, то существуют, как часто
говорят, значения функции "на берегах разрыва": ![]() и
и ![]() , но
точка
, но
точка ![]() не
является точкой непрерывности.
не
является точкой непрерывности.
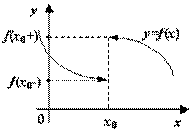
. ![]() -- точка разрыва
первого рода
-- точка разрыва
первого рода
Если значения на берегах
разрыва разные, то значение функции в точке ![]() может быть любым (или вообще
отсутствовать), всё равно
может быть любым (или вообще
отсутствовать), всё равно ![]() будет давать разрыв первого
рода. Если же значения на берегах разрыва совпадают, то для наличия разрыва
нужно, чтобы либо эти совпадающие значения были отличны от значения функции в
точке
будет давать разрыв первого
рода. Если же значения на берегах разрыва совпадают, то для наличия разрыва
нужно, чтобы либо эти совпадающие значения были отличны от значения функции в
точке ![]() ,
либо функция в этой точке была вовсе не определена. Если в этом случае
переопределить (или доопределить) функцию
,
либо функция в этой точке была вовсе не определена. Если в этом случае
переопределить (или доопределить) функцию ![]() в точке
в точке ![]() , положив
, положив ![]() , то полученная изменённая функция будет уже
непрерывна в точке
, то полученная изменённая функция будет уже
непрерывна в точке ![]() и разрыв в точке
и разрыв в точке ![]() исчезнет; отсюда и название
такого разрыва -- устранимый.
исчезнет; отсюда и название
такого разрыва -- устранимый.
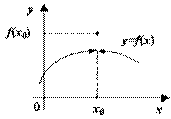
. ![]() -- точка устранимого
разрыва
-- точка устранимого
разрыва
Наконец, к разрывам второго
рода, как видно из определения, относятся все разрывы, которые не принадлежат к
разрывам первого рода; некоторые из возможных способов поведения функции в
окрестности точки ![]() , где происходит разрыв второго рода, представлены на следующем
рисунке.
, где происходит разрыв второго рода, представлены на следующем
рисунке.
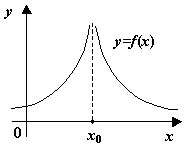
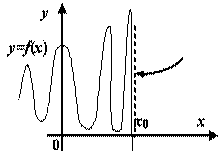
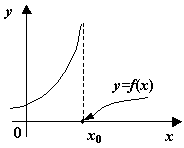
. ![]() -- точка разрыва
второго рода. Некоторые возможные варианты
-- точка разрыва
второго рода. Некоторые возможные варианты
Пример 7. Функция 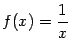 имеет при
имеет при ![]() разрыв
второго рода, так как
разрыв
второго рода, так как ![]() при
при ![]() и
и ![]() при
при ![]() .
.
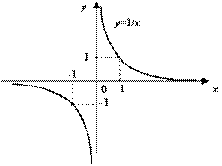
Рис. График функции ![]()
Пример 8.
Функция ![]() имеет
при
имеет
при ![]() разрыв
второго рода, так как
разрыв
второго рода, так как ![]() при
при ![]() и при
и при ![]() .
.
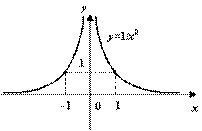
Рис. График функции ![]()
Задания для самостоятельной работы:
Задание 1. Найти пределы функций
|
I вариант |
II вариант |
III вариант |
|
«3» |
||
|
а) |
а) |
а) |
|
б) |
б) |
б) |
|
в) |
в) |
в) |
|
г) |
г) |
г) |
|
«4» |
||
|
а) |
а) |
а) |
|
б) |
б) |
б) |
|
в) |
в) |
в) |
|
г) |
г) |
г) |
|
«5» |
||
|
а) |
а) |
а) |
|
б) |
б) |
б) |
|
в) |
в) |
в) |
|
г) |
г) |
г) |
Задание 2. Исследовать функцию на непрерывность. Определить характер точек разрыва. Построить график функции
|
I вариант |
II вариант |
III вариант |
|
|
|
|
За каждое невыполненное задание снимается по 0,5 балла.
Тема: Составление уравнения касательной и нормали. Определение экстремумов функций. Вычисление наибольшего и наименьшего значений функций на заданном отрезке
Цели: научиться находить угловой коэффициент касательной и нормали к графику функции в заданной точке; составлять уравнения касательных к графику функции по заданным условиям.
Краткая теоретическая справка.
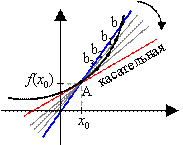
Строгое определение касательной:
Касательная к графику функции f, дифференцируемой в точке xо, - это прямая, проходящая через точку (xо; f(xо)) и имеющая угловой коэффициент f ′(xо).
Угловой коэффициент имеет прямая вида y = kx + b. Коэффициент k и является угловым коэффициентом этой прямой.
Угловой коэффициент равен тангенсу острого угла, образуемого этой прямой с осью абсцисс:
k = tg α= f ′(xо).
Здесь угол α – это угол между прямой y
= kx + b и положительным (то есть против
часовой стрелки) направлением оси абсцисс. Он называется углом наклона прямой.
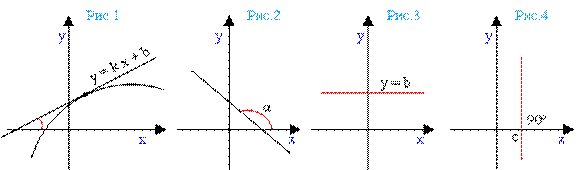 Если угол наклона
прямой y = kx + b острый, то угловой коэффициент
является положительным числом. График возрастает (рис.1).
Если угол наклона
прямой y = kx + b острый, то угловой коэффициент
является положительным числом. График возрастает (рис.1).
Если угол наклона прямой y = kx + b тупой, то угловой коэффициент является отрицательным числом. График убывает (рис.2).
Если прямая параллельна оси абсцисс, то угол наклона прямой равен нулю. В этом случае угловой коэффициент прямой тоже равен нулю (так как тангенс нуля есть ноль). Уравнение прямой будет иметь вид y = b (рис.3).
Если угол наклона прямой равен 90º (π/2), то есть она перпендикулярна оси абсцисс, то прямая задается равенством x = c, где c – некоторое действительное число (рис.4).
Уравнение касательной к графику функции y = f(x) в точке xо:
y = f(xо) + f ′(xо) (x – xо)
Уравнение нормали к графику функции y = f(x)
в точке xо:
y = f(xо)
![]() (x – xо)
(x – xо)
Алгоритм решения уравнения касательной к графику функции y = f(x):
1. Вычислить f(xо).
2. Вычислить производные f ′(x) и f ′(xо).
3. Внести найденные числа xо, f(xо), f ′(xо) в уравнение касательной и решить его.
Порядок выполнения работы.
1. Внимательно изучите теоретическую справку по теме.
2. Решите следующие задания.
Пример1. Найдем уравнение касательной к графику функции f(x) = x3 – 2x2 + 1 в точке с абсциссой 2.
Решение.
Следуем алгоритму.
1) Точка касания xо равна 2. Вычислим f(xо):
f(xо) = f(2) = 23 – 2 ∙ 22 + 1 = 8 – 8 + 1 = 1
2) Находим f ′(x). Для этого применяем формулы дифференцирования, изложенные в предыдущем разделе. Согласно этим формулам, х2 = 2х, а х3 = 3х2. Значит:
f ′(x) = 3х2 – 2 ∙ 2х = 3х2 – 4х.
Теперь, используя полученное значение f ′(x), вычислим f ′(xо):
f ′(xо) = f ′(2) = 3 ∙ 22 – 4 ∙ 2 = 12 – 8 = 4.
3) Итак, у нас есть все необходимые данные: xо = 2, f(xо) = 1, f ′(xо) = 4. Подставляем эти числа в уравнение касательной и находим окончательное решение:
у = f(xо) + f ′(xо) (x – xо) = 1 + 4 ∙ (х – 2) = 1 + 4х – 8 = –7 + 4х = 4х – 7.
Ответ. у = 4х – 7.
Пример 2. На рисунке изображены график функции y=f(x) и касательная к нему в точке с абcцисcой x0 . Найдите значение производной функции в точке x0 .
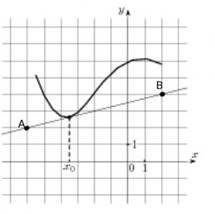
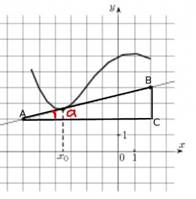
Значение производной функции y=f(x) в точке x0 равно тангенсу угла между касательной и положительным направлением оси ОХ. Чтобы его найти, выделим прямоугольный треугольник, гипотенуза которого лежит на касательной, а катеты параллельны осям координат. Обозначим точки с целыми координатами буквами А и В - эти точки выделены на касательной:
Проведем через точку А прямую параллельно оси ОХ, а через точку В - параллельно оси OY. Получим прямоугольный треугольник ABC. Угол А треугольника АВС равен углу между касательной и положительным направлением оси ОХ.
Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему. Длины катетов считаем по количеству клеточек
![]()
Ответ. 0,25.
Пример 3. Найти угловой коэффициент касательной, проведенной к графику функции
![]() в точке с
абсциссой х0=1.
в точке с
абсциссой х0=1.
Решение. Находим
производную функции
![]()
Тогда при x0=1
значение производной равно
![]()
Отсюда получаем, что угловой коэффициент касательной в точке с абсциссой х0=1 равен
![]()
Ответ. 1.
Пример 4. Прямая y= 8x-5 параллельна касательной к графику функции y=x2 +7x +7. Найдите абсциссу точки касания.
Решение. Условием параллельности двух прямых является равенство их угловых коэффициентов, следовательно k=8 . Угловой коэффициент касательной – это есть значение производной функции в точке x0. f ´(x0) = 2x0+7 =8, 2x0 = -1, x0 = -0,5.
Ответ. -0,5.
|
I вариант |
II вариант |
III вариант |
|
Задание № 1. Составьте уравнение касательной и нормали к графику функции y=f(x) в точке x0. (построить эти прямые) |
||
|
|
|
|
|
Задание №2. Найти угловой коэффициент касательной, проведенной к графику функции в точке x0. |
||
|
y=2x+7lnx, x0=14 |
y=6x-4cosx, x0= |
y=2-5x-lnx, x0=1 |
|
Задание №3. Прямая параллельна касательной к графику функции y=f(x). Найдите абсциссу точки касания. |
||
|
|
y=-3x -2, y =2 x2-11x+2 |
y=-5x+2, y = 3x2+7x+1 |
|
Задание № 4. |
||
|
1. Исследовать функцию на промежутки монотонности и экстремумы функции:
2. Определить промежутки возрастания функции и точку минимума:
|
1.
1. Исследовать функцию на промежутки
монотонности и экстремумы функции: 2. 2. Определить промежутки убывания и точку максимума:
|
1. Исследовать функцию на промежутки монотонности и экстремумы функции:
2. Определить промежутки возрастания и точки минимума:
|
Критерии оценки
|
«2» |
«3» |
«4» |
«5» |
|
0-2 |
3 |
4 |
5 |
Тема: Применение производной к исследованию функции и для нахождения наилучшего решения в прикладных задачах
Цель занятия: освоение алгоритма применения производной для нахождения наилучшего решения в прикладных задачах
Задания:
1. Рассмотрите теоретический материал по теме и примеры решения задач
(приведены ниже).
2. Решите практическую работу. Оформите решение письменно в тетради.
Задача 1. Представить число 76 в виде суммы трех положительных чисел так, чтобы сумма квадратов всех слагаемых была наименьшей, а отношение первого числа ко второму было равно 2:3.
Решение.
x>0 – коэффициент пропорциональности
2x - первое слагаемое.
3x – второе слагаемое.
76-2x-3x=76-5x – третье слагаемое, 76-5x> 0, x<15,2.
Сумма квадратов этих трех чисел равна (2x)2+(3x)2+(76-5x)2 = 38x2-760x+76
Сумма квадратов трех чисел будет наименьшей при том значении x, при котором функция f(x)= 38x2-760x+76 на интервале(0;15,2) достигает своего наименьшего значения.
f ' (x)=76x-760=76(x-10).
f ' (x)=0 при x=10.
Эта функция принимает наименьшее значение на промежутке (0;15,2) при x=10, т.к. эта точка является точкой минимума и единственной точкой экстремума функции f(x).
Или: Сумма квадратов этих трех чисел равна
(2x)2+(3x)2+(76-5x)2 = 38x2-760x+76 = 38(x2-20x+152)=38((x-10)2+52) – квадратичная функция, график – парабола, ветви направлены вверх. Следовательно, наименьшее значение функция будет достигать в вершине.
Для любого xЄR эта функция принимает наименьшее значение только при x=10.
Т.к. 10Є(0;15,2), то на промежутке (0;15,2) существует единственная точка x=10, в которой функция достигает своего наименьшего значения.
Следовательно, число 76 можно единственным образом представить в виде суммы согласно условиям задачи так 76=20+30+26.
Ответ: 76=20+30+26.
Задача 2. Имеются три раствора. Первый содержит 80% кислоты и 20% воды, второй-60% соли и 40%воды, третий - по 20%соли и кислоты и 60%воды. Из них необходимо приготовить новый раствор, содержащий 30%воды. Какое наименьшее и какое наибольшее процентное содержание соли может быть в этом новом растворе?
Решение:
1 способ решения: Обозначим за единицу массу нового раствора, х-масса I раствора, у-масса II раствора, z-масса III раствора, х ≥0, у≥0, z ≥0, тогда по условию х+у+z=1.
В новый раствор входит:
из I раствора 0,2х воды и 0,8х кислоты,
из II раствора 0,4у воды и 0,6у соли,
из III раствора 0,2z кислоты; 0,6z воды; 0,2z соли.
Масса воды в новом растворе 1*0,3=0,3
Тогда имеем: 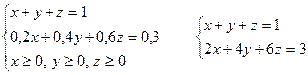
Пусть t – содержание соли в новом растворе, тогда t=0,6y+0,2z
Исключим из системы переменную х
![]()
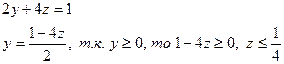
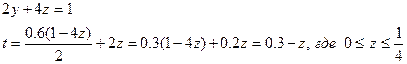
t=0.3-z – убывающая функция, значит наименьшее значение t принимает при z=1/4, а наибольшее
значение - при z=0.
![]()
![]()
Следовательно, ![]()
2 способ решения: Т.к. в новом растворе 30% воды, а во II-м и III-м соответственно 40% и 60%, то требуемый раствор невозможно получить только из II и III растворов, значит масса I-го раствора – ненулевая.
Обозначим за единицу массу первого раствора, х-масса II раствора, у-масса III раствора, x≥0, y≥0.
Тогда масса воды в новом растворе составляет 0,3(1+x+y)=0,2∙1+0,4∙x+0,6∙y ó x=1-3y.
Т.к. x≥0, то 1-3y≥0, y≤1/3.
Пусть Р – процентное
содержание соли в новом растворе, тогда ![]()
![]()
![]()
Найдем производную 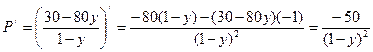
Так как ![]() на интервале
на интервале ![]() , то функция
убывает на отрезке
, то функция
убывает на отрезке ![]() .
.
Следовательно, наименьшее значение P(y) достигает в точке y=1/3, а наибольшее – в точке y=0.
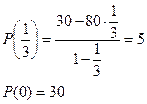
Итак, ![]()
Практическое задание
Каждое задание оценивается в 3 балла
Вариант 1
1. Представьте число52 в виде суммы трех положительных чисел так, чтобы сумма квадратов всех слагаемых была наименьшей, а отношение первого числа ко второму было равно 1:3.
2. Имеются три сплава. Первый сплав содержит 10% золота, 40% серебра и 50% меди, второй – 20% серебра и 80% меди, третий – 20% золота, 30% серебра и 50%меди. Из них получили новый сплав, содержащий 5% золота. Какое наибольшее и какое наименьшее процентное содержание серебра может быть в новом сплаве?
3. Участок в форме прямоугольника площадью 800 огорожен с трех сторон забором. Найдите наименьшую длину забора.
Вариант 2
1. Число 42 представьте в виде суммы трех положительных слагаемых так. Чтобы отношение первого числа ко второму было равно 3:4, а произведение всех трех чисел было наибольшим.
2. Имеются три раствора. Первый содержит 80% спирта и 20% воды, второй – поровну глицерина и воды, третий – по 10% спирта и глицерина и 80% воды. Из них необходимо приготовить новый раствор, содержащий 40% воды. Какое наибольшее и какое наименьшее процентное содержание глицерина может быть в этом новом растворе?
3. Периметр параллелограмма с острым углом 30˚ равен 4. Найти максимально возможное значение площади параллелограмма.
Критерии оценки
|
«2» |
«3» |
«4» |
«5» |
|
1-3 |
4-5 |
6-7 |
8-9 |
Тема: Вычисление неопределенных интегралов методом замены переменных и с помощью интегрирования по частям
Цель: совершенствование умений нахождения неопределенных интегралов методом замены переменной и по частям, совершенствование умений проверять действие интегрирования дифференцированием.
Теоретические сведения
Первообразная функции. Неопределенный интеграл
Функция
![]() , определенная на интервале
, определенная на интервале ![]() , называется первообразной для функции
, называется первообразной для функции ![]() , определенной на том же интервале
, определенной на том же интервале ![]() , если
, если ![]()
Если
![]() — первообразная для функции
— первообразная для функции ![]() , то любая другая первообразная
, то любая другая первообразная ![]() для функции
для функции ![]() отличается
от
отличается
от ![]() на некоторое постоянное слагаемое, т. е.
на некоторое постоянное слагаемое, т. е. ![]() где
где ![]() .
.
Неопределенным
интегралом от функции ![]() называется совокупность всех первообразных для этой
функции. Обозначается неопределенный интеграл:
называется совокупность всех первообразных для этой
функции. Обозначается неопределенный интеграл: ![]() где
где ![]()
Операция нахождений первообразной для данной функции называется интегрированием. Интегрирование является обратной операцией к дифференцированию:
![]()
Для проверки правильности выполненного интегрирования необходимо продифференцировать результат интегрирования и сравнить полученную функцию с подынтегральной.
Свойства неопределенного интеграла:
1.
![]()
2.
![]()
3.
![]()
4.
![]()
Таблица основных интегралов
1.
![]() 2.
2.
![]()
3.
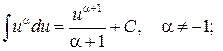
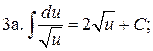
4.
![]() 5.
5.
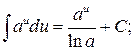
6.
![]() 7.
7.![]()
8.
![]() 9.
9.
![]()
10.
![]() 11.
11.
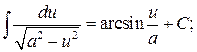
12.
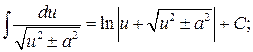 13.
13.
![]()
14.
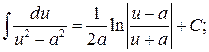 15.
15.
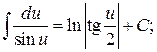
16.
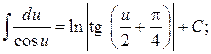 17.
17.
![]()
18.
![]()
Каждая из приведенных в таблице формул справедлива на промежутке, не содержащем точек разрыва подынтегральной функции. Вычисление интегралов с использованием таблицы и основных свойств называют непосредственным интегрированием.
Метод замены переменной
Теорема
1. Пусть ![]() монотонная,
непрерывно дифференцируемая функция, тогда
монотонная,
непрерывно дифференцируемая функция, тогда
![]() (1)
(1)
При
этом, если ![]() то
то ![]() где
где ![]() —
функция, обратная
—
функция, обратная ![]() .
.
Формула (1) называется формулой замены переменной в неопределенном интеграле.
Алгоритм замены переменной:
1)
Связать старую переменную интегрирования ![]() с новой переменной
с новой переменной ![]() с
помощью замены
с
помощью замены ![]() .
.
2)
Найти связь между дифференциалами ![]() .
.
3) Перейти под знаком интеграла к новой переменной.
4)
Проинтегрировать и в полученной первообразной вернуться к старой переменной,
подставив ![]()
Пример1. Проинтегрировать подходящей заменой переменной.
![]()
![]()
![]()
Решение:
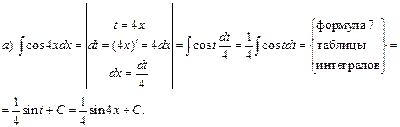
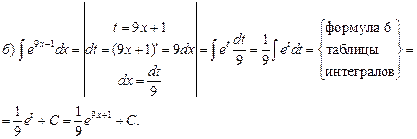
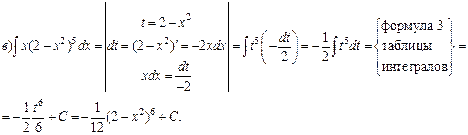
Интегрирование по частям
Некоторые виды интегралов, вычисляемых по частям
Если
производные функций ![]() и
и ![]() непрерывны, то справедлива
формула:
непрерывны, то справедлива
формула:
![]()
![]() (3)
(3)
называемая формулой интегрирования по частям.
В
качестве ![]() обычно выбирают
функцию, которая упрощается при дифференцировании.
обычно выбирают
функцию, которая упрощается при дифференцировании.
Некоторые
стандартные случаи функций, интегрируемых по частям, указаны в таблице 1. Там
же дается способ выбора множителей ![]() и
и ![]() .
.
Таблица 1
|
Вид интеграла |
|
|
|
|
|
|
|
Вид интеграла |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
![]() — многочлен от
— многочлен от ![]() степени
степени ![]() , т. е.
, т. е. ![]() , где
, где ![]() .
.
Пример 2. Проинтегрировать по частям.
![]()
![]()
Решение.
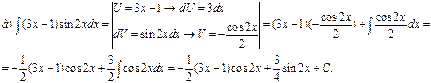
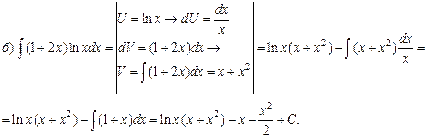
Задания для самостоятельной работы.
Задание 1. Проинтегрировать функции заменой переменной:
Вариант
1. ![]()
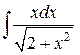
![]()
Вариант
2. ![]()
![]()
![]()
Вариант
3. ![]()
![]()
![]()
Задание 2. Найти интеграл интегрированием по частям:
Вариант
1. ![]()
![]()
Вариант 2. ![]()
![]()
Вариант3. ![]()
![]()
Критерии оценки
|
«2» |
«3» |
«4» |
«5» |
|
0-2 |
3 |
4 |
5 |
Тема: Построение криволинейной трапеции. Применение определенного интеграла к вычислению площадей плоских фигур и к вычислению объемов
знать:
- формулу Ньютона - Лейбница,
- формулы для вычисления объемов тел вращения с помощью определенного интеграла,
- таблицу неопределенных интегралов,
уметь:
- строить тела вращения
- вычислять объем тела вращения с помощью определенного интеграла
Содержание работы:
Краткие теоретические сведения
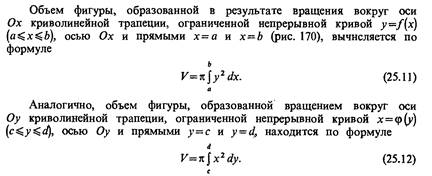

Алгоритм решения задач
1. Построить тело ращения, образованное вращением кривой вокруг указанной оси.
2. Определить пределы интегрирования. Если тело ограниченного двумя функциями, то данные пределы можно найти, решив систему уравнений.
3. Выразить переменную: если кривая вращается вокруг оси ОХ, то выражаем y; если кривая вращается вокруг оси OY, то выражаем переменную х.
4. Подставляем полученные значения в формулу 25.11, если кривая вращается вокруг оси OX, или в формулу 25.12, если кривая вращается вокруг оси OY.
5. Используя формулу Ньютона-Лейбница, вычислить объем тела.
Задания для самостоятельной работы (каждое задание по 3 балла):
Вариант 1
1. Вычислите площади фигур, ограниченных заданными линиями
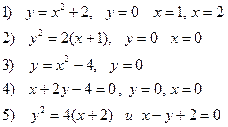
2. Вычислить объем тела, образованного вращением вокруг оси OY фигур, ограниченных линиями y=x2+1, y=5
Вариант 2
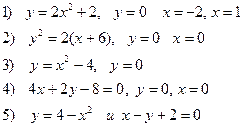
2. Вычислить объем тела, образованного вращением вокруг оси OY фигур, ограниченных линиями y=x2, y=1, y=4, x=0
Критерии оценки
|
«2» |
«3» |
«4» |
«5» |
|
0-7 |
8-12 |
13-15 |
16-18 |
Тема: Вычисление вероятностей сложных событий. Теоремы сложения и умножения вероятностей. Формула полной вероятности и формула Бернулли
Цель занятия: совершенствование умений применения теорем сложения и умножения вероятностей, а так же формулы полной вероятности и формулы Бернулли для решении вероятностных задач
Краткие теоретические сведения
Согласно классическому определению вероятности вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. Вероятность события А определяется формулой:
Р(А) = m/n,
где m – число элементарных исходов, благоприятствующих А;
n – число всех возможных элементарных исходов испытания.
1. Суммой A + B двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий.
a. Теорема сложения вероятностей несовместных событий. Вероятность появления одного из двух несовместных событий, равна сумме вероятностей этих событий:
Р (А + В) = Р(А) + Р(В)
b. Теорема сложения вероятностей совместных событий. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Р(А+В) = Р(А) + Р(В) – Р(АВ)
2. Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении этих событий.
a. Теорема произведения для независимых событий. Для независимых событий вероятность совместного появления событий равна произведению вероятностостей этих событий:
Р(АВ) = Р(А) Р(В).
b. Теорема умножения вероятностей. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Р(АВ) = Р(А) РА(В).
3. Вероятность появления хотя бы одного из независимых событий.
Если события А1, А2, А3,… Аn независимы в совокупности, причем Р(А1) = р1, Р(А2) = р2, Р(А3) = р3 и т.д.; q1, q2, q3, …, qn – вероятности противоположных событий.
Вероятность наступления события А, состоящего в наступлении хотя бы одного из событий А1, А2, А3,… Аn равна:
Р(А) = 1 – q1q2q3…qn.
4. Вероятность появления только одного из двух событий.
Р(А) = p1q2 + p2q1
Формула полной верятности позволяет определить вероятность события А, которое может наступить при условии появления одного из несовместных событий В1, В2, … Вn, образующих полную группу.
Р(А) = Р(В1)·РВ1(А) + Р(В2)·РВ2(А) + … + Р(Вn)·РВn(А)
Чтобы оценить вероятности гипотез В1, В2, … Вn, после того как стал известен результат испытания, используется формула Байеса.
![]()
Формула Бернулли позволяет рассчитать вероятность того, что при n испытаниях событие А осуществится ровно k раз. Формулой Бернулли удобно пользоваться, когда n и k<10.
![]()
Если n и k велики, то для нахождения вероятности появления события k раз в n испытаниях используется локальная теорема Муавра-Лапласа или асимптотическая формула Лапласа.
![]()
Если n велико, k мало и p<0,1, то для нахождения вероятности появления события k раз в n испытаниях удобно пользоваться формулой Пуассона.
![]()
Пример 1. В первом ящике содержится 20 деталей, из них 15 стандартных; во втором 30 деталей, из них 24 стандартных; в третьем – 10 деталей, из них 6 стандартных. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика – стандартная.
Решение
1. Обозначим через А – событие«взятая наудачу деталь стандартна»
Событие В1 – деталь извлечена из первого ящика;
Событие В2 – деталь извлечена из второго ящика
Событие В3 – деталь извлечена из третьего ящика
2. Определим вероятности событий В1, В2 и В3.
Вероятность того, что деталь взята из первого ящика Р(В1) = 1/3
Вероятность того, что деталь взята из первого ящика Р(В2) = 1/3
Вероятность того, что деталь взята из первого ящика Р(В3) = 1/3
3. Определим условные вероятности.
Условная
вероятность того, что из 1 ящика была извлечена стандартная деталь: РВ1(А)
= ![]()
Условная
вероятность того, что из 2 ящика была извлечена стандартная деталь: РВ2(А)
= ![]()
Условная вероятность того, что из 3 ящика была
извлечена стандартная деталь: РВ3(А) = ![]()
4. По формуле полной вероятности определим вероятность события А:
Р(А)
= ![]() =
= ![]() . Ответ: Р(А) = 0,72
. Ответ: Р(А) = 0,72
Пример 2. В классе 10 компьютеров. Для каждого компьютера вероятность того, что он в данный момент включен, равна 0,8. Найти вероятность, что в данный момент: а) включено 4 компьютера; б) включены все компьютеры; в) включено менее 3 компьютеров; г) включено не менее 3 компьютеров.
Решение
а) n = 10; k = 4; p = 0,8; q = 0,2
По формуле Бернулли: Р10(4) = ![]()
б) n = 10; k = 10; p = 0,8; q = 0,2
По формуле Бернулли: Р10(10) = ![]()
в) Р10(k<3) = Р10(0) + Р10(1) + Р10(2)
Р10(0)= ![]()
Р10(1)=
![]()
Р10(2)=
![]()
Р10(<3)
= ![]()
г) Т.к. события «включено менее 3 компьютеров» и «включено не менее трех компьютеров» являются противоположными, то
Р10(k≥3) = 1 - Р10(<3) = 1 – 0,000078 = 0,9999 = 99, 99%
Ответ:
Р10(4) = 0,55%; Р10(10) = 10,7%; Р10(k<3)
= ![]() ; Р10(k≥3) =
99,99%
; Р10(k≥3) =
99,99%
Задания для самостоятельной работы
|
|
I вариант |
II вариант |
|
1. |
Среди сотрудников фирмы 28% знают английский язык, 30% – немецкий; английский и немецкий – 8%. Найти вероятность того, что случайно выбранный сотрудник фирмы знает хотя бы один язык. |
Имеется 3 ящика, содержащих по 20 деталей. В первом ящике 12, во втором 5 и в третьем 9 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все детали окажутся стандартными. |
|
2. |
Производится бомбометание по трем складам боеприпасов, причем сбрасывается одна бомба. Вероятность попадания в первый склад 0,025; во второй – 0,03; в третий 0,019. При попадании в один из складов взрываются все три. Найти вероятность того, что склады будут взорваны. |
В электрическую цепь последовательно включены три элемента, работающие независимо один от другого. Вероятности отказов первого, второго и третьего элементов соответственно равны: р, = 0,1; р, = 0,15; р, = 0,2. Найти вероятность того, что тока в цепи не будет (не работает хотя бы 1 элемент). |
|
3. |
Имеется 3 ящика, содержащих по 15 деталей. В первом ящике 5, во втором 7 и в третьем 10 стандартных деталей. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все детали окажутся стандартными. |
Среди студентов группы 15% имеют отличные оценки по математике, 34% – по истории. При этом 12% являются отличниками по обеим дисциплинам. Найти вероятность того, что случайно выбранный студент учится на «отлично» хотя бы по одной дисциплине. |
|
4. |
Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,9. Найти вероятность того, что из двух проверенных изделий только одно стандартное. |
В ящике 10 деталей, из которых четыре окрашены. Сборщик наудачу взял три детали. Найти вероятность того, что хотя бы одна из взятых деталей окрашена. Решить задачу двумя способами. |
|
5. |
Устройство содержит два независимо работающих элемента. Вероятности отказа элементов соответственно равны 0,05 и 0,08. Найти вероятности отказа устройства, если для этого достаточно, чтобы отказал хотя бы один элемент. |
Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта, равна 0,8. Найти вероятность того, что из двух проверенных изделий только одно высшего сорта. |
|
6. |
В ящике содержится 12 деталей, изготовленных на заводе №1, 20 деталей – на заводе №2 и 18 деталей – на заводе №3. Вероятность того, что деталь, изготовленная на заводе №1, отличного качества, равна 0,9; для деталей, изготовленных на заводах №2 и №3, эти вероятности соответственно равны 0,6 и 0,9. Найти вероятность того, что извлеченная наудачу деталь окажется отличного качества. |
В магазин поступили телевизоры от 3 фирм. На долю 1 фирмы приходится 50% от общего числа поставок, на долю 2 фирмы – 20%, а на долю 3 фирмы – 30%. Из практики известно, что бракованными оказываются 4% поставляемых 1 фирмой, 3% поставляемых 2 фирмой и 5% поставляемых 3 фирмой. Найти вероятность того, что купленный в данном магазине телевизор окажется бракованным. |
|
7. |
Устройство, состоящее из пяти независимо работающих элементов. Вероятность отказа каждого из них за сутки равна 0,2. Найти вероятность того, что откажут: а) три элементы; б) не менее 4 элементов; в) менее 4 элементов |
Пусть вероятность того, что телевизор потребует ремонта в течение гарантийного срока, равна 0,2. Найти вероятность того, что в течение гарантийного срока из 6 телевизоров: а) 2 телевизора потребуют ремонта; б) не более одного потребует ремонта; б) более одного потребует ремонта. |
Критерии оценки
|
«2» |
«3» |
«4» |
«5» |
|
0-2 |
3-4 |
5-6 |
7 |
Тема: Составление статистического распределения выборки, построение полигона и гистограммы
Цель занятия: освоение алгоритма исследования статистического распределения выборки, построения гистограммы, полигона частот, функции распределения и куммулят
Краткие теоретические сведения
Статистическим распределением выборки или статистическим рядом называют перечень вариант и соответствующих им частот или относительных частот.
Пример 1. После группировки данных в выборке статистический ряд задан таблицей 1 (где объём выборки n = 15).
Таблица 1
|
xi |
2 |
3 |
4 |
6 |
|
ni |
1 |
4 |
2 |
3 |
В таблице 1 значения xi называют вариантами. Последовательность вариант, записанных в возрастающем порядке (вся строка xi) называется вариационным рядом. Число наблюдений ni называют частотами, i – номер варианты.
Учитывая,
что ![]()
n– это объем выборки, можно найти относительную частоту wi = ni/n, наблюдаемого значения xi – варианты, k – количество вариант.
Тогда таблица будет иметь вид:
Таблица 2
|
xi |
2 |
3 |
4 |
6 |
|
wi = ni/n |
0,1 |
0,3 |
0,4 |
0,6 |
Табличные данные могут быть представлены графически в виде полигона или гистограммы. Если выборка задана в виде отдельных точек, а не интервалов, тогда строят полигон частот. Полигоном относительных частот называется ломанная, отрезки которой соединяют точки (x; wi). На рис. 1 изображен полигон частот, приведённых в таблице 1.
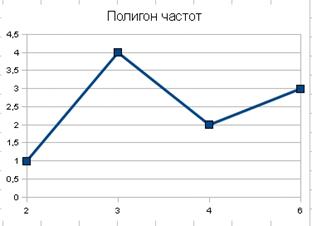
Рис. 1. Полигон
Пример 2. В этом примере наблюдаемые значения случайной величины после группировки данных в выборке разбиты на последовательные непересекающиеся частичные интервалы. В результате получается статистический ряд, который задан таблицей 3.
Таблица 3
|
xi |
[0¸2) |
[2¸4) |
[4¸6) |
[6¸8] |
|
ni |
5 |
10 |
12 |
3 |
Данную таблицу можно представить через относительную частоту wi =ni/n (где объём выборки n = 30) в таблице 4. Таблица 4
|
h=xi-xi-1 |
[0¸2) |
[2¸4) |
[4¸6) |
[6¸8] |
|
wi = ni/n |
0,17 |
0,33 |
0,4 |
0,1 |
При этом частоты wi удовлетворяют условию
![]() =1.
=1.
Если выборка задана в виде интервалов, тогда строят гистограмму.
Гистограмма частот
Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной h=xi-xi-1, а их высоты равны ni/h (для относительных частот - wi /h).
Если объем выборки из генеральной совокупности случайной непрерывной величины велик, то прибегают к предварительной группировке данных: размах выборки разбивают на k частичных интервалов Ji. Количество интервалов подсчитывается по формуле:
![]() или
или ![]() , [x] – целая
часть числа х.
, [x] – целая
часть числа х.
Подсчитывается, сколько значений из n1, n2,...,nm попало в каждый из к интервалов. Вариантами для выборки считают середины этих интервалов.
Задача: Рассмотреть все возможные варианты раскладки междуэтажных плит перекрытия по серии 1.141.1-89, если размеры помещения 8,76м на 7,6 м. Плиты размещаются вдоль меньшей стороны помещения. Номинальная ширина плит 1,0; 1,2; 1,5; 1,8; 2,4; 2,7; 3,0; 3,6.
Рассмотреть все возможные варианты. Найти относительную частоту повторяемости плит указанной ширины. Построить гистограмму, кумуляту, полигон частот и функцию распределения.
Найти моду, медиану и среднюю ширину плит. Найти математическое ожидание, дисперсию для каждого размера плит.
Подбор плит по их ширине произвести, исходя из размера 7,6м
|
№ |
1,0 |
1,2 |
1,5 |
1,8 |
2,4 |
2,7 |
3,0 |
3,6 |
швы |
всего |
|
1 |
4 |
|
|
|
|
|
|
1 |
6 |
5 |
|
2 |
1 |
3 |
|
|
|
|
1 |
|
6 |
5 |
|
3 |
1 |
|
2 |
|
|
|
|
1 |
5 |
4 |
|
4 |
1 |
|
|
1 |
2 |
|
|
|
5 |
4 |
|
5 |
1 |
|
|
|
|
|
1 |
1 |
4 |
3 |
|
6 |
1 |
1 |
|
3 |
|
|
|
|
6 |
5 |
|
7 |
4 |
|
|
2 |
|
|
|
|
7 |
6 |
|
8 |
1 |
|
1 |
|
1 |
1 |
|
|
5 |
4 |
|
9 |
1 |
1 |
|
|
|
2 |
|
|
5 |
4 |
|
10 |
1 |
4 |
|
1 |
|
|
|
|
7 |
6 |
|
11 |
4 |
1 |
|
|
1 |
|
|
|
7 |
6 |
|
12 |
1 |
|
|
2 |
|
|
1 |
|
5 |
4 |
|
13 |
1 |
1 |
2 |
|
1 |
|
|
|
6 |
5 |
|
14 |
1 |
1 |
|
|
1 |
|
1 |
|
5 |
4 |
|
15 |
1 |
1 |
|
1 |
|
|
|
1 |
5 |
4 |
|
16 |
1 |
2 |
1 |
|
|
1 |
|
|
6 |
5 |
|
17 |
4 |
3 |
|
|
|
|
|
|
8 |
7 |
|
18 |
1 |
3 |
2 |
|
|
|
|
|
8 |
6 |
|
19 |
1 |
|
2 |
2 |
|
|
|
|
6 |
5 |
|
20 |
1 |
2 |
|
1 |
1 |
|
|
|
6 |
5 |
|
итого |
32 |
23 |
10 |
13 |
7 |
4 |
4 |
4 |
|
97 |
Составим частотную таблицу по этой задаче.
Найдем относительную частоту и накопленную.
|
Xi |
1,0 |
1,2 |
1,5 |
1,8 |
2,4 |
2,7 |
3,0 |
3,6 |
|
Ni |
32 |
23 |
10 |
13 |
7 |
4 |
4 |
4 |
|
Ni/N |
0,330 |
0,237 |
0,103 |
0,135 |
0,072 |
0,041 |
0,041 |
0,041 |
|
Накопленная Ni/N |
0,330 |
0,567 |
0,670 |
0,805 |
0,877 |
0,918 |
0,959 |
1 |
Всего 97 плит.
Медианой является плита, стоящая на 49-м месте в вариационном ряду.
97/2=48 и остаток 1. Медиана 1,2.
Мода равна 1, т.к. плита, имеющая ширину 1м, встречается 32 раза.
Xср=(![]() =152/97=1,52
=152/97=1,52
Полигон частот
![]()
Функция распределения
![]()
Кумулята
![]()
Гистограмма
![]()
![]()
Задание для самостоятельной работы Рассмотреть все возможные варианты раскладки междуэтажных плит перекрытия по серии 1.141.1-89, если размеры помещения 8,76м на 7,6 м. Плиты размещаются вдоль меньшей стороны помещения. Номинальная ширина плит 1,0; 1,2; 1,5; 1,8; 2,4; 2,7; 3,0; 3,6.
Рассмотреть все возможные варианты. Найти относительную частоту повторяемости плит указанной ширины. Построить гистограмму, кумуляту, полигон частот и функцию распределения.
Найти моду, медиану и среднюю ширину плит. Найти математическое ожидание, дисперсию для каждого размера плит.
Вариант 1.
Подбор плит по их ширине производим, исходя из размера 9,9м
|
№ |
1,0 |
1,2 |
1,5 |
1,8 |
2,4 |
2,7 |
3,0 |
3,6 |
Швы |
Всего |
|
1 |
|
|
1 |
|
1 |
|
2 |
|
5 |
4 |
|
2 |
|
2 |
1 |
|
|
|
2 |
|
6 |
5 |
|
3 |
|
2 |
5 |
|
|
|
|
|
8 |
7 |
|
4 |
|
|
5 |
|
1 |
|
|
|
7 |
6 |
|
5 |
|
|
1 |
|
|
2 |
1 |
|
5 |
4 |
|
6 |
|
|
3 |
|
|
2 |
|
|
6 |
5 |
|
7 |
|
|
3 |
1 |
|
|
|
1 |
6 |
5 |
|
8 |
|
|
3 |
3 |
|
|
|
|
7 |
6 |
|
9 |
|
3 |
3 |
1 |
|
|
|
|
8 |
7 |
|
10 |
|
|
|
1 |
|
3 |
|
|
5 |
4 |
|
11 |
|
1 |
3 |
1 |
1 |
|
|
|
7 |
6 |
|
12 |
|
|
|
|
3 |
1 |
|
|
5 |
4 |
|
13 |
|
6 |
|
|
|
1 |
|
|
8 |
7 |
|
14 |
|
|
|
|
|
1 |
|
2 |
4 |
3 |
|
15 |
|
|
|
2 |
|
1 |
|
1 |
5 |
4 |
|
16 |
|
|
|
4 |
|
1 |
|
|
6 |
5 |
|
17 |
|
|
3 |
|
1 |
|
1 |
|
6 |
5 |
|
18 |
|
1 |
|
|
|
1 |
2 |
|
5 |
4 |
|
19 |
|
|
1 |
|
2 |
|
|
1 |
5 |
4 |
|
20 |
3 |
|
1 |
3 |
|
|
|
|
8 |
7 |
|
21 |
|
|
1 |
3 |
|
|
1 |
|
6 |
5 |
|
22 |
|
3 |
|
|
|
1 |
|
1 |
6 |
5 |
|
23 |
6 |
|
1 |
|
1 |
|
|
|
9 |
8 |
|
24 |
6 |
1 |
|
|
|
1 |
|
|
9 |
8 |
|
25 |
|
|
1 |
1 |
|
|
1 |
1 |
5 |
4 |
|
26 |
3 |
|
3 |
|
1 |
|
|
|
8 |
7 |
|
27 |
|
1 |
4 |
|
|
1 |
|
|
7 |
6 |
|
28 |
|
|
1 |
2 |
2 |
|
|
|
6 |
5 |
|
29 |
|
4 |
1 |
2 |
|
|
|
|
8 |
7 |
|
30 |
|
4 |
1 |
|
|
|
|
1 |
7 |
6 |
|
31 |
|
3 |
|
2 |
|
1 |
|
|
7 |
6 |
|
32 |
|
3 |
1 |
1 |
|
|
1 |
|
7 |
6 |
|
33 |
|
5 |
1 |
|
1 |
|
|
|
8 |
7 |
|
итого |
18 |
39 |
48 |
27 |
14 |
17 |
11 |
8 |
|
182 |
Задание для самостоятельной работы Рассмотреть все возможные варианты раскладки междуэтажных плит перекрытия по серии 1.141.1-89, если размеры помещения 8,76м на 7,6 м. Плиты размещаются вдоль меньшей стороны помещения. Номинальная ширина плит 1,0; 1,2; 1,5; 1,8; 2,4; 2,7; 3,0; 3,6.
Рассмотреть все возможные варианты. Найти относительную частоту повторяемости плит указанной ширины. Построить гистограмму, кумуляту, полигон частот и функцию распределения.
Найти моду, медиану и среднюю ширину плит. Найти математическое ожидание, дисперсию для каждого размера плит.
Вариант 2.
Подбор плит по их ширине производим, исходя из размера 8,8м
|
№ |
1,0 |
1,2 |
1,5 |
1,8 |
2,4 |
2,7 |
3,0 |
3,6 |
Всего |
швы |
|
1 |
1 |
1 |
|
|
|
|
1 |
1 |
4 |
5 |
|
2 |
4 |
|
2 |
1 |
|
|
|
|
7 |
8 |
|
3 |
4 |
4 |
|
|
|
|
|
|
8 |
9 |
|
4 |
1 |
2 |
|
|
1 |
|
1 |
|
5 |
6 |
|
5 |
1 |
|
2 |
|
2 |
|
|
|
5 |
6 |
|
6 |
1 |
|
|
|
2 |
|
1 |
|
4 |
5 |
|
7 |
1 |
4 |
2 |
|
|
|
|
|
7 |
8 |
|
8 |
1 |
3 |
|
1 |
1 |
|
|
|
6 |
7 |
|
9 |
1 |
|
|
1 |
1 |
|
|
1 |
4 |
5 |
|
10 |
1 |
1 |
1 |
|
1 |
1 |
|
|
5 |
6 |
|
11 |
1 |
|
|
1 |
|
|
2 |
|
4 |
7 |
|
12 |
1 |
|
2 |
1 |
|
|
1 |
|
5 |
6 |
|
13 |
1 |
4 |
|
|
|
|
1 |
|
6 |
7 |
|
14 |
1 |
1 |
|
2 |
|
|
1 |
|
5 |
6 |
|
15 |
1 |
|
|
|
1 |
2 |
|
|
4 |
5 |
|
16 |
4 |
|
|
1 |
|
|
1 |
|
6 |
7 |
|
17 |
1 |
2 |
|
3 |
|
|
|
|
6 |
7 |
|
18 |
1 |
1 |
|
|
1 |
1 |
|
|
5 |
6 |
|
19 |
7 |
|
|
1 |
|
|
|
|
8 |
9 |
|
20 |
1 |
5 |
|
1 |
|
|
|
|
7 |
8 |
|
21 |
1 |
|
4 |
1 |
|
|
|
|
6 |
7 |
|
22 |
1 |
|
|
3 |
1 |
|
|
1 |
6 |
7 |
|
23 |
4 |
1 |
|
|
|
|
|
1 |
6 |
7 |
|
24 |
1 |
1 |
2 |
|
|
|
|
1 |
5 |
6 |
|
25 |
1 |
|
1 |
|
|
1 |
|
1 |
4 |
5 |
|
26 |
4 |
|
|
|
2 |
|
|
|
6 |
7 |
|
27 |
1 |
1 |
|
1 |
2 |
|
|
|
5 |
6 |
|
28 |
1 |
1 |
2 |
2 |
|
|
|
|
6 |
7 |
|
29 |
1 |
3 |
1 |
|
|
1 |
|
|
6 |
7 |
|
30 |
4 |
2 |
|
|
1 |
|
|
|
7 |
8 |
|
31 |
1 |
2 |
|
|
1 |
|
1 |
|
5 |
6 |
|
32 |
1 |
|
1 |
2 |
|
1 |
|
|
5 |
6 |
|
33 |
4 |
1 |
|
2 |
|
|
|
|
7 |
8 |
|
34 |
1 |
2 |
|
1 |
|
|
|
|
5 |
6 |
|
итого |
61 |
42 |
21 |
25 |
17 |
7 |
10 |
7 |
190 |
|
1. Богомолов Н.В. Математика. Учебное пособие для ссузов. – М. Дрофа , 2010 г. – 400 с.
2. Богомолов Н.В. Практические занятия по математике. - М.: Высш. шк., 2012. - 495 с.
3. Богомолов Н.В. Сборник задач по математике. - М.: Дрофа, 2011 г. - 208 с.
4. Валуцэ И.И. Математика для техникумов. - М.: Наука. Гл. ред. Физ.-мат. Лит., 2010 - 576 с.
5. Кремер Н.Ш. Высшая математика для экономистов: учебник для вузов - М.: ЮНИТИ, 2009 - 471с.
6. Шипова Л.И. Математика: пособие для СПО. - Волгоград: Издательский дом "ИН-Фолио", 2012. - 224с
Ю.М.Колягин Математика в 2-х книгах, учебник для СПО, 2008, книга 1
И.Л.Соловейчик Сборник задач по математике для техникумов, -М, 2003
http://www.cleverstudents.ru
http://www.coolreferat.com
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.