Методические рекомендации по выполнению практический заданий «Гидравлика, теплотехника и аэродинамика»

МР-22-08.02.08-ОП.06

комитет по науке и высшей школе

Санкт-Петербургское государственное

БЮДЖЕТНОЕ профессиональное образовательное учреждение

 «Санкт-Петербургский техникум отраслевых технологий,

финансов и права»

методические рекомендации

по выполнению практических ЗАНЯТИЙ

по общепрофессионально дисциплине

ОП.06 ОСНОВЫ ГИДРАВЛИКИ, ТЕПЛОТЕХНИКИ И АЭРОДИНАМИКИ

Специальность 08.02.08 «Монтаж и эксплуатация оборудования и систем газоснабжения»

(квалификация техник)

 

Методические рекомендации по выполнению практических занятий для студентов составлены в соответствии с рабочей программой учебной дисциплины ОП. 06 «Основы гидравлики, теплотехники и аэродинамики» по специальности 08.02.08 «Монтаж и эксплуатация оборудования и систем газоснабжения», квалификация техник.

 

Разработчик: преподаватель СПбТОТФиП					А.С. Савватеев
				(подпись)
СОГЛАСОВАНО
На заседании цикловой комиссии № 08.02.08
Протокол №	6	от	10.02.2022
Председатель ЦК № 08.02.08					М.А. Шмелькова
				(подпись)

 

СОГЛАСОВАНО
На заседании цикловой комиссии № 08.02.09
Протокол №	6	от	02.02.2022
Председатель ЦК № 08.02.09					А.В. Бычков
				(подпись)
УТВЕРЖДЕНА
Учебно-методический совет техникума
Протокол №	7	от	03.03.2022
Методист					О.В. Корнилова

 

                    (подпись)

 

 

Оглавление

1. Пояснительная записка.. 4

2. ПЕРЕЧЕНЬ ПРАКТИЧЕСКИХ ЗАНЯТИЙ.. 5

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №1 Определение физических свойств жидкости. 6

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №2 Определение давления рабочей жидкости.. 12

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №3 Опытная иллюстрация уравнения Бернулли. Построение пьезометрических напорных линий. 18

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №4 Гидравлический расчет простого трубопровода. 23

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №5 Классификация, область применения, достоинства и недостатки насосов. 29

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №6 Испытание центробежного насоса. 35

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №7 Изучение работы и построение характеристик центробежного вентилятора. 39

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №8 Определение параметров пара. 45

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №9 Применение первого и второго закона термодинамики. 50

 

 

 

 

1. Пояснительная записка

 

Методические рекомендации к практическим занятиям предназначены в качестве методического пособия при проведении практических занятий по ОП. 06 «Основы гидравлики, теплотехники и аэродинамики» для специальности 08.02.08 «Монтаж и эксплуатация оборудования и систем газоснабжения»

Практические занятия проводятся после изучения соответствующих разделов и тем дисциплины. Выполнение обучающимися практических заданий позволяет им понять, где и когда изучаемые теоретические положения и практические умения могут быть использованы в будущей практической деятельности.  

Целью практических занятий является закрепление теоретических знаний и приобретение практических умений и навыков.

Методические рекомендации по каждому практическому занятию имеют теоретическую часть с необходимыми для выполнения работы формулами, пояснениями, таблицами; алгоритм выполнения заданий.

 

 

 

2. ПЕРЕЧЕНЬ ПРАКТИЧЕСКИХ ЗАНЯТИЙ

№ п/п	Наименование	Количество часов
1	Определение физических свойств жидкости	4
2	Определение давления рабочей жидкости	2
3	Гидростатические машины	4
4	Опытная иллюстрация уравнения Бернулли. Построение пьезометрических напорных линий	2
5	Гидравлический расчет простого трубопровода	4
6	Классификация, область применения, достоинства и недостатки объемных насосов	4
7	Испытание центробежного насоса	2
8	Изучение работы и построение характеристик центробежного вентилятора	2
9	Определение параметров пара	4
10	Применение первого и второго закона термодинамики	2

 

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №1 Определение физических свойств жидкости.

Цель:

Научиться рассчитывать и определять основные физические свойства жидкости.

Ход работы:

Вначале проводится опрос студентов с целью выявить их теоретические знания по теме, затем совместно решается задача и дается задание на самостоятельное решение

Необходимые материалы и оборудование:

1. Методические рекомендации по выполнению практических занятий

2. Справочные таблицы 

Пояснения к работе:

Жидкими телами или жидкостями называют физические тела, легко изменяющие свою форму под действием самой незначительной по величине силы. Можно сказать, что жидкость – это физическое тело, обладающее текучестью, имеющее определенный объем и заполняющая часть пространства (сосуда), равного ее объему.

Различают два вида жидкостей:

·               -жидкости капельные (малосжимаемые);

·               -жидкости газообразные (сжимаемые).

Плотность жидкости.

Важнейшими характеристиками механических свойств жидкости являются ее плотность и удельный вес. Они определяют "весомость" жидкости.

Плотность ρ характеризует распределение массы Δm жидкости по объему ΔW. Плотность однородной жидкости равна отношению массы m

жидкости к ее объему:

где m – масса жидкости, кг;

      V – объем жидкости, м³.

Плотность ρ во всех точках однородной жидкости одинакова. В общем случае плотность может изменяться в объеме жидкости от точки к точке и в каждой точке объема с течением времени. За единицу плотности в системе СИ принят 1 кг/м3.

Вместо плотности в формулах может быть использован также удельный вес γ (Н/м³), то есть вес жидкости G, приходящийся на единицу объема W:

Плотность жидкостей и газов зависит от температуры и давления. Все жидкости, кроме воды, характеризуются уменьшением плотности с увеличением температуры. Плотность воды максимальна при t =4 ºС и уменьшается как с уменьшением, так и с увеличением температуры от этого значения. В этом проявляется одно из аномальных свойств воды.

Плотность воды при t =4º С составляет 1000 кг/м³;

морской воды - 1020 … 1030 кг/м3;

нефти и нефтепродуктов – 650 … 900 кг/м3;

чистой ртути - 13600 кг/м3;

воздуха при t =0º С и атмосферном давлении – 1,29 кг/м3.

При изменении давления плотность жидкости изменяется незначительно.

Сжимаемость. Это свойство жидкостей изменять объем при изменении давления; характеризуется коэффициентом объемного сжатия (коэффициентом сжимаемости) βр (Па^-1); представляющим собой относительное изменение объема жидкости W при изменении давления на единицу:

где V – первоначальный объем жидкости, м³;

∆V – относительное изменение объема жидкости при изменении давления на величину ∆р, м³.

Знак "—" в формуле (1.3) указывает на то, что при увеличении давления объем жидкости уменьшается.

Величина, обратная коэффициенту объемного сжатия – модуль объемной упругости жидкости Е_о, Па:

Физический смысл объемного модуля упругости: величина, обратная изменению объема одного кубического метра жидкости при изменении давления на одну единицу.

Объемный модуль упругости жидкости зависит от типа жидкости, давления и температуры. Однако в большинстве случаев Ео считают постоянной величиной, принимая за нее среднее значение в данном диапазоне температур и давлений.

Различают изотермический и адиабатический модуль упругости. Причем для расчетов обычно используют изотермический модуль упругости Е_то, применяемый для анализа медленных процессов, при которых успевает завершиться теплообмен с окружающей средой. Для быстротечных процессов, при которых теплообмен не успевает завершиться, используют адиабатический модуль упругости Е_ао.

Температурное расширение. Это свойство жидкостей изменять объем при изменении температуры; характеризуется температурным коэффициентом объемного расширения βt (1/°С), представляющим собой относительное изменение объема жидкости при изменении температуры на единицу (1 ºС) и при постоянном давлении:

где V – первоначальный объем жидкости, м³;

∆V – относительное изменение объема жидкости при повышении температуры на ∆t, м³.

Для воды с увеличением давления при температуре до 50 ºС коэффициент βt растет, а при температуре выше 50 ºС уменьшается.

Вязкость. Это свойство жидкости оказывать сопротивление относительному сдвигу ее слоев.

Вязкость проявляется в том, что при относительном перемещении слоев жидкости на поверхностях их соприкосновения возникают силы сопротивления сдвигу, называемые силами внутреннего трения или силами вязкости. Благодаря этим силам слой жидкости, движущийся медленнее, "тормозит" соседний слой, движущийся быстрее. Силы внутреннего трения проявляются вследствие наличия межмолекулярных связей между движущимися слоями.

Кинематическая вязкость ν – отношение динамической вязкости µ к плотности жидкости ρ и определяется формулой: 

где µ - динамическая вязкость, Па·с;

ρ - плотность жидкости, кг/м³.

В международной системе единиц (СИ), кинематическая вязкость измеряется в квадратных метрах на секунду. 

 

 

 

 

 

 

 

 

 

Пример решения задачи:

Вариант 30

Определите массу жидкости, если её занимаемый объем W, а плотность - ρ.

Дано:                                Решение:

М

V =72 м³                       Воспользуемся формулой

ρ = 940 кг/м³        В этой формуле нам известные две величины: объем и

m- ?                      плотность. Тогда наша задача сводится к тому, чтобы

                             выразить неизвестную величину и найти ее. Тогда:

                                m = W∙ρ = 72*940 = 67680 кг  68 т

 

Ответ: m 68 т

 

Задание:

№1. В отопительной системе (котел, радиаторы и трубопроводы) небольшого дома содержится объем воды V. Определите сколько воды дополнительно войдет в расширительный сосуд при нагревании с t₁ до t₂?

№2. Определите удельный объем и удельный вес жидкости, если известна ее плотность ρ, ускорение свободного падения g=9,81 м/с².

№3. При гидравлическом испытании внутренних систем водоснабжения допускается падение испытательного давления на ∆р. Определите допустимую величину утечки ∆Wпри гидравлическом испытании системы вместимостью V.

№4. По условиям гидравлического испытания водопровода диаметром d и длиной lдавление должно быть поднято от атмосферного до p. Определите объем воды, который потребуется дополнительно подать в водопровод. Деформацией труб пренебречь.

№5. Определите изменение плотности воды при нагревании ее от t₁до t₂.

№6. Определите динамическую вязкость жидкости, если ее плотность ρ, а кинематическая вязкость ν.

            №7. Используя справочную литературу нужно построить зависимость W-p сжимаемости различных жидкостей от давления (1- глицерин, 2- вода, 3 – масло, 4- силиконовая рабочая жидкость).  Задание оформите в виде графика, выполненного в программном комплексе Microsoft Excel.

 

 

Варианты заданий:

№ п/п	V, м3	t1, 0С	t2, 0С	ρ, кг/м3	p, МПа	∆p, кПа	d, мм	l, м	υ, м2/с
1 вариант	72	13	73	850	3,3	54	100	1980	7,6
2 вариант	73	16	70	840	2,8	50	150	1740	7,7
3 вариант	79	18	86	800	2,6	60	200	850	10
4 вариант	89	18	89	990	3,3	40	100	930	9,9
5 вариант	76	10	88	810	3,7	50	150	2000	9,6
6 вариант	83	10	78	1000	2,9	57	200	1720	8,3
7 вариант	82	10	75	950	3,1	41	100	1040	9,2
8 вариант	88	15	76	1000	3	60	150	1580	7
9 вариант	86	11	87	970	2,1	42	200	1780	7,1
10 вариант	80	15	74	840	3,2	45	100	950	9,3
11 вариант	70	18	77	930	2,8	43	150	910	9,6
12 вариант	80	19	81	890	3,9	59	200	960	9,4
13 вариант	77	11	77	840	4	42	100	1980	9,1
14 вариант	83	16	76	900	2,2	53	150	1600	7
15 вариант	75	15	85	860	2,4	49	200	800	9,6
16 вариант	86	12	71	960	3,7	52	100	1320	7,9
17 вариант	70	13	82	880	2,7	54	150	1480	8
18 вариант	82	13	89	880	3	60	200	1330	8,4
19 вариант	71	18	90	870	3,7	40	100	1300	9,2
20 вариант	82	16	83	1000	3,8	44	150	1370	7,7
21 вариант	88	15	84	800	3,6	60	200	1640	9
22 вариант	73	13	87	1000	4	40	100	980	8,5
23 вариант	74	10	82	1000	2,9	45	150	1770	7,8
24 вариант	88	10	87	970	2	60	200	1010	9,9
25 вариант	88	14	87	900	4	50	100	1190	8,5
26 вариант	75	11	80	950	3,4	40	150	1430	8
27 вариант	79	15	81	1000	3,7	58	200	1070	7,7
28 вариант	90	20	88	900	2,9	59	100	1130	8,3
29 вариант	73	16	84	820	3,8	48	150	1250	8,4
30 вариант	72	18	70	940	3,7	59	200	1280	8,4

 

 

Контрольные вопросы:

1.        Сформулируйте определение жидкости.

2.        Назовите основные физические свойства жидкости.

3.        Сформулируйте физический смысл вязкости?

4.        Назовите физический смысл объемного модуля упругости?

5.        Назовите виды вязкости  жидкости?

6.        Определите, как изменяется коэффициент β_t с увеличением давления?

7.        Назовите, в чем измеряются основные физические свойства жидкости?

 

 

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №2 Определение давления рабочей жидкости.

Цель:

Ознакомиться с методами определения давления рабочей жидкости. Научиться определять давление жидкости в зависимости от заданных условий.

Ход работы:

Вначале проводится опрос студентов с целью выявить их теоретические знания по теме, затем совместно решается задача и дается задание на самостоятельное решение

Необходимые материалы и оборудование:

1. Методические рекомендации по выполнению практических занятий

2. Справочные таблицы 

Пояснения к работе:

Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости и их практическое применение.

В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением. Жидкость оказывает силовое воздействие на дно и стенки сосуда. Частицы жидкости, расположенные в верхних слоях водоема, испытывают меньшие силы сжатия, чем частицы жидкости, находящиеся у дна.

Гидростатическое давление обладает свойствами.

            Свойство 1. В любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости.

Свойство 2. Гидростатическое давление неизменно во всех направлениях.

Свойство 3. Гидростатическое давление в точке зависит от ее координат в пространстве.

Основное уравнение гидростатики

            Рассмотрим распространенный случай равновесия жидкости, когда на нее действует только одна массовая сила - сила тяжести, и получим уравнение, позволяющее находить гидростатическое давление в любой точке рассматриваемого объема жидкости. Это уравнение называется основным уравнением гидростатики.

            Пусть жидкость содержится в сосуде (рис.2.1) и на ее свободную поверхность действует давление P₀ . Найдем гидростатическое давление P в произвольно взятой точке М, расположенной на глубине h. Выделим около точки М элементарную горизонтальную площадку dS и построим на ней вертикальный цилиндрический объем жидкости высотой h. Рассмотрим условие равновесия указанного объема жидкости, выделенного из общей массы жидкости. Давление жидкости на нижнее основание цилиндра теперь будет внешним и направлено по нормали внутрь объема, т.е. вверх.

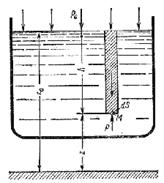
Рисунок  2.1 -  Схема для вывода основного уравнения гидростатики

            Запишем сумму сил, действующих на рассматриваемый объем в проекции на вертикальную ось:

            Последний член уравнения представляет собой вес жидкости, заключенный в рассматриваемом вертикальном цилиндре объемом hdS. Силы давления по боковой поверхности цилиндра в уравнение не входят, т.к. они перпендикулярны к этой поверхности и их проекции на вертикальную ось равны нулю. Сократив выражение на dS и перегруппировав члены, найдем

где р₀ – давление, действующеена свободную поверхность жидкости, Па;

      ρ– плотность жидкости, кг/м³;

      g– ускорение свободного падения, g = 9,81м/с²;

      h– высота столба жидкости, м;

      γ – удельный вес Н/м³.

            Полученное уравнение называют основным уравнением гидростатики. По нему можно посчитать давление в любой точке покоящейся жидкости. Это давление, как видно из уравнения, складывается из двух величин: давления P₀ на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости.

            Из основного уравнения гидростатики видно, что какую бы точку в объеме всего сосуда мы не взяли, на нее всегда будет действовать давление, приложенное к внешней поверхности P₀. Другими словами давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости по всем направлениям одинаково. Это положение известно под названием закона Паскаля.

Абсолютное давление складывается из двух других: избыточного и внешнего (атмосферного):

p = p_изб +p_вн     

где p_изб – избыточное давление в резервуаре, Па;

      p_вн – внешнее (атмосферное) давление в резервуаре, Па.

Избыточное давление определяется, как произведение удельного веса на высоту столба жидкости:

   

где γ – удельный вес, Н/м³;

ρ– плотность жидкости, кг/м³;

g– ускорение свободного падения, g = 9,81 м/с²;

h– высота столба жидкости, м.

Закон Архимеда.

  Тело, погруженное (полностью или частично) в жидкость, испытывает со стороны жидкости суммарное давление, направленное снизу вверх и равное весу жидкости в объеме погруженной части тела.

где V_погр – объем погруженного в жидкость тела, м³;

ρ_ж – плотность жидкости, кг/м³;

g– ускорение свободного падения, g = 9,81 м/с².

Пример решения задачи:

Вариант 30

            К всасывающей стороне цилиндра присоединен водяной вакууметр с показанием h. Определите разрежение под поршнем.

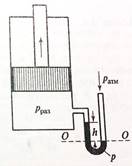
Рисунок  2.2 – Цилиндр к примеру решения задачи

 

 

 

Дано:                                Решение:

h =95 м                В данной задачи нам нужно найти разрежение под

р_раз- ?                   поршнем, по-другому его можно назвать избыточным

                              давлением, которое найдем по формуле (2.4)

                                Жидкость, находящаяся в цилиндре это вода, тогда ρ  = 1000 кг/м³, а g = 9,81 м/с²

                               Тогда,  = 931950 Па = 0,93 МПа

                     Ответ: р_раз = 0,93 Мпа

 

            

 

Задание

            №1. Определите избыточное давление воды в трубе по показаниям батарейного ртутного манометра. Отметки уровней ртути по оси трубы: Z₁, Z₂, Z₃, Z₄.

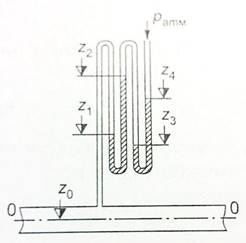
Рисунок  2.3 – Батарейный ртутныйма нометр, к задаче №1

            №2. Определите избыточное давление в забое скважины глубиной h, которая заполнена жидкостью плотностью ρ.

№3. Два горизонтальных цилиндрических трубопровода А и В содержат соответственно минеральное масло плотностью 900 кг/м³ и воду плотностью 1000 кг/м³. Высоты жидкостей, представленные на рисунке имеют следующие значения: h_м, h_рт, h_в. Зная, что гидростатическое давление на оси трубопровода А равно р, определите давление на оси трубопровода В.

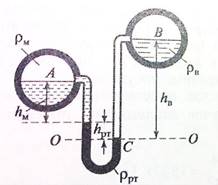
Рисунок  2.4 – Батарейный ртутный манометр, к задаче №3

            №4. Избыточное давление воды в океане на глубине h равно р.  Определите: плотность морской воды на этой глубине.

            №5. В обычных условиях человек поднимает без труда стальную гирю массой m₁. Проанализируйте, какой массы стальную гирю человек может поднять без труда под водой, если ρ_в = 10³ кг/м³,  ρ_ст = 7,8*10³ кг/м³?

 

Варианты заданий:

№ п/п	h, м	z1, м	z2, м	z3, м	z4, м	hм, м	hрт, м	hв, м	ρ, кг/м3	р, МПа	m1, кг
1 вариант	97	1,77	3,05	1,66	2,63	0,28	0,48	0,96	1080	0,55	13,5
2 вариант	81	1,94	3,12	1,59	2,69	0,29	0,45	0,96	950	0,56	10,1
3 вариант	84	1,78	3,26	1,68	2,64	0,3	0,44	0,98	820	0,61	11,7
4 вариант	98	1,8	3,09	1,5	2,6	0,3	0,41	0,99	990	0,59	12,9
5 вариант	93	1,87	3,03	1,58	2,61	0,29	0,5	0,92	940	0,64	10,8
6 вариант	91	1,99	3,14	1,62	2,67	0,3	0,44	0,94	1150	0,53	14,5
7 вариант	91	1,95	3,19	1,68	2,7	0,27	0,42	0,92	810	0,62	11,4
8 вариант	92	1,76	3,04	1,7	2,51	0,3	0,45	0,93	880	0,61	13
9 вариант	97	1,94	3,14	1,56	2,66	0,29	0,44	0,91	950	0,59	13,2
10 вариант	99	1,76	3,23	1,56	2,67	0,3	0,48	0,93	1150	0,58	11,8
11 вариант	88	1,97	3,18	1,59	2,58	0,27	0,41	0,94	1100	0,54	12,6
12 вариант	86	1,96	3,04	1,65	2,64	0,23	0,5	0,99	1150	0,5	13,3
13 вариант	95	1,89	3,18	1,68	2,58	0,27	0,48	0,92	800	0,53	13,9
14 вариант	81	1,77	3,09	1,65	2,57	0,25	0,48	0,99	1080	0,57	11,1
15 вариант	89	1,87	3,12	1,59	2,69	0,28	0,48	1	970	0,62	11,3
16 вариант	85	1,83	3,17	1,59	2,66	0,21	0,44	0,96	980	0,69	13
17 вариант	86	1,94	3,27	1,56	2,56	0,2	0,4	0,99	950	0,67	13,6
18 вариант	97	1,82	3,11	1,67	2,56	0,26	0,48	0,9	1200	0,68	14,2
19 вариант	97	1,88	3,29	1,6	2,54	0,29	0,4	0,9	800	0,59	10,6
20 вариант	93	1,97	3,02	1,69	2,58	0,23	0,41	0,95	1160	0,61	13,3
21 вариант	81	1,76	3,13	1,55	2,5	0,22	0,44	0,95	930	0,5	14,9
22 вариант	99	2	3,27	1,51	2,52	0,28	0,48	0,93	1140	0,69	11,9
23 вариант	99	1,75	3,15	1,68	2,68	0,26	0,41	0,98	930	0,52	14,6
24 вариант	84	1,77	3,26	1,5	2,58	0,21	0,5	0,99	830	0,51	13,2
25 вариант	83	1,92	3,17	1,61	2,64	0,22	0,49	1	1180	0,68	14,9
26 вариант	94	1,79	3,02	1,53	2,59	0,28	0,48	0,91	800	0,65	10,1
27 вариант	81	1,76	3,03	1,68	2,64	0,29	0,5	0,95	990	0,55	13,2
28 вариант	99	1,97	3,22	1,67	2,53	0,23	0,45	0,99	1130	0,64	13,4
29 вариант	84	1,78	3,14	1,62	2,58	0,21	0,48	0,95	830	0,54	14,7
30 вариант	95	1,77	3,21	1,66	2,65	0,21	0,49	0,95	970	0,69	12

 

Контрольные вопросы:

1.        Назовите определение гидростатического давления?

2.        Назовите свойства, которыми обладает гидростатическое давление.

3.        Напишите вывод основного уравнения гидростатики.

4.        Расскажите сущность закона Паскаля.

5.        Сформулируйте закон Архимеда.

6.        Назовите известные вам виды давлений?

 

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №3 Опытная иллюстрация уравнения Бернулли. Построение пьезометрических напорных линий.

Цель:

Научиться рассчитывать пьезометрический напор и строить пьезометрические напорные линии.

Необходимые материалы и оборудование:

1.                           Методические рекомендации по выполнению практических занятий

2.                           Справочные таблицы 

Ход работы:

Вначале проводится опрос студентов с целью выявить их теоретические знания по теме, затем совместно решается задача и дается задание на самостоятельное решение

Пояснения к работе:

Уравнение Бернулли для потока идеальной жидкости:

При движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию.

В результате полная удельная энергия жидкости в сечении 1 – 1 будет больше полной удельной энергии в сечении 2 – 2 на величину потерянной энергии.

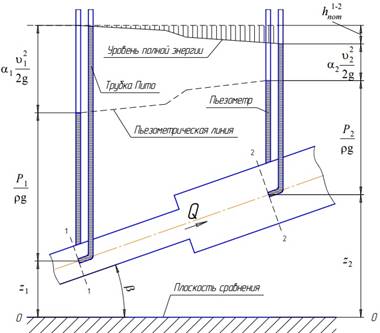
Рис.3.1

Уравнение Бернулли для реальной жидкости будет иметь вид:

где    – потерянная энергия или потерянный напор

Потерянный напор  складывается из линейных потерь , вызванных силой трения между слоями жидкости, и потерь , вызванных местными сопротивлениями (изменениями конфигурации потока)

Из рис. 3.1 видно, что по мере движения жидкости от сечения 1—1 до сечения 2 – 2 потерянный напор все время увеличивается (потерянный напор выделен вертикальной штриховкой).

Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между сечениями 1—1 и 2—2. Кроме этого в уравнение включены два коэффициента и , которые называются коэффициентами Кориолиса и учитывают неравномерность распределения скоростей в потоке вязкой жидкости. Эти коэффициенты зависят от режима течения жидкости ( .

Уравнение Бернулли для реальной жидкости применяется в технике, например для расчетов водопроводов, нефтепроводов, газопроводов и т.д.

Рассмотрим следующую задачу:

Из бака при постоянном напоре по прямому горизонтальному трубопроводу с вентилем вытекает вода в атмосферу (рис. 3.2).

Определить расход воды в трубопроводе при полном открытии вентиля и построить пьезометрическую и напорную линии.

Рис.3.2

Уравнение Бернулли для сечений 0—0 и 4—4 относительно плоскости сравнения 0’—0’, проведенной через ось трубы:

В данном случае

т.к. скорость движения воды в баке много меньше, чем скорость движения воды в трубе, то  

Тогда полный напор:

Потерянный напор:

Где  – суммарные потери напора на преодоление местных сопротивлений;  – потери напора на трение по длине трубопровода;         – сумма коэффициентов потерь в местных сопротивлениях.

Или полный напор:

Т.к.  , то

Учитывая, что  , расход жидкости определится:

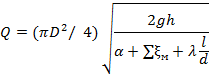
где

Для построения пьезометрической линии определим пьезометрический напор в любом сечении трубопровода:

Уравнение Бернулли для сечений 0—0 и х—х относительно плоскости сравнения 0’—0’:

т.к. пьезометрический напор зависит только от избыточного давления, то для всех сечений считаем  , тогда:

Пьезометрический напор в сечении 1—1:

где

Пьезометрический напор в сечении 2—2 определяется с учетом      

Пьезометрический напор в сечении 3—3 определяется с учетом                

В сечении 4 — 4  и

Исходные данные для расчетов

В качестве исходных данных задаются:

- длина горизонтального трубопровода ;

- диаметр трубопровода ;

- расстояние от начала трубопровода до вентиля ;

- постоянный напор ;

- коэффициент гидравлического трения ;

- коэффициент потерь в вентиле при его полном открытии ;

- коэффициент потерь на входе в трубу ;

- коэффициент неравномерности скоростей (Кориолиса) ;

Исходные данные представлены в таблице.

Вариант
1	100	80	0.10	5	0.030
2	150	120	0.15	10	0.035
3	120	100	0.12	8	0.030
4	180	140	0.2	8	0.040
5	200	150	0.2	10	0.042
6	160	100	0.15	6	0.034
8	130	90	0.1	10	0.030
9	100	70	0.3	4	0.035
10	140	100	0.2	8	0.040
11	150	100	0.15	5	0.035
12	180	150	0.1	7	0.06
13	170	120	0.3	9	0.052
14	230	210	0.2	10	0.044
15	200	150	0.15	8	0.033
16	110	85	0.35	9	0.045
17	160	120	0.4	10	0.025
18	200	160	0.5	13	0.030
19	210	130	0.1	4	0.034
20	220	200	0.3	5	0.038
21	90	85	0.5	8	0.044
22	50	20	0.6	9	0.045
23	230	200	0.8	10	0.024
24	250	240	0.25	4	0.020
25	240	120	0.1	6	0.036
26	300	250	0.3	8	0.047
27	155	100	0.16	9	0.040
28	260	220	0.2	7	0.031
29	320	300	0.3	8	0.028
30	310	50	0.25	9	0.024

 

Порядок проведения расчетов

1.             Найти расход воды в трубопроводе при полном открытии вентиля.

2.             Найти скорость течения воды.

3.             Вычислить пьезометрический напор в сечения 1—1 ; 2—2; 3—3.

4.             Вычислить скоростной (динамический) напор по формуле

Результаты расчетов

1.             Исходные данные и полученные данные занести в таблицу.

Вариант

2.             Откладывая полученные значения пьезометрического напора в каждом сечении от плоскости сравнения 0’ – 0’, построить пьезометрическую линию (в масштабе).

3.             С учетом равномерности напора в трубопроводе постоянного сечения, построить напорную линию параллельно пьезометрической и выше последней на величину скоростного напора (см. рис. 3.2).

 

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №4 Гидравлический расчет простого трубопровода.

Цель:

Научиться рассчитывать линейные потери напора в трубопроводах при различных режимах течения жидкости и различной шероховатости стенок труб

Необходимые материалы и оборудование:

1.                           Методические рекомендации по выполнению практических занятий

2.                           Справочные таблицы 

Ход работы:

Вначале проводится опрос студентов с целью выявить их теоретические знания по теме, затем совместно решается задача и дается задание на самостоятельное решение     

Пояснения к работе:

В природе существует два режима течения жидкостей: ламинарный и турбулентный.

Ламинарным называется слоистое течение без перемешивания частиц жидкости и без пульсации скорости и давления.

Турбулентным называется течение, сопровождающееся интенсивным перемешиванием жидкости с пульсациями скоростей и давления

Переход от ламинарного режима к турбулентному наблюдается при определенной средней скорости движения жидкости. Эта скорость называется критической .

Значение этой скорости прямо пропорционально кинематической вязкости жидкости и обратно пропорционально диаметру трубы.

где  кинематическая вязкость;

k – безразмерный коэффициент

d – внутренний диаметр трубы

Входящий в эту формулу безразмерный коэффициент k, называется критическим числом Рейнольдса Re_кр и определяется следующим образом:

Как показывает опыт, для труб круглого сечения

Таким образом, число Рейнольдса позволяет судить о режиме течения жидкости в трубе.

При Re < Re_кр течение является ламинарным, а при Re > Re_кр течение является турбулентным. Точнее говоря, вполне развитое турбулентное течение в трубах устанавливается лишь при Re примерно равным 4000, а при Re = 2300…4000 имеет место переходная, критическая область.

Режим движения жидкости напрямую влияет на степень гидравлического сопротивления трубопроводов.

При движении реальной вязкой жидкости в трубопроводе часть энергии жидкости затрачивается на преодоление силы трения между слоями жидкости и стенками трубы, а часть – на преодоление различных препятствий в трубопроводе (вентилей, всевозможных закруглений, сужений, расширений и т.д.).

 

Полные потери энергии или потерянный напор  определяется

где — линейные потери, вызванные силой трения между слоями жидкости

— потери, вызванные местными сопротивлениями (изменениями конфигурации потока)

Линейные потери напора определяются формулой Дарси−Вейсбаха:

где  – коэффициент гидравлического трения; l – длина трубопровода диаметром d; v – средняя скорость потока жидкости

СИ:[] = м

Линейные потери напора δp можно выразить в единицах давления:

На практике трубопроводы делятся на короткие и длинные.

К коротким относятся все трубопроводы, в которых местные потери напора превышают 5…10% потерь напора по длине. При расчетах таких трубопроводов обязательно учитывают потери напора в местных сопротивлениях.

К длинным относятся трубопроводы, в которых местные потери меньше 5…10% потерь напора по длине. Их расчет ведется без учета местных потерь. К таким трубопроводам относятся, например, магистральные водоводы, нефтепроводы.

Учитывая гидравлическую схему работы длинных трубопроводов, их можно разделить также на простые и сложные. Простыми называются последовательно соединенные трубопроводы одного или различных сечений, не имеющих никаких ответвлений. К сложным трубопроводам относятся системы труб с одним или несколькими ответвлениями, параллельными ветвями и т.д. К сложным относятся и так называемые кольцевые трубопроводы.

Средняя скорость потока жидкости:

где  — объемный расход жидкости, м³/с

—площадь живого сечения, м²

Для круглой трубы:

Коэффициент гидравлического трения λ зависит от числа Рейнольдса и от относительной шероховатости стенок трубы δ/d

Где δ – эквивалентная шероховатость стенок трубопровода, дается в таблице

Характерные значения δ (в мм) для труб из различных материалов приведены ниже:

Материал и вид труб	δ (в мм) пределы изменения
Стекло, цветные металлы	0,001…0,002
Трубы, тянутые из латуни, свинца и меди	0…0,002
Высококачественные бесшовные стальные трубы	0,06-0,2
Стальные трубы	0,1…0,5
Цельносварная стальная	0,04…0,1
Чугунные асфальтированные трубы	0,1…0,2
Чугунные трубы	0,2…1,0
Асбоцементные трубы	0,5…0,1
Керамическая	1,4
Бетонная и железобетонная	2,5

 

При ламинарном течении коэффициент гидравлического трения λ зависит от числа Рейнольдса Re и не зависит от относительной шероховатости и вычисляется по выражению:

При турбулентном движении в гидравлически гладких трубах в диапазоне чисел Рейнольдса 4000 < Re < 10d/δ коэффициент λ определяется по формуле Блазиуса:

Для круглых труб различной шероховатости в диапазоне чисел Рейнольдса                 10d/δ < Re < 560d/δ коэффициент λ зависит одновременно от двух параметров – числа Re и относительной шероховатости δ/d.

Для определения коэффициента λ в этой области может служить универсальная формула А.Д. Альтшуля:

Где δ – эквивалентная абсолютная шероховатость.

При больших Re > 560 δ/d, коэффициент λ не зависит от числа Re, а определяется лишь относительной шероховатостью. Определение λ для этой области производят по упрощенной формуле Альтшуля:

Исходные данные для расчетов

В качестве исходных данных задаются:

- два вида жидкостей: вода и нефть;

- плотность воды ; плотность нефти ;

- динамическая вязкость воды ; динамическая вязкость нефти                    ;

- длина трубопровода l

- диаметр трубопровода d;

- объемный расход Q;

- относительная шероховатость трубы δ/d

Исходные данные представлены в таблице.

 

 

Вариант	Вода				Нефть
	l,м	d,м	Q, м3/с	Материал и вид трубы	l,м	d,м	Q, м3/с	Материал и вид трубы
1	120	0,26	3,14∙10-4	Стекло	3	0,1	0,314	Бесшовные стальные трубы
2	300	0,2	1,57∙10-1	Латунь	50	0,2	3,14∙10-3	Стальная
3	240	0,13	3,90∙10-3	Бесшовные стальные трубы	2	0,3	1,256	Стекло
4	80	0,15	5,88∙10-2	Стальная	30	0,15	0,126	Латунь
5	150	0,1	1,56∙10-2	Цельносварная стальная	2,5	0,8	0,312	Чугунная труба
6	20	0,3	4,70∙10-2	Чугунная асфальтированная	20	0,5	1,26	Цельносварная стальная
7	15	20	5,24∙10-3	Чугунная труба	20	0,3	2,3	Керамическая
8	40	15	7,45∙10-2	Асбоцементная труба	30	0,25	1,54	Асбоцементная труба
9	88	36	5,12∙10-3	Керамическая	15	0,4	1,625	Бетонная и железобетонная
10	81	8	1,52∙10-1	Бетонная и железобетонная	60	0,1	2,2	Чугунная асфальтированная

 

 

Порядок проведения расчетов

1.             Зная диаметр трубопровода, найти площадь живого сечения.

2.             Зная объемный расход и площадь живого сечения найти среднюю скорость потомка.

3.             По заданным параметрам жидкости, известным диаметру трубопровода и средней скорости найти число Рейнольдса.

4.             Зная число Рейнольдса и относительную шероховатость, определить соответствующий частный случая для расчета коэффициента гидравлического трения λ и найти его значения.

5.             Рассчитать линейные потери напора, выраженные в единицах длины и в единицах давления.

Результаты расчетов

Исходные и полученные данные для каждой жидкости (воды и нефть) занести в таблицу.

Вариант №	l, м	d, м	Q, м3/с	δ/d	ω,	v, м/с	Re	λ	hлин, м	δp, Па
Вода
Нефть

 

 

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №5 Классификация, область применения, достоинства и недостатки насосов.

Цель:

Познакомиться с классификацией, принципом действия, областями применения и особенностями насосов.

Необходимые материалы и оборудование:

1.                           Методические рекомендации по выполнению практических занятий

2.                           Справочные таблицы 

Ход работы:

Вначале проводится опрос студентов с целью выявить их теоретические знания по теме, затем совместно решается задача и дается задание на самостоятельное решение

Пояснения к работе:

Динамические насосы

По характеру силового взаимодействия между рабочими органами и жидкостью динамические насосы подразделяются на:

1)      Лопастные насосы

2)      Насосы трения.

Лопастные насосы

Лопастные насосы получили наибольшее распространение в системах водоснабжения населения. Рабочим органом лопастной машины является вращающееся рабочее колесо, снабженное лопастями.

В зависимости от траектории движения жидкости в проточной части лопастные насосы делятся на центробежные и осевые.

Центробежные насосы

В центробежном лопастном насосе жидкость под действием центробежных сил перемещается через рабочее колесо от центра к периферии. Центробежные насосы наиболее распространены в машиностроении.

На рис. 5.1 изображена простейшая схема центробежного насоса.

Проточная часть насоса состоит из трех основных элементов – подвода 1, рабочего колеса 2 и отвода 3. По подводу жидкость подается в рабочее колесо из подводящего трубопровода. Рабочее колесо 2 передает жидкости энергию от приводного двигателя.

Рабочее колесо состоит из двух дисков а и  б, между которыми находятся лопатки в, изогнутые в сторону, противоположную направлению вращения колеса.

Жидкость движется через колесо из центральной его части к периферии. По отводу жидкость отводится от рабочего колеса к напорному патрубку 4 или, в многоступенчатых насосах, к следующему колесу.

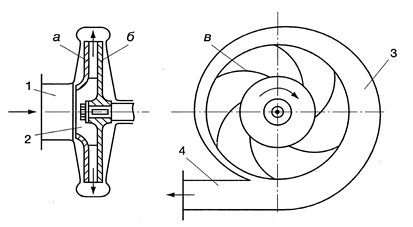
Рис. 5.1 - Схема центробежного насоса

Центробежные насосы могут быть предназначены для особых условий эксплуатации, например для перекачки нефти и нефтепродуктов, для работы с химически ки активными жидкостями, для работы при повышенной температуре и т.д. Их КПД лежит в пределах 0,70 … 0,85.

Центробежные насосы могут выпускаться вместе в приводным двигателем как единое изделие. Такое устройство называется насосным агрегатом.

Осевые насосы

В осевом лопастном насосе жидкость перемещается в основном вдоль оси вращения рабочего колеса (рис. 5.2).

Рабочее колесо осевого насоса похоже на винт корабля. Оно состоит из втулки 1, на которой закреплено несколько лопастей 2. Отводом насоса служит осевой направляющий аппарат 3, с помощью которого устраняется закрутка жидкости, и кинетическая энергия ее преобразуется в энергию давления.

Осевые насосы применяют при больших подачах и малых давлениях.

Осевые насосы могут быть жестколопастными, в которых положение лопастей рабочего колеса не изменяется, и поворотно-лопастными, в которых положение рабочего колеса может регулироваться.

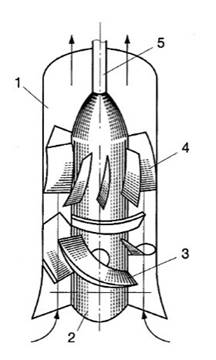
Рис.5.2 - Схема осевого насоса

По сравнению с объемными насосами лопастные насосы имеют ряд преимуществ и недостатков. Они имеют практически равномерную подачу и нетребовательны к чистоте рабочей жидкости (могут перекачивать весьма загрязненные жидкости).

Однако, эти насосы не могут перекачивать вязкие жидкости и не обладают самовсасыванием, т.е. работая без жидкости, не создают достаточного разрежения, за счет которого возможно подсасывание жидкости из емкости, расположенной ниже насоса. Поэтому перед началом работы всасывающий трубопровод насоса должен быть заполнен жидкостью.

Кроме того, подача насоса существенно зависит от его напора (и наоборот), т.е. при изменении сопротивления трубопровода меняется напор, а с ним и подача насоса.

Насосы трения

В насосах трения силовое взаимодействие происходит в проточной части за счет сил трения, причем их проточная часть постоянно сообщается с входом и выходом.

Т.к. в основе работы насосов лежит принцип трения, то эффективность их работы невысока, они имеют низкий КПД.

Поэтому насосы трения не получили широкого распространения в технике.

Из насосов этого типа наиболее широко используются вихревые и струйные насосы.

Вихревые насосы

Вихревые насосы по своему рабочему процессу и свойствами близки к центробежным (лопастным) насосам.

Однако, напор вихревого насоса в 4…6 раз больше, чем центробежного, при тех же габаритах и частоте вращения.

Кроме того, вихревые насосы обладают самовсасывающей способностью, что позволяет использовать их в качестве вакуум-насосов при заливе крупных центробежных насосов. Но у вихревых насосов относительно невысок КПД (0,30 … 0,45).

Выпускают комбинированные насосы, у которых в одном корпусе размещены и вихревые, и центробежные колеса.

На рис. 5.3 изображена простейшая схема вихревого насоса.

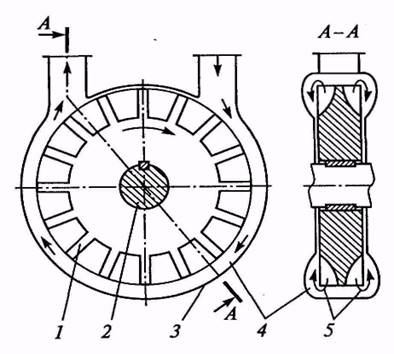
Рис. 5.3. Схема вихревого насоса

Основной деталью насоса является рабочее колесо 1 с радиальными или наклонными лопатками.

Колесо установлено в корпусе 3 и приводится во вращение валом 2.

Важным конструктивным элементом является концентрический канал 4, охватывающий колесо по большей части окружности – от входного отверстия до выходного. По меньшей части окружности канал (от выходного отверстия до входного) отсутствует, что служит уплотнением между напорной и всасывающей полостями.

При вращении рабочего колеса 1 в межлопаточных полостях и в концентрическом канале 4 образуются вихри 5, что приводит к непрерывному перемещению частиц жидкости из межлопаточных полостей колеса в канал и обратно.

За счет этого происходит передача энергии от колеса к жидкости в концентрическом канале. Жидкость в канале как бы увлекается образовавшимися вихрями и перемещается вместе с колесом от полости всасывания к полости нагнетания.

Струйные насосы

Струйные насосы не имеют вращающихся частей, а поток перекачиваемой жидкости перемещается за счет трения, возникающего между ним и другим (рабочим) потоком жидкости.

Рабочий поток жидкости подводится к насосу извне и должен обладать достаточной энергией для обеспечения перекачки жидкости с заданными параметрами. Его можно считать условным рабочим органом данного насоса.

Рабочий и перекачиваемый потоки могут быть одной и той же или разными жидкостями.

Существенным преимуществом струйных насосов является отсутствие подвижных и вращающихся частей. Они малочувствительны к загрязненным и агрессивным жидкостям.

Недостатки насосов: невысокие давления на выходе и крайне низкий к.п.д.  (0,20… 0,35).

На рис. 5.4 изображена простейшая схема струйного насоса.

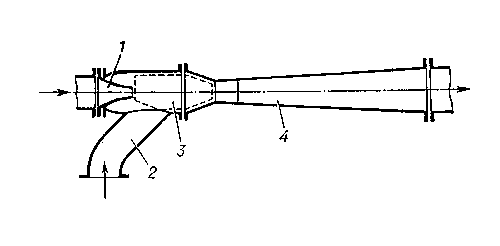
Рис.5.4. Схема струйного насоса

1-            всасывающий полость, 2- сопло, 3- смеситель, 4- диффузор, 5- труба

В струйном насосе рабочая жидкость под давлением подводится по трубе 1 к соплу 2, а из него с увеличенной скоростью попадает в цилиндрический участок – смеситель 3. Здесь из-за создавшегося разрежения вода из колодца или скважины подсасывается и перемешивается с рабочей жидкостью. Далее смешанный поток воды поступает в расширяющийся участок насоса – диффузор 4, где в связи с понижением скорости давление (напор) увеличивается до такого предела, который обеспечивает дальнейший подъем и перемещение воды по трубе 5 к потребителю.

Струйные насосы характеризуются простотой устройства и обслуживания, так как не имеют трущихся частей и клапанов. Они малочувствительны к загрязнению воды, и потому чих часто применяют для перекачки пульпы, угольного шлама, ливневых и сточных канализационных вод.

В практике сельского водоснабжения струйные насосы обычно используют в комбинации с центробежными для увеличения их высоты всасывания. Преимущество такой установки состоит в том, что в скважине нет вращающихся деталей, а центробежной насос и электродвигатель располагаются на земной поверхности, в удобном для осмотра месте.

В зависимости от вида рабочей и перекачиваемой жидкостей различают:

1)            эжектор – оба потока являются жидкостями;

2)            элеватор – рабочий поток – жидкость, перекачиваемый – пульпа (смесь жидкости с песком, шлаком и т.д.) или жидкость другой температуры (в системах отопления)

3)            инжектор – для рабочего потока используется газ (пар), который перекачивает жидкость.

Порядок выполнения работы.

1. Ознакомьтесь с классификацией, принципом действия, устройством и техническими характеристиками насосов, используя материал, представленный в описании данной практической работы.

2. Заполните таблицы 1 и 2.

Таблица 1 - Объемные насосы

Тип насоса (по характеру движения рабочего органа)	Принцип действия	Вид насоса (в зависимости от вида рабочего органа)	Давление насоса, к.п.д.	Назначение	Достоинства	Недостатки

 

Таблица 2 - Динамические насосы

Тип насоса (по характеру взаимодействия между рабочим органом и жидкостью)	Принцип действия	Вид насоса (в зависимости от наличия или отсутствия рабочего органа)	К.п.д.	Назначение	Достоинства	Недостатки

 

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №6 Испытание центробежного насоса.

Цель:

Ознакомиться с основными параметрами и характеристиками насосов, научиться их определять.

Необходимые материалы и оборудование:

1.                           Методические рекомендации по выполнению практических занятий

2.                           Справочные таблицы 

Ход работы:

Вначале проводится опрос студентов с целью выявить их теоретические знания по теме, затем совместно решается задача и дается задание на самостоятельное решение

Пояснения к работе:

Насосом называется гидравлическая машина, в которой происходит преобразование механической работы в энергию потока жидкости, предназначенную для подъема, нагнетания и перемещения жидкости.

Насосы классифицируются по принципу их действия:

1)            динамические – работают по принципу силового воздействия на перемещаемую среду:

·               лопастные насосы – центробежные, радиальные и осевые;

·               насосы трения – струйные, вихревые и дисковые.

2)            объемные – работают по принципу вытеснения жидкости:

·               поршневые насосы;

·               роторные.

         Основные технические характеристики центробежного насоса:

1.             Подача – это объем перекачиваемой в единицу времени жидкости, Q[м³/ч], [л/с].

2.             Полный напор:

·               для горизонтального насоса:

где  Н_d – гидростатическое давление на выходе из насоса, измеряемое у выходного патрубка и отнесенное к оси вала насоса, м;

Н_s – гидростатическое давление на входе, измеряемое у входного патрубка и отнесенное также к оси вала насоса, м;

v_d – скорость жидкости на выходе из насоса, измеряемое у выходного патрубка, м/с;

v_s – скорость жидкости на входе, м/с;

g – ускорение свободного падения, g = 9,81 м/с².

·         для вертикального насоса:

 

где  Н_d – гидростатическое давление на выходе из насоса, отнесенное к оси напорного колена, м;

Н_s – геометрическая высота всасывания (расстояние от уровня жидкости до центра рабочего колеса), м;

v_d – скорость жидкости на выходе из насоса, м/с;

g – ускорение свободного падения, g = 9,81, м/с².

3.      Коэффициент полезного действия –  это степень гидравлического и механического совершенства насоса определяется значением КПД.

Полный КПД насоса:

где  ρ – плотность жидкости, кг/м³;

Q – подача, м³/с;

Н – полный напор, м;

N – мощность, подведенная к валу насоса Вт.

4.      Характеристики – это зависимости напора от подачи при постоянном числе оборотов.

Законы подобия:

где  n₁ – первоначальное число оборотов, об/мин;

n₂ – конечное число оборотов, об/мин;

Q₁ – первоначальная подача жидкости при начальном числе оборотов, м³/с;

Q₂ – конечная подача ж при конченом числе оборотов, м³/с;

Н₁ – первоначальный напор жидкости при n, м;

Н₂ – конечный напор жидкости при конченом числе оборотов, м;

N₁ – первоначальная мощность при n₁, Вт;

N₂ – конечная мощность при конченом числе оборотов, Вт.

5.      Коэффициент быстроходности:

где  Q –подача жидкости, м³/с;

Н – напор жидкости, м.

6.      Кавитационный запас – это разность статического давления на всасывание насоса и упругости насыщенных паров.

Пример выполнения

Определите геометрическую высоту всасывания центробежного насоса, если его подача Q, диаметр всасывающего трубопровода d₁, а сумма потерь напора во всасывающем трубопроводе Σh_пот, а допустимая вакуумметрическая высота всасывания насоса H_вак.

Дано:                СИ:           Решение:

Q =62 л/с      0,062 м³/с     Геометрическая высота всасывания определяется

d₁ = 100 мм      0,1 м          по формуле:

Σh_пот = 1,2 м                       Для того, чтобы найти геометрическую высоту

Н_вак = 6,3 м                        всасывания насоса, нам нужно определить

Н_s - ?                                  скорость жидкости во всасывающем

                                           трубопроводе, скорость мы будем находить из

                                              уравнения расхода:

                                             Тогда, , так как площадь трубопровода, это                

                                             площадь поперечного сечения, т.е. круга: ,

                                             Следовательно,

Тогда, геометрическая высота всасывания насоса:

                                                                          Ответ: Н_s = 1,9 м

 

Задание:

№1. При частоте вращения вала n₁ , и подаче Q, центробежный насос развивает напор Н_d, и потребляет мощность N. Определите, как изменятся параметры насоса (∆Q,∆H, ∆N), если частота вращения снизится до n₂.

№2. Определите геометрическую высоту всасывания центробежного насоса, если его подача Q, диаметр всасывающего трубопровода d₁, а сумма потерь напора во всасывающем трубопроводе Σh_пот, а допустимая вакуумметрическая высота всасывания насоса H_вак.

№3. Определите коэффициент быстроходности вертикального центробежного насоса, если подача жидкости Q, давление на выходе из насоса Н_d, геометрическая высота всасывания Н_s, а диаметр всасывающего трубопровода d₂.

№4. Определите напор насоса, если его подача Q; диаметр всасывающего трубопровода d₁; диаметр нагнетательного трубопровода d₂, показания манометра соответствуют напору H_d, показания вакууметра H_s; расстояние по вертикали между центрами вакууметра и манометра ∆h.

Варианты заданий:

№ п/п	Q, л/с	d1, мм	d2, мм	Σhпот, м	Hвак, м	Hd, м	Hs, м	∆h, м	n1,мин-1	n2,мин-1	N, кВт
1 вариант	33	50	50	1	7,1	67	-9	0,1	2749	904	81
2 вариант	66	100	50	1,2	6,3	66	-5	0,2	2754	854	72
3 вариант	48	150	100	1,7	6,5	55	-7	0,2	2836	870	71
4 вариант	39	200	150	1	5,5	52	-10	0,2	2875	914	81
5 вариант	36	50	50	0,9	7,5	54	-4	0,3	2820	935	95
6 вариант	41	100	50	1,4	7	67	-7	0,3	2907	922	72
7 вариант	42	150	100	1,5	5,9	45	-3	0,3	2739	949	96
8 вариант	40	200	150	1,1	5,3	55	-7	0,3	2742	922	71
9 вариант	62	50	50	1,7	6,2	42	-4	0,3	2865	898	103
10 вариант	39	100	50	1,4	5,1	62	-9	0,2	2779	910	81
11 вариант	65	150	100	1,2	7,6	59	-10	0,1	2973	931	92
12 вариант	45	200	150	0,9	5,4	51	-4	0,2	2711	969	98
13 вариант	48	50	50	1,1	5,8	70	-4	0,1	2822	976	84
14 вариант	31	100	50	1,2	5,5	43	-10	0,3	2919	941	76
15 вариант	37	150	100	1,6	6,5	69	-6	0,3	2870	934	106
16 вариант	31	200	150	1	7,8	41	-5	0,1	2780	969	110
17 вариант	63	50	50	0,8	5,8	57	-8	0,3	2995	960	89
18 вариант	67	100	50	1,6	7,4	57	-9	0,1	2756	910	81
19 вариант	40	150	100	0,8	6,5	47	-5	0,2	2846	866	87
20 вариант	52	200	150	1,5	5,2	48	-5	0,1	2813	914	104
21 вариант	30	50	50	1,6	6,2	52	-4	0,3	2729	848	84
22 вариант	39	100	50	1,6	7,5	64	-9	0,3	2974	875	78
23 вариант	60	150	100	1,2	7,2	59	-7	0,2	2994	977	118
24 вариант	67	200	150	0,9	6,2	49	-3	0,2	2991	940	98
25 вариант	59	100	50	1,7	7,5	65	-3	0,1	2968	885	106
26 вариант	34	50	50	1,7	5,9	64	-3	0,1	2710	890	73
27 вариант	52	100	100	1,5	5,2	40	-9	0,3	2920	956	112
28 вариант	49	150	150	1,3	7,2	53	-9	0,1	2900	863	75
29 вариант	66	200	50	0,9	5,4	69	-10	0,2	2761	879	78
30 вариант	62	100	50	1,2	6,3	54	-6	0,3	2793	895	93

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №7 Изучение работы и построение характеристик центробежного вентилятора.

Цель:

Научиться определять характеристики центробежных вентиляторов, изучить виды вентиляторов и принцип их работы.

Необходимые материалы и оборудование:

1.                           Методические рекомендации по выполнению практических занятий

2.                           Справочные таблицы 

Ход работы:

Вначале проводится опрос студентов с целью выявить их теоретические знания по теме, затем совместно решается задача и дается задание на самостоятельное решение

Пояснения к работе:

Вентиляторами называют устройства, служащие для перемещения воздуха и других газов при давлении не более 0,15*10⁵ Па. Они, как и насосы, находят применение во многих отраслях народного хозяйства и, в частности, в системах теплогазоснабжения, вентиляции и кондиционирования воздуха. Вентиляторы разделяют на центробежные и осевые.

Центробежный вентилятор состоит из рабочего колеса (ротора) 2 с лопатками, спирального корпуса (кожуха) 3 и станины 1. Рабочее колесо насажено на вал 4, который установлен в подшипниках на станине.

 

 

 

 

 

 

 

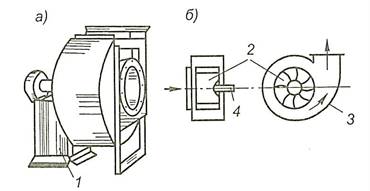
Рисунок 7.1 – а) Общий вид; б) схема устройства центробежного вентилятора

Центробежные вентиляторы применяются в вентиляционных системах промышленных и гражданских зданий, в агрегатах воздушного отопления и кондиционирования воздуха.

Конструктивное устройство центробежного вентилятора показано на рис. 7.2. Рабочее колесо вентилятора состоит из литой ступицы 1, жесткосопряженной с основным диском 2. Рабочие лопатки 3 крепятся к основномудиску 2 и к переднему диску 4, обеспечивающему необходимую жесткость

лопастной решетки 5. Корпус 6 вентилятора крепится к литой или сварнойстанине 9, на которой располагаются подшипники 10, несущие валвентилятора с посаженным на него рабочим колесом; 7 и 8 – фланцыкрепления всасывающей и напорной труб, 11 – шкив привода вентилятора.

Рисунок 7.2 – Конструктивное устройство центробежного вентилятора

Принцип работы центробежного вентилятора аналогичен принципу работы центробежного насоса. Воздух, поступивший через входное отверстие вентилятора в полость рабочего колеса, захватывается лопатками и приводится во вращение. Под действием возникающих сил при этом центробежных сил он сжимается, отбрасывается в спиральный кожух и через нагнетательный патрубок выходит в воздуховод.

Осевой вентилятор представляет собой расположенное в цилиндрическом кожухе 2 лопаточное колесо 1, при вращении которого поступающий через входное отверстие воздух под действием лопаток перемещается между ними в осевом направлении.

Рисунок 7.3 –  а) Общий вид; б) схема устройства осевого вентилятора

Колесо осевого вентилятора состоит из втулки, на которой закреплены наглухо или в которой встроены лопатки. Число лопаток на колесе от 2 до 32. Осевые лопатки с лопатками симметричного профиля называются – реверсивными, а с лопатками несимметричного профиля – нереверсивными.

Центробежные вентиляторы по сравнению с осевыми развивают большее давление, поэтому их целесообразно применять для подачи воздуха при значительном давлении, а осевые -  для подачи относительно большого объема воздуха при небольшом давлении.

Основные технические характеристики вентиляторов:

1.             Подача вентиляторов L, м³/ч, м³/с  - это объем воздуха, перемещаемого вентилятором.

2.             Полное давление:

где   – плотность воздуха, кг/м³;

– окружная скорость, м/с;

 – коэффициент давления вентилятора,  ;

  - гидравлический КПД вентилятора;

р_т – теоретическое давление, развиваемое вентилятором, Па;

– коэффициент закручивания потока.

3.             Теоретическая полезная мощность, передаваемая вентилятором перемещаемой среде:

где  р_п –полное давление, Па;

L – подача вентилятора, м³/с.

4.             КПД вентилятора – отношение полезной мощности к действительной:

5.             Установочная мощность двигателя:

где  К – коэффициент запаса, принимаемый для центробежных вентиляторов, К = 1,5 – 1,1, для осевых К = 1,2-1,05.

6.             Законы подобия:

где  n₁ – первоначальное число оборотов, об/мин;

n₂ – конечное число оборотов, об/мин;

L₁ – первоначальная подача воздуха при начальном числе оборотов, м³/с;

L₂ – конечная подача при конченом числе оборотов, м³/с;

р₁ – первоначальное давление воздуха, Па;

р₂ – конечный давление воздуха при конченом числе оборотов, Па;

N₁ – первоначальная мощность при n₁, Вт;

N₂ – конечная мощность при конченом числе оборотов, Вт.

7.             Критерий быстроходности:

где   – угловая скорость вращения, с^-1;

L – подача вентилятора, м³/с;

 – полное давление вентилятора, Па.

Для центробежных вентиляторов критерий быстроходности составляет до 80, а для осевых 80 - 300.

Характеристикой вентилятора называется зависимость основных величин, определяющих его работу, от расхода воздуха. Характеристика строится в координатах L, м³/с, и p, Па, причем проводят линии полного давления при различной частоте вращения, линия динамического давления, а также линии КПД и потребляемой мощности. Пользуясь универсальной аэродинамической характеристикой, можно всегда выбрать наиболее эффективный режим работы вентилятора, при котором будет максимальный КПД.

Пример задачи

Вариант 30

Определите критерий быстроходности вентилятора и какой вентилятор нужен, если его подача L, давление р_п и угловая частота вращения рабочего колеса .

Дано:                                Решение:

L = 1 м³/с             Критерий быстроходности определим по формуле:

р_п = 800 Па

 = 89 с^-1              Тогда,

 - ?                    Следовательно, можно выбрать центробежный вентилятор.

                               Ответ:

 

Задание:

№1. Определите критерий быстроходности вентилятораи какой вентилятор нужен, если его подача L, давление р_п и угловая частота вращения рабочего колеса .

№2. Определите давление, развиваемое центробежным вентилятором, если коэффициент давления Ψ, частота вращения рабочего колеса n₁, наружный диаметр колеса D, а плотность воздуха ρ.

№3. При частоте вращения вала n₁, и подаче L, центробежный вентилятор развивает давление p, и потребляет мощность N. Определите, как изменятся параметры насоса (∆L,∆p, ∆N), если частота вращения снизится до n₂.

№4. Постройте характеристику вентилятора p_п [Па] от L [тыс. м³/ч], если число оборотов вентилятора n, мощность N, а КПД ƞ. График выполните в программном комплексе Microsoft Excel.

Варианты заданий

№ п/п	L, м3/с	рп, Па	р, кПа	с-1	Ψ	n1, мин-1	n2, мин-1	D, м	ρ, кг/м3	N, кВт	ƞ
1 вариант	4	715	3,4	90	0,83	800	513	0,54	1,2	20	0,5
2 вариант	1	797	3,8	89	0,87	900	440	0,51	1,2	10	0,6
3 вариант	2	700	3,4	85	0,85	1000	446	0,45	1,2	4,5	0,43
4 вариант	1	790	3,3	85	0,78	1100	500	0,41	1,2	2,8	0,64
5 вариант	4	747	4,2	88	0,71	1200	464	0,52	1,2	14	0,5
6 вариант	2	787	3,1	91	0,76	1300	577	0,42	1,2	1	0,6
7 вариант	2	789	3,8	85	0,77	1400	569	0,4	1,2	1,7	0,43
8 вариант	1	748	4,4	89	0,72	800	545	0,5	1,2	20	0,64
9 вариант	2	780	3,6	91	0,85	900	560	0,52	1,2	10	0,64
10 вариант	5	792	4,7	95	0,79	1000	434	0,42	1,2	4,5	0,5
11 вариант	1	776	4,7	88	0,9	1100	433	0,4	1,2	2,8	0,6
12 вариант	3	800	3,7	95	0,7	1200	554	0,6	1,2	14	0,43
13 вариант	4	705	4,2	91	0,9	1300	512	0,34	1,2	1	0,64
14 вариант	3	728	3,9	92	0,79	1400	517	0,33	1,2	1,7	0,5
15 вариант	4	718	4,4	93	0,85	800	508	0,48	1,2	20	0,6
16 вариант	4	799	4,5	89	0,87	900	496	0,3	1,2	10	0,43
17 вариант	3	786	4,2	92	0,73	1000	486	0,52	1,2	4,5	0,64
18 вариант	2	791	3,2	89	0,78	1100	560	0,4	1,2	2,8	0,64
19 вариант	3	795	5	86	0,82	1200	417	0,48	1,2	14	0,5
20 вариант	5	712	3,3	89	0,76	1300	550	0,36	1,2	1	0,6
21 вариант	3	779	4,6	91	0,7	1400	526	0,4	1,2	1,7	0,43
22 вариант	1	718	3	92	0,79	800	542	0,37	1,2	20	0,64
23 вариант	5	791	3	89	0,71	900	513	0,34	1,2	10	0,5
24 вариант	3	758	4,9	86	0,7	1000	409	0,55	1,2	4,5	0,6
25 вариант	5	707	4,1	90	0,8	1100	460	0,5	1,2	2,8	0,43
26 вариант	3	787	4	87	0,89	1200	513	0,46	1,2	14	0,64
27 вариант	3	714	3,7	88	0,81	1300	566	0,46	1,2	1	0,64
28 вариант	4	705	4,5	91	0,74	1400	442	0,36	1,2	1,7	0,43
29 вариант	1	735	4,6	85	0,83	1400	437	0,4	1,2	20	0,5
30 вариант	1	800	3,6	89	0,73	1300	572	0,34	1,2	14	0,6

Контрольные вопросы:

1.        Назовите назначение вентилятора и их виды.

2.        Объясните принцип работы центробежного вентилятора.

3.        Расскажите классификацию центробежных вентиляторов.

4.        Назовите основные технические характеристики вентиляторов.

5.        Объясните, как определить полезную мощность и КПД вентилятора.

6.        Назовите, что характеризует критерий быстроходности вентилятора.

7.        Назовите, что называют характеристикой вентилятора?

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №8 Определение параметров пара.

Цель:

Научиться определять основные параметры пара и законы идеального газа. Понять в чем их отличие

Необходимые материалы и оборудование:

1.                           Методические рекомендации по выполнению практических занятий

2.                           Справочные таблицы 

 

Ход работы:

Вначале проводится опрос студентов с целью выявить их теоретические знания по теме, затем совместно решается задача и дается задание на самостоятельное решение

Пояснения к работе:

Теплотехника – это наука, изучающая процесс перехода теплоты в механическую работу.

Идеальный газ – это такой газ, в котором молекулы находятся на большом расстоянии друг от друга, не взаимодействуют межу собой.

            Основные параметры состояния идеального газа:

1)      Давление:

где  р_б – атмосферное (барометрическое давление Па, мм рт. ст., бар;

р_изб – избыточное давление Па, мм рт. ст., бар.

1        бар = 750 мм рт. ст.

2)      Температура:

где  t– температура по шкале Цельсия ⁰С.

3)      Удельный объем:

где  V – объем, занимаемый газом, м³;

m– масса газа, кг;

ρ– плотность газа, кг/м³.

            Основные законы идеального газа:

Закон Бойля – Мариотта:

где  υ – удельный объем, м³;

р – абсолютное давление, Па, мм рт. ст., бар;

t– температура, ⁰С, К.

Закон Гей-Люссака:

где  υ – удельный объем, м³;

t– температура, К;

р– абсолютное давление, Па, мм рт. ст., бар.

Закон Шарля:

где  р– абсолютное давление, Па, мм рт. ст., бар;

υ – удельный объем, м³;

t– температура, К.

Закон Авогадро:

где  μ – молярная масса, кг/моль;

р– абсолютное давление, Па, мм рт. ст., бар;

ρ– плотность газа, кг/м³;

t– температура, ⁰С, К.

Уравнение состояния идеального газа, или уравнение Клайперона:

где  V – объем, занимаемый газом, м³;

р– абсолютное давление, Па, мм рт. ст., бар;

ρ– плотность газа, кг/м³;

m– масса газа, кг;

R₀ – газовая постоянная, для каждого газа имеет свое значение, Дж/(кг*К);

T– температура, К.

Уравнение Менделеева-Клайперона:

где  V – объем, занимаемый газом, м³;

р– абсолютное давление, Па, мм рт. ст., бар;

ρ– плотность газа, кг/м³;

m– масса газа, кг;

μ – молярная масса, кг/моль;

R – универсальная газовая постоянная, R=8,314 Дж/(моль*К);

T– температура, К.

Пример решения задачи:

Вариант 30

Определите, как изменится объем жидкости при повышении температуры от t₁ до t₂, если изначально объем жидкости составлял V, давление осталось неизменным.

Дано:                                Решение:

V = 0,8 м³                 Так как p = const, то для нахождения изменения объема

t₁ = 15 ⁰C                мы применим законГей-Люссака:     

t₂ = 43⁰C                Для этого сначала переведем температуру в Кельвин:

∆V - ?                     Т₁ = 273+15 = 288 К

                               Т₂ = 273+43 = 316 К

                                 Т.к.    , то

                               Тогда ∆V = V₂ – V₁ = 0,878 – 0,8 = 0,078 м³

                                      Следовательно, при изменении температуры объем 

                               увеличился на 0,078 м³.

                               Ответ: ∆V = 0,078 м³

 

Здаание:

№1.Манометр, установленный на паровом котле, показывает давление р_изб. Определите давление пара в котле, если атмосферное давление р_атм.

№2.В баллоне содержится кислород массой m при давлении p и температуре t₁. Вычислите вместимость баллонаV.

№3.Давление воздуха, измеренное ртутным барометром, равно р_б при температуре ртути t₁. Выразите это давление в барах.

№4. В баллоне объемом V содержится аргон при определенных условиях массой m. Определите плотность и удельный объем аргона при этих условиях.

№5. Резервуар вместимостью V заполнен углекислым газом. Избыточное давление в резервуаре p_изб, температура t₁, а барометрическое давление p_атм. Определите:

а) массу газа

б) вес газа

в) удельный объем газа

№6. Определите, как изменится давление жидкости при повышении температуры от t₁ до t₂, если изначально давление жидкости составляло p, удельный объем остался неизменным.

№7. В баллоне объемом V находится гелий под давлением р при температуре t₁. После того, как из баллона был израсходован гелий массой m, температура в баллоне понизилась на ∆t. Определите давление p₂ гелия, оставшегося в баллоне. Молярная масса гелия μ= 0,004 кг/моль.

Варианты заданий:

№ п/п	p, МПа	ризб, кПа	ратм, кПа	рб, мм рт. ст.	t1, 0С	t2, 0С	∆t, 0С	V, м3	m,кг
1 вариант	3,9	1,4	100	696	20	53	10	1,3	0,91
2 вариант	10,4	2,2	94	665	15	49	9	0,7	1,04
3 вариант	7,4	1,9	102	655	10	55	7	0,9	0,6
4 вариант	1,4	1,6	96	661	15	50	5	0,6	0,9
5 вариант	10,8	1	107	704	30	42	20	1,8	0,53
6 вариант	3,9	1,2	119	665	25	44	15	1,3	0,5
7 вариант	7,1	1,8	115	671	20	49	9	0,8	0,99
8 вариант	2	2,2	88	697	15	58	8	1,4	1,03
9 вариант	7	1,5	96	670	15	51	7	1,5	0,82
10 вариант	4,3	2	112	689	10	57	5	0,8	0,62
11 вариант	6,3	2,2	80	702	25	41	20	0,6	0,46
12 вариант	7,5	0,9	114	660	10	55	7	0,8	0,71
13 вариант	7,2	1,9	92	692	30	49	17	0,7	0,75
14 вариант	10,5	1,4	83	703	10	43	8	0,7	0,73
15 вариант	1,3	1,4	107	690	15	54	9	1,8	0,58
16 вариант	1,8	1,1	86	660	15	41	4	1,2	0,66
17 вариант	4,6	1,2	115	717	25	58	22	1,4	1,03
18 вариант	3,2	1,6	106	659	10	57	7	1,2	0,86
19 вариант	9,7	1,6	116	681	25	51	11	1,1	0,76
20 вариант	2,7	1	85	647	30	40	10	1,8	0,89
21 вариант	5,3	1,5	111	718	30	55	14	1,4	0,51
22 вариант	9,8	1,4	90	681	15	54	9	0,6	0,7
23 вариант	8,5	2,1	88	652	20	44	14	1,3	0,8
24 вариант	8,6	1,7	84	710	25	41	8	1	0,56
25 вариант	2,5	2,3	97	665	30	57	7	1,5	0,62
26 вариант	4	1,5	92	710	15	44	10	1,4	0,47
27 вариант	2,9	1,3	83	645	10	58	4	1,5	0,56
28 вариант	7,6	1,2	118	685	20	55	19	1,8	0,59
29 вариант	1,3	1,3	102	676	30	51	15	1,3	0,88
30 вариант	10,9	1,2	106	655	15	43	7	0,8	0,53

 

Контрольные вопросы:

1.        Назовите, что изучает теплотехника?

2.        Сформулируйте, какой физический смысл лежит в основе термодинамики?

3.        Назовите, что такое термодинамическая система?

4.        Назовите какие бывают термодинамические состояния?

5.        Объясните отличие реального газа от идеального.

6.        Назовите какие две температурные шкалы применяют для измерения температуры?

7.        Назовите основные параметры состояния идеального газа?

8.        Сформулируйте закон Бойля-Мариотта

9.        Назовите, что утверждает закон Гей-Люссака?

10.     Сформулируйте закон Шарля.

11.    Объясните, какие параметры связывают уравнение идеального газа Клайперона?

 

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №9 Применение первого и второго закона термодинамики.

Цель:

Научиться применять 1 и 2 закон термодинамики для решения конкретных прикладных задач, изучить термодинамические процессы, и их особенности, понять, в чем заключается особенность цикла Карно, и что такое прямой и обратный циклы.

Необходимые материалы и оборудование:

1.                           Методические рекомендации по выполнению практических занятий

2.                           Справочные таблицы 

Ход работы:

Вначале проводится опрос студентов с целью выявить их теоретические знания по теме, затем совместно решается задача и дается задание на самостоятельное решение

Пояснения к работе:

Полная энергия системы:

E = E_к + Е_п + U

где  E_к – кинетическая энергия системы, Дж;

E_п – потенциальная энергия системы, Дж;

U – внутренняя энергия, Дж.

Внутренняя удельная энергия вещества:

 Дж/кг

где  U – внутренния энергия системы, Дж;

m – масса вещества,  кг.

Изменение внутренней энергии:

∆U = Дж

где  i – число степеней свободы;

R – универсальная газовая постоянная, R = 8,314 Дж/(моль*К);

m – масса вещества,  кг;

μ–молярная масса, кг/моль;

∆T – изменение температуры, К.

Удельная теплоемкость при постоянном давлении:

где  ∆Q – количество теплоты, Дж;

m – масса вещества,  кг;

∆T – изменение температуры, К.

Удельная теплоемкость при постоянном объеме:

где  ∆Q – количество теплоты, Дж;

m – масса вещества,  кг;

∆T – изменение температуры, К.

Показатель адиабаты:

где  с_р – удельная теплоемкость при постоянном давлении, Дж/кг*К;

с_v – удельная теплоемкость при постоянном объеме, Дж/кг*К.

Молярная теплоемкость:

 

где  с_р – удельная теплоемкость при постоянном давлении, Дж/кг*К;

μ–молярная масса, кг/моль.

Первый закон термодинамики:

где  ∆U – изменение внутренней энергии системы, Дж;

А – работа,  Дж.

 

Второй закон термодинамики:

где  ∆Q – количество теплоты, Дж;

Т –  температура,  К.

КПД тепловой машины:

Холодильный коэффициент:

 

 

 

 

 

 

Пример решения задачи:

Вариант 30

Найдите среднюю удельную теплоемкость кислорода при постоянном давлении при повышении его температуры от t₁до t₂.

Дано:                                Решение:

t₁ = 20⁰C                      Так как давлении постоянно p = const, то будем находить t₂ = 146⁰C среднюю удельную теплоемкость при постоянном

с_р - ?                     давлении с_р.

                             Искомую теплоемкость принимаем равной истинной

                             Удельной изобарной теплоемкости при средней

                               арифметической температуре .

                             Так как, в условии задачи нам даны t₁и t₂, то сначала

                               найдем среднюю температуру:= t₁ + t₂ = 20 + 146 = 83 ⁰C

                             Затем из приложения 13 (справочные данные), находим

                             истинную удельную изобарную теплоемкость для

                               кислорода при  = 83 ⁰C: с_р = 0,929 кДж/(кг*К)

                                      Это значение теплоемкости равно средней удельной

                              теплоемкости кислорода в интервале температур от 20

                              до 146 ⁰C.

                              Ответ: с_р = 0,929 кДж/(кг*К)

 

 

Задание:

№1.Определите внутреннюю энергию азота массой m, который вначале находится при температуре Т₁. Затем азот изобарно нагрели до Т₂. Определить изменение внутренней энергии газа. Молярная масса азота равна μ= 0,028 кг/моль.

№2. Определите расход воздуха в системе охлаждения дизеля Q, и массу m, мощностью N, если отводимая теплота составляет 75% полезной мощности двигателя, а температура охлаждающего воздуха повышается до ∆t. 

№3. В резервуаре емкостью V₁находится воздух при давлении p₁ и температуре t₁. Определите, как изменится температура t₂ и давление p₂  воздуха, если к нему подвести теплоту в количестве Q?

№4. Найдите среднюю киломольную изобарную теплоемкость углекислого газа (СО₂) при повышении его температуры от t₁ до t₂.

№5. Определите КПД обратимого цикла теплового двигателя, если температуры теплоотдачи t₁ , а теплоприемника t₂.

№6. Тепловая машина работает по некоторому обратимому прямому циклу, КПД которого ƞ. Вычислите величину холодильного коэффициента этой машины, если она будет совершать тот же цикл в обратном направлении?

№7. Кислород, занимающий объем V₁ под давлением Р₁, нагрели сначала при постоянном давлении до объема V₂, а затем при постоянном объеме до давления Р₂. Постройте графики процессов в Р – V координатах в программном комплексе Microsoft Excel. Определите: 1) изменение внутренней энергии U газа; 2) совершенную им работу A; 3) количество тепла Q, переданное газу. Молярная масса кислорода = 0,032 кг/моль.

Варианты заданий:

№ п/п	t1, 0С	t2, 0С	∆t, 0С	m,кг	N, кВт	V1, м3	V2, м3	p1, МПа	p2, МПа	ƞ, %	Q, Дж
1 вариант	56	105	52	0,85	65,00	0,70	3,60	0,80	6,80	17,00	240
2 вариант	45	180	27	0,63	40,00	1,90	4,30	0,70	5,20	39,00	235
3 вариант	42	300	48	0,43	42,00	1,40	3,30	1,10	4,70	23,00	258
4 вариант	43	135	26	0,80	62,00	0,90	3,40	0,70	5,80	18,00	299
5 вариант	70	291	49	0,45	53,00	1,70	4,10	1,00	4,30	38,00	302
6 вариант	60	114	60	0,57	38,00	1,30	5,50	1,90	5,00	24,00	304
7 вариант	53	117	82	0,42	33,00	2,10	5,20	1,40	4,70	41,00	308
8 вариант	56	254	58	0,58	36,00	1,00	5,00	1,70	4,10	37,00	325
9 вариант	51	243	27	0,84	48,00	1,90	4,80	0,50	4,70	16,00	242
10 вариант	62	249	96	0,90	65,00	2,50	4,20	0,50	4,30	16,00	309
11 вариант	44	127	21	0,57	62,00	0,60	5,40	1,10	6,00	24,00	195
12 вариант	34	190	28	0,58	33,00	2,20	4,10	1,80	6,10	18,00	290
13 вариант	12	205	22	0,90	34,00	0,50	5,30	1,40	6,40	35,00	313
14 вариант	64	116	43	0,56	35,00	0,50	5,00	1,60	6,60	23,00	350
15 вариант	17	145	71	0,65	37,00	0,80	3,70	1,50	5,70	25,00	390
16 вариант	23	120	52	0,55	58,00	1,90	3,10	0,70	4,50	38,00	380
17 вариант	56	234	28	0,90	50,00	0,90	5,10	0,70	5,90	16,00	372
18 вариант	30	178	83	0,80	71,00	2,30	3,70	0,70	6,20	24,00	350
19 вариант	13	228	13	0,92	43,00	2,30	4,60	1,70	5,70	20,00	375
20 вариант	59	211	20	0,56	48,00	0,90	3,00	1,70	4,00	23,00	198
21 вариант	68	230	68	0,58	70,00	1,00	4,60	1,40	5,70	35,00	171
22 вариант	54	159	62	0,70	70,00	1,50	5,30	1,10	4,00	27,00	153
23 вариант	16	153	77	0,80	50,00	2,40	4,60	1,60	5,70	35,00	203
24 вариант	66	193	75	0,90	50,00	1,80	5,50	1,60	4,00	39,00	231
25 вариант	11	102	97	0,86	63,00	1,90	3,60	0,60	7,00	24,00	255
26 вариант	52	279	71	0,49	43,00	0,80	5,00	1,20	5,30	20,00	281
27 вариант	27	174	29	0,53	67,00	1,90	3,80	1,80	6,20	39,00	292
28 вариант	18	215	45	0,68	72,00	2,00	3,60	1,00	4,80	35,00	300
29 вариант	68	297	86	0,63	57,00	2,30	5,20	1,80	5,70	27,00	302
30 вариант	20	146	95	0,57	55,00	0,70	5,50	0,60	6,80	24,00	307

 

Контрольные вопросы:

1.       Назовите из чего складывается полная внутренняя энергия системы?

2.       Объясните, что такое удельная внутренняя энергия?

3.       Объясните, как определить энтальпию газа?

4.       Назовите, что такое энтропия газа, в чем заключается ее физический смысл?

5.       Назовите определение теплоемкости газов. Виды.

6.       Сформулируйте первый закон термодинамики.

7.       Запишите уравнение изохорного процесса.

8.       Запишите основное уравнение для изобарного процесса.

9.       Объясните физическую сущность изотермического процесса.

10.   Запишите основное уравнение для адиабатического процесса.

11.   Объясните в чем сущность политропного процесса?

12.    Назовите, как определить термический КПД?

13.   Сформулируйте, что означает «холодильный коэффициент»?

14.   Назовите, в чем заключается сущность идеального цикла Карно?

15.   Назовите, какой процесс называют обратным, а какой прямым?

16.   Назовите известные вам трактовки второго закона термодинамики.

 

 

Скачано с www.znanio.ru