Министерство образования и науки Самарской области

Министерство имущественных отношений Самарской области

Государственное бюджетное профессиональное образовательное учреждение Самарской области

 «Чапаевский губернский колледж им. О.Колычева»

 

 

 

 

 

 

 

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ СТУДЕНТАМ

по выполнению лабораторных работ в табличном процессоре MS Excel (задачи оптимизации)

 МДК 04.01 Технология использования прикладного программного обеспечения для персонального компьютера

 

специальность 09.02.01 Компьютерные системы и комплексы

 

 

 

 

 

 

 

 

 

 

 

Чапаевск, 2021 год

Публикуется на основании решения

Методического совета ГБПОУ СОЧГК им. О.Колычева

Протокол № 2 от 20.01.2021

 

 

 

Составитель:   Дикова В.Г., преподаватель общепрофессиональных и специальных дисциплин образовательной программы среднего

                        профессионального образования ППССЗ ГБПОУ

                        СОЧГК им. О.Колычева

 

Редактор:       Захарова Е.М., зав. отделением по учебно-методической работе образовательной программы среднего профессионального образования ГБПОУ СОЧГК им. О.Колычева

 

 

Рецензент:      Денисов А.В., заместитель главного

                         специалиста отдела АСУ начальника отдела

                         АО «Промсинтез» г.о. Чапаевск  

 

 

Методические рекомендации предназначены для студентов специальности 09.02.01 Компьютерные системы и комплексы при формировании практических навыков использования функциональных возможностей табличного процессора MS Excel как представителя современного прикладного программного обеспечения персонального компьютера. Тематика лабораторных работ соответствует программе учебной дисциплины. При разработке пособия использовались учебники, рекомендуемые программой, и информационные ресурсы сети Интернет

 

Содержание

 

Пояснительная записка		4
Лабораторная работа №1. «Табличный процессор MS Excel. Построение простейших таблиц»		5
Лабораторная работа №2. «Табличный процессор MS Excel: автоматизация расчетов»		7
Лабораторная работа № 3. «Задачи оптимизации»		10
Лабораторная работа № 4. «Целочисленная оптимизация»		16
Лабораторная работа № 5. «Прибыль от вложения капитала»		19
Лабораторная работа  № 6. «Составление сметы и расчет себестоимости»		26
Список источников информации		30

Пояснительная записка

Методические рекомендации разработаны в помощь студентам специальности 09.02.01 Компьютерные системы и комплексы для использования функциональных возможностей табличного процессора MS Excel при решении задач оптимизации.

При разработке лабораторных работ учитывались требования к результатам освоения учебной дисциплины, сформулированные в ФГОС СПО III поколения.

В результате освоения раздела обучающийся должен овладеть общими и профессиональными компетенциями:

ОК 1.	Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.
ОК 2.	Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 3.	Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
ОК 4.	Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.
ОК 5.	Использовать информационно-коммуникационные технологии в профессиональной деятельности.
ОК 6.	Работать в коллективе и в команде, эффективно общаться с коллегами, руководством, потребителями.
ОК 7.	Брать на себя ответственность за работу членов команды (подчиненных), за результат выполнения заданий.
ОК 8.	Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.
ОК 9.	Ориентироваться в условиях частой смены технологий в профессиональной деятельности.

Лабораторные работы могут быть использованы  студентами и преподавателями данной дисциплины при подготовке к учебным занятиям.

 

Лабораторная работа №1

«Табличный процессор MS Excel. Построение простейших таблиц»

 

Цель работы: знакомство с интерфейсом табличного процессора MS Excel; формирование навыков составления и форматирования простейших таблиц

Постановка задачи: составить таблицу отчета некоторой фирмы по продажам фруктов в различных районах города.

Задания

 

1.       Запустите табличный процессор MS Excel. Внимательно изучите устройство пользовательского интерфейса процессора при помощи лекционного материала.

2.       На листе рабочей книги создайте заготовку для таблицы следующего форматирования и содержания:

	Яблоки	Груши	Виноград	Бананы	Апель сины
Северный
Южный
Восточный
Западный
Центральный
Итого:

3.       Поместите в таблицу информацию о продажах продукции (в килограммах) по различным районам города. Последняя строка должна содержать формулы вычисления итоговых сведений по каждому виду товара.

4.       Далее необходимо создать таблицу, вычисляющую валовую прибыль по видам продукции в целом по фирме. Для этого ниже создайте следующую таблицу:

	Количество	Цена	Стоимость
Яблоки
Груши
Виноград
Бананы
Апельсины

5.       Во второй столбец таблицы (Количество) поместите ссылки на соответствующие итоговые ячейки в предыдущей таблице.

6.       Заполните столбец Цена исходными данными по стоимости продукции.

7.       Значение ячеек в столбце Стоимость определите при помощи формул, перемножающих соответствующие ячейки в столбцах Цена и Количество.

8.       Далее необходимо снабдить отчет итоговыми значениями. Для этого необходимо создать следующую таблицу:

Район	Объем продаж
Северный
Южный
Восточный
Западный
Центральный
ИТОГО по фирме:

9.       Введите формулы расчета валового объема продаж по отдельным районам и фирме в целом.

10.   Используя инструмент Автоформатирования, приведите форматы таблиц к одному из предложенных образцов.

 

Лабораторная работа №2

«Табличный процессор MS Excel: автоматизация расчетов»

 

Цель работы: – формирование навыков использования электронных таблиц для автоматизации расчетов;

– закрепление навыков составления и форматирования таблиц, использования формул и функций.

Постановка задачи: Руководство коммерческой организации должно составить штатное расписание, т.е. определить, сколько сотрудников, на каких должностях и с каким окладом необходимо принять на работу. Общий фонд заработной платы составляет $10 000.

 

Модель решения задачи

Допустим, что для нормальной работы коммерческой организации необходимо:

1 генеральный директор;	1 технический директор;
1 коммерческий директор;	3 начальника отделов;
1 бухгалтер	10-12 менеджеров старшего звена;
8-10 клерков;	5-7 секретарей.

(На некоторых должностях число людей может меняться. Например, зная, что найти секретарей трудно, руководитель может принять решение сократить их число, чтобы увеличить оклад каждой из них.)

Итак, принимаем следующую модель решения задачи. За основу берем оклад секретаря, а все остальные вычисляются через него: во столько-то раз или на столько-то больше. Говоря математическим языком, каждый оклад является линейной функцией от оклада секретаря:

А * С + В, где С – оклад секретаря;

                         А и В – коэффициенты для каждой должности.

Допустим, руководство решило, что

 

	А	В
клерк должен получать в 1,5 раза больше секретаря	1,5	0
менеджер – в 3 раза больше секретаря	3	0
начальник отдела на $30 больше, чем менеджер	3	30
бухгалтер в 2 раза больше секретаря	2	0
технический директор на $40 больше бухгалтера	1,5	40
коммерческий директор в 4 раза больше секретаря	4	0
генеральный директор на $20 больше коммерческого директора	4	20

 

Задав количество человек для каждой должности можно составить уравнение:

N1*(A1*C+B1)+N2*(A2*C+B2)+…+N8*(A8*C+B8)=10000,

где N_i – количество каждой группы персонала; A_i, B_i – соответствующие коэффициенты.

Ясно, что при таком количестве неизвестных решить данное уравнение стандартными методами невозможно. Остается решать его путем подбора.

 

Выполнение работы

1.         Используя в качестве примера приведенный ниже рисунок, создайте структуру таблицы и заполните ее исходными данными (коэффициенты, должности, предполагаемое количество сотрудников, зарплату секретаря).

2.         В столбце Зарплата необходимо вычислить таковую по формуле А*С+В. Следует заметить, что ссылка на ячейку с зарплатой секретаря (С) должна быть абсолютной, тогда при копировании формулы не произойдет ошибки. Наиболее удачным способом абсолютной адресации является именование ячейки.

 

 

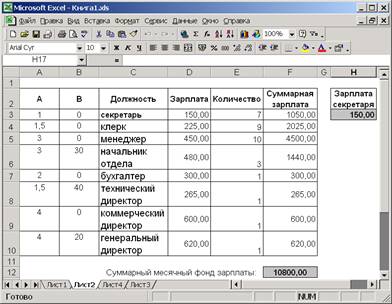
Ячейке с зарплатой секретаря (на рисунке – Н3) присвойте имя С. Для чего необходимо выделить эту ячейку, затем перейти в поле имени, щелкнув левой кнопкой мыши, и ввести имя ячейки, завершив ввод нажатием клавиши Enter.

В нашем примере (см. рисунок) в ячейку D3 необходимо ввести формулу А3*С+В3, а затем скопировать ее на диапазон D4:D10 (при копировании относительные ссылки изменятся, а абсолютная ссылка на ячейку с именем С – нет).

 

3.         В столбце Суммарная зарплата вычислите зарплату всех сотрудников по каждой должности.

4.         Определите суммарный месячный фонд заработной платы, воспользовавшись функцией автосуммирования.

5.         На этом построение таблицы закончено. Далее необходимо, изменяя заработную плату секретаря или количество тех или иных сотрудников добиться того, чтобы полученный суммарный месячный заработок был как можно более близок к расчетной сумме в $10 000.

6.         На другом листе рабочей книги подготовьте три варианта штатного расписания. Для этого при каждом удачном подборе скопируйте значения с исходной таблицы на другой лист.

7.         Сохраните файл.

8.         Завершите работу с MS Excel.

 

Лабораторная работа № 3. «Задачи оптимизации»

ПОСТАНОВКА ЗАДАЧИ

Фирма производит две модели А и В сборных книжных по­лок.

Их производство ограничено наличием сырья (высококаче­ственных досок) и временем машинной обработки. Для каждого изделия модели А требуется 3 м² досок, а для изделия модели В — 4м². Фирма может получать от своих поставщиков до 1700 м² досок в неделю. Для каждого изделия модели А требуется 12 мин машинного времени, а для изделия модели В — 30 мин. В неделю можно использовать 160 ч машинного времени. Сколько изделий каждой модели следует выпускать фирме в неделю, если каждое изделие модели А приносит 2 долл. прибыли, а каж­дое изделие модели В — 4 долл. прибыли?

Решение.

Составим математическую модель.

Обозначим:

х — количество изделий модели А, выпускаемых в течение неде­ли

у — количество изделий модели В.

Прибыль от этих изделий равна 2х+4у долл. Эту прибыль нужно максимизировать. Функ­ция, для которой ищется экстремум (максимум или минимум), носит название целевой функции. Беспредельному увеличению количества изделий препятствуют ограничения. Ограничено ко­личество материала для полок, отсюда неравенство

Зх + 4у < 1700.

Ограничено машинное время на изготовление полок. На изделие А уходит 0.2 часа, на изделие В — 0.5 часа, а всего не более 160 ч, поэтому

0.2* + 0.5у < 160.

Кроме того, ко­личество изделий — неотрицательное число, поэтому

х > 0, у > 0.

Формально наша задача оптимизации записывается так:

Теперь решим эту задачу в Excel.

Создайте новую рабочую книгу, сохраните ее. Дайте первому листу имя "Полки".

Введите в ячейки рабочего листа информацию (рис. 1). Ячейкам В2 и ВЗ присвойте имена х и у (необходимо присвоить имена ячейкам, установив тем самым абсолютную адресацию). В ячейках С6, С9 и С10 представлены формулы, занесенные в соответствующие ячейки столбца В.

 

Рис. 1

Выделим ячейку, в которой вычисляется целевая функция, и вызовем «Решатель» ("Сервис/Поиск решения"). В диалоговом окне в поле ввода "Установить целевую ячейку:" уже содержит­ся адрес ячейки с целевой функцией $В$6. Установим переклю­чатель: "Равной максимальному значению". Перейдем к полю ввода "Изменяя ячейки:". В нашем случае достаточно щелкнуть кнопку "Предположить" и в поле ввода появится адрес блока $В$2:$В$3.

Перейдем к вводу ограничений. Щелкнем кнопку "Доба­вить". Появится диалоговое окно "Добавление ограничения". В поле ввода "Ссылка на ячейку:" укажите $В$9. Правее распо­ложен выпадающий список с условными операторами (раскрой­те его и посмотрите). Выберем условие <=. В поле ввода "Огра­ничение:" введите число 1700. У нас есть еще одно ограничение, поэтому, не выходя из этого диалогового окна, щелкните кнопку "Добавить" и введите ограничение $В$10<=160. Ввод ограни­чений закончен, поэтому нажмите "ОК". Вы вновь окажетесь в диалоговом окне "Поиск решения". Вы увидите введенные ог­раничения $В$10<=160 и $В$9<=1700. Справа имеются кноп­ки "Изменить" и "Удалить". С их помощью Вы можете изменить ограничение или стереть его. (Если Вы используете Excel 5.0/7.0, то Вы должны ввести еще одно ограничение $В$2:$В$3>=0.)

Щелкните кнопку "Параметры". Вы окажетесь в диалоговом окне "Параметры поиска решения". Чтобы узнать назначение полей ввода этого окна, щелкните кнопку "Справка". Менять ничего не будем, только установим два флажка: "Линейная мо­дель" (так как наши ограничения и целевая функция являются линейными по переменным х и у) и "Неотрицательные значе­ния" (для переменных х и у). В Excel 5.0/7.0 этот последний флажок отсутствует, поэтому и нужно было вводить ограниче­ние $В$2:$В$3>=0.). Щелкнем "ОК" и окажемся в исходном окне.

Мы полностью подготовили задачу оптимизации. Нажимаем кнопку "Выполнить". Появляется диалоговое окно "Результаты поиска решения". В нем мы читаем сообщение "Решение найде­но. Все ограничения и условия оптимальности выполнены". На выбор предлагаются варианты: "Сохранить найденное решение" или "Восстановить исходные значения". Выбираем первое. Можно также вывести отчеты: по результатам, по устойчивости, по пределам. Выделите их все, чтобы иметь представление о том, какая информация в них размещена. Здесь мы не будем комментировать эти отчеты, так как их полное понимание тре­бует существенного углубления в методы оптимизации..

После нажатия "ОК" вид таблицы меняется: в ячейках х и у появляются оптимальные значения.

Числовые данные примера специально подобраны, поэтому в ответе получились круглые цифры: изделие А нужно выпускать в количестве 300 штук в неделю, а изделие В — 200 штук. Соответственно пересчиты­ваются все формулы. Целевая функция достигает значения 1400.

Замечание. Ограничения можно было ввести в Решатель быстрее. Нуж­но было ввести в В9:В10 формулы =3*х+4*у-1700 и =0.2*х+0.5*у-160. Тогда ограничения можно было задать бло­ком $В$9:$В$10<=0. В случае большого количества ограниче­ний это существенно ускорит подготовку задачи.

Упражнение 1. Недельный фонд времени уменьшился из-за планового ремонта и составляет 150 ч. Измените ограни­чение и убедитесь, что получатся дробные решения. Поэтому данную задачу нужно формулировать как целочисленную.

Упражнение 2. Фирме требуется уголь с содержанием фосфора не более 0,03% и с примесью пепла не более 3,25%. Доступны три сорта угля А, В, и С. по следующим ценам (за тонну):

Как их следует смешать, чтобы удовлетворить ограничениям на применение и минимизировать цену?

(Ответ: А – 1/12, В – 4/12, С – 7/12. Цена 38,75 за тонну.)

Упражнение 3. Фирма производит два продукта А и В, рынок сбыта которых неограничен. Каждый продукт должен быть обработан каждой машиной I, II и III. Время обработки в часах для каждого из изделий А и В приведено ниже:

Время работы машин I, II и III соответственно 40, 36 и 36 часов в неделю. Прибыль от изделий А и В составляет соответственно 5 и 3 доллара. Фирме надо определить недельные нормы выпуска изделий А и В, максимизирующие прибыль.

Упражнение 4. Фирма занимается составлением диеты, содержащий по крайней мере 20 ед. белков, 30 ед. углеводов, 10 ед. жиров, 40 ед. витаминов. Как дешевле достичь этого при указанных ценах на продукты:

 

 

 

ЛАБОРАТОРНАЯ РАБОТА № 4

«ЦЕЛОЧИСЛЕННАЯ ОПТИМИЗАЦИЯ»

 

Задача 1. Фирма выпускает два набора удобрений для газонов: обыч­ный и улучшенный. В обычный набор входят 3 фунта азотных, 4 фунта фосфорных и один фунт калийных удобрений, а в улуч­шенный — 2 фунта азотных, 6 фунтов фосфорных и 2 фунта ка­лийных удобрений. Известно, что для некоторого газона требуется, по меньшей мере, 10 фунтов азотных, 20 фунтов фосфорных и 7 фунтов калийных удобрений. Обычный набор стоит 3 долл., а улучшенный — 4 долл. Сколько и каких наборов удобрений надо купить, чтобы обеспечить эффективное питание почвы и минимизировать стоимость?

Решение. Как и в предыдущем примере, задачу нужно пере­вести на математический язык. Пусть х — количество обычных наборов удобрений, у — количество улучшенных наборов удоб­рений. f(x,y) = Зх + 4у à (min) при ограничениях:

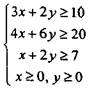
Можно непосредственно запрограммировать в Excel эти не­равенства, но мы воспользуемся возможностями Excel, чтобы сделать решение более выразительным.

 

Рисунок 1. Таблица значений

В таблице имеются формулы. В В6 =СУММПРОИЗВ( В2:ВЗ, $F$2:$F$3) - В5. Она скопирована в C6:D6. Она скопи­рована также в Е6 и там скорректирована (убрано вычитаемое Е5).

Выделим ячейку с целевой функцией и вызовем "Сервис/ Поиск решения". В диалоговом окне укажем: "Установить целе­вую ячейку:" $Е$6, "минимальное значение", "изменяя ячейки" $F$2:$F$3, "ограничения" $B$6:$D$6>=0. В окне "Параметры" установим флажок "Линейная модель" и "Неотрицательные зна­чения". Запустим выполнение. Поиск решения вернет результат: х= 1.5,у = 2.75. Целевая функция равна 15.5.

Но наборы удобрений нельзя покупать частями! Нужно на­ложить еще одно ограничение: х,у — целые числа. Вновь вызываем Решатель, нажимаем кнопку "Добавить" и в диалоговом окне "Добавление ограничения" указываем, что $F$2:$F$3 – целые (в том же выпадающем списке, откуда ранее мы выбира­ли символ для ограничения). Нажимаем "ОК.". Видим, что до­бавлено новое ограничение: $Р$2:$Р$3=целое. Запустим вы­полнение. На этот раз получим значение целевой функции 17 (естественно, оно ухудшилось), а количество наборов стало та­ким: х — 3, у = 2. Обратите внимание, что эти значения вовсе не являются результатом округления в большую сторону значений хну, полученных без ограничения целочисленности. (Проверь­те, что х = 2, у - 3 дают худший результат.)

ЗАДАЧА 2. В контейнер упакованы комплектующие изде­лия трех типов. Стоимость и вес одного изделия составляют 400 руб. и 12 кг для первого типа, 500 руб. и 16 кг для второго типа, 600 руб. и 15 кг для третьего типа. Общий вес комплектующих равен 326 кг. Определить максимальную и минимальную воз­можную суммарную стоимость находящихся в контейнере ком­плектующих изделий.

К задачам целочисленного программирования относят также задачи, где некоторые переменные могут принимать всего два значения: 0 и 1. Такие переменные называют булевыми, двоич­ными, бинарными.

ЗАДАЧА 3. Имеются 6 предметов, каждый из которых характеризуется весом и ценой. Нужно выбрать из них такие предметы, чтобы их общий вес не превышал 12, а суммарная цена была максимальной (так называемая "задача о рюкзаке").

Решение. В блоке А2:А6 размещены условные названия предметов, а в соседних столбцах — их вес и цена. В блоке D2:D6 фиксируется наличие (1) или отсутствие (0) предмета в наборе. Блокам даны имена в соответствии с их заголовками. В Решателе задаем: максимизировать $А$11 по переменным "на­личие" при ограничениях $А$9<=0 и наличие=двоичное. По­следнее ограничение задается так. В диалоговом окне "Добавление ограничения" сначала нажимаем F3 и вставляем имя "нали­чие", в выпадающем списке выбираем "двоич". После запуска решателя он выдает сообщение, что не смог найти решение. При этом значение целевой ячейки равно 23, а двоичные значения: 0, 1, 0, 0, 1, 0, т.е. нужно выбрать второй и пятый предметы.

 

Рисунок 2. Таблица формул

 

ЗАДАЧА 4. Наложите на блок "Наличие" пользователь­ский формат, чтобы вместо единиц и нулей выводились слова "да" и "нет". К счастью, в нашем примере всего шесть двоичных пере­менных, поэтому оптимальное решение можно получить пря­мым перебором.

ЗАДАЧА 5. Прямоугольный параллелепипед имеет длину а, ширину b и высоту h. Длина а может принимать только три значения: 4.25, 5.5, 6.75. Площадь поверхности параллелепипеда не превышает 5. Выбрать а, b и h так, чтобы объем параллеле­пипеда был максимален.

 

 

ЛАБОРАТОРНАЯ РАБОТА № 5.

«ПРИБЫЛЬ ОТ ВЛОЖЕНИЯ КАПИТАЛА»

 

Сначала постройте таблицу для расчета, реализующего «нулевой» вари­ант, т.е. задайте такое значение рентабельности капитала, при котором в конце последнего периода будет получена прибыль, равная нулю. Этот ре­зультат будет достигнут, если взять рентабельность капитала за период рав­ной процентной ставке за период (36% / 12). «Нулевой» вариант будет иг­рать роль контрольного (тестового), а полученную таблицу (рис. 56) в даль­нейшем можно использовать как инструмент для решения поставленной финансовой задачи.

 

Вы взяли кредит в банке  и хотите вложить деньги так, чтобы получить прибыль. Каким должен быть оборот денежных средств, чтобы не только расплатиться за кредит, но и получить прибыль?

Деньги вкладываются в бизнес, при этом в конце каждого периода на­растает доход, вычисляемый как процент от вложенной суммы. Назовем этот доход рентабельностью капитала за период.

Требуется найти такое значение рентабельности капитала, при котором удастся не только расплатиться за кредит, но и получить в конце последне­го из периодов некоторую заданную прибыль.

Решение задачи определения прибыли от вложения капитала можно разделить на этапы:

- построение расчетной таблицы,

- подбор значения рентабельности капитала,

- построение зависимости прибыли от рентабельности.

 

 

 

Этап 1. Построение расчетной таблицы

Исходные данные задачи:

Сумма кредита                      

PV= 10 000 руб.

Количество периодов выплат п = 12 месяцев.

Годовая процентная ставка г = 36%

Процесс построения таблицы для «нулевого» варианта состоит из сле­дующих шагов:

1. Откройте новую рабочую книгу и введите в ячейку В1 текст заголов­ка таблицы Прибыль от вложения капитала.

2. Присвойте рабочему листу имя Нулевой вариант и сохраните весь документ в личной папке, например, под именем profit (будет создан файл profitxls).

3. Откройте файл ЗАДАЧИ «ПОГАШЕНИЕ КРЕДИТА» и скопируйте из него блок ячеек (ВЗ:Е7), содержащий исходные данные, на такой же блок нового листа.

4. Значение периодического платежа, вычисляемого функцией ОПЛАТ, представлено в ячейке Е7 в виде отрицательного числа, т.к. это убыток. Для задания формул расчетной таблицы удобнее пользоваться денежными сум­мами как положительными величинами. Поэтому отредактируйте формулу в ячейке Е7, вставив знак «- » в формулу перед именем функции ППЛАТ.

5. Введите в ячейку В8 текст Рентабельность капитала за период.

6. Так как первоначально рентабельность капитала за период берется равной процентной ставке за период, введите в ячейку Е8 формулу

=Е6

7. Введите в ячейки В10:Е10 заголовки расчетной таблицы: Периоды, Доход, Дебетовое сальдо.

8. Отформатируйте заголовки столбцов в диапазоне B10:D10.

9. В диапазоне ячеек В11:В22 постройте числовой рад со значениями от 1 до 12.

10. Введите в ячейку С11 формулу для вычисления дохода в конце пер­вого периода

=$Е$4*$Е$8

11. Введите в ячейку D11 формулу для вычисления дебетового сальдо (лат. debet - он должен; итал. saldo - остаток) по доходам (деньги в оборо­те) и расходам (платежи по кредиту) в конце первого периода

=$Е$4+С11-$Е$7

12. Введите в ячейку С12 формулу для вычисления дохода в конце вто­рого периода

=D11*$E$8

13. Введите в ячейку D12 формулу для вычисления дебетового сальдо в конце второго периода

=D11+C12-$E$7

14. Выделите диапазон C12:D12 и скопируйте его на блок С13:Е22, протащив маркер заполнения. В ячейке D22 должен получиться 0 (нулевая прибыль).

15. В блоке ячеек C11:D22 установите Денежный формат.

 

Этап 2. Подбор значения рентабельности капитала

Теперь можно определить, какой должна быть рентабельность капита­ла, чтобы в конце последнего периода получить прибыль, например, рав­ную 5000 руб.

Для этого воспользуйтесь подбором параметра.

В поставленной задаче целевой ячейкой является ячейка D22, а изменяе­мой — ячейка Е8.

Для получения необходимого результата выполните следующие шаги:

1. Скопируйте рабочий лист Нулевой вариант и присвойте ему имя Подбор.

2. Удалите из ячейки Е8 формулу и вместо нее введите значение 3%.

3. Выполните команду Сервис/Подбор параметра...

4. В открывшемся диалоговом окне Подбор параметра заполните поля ввода следующим образом:

 

 

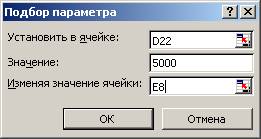
5. Нажмите кнопку ОК, и результат подбора параметра (7,30%) будет показан в одноименном окне.

6. Нажмите кнопку ОК для сохранения результата в ячейке Е8.

 

Этап 3. Построение зависимости прибыли от рентабельности

Построенную таблицу можно использовать для того, чтобы определить, какой будет прибыль при том или ином значении рентабельности капитала. Для этого можно изменять значение в ячейке Е8 и смотреть на результат расчета в ячейке D22.

Однако для проведения многократных расчетов следует воспользоваться таблицей подстановки с одним параметром (раздел 3.2).

В этой задаче параметром является рентабельность капитала за период (ячейка Е8), а функцией - вычисленное на конец последнего периода де­бетовое сальдо (ячейка D22).

Для анализа зависимости прибыли от рентабельности капитала постройте таблицу расчета прибыли (убытков) для рентабельности, изменяющейся от 1% до 12% с шагом 0,5%.

Поместите значения аргумента в диапазон В25:В47, а для значений функции отведите диапазон С25:С47. В этом случае (подстановка по стро­кам) формула, определяющая значение функции, помещается над диапа­зоном значений функции, т.е. в ячейку С24.

Процесс построения таблицы подстановки состоит из следующих шагов:

1. Скопируйте рабочий лист Нулевой вариант и присвойте ему имя Зависимость.

2. Постройте в диапазоне В25:В47 числовой ряд со значениями от 1% с шагом 0,5% до 12%.

3. Введите в ячейку С24 формулу

=022

определяющую ту ячейку таблицы, значение которой будет после расчета заноситься в соответствующую ячейку диапазона С25:С47.

4. Выделите блок ячеек В24:С47, выберите пункт меню ДанныеЯабли-ца подстановки..., в диалоговом окне Таблица подстановки укажите в поле ввода Подставлять значения по строкам в: ячейку Е8 и нажмите кнопку ОК.

Внимание! Нулевая прибыль получилась для значения аргумента, рав­ного 3%.

5. Отформатируйте диапазон С24:С47 в денежном формате.

6. Для полученной таблицы (диапазон В25:С47) постройте диаграмму зависимости прибыли от рентабельности капитала типа График или Точечная. Проанализируйте построенную диаграмму: переход через 0 должен вы­полняться для значения аргумента 3%.

7. Воспользуйтесь построенной диаграммой для получения ответа на вопрос, какова должна быть рентабельность капитала (значение на оси X) для получения намеченной прибыли 5 000 руб. (значение на оси Y).

Упражнение 10.1. Определите для исходных данных ЗАДАЧИ 10, какой должна быть рентабельность капитала, чтобы через год получить прибыль, равную 10 000 руб. (20 000 руб.).

Упражнение 10.2. Предположите, что банк изменил годовую процент­ную ставку, например, увеличил ее с 36% годовых до 50%. Какую прибыль вы можете получить при той же рентабельности капитала за период, что и в упражнении 10.1?

Упражнение 10.3. Решите ЗАДАЧУ 10 с учетом ежемесячных налоговых отчислений в размере 28%. Какова в этом случае должна быть рентабель­ность капитала, чтобы иметь в конце года хотя бы нулевую прибыль?

Упражнение 10.4. Предположите, что доход от вложения денег вы будете получать только в конце каждого квартала. Проведите расчеты для этого случая и сравните с вариантом ежемесячного получения дохода.

Упражнение 10.5. Пусть половина взятой в кредит суммы вкладывается с рентабельностью 6 %. Как распорядиться второй половиной кредита, чтобы в конце года получить прибыль 10 000 руб.?

Упражнение 10.6. Предположите, что вы кредит не брали, а хотите пус­тить в оборот накопленные деньги. Как в этом случае использовать расчет­ную таблицу ЗАДАЧИ 10 для подсчета прибыли?

 

     Лабораторная работа  № 6.

«Составление сметы и расчет себестоимости»

 

I. Составление сметы обучения на бухгалтерских курсах

 

Начальные условия задачи. Базовая стоимость разли­чается для разных курсов, отдельно оплачиваются дополнительные мате­риалы. Постоянным клиентам предо­ставляется скидка, а если не внесена предоплата, общая сумма увеличива­ется.

 

1. На первом шаге необходимо создать следующую заготовку на листе табличного процессора

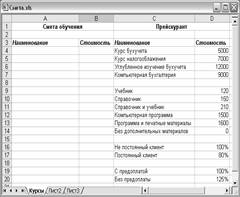2. В начале нужно выбрать, что за курс предполагается прослушать. В нашем примере эта информация вводится в ячейку А4. При этом, нужно указать, что в ячейку А4 можно вводить информацию только из ячеек С4, С5, С6 и С7. Любая другая ин­формация в этой ячейке недопустима.

Сделайте текущей ячейку А4, щелкнув на ней мышью, и выберите команду меню Данные > Проверка, чтобы открыть диалог настройки проверки вводимых значений. На вкладке Параметры этого диалога выберите в списке Тип данных вариант Список. Этим вы укажите, что в данную ячейку можно вводить значения только из определенного списка. Далее нужно указать, где расположен этот спи­сок. Щелкните мышью на поле Источник и выделите с помощью мыши ячейки с С4 по С7. Адреса ячеек появятся в поле. Вы также можете указать адрес списка вручную, введя в поле выражение =$С$4:$С$7. Установите флажок Список допус­тимых значений, и нажмите кнопку ОК. Диалог закроется, и теперь вы не сможе­те ввести в ячейку неправильное значение.

Когда вы сделаете активной ячейку А4, правее ячейки появится кнопка. Нажав ее, вы откроете список возможных вариантов. Выберите ва­риант, список закроется, и нужный вариант будет вставлен в ячейку. Попытай­тесь ввести неверное значение, и Excel сообщит об ошибке. Вы сможете только отменить неверный ввод, но никаким способом нельзя ввести ошибочную ин­формацию.

3. Аналогично нужно задать проверку для ячеек А5, А6 и А7. Единственное от­личие в том, что для каждой ячейки задаются свои собственные списки. После того как все списки заданы, введите в ячейки про­извольную информацию. Конечно, вы сможете ввести любую информацию, но только из спис­ков. С первой задачей мы справились, теперь ввод исходных данных для сметы стал значительно проще. Теперь нужно автоматизировать расчет сметы.

4. Введите в ячейку В4 формулу =ВПР(A4;C4:D7;2;ЛОЖЬ).

Функция ВПР очень полезна и будет использоваться во многих примерах. Она позволяет най­ти в таблице строку, содержащую нужное значение, и вернуть значение из дру­гой ячейки этой же строки. В нашем случае мы ищем название курса, а хотим узнать его цену, записанную в той же строке. Диапазон ячеек C4:D7 указывает на область таблицы, в которой будет выполняться поиск. Поиск осуществляет­ся по ячейкам первого столбца области, то есть по ячейкам столбца С. Значе­ние, которое будет искаться, указано в ячейке А4, что и задается первым аргу­ментом функции. Число 2 в качестве третьего аргумента указывает, что нужно взять содержимое второго столбца найденной строки, то есть столбца D. Сло­во ЛОЖЬ в формуле говорит, что список в указанном диапазоне ячеек может быть не отсортирован. Теперь, если вы введете в ячейку А4 значение Курс буху­чета, в ячейке В4 появится сумма из третьей строки столбца D, так как имен­но в этой строке в прейскуранте находится данное название. В нашем примере это будет число 5000.

5. Аналогично, в ячейку В5 нужно ввести формулу =ВПР(А5;С9:D14;2;ЛОЖЬ), чтобы вставить в смету стоимость дополнительных материалов.

6. Так как остальные вычисления предполагают увеличение или уменьшение базовой суммы, формулы получатся немного сложнее. В ячейку В6 введите фор­мулу =(В4+В5)*(ВПР(А6;С16:D17;2;ЛОЖЬ)-1). Сумма В4+В5 вычисляет стои­мость курса вместе с дополнительными материалами. Выражение ВПР(А6;С16:D17;2;ЛОЖЬ) возвращает процент, который должен уплатить кли­ент. Если вычесть из него единицу, то мы получим процент скидки, причем он будет отрицательный. Умножив первую часть формулы на вторую, мы получим размер предоставляемой скидки.

7. В ячейку В7 введите очень похожую формулу, вычисляющую наценку: =(В4+В5+В6)*(ВПР(А7;С19:D20;2;ЛОЖЬ)-1). В отличие от скидки, наценка по­лучается неотрицательной.

е составные части сметы рассчитаны, осталось их только просуммировать. Введите в ячейку В9 формулу =СУММ(В4:В7). Коммен­тарии тут не требуются. Далее вы можете добавить дополнительные вычисления, например, рассчитать НДС и НСП. Потратив немного времени, вы составили таблицу, существенно ускоряющую составление смет. Выбрав нужные значения из четырех списков, вы мгновенно получаете готовую смету.

 

           

Список источников информации

1.         Левин А. Самоучитель полезных программ. – СПб.: Питер, 2017.

2.         Грошев С.В., Коцюбинский А.О., Комягин В.Б. Современный самоучитель профессиональной работы на компьютере: Практ. пособ. – М.: Триумф, 2015.

3.         Столяров А., Столярова Е. Вы купили компьютер. – М.: Вербо, 2015.

4.         Стоцкий Ю.  Office 2000: Самоучитель. – СПб.: Питер, 2016.

5.         Журин А.А. Microsoft Excel 2000: Краткие инструкции для новичков. –  Аквариум ЛТД, 2017. 

6.         Могилев А., Пак Н., Хеннер Е. Практикум по информатике. – М.: ИЦ «Академия», 2015.