Государственное автономное профессиональное образовательное учреждение
Свердловской области
«Талицкий лесотехнический колледж им. Н.И.Кузнецова»

 

 

 

 

              Методические указания для студентов по проведению лабораторных работ и практических занятий

Специальность: 23.02.03 Техническое обслуживание и ремонт автомобильного транспорта

 

Дисциплина:      ОП 0.2 «Техническая механика»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

г.Тугулым.

Согласовано на заседании цикловой комиссии   23.02.03  «Техническое обслуживание и ремонт автомобильного транспорта» протокол №  1  от  28.08.2019г.      Председатель цикловой  Комиссии ___________Б.А. Астратов

УТВЕРЖДАЮ заведующий филиала ____________Колмакова И.В. 31.08.2019г .

 

Методические рекомендации для выполнения практических работ по учебной дисциплины «ОП.02 техническая механика» для специальности среднего профессионального образования «23.02.03 Техническое обслуживание и ремонт автомобильного транспорта»

 

Методические рекомендации для выполнения практических работ разработаны на основе рабочий программы учебной дисциплины и Федеральным государственного образовательного стандарта по специальности среднего профессионального образования (далее СПО) утвержденного приказом Министерства образования и науки РФ № 701 от 2 августа 2013 г., зарегистрировано Министерством юстиции (рег. № 29498 от 20 августа 2013г.).

 

 

Автор:   Астратов Борис Александрович, преподаватель

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ОГЛАВЛЕНИЕ

Тема	Наименование задания	страница	Кол-во часов
Тема 1.2. Плоская система сил	Практические занятия № 1. Определение проекций сил на оси x и y	5	2
	Практическое занятие № 2. Определение величины и направления действия уравновешивающих сил	6	2
Тема 1.4. Центр тяжести	Практическое занятие № 3. Определение момента силы и пары сил относительно точки	8	2
Тема 1.9. Динамика материальной точки	Практическое занятие № 4. Приведение к точке плоской системы произвольно расположенных сил	10	2
Тема 2.2. Растяжение и сжатие	Практическое занятие № 5. Определение главного вектора и главного момента произвольной системы сил	12	2
	Практическое занятие № 6. Сложение пространственной системы сходящихся сил	14	2
	Практическое занятие № 7. Момент силы относительно оси	16	2
	Практическое занятие № 8. Определение положения центра тяжести тела	18	2
	Практическое занятие № 9. Определение координат центра тяжести фигур	20	2
	Практическое занятие № 10. Определение траектории, скорости и ускорения точки	21	2
Тема 2.3. Срез и смятие	Практическое занятие № 11. Определение скорости и ускорения различных точек вращающегося тела	23	2
Тема 2.4. Геометрические характеристики плоских сечений.	Практическое занятие № 12. Определение скорости любой точки тела	25	2
	Практическое занятие № 13. Решение задач на прямолинейное движение точки	26	2
Тема 2.5. Кручение	Практическое занятие № 14. Решение задач на определение работы и мощности	28	2
Тема 2.6. Изгиб	Практическое занятие № 15. Решение задач на поступательное движение тела	30	2
	Практическое занятие № 16. Построение эпюр продольных сил, напряжений и перемещений	32	2
	Практическое занятие № 17. Определение усилий в стержнях	34	2
	Практическое занятие № 18. Расчет на прочность по предельному состоянию	37	2
Тема 3.2. Соединения деталей. Разъемные и неразъемные соединения	Практическое занятие № 19. Расчет на срез и смятие	40	2
	Практическое занятие № 20. Расчет на прочность и жесткость при кручении круглого бруса	41	2
Тема 3.3. Механические передачи	Практическое занятие № 21 Определение угловых и линейных скоростей и ускоренных точек вращающегося тела	43	2

 

 

 

ВВЕДЕНИЕ

 

Методические рекомендации по дисциплине «техническая механика» написаны в соответствии с программой по технической механике для студентов техникумов и колледжей и имеет цель оказать им помощь при получении первоначальных навыков решения задач по теоретической механике.

Пособие содержит общие методические указания и советы для решения задач. Решение задач сопровождается подробными пояснениями.

Каждое практическое занятие состоит из двух частей: теоретическая часть состоит из ряда вопросов, отражающих основные понятия, определения и формулы изученной темы; практическая часть содержит примеры решения задач и задания для самостоятельной работы по вариантам.

Данная система заданий, построенная с учетом современных дидактических требований, способствует осознанному и прочному усвоению теоретического материала, выработке практических умений и навыков.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ИНСТРУКЦИОННО-МЕТОДИЧЕСКАЯ КАРТА

по выполнению практического задания № 1

 

Наименование предмета: «Техническая механика».

Тема: «Плоская система сходящихся сил».

Наименование работы: «Определение проекций сил на оси x и y».

Время: 90 мин.

Цель (обучающая, развивающая, воспитательная): уметь определять направление и величину вектора по его проекциям, уметь записывать уравнение равновесия плоской системы сходящихся сил.

Форма отчета: тетрадь.

Рекомендуемая литература: А.И. Аркуша «Техническая механика».

Контрольные вопросы:

1.      Дайте определение силы в статике.

2.      Какими признаками характеризуется понятие силы?

3.      Как графически изображается сила и как она изображается в тексте?

4.      Что такое проекция силы на ось и как она определяется?

 

Порядок выполнения работы:

1. Повторить тему «Плоская система сходящихся сил».

2. Выпишите данные для вашего варианта (согласно нумерации в журнале).

№ варианта	F1, Н	F2, Н	F3, Н	F4, Н	№ варианта	F1, Н	F2, Н	F3, Н	F4, Н	№ варианта	F1, Н	F2, Н	F3, Н	F4, Н
1	100	50	45	60	11	90	85	70	105	21	110	30	50	95
2	90	100	50	45	12	60	90	85	70	22	105	110	30	50
3	85	90	100	50	13	45	60	90	85	23	70	105	110	30
4	70	85	90	100	14	50	45	60	90	24	85	70	105	110
5	105	70	85	90	15	100	50	45	60	25	90	85	70	105
6	110	105	70	85	16	90	100	50	45	26	60	90	85	70
7	30	110	105	70	17	85	90	100	50	27	45	60	90	85
8	50	30	110	105	18	70	85	90	100	28	50	45	60	90
9	95	50	30	110	19	105	70	85	90	29	100	50	45	60
10	100	95	50	30	20	110	105	70	85	30	90	100	50	45

 

3.      Рассмотрите пример решения.

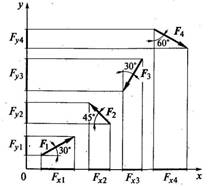
F₁ = F₂ = F₃ = F₄ = 100 Н.

F x ₁ = F₁× cos 30^o = F₁ × 0,866 = 100 × 0,866 = 86,6 Н.

F y₁ = F₁× cos 60^o = F₁ × 0, 5 = 100 × 0, 5 = 50 Н.

F x₂ = – F₂× cos 45^o = – F₂ × 0,707 = -100 × 0,707 = –70,7Н.

F y₂ = – F₂× cos 45^o = – F₂ × 0,707 = -100 × 0,707 = –70,7Н.

F x₃ = – F₃× cos 60^o = – F₃ ×0, 5 = -100 × 0, 5 = –50 Н.

F y₃ = – F₃× cos 30^o = – F₃ × 0,866 = -100 × 0,866 = –86,6 Н.

F x₄ = F₄ × cos 30^o = F₄ × 0,866 = 100 × 0,866 = 86,6 Н.

F y₄ = – F₃× cos 60^o = – F₃ × 0, 5 = –100 × 0, 5= –50 Н.

4.      Зарисуйте прямоугольную систему координат x – О – y, с указанием сил, углов и проекций сил.

5.      Определите проекции сил.

6.      Сделайте вывод.

 

ИНСТРУКЦИОННО-МЕТОДИЧЕСКАЯ КАРТА

по выполнению практического задания № 2

 

Наименование предмета: Техническая механика.

Тема: Плоская система сходящихся сил.

Наименование работы: Определение величины и направления действия уравновешивающих сил.

Время: 90 мин.

Цель (обучающая, развивающая, воспитательная): уметь определять величины и направления действия уравновешивающих сил графическим и аналитическим способами.

Форма отчета: тетрадь.

Рекомендуемая литература: А.И. Аркуша «Техническая механика»

Контрольные вопросы:

1.      Как найти равнодействующую трех сил?

2.      Что можно сказать о действии сил, когда их равнодействующая равна нулю?

3.      Опишите общий порядок решения задач о равновесии трех сил графическим способом.

4.      Каков общий порядок решения тех же задач аналитическим способом?

5.      Какой из указанных способов более точен?

6.      Приведите примеры частных случаев трех сил.

 

Порядок выполнения работы:

1.      Повторить тему «Плоская система сходящихся сил».

2.      Выпишите данные для вашего варианта (согласно нумерации в журнале).

№ варианта	F1, Н	№ варианта	F1, Н	№ варианта	F1, Н
1	22	11	32	21	27
2	23	12	33	22	28
3	24	13	34	23	29
4	25	14	35	24	30
5	26	15	36	25	31
6	27	16	22	26	32
7	28	17	23	27	33
8	29	18	24	28	34
9	30	19	25	29	35
10	31	20	26	30	36

3.      Рассмотрите пример решения.

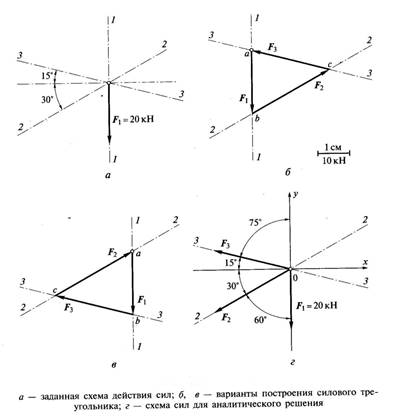
Пример решения: Найти величины и направления действия уравновешивающих сил F₂ и F₃ графическим и аналитическим способами, если заданы величина силы F₁ = 20 кН и линии действия сил F₂ и F₃ (рис. a).

Решение графическим способом.

Принимаем масштаб сил: в 1 см – 10 кН.

Из произвольной точки а откладываем в масштабе известную силу F₁, длина вектора которой равна длине отрезка аb = 2 cм (рис. б).

Через начало и конец вектора силы F_1,, т.е. через точки a и b, проводим линии, параллельные линиям действия сил F₂ и F_3, так, чтобы они пересекались в одной точке с. При этом силы F₂ и F₃ могут оказаться как справа от силы F₁ (см. рис. б), так и слева от нее (рис. в). Это не является ошибкой построения, поскольку оба полученных силовых треугольника являются двумя частями параллелограмма. Но, все же, правильнее, когда при обходе треугольника номера сил идут в нарастающем порядке, т.е. вариант F₁ F₂ F₃ предпочтительнее, чем второй вариант. Силы F₂ и F₃ являются уравновешивающими силу F₁.

Измеряем отрезки bc и ca: bc =2, 8 см, ca = 2,5 см. Так как 1 см соответствует 10 кН, получаем F₂ = 28 кН, F₃ = 25 кН.

Расставляем стрелки на отрезках bc и ca. Из условия равновесия все стрелки должны быть направлены в одну сторону при обходе треугольника. Поскольку направление силы F₁ задано (вниз), остальные силы должны быть направлены так, как показано на рис. б, в, при этом конец вектора силы F₃ будет совпадать с началом вектора силы F_1.

Ответ: F₂ = 28 кН, F₃ = 25 кН; направления этих сил показаны на силовом треугольнике.

Решение аналитическим способом.

Проводим оси координат О x и O y, традиционно направляя первую из них горизонтально, а вторую – вертикально. Силы направляем из начала координат по заданным линиям действия 3-3 и 2-2. Направление выбираем произвольно (допустим, влево – рис. г). Проставляем углы между направлениями всех сил и координатными осями.

Составляем уравнения:

–F₂ cos 30^o – F₃ cos 15^o = 0

–F_{1 –_}F₂  cos 60^o+ F₃ cos 75^o = 0

Из первого уравнения получаем выражение для F_2:

F₂ = – F₃ cos 15^o/ cos 30^o

Подставляем выражение для F₂ во второе уравнение:

–F₁ + F₃  cos 15^o / cos 30^o × cos 60^o + F₃ cos 75 ^o = 0;

F₃ = F₁/ (cos 15^o : cos 30^o × cos 60^o + cos 75^o) = 20/ (0,966: 0,866 × 0,5 + 0,259) = 24,48 кН

Определив F_{3 ,} находим F₂:

F₂ = – F₃ cos 15^o/ cos 30^o = 24, 48× 0,966: 0,866 = -27,31 кН

Ответ: F₂ = 27, 31 кН, эта сила направлена в сторону, противоположную показанной на рис, о чем говорит знак «минус» перед числовым значением; F₃ = 24,48 кН, сила направлена так же, как показано на рис. г, поскольку числовое значение получилось со знаком «плюс», который опущен.

 

4.      Перечертите рисунок с соблюдением масштаба.

5.      Решите задачу

6.      Сделайте вывод.

 

ИНСТРУКЦИОННО-МЕТОДИЧЕСКАЯ КАРТА

по выполнению практического задания № 3

 

Наименование предмета: «Техническая механика».

Тема: «Плоская система сходящихся сил».

Наименование работы: «Определение момента силы и пары сил относительно точки».

Время: 90 мин.

Цель (обучающая, развивающая, воспитательная): знать определения момента пары сил и момента относительно точки, уметь определять знак момента.

Форма отчета: тетрадь.

Рекомендуемая литература: А.И. Аркуша «Техническая механика».

Контрольные вопросы:

1.      Напишите формулу для определения момента силы относительно какой-либо точки тела.

2.      Как определяется знак момента силы относительно какой-либо точки?

3.      В чем сходство и отличие вращательных воздействий, оказываемых на тело силой и парой сил?

Указания к выполнению работы:

1.      Повторить тему «Момент силы относительно точки. Пара сил».

2.      Выпишите данные для Вашего варианта (согласно нумерации в журнале).

 

№ варианта	F1 кН	F2 кН	F3 кН	F4 кН	M кН м	a1 м	a2 м	a3 м	a4 м	a5 м	h4 м
1	20	10	30	40	15	1	2	3	4	5	0,5
2	15	20	10	30	40	5	1	2	3	4	0,8
3	40	15	20	10	30	4	5	1	2	3	0,7
4	30	40	15	20	10	3	4	5	1	2	0,6
5	20	30	40	15	20	2	3	4	5	1	0,3
6	10	20	30	40	15	1	2	3	4	5	0,4
7	50	10	20	30	40	5	1	2	3	4	0,5
8	40	50	10	20	30	4	5	1	2	3	0,6
9	30	40	50	10	20	3	4	5	1	2	0,3
10	25	30	40	50	10	2	3	4	5	1	0,4
11	10	25	30	40	50	1	2	3	4	5	0,5
12	20	10	25	30	40	2	1	2	3	4	0,6
13	35	20	10	25	30	3	2	1	2	3	0,7
14	40	35	20	10	25	4	3	2	1	2	0,8
15	30	40	35	20	10	5	4	3	2	1	0,3
16	50	30	40	35	20	1	5	4	3	2	0,4
17	15	50	30	40	35	2	1	5	4	3	0,5
18	20	15	50	30	40	3	2	1	5	4	0,6
19	30	20	15	50	30	4	3	2	1	5	0,7
20	40	30	20	15	50	5	4	3	2	1	0,8
21	45	40	30	20	15	1	5	4	3	2	0,3
22	50	45	40	30	20	2	1	5	4	3	0,4
23	10	50	45	40	30	3	2	1	5	4	0,5
24	20	10	50	45	40	4	3	2	1	5	0,6
25	30	20	10	50	45	5	4	3	2	1	0,7
26	40	30	20	10	50	1	5	4	3	2	0,8
27	45	40	30	20	10	2	1	5	4	3	0,3
28	50	45	40	30	20	3	2	1	5	4	0,4
29	10	50	45	40	30	4	3	2	1	5	0,5
30	20	10	50	45	40	5	4	3	2	1	0,6

 

3.      Рассмотрите пример решения.

F₁= 10 кН

F₂= 15 кН

F₃ = 20 кН

F₄ = 25 кН

M = 15 кНм

a₁ = 2 м

a₂ = 3 м

a₃ = 4 м

a₄ = 5 м

a₅ = 6 м

h₄ = 0,2 м

 

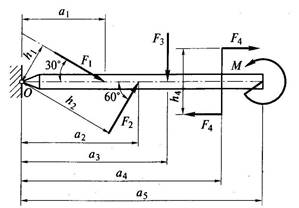
Находим плечи h₁ h₂ h₃

h ₁ = a ₁ sin 30 ^o= 2∙ 0,5 = 1 м

h ₂ = a ₂ sin 60 ^o= 3 ∙ 0,866 = 2,598 м

h ₃ = a ₃ = 4 м

Находим сумму моментов относительно точки О:

∑M_o = – F₁ h₁ + F₂ h_{2 –} F₃ h ₃ – F₄ h ₄ + M = – 10 ∙ 1 + 15 ∙ 2,598 – 20 ∙ 4 – 25 ∙ 0, 2 + 15 = – 41,03кНм.

4.      Перечертите рисунок.

5.      Определите сумму моментов всех сил относительно точки О.

6.      Сделайте вывод.

 

ИНСТРУКЦИОННО-МЕТОДИЧЕСКАЯ КАРТА

по выполнению практического задания № 4

 

Наименование предмета: Техническая механика.

Тема: Плоская система произвольно расположенных сил

Наименование работы: Приведение к точке плоской системы произвольно расположенных сил.

Время: 90 мин.

Цель (обучающая, развивающая, воспитательная): знать способы определения главного вектора и главного момента, уметь составить уравнения равновесия для двух и более сил.

Форма отчета: тетрадь.

Рекомендуемая литература: А.И. Аркуша «Техническая механика».

Контрольные вопросы:

1.      Как найти равнодействующую трех сил?

2.      Что можно сказать о действии сил, когда их равнодействующая равна нулю?

3.      Опишите общий порядок решения задач о равновесии трех сил графическим способом.

4.      Каков общий порядок решения тех же задач аналитическим способом?

5.      Какой из указанных способов более точен?

6.      Приведите примеры частных случаев действия трех сил.

 

Указания к выполнению работы:

1.      Повторить по учебнику тему «Плоская система произвольно расположенных сил».

2.      Выпишите данные для вашего варианта (согласно нумерации в журнале).

№ варианта	F1, кН	F2, кН	F3, кН	№ варианта	F1, кН	F2, кН	F3, кН
1	22	32	37	16	37	21	27
2	23	33	38	17	38	22	28
3	24	34	39	18	39	23	29
4	25	35	40	19	40	24	30
5	26	36	10	20	10	25	31
6	27	22	11	21	11	26	32
7	28	23	12	22	12	27	33
8	29	24	13	23	13	28	34
9	30	25	14	24	14	29	35
10	31	26	15	25	15	30	36
11	32	27	16	26	16	31	37
12	33	28	17	27	17	32	38
13	34	29	18	28	18	33	39
14	35	30	19	29	19	34	40
15	36	31	20	30	20	35	10

 

3.      Рассмотрите пример решения.

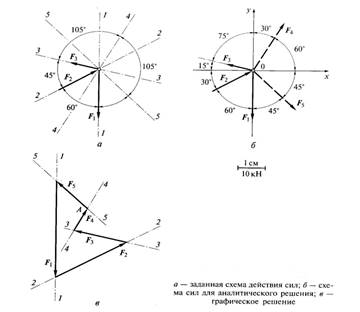
Пример. Определить величины и направления действия сил F₄ и F_5, уравновешивающих известные силы F_1, F₂ и F₃ (рис. а), если F₁= 40 кН, F₂ = 30 кН, F₃ = 20 кН.

 

Решение аналитическим способом (рис. б) Проводим оси координат, располагая их традиционно.

Составляем уравнение равновесия в форме:

F₂ cos 30 ^о – F₃ cos15^о + F₄ cos 60^о+F₅ cos 45^о = 0.

–F₁+F₂ cos 60^о +F₃ cos 75^о + F₄ cos 30 ^о- F₅ cos 45^o = 0.

Решать задачи принято в общем виде, но в данном случае проще выделить свободные члены и коэффициенты при неизвестных F₄ и F₅:

 

30 × 0,866 – 20 × 0,966 + F₄ × 0,5 + F₅ × 0,707 = 0;

–40 + 30 × 0,5 + 20 × 0,259 +

+ F₄ × 0,866 – F₅ × 0,707 = 0.

Отсюда

0,5F₄ + 0,707 F₅ = – 6, 66;

0,866 F₄ – 0,707 F₅ = 19, 82.

Такую систему проще решить не методом подстановки, а методом сложения. Сложив левую часть первого уравнения с левой частью второго, а правую часть с правой, получим

1,366 F₄ = 13,16 кН.

Отсюда F₄ = 13,66:1,366 = 9,63 кН.

 

Из первого уравнения определим F₅:

        - 6, 66 – 0,5F_{4        –} 6, 66 – 0,5 ∙ 9, 63

 F₅ = -------------------- = ---------------------- = – 16, 23 кН

             0,707                         0,707

Ответ: F₄ = 9, 63 кН, F₅ = -16, 23 кН, сила направлена в сторону, противоположную показанной на рисунке.

 

 

Решение графическим способом (рис. в) Масштаб: в 1 см – 10 кН.

Откладываем в масштабе силы F₁, F₂, F₃, соблюдая заданные направления.

Через начало вектора силы F₁ и конец вектора силы F₁ проводим линии, параллельные линиям действия сил F₄ и F₅ до пересечения в точке А.

Измеряем полученные отрезки в сантиметрах и с учетом масштаба находим величины силы F ₄ и F₅ в килоньютонах: F₄ = 10 кН, F₅ = 16 кН.

Стрелки на векторах сил F₄ и F₅ ставим так, чтобы они были направлены в одну сторону при обходе многоугольника. После простановки стрелок видно, что сила F₅ направлена в сторону, противоположную показанной на рис.

Ответ: F₄ = 10 кН, F₅ = 16 кН.

 

4.      Решите свой вариант сначала аналитическим способом, а затем графическим.

5.      Сравните способы решения.

6.      Ответьте на вопросы.

7.      Сделайте вывод.

 

ИНСТРУКЦИОННО-МЕТОДИЧЕСКАЯ КАРТА

по выполнению практического задания № 5

 

Наименование предмета: «Техническая механика».

Тема: «Плоская система произвольно расположенных сил».

Наименование работы: «Определение главного вектора и главного момента произвольной системы сил».

Время: 90 мин.

Цель (обучающая, развивающая, воспитательная): знать способы определения главного вектора и главного момента, уметь составить уравнения равновесия для двух и более сил.

Форма отчета: тетрадь.

Рекомендуемая литература: А.И. Аркуша «Техническая механика»

Контрольные вопросы:

1.      Дайте определение главного вектора.

2.      Чему равен главный момент?

3.      В чем сходство и в чем различие между главным вектором плоской системы сил и ее равнодействующей?

 

Указания к выполнению работы:

1.      Повторить по учебнику тему «Плоская система произвольно расположенных сил».

2.      Выпишите данные для вашего варианта (согласно нумерации в журнале).

 

 

 

№ варианта	F1, Н	F2, Н	F3, Н	F4, Н	F5, Н	№ варианта	F1, Н	F2, Н	F3, Н	F4 Н	F5, Н
1	22	32	37	10	20	16	37	21	27	11	19
2	23	33	38	11	21	17	38	22	28	12	20
3	24	34	39	12	22	18	39	23	29	13	21
4	25	35	40	13	23	19	40	24	30	14	22
5	26	36	10	14	24	20	10	25	31	15	23
6	27	22	11	15	25	21	11	26	32	16	24
7	28	23	12	16	26	22	12	27	33	17	25
8	29	24	13	17	27	23	13	28	34	18	26
9	30	25	14	18	28	24	14	29	35	19	27
10	31	26	15	19	29	25	15	30	36	20	28
11	32	27	16	20	30	26	16	31	37	21	29
12	33	28	17	21	31	27	17	32	38	22	30
13	34	29	18	22	32	28	18	33	39	23	31
14	35	30	19	23	33	29	19	34	40	24	32
15	36	31	20	24	34	30	20	35	10	25	33

 

3.      Рассмотрите пример решения.

Пример.

К точкам А, B, С и D, образующим прямоугольник со сторонами АB = 80 см, BC = 120 см, приложены пять сил, как показано на рис. Определить главный вектор и главный момент этой системы сил, если F ₁ = 50 Н, F₂ = 74 Н, F₃ = 60 Н, F₄ = 40 Н, F₅ = 51 Н и угол α = 60^о. При определении главного момента центр приведения выбрать наиболее рациональным образом.

Решение.

1.      Примем за центр приведения точку А (в этой точке пересекаются линии действия трех сил из пяти) и ее же примем за начало координат, совместив ось x со стороной АB прямоугольника, а ось y – cо стороной DA.

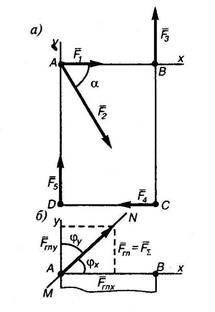2.      Найдем проекции всех заданных сил на ось x, Н:

F_1x = F₁ = 50; F_{2 x} = F₂ cos α = 74 ∙ cos 60^o = 37;

F_3x = 0; F_{4 x} = – F₄ = – 40; F_{5 x} = 0.

3.      Найдем проекции всех заданных сил на ось y, Н:

F_1y = 0; F_2y = -F₂ sin α = -74 sin 60^o = – 64;

F_3y = F₃ = 60; F_{4 y} = 0; F_5y = F₅ = 51.

4.      Найдем проекции главного вектора на оси x и y:

 

 F_глx = ∑ F _{k x} = 50 + 37 – 40 = 47 Н;

F_глy = ∑ F _{k y} = – 64 + 60 + 51 = 47 Н.

 

5.      Как видно проекции получаются положительными и равными между собой. Это значит, что главный вектор направлен под углом 45 ^o к каждой из осей, т.е.

φ _x = φ _y = 45 ^o

и модуль главного вектора

F_гл = F_глx √2 = 47 √2 = 66, 5 Н.

Вектор F_гл приложен в точке А, принятой за центр приведения (рис.).

6.      Находим главный момент, для этого предварительно определим моменты всех заданных сил относительно центра приведения (точки А);

T_A (F₁) = 0;

T_A (F₂) = 0;

T_A (F₃) = F₃ ∙ AB = 60 ∙ 0, 8 = 48 Н ∙ м;

T_A (F₄) = – F₄ ∙ AD = – 40 ∙ 1, 2 = – 48 Н ∙ м;

T_A (F₅) = 0.

Главный момент T _гл = ∑ T_A (F _k) = 48 – 48 = 0.

Таким образом, вследствие удачного выбора центра приведения сразу определяется равнодействующая F_{∑ :} ее модуль F_∑ = 66, 5 Н, линия ее действия MN проходит через точку A под углом φ _x = 45^o к стороне AB.

Ответ: F_гл = 66, 5 Н, T_гл = 0.

 

4.      Решите свой вариант.

5.      Ответьте на вопросы.

6.      Сделайте вывод.

 

ИНСТРУКЦИОННО-МЕТОДИЧЕСКАЯ КАРТА

по выполнению практического задания № 6

 

Наименование предмета: «Техническая механика».

Тема: «Пространственная система сил».

Наименование работы: «Сложение пространственной системы сходящихся сил».

Время: 90 мин.

Цель (обучающая, развивающая, воспитательная): научиться определять усилия в стержнях, вызванных действием груза, составлять уравнения равновесия для пространственной системы сходящихся сил.

Форма отчета: тетрадь.

Рекомендуемая литература: А.И. Аркуша «Техническая механика».

Контрольные вопросы:

1.      Что называют главным вектором системы?

2.      Чему равен главный момент системы?

3.      Чему равна равнодействующая произвольной плоской системы сил?

4.      Какая система сил называется пространственной?

 

Указания к выполнению работы:

1.      Повторить по учебнику тему «Пространственная система сил».

2.      Выпишите данные для вашего варианта (согласно нумерации в журнале).

 

 

№ варианта	m, кг	№ варианта	m, кг	№ варианта	m, кг
1	200	11	700	21	400
2	300	12	800	2	600
3	400	13	200	23	700
4	600	14	300	24	800
5	700	15	400	25	200
6	800	16	600	26	300
7	200	17	700	27	400
8	300	18	800	28	600
9	400	19	200	29	700
10	600	20	300	30	800

 

3.      Рассмотрите пример решения.

Пример.

 

 

 

 

 

 

 

 

 

 

 

 

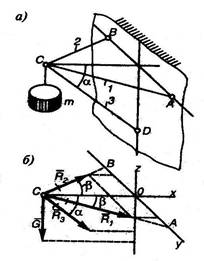
Груз, масса которого m = 500 кг, подвешен на кронштейне ABCD, состоящем из трех стержней 1, 2 и 3. Стержни 1 и 2 образуют в месте соединения прямой угол и расположены в горизонтальной плоскости. Стержень 3 образует с горизонтальной плоскостью угол α = 40^o (рис.а). Определить усилия в стержнях, вызванные действием груза. Соединения стержней между собой и с вертикальной стенкой шарнирные. Весом стержней пренебречь.

Решение.

1.      На точку C кронштейна действует вертикальная нагрузка, равная весу груза, поэтому

G = mg = 500 ∙ 9, 81 = 4900 Н = 4, 9 кН.

2.      Действие веса G на кронштейн уравновешивается реакциями трех стержней. Известно, что реакции направлены вдоль стержней (так как соединения стержней шарнирные). Нужно определить модуль и направление каждой реакции, т. Е. определить, какой из стержней сжат, а какой растянут.

Мысленно разрежем стержни вблизи точки C и изобразим узел C, образуемый соединением трех стержней отдельно (рис.) вместе с четырьмя действующими на него силами: вертикально вниз действует известная сила G = 4,9 кН, а вдоль стержней действуют три их реакции: R_1, R₂ и R_3. Причем условно считаем, что все стержни растянуты, поэтому на рис. все реакции направлены от узла C.

3.      Расположим оси координат, как показано на рис.161, б. Замечая, что осью x прямой угол ACB разделен пополам ( ACO = BCO = β = 45^o), составим три уравнения равновесия для пространственной системы сходящихся сил:

∑ F_kx = 0; R₁ cos β + R₂ cos β + R₃ cos α = 0; (1)

∑ F_ky = 0; R₁ sin β – R₂ sin β = 0; (2)

∑ F_kя = 0; – R₃ sin α – G = 0. (3)

4.      Решаем полученную систему уравнений.

Из уравнения (3)

R₃ = – G / sin α = – 4,9 / sin 40^o = – 7, 62 кН.

Знак «минус» показывает, что реакция R₃ направлена в сторону, противоположную той, которая изображена на рисунке. Значит стержень 3 сжат усилием 7,62 кН.

Из уравнения (2) R_{1 =} R_2.

Из уравнения (1) R₁ = R_2.= – R₃ cos α / 2 cos β = 7,62 cos 40^o/ 2 cos 45^o = 4,13 кН.

Числовые значения реакций R₁ и R₂ получились положительные, значит стержни 1 и 2 растянуты силами по 4,13 кН.

4.      Решите свой вариант.

5.      Ответьте на вопросы.

6.      Сделайте вывод.

 

ИНСТРУКЦИОННО-МЕТОДИЧЕСКАЯ КАРТА

по выполнению практического задания № 7

 

Наименование предмета: «Техническая механика».

Тема: «Пространственная система сил».

Наименование работы: «Момент силы относительно оси».

Время: 90 мин.

Цель (обучающая, развивающая, воспитательная): научиться определять моменты сил относительно осей x, y и z.

Форма отчета: тетрадь.

Рекомендуемая литература: А.И. Аркуша «Техническая механика».

Контрольные вопросы:

1.      Какие уравнения и сколько можно составить для уравновешенной пространственной системы сходящихся сил?

2.      Почему при определении момента силы относительно оси нужно обязательно проецировать силу на плоскость, перпендикулярную оси?

3.      Как нужно расположить ось, чтобы момент данной силы относительно этой оси равнялся нулю?

4.      Какие уравнения и сколько можно составить для уравновешенной системы параллельных сил, расположенных в пространстве?

5.      Какие уравнения и сколько можно составить для уравновешенной системы сил, расположенных в пространстве как угодно?

 

Указания к выполнению работы:

1.      Повторить по учебнику тему «Пространственная система сил».

2.      Выпишите данные для вашего варианта (согласно нумерации в журнале).

№ варианта	F1 кН	F2 кН	F3 кН	F4 кН	№ варианта	F1 кН	F2 кН	F3 кН	F4 кН	№ варианта	F1 кН	F2 кН	F3 кН	F4 кН
1	3	3	3	3	11	4	4	4	4	21	6	6	6	6
2	4	4	4	4	12	6	6	6	6	22	7	7	7	7
3	6	6	6	6	13	7	7	7	7	23	8	8	8	8
4	7	7	7	7	14	8	8	8	8	24	3	3	3	3
5	8	8	8	8	15	3	3	3	3	25	4	4	4	4
6	3	3	3	3	16	4	4	4	4	26	6	6	6	6
7	4	4	4	4	17	6	6	6	6	27	7	7	7	7
8	6	6	6	6	18	7	7	7	7	28	8	8	8	8
9	7	7	7	7	19	8	8	8	8	29	3	3	3	3
10	8	8	8	8	20	3	3	3	3	30	4	4	4	4

 

3.      Рассмотрите пример решения

Пример.

К вершинам квадрата ABCD (AB =AD = 2 м), расположенного в горизонтальной плоскости, приложены силы F₁, F_2, F₃ и F₄. Сила F₁ направлена по диагонали AC; сила F₂ действует вверх перпендикулярно к плоскости квадрата; сила F₃ действует в плоскости квадрата и ее направление образует с диагональю CA угол α = 20 ^o; сила F₄ действует в плоскости, перпендикулярной к плоскости квадрата, и направлена к стороне DC под углом α = 30 ^o. Определить моменты каждой силы относительно осей x, y и z. Модули сил

F₁= F₂ = F₃ = F₄ = 5 кН.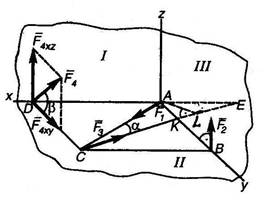

Решение.

1.      Замечаем, что расположение осей, показанное на рис. определяет положение трех взаимно перпендикулярных плоскостей; плоскости I, перпендикулярной к оси y, плоскости II, перпендикулярной к оси z, и плоскости III, перпендикулярной к оси x.

2.      Определяем моменты силы F₁. Сила F₁приложена в точке A пересечения всех трех осей, следовательно, согласно первому частному случаю

T_x (F₁) = 0; T_y (F₁) = 0; T_z (F₁) = 0.

3.      Определяем моменты силы F_2.

Сила F₂, приложенная в точке B, пересекает ось y и параллельна оси z. Следовательно, согласно первому и второму частным случаям

T_y (F₂) = 0; T_z (F₂) = 0.

Чтобы определить момент силы F₂ относительно оси x, необходимо найти проекцию F₂ на плоскость III, перпендикулярную к оси x. Сила F₂ расположена в этой плоскости и, следовательно, проецируется полностью F_{2yz =} F_2. Плечом является сторона AB квадрата. Знак момента положительный, так как если посмотреть от точки D вдоль оси x на плоскость III, то увидим, что сила F₂ поворачивает плечо AB против хода часовой стрелки. Поэтому

T_x (F₂) = F₂ ∙ AB = 5 ∙ 2 = 10 кН∙м

4.      Определяем моменты силы F₃

Сила F₃ расположена в горизонтальной плоскости. В этой же плоскости расположены оси x и y. Поэтому линия действия силы F₃ пересекает ось x (в точке E) и ось y (в точке K) Значит

T_x (F₃) = 0 и T_y (F₃) = 0.

Плоскость, в которой расположена сила F₃, перпендикулярна оси z,

значит F_{3xy =} F_3. Плечо AL силы F₃ найдем из треугольника ALC:

AL=AC sin α = AB √ 2 sin α

Знак момента положительный (если посмотреть на плоскость II со стороны оси z) Поэтому

T_z (F₃) = F₃ ∙ AL= F₃ ∙ AB √ 2 sin α = 5 ∙2 ∙ √ 2 sin 20^o = 4,83 кН м

5.                 Определяем моменты силы F_4.

Линия действия силы F₄ пересекает ось x, следовательно,

T_x (F₄) = 0.

Спроецируем силу F₄ на плоскости I и II:

F_4xz = F₄ sin β и F_4xy = F₄ cos β

Плечом силы F₄ является сторона квадрата AD

T_y (F₄ ) = – F_{4xz ∙} AD = -F₄ sin β ∙ AD = – 5 sin 30 ^o ∙2 = – 5 кН∙ м

T_z (F₄) = – F_4xy ∙ AD = – F₄ cos β ∙ AD = 5 cos 30 ^o ∙ 2 = 8,66 кН ∙ м

4.      Ответьте на вопросы.

5.      Сделайте вывод.

 

ИНСТРУКЦИОННО-МЕТОДИЧЕСКАЯ КАРТА

по выполнению практического задания № 8

 

Наименование предмета: «Техническая механика».

Тема: «Центр тяжести».

Наименование работы: «Определение положение центра тяжести тела».

Время: 90 мин.

Цель (обучающая, развивающая, воспитательная): уметь определять положение центра тяжести плоской фигуры.

Форма отчета: тетрадь.

Рекомендуемая литература: А.И. Аркуша «Техническая механика».

Контрольные вопросы:

1.      Дайте определение центра тяжести тела.

2.      Чему равен статический момент площади относительно оси абсцисс?

3.      В каких единицах измеряется статический момент плоской фигуры?

4.      Чему равен статический момент плоской фигуры относительно центральной оси?

Указания к выполнению работы:

1.      Повторить по учебнику тему «Центр тяжести».

2.      Выпишите данные для вашего варианта (согласно нумерации в журнале).

№ варианта	AB, см	BD, см	DE, см	EK, см	№ варианта	AB,	BD,	DE,	EK,	№ варианта	AB, см	BD, см	DE, см	EK, см
1	10	12	8	6	11	12	14	10	8	21	6	8	4	2
2	12	14	10	8	12	6	8	4	2	22	10	12	8	6
3	6	8	4	2	13	10	12	8	6	23	12	14	10	8
4	10	12	8	6	14	12	14	10	8	24	6	8	4	2
5	12	14	10	8	15	6	8	4	4	25	10	12	8	6
6	6	8	4	2	16	10	12	8	2	26	12	14	10	8
7	10	12	8	6	17	12	14	10	8	27	6	8	4	2
8	12	14	10	8	18	6	8	4	2	28	10	12	8	6
9	6	8	4	2	19	10	12	8	6	29	12	14	10	8
10	10	12	8	6	20	12	14	10	8	30	6	8	4	2

 

3.      Рассмотрите пример решения.

Пример.

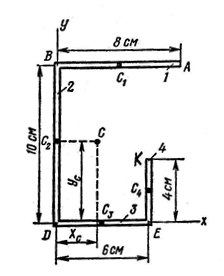
Определить положение центра тяжести плоской фигуры, изогнутой из тонкой проволоки

Решение.

1)      Фигура состоит из четырех прямых отрезков: AB = l₁ = 8 см; BD = l₂ = 10 см; DE = l₃ = 6 см; EK = l₄ = 4 см. На эти четыре части и разделим всю фигуру.

2)      Оси координат расположены так, чтобы они совпали с отрезками DE (ось x) и BD (ось y). Так как фигура плоская, третья ось здесь не нужна.

3)      Для центров тяжести C_1,, C_2,, C₃ и C₄ каждого отрезка соответственно найдем, исходя из размеров фигуры, их координаты. Обозначив x₁ и y₁ координаты C₁, найдем, что

x₁ = BA / 2 = 4 см; y₁ = DB = 10 см;

координаты C₂: x₂ = 0; y ₂ = DB / 2 = 5 см;

координаты C₃: x₃ = DE / 2 = 3 см; y₃ = 0;

координаты C₄: x₄ = DE = 6 см; y₄ = EK / 2 = 2 см.

Для удобства, а также ввиду того, что координаты центров тяжести можно определить непосредственно по рисунку, данные для подстановки в формулы следует представлять в таком виде:

l ₁ = 8 см; С₁ (4; 10);

l ₂ = 10 см; С₂ (0; 5);

l ₃ = 6 см; С₃ (3; 0);

l ₄ = 4 см; С₄ (6; 2).

4)      Подставим значения l_k,, x_k и y_k в формулы (2) и сделаем вычисления:

x _c = ( 8 · 4 + 10 · 0 + 6 · 3 + 4 · 6) / (8 + 10 + 6 + 4) = 2,64 см;

y_с = (8 · 10 +10 · 5 +6 · 0 + 4 ·2) / (8 +10 + 6 + 4) = 4,93 см.

5)      Отложив вдоль осей x и y найденные координаты, отметим на рис. положение центра тяжести C данной фигуры.

 

4.      Решите свой вариант.

5.      Ответьте на вопросы.

6.      Сделайте вывод.

 

ИНСТРУКЦИОННО-МЕТОДИЧЕСКАЯ КАРТА

по выполнению практического задания № 9

 

Наименование предмета: «Техническая механика».

Тема: «Центр тяжести».

Наименование работы: «Определение координат центра тяжести фигур».

Время: 90 мин.

Цель (обучающая, развивающая, воспитательная): уметь определять положение центра тяжести фигуры.

Форма отчета: тетрадь.

Рекомендуемая литература: А.И. Аркуша «Техническая механика».

Контрольные вопросы:

1.      Дайте определение центра тяжести тела.

2.      Чему равен статический момент площади относительно оси абсцисс?

3.      В каких единицах измеряется статический момент плоской фигуры?

4.      Чему равен статический момент плоской фигуры относительно центральной оси?

 

Указания к выполнению работы:

1.      Повторить по учебнику тему «Центр тяжести».

2.      Выпишите данные для вашего варианта (согласно нумерации в журнале).

№ варианта	x1, мм	x2, мм	y, мм	z1, мм	z3, мм	№ варианта	x1, мм	x2, мм	y, мм	z1, мм	z3, мм	№ варианта	x1, мм	x2, мм	y, мм	z1, мм	z3, мм
1	20	30	70	40	10	11	60	70	110	80	50	21	40	50	90	60	30
2	40	50	90	60	30	12	50	60	100	70	40	22	60	70	110	80	50
3	60	70	110	80	50	13	20	30	70	40	10	23	50	60	100	70	40
4	50	60	100	70	40	14	40	50	90	60	30	24	20	30	70	40	10
5	20	30	70	40	10	15	60	70	110	80	50	25	40	50	90	60	30
6	40	50	90	60	30	16	50	60	100	70	40	26	60	70	110	80	50
7	60	70	110	80	50	17	20	30	70	40	10	27	50	60	100	70	40
8	50	60	100	70	40	18	40	50	90	60	30	28	20	30	70	40	10
9	20	30	70	40	10	19	60	70	110	80	50	29	40	50	90	60	30
10	40	50	90	60	30	20	50	60	100	70	40	30	60	70	110	80	50

 

3.      Рассмотрите пример решения.

 

Пример.

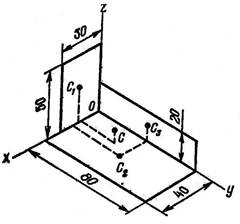
Определить положение центра тяжести фигуры, составленной из трех тонких плоских пластинок прямоугольной формы, пересекающихся друг с другом под прямыми углами; размеры – в мм.

Решение.

1)                Поместим начало координат в вершине трехгранного угла и расположим оси координат вдоль линий пересечения пластинок.

Фигура состоит из трех прямоугольников с центрами тяжести С₁, С₂ , С₃, расположенными на пересечении прямых, соединяющих середины противоположных сторон.

2)                Исходя из размеров фигуры, определим необходимые данные для подстановки в формулы (3): A _k – площади прямоугольников и координаты их центров тяжести:

A₁ = 3 ∙ 5 = 15 см²; C₁ (1, 5; 0; 2, 5);

A₂ = 4 ∙ 8 = 32 см²; C₂ (2; 4; 0);

A₃ = 8 ∙ 2 = 16 см²; C₃ 0; 4; 1).

3)                Подставим эти данные в формулы (4) и вычислим искомые координаты центра тяжести фигуры:

x _c = (15 ∙ 1,5 + 32 ∙ 2 + 16 ∙ 0) / (15 + 32 + 16) = 1, 37 см = 13,7 мм

y _c = (15 ∙ 0 + 32 ∙ 4 + 16 ∙ 4) / (15 + 32 + 16) = 3,04 см = 30,4 мм

z _c = (15 ∙ 2,5 + 32 ∙ 0 + 16 ∙ 1) / (15 + 32 + 16) = 0,85 см = 8,5 мм

Центр тяжести фигуры расположен в точке  С (13,7; 30,4; 8,5).

 

4.      Решите свой вариант.

5.      Ответьте на вопросы.

6.      Сделайте вывод.

 

 

ИНСТРУКЦИОННО-МЕТОДИЧЕСКАЯ КАРТА

по выполнению практического задания № 10

 

Наименование предмета: «Техническая механика».

Тема: «Кинематика точки».

Наименование работы: «Определение траектории, скорости и ускорения точки».

Время: 90 мин.

Цель (обучающая, развивающая, воспитательная): научиться определять время, необходимое для прохождения заданного расстояния, если задана скорость.

Форма отчета: тетрадь.

Рекомендуемая литература: А.И. Аркуша «Техническая механика»

Контрольные вопросы:

1.      Дайте определение кинематики.

2.      Что называют траекторией?

3.      В каких единицах измеряется скорость?

4.      Чему равен модуль средней скорости?

5.      В каких единицах измеряется ускорение?

 

Указания к выполнению работы:

1.      Повторить по учебнику тему «Кинематика точки».

2.      Выпишите данные для вашего варианта (согласно нумерации в журнале).

№ варианта	S, км	vА, км/ч	vВ,, км./ч	№ варианта	S, км	vА, км/ч	vВ,, км/ч	№ варианта	S, км	vА,, км/ч	v В, км/ч
1	110	30	20,4	11	130	34	24,8	21	110	30	20,4
2	120	32	22,6	12	140	36	26,2	22	120	32	22,6
3	130	34	24,8	13	110	30	20,4	23	130	34	24,8
4	140	36	26 2	14	120	32	22,6	24	140	36	26,2
5	110	30	20,4	15	130	34	24,8	25	110	30	20,4
6	120	32	22,6	16	140	36	26,2	26	120	32	22,6
7	130	34	24,8	17	110	30	20,4	27	130	34	24,8
8	140	36	26,2	18	120	32	22,6	28	140	36	26,2
9	110	30	20,4	19	130	34	24,8	29	110	30	20,4
10	120	32	22,6	20	140	36	26,2	30	120	32	22,6

 

3.      Рассмотрите пример решения.

Из двух пунктов А и В прямолинейного шоссе, находящихся один от другого на расстоянии 100 км, одновременно выезжают навстречу друг другу два велосипедиста и движутся с постоянными скоростями. Велосипедист, выезжающий из А, имеет скорость v _А, а велосипедист, выезжающий из В, – скорость v_В, = 26,6 км /ч. Определить, за какое время каждый из них проедет расстояние 100 км. Через сколько часов и где они встретятся?

Решение.

1.                 Находим время, затраченное первым велосипедистом на проезд от точки А до В:

t_АВ = S _АВ / v_А = 100 / 40 = 2,5 ч

2.                 Находим время, затраченное вторым велосипедистом на проезд от точки В до А:

t_ВА = S _ВA / v_B = 100 / 26,6 = 3,75 ч.

3.                 Время и место встречи велосипедистов наиболее просто определить графически. Расстояние между пунктами А и В, равное100 км, изобразим на оси ординат отрезком в 50 мм (рис.202), т.е. в масштабе μ_S = 2 км /мм (100 км = μ_S · 50 мм и … μ_S = 100 км / 50 км = 2 км /мм).

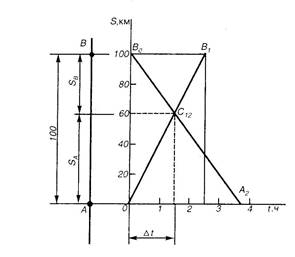По оси абсцисс отложим время в масштабе μ_t = 0,1 ч /мм (4 часа изображены отрезком 40 мм, поэтому 4 ч = μ_t · 40 мм и μ_t = 4 ч / 40 мм = 0,1 ч /мм)

Первый велосипедист расстояние от А до В проезжает за 2,5 ч. Его перемещение изображается на графике прямой OB₁.

Второй велосипедист расстояние от В до А проезжает за 3,75 ч и его перемещение изображается на графике прямой В₀ А₂

Точка С₁₂ пересечения обоих графиков указывает место и время встречи.

Встреча происходит на расстоянии S _А = 60 км от пункта А (или на расстоянии.

S _В = 40 км от пункта В) через Δt = 1,5 ч после начала движения велосипедистов.

Если вместо графического решения применить аналитическое, то можно рассуждать таким образом.

Допустим, что место встречи происходит на расстоянии S от пункта А, а время до встречи Δt , считая от начала движения. Тогда уравнение движения первого велосипедиста примет вид

S = v_А · Δt и уравнение движения второго велосипедиста S = S_{0 –} v_B · Δt где S₀ = 100 км – расстояние от местонахождения второго велосипедиста до пункта А в момент начала отсчета (при t = 0).

Так как левые части уравнения (1) и (2) равны, то v_А · Δt = S_{0 –} v_B · Δt.

Отсюда

Δt = S₀ / (v_А + v_B) = 100 / (40 + 26,6) = 1, 5 ч.

Из уравнения (1) определяем S:

S = v_А · Δt = 40 · 1,5 = 60 км.

 

4.      Решите свой вариант.

5.      Ответьте на вопросы.

6.      Сделайте вывод.

 

 

ИНСТРУКЦИОННО-МЕТОДИЧЕСКАЯ КАРТА

по выполнению практического задания № 11

 

Наименование предмета: «Техническая механика».

Тема: «Простейшие движения твердого тела».

Наименование работы: «Определение скорости и ускорения различных точек вращающегося тела».

Время: 90 мин.

Цель (обучающая, развивающая, воспитательная): научиться определять угловую скорость шкива двигателя.

Форма отчета: тетрадь.

Рекомендуемая литература: А.И. Аркуша «Техническая механика»

Контрольные вопросы:

1.      Дайте определение вращательного движения тела.

2.      Чему равна средняя угловая скорость?

3.      Чему равно угловое ускорение тела в данный момент?

4.      Дайте определение частоты вращения.

5.      Чему равна частота вращения?

 

Указания к выполнению работы:

1.      Повторить по учебнику тему «Простейшие движения твердого тела».

2.      Выпишите данные для вашего варианта (согласно нумерации в журнале).

№ варианта	d п	d2	d3	№ варианта	d п	d2	d3	№ варианта	d п	d2	d3
1	650	350	130	11	750	450	150	21	650	350	130
2	700	400	140	12	800	500	160	22	700	400	140
3	750	450	150	13	650	350	130	23	750	450	150
4	800	500	160	14	700	400	140	24	800	500	160
5	650	350	130	15	750	450	150	25	650	350	130
6	700	400	140	16	800	500	160	26	700	400	140
7	750	450	150	17	650	350	130	27	750	450	150
8	800	500	160	18	700	400	140	28	800	500	160
9	650	350	130	19	750	450	150	29	650	350	130
10	700	400	140	20	800	500	160	30	700	400	140

 

3.      Рассмотрите пример решения.

Пример.

Дисковая пила 1 имеет диаметр 600 мм. На валу пилы насажен шкив 2 диаметром 300 мм, а шкив соединен бесконечным ремнем со шкивом двигателя 3 (рис.) диаметром 120 мм. С какой угловой скоростью должен вращаться шкив двигателя, чтобы скорость зубьев пилы не превышала 15 м./ с?

Решение.

1. 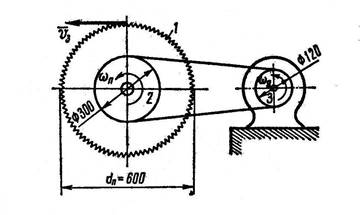                Так как пила 1 и шкив 2 насажены на одном валу, то они имеют одну и ту же угловую скорость ώ _п и скорость зубьев пилы v ₃ = 15 м /с зависит от ώ _п :

v ₃ = ρ ·ώ_п или v ₃ = d _п / 2 · ώ_п потому что ρ = d п / 2.

2.                 Находим угловую скорость шкива 2, который обеспечивает необходимую рабочую скорость зубьев пилы:

ώ _п = 2 v ₃ / d _п = 2 · 15 / 0, 6 = 50 с ^-1.

(d _п = 600 мм = 0,6 м).

3.                 Теперь найдем угловую скорость ώ _п шкива двигателя.

Шкивы 2 и 3 соединены бесконечным ремнем. Полагая, что ремень не растягивается и не проскальзывает на шкивах, можно считать, что все его точки движутся с одной и той же скоростью v_р. Это означает, что скорости точек, расположенных на поверхностях обоих шкивов, одинаковы равны v_р.

Поэтому применим зависимость v = ρ ·ώ

v_р = d₂ / 2 · ώ _п = d₃ / 2 · ώ _д

Отсюда

ώ _д = ώ _п · d₂ / d₃ = 50 · 300 / 120 = 125 c ^-1

4.                 Если перевести эту угловую скорость в мин ^-1, то

n _д = 30 ώ _д / π = 30 · 125 / π = 1200 мин ^-1.

Таким образом, для того, чтобы зубья пилы имели скорость 15 м./с, шкив двигателя должен вращаться с угловой скоростью 125 с ^-1 (или 1200 мин ^-1)

 

4.      Решите свой вариант.

5.      Ответьте на вопросы.

6.      Сделайте вывод.

 

ИНСТРУКЦИОННО-МЕТОДИЧЕСКАЯ КАРТА

по выполнению практического задания № 12

 

Наименование предмета: «Техническая механика».

Тема: «Сложное движение».

Наименование работы: «Определение скорости любой точки тела».

Время: 90 мин.

Цель (обучающая, развивающая, воспитательная): научиться определять скорость любой точки тела.

Форма отчета: тетрадь.

Рекомендуемая литература: А.И. Аркуша «Техническая механика».

Контрольные вопросы:

1.      Дайте определение относительного движения точки.

2.      Какое движение называют переносным?

3.      Какое движение называют сложным?

4.      Чему равна абсолютная скорость в каждый момент времени?

5.      Какое движение называют плоскопараллельным?

 

Указания к выполнению работы:

1.      Повторить по учебнику тему «Сложное движение».

2.      Выпишите данные для вашего варианта (согласно нумерации в журнале).

№ варианта	S, км	t 1, ч	t 2, ч	№ варианта	S, км	t 1, ч	t 2, ч	№ варианта	S, км	t 1, ч	t 2, ч
1	100	4	6	11	120	6	8	21	100	4	6
2	110	5	7	12	130	7	9	22	110	5	7
3	120	6	8	13	100	4	6	23	120	6	8
4	130	7	9	14	110	5	7	24	130	7	9
5	100	4	6	15	120	6	8	25	100	4	6
6	110	5	7	16	130	7	9	26	110	5	7
7	120	6	8	17	100	4	6	27	120	6	8
8	130	7	9	18	110	5	7	28	130	7	9
9	100	4	6	19	120	6	8	29	100	4	6
10	110	5	7	20	130	7	9	30	110	5	7

3.      Рассмотрите пример решения.

Пример.

Расстояние S = 90 км между пристанями, расположенными на реке, теплоход проходит без остановки в одном направлении (по течению) за t ₁ = 3 ч и в обратном направлении (против течения) за t ₂ = 5 ч. Определить скорость течения реки и собственную скорость теплохода.

Решение.

1.                 Теплоход, который принимаем за материальную точку, двигаясь по течению, имеет абсолютную скорость (скорость относительно берегов): v₁ = v _{T x} + v _р, где v _{T x} – искомая собственная скорость теплохода (относительная скорость); v _р – скорость течения реки (переносная скорость).

При движении против течения абсолютная скорость теплохода

v₂ = v _{T x} – v _р.

2.                 Движение теплохода по течению описывается уравнением (рис. а)

S = (v _{T x} + v _р) t ₁.

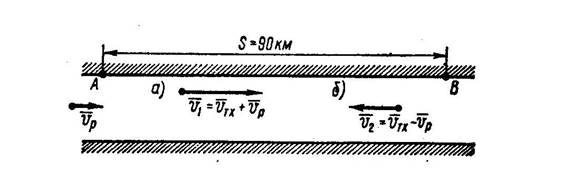
Движение теплохода против течения происходит по уравнению (рис. б)

S = (v _{T x} – v _р) t ₂.

3.                 Решаем полученную систему уравнений. Из (а) и (б)

v _{T x} + v _р = S / t ₁,

v _{T x –} v _р = S / t ₂ .

Сложим правые и левые части этих уравнений:

2 v _{T x} = S / t ₁ + S / t ₂ = 90 / 3 + 90 / 5 = 48 км / ч, v _р = 24 км / ч.

Вычитаем из верхнего равенства нижнее:

2 v _{T x} = S / t _{1 –} S / t ₂ = 90 / 3 – 90 / 5 = 12 км / ч, v _р = 6 км / ч.

Таким образом, собственная скорость теплохода составляет 24 км / ч, а скорость течения реки равна 6 км / ч.

 

4.      Решите свой вариант.

5.      Ответьте на вопросы.

6.      Сделайте вывод.

 

ИНСТРУКЦИОННО-МЕТОДИЧЕСКАЯ КАРТА

по выполнению практического задания № 13

 

Наименование предмета: «Техническая механика».

Тема: «Движение несвободной материальной точки».

Наименование работы: «Применение принципа Даламбера к решению задач на прямолинейное движение точки».

Время: 90 мин.

Цель (обучающая, развивающая, воспитательная): уметь составлять уравнения равновесия для решения задач на прямолинейное движение точки.

Форма отчета: тетрадь.

Рекомендуемая литература: А.И. Аркуша «Техническая механика».

Контрольные вопросы:

1.      Что изучает динамика?

2.      Какая система отсчета называется инерциальной?

3.      В чем состоит принцип инерции?

4.      В чем заключается основной закон динамики?

5.      Чему равно значение силы тяжести тела?

 

Указания к выполнению работы:

1.      Повторить по учебнику тему «Движение несвободной материальной точки».

2.      Выпишите данные для вашего варианта (согласно нумерации в журнале).

№ варианта	G, кН	F, кН	S, м	№ варианта	G, кН	F, кН	S, м	№ варианта	G, кН	F, кН	S, м
1	100	20	2	11	150	25	3	21	205	30	2
2	105	25	3	12	155	30	4	22	210	35	3
3	110	30	4	13	160	35	5	23	215	40	4
4	115	35	5	14	165	40	6	24	220	45	5
5	120	40	6	15	170	45	7	25	225	50	6
6	125	45	7	16	175	50	8	26	230	55	7
7	130	50	8	17	180	55	4	27	235	60	8
8	135	55	4	18	185	60	5	28	240	65	4
9	140	60	5	19	190	65	6	29	245	70	5
10	145	65	6	20	195	70	7	30	250	75	6

 

3.      Рассмотрите пример решения.

Пример.

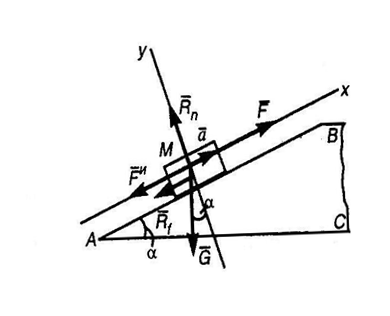
По наклонной плоскости AB длиной 4 м и углом подъема ά = 15^o равноускоренно поднимают груз M весом G = 200 кН, постоянной силой F = 65 кН, направленной параллельно наклонной плоскости. Определить, сколько времени потребуется, чтобы переместить груз на расстояние AB , если коэффициент трения при движении груза по наклонной плоскости f = 0,05.

Решение.

1.      Изобразим тело M на наклонной плоскости с приложенными к нему силами G и F, а также силой трения R _f и нормальной реакцией R _n наклонной плоскости.

Находясь под действием этих сил, тело движется по наклонной плоскости с постоянным ускорением a.

2.      Груз перемещается равноускоренно, без начальной скорости. Время его движения можно определить из уравнения движения

S = a t ² / 2, откуда t = √ 2S/a, но предварительно необходимо определить ускорение a.

3.      Так как груз движется с ускорением, то силы G и F, R _f и R _n, приложенные к нему, не образуют уравновешенной системы. Приложим к грузу M силу инерции F_и = ma = Ga / g, направив ее в сторону, противоположную ускорению a. Теперь система пяти сил G, F, R _f , R _n, F _и является уравновешенной.

4.      Выберем систему координат, как показано на рис, и спроецируем все силы на оси x и y. Тогда получим два уравнения равновесия:

∑F_kx = 0; F – G sin α – R _f – F_и = 0; (1)

∑F_ky = 0; R _n – G cos α = 0. (2)

5.      Из уравнения (1)

F_и = F – G sin α – R _f, но сила трения R _f = f R _n .

Нормальную реакцию R _n найдем из уравнения (2)

R _n = G cos α.

Поэтому

F_и = F – G sin α – f G cosα = F- G(sinα + f cosα).

Подставим в это уравнение числовые значения

F_и = 65 – 200 (sin 15^o+ 0,05 cos 15^o) = 65 – 61,4 = 3,6 кН

6.      Из выражения F_и = G/g · а найдем ускорение а:

а = (F _и · g) /G = (3,6 · 9,81) / 200 = 0,18 м / с ²

7.      Подставив значение ускорения а в выражение t = √2S/2, найдем время перемещения груза М по всей длине наклонной плоскости:

t = √2 S / а = √2 · 4 / 0,18  = 6,7 с.

4.      Решите свой вариант.

5.      Ответьте на вопросы.

6.      Сделайте вывод.

 

ИНСТРУКЦИОННО-МЕТОДИЧЕСКАЯ КАРТА

по выполнению практического задания № 14

 

Наименование предмета: «Техническая механика».

Тема: «Работа и мощность».

Наименование работы: «Решение задач на определение работы и мощности».

Время: 90 мин.

Цель (обучающая, развивающая, воспитательная): научиться решать задачи на определение работы.

Форма отчета: тетрадь.

Рекомендуемая литература: А.И. Аркуша «Техническая механика».

Контрольные вопросы:

1.      Дайте определение работы.

2.      В каких единицах выражается работа?

3.      Дайте определение мощности.

4.      В каких единицах выражается мощность?

5.      Что называют механическим коэффициентом полезного действия?

 

Указания к выполнению работы:

1.      Повторить по учебнику тему «Работа и мощность».

2.      Выпишите данные для вашего варианта (согласно нумерации в журнале).

№ варианта	m, кг	S, м	d, см	№ варианта	m, кг	S, м	d, см	№ варианта	m, кг	S, м	d, см
1	60	5	30	11	80	7	50	21	60	5	30
2	70	6	40	12	90	8	60	22	70	6	40
3	80	7	50	13	60	5	30	23	80	7	50
4	90	8	60	14	70	6	40	24	90	8	60
5	60	5	30	15	80	7	50	25	60	5	30
6	70	6	40	16	90	8	60	26	70	6	40
7	80	7	50	17	60	5	30	27	80	7	50
8	90	8	60	18	70	6	40	28	90	8	60
9	60	5	30	19	80	7	50	29	60	5	30
10	70	6	40	20	90	8	60	30	70	6	40

 

3.      Рассмотрите пример решения.

Пример.

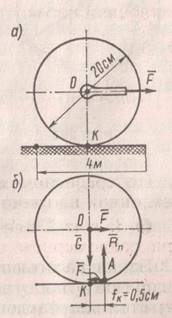
Определить работу, которую необходимо произвести, чтобы перекатить каток массой 50 кг на расстояние 4 м по горизонтальной негладкой поверхности. Считать, что сила, двигающая каток, приложена к оси катка и горизонтальна (рис). Диаметр катка 20 см, коэффициент трения f _k = 0,5 см.

Решение.

1)                Как известно из кинематики, движение катящегося катка называется плоскопараллельным и состоит из двух движений – поступательного и вращательного.

Ось катка передвигается поступательно, поэтому работу силы F, приложенной к оси, можно определить по формуле W = F S, но предварительно нужно найти численное значение силы F.

2)                На каток в неподвижном состоянии действуют две силы: вес катка G и реакция

R _n горизонтальной поверхности, приложения к катку в точке K (геометрическая точка касания катка с поверхностью). При качении на каток действуют уже четыре силы (рис. б): G – вес катка, F – движущая сила и две составляющие R _n и R _f  полной реакции поверхности, место приложения которой перемещается из точки К в точку А – вперед по ходу катка.

3)                Если спроецировать все силы на вертикальную и горизонтальную оси, то R _n = G и F = R _f , т. е. на катящийся каток действуют две пары сил: катящая пара (F, R _f ) с плечом ОК = d / 2 = 20 см / 2 = 10 см и пара сопротивления (G, R _n ) с плечом KA = f _k = 0,5 см. При равномерном перекатывании катка моменты этих пар численно равны между собой, т. е. F d / 2 = G f _k .

Отсюда находим силу F, выразив силу тяжести в Н (G = mg),

F= G f _k / ( d / 2) = 50 ∙ 9, 81 ∙ 0,5 / (20/2) = 24, 5 Н.

4)                 Таким образом, работа, произведенная при перемещении катка,

W = F S = 24, 5 ∙ 4 = 98 Дж.

 

4.      Решите свой вариант.

5.      Ответьте на вопросы.

6.      Сделайте вывод.

 

ИНСТРУКЦИОННО-МЕТОДИЧЕСКАЯ КАРТА

по выполнению практического задания № 15

 

Наименование предмета: «Техническая механика».

Тема: «Основные теоремы динамики».

Наименование работы: «Решение задач на поступательное движение тела».

Время: 90 мин.

Цель (обучающая, развивающая, воспитательная): рассмотреть пример решения задачи на поступательное движение тела.

Форма отчета: тетрадь.

Рекомендуемая литература: А.И. Аркуша «Техническая механика».

Контрольные вопросы:

1.      Что изучает динамика?

2.      Какая система отсчета называется инерциальной?

3.      Сформулируйте основной закон динамики

4.      В чем состоит принцип инерции?

 

Указания к выполнению работы:

1.      Повторить по учебнику тему «Общие теоремы динамики».

2.      Выпишите данные для вашего варианта (согласно нумерации в журнале).

 

№ варианта	s, м	h, м	v, м /с	№ варианта	s, м	h, м	v, м /с	№ варианта	s, м	h, м	v, м /с
1	550	3	13	11	650	5	15	21	550	3	13
2	600	4	14	12	700	6	16	22	600	4	14
3	650	5	15	13	550	3	13	23	650	5	15
4	700	6	16	14	600	4	14	24	700	6	16
5	550	3	13	15	650	5	15	25	550	3	13
6	600	4	14	16	700	6	16	26	600	4	14
7	650	5	15	17	550	3	13	27	650	5	15
8	700	6	16	18	600	4	14	28	700	6	16
9	550	3	13	19	650	5	15	29	550	3	13
10	600	4	14	20	700	6	16	30	600	4	14

 

3.      Рассмотрите пример решения.

Пример.

За 500 м до станции, стоящей на пригорке высотой 2 м, машинист поезда, идущего со скоростью 12 м / с, начинает тормозить. Как велико должно быть сопротивление от торможения, считаемое постоянным, чтобы поезд остановился у станции, если масса поезда равна 10 ⁶ кг, сопротивление трения 19600 Н.

Решение.

1.                 Решаем задачу, используя теорему об изменении кинетической энергии, так как в условии задачи задано не время торможения, а тормозной путь s = 500 м.

2.                 Поезд движется поступательно, поэтому достаточно рассмотреть движение его центра тяжести O. Приложим к точке O все действующие силы (рис.). Вес поезда G раскладываем на две составляющие G₁ и G₂. На поезд, в сторону, противоположную его движению, действуют три силы, составляющая веса G₁, сила трения R_f и искомая сила торможения F.

 

 

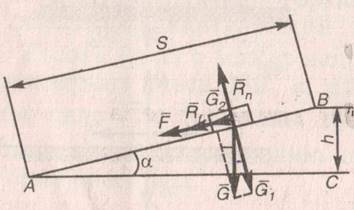
3.                 Равнодействующая этих сил, равная их сумме (F + R_f + G₂), действуя на расстоянии s, производит работу W = – (F + R_f + G₂) s (работа сил сопротивления отрицательна).

4.                 Работа W равна изменению кинетической энергии поезда:

W = mv ²/2 – mv_o ²/2.

Но так как конечная скорость поезда v = 0, то

– (F + R_f + G₂) s = – mv_o ²/2.

Из последнего уравнения можно найти силу торможения F:

F = mv_o ²/2s – R_f - G_2.

5.                 Но, предварительно нужно определить составляющую веса G_2:

G₂ = G sin α.

А, так как sin α = h/s, то

G₂ = G h/s.

Подставив полученное значение G₂ в формулу для определения силы F, получим

F = mv_o ²/2s – R_f   - G _.h/s.

Затем вычисляем величину силы F, учитывая, что G = mg.

F = mv_o ²/2s – R_f   - mgh / s = 10⁶ ∙12²/ (2 ∙ 500) – 19600 – 10⁶ ∙ 9, 81 ∙ 2 / 500 = 85100 Н.

 

4.      Решите свой вариант.

5.      Ответьте на вопросы.

6.      Сделайте вывод.

 

ИНСТРУКЦИОННО-МЕТОДИЧЕСКАЯ КАРТА

по выполнению практического задания № 16

 

Наименование предмета: «Техническая механика».

Тема: «Растяжение и сжатие».

Наименование работы: «Расчет на прочность при растяжении и сжатии».

Время: 90 мин.

Цель (обучающая, развивающая, воспитательная): научиться применять условие прочности при решении задач.

Форма отчета: тетрадь.

Рекомендуемая литература: А.И. Аркуша «Техническая механика».

Контрольные вопросы:

1.      Как нужно нагрузить прямой брус, чтобы он работал только на растяжение (сжатие)?

2.      Сформулируйте закон Гука. Каков физический смысл модуля продольной упругости?

3.      Что такое «предельное напряжение» и что такое «расчетное напряжение»?

4.      Что такое допускаемое напряжение и как оно выбирается в зависимости от свойств материалов?

5.      Как можно данную статически неопределимую систему превратить в статически неопределимую?

 

Указания к выполнению работы:

1.      Повторить по учебнику тему «Растяжение и сжатие».

2.      Выпишите данные для вашего варианта (согласно нумерации в журнале).

 

№ варианта	G, кН	F, кН	№ варианта	G, кН	F, кН	№ варианта	G, кН	F, кН
1	1,4	10	11	1,6	12	21	1,8	14
2	1,6	12	12	1,8	14	22	2,0	16
3	1,8	14	13	2,0	16	23	2,2	18
4	2,0	16	14	2,2	18	24	1,4	10
5	2,2	18	15	1,4	10	25	1,6	12
6	1,4	10	16	1,6	12	26	1,8	14
7	1,6	12	17	1,8	14	27	2,0	16
8	1,8	14	18	2,0	16	28	2,2	18
9	2,0	16	19	2,2	18	29	1,4	10
10	2,2	18	20	1,4	10	30	1,6	12

 

3.      Рассмотрите пример решения.

Пример.

Однородная жесткая плита AB силой тяжести G = 1, 2 кН нагружена силой F = 8 кН. Определить из условия прочности диаметр стержня CD, удерживающего плиту в горизонтальном положении; ά = 45^o, [σ] = 150 Н/мм ².

Решение.

1.                 Применяя метод сечений, рассечем стержень CD. Отбросив верхнюю его часть вместе с шарниром D, заменим  их действие на оставшуюся часть нормальной силой N. Сила тяжести плиты приложена посередине ее длины.

2.                 Для определения силы N составим уравнение моментов относительно точки A всех сил, действующих на плиту:

-                    G · AB / 2 + N · AC sin ά – F· AB = 0.

 

 

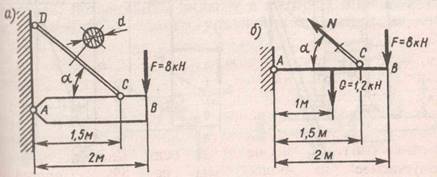
Отсюда

N = (G ·AB / 2 + F · AB) / (AC sin ά) = (1, 2 · 1 + 8 ·2) / (1, 5 sin 45^o) = 16,2 кН

3.                 Площадь поперечного сечения стержня, обеспечивающую его прочность, находим по расчетной формуле, имея в виду, что N = 16, 2 ·10³ Н и [σ] = 150 Н/мм ².

A ≥ N / [σ] = 16, 2∙ 10³ / 150 = 108 мм ².

4.                 Из формулы площади круга находим диаметр стержня:

d = √ 4 A / π = √ 4 ∙ 108 / π = 11, 8 мм.

Округляя до четного числа, принимаем значение диаметра d = 12 мм.

4.      Решите свой вариант.

5.      Ответьте на вопросы.

6.      Сделайте вывод.

 

ИНСТРУКЦИОННО-МЕТОДИЧЕСКАЯ КАРТА

по выполнению практического задания № 17

 

Наименование предмета: «Техническая механика».

Тема: «Растяжение и сжатие».

Наименование работы: «Определение усилий в стержнях».

Время: 90 мин.

Цель (обучающая, развивающая, воспитательная): научиться определять необходимые диаметры стержней.

Форма отчета: тетрадь.

Рекомендуемая литература: А.И. Аркуша «Техническая механика».

Контрольные вопросы:

1.      Сформулируйте закон Гука. Каков физический смысл модуля продольной упругости?

2.      Что такое «предельное напряжение» и что такое «расчетное напряжение»?

3.      Что такое допускаемое напряжение и как оно выбирается в зависимости от свойств материалов?

4.      Как можно данную статически неопределимую систему превратить в статически неопределимую?

 

Указания к выполнению работы:

1.      Повторить по учебнику тему «Растяжение и сжатие».

2.      Выпишите данные для вашего варианта (согласно нумерации в журнале).

№ варианта	F, кН	l1, м	l2, м	№ варианта	F, кН	l1, м	l2, м	№ варианта	F, кН	l1, м	l2, м
1	50	0,7	1,2	11	70	0,9	1,4	21	50	0,7	1,2
2	60	0,8	1,3	12	90	1,1	1,6	22	60	0,8	1,3
3	70	0,9	1,4	13	50	0,7	1,2	23	70	0,9	1,4
4	90	1,1	1,6	14	60	0,8	1,3	24	90	1,1	1,6
5	50	0,7	1,2	15	70	0,9	1,4	25	50	0,7	1,2
6	60	0,8	1,3	16	90	1,1	1,6	26	60	0,8	1,3
7	70	0,9	1,4	17	50	0,7	1,2	27	70	0,9	1,4
8	90	1,1	1,6	18	60	0,8	1,3	28	90	1,1	1,6
9	50	0,7	1,2	19	70	0,9	1,4	29	50	0,7	1,2
10	60	0,8	1,3	20	90	1,1	1,6	30	60	0,8	1,3

 

3.      Рассмотрите пример решения.

Пример.

Жесткий брус удерживается в равновесии двумя стальными стержнями круглого поперечного сечения одного и того же диаметра. Определить необходимые диаметры этих стержней, если [σ] = 150 Н/мм ².

Решение.

1)                Рассекая стержни и заменяя действие их отброшенных частей на жесткий брус нормальными силами N₁ и N₂, получаем расчетную схему, для которой запишем уравнение статики (уравнение моментов сил относительно точки A).

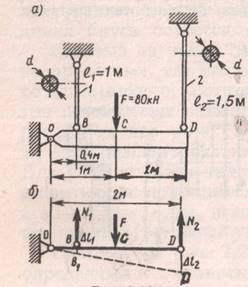N₁ · OB – F · OC + N₂ · OD = 0.

После подстановки числовых значений величин (F = 80 кН, OB = 0,4 м, OC = 1 м и

OD = 2 м) уравнение статики примет вид: N₁ + 5 N₂ = 200.

2)                Под действием силы F стержни 1 и 2 удлиняются соответственно на

 Δ l₁ = N₁ l₁ / AE и Δ l₂ = N₂ l₂ / AE.

Из подобия треугольников OBB₁ и ODD₁ получим уравнение перемещений

Δ l₁ ./ Δ l₂ = OB /OD.

Подставив сюда выражения Δ l₁ , Δ l₂ из п. 2, а также числовые значения

l₁ = 1 м, l₂ = 1, 5 м, OB = 0, 4 м и OD = 2м, получим

N₁ · 1 / N₂ ·15 = 0, 4 / 2, откуда N₁ = 0,3 N₂.

3)                Решив совместно уравнения статики и перемещений, найдем

N₂ = 37, 7 кН и N₁ = 11 кН.

4)                Из условия прочности более нагруженного стержня 2 по расчетной формуле находим требуемую площадь поперечного сечения

A₂ = N₂ / [σ] = 37, 7 · 10³ / 150 = 251 мм ².

5)                Диаметр стержня d = √ 4A/ π = √ 4 · 251 / π = 17, 9 мм.

6)                Округляя до четного числа, принимаем d₁ = d₂ = d = 18 мм.

 

4.      Решите свой вариант.

5.      Ответьте на вопросы.

6.      Сделайте вывод.

 

ИНСТРУКЦИОННО-МЕТОДИЧЕСКАЯ КАРТА

по выполнению практического задания № 18

 

Наименование предмета: «Техническая механика».

Тема: «Практические расчеты на срез и смятие».

Наименование работы: «Расчет на прочность по предельному состоянию».

Время: 90 мин.

Цель (обучающая, развивающая, воспитательная): научиться применять условие прочности при решении задач.

Форма отчета: тетрадь.

Рекомендуемая литература: А.И. Аркуша «Техническая механика».

1.      Что такое допускаемое напряжение и как оно выбирается в зависимости от свойств материалов?

2.      Как можно данную статически определимую систему превратить в статически неопределимую?

3.      На каких допущениях основаны расчеты на срез и смятие?

4.      Как определяется площадь смятия, если поверхность смятия: а) плоская;

б) цилиндрическая?

 

Указания к выполнению работы:

1.      Повторить по учебнику тему «Растяжение и сжатие».

2.      Выпишите данные для вашего варианта (согласно нумерации в журнале).

№ варианта	F, н	t1, мм	№ варианта	F, н	t1, мм	№ варианта	F, н	t1, мм
1	550	1,1	11	650	1,3	21	550	1,1
2	600	1,2	12	700	1,4	22	600	1,2
3	650	1,3	13	550	1,1	23	650	1,3
4	700	1,4	14	600	1,2	24	700	1,4
5	550	1,1	15	650	1,3	25	550	1,1
6	600	1,2	16	700	1,4	26	600	1,2
7	650	1,3	17	550	1,1,	27	650	1,3
8	700	1,4	18	600	1,2	28	700	1,4
9	550	1,1	19	650	1,3	29	550	1,1
10	600	1,2	20	700	1,4	30	600	1,2

 

3.      Рассмотрите пример решения.

Пример.

Дюралюминиевая пластина 1 толщиной t₁ = 1 мм склеена карбинольным клеем со стеклопластиковой пластиной 2. Определить толщину t₂ пластины 2, ширину b обеих пластин и длину клеевого шва, если F = 500 Н, допускаемое напряжение для дюралюминия [σ_р] = 100 н/мм², для стеклопластика [σ_р] _с = 75 н/мм², для клеевого шва [τ_ср]_кл = 5 н/мм².

Решение.

1)      Ширину листов b находим из условия прочности дюралюминиевого листа. Поперечное сечение листа 1 – прямоугольник площадью А₁ = t_1,b, нормальная сила в этом сечении N₁ = F. По расчетной формуле t₁ b ≥ N₁ / [σ_р]_д,

 

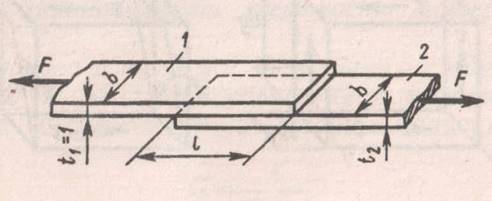
откуда b ≥ N₁ / ([σ_р]_д t₁) = 500/ (100 ∙ 1).

2)      Толщину листа 2 находим из условия его прочности. Площадь поперечного сечения  А₂ = t₂b, продольная сила N₂ = F. По формуле t₂ b ≥ N₂ / [σ_р]_c,

 откуда

t₂ ≥ N₂ / ( [σ_р]_c b) = 500 / (75 ∙ 5) = 1, 33 мм.

3)      Длину клеевого шва определяем из условия прочности соединения на срез. Площадь клеевого шва А _кл = bl. Сдвигающая сила Q = F. Из условия прочности, полагая

τ_ср = [τ _ср ] и А _ср = А _{кл ,} имеем

bl ≥ Q/ [τ_ср]_кл,

откуда

l ≥ Q/ b[τ_ср]_кл = 500/ (5 ∙ 5) = 20 мм

 

4.      Решите свой вариант.

5.      Ответьте на вопросы.

6.      Сделайте вывод.

 

 

 

 

 

 

ИНСТРУКЦИОННО-МЕТОДИЧЕСКАЯ КАРТА

по выполнению практического задания № 19

 

Наименование предмета: «Техническая механика».

Тема: «Практические расчеты на срез и смятие».

Наименование работы: «Расчет на срез и смятие».

Время: 90 мин.

Цель (обучающая, развивающая, воспитательная): научиться применять условие прочности при решении задач.

Форма отчета: тетрадь.

Рекомендуемая литература: А.И. Аркуша «Техническая механика».

1.      Что такое допускаемое напряжение и как оно выбирается в зависимости от свойств материалов?

2.      Как можно данную статически определимую систему превратить в статически неопределимую?

3.      На каких допущениях основаны расчеты на срез и смятие?

4.      Как определяется площадь смятия, если поверхность смятия: а) плоская;

б) цилиндрическая?

 

Указания к выполнению работы:

1.      Повторить по учебнику тему «Растяжение и сжатие».

2.      Выпишите данные для вашего варианта (согласно нумерации в журнале).

№ варианта	F, Кн	h, мм	№ варианта	F, Кн	h, мм	№ варианта	F, Кн	h, мм
1	3	3	11	3	3	21	3	3
2	4	4	12	4	4	22	4	4
3	5	5	13	5	5	23	5	5
4	6	6	14	6	6	24	6	6
5	7	7	15	7	7	25	7	7
6	3	3	16	3	3	26	3	3
7	4	4	17	4	4	27	4	4
8	5	5	18	5	5	28	5	5
9	6	6	19	6	6	29	6	6
10	7	7	20	7	7	30	7	7

 

3.      Рассмотрите пример решения.

Пример. Проверить прочность стержня на растяжение его головки на срез и опорной поверхности под головкой на смятие, если допускаемые напряжения

 

 [σ_р] = 110 Н/мм², [τ_ср] = 60 Н/мм²  и  [σ_см] = 120 Н/мм²  .

 

 

 

 

 

 

 

 

Решение

1.     Диаметр стержня   d = 5 мм, следовательно, площадь поперечного сечения стержня

 

A = p d²/4 = p 5²/4 = 19, 6 мм²,

 

а нормальная сила в этом сечении N = F = 2 кН = 2000 Н.

 

Рабочее напряжение в поперечном сечении

 

s = N/ A = 2000 / 19, 6 = 102 Н/ мм²  < [σ_р].

 

2.     Головка стержня может быть срезана по цилиндрической поверхности диаметром  d = 5 мм и высотой  h = 2 мм,

т.е. A_ср = p dh = p 5× 2 = 31, 4 мм ².

 

         Следовательно,  при  Q = F рабочее напряжение среза

 

[τ_ср] = Q / A_ср = 2000 / 31, 4 = 63, 7 Н/ мм ²  > [τ_ср].

 

Перегрузка составляет  [(63,7 – 60) / 60] × 100% = 6, 33 %, что не допустимо.  Необходимо, либо снизить нагрузку, либо взять стержень с более высокой головкой.

 

3.     Поверхность контакта между головкой стержня и опорой имеет форму плоского кольца, т.е. A _{см =} [p (D² – d²)] / 4.

  

           Рабочее напряжение определяем по формуле

 

               σ_см = ( F × 4) / [p (D² – d²)] = 2000 × 4 / [p (8² – 5²)] = 65 Н/ мм²   < [σ_см].

           

 

 

              (рис. 2.37, А. И. Аркуша).

 

 

4.      Решите свой вариант.

5.      Ответьте на вопросы.

6.      Сделайте вывод.

 

 

 

 

 

 

ИНСТРУКЦИОННО-МЕТОДИЧЕСКАЯ КАРТА

по выполнению практического задания № 20

 

Наименование предмета: «Техническая механика»

Тема: «Кручение»

Наименование работы: «Расчет на прочность и жесткость при кручении круглого бруса»

Время: 90 мин

Цель (обучающая, развивающая, воспитательная): научиться применять условие прочности при решении задач.

Форма отчета: тетрадь

Рекомендуемая литература: А.И. Аркуша «Техническая механика»

Контрольные вопросы:

1.  Дайте определение кручения .

2.  Как определяется полярный момент сопротивления?

3. От чего зависит значение касательного напряжения?

4. Запишите закон Гука при сдвиге.

5. Укажите зависимость между модулем упругости, модулем сдвига и коэффициентом 

    Пуассона.

 

Указания к выполнению работы:

 

1. Повторить по учебнику тему «Кручение»

2. Выпишите данные для вашего варианта (согласно нумерации в журнале)

 

№ варианта	P, кВт	n, об/мин	№ варианта	P, кВт	400	№ варианта	P, кВт	n, об/мин
1	60	400	11	80	600	21	60	400
2	70	500	12	90	700	22	70	500
3	80	600	13	60	400	23	80	600
4	90	700	14	70	500	24	90	700
5	60	400	15	80	600	25	60	400
6	70	500	16	90	700	26	70	500
7	80	600	17	60	400	27	80	600
8	90	700	18	70	500	28	90	700
9	60	400	19	80	600	29	60	400
10	70	500	20	90	700	30	70	500

 

3. Рассмотрите пример решения.

 

Пример. 

 

Определить диаметр вала для передачи мощности Р = 50 кВт при частоте вращения

 n = 300 об/мин, если [τ_к] = 30 Н/мм² и [φ ₀⁰] = 0,3 град/м, G = 0, 8·10 ⁶ Н/мм².

 

Решение. 1.  При передаче заданной мощности вал нагружен двумя скручивающимися моментами, каждый из которых определяют по формуле   T_вр = P/ω

 

 Так как ω = πn/30 и Р = 50 ·10³ Вт, то М₁  = М ₂ = Р/ω = 30 Р/πn = 30 · 50 · 10 ³ = 1590 Н · м.

 

2.   В любом сечении вала между приложенными к нему внешними моментами Т₁  и Т ₂   крутящий момент  М_к   равен любому из них, т. е.  М_к  = Т₁  =  Т ₂ = 1590  Н · м.

 

3. Определим диаметр d _п вала из условия прочности. Выразив крутящий момент  в Н · мм, по расчетной формуле    W = М_к /  [τ_к] находим требуемый полярный момент сопротивления:

 

              W_р  = М_к /  [τ_к] = 1590 ∙ 10³/ 30 = 53 ∙ 10³ мм.

 

Из формулы   W_р = πd³/ 16 находим диаметр вала, удовлетворяющий условию прочности:

             

               d _п  =  ³ √ 16 W_р / π =  ³√ 16  ∙ 53 ∙ 10³ / π = 10 ³√ 270 = 64, 6 мм.

 

     Округляя до целого числа мм, принимаем   d _п  = 65 мм.

4. Определяем диаметр  d_ж  вала из условия жесткости. По формуле [φ ₀⁰] = π / 180^o [φ ₀⁰]

    находим допускаемый угол закручивания:

 

               [φ ₀⁰] = π / 180^o [φ ₀⁰] = π ∙ 0,3 / 180 = 5, 23 ∙ 10^-3 рад/ мм.

 

По расчетной формуле  J_р = М_к / G [φ ₀]  находим требуемый полярный момент инерции сечения:

 

               J_р = М_к / (G [φ ₀]) = 1590 ∙ 10³ / (0, 8 ∙10⁵ ∙ 5, 23 ∙10^-4) = 380 ∙  10⁴ мм⁴.

 

Из формулы   J_р =  πd⁴/ 32

 

находим диаметр вала, удовлетворяющий условию жесткости:

 

              d_ж = ⁴√ 32 J_р / π =  ⁴√ 32 ∙  380 ∙ 10⁴ / π = 79 мм.

 

Принимаем  d_ж = 80 мм.

 

5. Из двух найденных значений диаметра вала необходимо взять большее, так как оно удовлетворяет обоим условиям, таким образом, конструктивный диаметр вала d = 80 мм.

 

 

4. Решите свой вариант.

5. Ответьте на вопросы.

6. Сделайте вывод.

 

Практическая работа № 21

Определение угловых и линейных скоростей и

ускоренных точек вращающегося тела

 

Тема: Кинематика. Вращательное движение твердого тела.

Цель работы: Научится определять угловые скорости и ускорения точек вращающегося, тела, а также их линейные скорости, касательное, нормальное и полное ускорение.

Задание: Движение груза задано уравнением у=f(t). Определить скорость и ускорение груза в момент времени t₁, а также скорость и ускорение точки В на ободе шкива. Данные для своего варианта принять по таблице.

 

Порядок выполнения

 

1. Изобразить в произвольном масштабе схему.

2. Для груза А изобразить вектор скорости и ускорения .

3. Из уравнения движения у=f(t) найти для груза скорость движения: 

и ускорение движения: .

4. Подставить в полученные выражения значения времени t, и найти численное значение скорости и ускорения.

5. Из условия совместимости движения троса с грузом и точек обода шкива при отсутствии проскальзывания определяем V_B=V_A;    

Откладываем на эскизе вектор  и .

6. Определяем угловую скорость шкива:      

7. Определение углового ускорения шкива:      

8. Определение нормального ускорения точки В:

9. Определение полного ускорения точки В:

10. Нанести векторы скорости ускорения точки В на эскиз.

11. Ответ.

12. Вывод.

 

Задания к практической работе № 21

Движение груза А, опускающегося при помощи лебедки, задано уравнением у=at²+bt+c, где у — в м, t — в с. Определить скорость и ускорение груза в момент времени t₁, а также скорость и ускорение точки В на ободе шкива (табл.)

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант задания	1 11 21	2 12 22	3 13 23	4 14 24	5 15 25	6 16 26	7 17 27	8 18 28	9 19 29	10 20 30
а, м/с2	2	0	3	0	3	3	2	0	4	0
b, м/с	0	3	4	2	0	4	0	3	4	2
c, м	3	4	0	5	2	0	4	2	0	3
r, м	0,5	0,8	0,8	0,8	0,5	0,5	0,4	0,6	0,8	0,5
t1, с	1,5	1	1,5	2	1,5	1	1,5	1	1,5	1

 

Критерии оценок при выполнении практических:  «Отлично»

- успешное и систематическое применение навыков, сформированное умение использовать полученные знания при овладении математическими  умениями, владении  навыками познавательной, учебно-исследовательской и проектной деятельности. «Хорошо» -   в целом успешное, но содержащее определенные пробелы применения навыков,  студент совершает незначительные ошибки, погрешности, и после замечаний может самостоятельно их исправить.

«Удовлетворительно» -  в целом успешное, но не систематическое применение навыков,  при выполнении  работ студенту необходима помощь преподавателя, возможность пользоваться учебником и тетрадью, справочными таблицами и т.д.

«Неудовлетворительно» - фрагментарные  умения, навыки; студент  не может выполнить  задание, не умеет пользоваться учебником, справочной литературой.

 

 

 

 

СПИСОК ЛИТЕРАТУРЫ

 

1.                  1.                                                                                                              Сорокин Н.П., Ольшевский Е.Д., Заикина А.Н., Шибанова Е.И. Инженерная графика. Учебник. 4-е изд., стер. — СПб.: Издательство «Лань», 2017. — 400 с.

2.                  Боголюбов С.К. Индивидуальные задания по курсу черчения Учебное пособие для средних специальных учебных заведений. 3-е изд. М.: ООО ИД "Альянс", 2017. - 368 с.

3.                  Куликов В.П., Кузин А. В.. Инженерная графика Учебник для учреждений СПО - 3-е изд., испр. - Москва: ФОРУМ, 2016. - 368 с.

4.                  Куликов В.П. Стандарты инженерной графики. 3-е издание Профессиональное образование Издательство: Форум, 2016 г. , 240 с.

5.                  Краснов М.Н. Руководство для выполнения заданий по инженерной и компьютерной графике. Учебное пособие - Пенза: Изд-во Пенз. гос. ун-та, 2017. - 116 с.

Дополнительные источники:

1.                  Апатов К.Ю., Иванова-Польская В.А. Практикум по начертательной геометрии и инженерной графике Киров: Изд-во ВятГУ, 2017. - 76 с.

2.                  Бударин А.М. и др. Сборочные чертежи машиностроительных изделий

Сборочные чертежи машиностроительных изделий: методические указания для студентов машиностроительных специальностей / сост. А. М. Бударин, Г. М. Горшков, Д. А. Коршунов. - Ульяновск: УлГТУ, 2017. - 22 с.

3.                  Горшков Г.М., Бударин А.М. Справочные материалы по инженерной графике Ульяновск: Ул- ГТУ, 2016. – 55 с.

4.                  Войцехович И.В., Гуща Ю.А. Инженерная графика .Методические указания- Выполнение чертежей железобетонных конструкций. Могилев: ГУ ВПО "Белорусско- Российский университет",2017 г, -13 с.

5.                  Абрамов А.Е. Учебно-методический комплекс по дисциплине: Компьютерная графика. Учебно-методический комплекс по дисциплине: Компьютерная графика\Абрамов А. Е. Ульяновск: ФГОУ ВПО Ульяновская ГСХА, 2016- 50 с.

6.                  Электронные ресурсы «Инженерная графика». Форма доступа: www.Ing-Grafika.ru

 

Скачано с www.znanio.ru