
 МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РЕСПУБЛИКИ САХА (ЯКУТИЯ)
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РЕСПУБЛИКИ САХА (ЯКУТИЯ)
ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ
ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
РЕСПУБЛИКИ САХА (ЯКУТИЯ)
РАССМОТРЕНО И РЕКОМЕНДОВАННО .
К ИСПОЛЬЗОВАНИЮ на заседании кафедры/МО «_________»
Протокол №_____________ от
«_____»______________________2022 г.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по выполнению индивидуальных практических заданий по разделу «Основы тригонометрии» общеобразовательной дисциплины «Математика»
Составитель:
преподаватель естественно-научных дисциплин Москалёва А.М.
Мирный
2022 год
Аннотация
Методические указания содержат краткий теоретический материал (понятия, схемы, таблицы, формулы, графики), задачи и упражнения по всем основным темам раздела «Тригонометрия» Подробные решения примеров помогут студентам при подготовке к практическим, лабораторным занятиям, при сдаче зачетов и экзаменов, а также для выполнения самостоятельных работ. Индивидуальные задания по каждой теме являются обязательными зачетными работами. Номер индивидуального задания соответствует номеру зачетной работы. Каждому индивидуальному заданию соответствуют практические задания (далее – номер). В каждом номере предусмотрены 30 вариантов практических заданий. Номер может служить вариантом индивидуальной работы студента.
Пояснительная записка
Дисциплина «Математика» входит в состав общих общеобразовательных учебных дисциплин, формируемых из обязательных предметных областей ФГОС среднего общего образования, для профессий СПО или специальностей СПО соответствующего профиля профессионального образования, и играет ведущую роль в общей и профессиональной системах образования студентов среднего профессионального образования.
Содержание программы «Математика» направлено на достижение следующих целей:
• обеспечение сформированности представлений о социальных, культурных и исторических факторах становления математики;
• обеспечение сформированности логического, алгоритмического и математического мышления;
• обеспечение сформированности умений применять полученные знания при решении различных задач;
• обеспечение сформированности представлений о математике как части общечеловеческой культуры, универсальном языке науки, позволяющем описывать и изучать реальные процессы и явления.
Раздел «Основы тригонометрии» (темы в отношении тригонометрических функций), включенные в содержание учебной дисциплины и отраженные в практических заданиях данного методического пособия, являются общими для всех профилей профессионального образования и при всех объемах учебного времени независимо от того, является ли учебная дисциплина «Математика» базовой или профильной.
Наряду с обеспечением высокой математической подготовки обучающихся, которые в дальнейшем в своей профессиональной деятельности будут пользоваться математическими знаниями и навыками, важнейшей задачей обучения является обеспечение некоторого гарантированного уровня математической подготовки независимо от специальности.
Федеральный государственный образовательный стандарт третьего поколения среднего профессионального образования подразумевает компетентностный подход в обучении. Основной задачей преподавателя является не передача, "трансляция" знаний, а формирование у обучающихся профессиональных компетенций, методов и способов самостоятельного поиска и получения новых знаний, умения применять теоретические знания при решении практических задач. При изучении дисциплины «Математика» наибольшие трудности у студентов возникают при решении практических задач. Вместе с тем именно решение задач в значительной степени способствует развитию технического, инженерного мышления.
Целью данного пособия является помощь студенту в организации его практической зачетной работы по разделу дисциплины «Основы тригонометрии». В методических указаниях представлены все темы практических работ раздела «Основы тригонометрии», способствующие оценки качества обученности по предметным результатам в отношении дидактических единиц раздела:
|
Содержание обучения (ДЕ) по разделу «Основы тригонометрии» |
Характеристика основных видов деятельности студентов (на уровне учебных действий) |
|
Основные понятия |
Изучение радианного метода измерения углов вращения и их связи с градусной мерой. Изображение углов вращения на окружности, соотнесение величины угла с его расположением. Формулирование определений тригонометрических функций для углов поворота и острых углов прямоугольного треугольника и объяснение их взаимосвязи |
|
Основные тригонометрические тождества |
Применение основных тригонометрических тождеств для вычисления значений тригонометрических функций по одной из них |
|
Преобразования простейших тригонометрических выражений |
Изучение основных формул тригонометрии: формулы сложения, удвоения, преобразования суммы тригонометрических функций в произведение и произведения в сумму и применение при вычислении значения тригонометрического выражения и упрощения его. Ознакомление со свойствами симметрии точек на единичной окружности и применение их для вывода формул приведения |
|
Тригонометрические уравнения и неравенства |
Решение по формулам и тригонометрическому кругу простейших тригонометрических уравнений. Применение общих методов решения уравнений (приведение к линейному, квадратному, метод разложения на множители, замены переменной) при решении тригонометрических уравнений. Умение отмечать на круге решения простейших тригонометрических неравенств |
|
Арксинус, арккосинус, арктангенс числа |
Ознакомление с понятием обратных тригонометрических функций. Изучение определений арксинуса, арккосинуса, арктангенса числа, формулирование их, изображение на единичной окружности, применение при решении уравнений |
|
Тригонометрические функции. Обратные тригонометрические функции |
Ознакомление с понятием непрерывной периодической функции, формулирование свойств синуса и косинуса, построение их графиков. Ознакомление с понятием гармонических колебаний и примерами гармонических колебаний для описания процессов в физике и других областях знания. Ознакомление с понятием разрывной периодической функции, формулирование свойств тангенса и котангенса, построение их графиков. Применение свойств функций для сравнения значений тригонометрических функций, решения тригонометрических уравнений. Построение графиков обратных тригонометрических функций и определение по графикам их свойств. Выполнение преобразования графиков |
В настоящих методических указаниях дан краткий теоретический материал, необходимый для выполнения заданий, и подробно рассмотрены решения типовых заданий, а также изложены требования к выполнению и оформлению индивидуальных практических работ. Индивидуальные задания по каждой теме являются обязательными зачетными работами. Номер индивидуального задания соответствует номеру зачетной работы. Каждому индивидуальному заданию соответствуют практические задания (далее – номер). В каждом номере предусмотрены 30 вариантов практических заданий. Номер может служить вариантом индивидуальной работы студента.
Содержание.
§ 1. Единичная тригонометрическая окружность. Тригонометрические функции числового аргумента. Основные формулы тригонометрии………....4 6
ИЗ №1…………………………………………………………..……Индивидуальные практические задания №1 …………….9 12
§2. Тригонометрические функции, их свойства и графики. Построение графиков тригонометрических функций с помощью геометрических преобразований графиков…………………………………………….................17 19
2.1. Тригонометрические функции, их свойства и графики………………..…17 19 2.2. Построение графиков тригонометрических функций с помощью геометрических преобразований графиков……………………….…………...19 21
Индивидуальные практические задания №2ИЗ №2…………………………………………………………………………….27 29
§ 3. Обратные тригонометрические функции…………………………………30 32
Индивидуальные практические задания №3ИЗ №3…………………………………………………………………………….33 35
§ 4. Тригонометрические уравнения…………………………………………....36 38
4.1. Простейшие тригонометрические уравнения……………………….….....36 38
4.2. Тригонометрические уравнения, приводимые к квадратным……………..37 39
4.3. Однородные тригонометрические уравнения……………………...….….38 40
4. 4.Решение тригонометрических уравнений, введением вспомогательного
угла……………………………………………………39 42
4.5. Решение тригонометрических уравнений, используя формулы преобразования произведения в сумму и обратно…………………….………40 42
4.6.Решение тригонометрических уравнений с помощью универсальной
подстановки……………………………………………………………….….…..41 43
ИЗ №4…………………………………………………………...……………….42 44
Индивидуальные практические задания №4
§ 5. Тригонометрические неравенства…………………………………….…...47 50
5.1 . Неравенства вида sin x a, sin x a, sin x a, sin x a…………….…….48 50
5.2. Неравенства вида cosx a, cosx a, cosxa, cosxa…….……….........50 52
5.3. Неравенства вида tgx a, tgx a, tgx a, tgx a……….……...………....52 54 5.4. Неравенства вида ctgx a, ctgx a, ctgx a, ctgx a………………….…54 56
ИЗ №5……………………………………………………………………Индивидуальные практические задания №5 ……….56 58
3
§ 1. Единичная тригонометрическая окружность.
Тригонометрические функции числового аргумента.
Основные формулы тригонометрии.
Единичная тригонометрическая окружность – это окружность, с радиусом 1 и центром в начале координат.
Горизонтальный (ось Ох) и вертикальный (ось Оу) диаметры делят числовую окружность на четыре четверти.
Начальная точка А единичной тригонометрической окружности находится на оси x и имеет координаты (1; 0).
Отсчет по единичной тригонометрической окружности может вестись как по часовой стрелке, так и против часовой стрелки.
Отсчет от точки А против часовой стрелки называется положительным направлением. Отсчет от точки А по часовой стрелке называется отрицательным направлением.
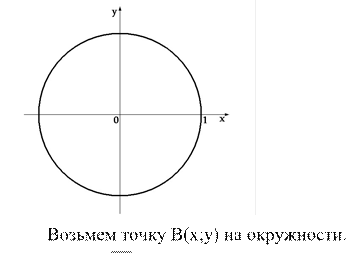
Вектор OB, соединяющий начало координат с произвольно выбранной точкой плоскости В(х,y), называется радиус-вектором этой точки . Опустим перпендикуляры на оси координат. Проекции точки В(х;у) на оси координат равны х и у соответственно. Рассмотрим прямоугольный треугольник ОАВ.
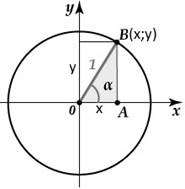 OA x AB y
OA x AB y
![]()
![]() cos
x;
sin
y
cos
x;
sin
y
OB 1 OB 1
4
Синус угла , образованного радиус-вектором точки на единичной окружности с положительным направлением оси Ox, есть ордината этой точки, т.е. : sin y.
Косинус угла , образованного радиус-вектором точки на единичной окружности с положительным направлением оси Ox, есть абсцисса этой точки: cos y.
Синус и косинус определены для любого угла и связаны между собой (по теореме Пифагора) равенством: sin2cos21, которое называется основным тригонометрическим тождеством.
Отношение синуса угла к косинусу того же угла называется
тангенсом
угла : tg
![]() sin
или tg
sin
или tg
![]() y .
y .
cos x
Тангенс
определен для всех углов, кроме ![]() n,
nZ
,
где
n,
nZ
,
где
2
cos![]() n
0,
Z
- множество целых чисел.
n
0,
Z
- множество целых чисел.
2
Отношение косинуса угла к синусу угла называется котангенсом
угла
:
tg
![]() cos
или tg
cos
или tg
![]() x . sin y
x . sin y
Котангенс определён для всех углов, кроме n, nZ , где sinn 0, Z - множество целых чисел.
![]() Так как точка В лежит на
единичной тригонометрической окружности 1
x
1,
1
y
1.
Следовательно, sin1,
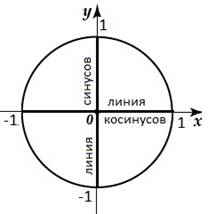
cos1. Отрезок на оси Оx от -1 до 1 называется линией
косинусов.
Так как точка В лежит на
единичной тригонометрической окружности 1
x
1,
1
y
1.
Следовательно, sin1,
cos1. Отрезок на оси Оx от -1 до 1 называется линией
косинусов.
Отрезок на оси Оy от -1 до 1 называется линией синусов.
![]()
![]() AB y sin
OA x cos
tg
, cos
0, ctg
, sin
0.
AB y sin
OA x cos
tg
, cos
0, ctg
, sin
0.
OA x cos AB y sin
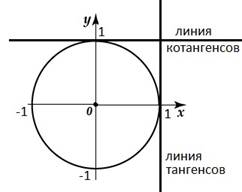
Линия тангенсов параллельна оси Оy и проходит через точку (1;0)
Линия котангенсов параллельна оси Оx и проходит через точку (0;1)
5
Радианная мера угла.
Угол в 1 радиан – центральный угол, длина дуги которого равна радиусу окружности. Радианная и градусная меры связаны зависимостью 1800 радиан.
1радиан
180![]() 0 , 10
0 , 10
![]() радиан.
радиан.
180
Периодичность тригонометрических функций .
Период косинуса равен 2: сos(2n) cos.
Период синуса равен 2:sin(2n) sin.
Период тангенса равен :tg(n) tg. Период котангенса равен :ctg(n) ctg.
Четность и нечетность тригонометрических функций. сos() cos, sin() sin, tg() tg, ctg() ctg
![]() Знаки
тригонометрических функций.
Знаки
тригонометрических функций.
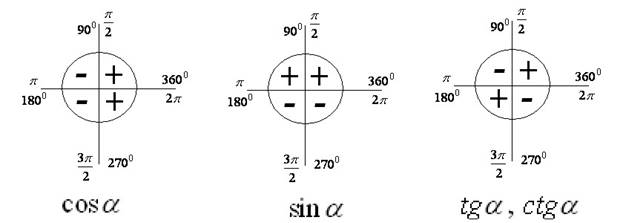
Значения тригонометрических функций при некоторых углах.

6
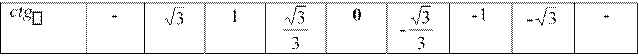
Формулы приведения.
|
Функции |
|
У |
гол |
|
|
2 |
|
3
2 |
2 |
|
|
sin |
cos |
m sin |
-cos |
sin |
|
cos |
m sin |
-cos |
sin |
cos |
|
tg |
m ctg |
tg |
m ctg |
tg |
|
ctg |
m tg |
ctg |
m tg |
ctg |
Основные тригонометрические тождества.
cos2sin21,
1tg2
![]() cos12 ,
1ctg2
cos12 ,
1ctg2
![]() sin12,
sin12,
tg
![]() sin,
ctg
sin,
ctg
![]() cos,
ctg
cos,
ctg ![]() 1 . cos sin tg
1 . cos sin tg
Формулы для суммы и разности элементов.
sin()
sincoscossin,
sin()
sincoscossin,
cos()
coscossinsin,
cos()
coscossinsin,
tg()
![]() tgtg
,
tg()
tgtg
,
tg()
![]() tgtg
,
tgtg
,
1tgtg 1tgtg
ctg()
![]() ctgctg1,
ctg()
ctgctg1,
ctg()
![]() ctgctg1.
ctgctg1.
ctg ctg ctgctg
Формулы двойных, тройных и половинных аргументов. sin2 2sincos, cos2 cos2sin212sin2 2cos21,
tg2
1![]() 2tg2 ,
ctg2
2tg2 ,
ctg2
![]() ctg2ctg21,
sin2
1
ctg2ctg21,
sin2
1![]() cos2
2, cos2
1
cos2
2, cos2
1![]() cos2
2,
cos2
2,
![]() tg sin2
1cos2,
tg sin2
1cos2,
1cos2 sin2
sin33sin4sin3, cos3 4cos34cos.
Формулы преобразования произведения в сумму и обратно.
sincos
![]() sin()
sin(),
coscos
sin()
sin(),
coscos
![]() cos()
cos(),
cos()
cos(),
sinsin
![]() cos()cos().
cos()cos().
![]()
![]() sin
sin
2sincos coscos
2coscos
sin
sin
2sincos coscos
2coscos
2 2 2 2
![]()
![]() sinsin
2sincos coscos
2sinsin
sinsin
2sincos coscos
2sinsin
2 2 2 2
7
Примеры.
1.
![]()
![]()
![]() Выразите в радианной мере величины углов: 500,
2160,
720. Решение:500
50
5, 2160
216
6, 720
72
2.
Выразите в радианной мере величины углов: 500,
2160,
720. Решение:500
50
5, 2160
216
6, 720
72
2.
180 18 180 5 180 5
2.
![]() Выразите
в градусной мере величины углов: 7,
5,
0,2.
Выразите
в градусной мере величины углов: 7,
5,
0,2.
12 4
![]()
![]()
![]() Решение:
7
71800
0, 5
51800
2250, 0,2
1800
360 105
Решение:
7
71800
0, 5
51800
2250, 0,2
1800
360 105
12 12 4 4 5 5
3. Приведите тригонометрическую функцию произвольного аргумента к
тригонометрической функции острого угла: sin4050,
tg8630,
cos18![]() ,
,
5
21
ctg ![]() .
.
4
Решение: sin4150
sin(3600 550)
sin550,
tg8630
tg51800 370
tg370
tg370, cos18![]()
cos4
cos4
![]() 2
cos
2
cos ![]() 2
cos
2
cos ![]() 2,
2,
5 5 5 5
ctg
![]() 21
ctg5
21
ctg5![]()
ctg
ctg ![]() 5.
5.
4 4 4
4. Найдите значения других трех основных тригонометрических функций,
3 3
если sin
![]() ,
, ![]() .
.
5 2
![]() Решение: Из
основного тригонометрического тождества получим cos
1sin2
. Угол :
Решение: Из
основного тригонометрического тождества получим cos
1sin2
. Угол :
![]() 3
находится в III четверти, 2
3
находится в III четверти, 2
следовательно cos 0, tg 0, ctg 0. Таким образом,
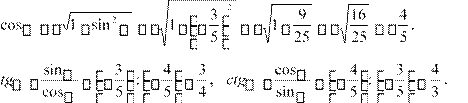
5.
Упростите выражение 1![]() coscos2. sin2sin
coscos2. sin2sin
Решение:
![]() 1cos
cos2
1cos
2cos21
2cos2cos
cos2cos1
1cos
cos2
1cos
2cos21
2cos2cos
cos2cos1
sin2sin 2sincossin sin2cos1 sin2cos1
![]() sin
tg.
sin
tg.
cos
8
6. Упростите выражение
2 2
![]()
![]() sin
3cos
2
cos
3sin
2
cos cos
3sin
sin
3
.
sin
3cos
2
cos
3sin
2
cos cos
3sin
sin
3
.
10 5 10 5 10 5 10 5
Решение:
![]()
![]() sin
3cos
2
cos
3sin
22
cos
cos
3sin
sin
32
sin
3cos
2
cos
3sin
22
cos
cos
3sin
sin
32
10 5 10 5 10 5 10 5
2 2
![]()
![]() sin310
25
cos10
35
sin2
sin310
25
cos10
35
sin2 ![]() 710
cos2
710
cos2 ![]() 710
1.
710
1.
7.
![]() Докажите
тождество tgtg
tgtg
2. tg tg
Решение:
Докажите
тождество tgtg
tgtg
2. tg tg
Решение:
tgtg tgtg tgtg tgtg
![]()
tgtg:
tgtg: ![]() tgtg:
tgtg: ![]()
tg tg 1tgtg 1tgtg
tgtg 1tgtg tgtg 1tgtg
![]() 1tgtg1tgtg
2.
1tgtg1tgtg
2.
1 tgtg 1 tgtg
ИЗ №Индивидуальные практические задания №1 1.
1. Выразите в радианной мере величины углов.
1.1. 100, 135 0, 600; 1.15. 450, 160 0, 750;
1.2. 180, 150 0, 900; 1.16. 2160, 150, 600;
1.3. 300, 144 0, 1300; 1.17. 1300, 720, 1800;
1.4. 540, 135 0, 360; 1.18. 540, 1200, 1500;
1.5. 150, 120 0, 1800; 1.19. 180, 1080, 300;
1.6. 200, 125 0, 360; 1.20. 2520, 450, 2400;
1.7. 400, 225 0, 300; 1.21. 2100, 150, 600;
1.8. 450, 240 0, 180; 1.22. 500, 1440, 1200;
1.9. 360, 150 0, 2100; 1.23. 1080, 1350, 3000;
1.10. 600, 72 0, 2520; 1.24. 300, 3150, 360;
1.11. 720, 108 0, 2700; 1.25. 100, 2160, 180;
1.12. 1200, 135 0, 1440; 1.26. 550, 150 0, 1350;
1.13. 750, 2100, 360; 1.27. 720, 540, 300;
1.14. 1000, 540, 900; 1.28. 600, 75 0, 1440;
9
1.29. 2100, 500, 900 1.30. 150, 3000, 1000.
2. Выразите в градусной мере величины углов.
![]()
![]() 2.1. 7,
,
0,3; 2.16. 5,
,
0,4
2.1. 7,
,
0,3; 2.16. 5,
,
0,4
6 5 3 3
![]()
![]() 2.2. 5,
7,
0,2; 2.17. 19,
7,
1,1
2.2. 5,
7,
0,2; 2.17. 19,
7,
1,1
18 9 36 6
![]()
![]() 2.3. 5,
11,
1,4; 2.18. ,
13,
1,25
2.3. 5,
11,
1,4; 2.18. ,
13,
1,25
9 18 3 18
![]()
![]() 2.4. 5,
4,
1,5; 2.19. 11,
3,
1,125
2.4. 5,
4,
1,5; 2.19. 11,
3,
1,125
36 5 6 5
![]()
![]() 2.5. 7,
2,
0,8; 2.20. 4,
29,
0,6
2.5. 7,
2,
0,8; 2.20. 4,
29,
0,6
9 3 5 36
![]()
![]() 2.6. 7,
5,
1,7; 2.21. 19,
5,
1,8
2.6. 7,
5,
1,7; 2.21. 19,
5,
1,8
36 18 18 9
![]()
![]() 2.7. 2,
4,
0,25; 2.22. 5,
,
0,3
2.7. 2,
4,
0,25; 2.22. 5,
,
0,3
3 5 36 4
![]()
![]() 2.8. 8,
,
0,125; 2.23. 11,
3,
0,9
2.8. 8,
,
0,125; 2.23. 11,
3,
0,9
9 6 18 4
![]()
![]() 2.9. ,
6,
0,6; 2.24. 23,
4,
1,7
2.9. ,
6,
0,6; 2.24. 23,
4,
1,7
18 5 36 9
![]()
![]() 2.10. ,
11,
1,4 2.25. 2,
11,
1,4
2.10. ,
11,
1,4 2.25. 2,
11,
1,4
9 36 5 9
![]()
![]() 2.11. 3,
2,
0,5 2.26. 17,
,
1,2
2.11. 3,
2,
0,5 2.26. 17,
,
1,2
4 9 36 5
![]()
![]() 2.12. 2,
5,
0,9 2.27. 8,
19,
0,1
2.12. 2,
5,
0,9 2.27. 8,
19,
0,1
5 9 9 36
![]()
![]() 2.13. 4,
3,
0,7 2.28. 5,
3,
1,25
2.13. 4,
3,
0,7 2.28. 5,
3,
1,25
9 5 18 4
![]()
![]() 2.14. 7,
13,
1,2 2.29. 13,
11,
0,4
2.14. 7,
13,
1,2 2.29. 13,
11,
0,4
18 36 9 36
![]()
![]() 2.15. 17,
2,
1,3 2.30. ,
5,
1,46
2.15. 17,
2,
1,3 2.30. ,
5,
1,46
36 5 18 9
3. Приведите тригонометрическую функцию произвольного аргумента к тригонометрической функции острого угла:
3.1.
sin3400,
cos11![]() ,
tg(5230),
ctg 18
,
tg(5230),
ctg 18![]() ;
;
9 7
10
3.2.
cos2950,
sin13![]() ,
ctg4470, tg 11
,
ctg4470, tg 11![]() ;
;
8 6
3.3.
sin(3050),
cos15![]() ,
tg3920, ctg17
,
tg3920, ctg17![]() ;
;
8 6
3.4.
sin(2670),
cos13![]() ,
ctg(6820),
tg11
,
ctg(6820),
tg11![]() ;
;
3 5
3.5.
cos(3050),
sin17![]() ,
ctg2870,
tg
,
ctg2870,
tg
![]() 9;
9;
4 5
3.6.
cos3650,
sin13![]() ,
tg(4510),
ctg
,
tg(4510),
ctg ![]() 7;
7;
4 5
3.7.
sin(3190),
cos15![]() ,
ctg(3410),
tg12
,
ctg(3410),
tg12![]() ;
;
7 5
3.8.
cos2790,
sin17![]() ,
tg7000, ctg10
,
tg7000, ctg10![]() ;
;
4 3
3.9.
sin3510,
cos17![]() ,
tg(5070),
ctg13
,
tg(5070),
ctg13![]() ;
;
4 3
3.10.
cos2840,
sin16![]() ,
tg(4510),
ctg 17
,
tg(4510),
ctg 17![]() ;
;
7 6
3.11.
sin(3530),
cos14![]() ,
ctg(6050),
tg 12
,
ctg(6050),
tg 12![]() ;
;
3 5
3.12.
cos(5000),
sin12![]() ,
tg(3610),
ctg 16
,
tg(3610),
ctg 16![]() ;
;
7 3
3.13.
cos4230,
sin11![]() ,
ctg(2350),
ctg 19
,
ctg(2350),
ctg 19![]() ;
;
4 6
3.14.
sin(2890),
cos16![]() ,
tg(5060),
ctg 12
,
tg(5060),
ctg 12![]() ;
;
5 5
3.15.
cos3040,
sin19![]() ,
tg(5210),
ctg 11
,
tg(5210),
ctg 11![]() ;
;
6 3
3.16.
sin3120,
cos15![]() ,
tg(4240),
ctg 12
,
tg(4240),
ctg 12![]() ;
;
9 5
3.17.
cos3120,
sin15![]() ,
ctg3080,
tg 10
,
ctg3080,
tg 10![]() ;
;
8 3
3.18.
sin(3160),
cos17![]() ,
tg2890,
ctg15
,
tg2890,
ctg15![]() ;
;
7 6
3.19.
sin(2090),
cos12![]() ,
ctg(6030),
tg14
,
ctg(6030),
tg14![]() ;
;
5 5
11
3.20.
cos(2350),
sin13![]() ,
ctg2470,
tg11
,
ctg2470,
tg11![]() ;
;
6 5
3.21.
cos2840,
sin11![]() ,
tg(5210),
ctg13
,
tg(5210),
ctg13![]() ;
;
4 5
3.22.
sin(3060),
cos14![]() ,
ctg(3110),
tg17
,
ctg(3110),
tg17![]() ;
;
5 6
3.23.
cos2990,
sin
![]() 21,
tg6000, ctg12
21,
tg6000, ctg12![]()
;
;
5 7
3.24.
sin4510,
cos17![]() ,
tg(5200),
ctg14
,
tg(5200),
ctg14![]() ;
;
6 5
3.25.
cos2860,
sin17![]() ,
tg(4230),
ctg 18
,
tg(4230),
ctg 18![]() ;
;
7 5
3.26.
sin(3440),
cos12![]() ,
ctg(6120),
tg 19
,
ctg(6120),
tg 19![]() ;
;
7 6
3.27.
cos(5010),
sin13![]() ,
tg(3450),
ctg 18
,
tg(3450),
ctg 18![]() ;
;
7 5
3.28.
cos4030,
sin15![]() ,
ctg(3350),
ctg 11
,
ctg(3350),
ctg 11![]() ;
;
4 5
3.29.
sin(2790),
cos13![]() ,
tg(5160),
ctg 11
,
tg(5160),
ctg 11![]() ;
;
5 5
3.30.
cos3340,
sin17![]() ,
tg(5520),
ctg 10
,
tg(5520),
ctg 10![]() .
.
6 3
4. Найдите значения других трех основных тригонометрических
функций, если
4.1.
![]() sin
12 ,
;
sin
12 ,
;
13 2
4.2.
cos
0,6, ![]() ; 2
; 2
4.3.
![]() sin
3 , 3
2;
sin
3 , 3
2;
5 2
4.4.
sin
0,8,
![]() 3;
2
3;
2
4.5.
cos
![]() 5 ,
5 ,
![]() 3;
3;
13 2
4.6.
![]() cos
12 , 3
2;
cos
12 , 3
2;
13 2
4.7.
sin
0,6,
![]() 3;
3;
2
4.8.
![]() sin
5
,
;
sin
5
,
;
13 2
4.9.
![]() cos
3 ,
;
cos
3 ,
;
5 2
4.10.
![]() sin
12
,
3
2;
sin
12
,
3
2;
13 2
4.11.
cos
0,8, ![]() ;
2
;
2
4.12.
sin
12![]() ,
,
![]() 3;
3;
13 2
12
4.13.
cos
0,6,
![]() 3;
4.22. sin
0,8,
3;
4.22. sin
0,8,
![]() ;
;
2 2
4.14.
![]()
![]() cos
4
,
;
4.23. cos
4 , 3
2;
cos
4
,
;
4.23. cos
4 , 3
2;
5 2 5 2
4.15.
sin
![]() 5 ,
5 ,
![]() 3;
4.24. sin
3;
4.24. sin
![]() 4 ,
4 ,
![]() 3;
3;
13 2 5 2
4.16.
![]() sin
3
,
;
4.25. cos
0,8,
sin
3
,
;
4.25. cos
0,8,
![]() 3;
3;
5 2 2
4.17.
cos
12![]() ,
,
![]() 3;
4.26. sin
3;
4.26. sin
![]() 3 ,
3 ,
![]() 3;
3;
13 2 5 2
4.18.
cos
![]() 3 ,
3 ,
![]() 3;
4.27. cos
3;
4.27. cos
![]() 4 ,
4 ,
![]() 3;
3;
5 2 5 2
4.19.
![]() sin
4
,
;
4.28. cos
0,8,
sin
4
,
;
4.28. cos
0,8,
![]() 3
2;
3
2;
5 2 2
4.20.
![]() sin
0,6,
sin
0,6,
![]() ;
4.29.
sin
4 , 3
2;
;
4.29.
sin
4 , 3
2;
2 5 2
4.21.
![]()
![]() cos
5 ,
; 4.30. cos
12 ,
.
cos
5 ,
; 4.30. cos
12 ,
.
13 2 13 2
5. Упростите выражение
5.1. sincos2 sin2; 5.10. cos2ctg2sin2sin2;
5.2. 1 cos1 cos; 5.11. cos2cos4sin4;
![]()
sin 5.12. sin2tg2sin2ctg;
5.3.
![]() 1 sin
; 1 2cos2
tg
1
cos 5.13.
1 sin
; 1 2cos2
tg
1
cos 5.13. ![]() ;
;
cossin
5.4.
1![]()
2sincos
cos; sin24
1
2 ; sincos 5.14.
2sincos
cos; sin24
1
2 ; sincos 5.14. ![]() tg
tg
cos
5.5.
![]() (1sin)(1sin)
; 1cos
cos2
cos 5.15.
(1sin)(1sin)
; 1cos
cos2
cos 5.15. ![]() ;
;
sin2sin
5.6.
1![]() sin2(costg)2;
5.16. ctg21cos2cos2;
sin2(costg)2;
5.16. ctg21cos2cos2;
cos2
5.17. tg2sin2tg2sin2;
5.7.
![]() tgβctgβ;
2 2
tgβctgβ;
2 2
5.18. 3sin 2cos 2sin3cos
;
5.8.
![]() 1sin22
tgctg
; costg
1sin22
tgctg
; costg
1
cos
5.19. ![]() ctgcos;
ctgcos;
5.9. 1sin21tg2; sin2
13
5.20. sin
cos2 sin2; 5.26. cos4sin4; 5.21. 1cos21ctg2; 5.27. ![]() 1sin2
;
1sin2
;
cossin
5.22.
![]() sinsin2ctgsin; 5.28. sin21ctgcos21tg;
sinsin2ctgsin; 5.28. sin21ctgcos21tg;
5.23.
![]() sin2
2ctg; 5.29.
sin2
2ctg; 5.29. ![]() cos4cos2sin4; cos
cos4cos2sin4; cos
5.24.
![]() sin1sin
cos22
; 5.30.
sin1sin
cos22
; 5.30. ![]() cos12cos
cos22.
cos12cos
cos22.
5.25.
![]() cos2 ;
cos2 ;
cossin
6. Упростить выражение.
6.1. sin2cos3cos2sin3sin;
6.2. sin2sin3cos2cos3cos5;
6.3.
![]() sin 2cos
cos
2sin;
sin 2cos
cos
2sin;
15 5 15 5
6.4.
![]() coscos
sinsin
;
coscos
sinsin
;
7 42 7 42
2
6.5.
![]() sincos
4
cossin
4
;
sincos
4
cossin
4
;
7 21 7 21
6.6.
![]() cos540 cos90 sin540 sin90 2
;
cos540 cos90 sin540 sin90 2
;
6.7. 2sin120 cos180 cos120 sin180;
6.8.
![]() cos6500coscos40800
cossin176500
sinsin8400
0 ;
cos6500coscos40800
cossin176500
sinsin8400
0 ;
sin17
6.9. sin xsin2xsin3xcos xcos2x;
6.10. sin380 cos120 cos380 sin1202 cos400 cos100 sin400 sin1002;
6.11. cos xsin2x sin xcos2xsin x;
6.12.
cos![]() xcos
xcos![]() x sin
x sin![]() xsin
xsin![]() x
x
![]() cos
cos![]() x;
x;
6.13. sin7sin4cos4cos7cos11;
6.14.
![]() cos4000
coscos131700
cossin104000sinsin131700
;
cos4000
coscos131700
cossin104000sinsin131700
;
sin10
6.15. sin7cos4sin4cos73sin11;
14
2
6.16.
![]() sincos
cossin
;
sincos
cossin
;
3 12 3 12
6.17.
![]() cos 2cos
5sin
2sin
5;
cos 2cos
5sin
2sin
5;
7 42 7 42
6.18.
![]() 2sin
2cos
cos
2sin
;
2sin
2cos
cos
2sin
;
5 15 5 15
6.19.
![]() coscos
sinsin
2
;
coscos
sinsin
2
;
5 20 5 20
6.20.
![]() sin1500
coscos102000cossin15500sinsin201000
;
sin1500
coscos102000cossin15500sinsin201000
;
cos5
6.21. sin1230 cos330 cos1230 sin3302;
6.22. sin2xcos3x2sin5xcos2xsin3x;
6.23.
![]() cos3900
coscos151200
cossin123900
sinsin151200
;
cos3900
coscos151200
cossin123900
sinsin151200
;
sin12
6.24. cos2,5xcos1,5x cos x sin1,5xsin2,5x;
6.25. sin350 cos100 cos350 sin100 2 cos150 cos100 sin150 sin100 2 ;
6.26. cos4xcos7xcos3xsin4xsin7x;
6.27. cos1040 cos140 sin1040 sin140 3;
6.28. sin280 cos120 cos280 sin120 sin400 ;
![]()
2
6.29.
![]() sin3800coscos121000
cossin384000
sinsin121000
;
sin3800coscos121000
cossin384000
sinsin121000
;
cos40
6.30. sin4xcos3xsin7xcos4xsin3x.
7. Докажите тождество.
7.1. sincos2 sincos2 2;
7.2.
ctg2
cos2
![]() sin12
sin2;
sin12
sin2;
7.3.
2sincoscos2
![]() sin4;
sin4;
7.4.
![]() 1 cosctg
sin; sin
1 cosctg
sin; sin
7.5.
![]() 1
cos
cos
tg;
2
1sin
1sin
1
cos
cos
tg;
2
1sin
1sin
7.6. 4cos2cossin sin4;
7.7.
![]() 1 sintg
cos; cos
1 sintg
cos; cos
15
7.8.
1![]()
cos2sin2
ctg;
cos2sin2
ctg;
1cos2sin2
7.9.
![]() sin
sin
cos
2ctg;
sin
sin
cos
2ctg;
1 cos 1cos
7.10.
1![]() cossin22costg2
cos2;
cossin22costg2
cos2;
7.11.
![]() 1
sin
1
;
tg
1
cos
sin
7.12.
1
sin
1
;
tg
1
cos
sin
7.12. ![]() 2sin21
cos
sin;
sincos
7.13.
2sin21
cos
sin;
sincos
7.13. ![]() cos3sin3sin
cos;
cos3sin3sin
cos;
1sincos
7.14. ctgcos![]() sincos2tg
cos2;
sincos2tg
cos2;
cos4sin4 1;
7.15. ![]()
cos2
7.16.
1![]()
sin2
cos2
tg;
sin2
cos2
tg;
1 sin2 cos2
7.17.
![]() 1sin2
2
1;
1sin2
2
1;
sin cos
7.18.
![]() 1 tgtg22 1ctgctg22
tg2;
1 tgtg22 1ctgctg22
tg2;
7.19. cos4sin4 cos2;
7.20.
![]() cos2
sin
cos; cossin
cos2
sin
cos; cossin
7.21.
tg2sin2
![]() cos12
cos2;
cos12
cos2;
7.22.
![]() 1
sin
ctg; sin
1
cos
1
sin
ctg; sin
1
cos
1 2sin2
7.23.
![]() sin
cos;
sin
cos
sin
cos;
sin
cos
7.24.
![]() sin22cossinsin
cos22
2cos;
sin22cossinsin
cos22
2cos;
7.25.
![]() cos2
2sin2
1
;
ctgtg
cos2
cos2
2sin2
1
;
ctgtg
cos2
7.26. sin2tg2sin2ctg tg;
7.27. cos2cos4sin4 sin2;
7.28.
![]() 1sin2
cos
sin;
sincos
1sin2
cos
sin;
sincos
7.29.
![]() 1 tgtg22
1ctgctg22
1;
1 tgtg22
1ctgctg22
1;
7.30. 1ctg2tg2cos2 ctg2.
16
§2. Тригонометрические функции, их свойства и графики.
Построение графиков тригонометрических функций с помощью геометрических преобразований графиков.
2.1. Тригонометрические функции, их свойства и графики.
Основными тригонометрическими функциями являются функции y=sin(x), y=cos(x), y=tg(x), y=ctg(x).
1. Функция y=sin(x). График функции y=sin(x) – синусоида:
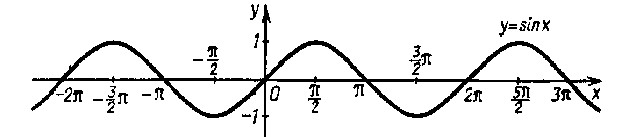
Основные свойства:
1. Область определения вся числовая ось.
2. Функция ограниченная. Множество значений – отрезок [-1;1].
3. Функция нечетная.
4.Функция периодическая с наименьшим положительным периодом равным 2π.
5. Нули функции: (πk;0) , где k – целое.
6. Интервалы знакопостоянства: sin x 0приx2n; 2n, nZ ; sin x 0приx 2n;2 2n, nZ .
2. Функция y= cos(x). График функции y= cos(x):
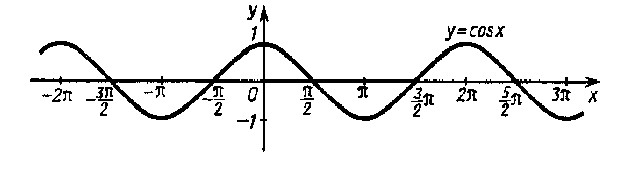
Основные свойства:
1. Область определения вся числовая ось.
2. Функция ограниченная. Множество значений – отрезок [-1;1].
3. Функция четная.
4.Функция периодическая с наименьшим положительным периодом равным 2π.
17
![]()
k;0,
где k – целое. 5. Нули функции: 2
k;0,
где k – целое. 5. Нули функции: 2
6. Интервалы знакопостоянства: cosx
0приx![]() 2
2n;
2
2n;![]() 2
2n,
nZ
;
2
2n,
nZ
;
cosx 0приx![]() 2
2n;
2
2n;![]() 32
2n,
nZ
.
32
2n,
nZ
.
3. Функция y=tg(x).
График функции y=tg(x) – тангенсоида:
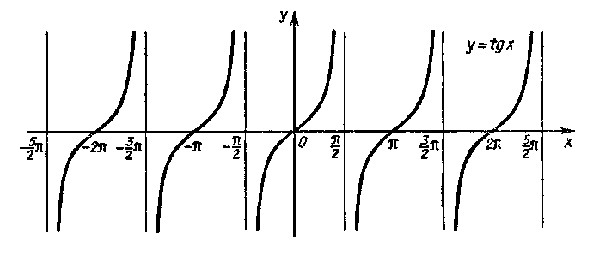
Основные свойства:
1. Область определения вся числовая ось, за исключением точек вида
x ![]() k
,
где k – целое.
k
,
где k – целое.
2
2. Функция неограниченная. Множество значение вся числовая прямая.
3. Функция нечетная.
4.Функция периодическая с наименьшим положительным периодом равным π.
5. Нули функции: (πk;0) , где k – целое.
6.
Интервалы
знакопостоянства: tgx 0приxn;![]() 2
n,
nZ
;
2
n,
nZ
;
tgx 0приx![]() 2
n;n,
nZ
.
2
n;n,
nZ
.
4. Функция y=ctg(x).
График функции y=ctg(x):
18
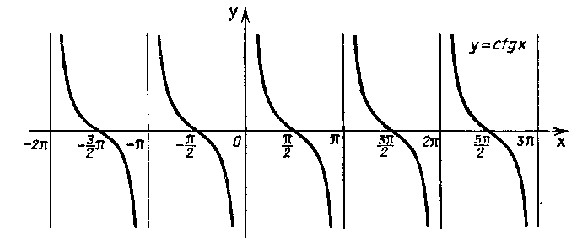
Основные свойства:
1. Область определения вся числовая ось, за исключением точек вида x=πk, где k – целое.
2. Функция неограниченная. Множество значение вся числовая прямая.
3. Функция нечетная.
4.Функция периодическая с наименьшим положительным периодом равным π.
![]()
k;0,
где k – целое.
k;0,
где k – целое.
5. Нули функции: 2
6.
Интервалы
знакопостоянства: ctgx 0приxn;![]() 2
n,
nZ
;
2
n,
nZ
;
ctgx 0при
x![]() 2
n;
2n,
nZ
.
2
n;
2n,
nZ
.
2.2. Построение графиков тригонометрических функций с помощью геометрических преобразований графиков.
Виды преобразований графиков функций.
1. Сжатие графика к оси ординат.
Правило: чтобы построить график функции f kx, где k 1, нужно график функции f x сжать к оси Оу в k раз.
Пример 1
Построить график функции y sin2x . Сначала строим график y sin x. Период T 2.
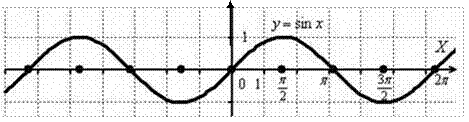
Сжимаем синусоиду к оси Оу в 2 раза:
19
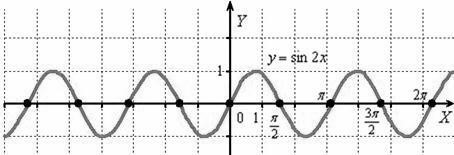
Таким образом, график функции y sin2x получается путём сжатия графика y sin x к оси ординат в два раза.
Период функции y sin2x равен.
В целях самоконтроля можно взять 2-3 значения «икс» и устно либо на черновике выполнить подстановку:
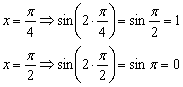
Смотрим на чертёж, и видим, что это действительно так.
Пример 2
Построить график функции y cos3x.
График функции y cos x сжимается к оси Оу в 3 раза:
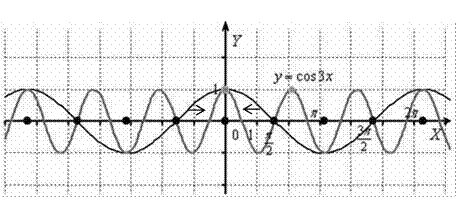
Период T функции y cos x равен 2, период функции y cos3x
2
составляет
![]() . 3
. 3
2. Растяжение графика функции от оси ординат
Правило: чтобы построить
график функции f
![]() 1 x
,
где k
1,
нужно
1 x
,
где k
1,
нужно
k
график функции f x растянуть от оси Оу в k раз.
Пример 3 Построить
график функции y sin
![]() x .
Строим 2
x .
Строим 2
график y sin x.
20
Период T 2.
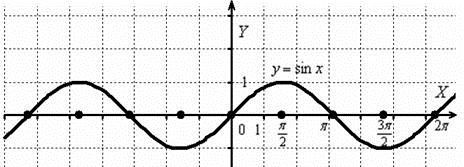
И растягиваем синусоиду от оси Оу в 2 раза:
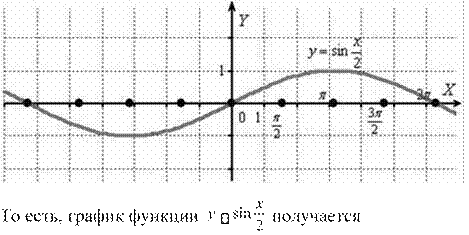
путём растяжения графика y sin x от оси ординат в два раза.
Период итоговой функции увеличивается в 2 раза: T 22 4.
3. Сдвиг графика влево/вправо вдоль оси абсцисс Если к аргументу функции добавляется постоянная, то происходит сдвиг (параллельный перенос) графика вдоль оси Ох.
Рассмотрим функцию y f (x) и положительное число b : Правило:
1) чтобы построить график функции y f (x b), нужно график y f (x) сдвинуть вдоль оси Ох на b единиц влево; 2) чтобы построить график функции y f (x b) , нужно график y f (x)сдвинуть вдоль оси ОХ на b единиц вправо. Пример 4
Построить график функции y
sinx
![]() .
.
2
График синуса y
sin
x
сдвинем вдоль оси Ох на ![]() влево:
влево:
2
21
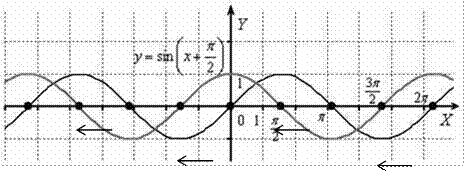
Внимательно присмотримся к полученному красному
графику y
sinx
![]() Это
в точности график косинуса y cos
x.
Мы
Это
в точности график косинуса y cos
x.
Мы
2
получили геометрическую иллюстрацию формулы
приведенияsinx
![]()
cos
x.
cos
x.
2
График функции y cos x получается путём сдвига
синусоиды y
sin
xвдоль
оси Ох на ![]() единиц влево. 2
единиц влево. 2
Рассмотрим композиционное правило, когда аргумент представляет собой линейную функцию: f (kxb), при этомk 0,b 0.
Функцию
f
(kxb)
необходимо представить в виде f (kxb)
f
kx
![]() bk
и последовательно выполнить следующие преобразования:
bk
и последовательно выполнить следующие преобразования:
1) График функции f (x) сжимаем (или растягиваем) к оси (от оси) ординат: f (kx).
2) График
полученной функции f (kx)
сдвигаем влево (или вправо) вдоль оси абсцисс на ![]() b
единиц, в результате чего будет построен k
b
единиц, в результате чего будет построен k
искомый график f (kxb). Пример 5
Построить график функции y
sin2x
![]()
2
Представим функцию в виде y
sin2x
![]() 4
и выполним следующие
4
и выполним следующие
преобразования: синусоиду y sin x сожмём к оси Оу в два раза: y sin2x.
2) сдвинем вдоль оси Ох на ![]() влево:
y
sin2x
влево:
y
sin2x
![]()
.
.
4 2
22
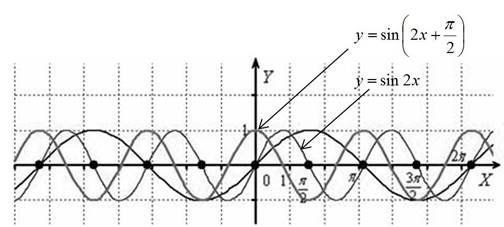
Пример, вроде бы, несложный, а сделать ошибку в параллельном
![]()
![]() .
переносе легко. График сдвигается на , а вовсе не на
.
переносе легко. График сдвигается на , а вовсе не на
4 2
4. Растяжение графика вдоль оси ординат.
Правило: чтобы построить график функции y mf (x), где m 1, нужно график функции y f (x) растянуть вдоль оси Оу в m раз.
Пример 6
Построить график функции y 2sin x. Строим график функции y sin x:
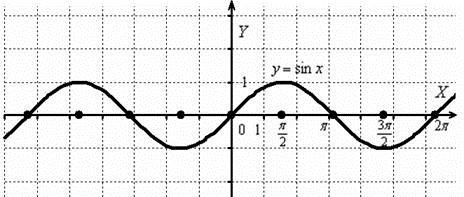
И вытягиваем синусоиду вдоль оси Оу в 2 раза:
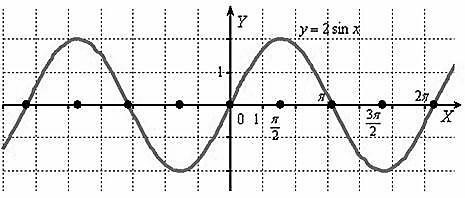
Период функции y 2sin x не изменился и составляет T 2, а вот
23
значения (все, кроме нулевых) увеличились по модулю в два раза. Область значений функции y 2sin x: E(y) 2;2.
5. Сжатие графика вдоль оси ординат.
Правило:
чтобы построить график функции y
![]() f (x)
,
где m
1,
m
f (x)
,
где m
1,
m
нужно график функции y f (x) сжать вдоль оси Оу вm раз.
Пример 7
Построить график функции y
![]() sin x.
sin x.
Строим график функции y sin x:
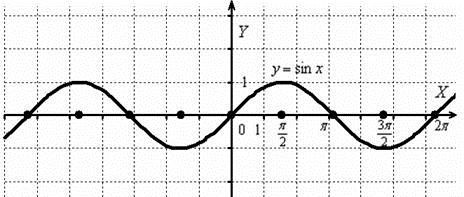
Теперь сжимаем синусоиду вдоль оси Оу в 2 раза:
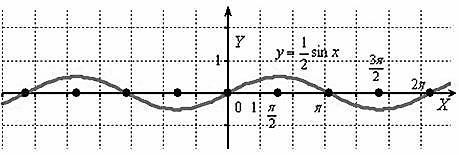
![]()
![]() Аналогично,
период T 2
не изменился, а область значений функции y sin
x:
E(y)
12;12
.
Аналогично,
период T 2
не изменился, а область значений функции y sin
x:
E(y)
12;12
.
6. Симметричное отображение графика относительно оси абсцисс
Правило: чтобы построить график функции y f (x), нужно график y f (x) отобразить симметрично относительно оси Ох.
Пример 8
Построить график функции y sin x.
Отобразим синусоиду симметрично относительно оси Ох:
24
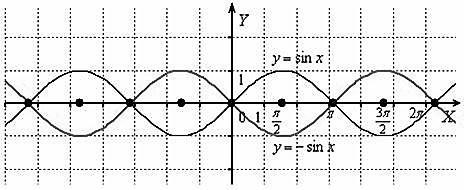
7. Сдвиг графика вверх/вниз вдоль оси ординат Правило:
1) чтобы построить график функции y f (x) c, нужно график y f (x) сдвинуть ВДОЛЬ оси Оу на c единиц вверх; 2) чтобы построить график функции y f (x)c, нужно график y f (x) сдвинуть ВДОЛЬ оси Оу на c единиц вниз.
Пример 9.
Построить графики функций y sin x 2, y sin x 1.
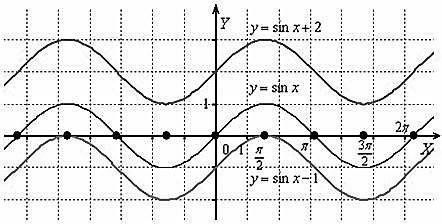
Комбинационное построение графика y mf (x) c в общем случае осуществляется очевидным образом:
1) График функции y f (x) растягиваем (сжимаем) вдоль оси Оу. Если множитель отрицателен, дополнительно осуществляем симметричное отображение относительно оси Ох.
2) Полученный на первом шаге график y mf (x) сдвигаем вверх или вниз в соответствии со значением константы c. Пример 10
Построить график функции y
![]() cos x
2
cos x
2
Строим график косинуса y cos x:
25
1)
Растягиваем
вдоль оси Оу в 1,5 раза: y ![]() cos x;
cos x;
2)
Сдвигаем
вдоль оси Оу на 2 единицы вниз: y
![]() cos x
2.
cos x
2.
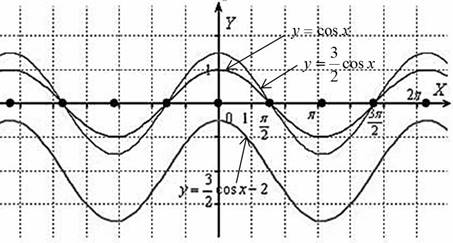
Общая схема построения графика функции с помощью геометрических преобразований
Рассмотрим функцию y mf (kxb)c, которая «базируется» на некоторой функции y f (x).
Для построения графика функции y mf (kxb) c
– на первом шаге выполняем преобразования, связанные с аргументом функции, в результате чего получаем график функции y f (kxb);
– на втором шаге выполняем преобразования, связанные с самой функцией, и получаем график функции y mf (kxb) c.
Пример 11. Найдите множество значений функции y 3sin 5x 0,1.
Решение:
Область значений функции y sin5x, как и функции y sin x равна 1;1. Так как при умножении на -3 происходит растяжение в 3 раза вдоль Оу графика функции y sin5x и симметричное отображение графика функции y 3sin5xотносительно оси абсцисс, область значений функции y 3sin5x - отрезок 3;3. А после сдвига вдоль Оу вниз на0,1 графика последней функции, получаем окончательный ответ 3,1;2,9.
Пример 12. Используя четностью/нечетность тригонометрических функций, исследовать на четностью/нечетность функцию
y(x)
![]() x sin
x .
x sin
x .
3cos x
26
Решение:
Поменяем знак аргумента, получим,
![]() y(x)
x sin(x)
x sin
x x
sin
x y(x),
следовательно функция
y(x)
x sin(x)
x sin
x x
sin
x y(x),
следовательно функция
3cos(x) 3cos x 3cos x нечетная.
Индивидуальные практические задания №2ИЗ № 2.
1. Построить график функции
1.1.
![]() y
sin2x
y
sin2x
![]() 1.17. 6
1.18. y
sin1
x
1.17. 6
1.18. y
sin1
x
1.2.
y cos2x
![]()
2 3
2 3
6
1.19. y
cos2x
![]() 5
5
1.3.
y sin3x
![]() 6
6
![]() 6
1.20. y
sin
1
x
6
1.20. y
sin
1
x
1.4.
![]() y
cos2x
y
cos2x
![]() 5
2
3
6 1.21. y
cos1
x
5
2
3
6 1.21. y
cos1
x
1.5.
y sin2x
![]()
2 3
2 3
![]() 3
1.22. y
sin1
x
3
1.22. y
sin1
x
1.6.
![]() y
cos
1
x 2
2 6
y
cos
1
x 2
2 6
![]()
2 3
1.23. y
cos1
x
2 3
1.23. y
cos1
x
1.7.
y sin2x
![]()
2 3
2 3
3
1.24. y
sin3x
![]()
1.8.
y cos3x
![]() 6
6
6
1.25. y
cos3x
![]()
1.9.
y sin2x
![]() 2 6
2 6
3
1.26. y
cos2x
![]()
1.10.
![]() y
cos
1
x 2 3
y
cos
1
x 2 3
![]()
2 3
1.27. y
sin
1
x 2
2 3
1.27. y
sin
1
x 2
1.11.
y sin2x
![]() 2
2 3
2
2 3
![]() 3
1.28. y
sin1
x 2
3
1.28. y
sin1
x 2
1.12.
![]() y
cos1
x 5
2 3
y
cos1
x 5
2 3
![]()
2 6
1.29. y
cos1
x
2 6
1.29. y
cos1
x
1.13.
y sin3x
![]() 5
2 6
5
2 6
![]() 6
1.30. y
sin
1
x 5
6
1.30. y
sin
1
x 5
1.14.
y cos3x
![]()
2 6
2 6
6
1.31. y
cos2x
![]() 2
2
1.15.
y sin2x
![]() 5 3
5 3
6
1.16.
y cos2x
![]()
6
27
2.
Построить
график функции. 2.1. y
2sinx
![]()
6
2.2.
y 3cosx
![]() 2
2
3
2.3.
y 2sinx
![]()
6
2.4.
y ![]() 1
cosx
1
cosx
![]() 2
2
2 3
2.5.
y 3sinx
![]()
3
2.6.
y ![]() 1
cosx
1
cosx
![]()
2 6
2.7.
y 2sinx
![]()
3
2.8.
y 2cosx
![]() 5
5
6
2.9.
y 2sinx
![]() 2
2
3
2.10.
y 2cosx
![]()
6
2.11.
y 2sinx
![]() 2
2
3
2.12.
y 2cosx
![]()
3
2.13.
y 2sinx
![]() 5
5
6
2.14.
y 3cosx
![]() 5
5
6
2.15.
y 3sinx
![]() 5
5
6
3. Построить график функции
3.1.
![]() y
cos1
x 2
1
y
cos1
x 2
1
2 3
3.2.
y 2sin
![]() x 1
x 1
3.3.
y 3sinx
![]()
1
1
3
3.4.
y 2sinx
![]()
1
1
6
3.5.
y sin2x
![]() 2
1
2
1
3
28
2.16.
y 3cosx
![]()
6
2.17.
y ![]() 1
sinx
1
sinx
![]()
2 6
2.18. y
![]() 1 cosx
1 cosx
![]()
2 3
2.19.
y 3sinx
![]()
6
2.20.
y 3cosx
![]()
3
2.21.
y ![]() 1
sinx
1
sinx
![]()
2 3
2.22.
y 2cosx
![]() 5
5
6
2.23.
y ![]() 1sinx
1sinx
![]()
2 3
2.24.
y 2cosx
![]() 2
2
3
2.25.
y 3sinx
![]() 2
2
3
2.26.
y ![]() 1
cosx
1
cosx
![]() 2
2
2 3
2.27. y
![]() 1 sinx
1 sinx
![]() 2
2
2 3
2.28. y
![]() 1 cosx
1 cosx
![]() 5
5
2 6
2.29. y
![]() 1 sinx
1 sinx
![]() 5
5
2 6
2.30. y
![]() 1 cosx
1 cosx
![]()
2 6
3.6.
y 3sinx
![]() 5
2
5
2
6
3.7.
y sin2x
![]() 5
2
5
2
6
3.8.
y 2cos3x
![]() 5
5
6
3.9.
y sin3x
![]()
2
2
6
3.10. y 2cos3x 2
|
3.11. y
cos2x
6 6 3.12. y
2 3 6
6 2 6 3.14. y
cos2x
6 6 3.15. y
2sinx
6 6
3.17. y
sin2x
1
3.28. y
2sin2x
3
2 3 2 6 3.19. y 3cos2x 1 5
2cos3x |
3.20.
y sin3x
![]()
2
2
6
3.21.
y 2cosx
![]()
1
1
3
4. Найдите область значений функции.
4.1.
y ![]() 1
cosx
1
cosx
![]() 0,2;
4.12.
0,2;
4.12.
2 3 4.13.
4.2.
y 2,5sinx
![]()
0,4;
0,4;
6 4.14.
4.3. y 5cos3x 0,7;
4.4.
y cos2x
![]()
2,2; 4.15.
2,2; 4.15.
4
4.5.
y 3,4sin
![]() x 1,5;
4.16.
x 1,5;
4.16.
2
4.6.
y 2cos![]()
x
1; 4.17.
x
1; 4.17.
3
4.7.
y 4,2sin
![]() x
2,5;
4.18.
x
2,5;
4.18.
3
0,1; 4.19.
4.8.
y 0,6sin ![]() x
x
4 5; 4.20.
4.9.
y 3
2sinx
![]()
6 4.21.
4.10.
y 4cos2x
2,7;
4.11.
y
sin3x
![]()
1,6; 4.22.
1,6; 4.22.
5
29
6
y 13cos2x;
y 7,1cosx
![]() 2
3,2;
2
3,2;
3
x
y
5cos
![]() 2,3; 4 y
5,2sin
2,3; 4 y
5,2sin![]()
x
3;
x
3;
4
y 2cosx
![]()
0,4;
0,4;
3
y 2sinx
![]()
0,6;
0,6;
6
y 2cos5x 3,7;
y sin2x
![]() 3
2,4;
3
2,4;
4
4 x
![]() y cos 3;
y cos 3;
5 5
y 2sin![]()
x
1,5;
x
1,5;
4 x
y
4,1cos ![]() 0,5;
0,5;
3
|
4.23. y
2,2sin
3 3 4.24. y
53sinx
3 4 4.25. y
0,5cos2x
2;
4.30. y
2,5sin 4.26. y
sin4x
5 4.27. y 43,5cos3x;
5. Исследуйте функцию на четностью/нечетность. |
5.1. y(x)
![]() 3tgxcossinx
x ;
3tgxcossinx
x ;
5.2. y(x) tgx sin x ctg2x;
5.3. y(x) 3cos xsin x tgx;
5.4. y(x)
![]() cgx3sin
tgxx
;
cgx3sin
tgxx
;
5.5. y(x)
![]() tg2xsin5xcos
x ;
tg2xsin5xcos
x ;
5.6. y(x) xctgx 2cos x;
5.7. y(x) sin2 x cos x x3 tgx
;
5.8. y(x)
![]() 27tgx
cos
xx3
;
27tgx
cos
xx3
;
5.9. y(x) 2sin x cos x;
5.10. y(x) x3 tgx 6cos x;
5.11. y(x)
![]() 2tgxsin2ctgxx ;
2tgxsin2ctgxx ;
5.12. y(x)
![]() xx3 sincosxx
;
xx3 sincosxx
;
5.13. y(x) 5cos2 x xtgx;
5.14. y(x) 2sin x xcos x 5tgx;
5.15. y(x)
![]() 2ctgxtgx2x
;
2ctgxtgx2x
;
![]() 5.16. y(x)
tg2x
sin2
x
5.16. y(x)
tg2x
sin2
x
cos x ;
5.17. y(x) 3xsin x 5ctg2x;
5.18. y(x) tg2xsin x 5ctgx ;
5.19. y(x)
![]() ctgxsin3 x4x
;
ctgxsin3 x4x
;
5.20. y(x)
![]() tgx3sin1xcos5x;
tgx3sin1xcos5x;
5.21. y(x) 3x2 ctgx 2xcos x;
5.22. y(x)
![]() sin2
x 3cos
x ; 7x
sin2
x 3cos
x ; 7x
5.23. y(x)
![]() 7x42tgxcos
x ;
7x42tgxcos
x ;
5.24. y(x) x2 sin x 5cos x;
5.25. y(x)
![]() x3 tgx
;
1
7ctgx
x3 tgx
;
1
7ctgx
5.26. y(x)
![]() 2tgsin3x
x2x
;
2tgsin3x
x2x
;
5.27. y(x)
![]() sinxxcos
2tgxx ;
sinxxcos
2tgxx ;
5.28. y(x) 5x2 cos x 3xctgx
;
5.29. y(x) 2sin2 x xcos x;
5.30. y(x)
![]() sinx2x3tgx5x2 .
sinx2x3tgx5x2 .
§ 3. Обратные тригонометрические функции.
![]()
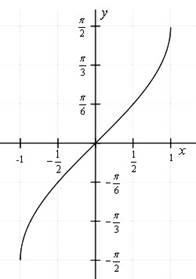
![]() Арксинусом
числа a1;1называется
угол x2
;2,
синус которого равен a. Т.е. arcsin
a x
sin
x a,
x2
;2.
Арксинусом
числа a1;1называется
угол x2
;2,
синус которого равен a. Т.е. arcsin
a x
sin
x a,
x2
;2.
График функции y arcsin x.
30
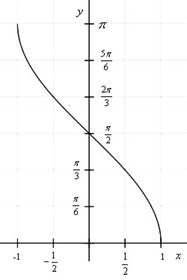
Арккосинусом числа a1;1называется угол x0;, косинус которого равен a. Т.е. arccos x cos x a, x0;.
График функции yarccosx.
![]() Арктангенсом
числа a;называется
угол x;,
Арктангенсом
числа a;называется
угол x;,
2 2
![]() тангенс
которого равен a. Т.е. arctga
x
tgx
a,
x;.
тангенс
которого равен a. Т.е. arctga
x
tgx
a,
x;.
2 2
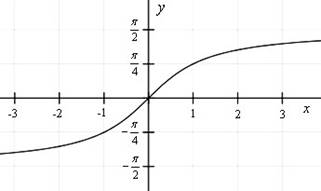
График функции y arctgx.
31
Арккотангенсом числа a;называется угол x0;, котангенс которого равен a. Т.е. arcctga x ctgx a,x0;.
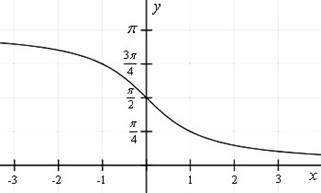
График функции y arcctgx .
Формулы, связывающие обратные тригонометрические функции.
arcsin(x)
arcsin
x,
arcsin
x ![]() arccos
x
2
arccos
x
2
![]()
![]() arcsin x
arccos
1
x2
arctg
x , x
0 1
x2
arcsin x
arccos
1
x2
arctg
x , x
0 1
x2
arccos(x) arccos x, arccos x arcsin x 2
![]()
![]() arccos x
arcsin
1
x2
arcctg
x , x
0 1
x2
arccos x
arcsin
1
x2
arcctg
x , x
0 1
x2
arctg(x) arctgx, arctgx arcctgx
2
1 x 1
![]()
![]() arctgx
arcctg
arctgx
arcctg
![]() arcsin
arccos ,
x
0 x 1
x2 1
x2
arcsin
arccos ,
x
0 x 1
x2 1
x2
arcctg(x)
arcctgx
,
arcctgx
![]() arctgx
arctgx
|
2 |
|
|
1 1 x
arcctgx arctg |
x 0 |
![]()
![]()
x Примеры.
![]() 3
3
1. Вычислите arcsin 2 2arccos 2 arctg 3 .
Решение:
![]()
![]()
![]() arcsin
23
2arccos
22
arctg 33
3
2
34
6
3
32
6
arcsin
23
2arccos
22
arctg 33
3
2
34
6
3
32
6
29 10 5
![]()
.
.
6 6 3
2.
Вычислите
cosarcsin
![]() 4,
sinarcctg(2).
4,
sinarcctg(2).
5
Решение:
32
![]() cosarcsin
cosarcsin
![]()
![]()
![]() 54 cosarccos 1
542
cosarccos 1
1625
cosarccos 259
54 cosarccos 1
542
cosarccos 1
1625
cosarccos 259
![]()
cosarccos
3
3;
cosarccos
3
3;
5 5
1 1
![]() sinarcctg(2)
sin
arcctg2
sin(arcctg2)
sinarcsin
1
22
5
.
ИЗ № 3.
sinarcctg(2)
sin
arcctg2
sin(arcctg2)
sinarcsin
1
22
5
.
ИЗ № 3.
Индивидуальные практические задания №3
1. Вычислите
1.1.
![]()
![]() 2arctg
33
arccos 0
arcctg 3 ;
2arctg
33
arccos 0
arcctg 3 ;
2 1 arcsin arccos
arctg1
1.2. 2 2 ;
1.3.
![]() 2arccos1
arctg(
3)
arcctg 3 ; 3
2arccos1
arctg(
3)
arcctg 3 ; 3
1.4.
arcsin
![]() 1 arccos
23
arcctg(1);
1 arccos
23
arcctg(1);
2
arcctg 33 arcsin 1
1.5. 2 ;
arccos 0
1.6.
![]() arctg
3
2arcsin
22
arccos
0;
arctg
3
2arcsin
22
arccos
0;
1.7.
![]() 3arcsin
12
arccos
23
arcctg0;
3arcsin
12
arccos
23
arcctg0;
2
arccos arcsin 0
2
1.8. ;
arctg1
1.9. arcsin
![]() 1 arccos
23
arcctg(1);
1 arccos
23
arcctg(1);
2
![]()
![]()
![]() 1.10. 3arctg
33
2arccos
22
arcctg(
3);
1.10. 3arctg
33
2arccos
22
arcctg(
3);
arctg 3 arccos 1
![]() 1.11. 2
;
1.11. 2
;
2
arcsin
2
33
![]() 1.12. arcsin1
arccos
22
4arcctg(1)
;
1.12. arcsin1
arccos
22
4arcctg(1)
;
![]()
![]()
![]() 1.13. 2arccos
arctg 3
2arcctg 3
;
1.13. 2arccos
arctg 3
2arcctg 3
;
3
![]() 1.14. 2arcsin 2
arccos
23
arcctg 3 ;
1.14. 2arcsin 2
arccos
23
arcctg 3 ;
2
arccos 23 arcsin 1
1.15. 2 ;
3 arctg 3
![]()
![]() 1.16. 2arccos
22
arctg0
arcsin 23 ;
1.16. 2arccos
22
arctg0
arcsin 23 ;
2
arccos arctg(1)
1.17. 2 ;
arcsin ![]()
1.18. ![]()
![]() 1.19. 1
1.19. 1 ![]()
1.20.
1.21. arcctg(1) 2arccos
1.22. 1 arctg0;
2
1.23.
1.24. 1.25.
2
34
1.30. .
arcctg1
2. Вычислите
2.1.
![]()
![]() sinarccos12,
tgarcsin(0,6);
2.12. cosarcctg(4),
tgarcsin
3;
sinarccos12,
tgarcsin(0,6);
2.12. cosarcctg(4),
tgarcsin
3;
13 5
2.2.
![]()
![]() cosarctg(2),
ctgarcsin
3;
2.13. sinarccos(0,8),
tgarcsin
12;
cosarctg(2),
ctgarcsin
3;
2.13. sinarccos(0,8),
tgarcsin
12;
5 13
2.3.
![]() sinarctg3,
cosarcsin(0,8);
2.14. cosarctg4,
ctgarcsin
54;
sinarctg3,
cosarcsin(0,8);
2.14. cosarctg4,
ctgarcsin
54;
2.4.
![]() tgarccos
5
,
cosarcctg(3);
tgarccos
5
,
cosarcctg(3);
13 2.15. sinarctg3, cosarcsin(0,8);
2.5.
![]()
![]()
![]() ctgarccos
54,
sinarctg2;
2.16. tgarccos1213,
cosarcctg
12;
ctgarccos
54,
sinarctg2;
2.16. tgarccos1213,
cosarcctg
12;
2.6.
![]()
![]() cosarcctg(3),
tgarcsin
12;
2.17. ctgarccos1213,
sinarctg4;
cosarcctg(3),
tgarcsin
12;
2.17. ctgarccos1213,
sinarctg4;
13
2.7.
![]()
![]() sinarccos
53,
tgarcsin 0,6;
2.18. cosarcctg
12,
tgarcsin 0,8;
sinarccos
53,
tgarcsin 0,6;
2.18. cosarcctg
12,
tgarcsin 0,8;
![]()
![]() 2.8. cosarctg3,
ctgarcsin
53;
2.19.
sinarccos1213,
tgarcsin(0,6);
2.8. cosarctg3,
ctgarcsin
53;
2.19.
sinarccos1213,
tgarcsin(0,6);
![]()
![]() 2.9. sinarcctg(3),
cosarcsin
5
;
2.20.
cosarctg
1,
ctgarcsin0,8;
2.9. sinarcctg(3),
cosarcsin
5
;
2.20.
cosarctg
1,
ctgarcsin0,8;
13 2
![]()
![]() 2.10. tgarccos135
,
cosarcctg2;
2.21.
sinarcctg2,
cosarcsin135
;
2.10. tgarccos135
,
cosarcctg2;
2.21.
sinarcctg2,
cosarcsin135
;
![]() 2.11. ctgarccos
54,
sinarctg2;
2.22. tgarccos 0,63,cosarcctg 51;
;
2.11. ctgarccos
54,
sinarctg2;
2.22. tgarccos 0,63,cosarcctg 51;
;
![]()
![]() 2.23. ctgarccos
5,
sinarctg
2
2.23. ctgarccos
5,
sinarctg
2
![]() 1.26. ;
1.26. ;
2
![]()
![]()
![]()
![]() 1.27. arcsin
12
arccos
23
arcctg(
3)
;
1.27. arcsin
12
arccos
23
arcctg(
3)
;
1.28. 2arcsin arctg 3 2arcctg
3
![]()
![]()
![]() 1.29. 2arcsin
22
arccos
23
arctg
3
;
1.29. 2arcsin
22
arccos
23
arctg
3
;
arcsin 23 arccos 12
35
2.24. cosarcctg4,
tgarcsin1213![]() ;
;
2.25. cosarcctg
![]() 1,
ctgarccos0,6;
1,
ctgarccos0,6;
2
2.26. sinarctg0,5,
cosarcsin1213![]() ;
;
2.27. tgarccos
![]() 53,
cosarcctg
53,
cosarcctg
![]() 12
;
12
;
2.28. ctgarccos13![]() 5 ,
sinarctg3;
5 ,
sinarctg3;
2.29. cosarcctg(5),
tgarcsin
12![]() ;
;
13
2.30. sinarccos0,8, cosarctg(4).
§ 4. Тригонометрические уравнения.
Определение: Тригонометрическим называется уравнение, в котором неизвестные находятся под знаком тригонометрических функций.
4.1. Простейшие тригонометрические уравнения.
Простейшими тригонометрическими уравнениями называют уравнения вида: sin x a, cosxa, tgx a, ctgx a. Решить простейшее тригонометрическое уравнение – значит найти множество всех углов (дуг), имеющих данное значение тригонометрической функции.
1) sin x a
Если a 1 уравнение корней не имеет.
![]() Если
a
1,
решение находим по формуле: x (1)n arcsin
a n,
nZ
.
Если
a
1,
решение находим по формуле: x (1)n arcsin
a n,
nZ
.
sin x 0 x n;
Частные
случаи: sin
x 1
x
![]()
2n;
2n;
2
sin
x 1
x
![]() 2 2n.
2 2n.
2) cos x a
Если a 1 уравнение корней не имеет.
![]() Если a
1,
решение находим по формуле: x
arccosa2n,
nZ
.
Если a
1,
решение находим по формуле: x
arccosa2n,
nZ
.
cos
x 0
x
![]() 2 2n;
2 2n;
Частные случаи: cos x 1 x 2n;
cos x 1 x 2n.
3)tgx a x arctga n,nZ .
36
4)ctgx a x arcctga n,nZ .
Примеры.
1.
![]() Решить
уравнение sin x 2 .
2
Решить
уравнение sin x 2 .
2
![]() Решение: x
1n
arcsin 2 n,nZ
,
т.е. x
1n
Решение: x
1n
arcsin 2 n,nZ
,
т.е. x
1n
![]() n,nZ
.
n,nZ
.
2 4
2.
![]() Решить
уравнение cos x2x
3
Решить
уравнение cos x2x
3
4 2
Решение:
![]() 2x
2x
![]()
arccos
23
2n,nZ
;
arccos
23
2n,nZ
;
4
![]() 2x
5
2n,nZ
;
2x
5
2n,nZ
;
![]() 4 6 x
5
n,nZ
.
4 6 x
5
n,nZ
.
8 6
4.2. Тригонометрические уравнения, приводимые к квадратным.
Уравнения вида Asin2 x Bsin x C 0, где A 0, решаются приведением к квадратному путем замены sin x y. (аналогично решаются уравнения с другими тригонометрическими функциями).
Примеры.
3. Решить уравнение 2sin2 x sin x 1 0.
Решение:
Введем новую переменную y sin x. Тогда данное уравнение можно записать в виде 2y2 y 1 0. Мы получили квадратное уравнение. Его
![]()
![]() 1
и y2 1.
Следовательно, sin x
или sinx
1.
корнями служат y1
1
и y2 1.
Следовательно, sin x
или sinx
1.
корнями служат y1
2
В первом случае получим решения
x
1k
arcsin ![]() n,
n,
т.е. x
1n ![]() n, nZ . 6
n, nZ . 6
Во втором случае имеем: x
![]()
2n,
nZ
.
2n,
nZ
.
2
4. Решить уравнение 6sin2 x 5cos x 2 0. Решение:
Заменяя sin2 x 1cos2 x , получим относительно cos x квадратное уравнение 6(1cos2 x) 5cos x 2 0
6cos2 x 5cos x 4 0 6cos2 x 5cos x 4 0
37
Введем новую переменную y
cos
x.
Тогда 6y2 5y
4
0,
откуда y1
![]() или y2
1
или y2
1![]() . Уравнение cos
x 1
. Уравнение cos
x 1![]() не имеет решений, т.к.1
не имеет решений, т.к.1![]() 1
.
1
.
Решая
уравнение cos
x ![]() находим:
находим:
x arccos
![]() 1
2n
x
1
2n
x
![]() 2
2n,nZ
.
2
2n,nZ
.
2 3
5. Решить уравнение tgx 3ctgx 0.
1 3
Решение:
Заменяя ctgx ![]() , получим tgx
, получим tgx
![]() 0,
откуда, т.к.
0,
откуда, т.к.
tgx tgx
![]() tgx
0,
получаем tg2x3
0.
Введем новую переменную y tgx.
Тогда y2
3,
откуда y1
3
или y2
3.
Следовательно,
tgx
0,
получаем tg2x3
0.
Введем новую переменную y tgx.
Тогда y2
3,
откуда y1
3
или y2
3.
Следовательно,
![]()
![]() tgx
3
x
tgx
3
x
![]() n,
nZ
и tgx
3 x
n,
nZ
.
n,
nZ
и tgx
3 x
n,
nZ
.
33
4.3. Однородные тригонометрические уравнения.
Однородные тригонометрические уравнения имеют ту же структуру, что и однородные уравнения любого другого вида. Отличительные признаки однородных уравнений:
а) все одночлены имеют одинаковую степень,
б) свободный член равен нулю,
в) в уравнении присутствуют степени с двумя различными основаниями.
Однородное тригонометрическое уравнение – это уравнение двух видов: asin x bcos x 0, ab 0 (однородное уравнение первой степени) либо
asin2 x bsin xcos x ccos2 x 0, abc 0 (однородное уравнение второй степени).
Алгоритм решения однородного уравнения первой степени: 1) разделить обе части уравнения на cosx (или на sin x). Делить можно на число, не равное 0, а cosx 0, т.к. в противном случае
asinx b0 0 и sinx 0, следовательно sin2 x cos2 x 0, что неверно;
sin x cos x
2)
воспользоваться
формулой tgx ![]() (ctgx
(ctgx ![]() );
);
cos x sin x
3) решить получившееся уравнение.
Пример.
6.
![]() Решить
уравнение sin x 3cos
x 0.
Решить
уравнение sin x 3cos
x 0.
![]() Решение: sin
x 3cos x
0
- однородное уравнение. Разделить обе части уравнения на cosx.
Решение: sin
x 3cos x
0
- однородное уравнение. Разделить обе части уравнения на cosx.
|
sin x
cos x |
38 |
|
![]() x
arctg(
3)
n,
nZ
,
x
x
arctg(
3)
n,
nZ
,
x
![]() n,
nZ
.
3
n,
nZ
.
3
Ответ: x n, nZ
3 Алгоритм решения однородного уравнения второй степени: 1) разделить обе части уравнения на cos2 x (или на sin2 x). Делить можно на число, не равное 0, а cos2 x 0, т.к. в противном случае
cos x 0,asin2 x bsin x0c0 0 и sin x 0, следовательно sin2 x cos2 x 0, что неверно;
2)
воспользоваться
формулой tgx ![]() sin x
(ctgx
sin x
(ctgx
![]() cos x );
cos x );
cos x sin x
3) решить получившееся уравнение.
Примеры.
7. Решить уравнение 4sin2 x 3sin xcos x 7cos2 x 0. Решение:
4sin2 x 3sin xcos x 7cos2 x 0 - однородное уравнение. Разделим обе части уравнения на cos2 x.
sin2 x sin xcos x cos2 x
![]() Получим
4cos2 x
3 cos2 x 7
cos2 x
0.
Получим
4cos2 x
3 cos2 x 7
cos2 x
0.
4tg2x 3tgx 7 0. Замена переменной : y tgx
4y2 3y 7 0
![]() D
b2
4ac
9112
121,
y
b
D
311,
y1
1,
y2
1
D
b2
4ac
9112
121,
y
b
D
311,
y1
1,
y2
1![]() 3
3
2a 8 4
tgx
1
, x
![]() n,
nZ
;
n,
nZ
;
4
3
![]()
![]() 13
n,
nZ
.
13
n,
nZ
.
tgx 1 , x arctg
4 4
Ответ: x
![]() n,
nZ
;
x
arctg1
n,
nZ
;
x
arctg1![]() 3
n,
nZ
.
3
n,
nZ
.
4 4
8. Решить уравнение 2sin2 x sin2x 2cos2 x 1.
Решение:
Применим формулы sin2x 2sin xcos x, 1 cos2 x sin2 x. Получим
2sin2 x 2sin xcos x 2cos2 x cos2 x sin2 x, sin2 x 2sin xcos x 3cos2 x 0- однородное уравнение. Разделим обе части уравнения на cos2 x. sin2 x sin xcos x cos2 x
![]() Получим
cos2 x
2 cos2 x 3cos2 x
0.
Получим
cos2 x
2 cos2 x 3cos2 x
0.
tg2x 2tgx 3 0. Замена переменной : y tgx
y2 2y 3 0 y1 1, y2 3
tgx 1
, x
![]() n, nZ ;
4
n, nZ ;
4
tgx 3 , x arctg3n, nZ .
39
Ответ: x
![]() n,
nZ
;
x
arctg3n,
nZ
.
n,
nZ
;
x
arctg3n,
nZ
.
4
4.4. Решение тригонометрических уравнений, введением вспомогательного угла.
Рассмотрим уравнение вида: asin x bcos x c, a,b,c 0.
![]() Разделим
обе части уравнения на a2 b2 .
Получим a b c sin x cos
x .
Разделим
обе части уравнения на a2 b2 .
Получим a b c sin x cos
x .
![]()
![]() 14a224b32 14a224b32 14a224b32
14a224b32 14a224b32 14a224b32
cos sin C
Теперь коэффициенты уравнения обладают свойствами синуса и кос инуса, а именно: модуль ( абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1. Тогда можно обозначить их соответственно как cos иsin ( здесь - так называемый вспомогательный угол ), и наше уравнение принимает вид: cossin x sincos x C или sinx C и его решение
x 1n arcsinC n, nZ , где arccos a arcsin b .
![]()
![]() a2 b2 a2 b2
a2 b2 a2 b2
Заметим, что cos иsin взаимно заменяемы.
Пример.
![]() 9. Решить
уравнение 3sin x cos
x 1.
9. Решить
уравнение 3sin x cos
x 1.
![]() Решение:
Здесь a 3,
b 1, a2 b2
2.
Решение:
Здесь a 3,
b 1, a2 b2
2.
3
![]()
![]()
![]() Делим
обе части уравнения на 2. Получим sin x cos
x , 2
Делим
обе части уравнения на 2. Получим sin x cos
x , 2
откуда
![]() cos
cos![]() sin x sin
sin x sin![]() cos x
cos x
![]() 1 и
sinx
1
.
1 и
sinx
1
.
6 6 2 6 2
Решив последнее уравнение, получим
x ![]()
1n
arcsin
1n
arcsin ![]() 1
n,
nZ
;
1
n,
nZ
;
![]() 6 2 x
1n
n,
nZ
.
6 2 x
1n
n,
nZ
.
6 6
4.5. Решение тригонометрических уравнений, используя формулы преобразования произведения в сумму и обратно.
Примеры.
10. Решить уравнение 2sin2xsin6x cos4x
Решение: Используя формулу sinsin
![]() cos()
cos(),
cos()
cos(),
40
получим 2sin2xsin6x
2![]() cos(4x)
cos8x
cos4x
cos8x.
Тогда уравнение примет вид cos4x cos8x
cos4x,
откуда cos8x
0,
cos(4x)
cos8x
cos4x
cos8x.
Тогда уравнение примет вид cos4x cos8x
cos4x,
откуда cos8x
0,
![]() 8x
8x
![]() n,
nZ
,
x
n
, nZ
.
n,
nZ
,
x
n
, nZ
.
2 16 8
11. Решить уравнение cos2xcos4xcos6xcos8x 0
Решение:
![]() cos2xcos4xcos6xcos8x
0
Применим формулу cos
cos
2coscos.
cos2xcos4xcos6xcos8x
0
Применим формулу cos
cos
2coscos.
2 2
2cos5xcos3x2cos5xcosx 0
2cos5x(cos3x cos x) 0
![]() Еще
раз применим формулу cos
cos
2coscos,
получим
Еще
раз применим формулу cos
cos
2coscos,
получим
2 2
4cos5xcos2xcosx 0
cos5x 0 или cos2x 0 или cos x 0
5x
![]() n,
nZ
2x
n,
nZ
2x
![]() n,
nZ
x
n,
nZ
x
![]() n,
nZ
n,
nZ
2 2 2
![]()
![]() x
n
, nZ
x
n
, nZ
x
n
, nZ
x
n
, nZ
10 5 4 2
4.6. Решение тригонометрических уравнений с помощью x 2 x
2tg 1tg
![]()
![]() универсальной
подстановки sin x 2
, cos
x 2
.
универсальной
подстановки sin x 2
, cos
x 2
.
1 tg2 x 1 tg2 x
2 2
Пример.
12. Решить уравнение 3sinx 4cosx 3. Решение: Возможны 2 случая:
![]() 1) tg
1) tg
![]() x не
существует, т.е. x
k
,
x
2k
.
Тогда
x не
существует, т.е. x
k
,
x
2k
.
Тогда
2 2 2
3sin( 2k) 4cos( 2k) 4 3.
2tg x 1tg2 x
![]()
![]() 2) tg
2) tg
![]() x
существует и sin x 2
, cos
x 2
.
x
существует и sin x 2
, cos
x 2
.
2 1 tg2 x 1 tg2 x
2 2
2tg x 1tg2 x
![]() Тогда уравнение примет
вид: 3 2
4 2
3.
Тогда уравнение примет
вид: 3 2
4 2
3.
1 tg2 x 1 tg2 x
2 2
Откуда
6tg
![]() x
4
4tg2
x
4
4tg2
![]() x
33tg2
x
33tg2
![]() x ;
x ;
2 2 2
41
![]() tg2
x 6tg
x 7
0.
tg2
x 6tg
x 7
0.
2 2
![]() x 2 6y
7
0,
y1 1,
y2 7.
x 2 6y
7
0,
y1 1,
y2 7.
Делаем замену: tg y. Имеем y 2
![]() x и
tg
x 7
x
2arctg7
2n,
nZ
.
x и
tg
x 7
x
2arctg7
2n,
nZ
.
![]()
![]() Тогда
tg 1
x
2n,
nZ
Тогда
tg 1
x
2n,
nZ
2 2 2
Индивидуальные практические задания №4 ИЗ № 4.
1. Решите простейшее тригонометрическое уравнение.
1.1. 2sin x 2 0; 1.16. 3tgx 3 0;
![]()
![]() 1.2. 3
3ctgx
0;
1.17. 2cos
x
3
0;
1.2. 3
3ctgx
0;
1.17. 2cos
x
3
0;
1.3. 2cos x 3 0; 1.18. 2 2cosx 0;
1.4. 3tgx 3 0; 1.19. 3tgx 3 0;
1.5. 3 2sin x 0; 1.20. 3tgx 3 0;
1.6. 3ctgx 3 0; 1.21. 3 2sin x 0; 1.7. 2cosx 2 0; 1.22. 12sinx 0;
![]() 1.8. 12cosx
0;
1.23. 2sin
x 3
0;
1.8. 12cosx
0;
1.23. 2sin
x 3
0;
1.9. 2sin x 3 0; 1.24. 2sinx1 0;
1.10. 3ctgx 3 0; 1.25. 2 2sin x 0;
![]()
![]() 1.11. 3ctgx
3
0;
1.26.
3
tgx
0;
1.12.
2sinx1
0;
1.27.
2cosx
2
0;
1.11. 3ctgx
3
0;
1.26.
3
tgx
0;
1.12.
2sinx1
0;
1.27.
2cosx
2
0;
![]()
![]() 1.13. 2sin
x
2
0;
1.28. 3 2cos
x 0;
1.14.
3tgx
3
0;
1.29.
3ctgx
3
0
;
1.15.
3
2cos
x 0;
1.30. 2cosx1
0.
1.13. 2sin
x
2
0;
1.28. 3 2cos
x 0;
1.14.
3tgx
3
0;
1.29.
3ctgx
3
0
;
1.15.
3
2cos
x 0;
1.30. 2cosx1
0.
2. Решите простейшее тригонометрическое уравнение.
2.1. sin 1 х 1 ; 2.7. sin2х 1 ;
2 6 2 6 2
![]()
![]() 2.2. cos
1
х
2 ; 2.8. cos
1
х 3
;
2.2. cos
1
х
2 ; 2.8. cos
1
х 3
;
2 4 2 2 4
2.3. sin 1 х 5 3 ; 2.9. sin 1 х 2 2 ;
2 6 2 2 3 2
![]()
![]() 2.4. sin
1
х
1 ; 2.10. cos
1
х
1 ;
2.4. sin
1
х
1 ; 2.10. cos
1
х
1 ;
2 3 2 2 3 2
![]() 2.5. cos
1
х
1 ; 2.11. sin2х
1 ;
2.5. cos
1
х
1 ; 2.11. sin2х
1 ;
2 6 2 3 2
![]()
![]() 2.6. sin
1
х 3
; 2.12. cos2х
3
12 ;
2.6. sin
1
х 3
; 2.12. cos2х
3
12 ;
2 4
42
![]() 2.13. cos
1
х 2
2 ; 2.22. sin
х
2 ;
2.13. cos
1
х 2
2 ; 2.22. sin
х
2 ;
2 3 2 3 6 2
![]() 2.14. cos2х
2
2 ; 2.23. cos2х
6
12 ;
2.14. cos2х
2
2 ; 2.23. cos2х
6
12 ;
3 2
![]() 2.15. sin2х
2 ; 2.24. sin
3х
4
23 ;
2.15. sin2х
2 ; 2.24. sin
3х
4
23 ;
4 2
2.16. cos2х 5 3 ; 2.25. cos3х 56 12 ;
6 2
2.17. cos2х 2 ; 2.26. sin2х 23 22 ;
4 2
![]() 2.18. sin
1
х
2 ; 2.27. cos
3х
23
22 ;
2.18. sin
1
х
2 ; 2.27. cos
3х
23
22 ;
2 4 2
2.19. cos2х 3 3 ; 2.28. sin2х 56 23 ;
4 2
2.20. sin3х 2 1 ; 2.29. cos 3х 6 23 ;
3 2
![]() 2.21. cos
1
х 5
3 ; 2.30. sin2х
34
23 .
2.21. cos
1
х 5
3 ; 2.30. sin2х
34
23 .
2 6 2
3. Решить простейшее тригонометрическое уравнение.
![]() 3.1. tg2х
2
3 ; 3.11. ctg2х
3.1. tg2х
2
3 ; 3.11. ctg2х
![]() 6
0;
6
0;
3 3
![]()
![]() 3.2. ctg
х
2
1; 3.12. tg
3х
4
3 ;
3.2. ctg
х
2
1; 3.12. tg
3х
4
3 ;
3 3
![]() 3.3. tg2х
5
3
;
3.13. ctg
12
х 6
1;
3.3. tg2х
5
3
;
3.13. ctg
12
х 6
1;
6
![]()
![]() 3.4. ctg
х
3 ; 3.14. ctg
12
х 4
33 ;
3.4. ctg
х
3 ; 3.14. ctg
12
х 4
33 ;
3 6 3
![]() 3.5. ctg2х
3 ; 3.15. tg
12
х 56
0;
3.5. ctg2х
3 ; 3.15. tg
12
х 56
0;
4 3
![]()
![]() 3.6. tg
1
х
1; 3.16. tg
12
х 3
1;
3.6. tg
1
х
1; 3.16. tg
12
х 3
1;
2 4
![]()
![]() 3.7. ctg2х
3
3; 3.17. ctg12
х 6
0;
3.7. ctg2х
3
3; 3.17. ctg12
х 6
0;
4
![]() 3.8. tg3х
3.8. tg3х
![]() 2
1; 3.18. ctg
12
х 34
3 ;
2
1; 3.18. ctg
12
х 34
3 ;
3
![]() 3.9. ctg
1
х 5
3 ; 3.19. tg2х
3.9. ctg
1
х 5
3 ; 3.19. tg2х
![]() 6
1;
6
1;
2 6 3
![]()
![]() 3.10. tg
х
1;
3.20. ctg
12
х 34
33 ;
3.10. tg
х
1;
3.20. ctg
12
х 34
33 ;
3 6
43
![]() 3.21. tg
1
х 2
3 ; 3.27.
3.21. tg
1
х 2
3 ; 3.27.
2 3
![]() 3.22. ctg
1 х
1;
3.28. 2 3
3.23. tg2х
3.22. ctg
1 х
1;
3.28. 2 3
3.23. tg2х
![]()
1; 3.29.
1; 3.29.
3
3.24. ctg2х 3 ; 3.30.
3
![]() 3.25. cos
1
х 2
2 ;
3.25. cos
1
х 2
2 ;
2 3 2
3.26. ctg2х 2 3 ;
3 3
4. Решить тригонометрическое уравнение:
![]() 4.1. 2sin2
x 5sin
x 2
0;
4.16.
4.2. cos2
x 3cos
x 2
0;
4.17.
4.3. 2sin2
x 3sin
x 1
0;
4.18.
4.4. tg2x
3tgx
2
0;
4.19.
4.5. 2cos2
x 3cos
x 2
0;
4.20.
4.6. 2cos2 x
2cos
x 0
4.21.
4.7. 4sin2
x 4sin
x 3
0;
4.22.
4.8. 2sin2
x 5sin
x 3
0
4.23.
4.9. 2sin2
x 3sin
x 2
0
4.24.
4.10. 2sin2sin
x 1
0;
4.25.
4.11. cos2
x cos
x 2
0
4.26.
4.12. 2sin2
x sin
x 0;
4.27.
4.13. 2cos2
x 3cos
x 1
0;
4.28.
4.14. 4cos2
x 8cos
x 3
0;
4.29.
4.15. 3ctg2x
5ctgx
2
0;
4.30.
4.1. 2sin2
x 5sin
x 2
0;
4.16.
4.2. cos2
x 3cos
x 2
0;
4.17.
4.3. 2sin2
x 3sin
x 1
0;
4.18.
4.4. tg2x
3tgx
2
0;
4.19.
4.5. 2cos2
x 3cos
x 2
0;
4.20.
4.6. 2cos2 x
2cos
x 0
4.21.
4.7. 4sin2
x 4sin
x 3
0;
4.22.
4.8. 2sin2
x 5sin
x 3
0
4.23.
4.9. 2sin2
x 3sin
x 2
0
4.24.
4.10. 2sin2sin
x 1
0;
4.25.
4.11. cos2
x cos
x 2
0
4.26.
4.12. 2sin2
x sin
x 0;
4.27.
4.13. 2cos2
x 3cos
x 1
0;
4.28.
4.14. 4cos2
x 8cos
x 3
0;
4.29.
4.15. 3ctg2x
5ctgx
2
0;
4.30.
5. Решить тригонометрическое уравнение:
5.1. 2cos2 x sin x 1 0; 5.11. 5.2. 4sin2 x 8cos x 7 0; 5.12. 5.3. cos2 x 3sin x 3 0; 5.13.
5.4. tgx 3ctgx 4; 5.14.
5.5. 2sin2 x cos x 1 0; 5.15. 5.6. 5sin2 x 6cos x 6 0; 5.16. 5.7. tgx 4ctgx 5 0; 5.17.
5.8. cos2 x sin x 1 0; 5.18. 5.9. 2cos2 x 3sin x 3 0; 5.19. 5.10. tgx 2ctgx 1 0; 5.20.
44
tg2х
![]()
1;
1;
4
ctg2х
![]() 5
0;
5
0;
6
![]() tg2х
3
3 ;
tg2х
3
3 ;
4
ctg3х
![]() 2
1.
2
1.
3
4sin2 x 4sin x 3 0; 2cos2 x cos x 1 0;
![]() 2sin2 x
2sin
x 0 2sin2
x 3sin
x 2
0
2sin2 x
2sin
x 0 2sin2
x 3sin
x 2
0
3tg2x tgx 2 0;
2cos2 x cos x 3 0
2sin2 x 3sin x 1 0;
4sin2 x 3 0; 4cos2 x 8cos x 3 0; sin2 x sin x 2 0; ctg2x 5ctgx 6 0;
2cos2 x cos x 0; sin2 x 3sin x 2 0; 2cos2 x 5cos x 3 0; 2sin2 x sin x 3 0.
2sin2 x 3cos x 0 tgx 4ctgx 5 0; 8sin2 x cos x 1 0; tgx 4ctgx 5 0; 2cos2 x sin x 1 0; sin2 x cos x 4 0; tgx 4ctgx 3 0; 2cos2 x 5sin x 0; tgx 2ctgx 3 0; sin2 x 3cos x 1 0;
5.21. 2cos2 x 3sin x 3 0; 5.26. tgx 2ctgx 3;
5.22. 2sin2 x 3cos x 0; 5.27. 6sin2 x 5cos x 2 0;
5.23. 2ctgx 3tgx 5 0; 5.28. 2sin2 x 3cos x 3 0; 5.24. 4cos2 x 4sin x 1 0; 5.29. 2cos2 x sin x 1 0;
5.25. 2cos2 x 5sin x 5 0 5.30. tgx 5ctgx 6 0.
6. Решить тригонометрическое уравнение:
6.1. sinx 5cosx 0; 6.16. 3sinx cosx 0;
6.2.
![]() sin
x 3cos x
0;
6.17.
2sinx
3cosx
0;
sin
x 3cos x
0;
6.17.
2sinx
3cosx
0;
6.3. sinx 2cosx 0; 6.18. sin x 4cos x 0;
6.4.
![]() sin
x cos x
0;
6.19. 3sin x cos
x 0;
sin
x cos x
0;
6.19. 3sin x cos
x 0;
6.5. 4sinx cosx 0; 6.20. sinx 2cosx 0;
6.6. 5sin x cos x 0; 6.21. 5sin x 2cos x 0;
6.7. 3sinx 2cosx 0; 6.22. 4sinx cosx 0;
6.8. 3sinx cosx 0; 6.23. 3sinx 2cosx 0;
6.9.
![]()
![]() 3sin x 3cos
x 0;
6.24.
3sin
x cos x
0;
3sin x 3cos
x 0;
6.24.
3sin
x cos x
0;
6.10. 2sinx cosx 0; 6.25. 2sinx cosx 0;
6.11. sin x cos x 0; 6.26. sin x 3cos x 0; 6.12. 5sinx 3cosx 0; 6.27. sinx 4cosx 0;
6.13. sin x 3cos x 0; 6.28. 5sin x cos x 0;
6.14. ![]() 3sin x 3cos
x 0;
6.29.
3sinx
5cosx
0;
6.15.
sinx
5cosx
0;
6.30.
2sinx
3cosx
0.
3sin x 3cos
x 0;
6.29.
3sinx
5cosx
0;
6.15.
sinx
5cosx
0;
6.30.
2sinx
3cosx
0.
7. Решить тригонометрическое уравнение:
7.1. 2sin2 x 3sin xcos x 5cos2 x 0; 7.16. sin2 x 5sin xcos x 4cos2 x 0;
7.2. 3sin2 x sin xcos x 2cos2 x 0; 7.17. 3sin2 x 5sin xcos x 8cos2 x 0;
7.3. sin2 x 4sin xcos x 5cos2 x 0; 7.18. sin2 x 5sin xcos x 6cos2 x 0;
7.4. 4sin2 x 3sin xcos x 7cos2 x 0; 7.19. 2sin2 x 3sin xcos x cos2 x 0;
7.5. 3sin2 x 2sin xcos x cos2 x 0; 7.20. 3sin2 x sin xcos x 4cos2 x 0;
7.6. 2sin2 x 3sin xcos x cos2 x 0; 7.21. sin2 x 4sin xcos x 3cos2 x 0;
7.7. sin2 x 7sin xcos x 6cos2 x 0; 7.22. 2sin2 x sin xcos x 3cos2 x 0;
7.8. 3sin2 x 4sin xcos x 7cos2 x 0; 7.23. 3sin2 x 5sin xcos x 2cos2 x 0;
7.9. 4sin2 x 3sin xcos x cos2 x 0; 7.24. 4sin2 x sin xcos x 5cos2 x 0;
7.10. 2sin2 x 5sin xcos x 7cos2 x 0; 7.25. sin2 x 7sin xcos x 8cos2 x 0;
7.11. 3sin2 x 4sin xcos x cos2 x 0; 7.26. 2sin2 x 3sin xcos x 5cos2 x 0;
7.12. 4sin2 x 5sin xcos x cos2 x 0; 7.27. 4sin2 x sin xcos x 3cos2 x 0;
7.13. 3sin2 x 2sin xcos x 5cos2 x 0; 7.28. 3sin2 x 2sin xcos x 5cos2 x 0;
7.14. sin2 x 7sin xcos x 6cos2 x 0; 7.29. 2sin2 x 5sin xcos x 7cos2 x 0; 7.15. 3sin2 x 5sin xcos x 2cos2 x 0; 7.30. 4sin2 x 5sin xcos x 9cos2 x 0.
8. Решить тригонометрическое уравнение:
45
8.1. 4sin2 x sin2x 3; 8.16. 8.2. sin2x 8sin2 x 5; 8.17. 8.3. 10cos2 x 2sin2x 3; 8.18. 8.4. cos2x 8sin2 x 6 2sin2x; 8.19. 8.5. sin2x2cos2x 1; 8.20. 8.6. sin2x cos2x 2cos2 x; 8.21. 8.7. 6cos2 x sin2x cos2x 2 8.22. 8.8. cos2 x 3sin2 x 2sin2x; 8.23. 8.9. 6sin2 x 2sin2x 5; 8.24. 8.10. 4sin2 x sin2x 1; 8.25. 8.11. cos2x2sin2x2 0; 8.26. 8.12. 2cos2 x 2sin2x 3; 8.27. 8.13. 2cos2x 2sin2 x 5 4sin2x; 8.28. 8.14. sin2x 4cos2 x 1; 8.29. 8.15. 2sin2x 32sin2 x; 8.30.
4cos2 x 2sin2 x 3sin2x;
1 4sin2 x 3sin2x;
2sin2x 2cos2 x 1;
3sin2 x sin2x 2; 2cos2 x 4sin2x 2cos2x 3; sin2x 4sin2 x 1; 2sin2 x 2sin2x 1 0; cos2x 4sin2 x sin2x; 6sin2 x cos2x 3sin2x 0; cos2x 2sin2x 8cos2 x 2;
4sin2 x 3 2sin xcos x;
4cos2 x sin2x 1;
2sin2 x 2sin2x 1;
4cos2 x 1 3sin2x;
|
9. Решить тригонометрическое уравнение:
9.1. 3sin x cos x 1; 9.16. sin x cos x 1; 9.2.
9.3.
9.4. sin x cos x 1; 9.19. sin x 3cos x 2; 9.5. 3sin x cos x 2 ; 9.20. sin x 3cos x 1; 9.6. sin x 3cos x 1; 9.21. 3sin x cos x 3 ; 9.7. 3sin x cos x 2 ; 9.22. 3sin x cos x 2; 9.8.
9.9. 3sin x cos x 3; 9.24. 3sin x cos x 1; 9.10.
9.11. 3sin x cos x 3; 9.26. 3sin x cos x 2; 9.12. sin x 3cos x 2 ; 9.27. sinx cosx 1; 9.13.
9.14. sinx cosx 1; 9.29. sin x 3cos x 3 ; 9.15. 3sin x cos x 2; 9.30. 3sin x cos x 2
10. Решить тригонометрическое уравнение:
10.1. 2sin3xsin5x cos2x 0; 10.8. 2sinxsin5xcos6x 0; 10.2. 2cos2xcos4x cos6x 0; 10.9. 2cos3xsin4xsin7x 0; 10.3. 2sin2xsin4xcos2x 0; 10.10. 10.4. 2cos3xcos7x cos4x 0; 2cos5xcos7x cos12x 0; 10.5. 2sin3xsin4xcos7x 0; 10.11. 2sin xsin2x cos3x 0; 10.6. 2cos2xsin4x sin2x 0; 10.12. 2cos3xcos5x cos2x 0; 10.7. 2sin2xsin4xcos6x 0; 10.13. 2sinxcos3x sin4x 0; 46 |
10sin2 x
3
2sin2x.
10.14. 2cos2xcos4xcos2x 0;
10.15. 2sin3xsin7xcos4x 0;
10.16. 2sinxcos3x sin2x 0;
10.17. 2cos xcos3xcos4x 0;
10.18. 2sinxsin3xcos2x 0;
10.19. 2cosxcos5x cos6x 0;
10.20. 2cos xsin5x sin6x 0;
10.21. 2sin5xsin7xcos12x 0;
10.22. 2cos3xcos4x cos7x 0;
10.23. 2cos3xsin5xsin2x 0;
10.24. 2sin xsin3x cos4x 0;
10.25. 2cosxcos2xcos3x 0
10.26. 2sin3xcos7xsin4x 0;
10.27. 2sinxsin4x cos3x 0;
10.28. 2cosxcos3xcos2x 0;
10.29. 2cos2xsin4x sin6x 0;
10.30. 2cos xcos4xcos3x 0.
11. Решить тригонометрическое уравнение:
11.1. sin xsin3xsin5xsin7x 0; 11.16. cos3xcos5x sin x;
11.2. cos2xcos6x cos4x; 11.17. cos3xcos5xcos7xcos9x 0;
11.3. sin5x sin3x cos4x; 11.18. cos7x cosx cos3x;
11.4. sin xsin3xsin5xsin7x 0; 11.19. cos4xcos10x 2cos7x;
11.5. cosx cos3x cos2x; 11.20. cosxcos3xcos5xcos7x 0;
11.6. sin6x sin2x 2cos4x; 11.21. sin2x sin4x sin3x;
11.7. cos2xcos4x cos6xcos8x 0; 11.22. sin3xsin5xsin7xsin9x 0;
11.8. sin5x sinx 2cos3x; 11.23. cos2x cos6x sin4x;
11.9. cosx cos5x sin3x; 11.24. sin2xsin4x sin6x sin8x 0;
11.10. cos3xcos5xcos7xcos9x 0; 11.25. cos xcos7x 2sin4x;
11.11. sin2x sin8x sin5x; 11.26. sin3xsin5xsin7xsin9x 0;
11.12. sin7x sinx cos4x; 11.27. sin3x sin7x 2sin5x;
11.13. cos xcos9x 2cos5x; 11.28. cos xcos3xcos5xcos7x 0;
11.14. sin2xsin4xsin6xsin8x 0; 11.29. sin5x sinx cos3x; 11.15. sin7x sinx sin4x; 11.30. cosx cos9x 2sin5x.
12. Решить тригонометрическое уравнение:
12.1. 3cos x 2sin x 2; 12.15. 43cos x 4sin x;
12.2. 3sinx cosx 3; 12.16. 4sinx 5cosx 4;
12.3. 2cos x sin x 1; 12.17. 5cos x sin x 1;
12.4. 4cos x 3sin x 3; 12.18. 3cos x sin x 1;
12.5. 33sinx 2cosx; 12.19. 7cosx 3sinx 3;
12.6. 5sinx 7cosx 5; 12.20. cosx 3sinx 3;
12.7. 2sin x 3cos x 2; 12.21. 5cos x 3sin x 3;
12.8. sinx 2cosx 1; 12.22. 3sinx cosx 3;
12.9. 3sin x 2cos x 3; 12.23. 7cos x 5sin x 5;
12.10. 3sin x 4cos x 3; 12.24. 2sin x cos x 2;
12.11. 3cosx 2sinx 2; 12.25. 3sinx 5cosx 3;
12.12. 7sinx 5cosx 7; 12.26. 5sinx 53cosx;
12.13. 5cos x 4sin x 4; 12.27. 2sin x cos x 2;
12.14. 43cosx 4sinx; 12.28. 2cosx 2sinx;
47
12.29. 7sin x 9cos x 7; 12.30. 9cos x 7sin x7.
§ 5. Тригонометрические неравенства. Определение: Неравенство, в котором неизвестная переменная находится под знаком тригонометрической функции, называется тригонометрическим неравенством.
К простейшим тригонометрическим неравенствам относятся следующие 16 неравенств: sin x a, sin x a, sin x a, sin x a ; cosxa, cosxa, cosxa, cosxa ; tgx a, tgx a, tgx a, tgx a ; ctgx a, ctgx a, ctgx a, ctgx a ;
Здесь x является неизвестной переменной, a может быть любым действительным числом.
5.1. Неравенства вида sin x a, sin x a, sin x a, sin x a.
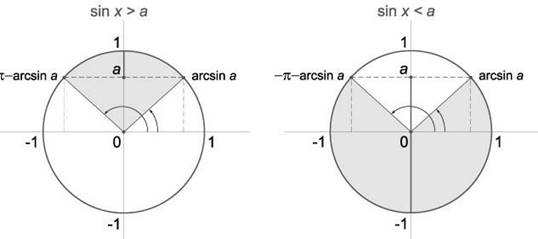
Рис.1 Рис.2
1. Неравенство sin x a.
При a 1 неравенство sin x a не имеет решений.
При a 1 решением неравенства sin x a является любое действительное число.
При 1 a 1 решение неравенства sin x a выражается в виде arcsin a2n x arcsina2n, nZ (рис.1).
2. Неравенство sin x a.
При a 1 неравенствоsin x a не имеет решений. При a 1 решением неравенстваsin x a является любое действительное число.
При a 1 решение неравенства sin x a сводится к решению уравнения sin x 1
48
При 1 a 1 решение неравенстваsin x a выражается в виде arcsin a2n x arcsin a 2n, nZ (рис.1).
3. Неравенство sin x a.
При a 1 неравенствоsin x a не имеет решений. При a 1 решением неравенстваsin x a является любое действительное число.
При 1 a 1 решение неравенстваsin x a выражается в виде arcsin a2n x arcsin a 2n, nZ (рис.2).
4. Неравенство sin x a.
При a 1 неравенствоsin x a не имеет решений. При a 1 решением неравенстваsin x a является любое действительное число.
При a 1 решение неравенства sin x a сводится к решению уравнения sin x 1.
При 1 a 1 решение неравенстваsin x a выражается в виде arcsin a2n x arcsin a 2n, nZ (рис.2).
Примеры.
1.
![]() Решить
неравенство sin x 23
.
Решить
неравенство sin x 23
.
Решение.
![]()
![]()
![]() Отмечаем на оси синусов значение
23
.
Все значения sin x
Отмечаем на оси синусов значение
23
.
Все значения sin x
2.
![]() Решить
неравенство sin1
x 3
2
.
Решить
неравенство sin1
x 3
2
.
3 4 2
49
Решение.
![]()
![]() Обозначим x
Обозначим x
![]() 3 за u . Получим неравенствоsinu
2
.
3 за u . Получим неравенствоsinu
2
.
4 2
![]() Отмечаем на
оси синусов значение 22 .
Все значения sinu
Отмечаем на
оси синусов значение 22 .
Все значения sinu
![]()
![]()
![]() меньшие расположены ниже точки 2 на оси синусов. 2
меньшие расположены ниже точки 2 на оси синусов. 2
4 3 4 4
-
![]()
![]() 5
3
2n
1
x
3
2n,
nZ
;
5
3
2n
1
x
3
2n,
nZ
;
4 4 3 4 4
1
-
![]() 2
2n
x
2n,
nZ
;
2
2n
x
2n,
nZ
;
3 2
3 Ответ:
6
6n
x
![]() 6n, nZ .
6n, nZ .
2
5.2. Неравенства вида cosx a, cosx a, cosxa, cosxa.
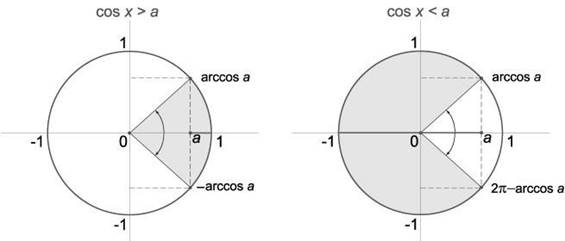
Рис.3 Рис.4
1. Неравенство cosx a.
50
При a 1 неравенство cosx a не имеет решений.
При a 1 решением неравенства cosx a является любое действительное число.
При 1 a 1 решение неравенства cosx a выражается в виде arccosa2n x arccosa2n, nZ (рис.3).
2. Неравенство cosxa.
При a 1 неравенствоcosxa не имеет решений. При a 1 решением неравенстваcosxa является любое действительное число.
При a 1 решение неравенства cosxa сводится к решению уравнения cos x 1
При 1 a 1 решение неравенстваsin x a выражается в виде arccosa2n x arccosa2n, nZ (рис.3).
3. Неравенство cosxa.
При a 1 неравенствоcosxa не имеет решений. При a 1 решением неравенстваcosx a является любое действительное число.
При 1 a 1 решение неравенстваcosx a выражается в виде arccosa 2n x 2arccosa 2n, nZ (рис.4).
4. Неравенство cosxa.
При a 1 неравенствоcosxa не имеет решений. При a 1 решением неравенстваcosxa является любое действительное число.
При a 1 решение неравенства cosxa сводится к решению уравнения cos x 1.
При 1 a 1 решение неравенстваcosxa выражается в виде arccosa2n x 2arccosa2n, nZ (рис.4).
Примеры.
3. Решить
неравенство cos x ![]() .
.
Решение.
Отмечаем на оси косинусов значение ![]() .
Все значения cosx меньшие
.
Все значения cosx меньшие ![]() расположены левее точки
расположены левее точки ![]() на оси косинусов.
на оси косинусов.
![]()
![]() arccos
1
,
2arccos
arccos
1
,
2arccos
![]() 1 2
5.
1 2
5.
2 3 2 3 3
51
![]()
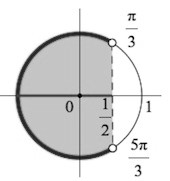
2n, nZ
![]() 4. Решить
неравенство cos3x
53
22
.
4. Решить
неравенство cos3x
53
22
.
Решение.
![]() Обозначим 3x
Обозначим 3x
![]() 5 за u . Получим неравенствоcosu
2
.
5 за u . Получим неравенствоcosu
2
.
3 2
![]() Отмечаем на оси косинусов значение .
Все значения cosu
Отмечаем на оси косинусов значение .
Все значения cosu
![]() 2
34.
2
34.
2
5.3. Неравенства вида tgx a, tgx a, tgx a, tgx a.
52
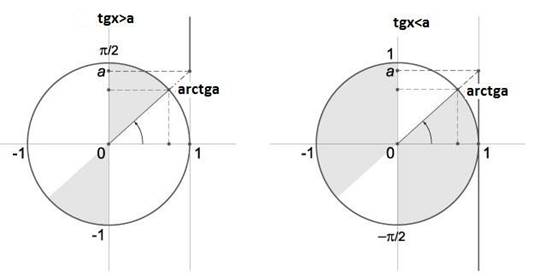
Рис.5 Рис.6
1. Неравенство tgx a.
При любом действительном a решение неравенства имеет вид:
arctga
n
x
![]() n,
nZ
(рис.5).
n,
nZ
(рис.5).
2
2. Неравенство tgx a.
При любом действительном a решение неравенства имеет вид:
arctga
n
x
![]() n,
nZ
(рис.5).
n,
nZ
(рис.5).
2
3. Неравенство tgx a.
При любом действительном a решение неравенства имеет вид:
![]() n
x
arctga
n,
nZ
(рис.6).
n
x
arctga
n,
nZ
(рис.6).
2
4. Неравенство tgx a.
При любом действительном a решение неравенства имеет вид:
![]() n
x
arctga
n,
nZ
(рис.6).
n
x
arctga
n,
nZ
(рис.6).
2 Примеры.
5. Решить неравенство tgx 1. Решение.
Отмечаем на оси тангенсов значение 1. Указываем все значения тангенса, меньшие 1 –ниже 1.
53
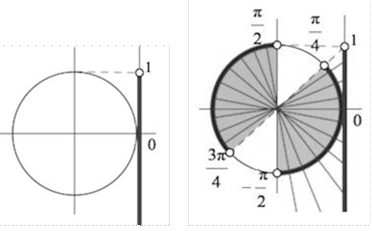
Отмечаем все точки тригонометрического круга, значение тангенса в которых будет меньше 1. Для этого мы соединяем каждую точку оси тангенсов ниже 1 с началом координат; тогда каждая проведенная прямая пересечет дважды тригонометрический круг.
Учитывая, что период тангенса равен , запишем ответ в
виде:![]() n
x
n
x
![]() n,
nZ
.
n,
nZ
.
2 4
6.
![]() Решить
неравенство tg2x
2
3.
Решить
неравенство tg2x
2
3.
3
Решение.
2
![]() Обозначим 2x
Обозначим 2x
![]() за u .
Получим неравенствоtgu
3. 3
за u .
Получим неравенствоtgu
3. 3
![]() Отмечаем на
оси тангенсов значение 3
. Указываем все
Отмечаем на
оси тангенсов значение 3
. Указываем все
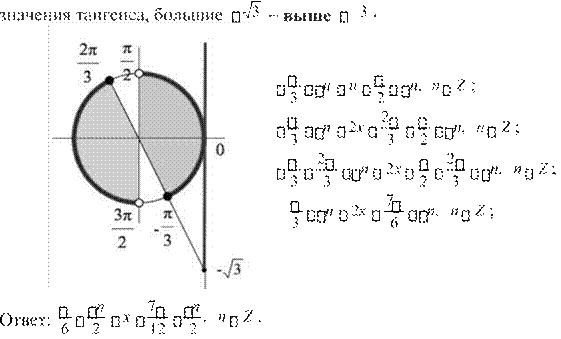
5.4. Неравенства вида ctgx a, ctgx a, ctgx a, ctgx a.
54
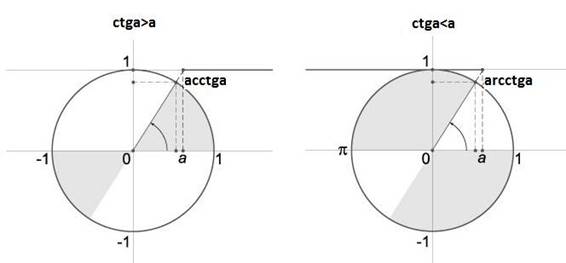
Рис.7 Рис.8
1. Неравенство ctgx a.
При любом действительном a решение неравенства имеет вид: n x arcctga n, nZ (рис.7).
2. Неравенство ctgx a.
При любом действительном a решение неравенства имеет вид: n x arcctga n, nZ (рис.7).
3. Неравенство ctgx a.
При любом действительном a решение неравенства имеет вид:
arcctga n x n, nZ (рис.8).
4. Неравенство ctgx a.
При любом действительном a решение неравенства имеет вид:
arcctga n x n, nZ (рис.8).
Примеры.
7.
![]() Решить
неравенство ctgx 3
.
Решить
неравенство ctgx 3
.
3 Решение:
3
![]() Отмечаем на
оси котангенсов значение . Указываем все значения 3
Отмечаем на
оси котангенсов значение . Указываем все значения 3
![]()
![]() котангенса,
большие 3 – правее 3
.
котангенса,
большие 3 – правее 3
.
3 3
55
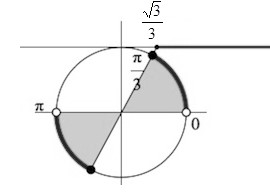
Учитывая, что период котангенса равен , запишем ответ в виде:
n
x
![]() n,
nZ
.
n,
nZ
.
3
8.
Решить
неравенство ctg3x
![]() 1.
1.
6
Решение:
Обозначим 3x
![]() за u .
Получим неравенствоctgu 1. 6
за u .
Получим неравенствоctgu 1. 6
Отмечаем на оси котангенсов значение -1. Указываем все значения котангенса, меньшие -1 – левее -1.
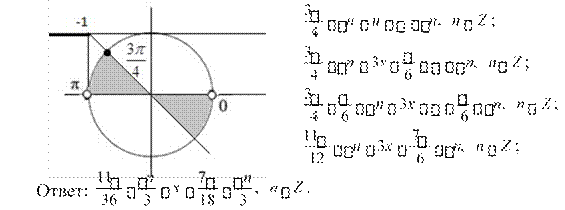
Индивидуальные практические задания №5ИЗ № 5.
1. Решите простейшее тригонометрическое неравенство.
1.1. 3tgx 3 0; 1.10. 2 2sin x 0;
1.2.
![]()
![]() 2cos x
3
0;
1.11. 3 tgx
0;
2cos x
3
0;
1.11. 3 tgx
0;
1.3. 2 2cosx 0; 1.12. 2cosx 2 0;
1.4. 3tgx 3 0; 1.13. 3 2cos x 0;
1.5. 3tgx 3 0; 1.14. 3ctgx 3 0;
1.6. 3 2sin x 0; 1.15. 2cosx1 0;
1.7. 12sinx 0; 1.16. 2sin x 2 0;
1.8.
![]()
![]() 2sin x 3
0;
1.17.
3
3ctgx
0;
2sin x 3
0;
1.17.
3
3ctgx
0;
1.9. 2sinx1 0; 1.18. 2cos x 3 0;
56
1.19.
![]() 3tgx
3
0;
1.25.
3ctgx
3
0;
3tgx
3
0;
1.25.
3ctgx
3
0;
1.20.
![]() 3
2sin
x 0;
1.26. 3ctgx 3
0;
3
2sin
x 0;
1.26. 3ctgx 3
0;
1.21.
![]() 3ctgx
3
0;
1.27. 2sinx1
0;
3ctgx
3
0;
1.27. 2sinx1
0;
1.22. 2cos x 2 0; 1.28. 2sin x 2 0;
1.23.
![]()
![]() 12cosx
0;
1.29.
3tgx
3
0;
1.24.
2sin
x 3
0;
1.30.
3
2cos
x 0.
12cosx
0;
1.29.
3tgx
3
0;
1.24.
2sin
x 3
0;
1.30.
3
2cos
x 0.
2.
3. Решить тригонометрическое неравенство.
![]() 3.1.2.1 tg2х
2
3
;
3.11.2.11 ctg2х
3.1.2.1 tg2х
2
3
;
3.11.2.11 ctg2х
![]() 6
1;
6
1;
3 3
![]()
![]() 3.2.2.2 ctg
х
2
1; 3.12.2.12 tg
3х
4
3 ;
3.2.2.2 ctg
х
2
1; 3.12.2.12 tg
3х
4
3 ;
3 3
![]() 3.3.2.3 tg2х
5
3
;
3.13.2.13 ctg
12
х 6
1;
3.3.2.3 tg2х
5
3
;
3.13.2.13 ctg
12
х 6
1;
6
![]()
![]() 3.4.2.4 ctg
х
3
;
3.14.2.14 ctg
12
х 4
33 ;
3.4.2.4 ctg
х
3
;
3.14.2.14 ctg
12
х 4
33 ;
3 6 3
![]() 3.5.2.5 ctg2х
3 ; 3.15.2.15 tg
12
х 56
1;
3.5.2.5 ctg2х
3 ; 3.15.2.15 tg
12
х 56
1;
4 3
![]()
![]() 3.6.2.6 tg1
х
1; 3.16.2.16 tg
12
х 3
1;
3.6.2.6 tg1
х
1; 3.16.2.16 tg
12
х 3
1;
2 4
![]()
![]() 3.7.2.7 ctg2х
3
3 ; 3.17.2.17 ctg
12
х 6
3 ;
3.7.2.7 ctg2х
3
3 ; 3.17.2.17 ctg
12
х 6
3 ;
4
3.8.2.8 tg3х
![]() 2
1;
3.18.2.18 ctg12
х 34
3 ;
2
1;
3.18.2.18 ctg12
х 34
3 ;
3
![]() 3.9.2.9 ctg
1
х 5
3
;
3.19.2.19 tg2х
3.9.2.9 ctg
1
х 5
3
;
3.19.2.19 tg2х
![]() 6
1;
6
1;
2 6 3
![]()
![]() 3.10.2.10 tg
х
1; 3.20.2.20 ctg
12
х 34
33 ;
3.10.2.10 tg
х
1; 3.20.2.20 ctg
12
х 34
33 ;
3 6
57
![]()
![]() 3.21.2.21 tg
1
х 2
3
;
3.26.2.26 ctg2х
2
3
;
3.21.2.21 tg
1
х 2
3
;
3.26.2.26 ctg2х
2
3
;
2 3 3 3
![]() 3.22.2.22 ctg
1
х
1; 2.273.27. tg2х
3.22.2.22 ctg
1
х
1; 2.273.27. tg2х
![]()
1;
1;
2 3 4
![]() 3.23.2.23 tg2х
3.23.2.23 tg2х
![]() 1;
2.283.28. ctg2х
5
3
;
1;
2.283.28. ctg2х
5
3
;
3 6 3
![]() 3.24.2.24 ctg2х
3 ; 2.293.29. tg2х
34
3 ;
3.24.2.24 ctg2х
3 ; 2.293.29. tg2х
34
3 ;
3
3.25.2.25 cos
1
х 2
2
;
3.30.2.30 ctg3х
![]() 2
1.
2
1.
2 3 2 3
58
Список литературы 1. Башмаков М.И. Математика: учебник для студ. учреждений сред. проф.
образования. — М., 2014.
2. Башмаков М.И. Математика. Сборник задач профильной направленности: учеб. Пособие для студ. учреждений сред. проф. образования. — М., 2014.
3. Башмаков М.И. Математика. Задачник: учеб. пособие для студ. учреждений сред.
проф. образования. — М., 2014.
4. Башмаков М.И. Математика. Электронный учеб.-метод. комплекс для студ.
учреждений сред. проф. образования. — М., 2015.
5. Башмаков М.И. Математика (базовый уровень). 10 класс. — М., 2014.
6. Башмаков М.И. Математика (базовый уровень). 11 класс. — М., 2014.
7. Башмаков М.И. Алгебра и начала анализа, геометрия. 10 класс. — М., 2013.
8. Башмаков М.И. Математика (базовый уровень). 10 класс. Сборник задач: учеб.
пособие. — М., 2008.
9. Башмаков М.И. Математика (базовый уровень). 11 класс. Сборник задач: учеб.
пособие. — М., 2012.
10. Башмаков М.И. Математика: кн. для преподавателя: метод. пособие. — М., 2013 Башмаков М.И., Цыганов Ш.И. Методическое пособие для подготовки к ЕГЭ. — М., 2011.
11. Галицкий М.Л. Сборник задач по алгебре и началам анализа 10-11 класс: Учеб.
пособие. – М.: Просвещение, 1999.
12. Гусев В.А., Григорьев С.Г., Иволгина С.В. Математика для профессий и специальностей социально-экономического профиля: учебник для студ. учреждений сред. проф. образования. — М., 2014.2. Алгебра и начала анализа. 10–11 кл.: Учеб.-метод. пособие/ М.И. Башмаков, Т.А. Братусь, Н.А. Жарковская и др. – М.: Дрофа, 2001. – 240 с.: ил. – (Дидактические материалы).
13. Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по алгебре и началам анализа для 10–11 классов. М.: Илекса, 2005г.
14. Контрольные и самостоятельные работы по алгебре: 10 класс: к учебнику А.Г. Мордковича «Алгебра и начала анализа. 10–11 классы» /М.А. Попов. – М.: Издательство «Экзамен», 2008.
15. Сканави М.И. «Математика в задачах для поступающих в вузы», – М.:
издательство «АСТ», 2010г.
Интернет-ресурсы www.fcior. edu. ru (Информационные, тренировочные и контрольные материалы). www.school-collection.edu.ru (Единая коллекции цифровых образовательных ресурсов).
www.math-ege.sdamgia.ru (Образовательный портал для подготовки к экзаменам) www.resh.edu.ru (Российская электронная школа)
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.