Федеральное государственное автономное образовательное учреждение высшего образования «Национальный исследовательский Нижегородский государственный

университет им. Н.И. Лобачевского»

 

Арзамасский филиал

 

Отделение среднего профессионального образования

(Арзамасский политехнический колледж им. В.А. Новикова)

 

 

 

 

 

 

 

 

 

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ РАБОТ

 

по учебной дисциплине

ОП.02 Техническая механика  по специальности:

35.02.08 Электрификация и автоматизация сельского хозяйства

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Разработчик(и):

 

 

АФ ННГУ отделение СПО

«Арзамасский политехнический

колледж им. В.А. Новикова»             преподаватель                    Д.И Артюхин_________

    (место работы)                        (занимаемая должность)                (инициалы, фамилия)

 

 

 

 

Содержание

 

Пояснительная записка

 

Практическая работа №1 «Определение равнодействующей плоской системы сходящихся сил».

Практическая работа №2 «Определение реакций опор балки».

Практическая работа №3 «Определение параметров вращательного движения».

Практическая работа №4 «Определение перемещений свободного конца бруса»

Практическая работа №5 «Расчет бруса круглого поперечного сечения при сочетании основных деформаций»

 

 

 

Пояснительная записка

 

Методические указания предназначены в помощь обучающимся среднего специального образования, входящей в укрупненную группу специальностей при выполнении практических работ  по дисциплине «Техническая механика». Они составлены на основе программы по дисциплине «Техническая механика», разработанной в соответствии с Федеральными государственными образовательными стандартами  для данной специальности.

Дисциплина «Техническая механика» является общепрофессиональной дисциплиной и при ее изучении отводится значительное место решению практических задач, в том числе в рамках проведения практических работ.

Обучающиеся, выполняя практические работы, реализуют следующие цели:

-             обобщать, систематизировать, закреплять полученные теоретические зна­ния по конкретным темам дисциплины;

-             формировать умения применять полученные знания на практике, реализуя единство интеллектуальной и практической деятельности;

-             развивать аналитические, умения у будущих специа­листов;

-             демонстрировать при решении поставленных задач умения, направленные на формирование профессиональных компетенций, предусмотренных программой дисциплины «Техническая механика»;

-             вырабатывать такие профессионально значимые качества, как самостоятельность, ответственность, точность, творческая инициатива, необходимые при формировании общих компетенций.

Использование методических указаний позволяет обучающимся при  минимальных затратах учебного времени самостоятельно выполнять практические работы, даёт возможность преподавателю и обучающимся контролировать и оценивать знания и умения по данной

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Практическая работа №1

«Определение равнодействующей плоской системы сходящихся сил».

 

Цель работы: Закрепить теоретические знания  и умения определять равнодействующую системы сходящихся сил аналитическим и геометрическим способами

Краткие теоретические и справочно-информационные материалы по теме:

Системой сходящихся сил  называется система, в которой линии действия сил пересекаются в одной точке, называемой центром системы.

Система сходящихся сил имеет равнодействующую, равную геометрической сумме   этих сил и приложенную в точке их пересечения. 

Равнодействующая системы сходящихся сил аналитическим способом определяется по величинам сумм проекций на ось χ и Y по формуле:    .

Направление равнодействующей определяется значением угла равнодействующей с осью Ох по формуле:cos.

Равнодействующую системы сходящихся сил можно определить геометрическим способом.  Для этого  необходимо  построить многоугольник сил заданной  системы сходящихся сил. 

Многоугольник сил строится в следующей последовательности: вычерчиваются векторы сил заданной системы в определённом масштабе один за другим так, чтобы конец предыдущего вектора совпадал с началом последующего. Вектор равнодействующей замыкает полученную ломаную линию, он соединяет начало первого вектора с концом последнего и направлен ему навстречу.

 Измеряя полученный при построении  равнодействующий вектор  сил,  учитывая выбранный масштаб,  определяется  его величина.

Проверка знаний и умений (необходимых для выполнения практической работы)

 

№ п/п	Задание	Вариант ответа
1.	Чему равен модуль равнодействующей сил F1 и F2, если F1 = F2 = 5 кН, α = 600?	А. 7,1 кН В. 9,7 кН С. 7,9 кН Д. 8,7 кН
2.	Какой вид имеют уравнения равновесия сходящейся системы сил?
3.	Чему равна равнодействующая трёх сил, если  R = 10 Н, F1 = F2 = 20 Н, угол  = 30o?	А. 30 Н С. 90 Н В. 0  Н Д. 60 Н

 

Задание: Определить равнодействующую системы сходящихся сил геометрическим и аналитическим способами. Определить погрешность вычислений двумя способами.

 

Порядок выполнения работы:

1)      По данным варианта вычертить систему сходящихся сил.

2)      Определить равнодействующую геометрическим способом.

3)      Определить проекции всех сил системы на ось Ох.

4)      Определить проекции всех сил системы на ось Оу.

5)      Определить модуль равнодействующей по величинам сумм проекций на ось χ и Y.

6)      Определить значение угла равнодействующей с осью Ох аналитическим способом.

7)      Определить погрешность вычислений по формуле.

.

Пример расчета:

F1	=	20	кН
F2	=	5	кН
F3	=	10	кН
F4	=	15	кН
F5	=	10	кН
α1	=	0	°
α2	=	60	°
α3	=	75	°
α4	=	150	°
α5	=	210	°

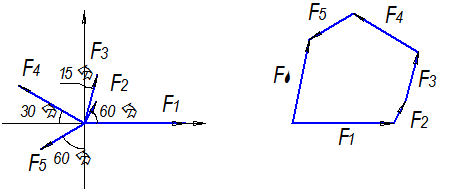
1. Определение равнодействующей геометрическим способом.

Используя свойства векторной суммы сил, вычерчиваем векторы сил в масштабе    2 мм = 1 кН последовательно друг за другом.

Равнодействующей вектор соединяет начало первого вектора с концом последнего и направлен ему навстречу.

С помощью линейки определяем модуль равнодействующей силы, а транспортира угол наклона к её оси.

F_Σгр = 16,5 кН     α_Σх = 79°.

 

 2. Определение равнодействующей аналитическим способом:

 а) Определяем проекции всех сил системы на ось Ох:

 F_1х= F₁· соs 0° = 20 ·1 = 20 кН

 F_2х= F₂ · соs 60° = 5 · 0,5 = 2,5 кН

 F_3х= F₃ · соs 75° = 10 · 0,26 = 2,6 кН

 F_4х= - F₄ · соs 30° = - 15 · 0,866 = - 13 кН

 F_5х= - F₅ · соs 30° = - 10 · 0,866 = - 8,66 кН

 Сложив алгебраические проекции, получим проекцию равнодействующей на ось Ох:

 F_Σх = F_1х + F_2х + F_3х + F_4х + F_5х ; F_Σх = 20 + 2,5 + 2,6 – 13 – 8,66 = 3,44 кН.

 Знак проекции соответствует направлению вправо.

 

 б) Определяем проекции всех сил системы на ось Оу:

 F_1у= F₁ · соs 90° = 20 · 0 = 0

 F_2у= F₂ · соs 30° = 5 · 0,866 = 4,33 кН

 F_3у= F₃ · соs 15° = 10 · 0,966 = 9,66 кН

 F_4у= F₄ · соs 60° = 15 · 0,5 = 7,5 кН

 F_5у= - F₅ · соs 60° = - 10 · 0,5 = - 5 кН

 Сложив алгебраические проекции, получим проекцию равнодействующей на ось Оу:

 F_Σу = F_1у + F_2у + F_3у + F_4у + F_5у ; F_Σу = 0 + 4,33 + 9,66 + 7,5 – 5 = 16,49 кН.

 Знак проекции соответствует направлению вверх.

 

 в) Определяем модуль равнодействующей по величине проекции:

 ;  

 г) Определяем значение угла равнодействующей с осью Ох:

  

  3. Определение погрешности вычислений.

 

Вывод: равнодействующая определена правильно.

 

Контрольные вопросы:

 

1. Какая система сил является системой сходящихся сил?

2. Сформулируйте условие равновесия системы сходящихся сил в аналитической и геометрической формах.

3. Сформулируйте правила построения силового многоугольника.

4. Приведите формулу для определения равнодействующей системы сходящихся сил.

5. В каком случае проекция силы равна 0?

6. В каком случае проекция силы положительна?

 

Практическая работа №2

«Определение реакций опор балки».

 

Цель: Сформировать умения по выполнению расчетов для определения реакций опор балочной системы.

 

Для заданной двухопорной балки определить реакции опор.

 

Пример выполнения задания

 

Двухопорная  балка с шарнирными  опорами А и В нагружена сосредоточенной силой F, распределенной нагрузкой с интенсивностью q и парой силой с моментом m. Определить реакции опор.

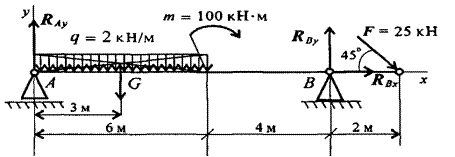
Рисунок

 

Решение

 

1.Левая опора (точка А) – подвижный шарнир. В таком случае, реакция R_ay направлена перпендикулярно опорной поверхности.

       Правая опора (точка В) – неподвижный шарнир. В таком случае, возникает две  реакции R_Byи R_Bx, которые направлены вдоль осей координат.

       2. Заменим равномерно распределенную нагрузкуqсосредоточенной силой G.

G=ql

G=2*6=12кН – сосредоточенная сила размещается в середине пролета.

        Далее задача решается с сосредоточенными силами.

3.Составим уравнение моментов относительно  точки  А.

=G*3+m- R_By*10+F*12*sin45˚=0

 

R_By*10=G*3+m+F*12*sin45˚

R_By*10=12*3+100+25*12*0.7

R_By==34,6кН – реакция направлена верно.

4. Составим уравнение моментов относительно точки В.

=R_ay*10-G*7+m+F*2*sin 45˚=0

R_ay*10=G*7-m-F*2*sin 45˚

R_ay*10=12*7-100-50*0.7

R_ay=-=-5.1кН - реакция отрицательная, следовательно R_ayнужно направить в противоположную сторону.

5.Используя уравнение проекций , определим реакцию R_Bx.

=R_Bx+Fcos45˚=0

R_Bx=-Fcos45˚

R_Bx= - 17,5кН – реакция отрицательная, следовательно ее направление будет противоположно выбранному.

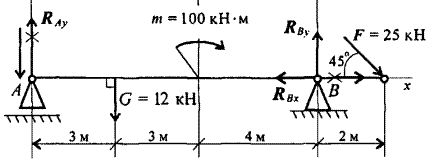
Рисунок

 

6. Проверка

Составим уравнение проекций на ось У.

=0

-R_ay-G+ R_By- Fcos45˚=0

-5.1-12+34.6-25*0.7=0 – решение верно.

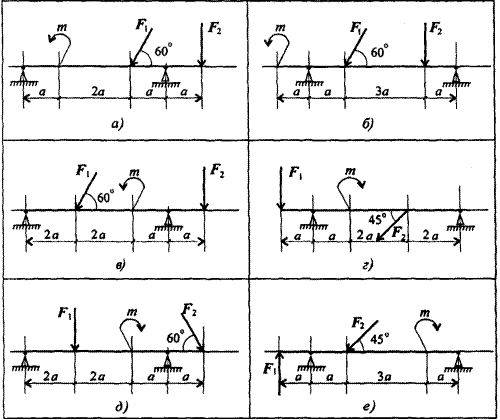
Задание: Определить реакции в опорах по вариантам

 

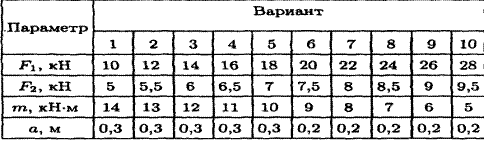
Содержание отчета

1. Наименование работы.

2. Цель работы.

3. Номер варианта.

4.Расчеты

5. Вывод

Контрольные вопросы:

1. Дать определение условию равновесия  плоской системы параллельных сил?

2. Что такое связь?

3. Реакции в связях?

4. Классификация балок, реакции в балках?

5.  Абсолютно твердым телом называется, такое тело в котором:

а) расстояние между каждыми двумя точками  остаются всегда неизменными;

б) размеры каждого очень мало по сравнению другими телами;

в) форма тело остается постоянной;

г) в котором можно пренебречь формой;

д) которое деформируется.

6.Сформулируйте аксиомы статики?

7. Что такое абсолютно твердое тело?

8.Приведите определение понятия «сила»?

9. Что такое равнодействующая и уравновешивающая сила?

10. Дайте определение внешней и внутренней силы?

Практическая работа №3

«Определение параметров вращательного движения».

Цель: знать формулы для определения параметров поступательного и вращательного движений и кинематические графики.

Уметь определять кинематические параметры тела при по­ступательном и вращательном движениях, определять парамет­ры любой точки тела.

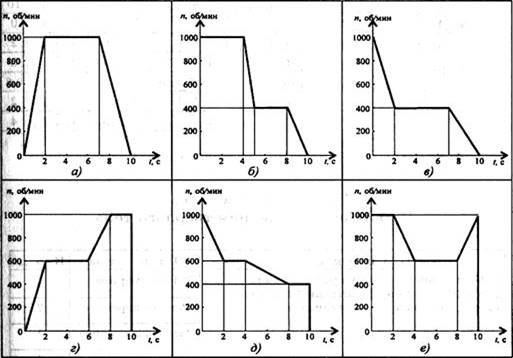
Задание 1. Частота вращения шкива диаметром d меняется со­гласно графику. Определить полное число оборотов шкива за время движения и среднюю угловую скорость за это же время. Построить график угловых перемещений и угловых ускорений шкива. Опреде­лить ускорения точек обода колеса в моменты времени t₁ и t₂.

 

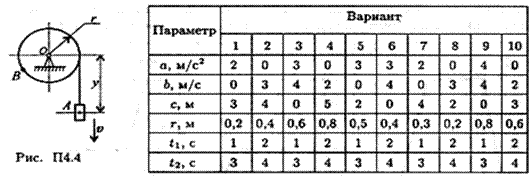
Задание 2. Движение груза А задано уравнением

Определить скорость и ускорение груза в моменты времени t₁ и t₂, а также скорость и ускорение точки В на ободе барабана лебедки (рис. П4.4).

При защите работы ответить на вопросы тестового задания.

Тема 1.9. Кинематика. Простейшие движения твердого тела

Практическая работа № 4

«Определение перемещения свободного конца бруса».

Цель работы: Закрепить теоретические знания  и  умения строить эпюры и выполнять расчёты на прочность при растяжении и сжатии

Краткие теоретические и справочно-информационные материалы по теме:

Растяжением или сжатием называют вид нагружения, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор — продольная сила.

Если внешняя сила направлена от сечения, то продольная сила положительна,  брус растянут; если внешняя сила направлена к сечению, то продольная сила отрицательна, брус сжат.

Эпюрой продольной силы называется график распределения продольной силы вдоль оси бруса.

Ось эпюры параллельна продольной оси бруса.

 Нулевая линия проводится тонкой линией. Значения сил откладывают от оси, положительные - вверх, отрицательные - вниз.

В пределах одного участка значение силы не меняется, поэтому эпюра очерчивается отрезками прямых линий, параллельными оси Oz.

На эпюре проставляются значения Nz. Величины продольных сил откладывают в заранее выбранном масштабе.

 Эпюра по контуру обводится толстой линией и заштриховывается поперек оси.

При растяжении и сжатии в сечении действует только нормальное напряжение, которое определяется по формуле:

,

где N – продольная сила в сечении,

      А  - площадь поперечного сечения.

При определении напряжений брус разбивают на участки нагружений, в пределах которых продольные силы не изменяются, и учитывают места изменений площади поперечных сечений. Рассчитывают напряжения по сечениям, и расчет оформляют в виде эпюры нормальных напряжений.

Строится и оформляется такая эпюра так же, как и эпюра продольных сил.

Расчеты на прочность ведутся по условиям прочности - неравенствам, выполнение которых гарантирует прочность детали при данных условиях.

Для обеспечения прочности расчетное напряжение не должно превышать допускаемого напряжения:

σ ≤ [σ],   где σ =

Расчетное напряжение σ зависит от нагрузки и размеров поперечного сечения, допускаемое только от материала детали и условий работы.

 Существуют три вида расчета на прочность.

 1. Проектировочный расчет - задана расчетная схема и нагрузки. Необходимо  подобрать размеры детали:  

А=

 2. Проверочный расчет - известны нагрузки, материал, размеры детали; необходимо проверить, обеспечена ли прочность.

 Проверяется неравенство σ ≤ [σ]

 3. Определение нагрузочной способности (максимальной нагрузки): [N] = [σ]А.

 

Литература:  Олофинская В.П. Техническая механика. Курс лекций с вариантами практических и тестовых заданий: учебное пособие. - 2-е изд. - М.: ФОРУМ: ИНФРА-М, 2012. 

 

Проверка знаний и умений (необходимых для выполнения практической работы)

 

№ п/п	Задание	Вариант ответа
1.	Какая из эпюр, приведенных на рисунке, соответствует эпюре продольных сил стержня?	A.   Б. B.
2.	Укажите эпюру,  соответствующую эпюре нормальных напряжений для данного бруса	A.   Б. B.
3.	Обеспечена ли прочность бруса в сечении С-С, если допустимое напряжение [σ] = 260 МПа?	A. σ < [σ] .   B.   σ = [σ];    С.  σ > [σ];

 

Задание.

Для стального бруса круглого поперечного сечения диаметром D  требуется:

1) построить эпюры продольных сил  и нормальных напряжений;

2) проверить прочность стержня, если [σ] = 160МПа. Данные своего варианта взять из таблицы.

 

Порядок выполнения работы:

1.      Изобразить расчётную схему.

2.      Разделить брус на участки нагружения, границы которых находятся в точках приложения сил.

3.      Определить продольные силы на участках бруса, используя метод сечений.

4.      Провести нулевую линию параллельно оси бруса.

5.      Найденные величины продольных сил отложить в масштабе в виде ординат, перпендикулярных оси бруса (положительные значения вверх от нулевой линии, отрицательные вниз). Через концы ординат провести линии параллельно оси бруса; поставить знаки и заштриховать эпюру параллельно ординатам.

6.      Разделить брус на участки нагружения для построения эпюры нормальных напряжений, с учётом площади поперечного сечения бруса.

7.      Найти значение нормальных напряжений для каждого участка нагружения.

8.      Построить эпюру нормальных напряжений по найденным значениям.

9.      Определить опасный участок.

10.  Сравнить расчётное напряжение с допустимым напряжением. 

11.  Сделать вывод о прочности бруса.

 

Пример расчета:

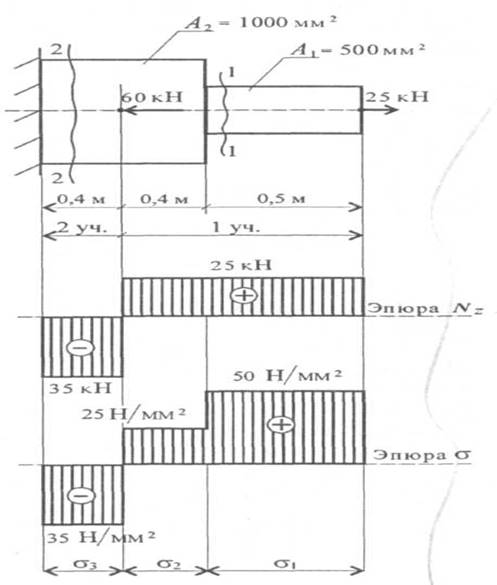
Для стального ступенчатого бруса нагруженного осевыми внешними силами  F₁ = 25 кН и F₂ = 60 кН   при  площадях поперечных сечений  A₁ = 500 см², A₂ = 1000 см² определить  продольные силы  и   напряжения. Построить   эпюры  продольных сил и нормальных напряжений. Проверьте прочность бруса, если если [σ] = 160МПа

 

Решение:

1.    Два участка нагружения для продольной силы:

участок 1: N₁ = + 25 кН; растянут;

участок 2: 25 – 60 + N₂ = 0; N₂ = - 35 кН; сжат.

2. Три участка нагружения по напряжениям:

 =   =

 =   =

 =   =

2.    На опасном участке напряжение <[ 160МПа, значит прочность бруса обеспечена.

 

 

 

 

Контрольные вопросы:               

 

1.      Сформулируйте условие прочности при растяжении и сжатии. Отличаются ли условия прочности при расчете на растяжение и расчете на сжатие.

2.      Какие внутренние силовые факторы возникают в сечении бруса при растяжении и сжатии?

3.      Как распределены напряжения по сечению при растяжении и сжатии?

4.      Запишите формулу для расчета нормальных напряжений при растяжении и сжатии.

5.      Как назначаются знаки продольной силы и нормального напряжения?

6.      Что показывает эпюра продольной силы?

7.      Как изменится величина напряжения, если площадь поперечного сечения возрастет в 4 раза?

 

 

Практическая работа №5

Цель: Уметь рассчитать брус круглого поперечного сечения на прочность при сояетании основных деформаций

«Расчет бруса круглого поперечного сечения при сочетании основных деформаций»

Геометрические характеристики круга и кольца

Круг (рисунок 10.1)

- круг;

Рисунок 10.1

Кольцо (рисунок 10.2)

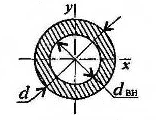
Рисунок 10.2

Моменты сопротивления:

Площади сечения

Условие прочности при совместном действии изгиба и кручения.

Эквивалентные моменты

 

 

Расчетно-графическая работа

Для промежуточного вала редуктора, передающего мощность Р при угловой скорости ω, определить вертикальную и горизонтальную составляющие реакции подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметры вала по сечениям, приняв [σ] – 60 МПа и полагая F_T- 0,364 F_t. Расчёт произвести по гипотезе максимальных касательных напряжений.

 

Рисунок 10.3

 

Указание: Окружную силу определить по формуле

 

Скачано с www.znanio.ru