Федеральное государственное автономное образовательное учреждение высшего образования «Национальный исследовательский Нижегородский государственный

университет им. Н.И. Лобачевского»

 

Арзамасский филиал

 

Отделение среднего профессионального образования

(Арзамасский политехнический колледж им. В.А. Новикова)

 

 

 

 

 

 

 

 

 

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ РАБОТ

 

по учебной дисциплине

ОП.02 Техническая механика  по специальности:

20.02.04 Пожарная безопасность

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Разработчик(и):

 

 

АФ ННГУ отделение СПО

«Арзамасский политехнический

колледж им. В.А. Новикова»             преподаватель                    Д.И Артюхин_________

    (место работы)                        (занимаемая должность)                (инициалы, фамилия)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Одобрено на заседании  методической комиссии

_____________________________________________

Протокол №_______ от «_____» _________ 20____г.

Председатель МК ________________ / С.А. Ефремова /

 

 

 

 

 

Содержание

 

Пояснительная записка

Практическая работа №1 «Определение равнодействующей сходящейся системы сил».

Практическая работа №2 «Определение реакций опор балки».

Практическая работа №3 «Определение центра тяжести плоских сечений».

Практическая работа № 4 «Определение перемещения свободного конца бруса».

Практическая работа №5 «Выбор рационального сечения вала».

Практическая работа №6 «Расчёт привода»

Практическая работа №7 «Определение параметров зубчатых колёс».

Практическая работа №8 «Подшипники качения».

Практическая работа №9 «Резьбовые соединения».

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Пояснительная записка

Методические указания предназначены в помощь обучающимся среднего специального образования, входящей в укрупненную группу специальностей при выполнении практических работ  по дисциплине «Техническая механика». Они составлены на основе программы по дисциплине «Техническая механика», разработанной в соответствии с Федеральными государственными образовательными стандартами  для данной специальности.

Дисциплина «Техническая механика» является общепрофессиональной дисциплиной и при ее изучении отводится значительное место решению практических задач, в том числе в рамках проведения практических работ.

Обучающиеся, выполняя практические работы, реализуют следующие цели:

-             обобщать, систематизировать, закреплять полученные теоретические зна­ния по конкретным темам дисциплины;

-             формировать умения применять полученные знания на практике, реализуя единство интеллектуальной и практической деятельности;

-             развивать аналитические, умения у будущих специа­листов;

-             демонстрировать при решении поставленных задач умения, направленные на формирование профессиональных компетенций, предусмотренных программой дисциплины «Техническая механика»;

-             вырабатывать такие профессионально значимые качества, как самостоятельность, ответственность, точность, творческая инициатива, необходимые при формировании общих компетенций.

Использование методических указаний позволяет обучающимся при  минимальных затратах учебного времени самостоятельно выполнять практические работы, даёт возможность преподавателю и обучающимся контролировать и оценивать знания и умения по данной

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Практическая работа №1

«Определение равнодействующей плоской системы сходящихся сил».

 

Цель работы: Закрепить теоретические знания  и умения определять равнодействующую системы сходящихся сил аналитическим и геометрическим способами

Краткие теоретические и справочно-информационные материалы по теме:

Системой сходящихся сил  называется система, в которой линии действия сил пересекаются в одной точке, называемой центром системы.

Система сходящихся сил имеет равнодействующую, равную геометрической сумме   этих сил и приложенную в точке их пересечения. 

Равнодействующая системы сходящихся сил аналитическим способом определяется по величинам сумм проекций на ось χ и Y по формуле:    .

Направление равнодействующей определяется значением угла равнодействующей с осью Ох по формуле:cos.

Равнодействующую системы сходящихся сил можно определить геометрическим способом.  Для этого  необходимо  построить многоугольник сил заданной  системы сходящихся сил. 

Многоугольник сил строится в следующей последовательности: вычерчиваются векторы сил заданной системы в определённом масштабе один за другим так, чтобы конец предыдущего вектора совпадал с началом последующего. Вектор равнодействующей замыкает полученную ломаную линию, он соединяет начало первого вектора с концом последнего и направлен ему навстречу.

 Измеряя полученный при построении  равнодействующий вектор  сил,  учитывая выбранный масштаб,  определяется  его величина.

Проверка знаний и умений (необходимых для выполнения практической работы)

 

Вариант ответа

1.       

Чему равен модуль равнодействующей сил F₁ и F₂, если F₁ = F₂ = 5 кН, α = 60^0?

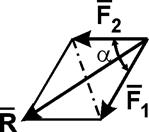
Вариант ответа

 

А. 7,1 кН

В. 9,7 кН

С. 7,9 кН

Д. 8,7 кН

2.       

Какой вид имеют уравнения равновесия сходящейся системы сил?

Вариант ответа

 

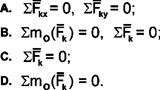
3.       

Чему равна равнодействующая трёх сил, если  R = 10 Н, F₁ = F₂ = 20 Н, угол  = 30^o? 

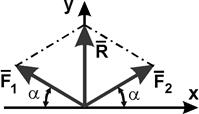
Вариант ответа

 

А. 30 Н

С. 90 Н

В. 0  Н

Д. 60 Н

 

Задание: Определить равнодействующую системы сходящихся сил геометрическим и аналитическим способами. Определить погрешность вычислений двумя способами.

 

Порядок выполнения работы:

1)      По данным варианта вычертить систему сходящихся сил.

2)      Определить равнодействующую геометрическим способом.

3)      Определить проекции всех сил системы на ось Ох.

4)      Определить проекции всех сил системы на ось Оу.

5)      Определить модуль равнодействующей по величинам сумм проекций на ось χ и Y.

6)      Определить значение угла равнодействующей с осью Ох аналитическим способом.

7)      Определить погрешность вычислений по формуле.

.

Пример расчета:

F1	=	20	кН
F2	=	5	кН
F3	=	10	кН
F4	=	15	кН
F5	=	10	кН
α1	=	0	°
α2	=	60	°
α3	=	75	°
α4	=	150	°
α5	=	210	°

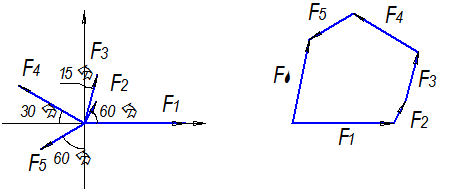
1. Определение равнодействующей геометрическим способом.

Используя свойства векторной суммы сил, вычерчиваем векторы сил в масштабе    2 мм = 1 кН последовательно друг за другом.

Равнодействующей вектор соединяет начало первого вектора с концом последнего и направлен ему навстречу.

С помощью линейки определяем модуль равнодействующей силы, а транспортира угол наклона к её оси.

F_Σгр = 16,5 кН     α_Σх = 79°.

 

 2. Определение равнодействующей аналитическим способом:

 а) Определяем проекции всех сил системы на ось Ох:

 F_1х= F₁· соs 0° = 20 ·1 = 20 кН

 F_2х= F₂ · соs 60° = 5 · 0,5 = 2,5 кН

 F_3х= F₃ · соs 75° = 10 · 0,26 = 2,6 кН

 F_4х= - F₄ · соs 30° = - 15 · 0,866 = - 13 кН

 F_5х= - F₅ · соs 30° = - 10 · 0,866 = - 8,66 кН

 Сложив алгебраические проекции, получим проекцию равнодействующей на ось Ох:

 F_Σх = F_1х + F_2х + F_3х + F_4х + F_5х ; F_Σх = 20 + 2,5 + 2,6 – 13 – 8,66 = 3,44 кН.

 Знак проекции соответствует направлению вправо.

 

 б) Определяем проекции всех сил системы на ось Оу:

 F_1у= F₁ · соs 90° = 20 · 0 = 0

 F_2у= F₂ · соs 30° = 5 · 0,866 = 4,33 кН

 F_3у= F₃ · соs 15° = 10 · 0,966 = 9,66 кН

 F_4у= F₄ · соs 60° = 15 · 0,5 = 7,5 кН

 F_5у= - F₅ · соs 60° = - 10 · 0,5 = - 5 кН

 Сложив алгебраические проекции, получим проекцию равнодействующей на ось Оу:

 F_Σу = F_1у + F_2у + F_3у + F_4у + F_5у ; F_Σу = 0 + 4,33 + 9,66 + 7,5 – 5 = 16,49 кН.

 Знак проекции соответствует направлению вверх.

 

 в) Определяем модуль равнодействующей по величине проекции:

 ;  

 г) Определяем значение угла равнодействующей с осью Ох:

  

  3. Определение погрешности вычислений.

 

Вывод: равнодействующая определена правильно.

 

Контрольные вопросы:

 

1. Какая система сил является системой сходящихся сил?

2. Сформулируйте условие равновесия системы сходящихся сил в аналитической и геометрической формах.

3. Сформулируйте правила построения силового многоугольника.

4. Приведите формулу для определения равнодействующей системы сходящихся сил.

5. В каком случае проекция силы равна 0?

6. В каком случае проекция силы положительна?

 

Практическая работа №2

«Определение реакций опор балки».

 

Цель: Сформировать умения по выполнению расчетов для определения реакций опор балочной системы.

 

Для заданной двухопорной балки определить реакции опор.

 

Пример выполнения задания

 

Двухопорная  балка с шарнирными  опорами А и В нагружена сосредоточенной силой F, распределенной нагрузкой с интенсивностью q и парой силой с моментом m. Определить реакции опор.

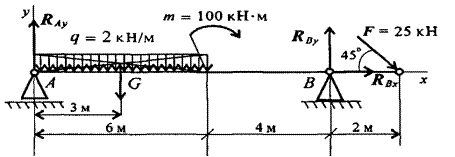
Рисунок

 

Решение

 

1.Левая опора (точка А) – подвижный шарнир. В таком случае, реакция R_ay направлена перпендикулярно опорной поверхности.

       Правая опора (точка В) – неподвижный шарнир. В таком случае, возникает две  реакции R_Byи R_Bx, которые направлены вдоль осей координат.

       2. Заменим равномерно распределенную нагрузкуqсосредоточенной силой G.

G=ql

G=2*6=12кН – сосредоточенная сила размещается в середине пролета.

        Далее задача решается с сосредоточенными силами.

3.Составим уравнение моментов относительно  точки  А.

=G*3+m- R_By*10+F*12*sin45˚=0

 

R_By*10=G*3+m+F*12*sin45˚

R_By*10=12*3+100+25*12*0.7

R_By==34,6кН – реакция направлена верно.

4. Составим уравнение моментов относительно точки В.

=R_ay*10-G*7+m+F*2*sin 45˚=0

R_ay*10=G*7-m-F*2*sin 45˚

R_ay*10=12*7-100-50*0.7

R_ay=-=-5.1кН - реакция отрицательная, следовательно R_ayнужно направить в противоположную сторону.

5.Используя уравнение проекций , определим реакцию R_Bx.

=R_Bx+Fcos45˚=0

R_Bx=-Fcos45˚

R_Bx= - 17,5кН – реакция отрицательная, следовательно ее направление будет противоположно выбранному.

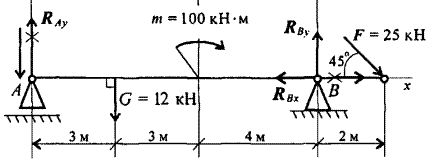
Рисунок

 

6. Проверка

Составим уравнение проекций на ось У.

=0

-R_ay-G+ R_By- Fcos45˚=0

-5.1-12+34.6-25*0.7=0 – решение верно.

Задание: Определить реакции в опорах по вариантам

 

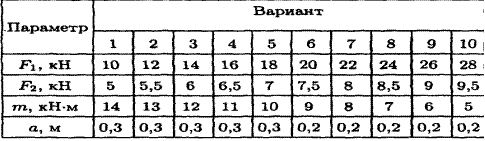
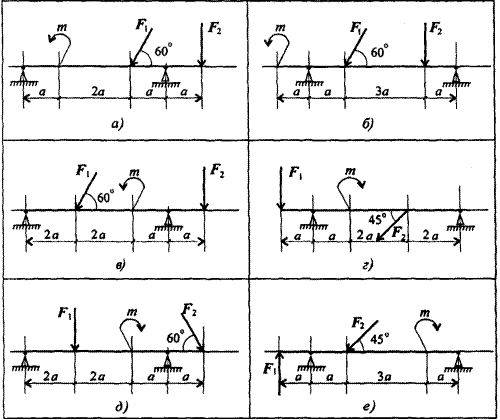
Содержание отчета

1. Наименование работы.

2. Цель работы.

3. Номер варианта.

4.Расчеты

5. Вывод

Контрольные вопросы:

1. Дать определение условию равновесия  плоской системы параллельных сил?

2. Что такое связь?

3. Реакции в связях?

4. Классификация балок, реакции в балках?

5.  Абсолютно твердым телом называется, такое тело в котором:

а) расстояние между каждыми двумя точками  остаются всегда неизменными;

б) размеры каждого очень мало по сравнению другими телами;

в) форма тело остается постоянной;

г) в котором можно пренебречь формой;

д) которое деформируется.

6.Сформулируйте аксиомы статики?

7. Что такое абсолютно твердое тело?

8.Приведите определение понятия «сила»?

9. Что такое равнодействующая и уравновешивающая сила?

10. Дайте определение внешней и внутренней силы?

 

Практическая работа №3

«Определение центра тяжести плоских сечений».

Цель: Сформировать умения, по выполнению расчетов для определения положения центра тяжести фигуры составленной из простых геометрических фигур.

 

Пример выполнения задания

     Определить положение центра тяжести плоской фигуры, показанной на рисунке.

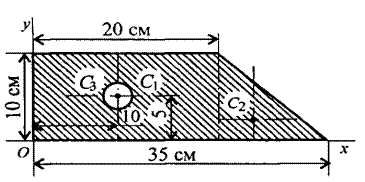
Рисунок

 

Решение:

1.Разбиваем фигуру на три части

1-прямоугольник

2-треугольник

3-круг

2.Определим площадь каждой фигуры

А₁=10*20=200см²

А₂=10*15=75см²

А₃=3,14*3²=28,3см²

3. Определим центр тяжести каждой фигуры

Фигура 1 – прямоугольник: х₁=10 см; у₁=5 см.

Фигура 2 – треугольник: х₂=20+*15=25 см; у₂=*10=3,3 см.

Фигура 3 – круг: х₃=10 см; у₃=5 см.

4. Определим центр тяжести всей фигуры пользуясь формулами

 

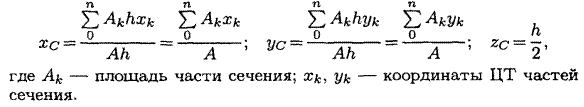
Х_с==14,5см;

Аналогично определяем  у_с=4,5см.

Задание: Определить центр тяжести фигуры по вариантам

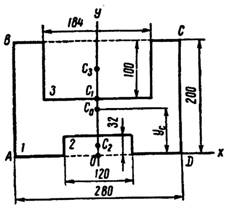
          Вариант  1                                                         Вариант 2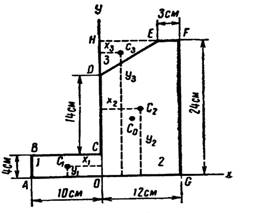

 

 

Вариант 3                                                        Вариант 4

 

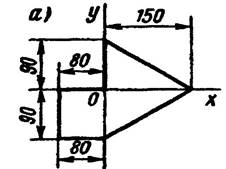
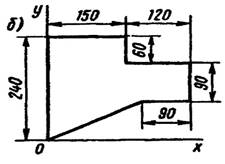
                                     Вариант   6

Вариант 5

 

 

 

 

 

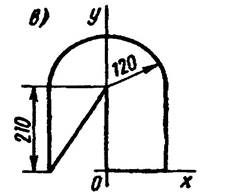
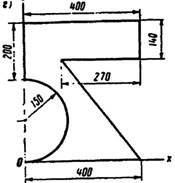
Содержание отчета

1. Наименование работы.

2. Цель работы.

3. Номер варианта.

4.Расчеты

5. Вывод

Контрольные вопросы:

1.Что называется центром параллельных сил?

2.  Как определяются координаты центра параллельных сил?

3. Что называется центром тяжести тела?    

4. Запишите формулу для определения положения центра тяжести простых геометрических фигур: прямоугольника, треугольника, трапеции и половины круга?

5.Как определить положение центра тяжести площади, если известно положение центров тяжести отдельных ее частей?

6. Где расположен центр тяжести дуги окружности?

7. Каким графическим построением можно найти центр тяжести треугольника?

 

 

Практическая работа № 4

«Определение перемещения свободного конца бруса».

Цель работы: Закрепить теоретические знания  и  умения строить эпюры и выполнять расчёты на прочность при растяжении и сжатии

Краткие теоретические и справочно-информационные материалы по теме:

Растяжением или сжатием называют вид нагружения, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор — продольная сила.

Если внешняя сила направлена от сечения, то продольная сила положительна,  брус растянут; если внешняя сила направлена к сечению, то продольная сила отрицательна, брус сжат.

Эпюрой продольной силы называется график распределения продольной силы вдоль оси бруса.

Ось эпюры параллельна продольной оси бруса.

 Нулевая линия проводится тонкой линией. Значения сил откладывают от оси, положительные - вверх, отрицательные - вниз.

В пределах одного участка значение силы не меняется, поэтому эпюра очерчивается отрезками прямых линий, параллельными оси Oz.

На эпюре проставляются значения Nz. Величины продольных сил откладывают в заранее выбранном масштабе.

 Эпюра по контуру обводится толстой линией и заштриховывается поперек оси.

При растяжении и сжатии в сечении действует только нормальное напряжение, которое определяется по формуле:

,

где N – продольная сила в сечении,

      А  - площадь поперечного сечения.

При определении напряжений брус разбивают на участки нагружений, в пределах которых продольные силы не изменяются, и учитывают места изменений площади поперечных сечений. Рассчитывают напряжения по сечениям, и расчет оформляют в виде эпюры нормальных напряжений.

Строится и оформляется такая эпюра так же, как и эпюра продольных сил.

Расчеты на прочность ведутся по условиям прочности - неравенствам, выполнение которых гарантирует прочность детали при данных условиях.

Для обеспечения прочности расчетное напряжение не должно превышать допускаемого напряжения:

σ ≤ [σ],   где σ =

Расчетное напряжение σ зависит от нагрузки и размеров поперечного сечения, допускаемое только от материала детали и условий работы.

 Существуют три вида расчета на прочность.

 1. Проектировочный расчет - задана расчетная схема и нагрузки. Необходимо  подобрать размеры детали:  

А=

 2. Проверочный расчет - известны нагрузки, материал, размеры детали; необходимо проверить, обеспечена ли прочность.

 Проверяется неравенство σ ≤ [σ]

 3. Определение нагрузочной способности (максимальной нагрузки): [N] = [σ]А.

 

Литература:  Олофинская В.П. Техническая механика. Курс лекций с вариантами практических и тестовых заданий: учебное пособие. - 2-е изд. - М.: ФОРУМ: ИНФРА-М, 2012. 

 

Проверка знаний и умений (необходимых для выполнения практической работы)

 

№ п/п	Задание	Вариант ответа
1.	Какая из эпюр, приведенных на рисунке, соответствует эпюре продольных сил стержня?	A.   Б. B.
2.	Укажите эпюру,  соответствующую эпюре нормальных напряжений для данного бруса	A.   Б. B.
3.	Обеспечена ли прочность бруса в сечении С-С, если допустимое напряжение [σ] = 260 МПа?	A. σ < [σ] .   B.   σ = [σ];    С.  σ > [σ];

 

Задание.

Для стального бруса круглого поперечного сечения диаметром D  требуется:

1) построить эпюры продольных сил  и нормальных напряжений;

2) проверить прочность стержня, если [σ] = 160МПа. Данные своего варианта взять из таблицы.

 

Порядок выполнения работы:

1.      Изобразить расчётную схему.

2.      Разделить брус на участки нагружения, границы которых находятся в точках приложения сил.

3.      Определить продольные силы на участках бруса, используя метод сечений.

4.      Провести нулевую линию параллельно оси бруса.

5.      Найденные величины продольных сил отложить в масштабе в виде ординат, перпендикулярных оси бруса (положительные значения вверх от нулевой линии, отрицательные вниз). Через концы ординат провести линии параллельно оси бруса; поставить знаки и заштриховать эпюру параллельно ординатам.

6.      Разделить брус на участки нагружения для построения эпюры нормальных напряжений, с учётом площади поперечного сечения бруса.

7.      Найти значение нормальных напряжений для каждого участка нагружения.

8.      Построить эпюру нормальных напряжений по найденным значениям.

9.      Определить опасный участок.

10.  Сравнить расчётное напряжение с допустимым напряжением. 

11.  Сделать вывод о прочности бруса.

 

Пример расчета:

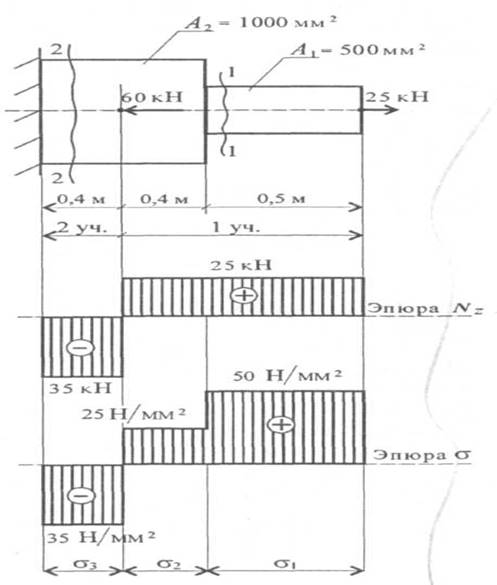
Для стального ступенчатого бруса нагруженного осевыми внешними силами  F₁ = 25 кН и F₂ = 60 кН   при  площадях поперечных сечений  A₁ = 500 см², A₂ = 1000 см² определить  продольные силы  и   напряжения. Построить   эпюры  продольных сил и нормальных напряжений. Проверьте прочность бруса, если если [σ] = 160МПа

 

Решение:

1.    Два участка нагружения для продольной силы:

участок 1: N₁ = + 25 кН; растянут;

участок 2: 25 – 60 + N₂ = 0; N₂ = - 35 кН; сжат.

2. Три участка нагружения по напряжениям:

 =   =

 =   =

 =   =

2.    На опасном участке напряжение <[ 160МПа, значит прочность бруса обеспечена.

 

 

 

 

Контрольные вопросы:               

 

1.      Сформулируйте условие прочности при растяжении и сжатии. Отличаются ли условия прочности при расчете на растяжение и расчете на сжатие.

2.      Какие внутренние силовые факторы возникают в сечении бруса при растяжении и сжатии?

3.      Как распределены напряжения по сечению при растяжении и сжатии?

4.      Запишите формулу для расчета нормальных напряжений при растяжении и сжатии.

5.      Как назначаются знаки продольной силы и нормального напряжения?

6.      Что показывает эпюра продольной силы?

7.      Как изменится величина напряжения, если площадь поперечного сечения возрастет в 4 раза?

 

 

Практическая работа №5

«Выбор рационального сечения вала».

Цель: Сформировать умения по выполнению расчетов на кручение и построению эпюр крутящих моментов.

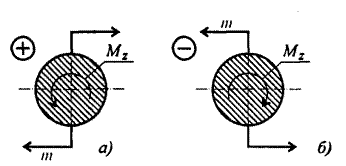
Крутящий момент считаем положительным, если моменты внешних пар сил направлены по часовой стрелке, в этом случае  момент внутренних сил упругости направлен против часовой стрелки.

Правила знаков

Построение эпюр

Порядок построения эпюры моментов аналогичен построению эпюр продольных сил.Ось эпюры параллельна оси бруса, значения моментов откладывают от оси вверх или вниз.

Пример выполнения задания

      На распределительном валу установлены четыре шкива,  на вал через шкив 1 подается мощность 12 кВт, которая  через шкивы 2,3,4 передается потребителю . Мощности распределяются следующим образом: Р₂=8кВт,   Р₃=3кВт,   Р₄=1кВт, вал вращается с постоянной скоростью ω=25рад/с. Построить эпюру крутящих моментов на валу.

 

 

 

 

 

 

 

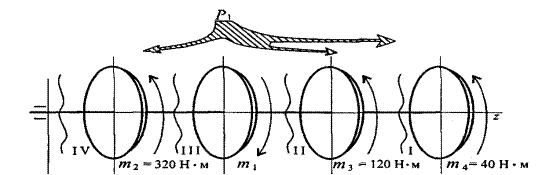
Решение

1.Определяем моменты пар сил на шкивах Р=mω, m=

m₁==480 Н*м                                      m₂==320Н*м

m₃==120 Н*м                                      m₄==40 Н*м

m₁=m₂+m₃+m₄

m₁=320+120+40=480 Н*м

2. Определяем крутящие моменты в поперечных сечениях бруса с помощью метода сечений

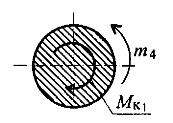
-m4+Мк1=0 Мк1=-m4 Мк1=-40 Н*м

Сечение 1

-m4-m3+Mк2=0 Mк2=-m4-m3 Mк2=-40-120=-160 Н*м

Сечение 2

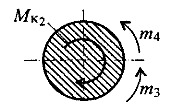
Сечение 3

-m4-m3+m1-Mk3=0 Mk3=-m4-m3+m1 Mk3=-40-120+480=320 Н*м

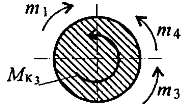
Сечение 4

M_k4=-m₄-m₃+m₁-m₂=0

3. Построим эпюру крутящих моментов.

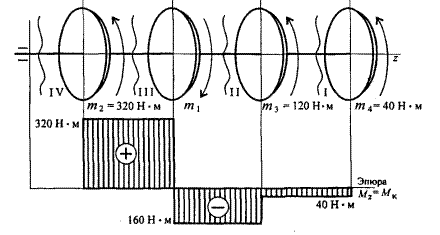
Решить самостоятельно по вариантам:

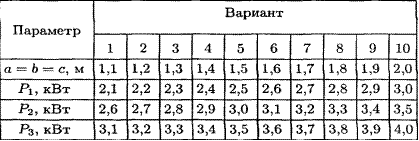
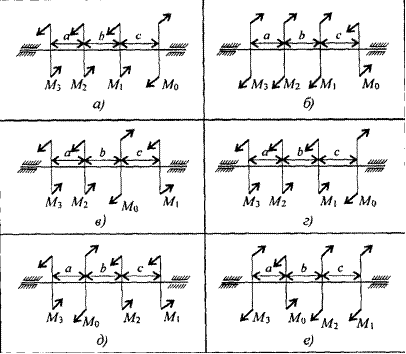
Содержание отчета

1. Наименование работы.

2. Цель работы.

3. Номер варианта.

4.Расчеты

5. Вывод

Контрольные вопросы:

1.Какие внутренние усилия возникают при кручении?

2. Что  называется  жесткостью при  кручении?

3. Условие прочности вала при кручении?

4.Какие деформации возникают при кручении?

5.Какой вид нагружения называется кручением?

6.Как вычисляют значение крутящего момента в поперечном сечении вала?

7. Опишите технику построения эпюры крутящих   моментов?

 

Практическая работа №6

«Расчёт привода»

Цель:Сформировать умения, по выполнению расчетов для определения совместного действия изгиба и кручения на валу.

Пример выполнения задания

Из условия прочности рассчитать необходимый диаметр вала . На валу установлены два колеса. На колеса действуют две окружные силы F_t1=1,2 кН   F_t2=2кН, и две радиальные силы F_r1=0,43 кН    F_r2=0,72кН. Диаметры колес соответственно равны d₁=0,1м ,   d₂=0,06м,  [σ]=50Мпа.

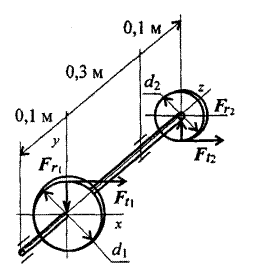
Решение

1.Составим расчетную схему вала.

 

     2.Определим крутящий момент на валу

М_к=М_вр=F_t1=F_t2

М_к=1,2₌0,06кН*м=60 Н*м

3. Изгиб рассматриваем в двух плоскостях:  горизонтальной  (плоскость Н) и вертикальной (плоскостьV)

      В горизонтальной плоскости определяем реакции в опоре

=F_t1*a-R_B^H(a+b)+F_t2(a+b+c)=0

1,2*0,1-R_B^H*0,4+2*0,5=0

R_B^H=2,8кН

= R_А^H(а+b)-F_t1*b+F_t2*c=0

R_А^H*0,4-1,2*0,3+2*0,1=0

R_А^H=0,4кН

 Определяем изгибающие моменты в точках В и С

М_С^Н=400*0,1=40 Н*м

М_В^Н=-2000*0,1=200 Н*м

    В вертикальной плоскости определяем реакции в опоре

= F_r1*a-R_B^V(a+b)-F_r2(a+b+c)=0

-R_B^V*0,4+0,43*0,1-0,72*0,5=0

R_B^V=-0,79кН

= R_А^V(a+b)- F_r1*b-F_r2*c=0

    R_А^V*0,4-0,43*0,3-0,72*0,1=0

R_А^V=0,5кН

   Определяем изгибающие моменты в точках С и В

М_С^V= R_А^V*aМ_С^V=500*0.1=50 Н*м

М_B^V= F_r2*cМ_B^V=720*0.1=72 Н*м

    Определяем суммарные изгибающие моменты в точках В и С

М_С= =63 Н*м

М_В==215 Н*м

   В точке В максимальный изгибающий момент, здесь же действует и крутящий момент.

    Расчет диаметра вала ведем по наиболее нагруженному сечению.

 

 

 

 

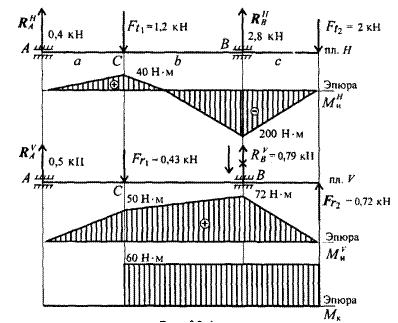
4.Эквивалентный момент в точке В по третьей теории прочности

М_{экв 111}=

М_{экв 111}==223 Н*м

 

5. Определяем диаметр вала  круглого поперечного сечения из условия прочности

σ_экв=≤[σ], W_х=0,1d³,≤[σ]

d ≥  d≥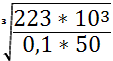=35,5мм

Округляем полученную величину: d=36мм

6. Определяем необходимые размеры вала кольцевого сечения при с=0,8

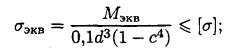
W_х=0,1d³(1-с⁴) – кольцо

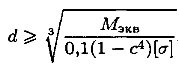
Диаметр вала кольцевого сечения можно определить по формуле

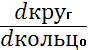=d_кольцо=d_круг⁴

 

d_кольцо=36⁴       d ≥42,5мм

Примем d=42мм

Перегрузка незначительная d_вн=0,8d=0,8*42=33,6мм≈33мм

7. Сравним затраты металла  по площадям сечения вала в обоих  случаях

       Площадь поперечного сечения сплошного вала

     А_1круга===1018мм²

       Площадь поперечного сечения полого вала

 А_{2кольца}=(d²-d²_внутр)

         А_{2кольца}==530мм

      Площадь поперечного сечения сплошного вала почти в два раза больше вала кольцевого сечения

=≈2

Задание: решить самостоятельно по вариантам

Вариант 2

 

Вариант 3

Содержание отчета

1. Наименование работы.

2. Цель работы.

3. Номер варианта.

4.Расчеты

5. Вывод

Контрольные вопросы:

1. Что такое сложное сопротивление?

2.Какие виды деформации бруса называют сложным со­противлением? 

3. Какой изгиб называется косым?

4. Сформулируйте принципы,  на  которых строится  рас­чет брусьев при сложном сопротивлении?

5.  Какие внутренние усилия возникают в стержне в  случае сложного сопротивления?

6. По каким формулам определяются нормальные напряжения при косом изгибе?

7.Когда возникает косой изгиб? 

 

Практическая работа №7

«Определение параметров зубчатых колёс».

Цель работы: Сформировать навыки по определению конструкции цилиндрических редукто­ров, кинематической схемы редукто­ра, изучить расчетные формулы геометрических параметров редуктора. Сделать вывод.

Зубчатый редуктор – это механизм, состоящий из зубчатых передач и предназначенный для понижения угловых скоростей и увеличения крутящих моментов с постоянным передаточным отношением, выполненный в виде отдельного агрегата.

Зубчатые редукторы бывают одноступенчатые, выполненные из одной зубчатой передачи, и многоступенчатые, выполненные из нескольких

последовательно соединенных зубчатых передач.

На рис. показан цилиндрический двухступенчатый зубчатый редуктор с

параллельными осями внешнего зацепления с косыми зубьями (обозначение

приведено согласно ГОСТу 2.770-68).

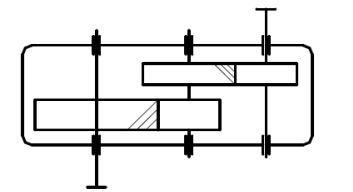
        Рисунок 1 - Зубчатый цилиндрический двухступенчатый редуктор с параллельными осями внешнего зацепления с косыми зубьями.

Передаточное число любой ступени редуктора определяется по формуле:

                                                            И=

    где z1– число зубьев меньшего зубчатого колеса – шестерни;

z2– число зубьев большего зубчатого колеса – колеса.

    Общее передаточное число редуктора определяется по формуле:

Ир=И1*И2

где  И1, И2-     передаточные числа отдельных ступеней.

Окружной модуль зацепления передачи определяется по формуле:

m_t=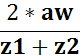

где aw- межосевое расстояние рассматриваемой ступени редуктора.

Допустимое значение мощности, которая может длительно передаваться

редуктором определяется из условия прочности по формуле:

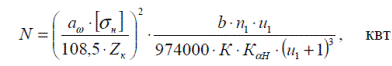
где σ_н– допускаемые контактные напряжения материала зубчатых колес, кгс/мм2;

b – наименьшая ширина зубчатого колеса ступени, мм;

n1 – частота вращения ведущего вала редуктора, об/мин;

z к– коэффициент, учитывающий специфику косозубого зацепления;

K – коэффициент нагрузки;

     КaН -коэффициент неравномерности распределения нагрузки между

зубьями.

Корпус редуктора воспринимает силы, действующие в зацеплении и

обеспечивает правильное взаимное расположение деталей.На верхней плоскости крышки корпуса для осмотра колес и других деталейредуктора и для заливки масла делают окно максимальных размеров.Точность фиксирования крышки относительно корпуса редуктора (для предотвращения деформации наружных колец подшипников и перекоса крышек подшипников при смещении крышки относительно корпуса) достигается двумя штифтами, которые предохраняли крышку и корпус от сдвига при растачивании. Для плотного прилегания в зоне сопряжения корпуса с крышкой

поверхности шабрят или шлифуют. Для уплотнения их смазывают герметиком.

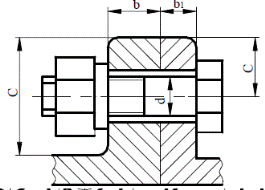
         Рисунок 2 - Крепление крышки и корпуса редуктора

           Для крепления корпуса к плите или раме в опорной поверхности корпуса

делают фланцы с отверстиями для крепежных болтов.

         Для упрочнения опорных фланцев и приливов подшипниковых гнезд выполняют ребра жесткости, которые одновременно увеличивают общую жесткость корпуса.

Для уменьшения потерь мощности на трение, снижения износа, предохранения от коррозии, заедания и лучшего отвода тепла трущиеся   поверхности смазывают маслами. 

В корпус редуктора заливают масло из условия 0,3…0,7 литра на 1 квт

передаваемой мощности. При вращении колес масло разбрызгивается зубьями.

Внутри корпуса образуется масляный туман. Частицы масла покрывают   поверхности всех деталей внутри корпуса.

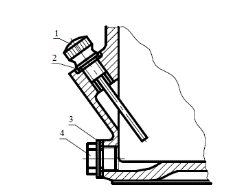
          Рисунок 3 – Маслоуказатель и пробка: 1 – маслоуказатель; 2 – прокладка; 3 – прокладка; 4 – пробка.

         При работе редуктора масло постепенно загрязняется продуктами износа и

с течением времени стареет, свойства его ухудшаются. Для слива отработанного

масла в корпусе редуктора имеется сливное отверстие, закрываемое пробкой.

         Для подъема и транспортировки крышки корпуса и собранного редуктора

применяют проушины . Допускается применение специальных грузовых

болтов.

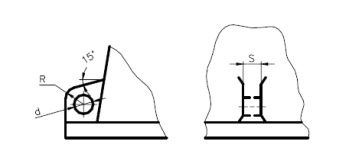
          Рисунок 4 – Проушина крышки

           Во время работы редуктора внутри корпуса в результате нагрева воздуха и

масла повышается давление. Чтобы избежать выбрасывания масла через

уплотнения и стыки, внутреннюю полость корпуса сообщают с внешней средой

отдушиной . Для наблюдения за уровнем масла в корпусе устанавливается

жезловый маслоуказатель,  для которого на корпусе делается специальный прилив. Уровень масла контролируется двумя рисками, нанесенными на стержне

маслоуказателя.

           Для осевого фиксирования зубчатых колес в редукторе используют буртики

на валу, распорные втулки и торцы колец подшипников.    В качестве опор валов редуктора широкое распространение получили  радиальные однородные шарикоподшипники. В системе соединений подшипников с валом и корпусом кольца принимают за основные детали.Различные посадки обеспечиваются выбором соответствующих отклонений цапф валов и отверстий корпусов. Посадка внутренних колец подшипников осуществляется в системе отверстия, а наружных – в системе вала. Расчетный ресурс подшипника может быть обеспечен правильным выбором характера

посадок его колец. Посадки колец зависят в основном от условия нагружения

кольца. Если нагружение кольца местное, то есть кольцо не вращается

относительно радиальной нагрузки (неподвижное кольцо), то следует применять

посадки с зазором. Это обеспечивает более равномерный износ по окружности

дорожки качения. Если нагрузкациркулярная, то есть   кольцо воспринимает радиальную нагрузку последовательно всей окружностью  дорожки качения (кольцо вращается), то следует применять посадки с натягом.

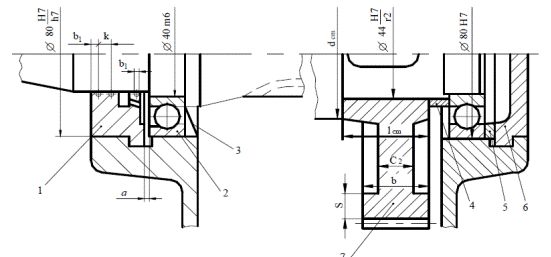
      Рисунок 5 – Опоры валов: 1 – крышка закладная с отверстием; 2 – шарикоподшипник радиальный однорядный; 3 – шайба маслозащитная; 4 – втулка; 5 – кольцо регулировочное; 6– крышка закладная глухая; 7 – колесо зубчатое; а – температурный зазор; в –ширина зубчатого венца.

      При картерной смазке зубчатых колес подшипники качения смазываются

брызгами масла. Для косозубых колес с целью предотвращения попадания в

подшипник продуктов износа, а также излишков масла, подшипники защищают

маслозащитными шайбами . Конструкция маслозащитных шайб зависит от

конструкции подшипникового узла.Для предохранения вытекания масла из подшипниковых узлов наружу, а также для защиты от попадания пыли и влаги извне в изучаемом редукторе применяются бесконтактные (щелевые) уплотнительные устройства, принцип работы которых основан на создании сопротивления протекающего через них масла. Для увеличения сопротивления передвижению масла в уплотнении применены кольцевые цилиндрические канавки . Сопротивление

увеличивается в результате последовательного расширения и сужения потока

масла.

Содержание отчета

1. Наименование работы.

2. Цель работы.

3.Описание работы

4. Вывод

Контрольные вопросы:

1. Каковы основные достоинства и недостатки  зубчатых передач  по сравнению с другими передачами?

2.Чем отличается закрытая передача от открытой?

3. Что такое эвольвента окружности и какими свойствами она обладает?

4.С какой целью производят смазывание зубчатых передач?

5. Каково влияние числа зубьев на их форму и прочность?

6.  Почему эвольвентное зацепление имеет преимущественное применение?

7.По каким признакам классифицируют зубчатые передачи?

 

Практическая работа №9

«Резьбовые соединения».

Цель работы: Познакомиться с конструктивными элементами резьбовых соединений и научиться рассчитывать резьбовые соединения

Порядок выполнения практической работы:

1.  Из таблицы 1 в соответствии с номером варианта выбираются номера задач для практической работы.
2.  Условия задач представлены ниже таблицы
3.  Перед решением задач следует определить к какому из 4 случаев относится условие задачи
4.  Последовательность решения приводится в примерах расчета

ЗАДАНИЯ

№вар	№№задач	№вар	№№ задач	№вар	№№ задач
1	1,2,3,4	12	4,6,9,12,	23	3,12,17,23
2	2,6,8,24	13	3,5,9,11	24	5,17,19,22
3	1,2,10,20	14	9,13,15,22	25	6,10,15,17,
4	1,6,8,15	15	8,9,16,20	26	2,14,17,20
5	1,5,6,14	16	3,9,14,15	27	3,5,13,24
6	6,11,12,24	17	2,9,19,22	28	8,16,17,22
7	7,13,15,22	18	4,12,21,20	29	2,18,19,20
8	4,6,7,12	19	2,6,10,21,	30	3,12,18,23
9	7,8,15,20	20	3,5, 13,24	31	5,10,18,22
10	6,7,10,16	21	12,14,21,22	32	11,15,18,20
11	5,7,11,22	22	16,19,20,21	33	3,13,16,18,

УСЛОВИЯ ЗАДАЧ

Задача 1

Рассчитать диаметр болта (болт предварительно затянут) для соединения двух деталей из чугуна с упругой прокладкой из резины, если максимальная осевая сила растяжки F_max=12кH, число болтов z=4, материал болтов сталь 4.6 класса прочности. Нагрузка постоянная. [s]_т=400МПа. 6мм<d<16мм

Задача 2

Три детали соединяются двумя болтами из Ст.5, коэффициент трения f=0,15, материал болтов 5.6 класса прочности. Действует постоянная поперечная сила F=3kH. [s]_т=500МПа. 16мм<d<32мм.

Задача 3

Рассчитать диаметр болта d₀ -диаметр отверстия болтового соединения без зазора, соединяющего две детали двумя болтами под действием поперечной силы F=12kH. Сталь болтов соответствует 4.6 классу прочности. [s]_т=400МПа.

Задача 4.

Определить диаметр болта, соединяющего две детали без приложения нагрузок, если F_зат=10KH. Сталь болтов соответствует 4.6 классу прочности. [s]_т=400МПа. 16мм<d<30мм.

Задача5

Определить требуемый диаметр болта из Ст. 3 для соединения двух пластин исходя из условия, что при коэффициенте трения f=0,18 сдвигающая сила F=3,4kH. Затяжка болта неконтролируемая. [s]_т=250МПа.

Задача 6

Определить диаметр болтов d₀, устанавливаемых без зазора в отверстие из-под развертки для двух пластин, если число болтов z=3, [i]_cp⁼50 МПа, F=15kH.

Задача 7

Крышка цилиндрического резервуара прикреплена к его фланцу 16 болтами из Ст.З. Определить диаметр болтов, если избыточное давление газа в резервуаре р=2,5Ч10^-6 н/м². Между фланцами и крышкой резервуара имеется асбестовая прокладка. Диаметр резервуара 250 мм.

Задача 8

Рассчитать   болт   грузовой   скобы   воспринимающей максимальную   нагрузку   F=20kH.   Материал   болта   Ст.3.

[s]_т=250МПа.

Задача 9

Подобрать диаметр болтов для крепления крышки к цилиндру высокого давления судовой паровой машины с прокладкой из резины, число болтов z =16, диаметр крышки D=690   мм,   [s]_т=290МПа,   наибольшее   давление   пара    в цилиндре р_mах=1,32н/мм²

Задача 10

Болты установлены в отверстия из-под развертки. Число болтов z=16. Болты соединяют две детали. Определить диаметр отверстия, если [i]_cp=50 МПа, поперечная сила, действующая на соединение F=15kH

Задача11

Рассчитать номинальный диаметр резьбы хвостовика крюка грузоподъемного крана, если нагрузка F=40kH, крюк изготовлен из ст З,  [s]_т=240МПа

Задача 12

Рассчитать диаметр болта для соединения трех пластин, если поперечная сила действующая на соединение F=3 кН, коэффициент трения f=0,2, затяжка неконтролируемая [s]_т= 240МПа

Задача 13.

Рассчитать винты крепления корпуса длиннофокусного микроскопа к станине экспериментальной установки Число винтов z = 4. По техническим условиям для нормальной работы   микроскопа  необходимо  создать  силу  прижатия F = 0,8 кН. Материал винтов — сталь Ст З, затяжка неконтролируемая.

Задача 14.

Рассчитать болты крепления рамы основания привода цепного конвейера. Максимальная сила на болт F=12 кН. Материал болтов сталь Ст З, затяжка неконтролируемая, коэффициент запаса прочности принять минимальным.

Задача 15.

Рассчитать болты крепления венца зубчатого колеса с колесным центром (рис. 1); диаметр окружности центров болтов D_o = 300 мм, вращающий момент, передаваемый червячным колесом М = 9 кНм (М = F Ч D₀/2),    коэффициент  трения  между  венцом  и  центром  f = 0,08, материал болтов — сталь 20. Число болтов z = 8.

Рис. 1. Болтовое соединение венца зубчатого колеса с центром:

1 — вал; 2 — центр колеса; 3 — болт; 4 - венец колеса

Задача 16.

Рассчитать болт соединения ухо - серьга (рис. 2), используемого для крепления троса подвески контактной сети. Сила, действующая на соединение, F = 3 кН, серьга податливая (легко деформируется силой затяжки болта). Материал болта — сталь 10, коэффициент трения между ухом и серьгой f= 0,2, затяжка неконтролируемая.

Рис. 2.  Болтовое соединение  подвески контактной сети:

1 — ухо; 2 — серьга

Задача 17

Подобрать диаметр  болтов крепления днища автоклава. Внутренний диаметр прокладки D= 520 мм, рабочее давление в автоклаве р =4Н/мм², число болтов z = 36. Болты выполнены из стали Ст З, коэффициент внешней нагрузки c = 0,5 (прокладка податливая из резины); затяжка неконтролируемая.

Задача 18.

Выполнить проверочный расчет болтов фланцевого соединения находящегося    под    действием   переменной   осевой   нагрузки   F = 90 кН. Число болтов z = 24; затяжка неконтролируемая; материал болтов — сталь 20, материал прокладки – асбест.

Задача 19

Рассчитать винты кольца крепления стекла в смотровом окне вакуум – камеры. Общее усилие прижатия кольца должно составлять F=8кН, число винтов z=6, материал винтов - сталь 45.

Задача 20

Рассчитать болты дисковой муфты, устанавливаемые в отверстия   без   зазора,   если   передаваемая   муфтой   мощность  Р = 40 кВт (Р = М Чw), частота вращения соединяемых муфтой валов n=300об/мин (n = 30Чp¤w), болты расположены по диаметру D₀ = 240 мм и число болтов z=4. Условия приложения нагрузки считать статическими.

Вращающий момент М = FD₀/2.

Задача 21

Рассчитать болты фланцевого соединения водопроводных труб, находящихся под постоянным давлением р = 2 Н/мм², прокладка тонкая из паронита диаметром D₀ = 240 мм, число болтов z=6.

Задача 22

Определить требуемый диаметр болтов d_o, устанавливаемых в отверстие из-под развертки, если число болтов z=3, [i]_ср = 50 МПа, F = 15 кН

Задача 23

Определить диаметр резьбы болта хвостовика грузоподъемного устройства, нагруженного силой F = 30 кН, изготовленного из стали Ст3

Задача 24

Рассчитать болты, соединяющие  крышку с цилиндрическим сосудом для сжатого воздуха при следующих данных: давление сжатого воздуха в цилиндре р=0,5 Н/мм²., внутренний диаметр цилиндра D = 450 мм, число болтов z = 16, материал болтов сталь 20, прокладка из резины.

 

 

ПРИМЕРЫ РАСЧЕТА

Случай 1

Болт затянут силой F₀, внешняя нагрузка отсутствует

Задача 1

Винтовая стяжка имеет правую и левую метрическую резьбу с крупным шагом. Определить диаметр резьбы, если максимальная осевая нагрузка F=20 кН. Материал винтов класса прочности 4.6. Нагрузка постоянная.

Решение:

1. Для   резьбового   соединения   с   неконтролируемой затяжкой   по   таблице   2   принимаем   [n]=3   в   предположении,   что наружный   диаметр    резьбы  d  находится в интервале 16...30 мм. По таблице 3 определяем [s]_т=240 МПа

Допускаемое напряжение [s]_р=[s]_т/[n]=240/З МПа=80 МПа

1.  Расчетная нагрузка

F_расч=1,3F=1,3Ч20кН=26кН

З.Расчетный диаметр резьбы винтов 

По таблице 4  принимаем  резьбу М24 с шагом  р=3мм, для которой

 d_p=d-0,94p=24-0,94Ч 3=21,18мм >20,1мм.

 Резьба М24 пригодна

Случай 2

Болтовое соединение нагружено поперечной силой F

Задача 2

Три стальные полосы растянуты силой F=2,8kH, крепятся с помощью двух болтов, материал болтов класса прочности 4.6. Нагрузка постоянная.

Решение:

1. Для болтового соединения с неконтролируемой затяжкой по таблице 2 принимаем [n]=3, в предположении, что наружный диаметр резьбы находится в интервале 16...30 мм. По таблице 3  определяем [s]_т=240МПа

Допускаемое напряжение

[s]_р= [s]_т/[n]=240/3 МПа=80 МПа

2.Принимаем коэффициент запаса по сдвигу листов К=1,6 (коэффициент запаса по сдвигу К=1,4...2) и коэффициент трения f=0,16, (для стальных и чугунных поверхностей f=0,15...0,20), i - число стыков, z - число болтов

Необходимая сила затяжки болтов: F₀=FK/fЧiЧz=2,8Ч1,6/0,16Ч2Ч2 =7 кН

3. Расчетная сила затяжки болта

F_Pасч=l,3F=l,3Ч7 кН=9,1кН

4.Расчетный диаметр резьбы

По таблице 4 принимаем резьбу М16 с шагом р=2 мм, для которой

d_p=d-0,94p=16-0,94Ч2=14,12мм >13,15мм.

Резьба М16 пригодна

Случай З

Болтовое соединение повышенной точности для отверстий из-под развертки (без зазора)

Задача 3

Определить диаметр болта d₀ - диаметр отверстия болтового соединения без зазора, для соединения двух деталей двумя болтами под действием поперечной силы F=10kH. Сталь болтов соответствует 5.6 классу прочности. [s]_т=300МПа

Решение

1.  Допускаемое касательное напряжение на срез стержня болта

[i]_ср=(0,2 - 0,3) [s]_т=0,25Ч300=75 МПа

1.  Диаметр стержня болта d₀

где  i - число стыков, z - число болтов

Резьба М10 пригодна

Случай 4

Болтовое соединение предварительно затянуто при сборке и нагружено внешней осевой растягивающей силой. В соединении используется прокладка из упругого материала.

Задача 4

Определить диаметр резьбы болтов крепящих крышку резервуара,   если   максимальная   сила давления газа на крышку F_max=38 кН, число болтов z=12, материал болтов - сталь класса прочности 5.6, материал прокладок - асбест

Решение

1. Для   резьбового   соединения   с   неконтролируемой затяжкой по таблице 2 принимаем [n]=4,5 в предположении, что наружный диаметр резьбы находится в интервале 6... 16 мм, по таблице 3 [s]_т=300МПа

Допускаемое напряжение [s]_р=[s]_т/[n]=300/4,5МПа=66,7МПа

2. Расчетная нагрузка F_pacч=F_max/z=38/12 кН=3,18 кН

где z – число болтов

З.Для герметичности соединения болты ставятся с предварительной затяжкой при сборке. Учитывая упругую асбестовую прокладку в соединении, принимаем c=0,45. При постоянной нагрузке Кзат⁼1,75.

При приближенных расчетах принимают: для соединений стальных и чугунных деталей без упругих прокладок c=0,2 - 0,3

Для соединений стальных и чугунных деталей с упругими прокладками (асбест, паронит, резина и др.) c=0,4 - 0,5

К_зат- коэффициент запаса предварительной затяжки:

При постоянной нагрузке К_зат=1,25 - 2

При переменной нагрузке К_зат=2 - 4

4.Сила предварительной затяжки

F₀=K_зат(1 -c)F = 1,75Ч(1 - 0,45)Ч 3,18 =3,06 кН

5.Расчетная сила

F_pacч=l,3F₀ + cF = (1,3Ч 3,06 + 0,45Ч3,18)кН =5,4 кН

1.  Расчетный диаметр резьбы болта

По таблице 4 принимаем резьбу М12 с шагом р=1,75, для которой

d_p=d - 0,94p=12 - 0,94Чl,75=10,35мм >10,2мм

Резьба М12 пригодна

ПРИЛОЖЕНИЯ

Значения требуемого коэффициента запаса прочности [n] при расчёте болтов с неконтролируемой затяжкой

Таблица 2

Сталь	Постоянная нагрузка	Переменная нагрузка
	Диаметр резьбы d, мм
	6...16	16...30	30...60	6...16	16...30	30...60
Углеродистая	5...4	4...2,5	2,51...1,6	10...6,5	6,5	6,5...5
Легированная	6,6..5	5    3,3	3,3	7,5...5	5	5...4

Классы прочности и механические свойства болтов из углеродистых и легированных сталей

Таблица 3

Класс прочности	Предел текучести [s]T, МПа	Марка стали
		Болта	Гайки
3,6	200	СтЗ	СтЗ
3,6	200	10	СтЗ
4,6	240	20	СтЗ
5,6	300	30;35,45	10

Резьба метрическая (мм)

Таблица 4

Номинальный	Резьба с крупным шагом	Резьба с мелким шагом
диаметр резьбы	Шаг резьбы р	Средний диаметр d2	Шаг резьбы р	Средний диаметр d2
6(7)	1	5,35(6,35)	0,75	5,35(6,35)
8(9)	1,25	7,188(8,188)	1,25	9,188
10	1,5	9,026	1,25	9,188
11	1,5	10,026	1,25	10,861
12	1,75	10,863	1,25	11,188
14	2	12,701	1,25	13,565
16	2	14,701	1,5	15,026
18	2,5	16,376	2	17,026
20	2,5	18,376	1,5	19,026
22	2,5	20,376	2	21,043
24	3	22,051	2	22,701
27	3	25,051	2	25,688
30	3,5	27,727	2	28,988
33	3,5	30,727	2	31,633
36	4	33,402	3	34,544
39(40)	4	36,402	3	36,402
42	4,5	39,077	4	39,077

Контрольные вопросы:

1.  Назовите основные параметры резьбы
2.  Классификация резьбы
3.  Какой тип резьбы применяют на болтах?
4.  По каким видам деформации производится проверка на прочность?
5.  Для чего нужен средний диаметр резьбы и как он обозначается?
6.  Из каких элементов состоит болтовое соединение?
7.  Какие случаи действия нагрузок на резьбовые соединения рассматривает курс «Детали машин»?
8.  Какие напряжения должны учитываться в каждом случае?
9.  Приведите примеры использования резьбовых соединений
10.  Чему равен диаметр отверстия в болтовом соединении без зазора?
11.  Как выбрать коэффициент запаса прочности?
12.  Как подобрать размер резьбы по среднему диаметру?
13.  Какие материалы используют для прокладок?
14.  как  обозначается коэффициент трения?
15.  Как определить допускаемое напряжение, если известен материал конструкции?
16.  Чему равно количество стыков, если соединяются три пластины?
17.  Нужно ли учитывать количество болтов при расчетах?

 

 

Скачано с www.znanio.ru