Федеральное государственное автономное образовательное учреждение высшего образования «Национальный исследовательский Нижегородский государственный

университет им. Н.И. Лобачевского»

 

Арзамасский филиал

 

Отделение среднего профессионального образования

(Арзамасский политехнический колледж им. В.А. Новикова)

 

 

 

 

 

 

 

 

 

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ РАБОТ

 

по учебной дисциплине

ОП.02 Техническая механика  по специальности:

23.02.03 ТЕХНИЧЕСКОЕ ОБСЛУЖИВАНИЕ И РЕМОНТ АВТОМОБИЛЬНОГО ТРАНСПОРТА

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Разработчик(и):

 

 

АФ ННГУ отделение СПО

«Арзамасский политехнический

колледж им. В.А. Новикова»             преподаватель                    Д.И Артюхин_________

    (место работы)                        (занимаемая должность)                (инициалы, фамилия)

 

 

 

Содержание

 

Пояснительная записка

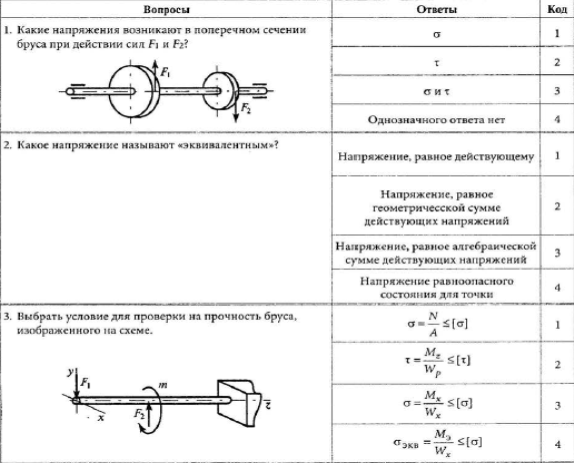
Практическая работа №1 «Определение равнодействующей плоской системы сходящихся сил».

Практическая работа №2 «Расчёт стержневых систем»

Практическая работа №3 «Определение реакций опор балки».

Практическая работа №4 «Определение центра тяжести плоских сечений».

Практическая работа №5 «Простейшие движения твёрдого тела».

Практическая работа №6 «Метод кинетостатики».

Практическая работа  №7 «Определение мощности двигателя торможением».

Практическая работа №8 «Определение перемещений свободного конца бруса»

Практическая работа  №9 «Расчёты на прочность при растяжении»

Практическая работа №10 «Расчёт заклепочных, болтовых соединений»

Практическая работа №11 «Расчёты на жёсткость при кручении».

Практическая работа №12 «Выбор рационального сечения вала».

Практическая работа №13 «Расчёт винтовых пружин».

Практическая работа №14 «Эпюры поперечных сил и изгибающих моментов».

Практическая работа №15 «Расчёты на прочность при изгибе».

Практическая работа №16 «Выбор рационального сечения балки».

Практическая работа №17 «Расчёт вала на изгиб и кручение».

Практическая работа №18 «Расчёт на устойчивость».

Практическая работа №19 «Механические передачи. Расчёт привода».

Практическая работа №20 «Прямозубая передача».

Практическая работа №21 «Косозубая и шевронная передача».

 

 

Пояснительная записка

 

Методические указания предназначены в помощь обучающимся среднего специального образования, входящей в укрупненную группу специальностей при выполнении практических работ  по дисциплине «Техническая механика». Они составлены на основе программы по дисциплине «Техническая механика», разработанной в соответствии с Федеральными государственными образовательными стандартами  для данной специальности.

Дисциплина «Техническая механика» является общепрофессиональной дисциплиной и при ее изучении отводится значительное место решению практических задач, в том числе в рамках проведения практических работ.

Обучающиеся, выполняя практические работы, реализуют следующие цели:

-             обобщать, систематизировать, закреплять полученные теоретические зна­ния по конкретным темам дисциплины;

-             формировать умения применять полученные знания на практике, реализуя единство интеллектуальной и практической деятельности;

-             развивать аналитические, умения у будущих специа­листов;

-             демонстрировать при решении поставленных задач умения, направленные на формирование профессиональных компетенций, предусмотренных программой дисциплины «Техническая механика»;

-             вырабатывать такие профессионально значимые качества, как самостоятельность, ответственность, точность, творческая инициатива, необходимые при формировании общих компетенций.

Использование методических указаний позволяет обучающимся при  минимальных затратах учебного времени самостоятельно выполнять практические работы, даёт возможность преподавателю и обучающимся контролировать и оценивать знания и умения по данной

 

 

 

 

 

Практическая работа №1

«Определение равнодействующей плоской системы сходящихся сил».

 

Цель работы: Закрепить теоретические знания  и умения определять равнодействующую системы сходящихся сил аналитическим и геометрическим способами

Краткие теоретические и справочно-информационные материалы по теме:

Системой сходящихся сил  называется система, в которой линии действия сил пересекаются в одной точке, называемой центром системы.

Система сходящихся сил имеет равнодействующую, равную геометрической сумме   этих сил и приложенную в точке их пересечения. 

Равнодействующая системы сходящихся сил аналитическим способом определяется по величинам сумм проекций на ось χ и Y по формуле:    .

Направление равнодействующей определяется значением угла равнодействующей с осью Ох по формуле:cos.

Равнодействующую системы сходящихся сил можно определить геометрическим способом.  Для этого  необходимо  построить многоугольник сил заданной  системы сходящихся сил. 

Многоугольник сил строится в следующей последовательности: вычерчиваются векторы сил заданной системы в определённом масштабе один за другим так, чтобы конец предыдущего вектора совпадал с началом последующего. Вектор равнодействующей замыкает полученную ломаную линию, он соединяет начало первого вектора с концом последнего и направлен ему навстречу.

 Измеряя полученный при построении  равнодействующий вектор  сил,  учитывая выбранный масштаб,  определяется  его величина.

Проверка знаний и умений (необходимых для выполнения практической работы)

 

№ п/п	Задание	Вариант ответа
1.	Чему равен модуль равнодействующей сил F1 и F2, если F1 = F2 = 5 кН, α = 600?	А. 7,1 кН В. 9,7 кН С. 7,9 кН Д. 8,7 кН
2.	Какой вид имеют уравнения равновесия сходящейся системы сил?
3.	Чему равна равнодействующая трёх сил, если  R = 10 Н, F1 = F2 = 20 Н, угол  = 30o?	А. 30 Н С. 90 Н В. 0  Н Д. 60 Н

 

Задание: Определить равнодействующую системы сходящихся сил геометрическим и аналитическим способами. Определить погрешность вычислений двумя способами.

 

Порядок выполнения работы:

1)      По данным варианта вычертить систему сходящихся сил.

2)      Определить равнодействующую геометрическим способом.

3)      Определить проекции всех сил системы на ось Ох.

4)      Определить проекции всех сил системы на ось Оу.

5)      Определить модуль равнодействующей по величинам сумм проекций на ось χ и Y.

6)      Определить значение угла равнодействующей с осью Ох аналитическим способом.

7)      Определить погрешность вычислений по формуле.

.

Пример расчета:

F1	=	20	кН
F2	=	5	кН
F3	=	10	кН
F4	=	15	кН
F5	=	10	кН
α1	=	0	°
α2	=	60	°
α3	=	75	°
α4	=	150	°
α5	=	210	°

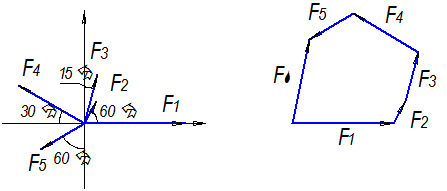
1. Определение равнодействующей геометрическим способом.

Используя свойства векторной суммы сил, вычерчиваем векторы сил в масштабе    2 мм = 1 кН последовательно друг за другом.

Равнодействующей вектор соединяет начало первого вектора с концом последнего и направлен ему навстречу.

С помощью линейки определяем модуль равнодействующей силы, а транспортира угол наклона к её оси.

F_Σгр = 16,5 кН     α_Σх = 79°.

 

 2. Определение равнодействующей аналитическим способом:

 а) Определяем проекции всех сил системы на ось Ох:

 F_1х= F₁· соs 0° = 20 ·1 = 20 кН

 F_2х= F₂ · соs 60° = 5 · 0,5 = 2,5 кН

 F_3х= F₃ · соs 75° = 10 · 0,26 = 2,6 кН

 F_4х= - F₄ · соs 30° = - 15 · 0,866 = - 13 кН

 F_5х= - F₅ · соs 30° = - 10 · 0,866 = - 8,66 кН

 Сложив алгебраические проекции, получим проекцию равнодействующей на ось Ох:

 F_Σх = F_1х + F_2х + F_3х + F_4х + F_5х ; F_Σх = 20 + 2,5 + 2,6 – 13 – 8,66 = 3,44 кН.

 Знак проекции соответствует направлению вправо.

 

 б) Определяем проекции всех сил системы на ось Оу:

 F_1у= F₁ · соs 90° = 20 · 0 = 0

 F_2у= F₂ · соs 30° = 5 · 0,866 = 4,33 кН

 F_3у= F₃ · соs 15° = 10 · 0,966 = 9,66 кН

 F_4у= F₄ · соs 60° = 15 · 0,5 = 7,5 кН

 F_5у= - F₅ · соs 60° = - 10 · 0,5 = - 5 кН

 Сложив алгебраические проекции, получим проекцию равнодействующей на ось Оу:

 F_Σу = F_1у + F_2у + F_3у + F_4у + F_5у ; F_Σу = 0 + 4,33 + 9,66 + 7,5 – 5 = 16,49 кН.

 Знак проекции соответствует направлению вверх.

 

 в) Определяем модуль равнодействующей по величине проекции:

 ;  

 г) Определяем значение угла равнодействующей с осью Ох:

  

  3. Определение погрешности вычислений.

 

Вывод: равнодействующая определена правильно.

 

Контрольные вопросы:

 

1. Какая система сил является системой сходящихся сил?

2. Сформулируйте условие равновесия системы сходящихся сил в аналитической и геометрической формах.

3. Сформулируйте правила построения силового многоугольника.

4. Приведите формулу для определения равнодействующей системы сходящихся сил.

5. В каком случае проекция силы равна 0?

6. В каком случае проекция силы положительна?

 

Практическая работа №2 «Расчёт стержневых систем»

Тема: Статика. Плоская система сходящихся сил.

 

Цель работы: Научится определять усилия в стержнях конструкции аналитическим методом.

 

Задание: Определить усилия в стержнях заданной конструкции аналитическим способом. Схему выбрать в соответствии с номером студента по списку журнала.

 

Порядок выполнения:

 

1. Изобразить заданную схему в соответствии с вариантом.

2. Выделить материальную точку, к которой приложена внешняя сила.

3. Определить тип связей, удерживающих точку.

4. Отбросить связи, заменить их действие силами реакции.

5. Составить расчетную схему, выделив точку, находящуюся в равновесии. Приложить к ней все действующие силы.

6. Выбрать оси координат.

7. Записать уравнения равновесия: 

8. Из уравнений равновесия найти величину сил реакции.

9. Записать величину усилий в стержнях.

10. Вычертить многоугольник сил, приложенных к точке.

11 .Вывод.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Задания к практической работе № 1

 

1	2	3
4	5	6
7	8	9
10	11	12
13	14	15

 

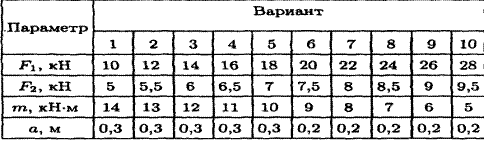
Практическая работа №3 «Определение реакций опор балки».

 

                                                      

Цель: Сформировать умения по выполнению расчетов для определения реакций опор балочной системы.

 

Для заданной двухопорной балки определить реакции опор.

 

Пример выполнения задания

 

Двухопорная  балка с шарнирными  опорами А и В нагружена сосредоточенной силой F, распределенной нагрузкой с интенсивностью q и парой силой с моментом m. Определить реакции опор.

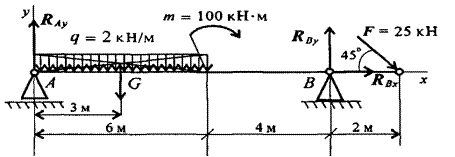
Рисунок

 

Решение

 

1.Левая опора (точка А) – подвижный шарнир. В таком случае, реакция R_ay направлена перпендикулярно опорной поверхности.

       Правая опора (точка В) – неподвижный шарнир. В таком случае, возникает две  реакции R_Byи R_Bx, которые направлены вдоль осей координат.

       2. Заменим равномерно распределенную нагрузкуqсосредоточенной силой G.

G=ql

G=2*6=12кН – сосредоточенная сила размещается в середине пролета.

        Далее задача решается с сосредоточенными силами.

3.Составим уравнение моментов относительно  точки  А.

=G*3+m- R_By*10+F*12*sin45˚=0

 

R_By*10=G*3+m+F*12*sin45˚

R_By*10=12*3+100+25*12*0.7

R_By==34,6кН – реакция направлена верно.

4. Составим уравнение моментов относительно точки В.

=R_ay*10-G*7+m+F*2*sin 45˚=0

R_ay*10=G*7-m-F*2*sin 45˚

R_ay*10=12*7-100-50*0.7

R_ay=-=-5.1кН - реакция отрицательная, следовательно R_ayнужно направить в противоположную сторону.

5.Используя уравнение проекций , определим реакцию R_Bx.

=R_Bx+Fcos45˚=0

R_Bx=-Fcos45˚

R_Bx= - 17,5кН – реакция отрицательная, следовательно ее направление будет противоположно выбранному.

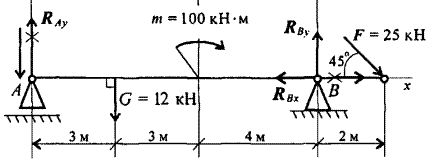
Рисунок

 

6. Проверка

Составим уравнение проекций на ось У.

=0

-R_ay-G+ R_By- Fcos45˚=0

-5.1-12+34.6-25*0.7=0 – решение верно.

Задание: Определить реакции в опорах по вариантам

 

Содержание отчета

1. Наименование работы.

2. Цель работы.

3. Номер варианта.

4.Расчеты

5. Вывод

Контрольные вопросы:

1. Дать определение условию равновесия  плоской системы параллельных сил?

2. Что такое связь?

3. Реакции в связях?

4. Классификация балок, реакции в балках?

5.  Абсолютно твердым телом называется, такое тело в котором:

а) расстояние между каждыми двумя точками  остаются всегда неизменными;

б) размеры каждого очень мало по сравнению другими телами;

в) форма тело остается постоянной;

г) в котором можно пренебречь формой;

д) которое деформируется.

6.Сформулируйте аксиомы статики?

7. Что такое абсолютно твердое тело?

8.Приведите определение понятия «сила»?

9. Что такое равнодействующая и уравновешивающая сила?

10. Дайте определение внешней и внутренней силы?

 

Практическая работа №4 «Определение центра тяжести плоских сечений».

 

Цель: Сформировать умения, по выполнению расчетов для определения положения центра тяжести фигуры составленной из простых геометрических фигур.

 

Пример выполнения задания

     Определить положение центра тяжести плоской фигуры, показанной на рисунке.

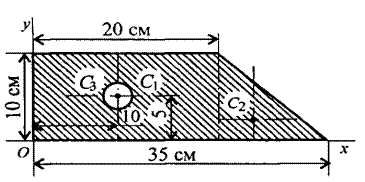
Рисунок

 

Решение:

1.Разбиваем фигуру на три части

1-прямоугольник

2-треугольник

3-круг

2.Определим площадь каждой фигуры

А₁=10*20=200см²

А₂=10*15=75см²

А₃=3,14*3²=28,3см²

3. Определим центр тяжести каждой фигуры

Фигура 1 – прямоугольник: х₁=10 см; у₁=5 см.

Фигура 2 – треугольник: х₂=20+*15=25 см; у₂=*10=3,3 см.

Фигура 3 – круг: х₃=10 см; у₃=5 см.

4. Определим центр тяжести всей фигуры пользуясь формулами

 

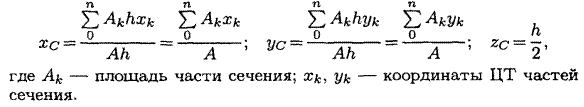
Х_с==14,5см;

Аналогично определяем  у_с=4,5см.

Задание: Определить центр тяжести фигуры по вариантам

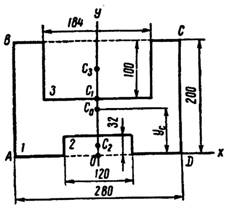
          Вариант  1                                                         Вариант 2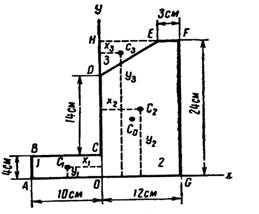

 

 

Вариант 3                                                        Вариант 4

 

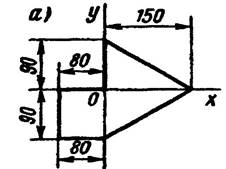
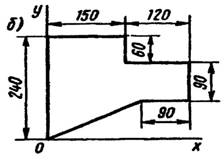
                                     Вариант   6

Вариант 5

 

 

 

 

 

Содержание отчета

1. Наименование работы.

2. Цель работы.

3. Номер варианта.

4.Расчеты

5. Вывод

Контрольные вопросы:

1.Что называется центром параллельных сил?

2.  Как определяются координаты центра параллельных сил?

3. Что называется центром тяжести тела?    

4. Запишите формулу для определения положения центра тяжести простых геометрических фигур: прямоугольника, треугольника, трапеции и половины круга?

5.Как определить положение центра тяжести площади, если известно положение центров тяжести отдельных ее частей?

6. Где расположен центр тяжести дуги окружности?

7. Каким графическим построением можно найти центр тяжести треугольника?

 

Практическая работа №5 «Простейшие движения твёрдого тела».

Знать формулы для определения параметров поступательного и вращательного движений и кинематические графики.

Уметь определять кинематические параметры тела при по­ступательном и вращательном движениях, определять парамет­ры любой точки тела.

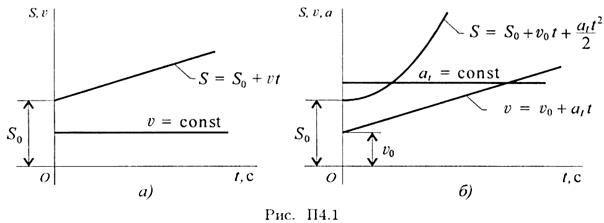
Расчетные формулы для определения параметров поступательного движения тела

Все точки тела движутся одинаково. Закон равномерного движения:

Закон равнопеременного движения:

Здесь So — путь, пройденный до начала отсчета, м;

v₀ — начальная скорость движения, м/с;

a_t — постоянное касательное ускорение, м/с²

Скорость:

Ускорение:

Закон неравномерного движения:

Кинематические графики поступательного движения представ­лены на рис. П4.1.

Точки тела движутся по окружностям вокруг неподвижной оси (оси вращения).

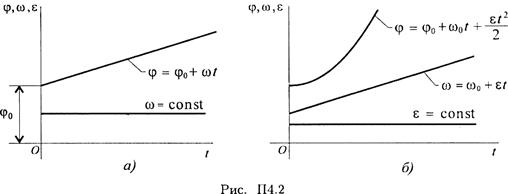
Закон равномерного вращательного движения:

Закон равнопеременного вращательного движения:

Закон неравномерного вращательного движения:

Здесь φ — угол поворота тела за время t, рад;

ω — угловая скорость, рад/с;

φ_о — угол поворота, на который развернулось тело до начала отсчета;

ω₀ — начальная угловая скорость;

ε — угловое ускорение, рад/с2;

Угловая скорость:

Угловое ускорение:

Кинематические графики вращательного движения представле­ны на рис. П4.2.

Число оборотов вращения тела:

 Угловая частота вращения: п, об/мин.

Параметры движения точки вращающе­гося тела (рис. П4.3):

Задание 1.

1.      Определить вид движения на каждом участке по приведенно­му кинематическому графику.

2.      Записать законы движения шкива на каждом участке. Па­раметры движения в конце каждого участка являются начальными параметрами движения на каждом последующем.

3.      Определить полный угол поворота шкива за время вращения. Использовать формулу для перехода от угловой частоты вращения к угловой скорости.

4.      Определить полное число оборотов шкива, используя формулу

1.      Построить графики угловых перемещений и угловых ускоре­ний.

2.      Определить нормальное и касательное ускорения точки на ободе шкива в указанные моменты времени.

Задание 2.

1.      Подставив заданные коэффициенты в общее уравнение дви­жения, определить вид движения.

2.      Определить уравнения скорости и ускорения груза.

Практическая работа №6 «Метод кинетостатики».

Тема: Динамика. Сила инерции. Принцип Даламбера.

 

Цель работы: Научится определять силу инерции для различных случаев движения и применять принцип Даламбера.

 

Задание: Решить задачу № 6 в соответствии со своим вариантом.

 

Порядок выполнения:

 

1. Выделить материальную точку, движение которой рассматривается и изобразить ее на рисунке.

2. Выявить все активные силы и изобразить их приложенными к точке.

3. Освободить точку от связей, заменить связи их реакциями.

4. Определить скорость и ускорения нити и изобразить их приложенными к точке.

5. Определить силу инерции F_ин=m·a.

6. Приложить силу инерции к движущейся точке.

7. Применить метод кинетостатики и рассмотреть равновесие полученной системы сил. Составить уравнения равновесия    

8. Из уравнений равновесия найти требуемую величину.

9. Записать ответ.

10. Вывод.

 

 

Задания к практической работе № 6

 

Вариант 1, 11, 21.

К потолку вагона на тонкой нити подвешен груз. При прямолинейном движении вагона с постоянным ускорением а=5м/сек² нить отклоняется от вертикали на некоторый угол α. Найти этот угол и натяжение нити, если масса груза 1кг. Массой нити пренебречь.

Вариант 2, 12, 22.

К потолку вагона на тонкой нити подвешен шарик, масса которого 2кг. При равноускоренном прямолинейном движении вагона нить отклонилась на угол α=18⁰. Определить ускорение вагона и натяжение нити.

 

Вариант 3,13, 23.

Груз в 5т, будучи подвешенным на тросе, длина которого 4м совершает колебательные движения около положения равновесия. При переходе через положение равновесия груз имеет скорость 1,6м/сек. Определить в этот момент натяжение троса.

 

Вариант 4, 14, 24.

Груз в 12т, подвешенный на тросе, опускается вертикально вниз с постоянным ускорением 4,4м/сек². Определить натяжение троса.

 

Вариант 5, 15, 25.

Гирю в 2кг взвешивают на пружинных весах, находясь в лифте, который поднимается вверх с ускорением 6м/сек². Определить показание пружинных весов.

 

Вариант 6, 16, 26.

Шарик, масса которого 0,5кг, привязан к нити и вращается вместе с ней в вертикальной плоскости с угловой скоростью 150об/мин. Длина нити 50см. Определить наибольшее натяжение нити.

 

Вариант 7, 17, 27.

Шарик, масса которого 1,2кг, привязали к нити длиной 40см. Шарик с нитью вращается в вертикальной плоскости с угловой скоростью 300рад/сек. Определить наименьшее натяжение нити.

 

Вариант 8, 18, 28.

Шарик массой 0,8кг привязан к нити, которая может выдержать максимальное натяжение 5кн. При какой угловой скорости вращения в вертикальной плоскости возникает опасность разрыва нити, если ее длина 80см?

 

Вариант 9,19, 29.

С какой скоростью должен проехать мотоциклист по арочному мостику радиусом 25м, чтобы в самой верхней точке мостика давление мотоцикла на мостик стало в два раза меньше его общего веса.

Вариант 10, 20, 30.

Масса мотоциклиста вместе с мотоциклом 280кг. Когда мотоциклист проезжает по легкому мостику со скоростью 108км/час, то мостик прогибается, образуя дугу радиусом 60м. Определить максимальное давление, производимое мотоциклом на мостик.

 

Практическая работа №7 «Определение мощности двигателя торможением».

 

Грузоподъемность лебедки: F=10КН

Скорость подъема v=1.2 м/с

Диаметр барабана D=200 мм

Угол наклона ременной передачи

=60

Ресурс работы привода L=3000 ч

Типовой режим нагружения-2I.

1. Определим требуемую мощность

Требуемая мощность

,

где

3 пары подшипников=0,99³

КПД клиноременной передачи=0,96

КПД муфты=0,98

КПД червячной передачи=0,9

Итого

2. Найдем угловую скорость и число оборотов в мин барабана

 

3. Подбор двигателя. Предпочтительные варианты:

Двигатель, КВт	Типоразмер	Частота, об/мин	s, %	Tn/Tн
15	4A160S2	3000	2.1	1.6
15	4A160S4	1500	2.3	2

а) двигатель 4A160S2 с числом оборотов 3000

б) двигатель 4A160S4 с числом оборотов 1500

Номинальная частота вращения:

а) n_ном =3000*(1-0,021)=2937 об/мин

б) n_ном =1500*(1-0,023)=1465 об/мин

Выбираем двигатель с числом оборотов 1500 4A160S4(четырехполюсный) и считаем передаточное число привода:

Возьмем из списка передаточных чисел червячного редуктора u₁ =8, тогда передаточное число клиноременной передачи равно:

u₂ =u/u₁ =12,8/8=1,6

Полученный двигатель имеет следующие размеры:

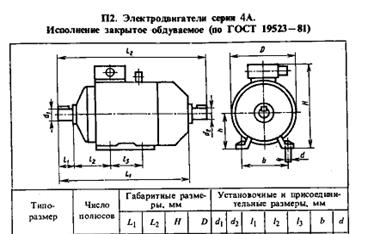
L1=110 мм, d1=48 мм

Кинематическая схема привода:

Вал 1(двигатель) P=14.6 КВт	n=1465 об/мин
Вал2(передача) P=14,6 КВт
Вал3(редуктор) P=14.6 КВт

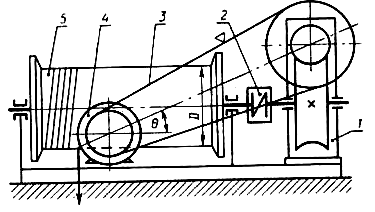
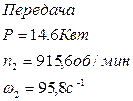
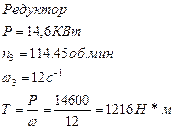
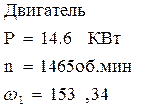
2. РАСЧЕТ КЛИНОРЕМЕННОЙ ПЕРЕДАЧИ

1. По номограмме в зависимости от частоты вращения меньшего шкива n₁ (в нашем случае n ₁ = n_дв =1465 об/мин) и передаваемой мощности Р= Р _дв =14,6 КВт принимаем сечение клинового ремня Б. Вращающий момент:

2. Диаметр меньшего шкива определяют по эмпирической формуле:

Диаметр большего шкива

Принимаем d₂ =360 мм

3. Уточняем передаточное отношение

При этом угловая скорость вала будет:

Расхождение с тем, что было получено по первоначальному расчету,

,

что менее допускаемого на плюс-минус 3 %

Следовательно, окончательно принимаем диаметры шкивов d₁ =224мм, d₂ =360мм.

4. Межосевое расстояние  следует принять в интервале:

Принимаем предварительно близкое значение 

5. Расчетная длина ремня определяется по формуле:

Принимаем по стандарту ГОСТ 1284.1-80 значение длины ремня 2240 мм

6. Уточняем значение межосевого расстояния  с учетом стандартной длины ремня L:

,

где

и .

Тогда

При монтаже передачи необходимо обеспечить возможность уменьшения межосевого расстояния на 0,01L=0.01*2240=22,4мм для облегчения надевания ремней на шкивы и возможность увеличения его на 0.025L=0.025*2240=56мм для увеличения натяжения ремней.

7. Угол обхвата меньшего шкива

8. Коэффициент режима работы, учитывающий условия эксплуатации передачи:

Коэффициент, учитывающий влияние длины ремня:

С_L =1

Коэффициент, учитывающий влияние угла обхвата: С=0,98

Коэффициент, учитывающий число ремней С_z =0.95

9. Число ремней в передаче

Р₀ =6,6 из таблицы 7.8, принимаем число ремней равным 3.

10. Натяжение ветви клинового ремня находим по формуле:

,

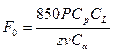где скорость

Коэффициент, учитывающий центробежную силу:

 для сечения ремня Б, тогда

11. Давление на валы

12. Ширина шкивов

13. Найдем долговечность ремней

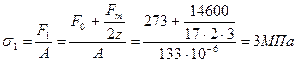, где 

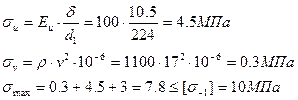
Ресурс работы привода считается по формуле:

,

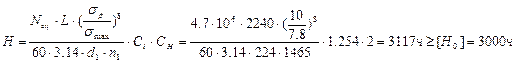Где

и  для сечения ремня Б

Оформим полученные значения в таблице:

Параметр	Формула	Значение
Сечение ремня	номограмма	Б
Вращающий момент, Н*м		95,2 Н*м
Диаметр меньшего шкива, мм
Диаметр большего шкива, мм
Передаточное отношение (уточненное)
Межосевое расстояние, мм
Длина ремня, мм		2240 мм
Уточненное межосевое расстояние, мм		658 мм
Угол обхвата, o		168o
Число ремней		3 шт
Натяжение ветви ремня, Н		273Н
Сила, действующая на вал, Н		1.6к Н
Ширина шкивов,мм		63мм
		3МПа
		4,5Мпа
		0,3МПа
Условие прочности
Ресурс привода		3117ч

3. РАСЧЕТ ЧЕРВЯЧНОГО РЕДУКТОРА

При расчете использовалась программа для расчета цилиндрических, конических и червячных редукторов. Полученные данные частично присутствуют в дальнейших расчетах.

Число витков червяка принимаем равным  при передаточном отношении u=8. Число зубьев червячного колеса

Вращающий момент на тихоходном валу:

Вращающий момент на валу червячного колеса

Выбираем материал червяка и венца червячного колеса.

Принимаем для червяка сталь 45 с закалкой до твердости менее HRC 45 с последующим шлифованием. Так как к редуктору не предъявляются специальные требования, то в целях экономии принимаем для венцачервячного колеса бронзу БР010Ф1 (отливка в кокиль).

Посчитаем напряжения для БРО10Ф1(см табл 4.8):

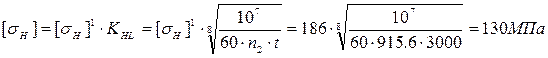
Принимаем предварительно коэффициент диаметра червяка равным 8.

Определяем межосевое расстояние:

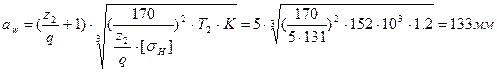
Модуль

Принимаем по ГОСТ 2144-76 стандартные значения m=8 и q=8, тогда межосевое расстояние будет равно

Основные размеры червяка:

Делительный диаметр червяка

d₁ =q*m = 8*8 = 64 мм;

Диаметр вершин витков червяка

Диаметр впадин витков червяка

Длина нарезанной части шлифованного червяка равна:

Делительный угол подъема витка у (по табл. 4.3): при z1=4 и q = 8 => 

Основные размеры венца червячного колеса:

Делительный диаметр червячного колеса

d₂ = z₂ *m = 32*8=256 мм;

Диаметр вершин зубьев червячного колеса

Диаметр впадин зубьев червячного колеса

Ширина венца червячного колеса принимается по соотношениям:

Окружная скорость червяка равна по формуле

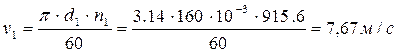
Скорость скольжения определяется из соотношения:

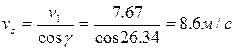
КПД редуктора равен 0,91%

При степени точности (табл. 4,7) равной 7 коэффициент динамичности 

Коэффициент неравномерности распределения нагрузки(x=0,3):

Коэффициент нагрузки равен

Проверяем контактные напряжения:

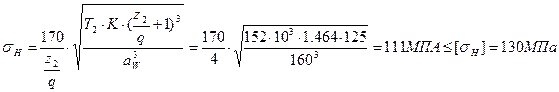
При этом расчетное напряжение ниже допускаемого на 14%, что считается удовлетворительным.

Проверка прочности зубьев червячного колеса на изгиб.

Эквивалентное число зубьев:

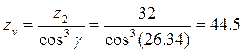
Коэффициент формы зуба по табл. 4.5 

Расчетные значения допускаемых напряжений изгиба

 

 

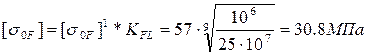
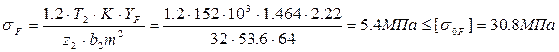
Практическая работа № 8 «Определение перемещения свободного конца бруса».

 

Цель работы: Закрепить теоретические знания  и  умения строить эпюры и выполнять расчёты на прочность при растяжении и сжатии

Краткие теоретические и справочно-информационные материалы по теме:

Растяжением или сжатием называют вид нагружения, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор — продольная сила.

Если внешняя сила направлена от сечения, то продольная сила положительна,  брус растянут; если внешняя сила направлена к сечению, то продольная сила отрицательна, брус сжат.

Эпюрой продольной силы называется график распределения продольной силы вдоль оси бруса.

Ось эпюры параллельна продольной оси бруса.

 Нулевая линия проводится тонкой линией. Значения сил откладывают от оси, положительные - вверх, отрицательные - вниз.

В пределах одного участка значение силы не меняется, поэтому эпюра очерчивается отрезками прямых линий, параллельными оси Oz.

На эпюре проставляются значения Nz. Величины продольных сил откладывают в заранее выбранном масштабе.

 Эпюра по контуру обводится толстой линией и заштриховывается поперек оси.

При растяжении и сжатии в сечении действует только нормальное напряжение, которое определяется по формуле:

,

где N – продольная сила в сечении,

      А  - площадь поперечного сечения.

При определении напряжений брус разбивают на участки нагружений, в пределах которых продольные силы не изменяются, и учитывают места изменений площади поперечных сечений. Рассчитывают напряжения по сечениям, и расчет оформляют в виде эпюры нормальных напряжений.

Строится и оформляется такая эпюра так же, как и эпюра продольных сил.

Расчеты на прочность ведутся по условиям прочности - неравенствам, выполнение которых гарантирует прочность детали при данных условиях.

Для обеспечения прочности расчетное напряжение не должно превышать допускаемого напряжения:

σ ≤ [σ],   где σ =

Расчетное напряжение σ зависит от нагрузки и размеров поперечного сечения, допускаемое только от материала детали и условий работы.

 Существуют три вида расчета на прочность.

 1. Проектировочный расчет - задана расчетная схема и нагрузки. Необходимо  подобрать размеры детали:  

А=

 2. Проверочный расчет - известны нагрузки, материал, размеры детали; необходимо проверить, обеспечена ли прочность.

 Проверяется неравенство σ ≤ [σ]

 3. Определение нагрузочной способности (максимальной нагрузки): [N] = [σ]А.

 

Литература:  Олофинская В.П. Техническая механика. Курс лекций с вариантами практических и тестовых заданий: учебное пособие. - 2-е изд. - М.: ФОРУМ: ИНФРА-М, 2012. 

 

Проверка знаний и умений (необходимых для выполнения практической работы)

 

№ п/п	Задание	Вариант ответа
1.	Какая из эпюр, приведенных на рисунке, соответствует эпюре продольных сил стержня?	A.   Б. B.
2.	Укажите эпюру,  соответствующую эпюре нормальных напряжений для данного бруса	A.   Б. B.
3.	Обеспечена ли прочность бруса в сечении С-С, если допустимое напряжение [σ] = 260 МПа?	A. σ < [σ] .   B.   σ = [σ];    С.  σ > [σ];

 

Задание.

Для стального бруса круглого поперечного сечения диаметром D  требуется:

1) построить эпюры продольных сил  и нормальных напряжений;

2) проверить прочность стержня, если [σ] = 160МПа. Данные своего варианта взять из таблицы.

 

Порядок выполнения работы:

1.      Изобразить расчётную схему.

2.      Разделить брус на участки нагружения, границы которых находятся в точках приложения сил.

3.      Определить продольные силы на участках бруса, используя метод сечений.

4.      Провести нулевую линию параллельно оси бруса.

5.      Найденные величины продольных сил отложить в масштабе в виде ординат, перпендикулярных оси бруса (положительные значения вверх от нулевой линии, отрицательные вниз). Через концы ординат провести линии параллельно оси бруса; поставить знаки и заштриховать эпюру параллельно ординатам.

6.      Разделить брус на участки нагружения для построения эпюры нормальных напряжений, с учётом площади поперечного сечения бруса.

7.      Найти значение нормальных напряжений для каждого участка нагружения.

8.      Построить эпюру нормальных напряжений по найденным значениям.

9.      Определить опасный участок.

10.  Сравнить расчётное напряжение с допустимым напряжением. 

11.  Сделать вывод о прочности бруса.

 

Пример расчета:

Для стального ступенчатого бруса нагруженного осевыми внешними силами  F₁ = 25 кН и F₂ = 60 кН   при  площадях поперечных сечений  A₁ = 500 см², A₂ = 1000 см² определить  продольные силы  и   напряжения. Построить   эпюры  продольных сил и нормальных напряжений. Проверьте прочность бруса, если если [σ] = 160МПа

 

Решение:

1.    Два участка нагружения для продольной силы:

участок 1: N₁ = + 25 кН; растянут;

участок 2: 25 – 60 + N₂ = 0; N₂ = - 35 кН; сжат.

2. Три участка нагружения по напряжениям:

 =   =

 =   =

 =   =

2.    На опасном участке напряжение <[ 160МПа, значит прочность бруса обеспечена.

 

 

 

 

Контрольные вопросы:               

 

1.      Сформулируйте условие прочности при растяжении и сжатии. Отличаются ли условия прочности при расчете на растяжение и расчете на сжатие.

2.      Какие внутренние силовые факторы возникают в сечении бруса при растяжении и сжатии?

3.      Как распределены напряжения по сечению при растяжении и сжатии?

4.      Запишите формулу для расчета нормальных напряжений при растяжении и сжатии.

5.      Как назначаются знаки продольной силы и нормального напряжения?

6.      Что показывает эпюра продольной силы?

7.      Как изменится величина напряжения, если площадь поперечного сечения возрастет в 4 раза?

Практическая работа №9 «Расчёты на прочность при растяжении»

Цель работы: усвоить теорию, научиться решать задачи на прочность при растяжении и сжатии.

Ход работы:

1.      Изучить теорию.

2.      Решить задачи.

3.      Оформить работу.

4.      Написать вывод.

Краткая теория:

Напряжение, при котором материал разрушается или в нем возникают заметные пластические деформации, называется предельным. При растяжении (сжатии) элемента конструкции статической нагрузкой предельным напряжением является одна из следующих механических характеристик материала.

Отношение предельного напряжения к максимальному расчетному напряжению σ_max , возникающему в элементе конструкции при его нагружении, называется коэффициентом запаса прочности:

Условие прочности выражается неравенством

Где [n] – нормативный (требуемый) коэффициент запаса прочности, зависящий от назначения рассчитываемой конструкции, условий ее работы, точности применяемых методов расчета, надежности определения рабочих нагрузок, достоверности сведений о механических свойствах материала.

Наиболее распространенная форма записи условия прочности

Где – допускаемое напряжение, т.е. такое напряжение, при котором обеспечивается безопасная работа конструкции.

Допускаемое напряжение равно предельному, деленному на нормативный коэффициент запаса:

В зависимости от поставленной задачи различают три вида расчетов на прочность:

А) проверка прочности (проверочный расчет);

Б) определение требуемых размеров поперечного сечения (проектный расчет);

В) определение допускаемой нагрузки.

Проверочный расчет. При этом расчете нагрузка бруса, его материал и размеры известны и требуется проверить, выполняется ли условие

Для этого определяем наибольшее расчетное напряжение

В поперечном сечении бруса и сравниваем с допускаемым. Наибольшее расчетное напряжение не должно быть больше допускаемого, расчетное напряжение считают не опасным, если оно превышает допускаемое не более чем на 5%. Поперечное сечение бруса, в котором возникает наибольшее расчетное напряжение при растяжении/сжатии, называется опасным.

Проектировочный расчет. При этом расчете известны нагрузки, действующие на брус, заданы или выбраны материал, допускаемое напряжение или нормативный запас прочности. Размеры поперечного сечения бруса, обеспечивающие требуемую прочность, определяем по формуле:

Определив из этой формулы требуемую площадь поперечного сечения, в зависимости от формы (круг, квадрат и др.) находим его размеры.

Определение допускаемой нагрузки. В этом случае известны размеры бруса и его материал, а требуется определить максимально допустимую нагрузку:

Затем с помощью метода сечения по найденному допускаемому значению продольной силы определяем допускаемое значение нагрузки.

Задача №1.

Проверить прочность стальных брусьев если . Построить эпюры продольных сил и нормальных напряжений. Данные для своего варианта взять из таблицы, рисунок 1.

Задача №2.

Проверить прочность стального бруса (рисунок 2), если , Данные для своего варианта взять из таблицы. Построить эпюры σ, ∆l, N. Е=2∙10⁵МПа.

Рис.1.

Рисунок 2.

 

Практическая работа №10 «Расчёт заклепочных, болтовых соединений»

 

Цель работы – научиться рассчитывать на прочность болтовые, заклёпочные и болтовых соединения при срезе и смятии.

В результате выполнения работы студент должен:

знать напряжения и деформации, возникающие при работе на срез и смятие соединений; условие прочности при срезе и смятии;

уметь производить расчёты на прочность по предельному состоянию заклёпочных, болтовых (без зазора), сварных соединений.

Теоретическое обоснование:

Многие элементы конструкции, служащие для соединения деталей (бол­ты, винты, заклепки, шпонки, швы сварных, клеевых соединений и т.д.), испытывают в процессе работы деформацию среза и смятия.

Рассмотрим практические расчеты на прочность при срезе и смятии на примере соединения заклепками.

Под действием внешней силы F, действующей на соединенные листы, заклепка испытывает деформацию среза по поперечному сечению аb (рис. 1). В этом сечении возникает один ВСФ − поперечная сила Q = F.

Рис. 1

Под действием поперечной силы Q в сечении заклепки ab возникает касательное напряжение

где А_ср − площадь среза.

Боковая поверхность заклепки под действием внешних сил F испытыва­ет деформацию смятия.

Смятие − это местная деформация сжатия на участках передачи давления одним элементом другому. На боковой поверхности заклепки возникает нормальное напряжение смятия

где А_см − площадь смятия.

Условие прочности на срез:

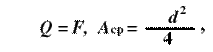
где п − количество срезов данного элемента;

т − количество элементов в данном соединении.

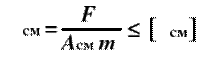
Условие прочности на смятие:

где δ − толщина листов.

Пример 1. Определить потребное количество заклепок для пе­редачи внешней нагрузки 120 кН. Заклепки расположить в один ряд. Проверить прочность соединяемых листов. Известно: [σ] = 160 МПа; [σ_см] = 300 МПа; [τ_ср] = 100 МПа; диаметр заклепок 16 мм.

Решение. 1. Определить количество заклепок из расчета на сдвиг (рис. 2).

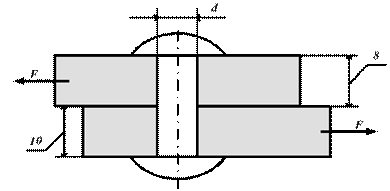
Рис. 2

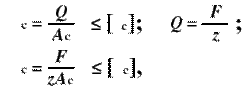
где А_с = 7πr²;

z − количество заклепок.

 

 

 

 

 

 

 

 

 

 

 

 

Практическая работа №11 «Расчёты на жёсткость при кручении».

1 Цель работы

 

1.1 Формирование умений выполнять расчеты валов на прочность при кручении

1.2 Развитие умений анализировать, сравнивать и делать выводы.

 

2 Задание

 

2.1 Для стального вала (рис.1) построить эпюру крутящих моментов; определить диаметр вала на каждом участке и полный угол закручивания. Данные для различных вариантов указаны в табл. 1.

Мощность на зубчатых колесах принять Р₂=0,5Р₁; Р₃=0,3Р₁; Р₄=0,2Р_1.

Указание. Полученное расчетное значение диаметра (в мм) округлить до ближайшего большого числа, оканчивающегося на 0, 2, 5, 8, или по СТС-В 208-75

 

3 Порядок выполнения работы

 

3.1 Определить вращающие моменты на шкивах

3.2 Построить эпюры крутящих моментов

3.3 Определить диаметры вала на каждом участке, используя условие прочности на кручение.

 

4 Ход работы

 

4.1 Вал вращается с постоянной угловой скоростью, следовательно, система вращающих моментов уравновешена. Мощность, подводимая к валу без потерь на трение, равна сумме мощностей, снимаемых с вала:

Р₁=Р₂+Р₃+Р₄ кВт.

4.2 Определяем вращающие моменты на шкивах:

4.3 Для построения эпюры крутящих моментов разбиваем брус на три участка, границами которых являются сечения, в которых приложены внешние моменты. В пределах каждого участка значения крутящих моментов таковы:

М_кр1 Нм;

М_кр2 Нм;

М_кр3= Нм;

По найденным значениям строим эпюру крутящих моментов (рис. 3, б).

4. 4 Из условия прочности на кручение

 

 

 

 

 

 

 

 

 

 

 

5 Вывод

 

Пример выполнения практического задания

(4 Ход работы)

 

2 Задание Для стального вала (рис. 3, а) построить эпюру крутящих моментов, определить из условия прочности требуемые диаметры каждого участка и углы закручивания этих участков.

Угловую скорость вала принять ω=100 рад/с, допускаемое напряжение [τ_кр] = 30МПа, модуль сдвига G=0,8*10⁵Мпа.

 

4 Ход работы

 

4.1 Вал вращается с постоянной угловой скоростью, следовательно, система вращающих моментов уравновешена. Мощность, подводимая к валу без потерь на трение, равна сумме мощностей, снимаемых с вала:

Р₁=Р₂+Р₃+Р₄=10+12+8=30кВт.

4.2 Определяем вращающие моменты на шкивах:

 

 

 

 

4.3 Для построения эпюры крутящих моментов разбиваем брус на три участка, границами которых являются сечения, в которых приложены внешние моменты. В пределах каждого участка значения крутящих моментов таковы:

М_кр1=-М₄=-80 Нм;

М_кр2=-М₄-М₃=-80-120=-200 Нм;

М_кр3=-М₄-М₃+М₁=-80-120+300=100 Нм;

По найденным значениям строим эпюру крутящих моментов (рис. 3, б).

4.4 Из условия прочности на кручение

 

 

 

 

 

 

 

 

 

 

Практическая работа №12 «Выбор рационального сечения вала».

Цель: Сформировать умения по выполнению расчетов на кручение и построению эпюр крутящих моментов.

Правила знаков

Крутящий момент считаем положительным, если моменты внешних пар сил направлены по часовой стрелке, в этом случае  момент внутренних сил упругости направлен против часовой стрелки.

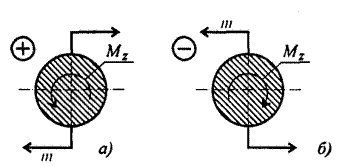
Построение эпюр

Порядок построения эпюры моментов аналогичен построению эпюр продольных сил.Ось эпюры параллельна оси бруса, значения моментов откладывают от оси вверх или вниз.

Пример выполнения задания

      На распределительном валу установлены четыре шкива,  на вал через шкив 1 подается мощность 12 кВт, которая  через шкивы 2,3,4 передается потребителю . Мощности распределяются следующим образом: Р₂=8кВт,   Р₃=3кВт,   Р₄=1кВт, вал вращается с постоянной скоростью ω=25рад/с. Построить эпюру крутящих моментов на валу.

 

 

 

 

 

 

 

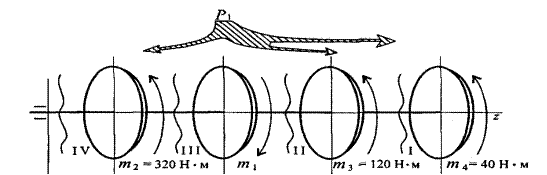
Решение

1.Определяем моменты пар сил на шкивах Р=mω, m=

m₁==480 Н*м                                      m₂==320Н*м

m₃==120 Н*м                                      m₄==40 Н*м

m₁=m₂+m₃+m₄

m₁=320+120+40=480 Н*м

2. Определяем крутящие моменты в поперечных сечениях бруса с помощью метода сечений

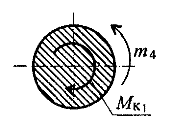
-m4+Мк1=0 Мк1=-m4 Мк1=-40 Н*м

Сечение 1

-m4-m3+Mк2=0 Mк2=-m4-m3 Mк2=-40-120=-160 Н*м

Сечение 2

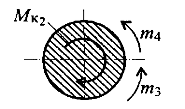
Сечение 3

-m4-m3+m1-Mk3=0 Mk3=-m4-m3+m1 Mk3=-40-120+480=320 Н*м

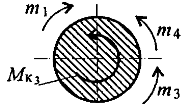
Сечение 4

M_k4=-m₄-m₃+m₁-m₂=0

3. Построим эпюру крутящих моментов.

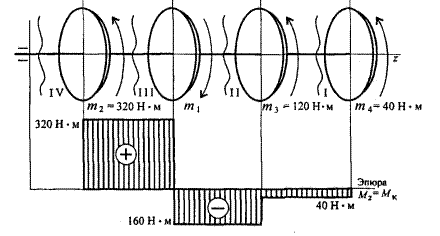
Решить самостоятельно по вариантам:

Содержание отчета

1. Наименование работы.

2. Цель работы.

3. Номер варианта.

4.Расчеты

5. Вывод

Контрольные вопросы:

1.Какие внутренние усилия возникают при кручении?

2. Что  называется  жесткостью при  кручении?

3. Условие прочности вала при кручении?

4.Какие деформации возникают при кручении?

5.Какой вид нагружения называется кручением?

6.Как вычисляют значение крутящего момента в поперечном сечении вала?

7. Опишите технику построения эпюры крутящих   моментов?

 

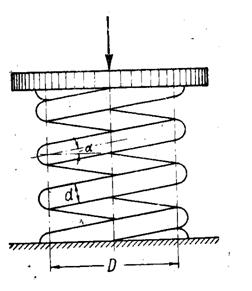
Практическая работа №13«Расчёт винтовых пружин».

 ЦЕЛЬ РАБОТЫ

Теоретическое и опытное определение осадки цилиндрической винтовой пружины и вычисление напряжений в витках. 

 ОБОРУДОВАНИЕ

1. Пружина сжатия винтовая цилиндрическая

2. Приспособление для сжатия пружин

3. Штангенциркуль

4. Линейка 

  ХАРАКТЕРИСТИКА ПРУЖИНЫ

Тип: пружина сжатия винтовая цилиндрическая.

Средний диаметр : D = мм

Поперечное сечение: круг диаметром d = мм

Число витков: n = 

 ПОЯСНЕНИЯ К РАБОТЕ

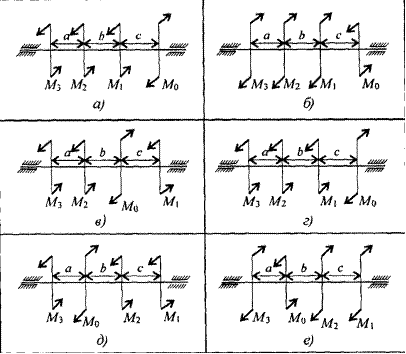
В различных машинах, механизмах, приборах пружины применяют для создания постоянных сил (тормоза, фрикционные передачи), в качестве элементов, смягчающих толчки и удары (амортизаторы, рессоры), для возврата движущихся деталей в исходное положение (клапанные пружины двигателей), для измерения величины силы (в динамометрах), в качестве устройств, аккумулирующих энергию (боевые пружины огнестрельного оружия), а также в элементах регистрирующих и записывающих приборов. 

По форме винтовые пружины делятся на цилиндрические, конические и фасонные. Наиболее широко в технике применяются цилиндрические винтовые пружины, воспринимающие осевую нагрузку и работающие на растяжение (рис. 1а) или на сжатие (рис. 2а). Пружины растяжения навивают без просвета между витками, пружины сжатия – с просветом.

 

Рис. 1. Цилиндрические винтовые пружины:

а) – растяжения; б) – сжатия.

Пружины изготавливают из высококачественной стали марок 65Г, 65С, 60С2, имеющих высокие значения допускаемых касательных напряжений:

  [] = 200…1000 МПа

Для большинства пружин угол  наклона витков небольшой (15º), поэтому для их расчета используется приближенная теория.

Расчет пружин растяжения и сжатия на прочность и жесткость одинаков, но для пружин сжатия при H : D  2,6 ( H – высота пружины в свободном состоянии, D – ее средний диаметр) возникает опасность потери устойчивости (выпучивания). Такие высокие пружины монтируют в гильзах или на оправках, препятствующих выпучиванию пружин.

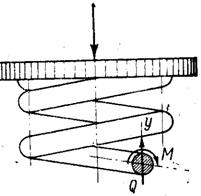
Рассмотрим пружину, нагруженную сжимающей силой F (рис. 2). Рассечем виток пружины (рис. 2а) плоскостью, проходящей через ее ось. Считая это сечение для витка поперечным, т.е. принимая  = 0 и рассматривая пружину как бы состоящую из колец, рассмотрим равновесие отсеченной части (рис. 2б).

 F F

 а) б)

 Рис. 2

В сечении пружины возникают два внутренних силовых фактора:

поперечная сила

 Q = F

и крутящий момент М = FD/2.

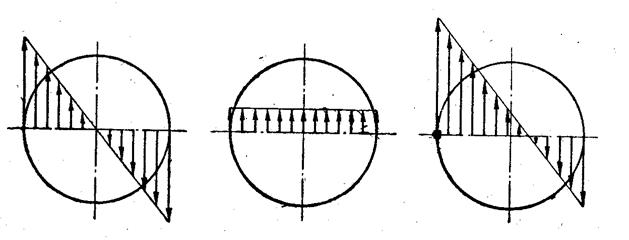
Касательные напряжения, связанные с наличием крутящего момента М, определяются так же, как при кручении бруса круглого поперечного сечения. Эпюра этих напряжений для точек диаметра витка показана на рис. 3а.

Касательные напряжения, связанные с наличием поперечной силы Q, распределены по сечению равномерно. Эпюра этих напряжений дана на рис. 3б.

Суммируя касательные напряжения, получаем результирующую эпюру, показанную на рис. 3в.

Опасной является точка А, ближайшая к оси пружины. Касательные напряжения в этой точке:

 А = max = maxM + Q (1)

 maxM

 

 а) б) в)

Рис. 3. Эпюры касательных напряжений в сечении витка пружины:

а) – от крутящего момента М = FD/2; б) – от поперечной силы Q = F;

в) – суммарная эпюра касательных напряжений.

Учитывая, что

 maxM =  

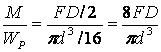
и Q = ,

получаем: А = max =  (2)

Отношение среднего диаметра пружины (D) к диаметру проволоки (d) называется индексом пружины и обозначается сп.

 сп = D/d

Тогда max = 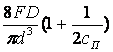 (3)

 Обычно сп = 5…12. При указанных значениях сп второе слагаемое в скобках составляет не более 0,1 от первого. Если пренебречь вторым слагаемым, т.е. учитывать только напряжения кручения, получится приближенная формула: 

 max  (4)

Формула (4) дает величину напряжений, меньшую действительной, т.к. в ней не учтено влияние поперечной силы и кривизна витков пружины. Исследования, выполненные методами теории упругости, позволяют уточнить значение max путем введения в формулу (4) поправочного коэффициента k, зависящего от индекса пружины и угла подъема витков. Его значение можно принимать по следующим данным:

Индекс сп	4	5	6	8	10	12
Коэффициент k	1,37	1,29	1,24	1,17	1,14	1,11

Несколько менее точное, но вполне приемлемое для практических расчетов значение k получается по формуле

 

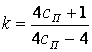
При более точных расчетах учитывают кривизну витков. Тогда значение поправочного коэффициента определяют по формуле

 k ≈ 1 + 1,45/сп (5)

С учетом указанного коэффициента условие прочности пружины примет вид

 max   [] (6)

Для определения изменения высоты пружины под нагрузкой (у пружин сжатия эта величина называется осадкой и обозначается ) воспользуемся соотношениями. Работа внешней статически приложенной силы F определяется по теореме Клапейрона

 W =  (7)

Эта работа равна энергии деформации пружины

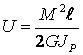 , (8)

где G – модуль сдвига, JР – полярный момент инерции поперечного сечения витка.

В выражении (7) под длиной пружины ℓ понимается полная длина проволоки пружины ℓ ≈ πDn, где n – число рабочих витков пружины. Для пружин растяжения во внимание не принимается отогнутая часть витков. Для пружин сжатия из полного числа витков исключается примерно 3/4 витка с каждого торца, поскольку эти витки при навивке поджимаются к соседним и свободно деформироваться не могут. Таким образом предполагается, что 1,5 витка в работе не участвуют.

Приравнивая правые части выражений (6) и (7), получим:

  = 

Учитывая, что М = FD/2 и 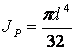, имеем: 

 = ,

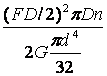откуда осадка пружины

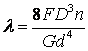  (9)

ЗАДАНИЕ

При подготовке к лабораторной работе студент должен:

 – знать виды пружин и области их применения;

– знать внутренние силовые факторы, возникающие в поперечных сечениях витков пружины при приближенном расчете;

– знать основные параметры цилиндрических винтовых пружин;

– знать формулу для определения коэффициента k, учитывающего кривизну витков и напряжения среза;

– уметь строить эпюры касательных напряжений в сечениях витков;

– уметь определять напряжения в наиболее опасной точке витка;

– уметь определять осадку пружины;

– ответить на контрольные вопросы;

– правильно оформить отчет по лабораторной работе. 

РАБОТА В ЛАБОРАТОРИИ

1. Установить пружину в приспособление для сжатия пружин.

2. Дать нагрузку F = H

3. Измерить величину осадки пружины 

4. Найти индекс пружины сп

5. Определить значение поправочного коэффициента k по формуле (5)

6. Рассчитать величину осадки р пружины по формуле (9) и сравнить полученную величину с найденной экспериментально.

7. Вычислить значение наибольших касательных напряжений в витках пружины по формуле (6) и сравнить их с допускаемыми [] = 300 МПа

8. Сделать выводы.

РЕЗУЛЬТАТЫ  РАБОТЫ

Расчетные формулы

1. Индекс пружины cп =  =

2. Поправочный коэффициент, учитывающий индекс пружины и кривизну витков k = 1 + 1,45/ cп = 1 + 1,45/ =

3. Расчетное значение осадки пружины

 P =  =

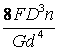4. Значение наибольших касательных напряжений в точке А приужины

 A =  =

 ТАБЛИЦА РЕЗУЛЬТАТОВ

D, мм	d, мм	n	F, Н	, мм	cп	k	P, мм	A, МПа

В Ы В О Д Ы

1. Величины осадки пружины, определенные опытным и расчетным путем, оказались примерно одинаковыми. Значит, формула (9) верна.

2. Значения максимальных касательных напряжений в точках, находящихся ближе к центру, не превысили допускаемых. Значит, условие прочности пружины не нарушено.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какая деталь называется пружиной?

2. Назовите типы пружин и области их применения.

3. Из какого металла изготавливают пружины?

4. Чем отличаются пружины сжатия от пружин растяжения?

5. Какое число витков у пружин растяжения и сжатия исключается при расчете и почему?

6. Что такое индекс цилиндрической винтовой пружины и каково его значение?

7. На какой вид деформации работают витки пружины?

8. В чем заключается приближенный расчет пружин?

9. По каким формулам вычисляется поправочный коэффициент k, учитывающий индекс пружины сп, влияние поперечной силы Q и угол α наклона витков?

10. Что такое осадка  пружины и по какой формуле она вычисляется?

 

 

 

 

 

 

Практическая работа №14 «Эпюры поперечных сил и изгибающих моментов».

 

Цель работы:

определить опорные реакции и построить эпюры поперечных сил (Q) и изгибающих моментов (М) для балки на двух опорах.

Теоретическое обоснование.

Для проверки прочности элементов, подверженных деформации «прямой изгиб», следует выявить опасные сечения.  Если будет обеспечена прочность в этих сечениях, то она будет обеспечена во всех остальных сечениях балки.

Ответить на вопросы полными предложениями:

1.      Что следует сделать для выявления опасных сечений?

2.      Какие внутренние силовые факторы возникают при прямом поперечном изгибе?

3.      Что такое эпюра?

4.      Чему равна поперечная сила в сечении бруса, подверженного деформации «прямой поперечный изгиб»?

5.      Чему равен изгибающий момент в сечении бруса, подверженного деформации «прямой поперечный изгиб»?

 

Порядок выполнения.

1.      Определить опорные реакции.

2.      Разделить брус на участки в пределах нагрузки.

3.      Определить Q (кН) на каждом участке. Построить эпюру Q.

Правило знаков для Q:

 

4.   Определить М, (кН·м) на каждом участке. Построить эпюру М. Правило знаков для М:

 

Если на участке с распределенной нагрузкой есть Q=0, необходимо подсчитать М_экстр.

                                       Пример решения задачи.

 

 

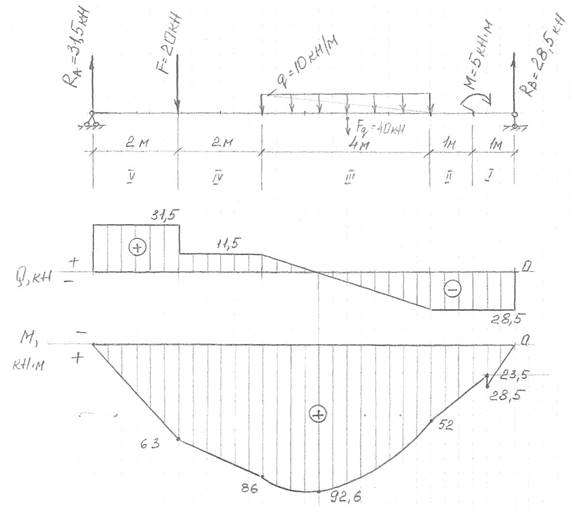
1.     Определяем реакции опор R_A и R_B, составив и решив уравнения равновесия вида   и . Делаем Проверку, составив уравнение .

;  R_B=28,5 (кН)

;  R_A=31,5 (кН)

Проверка:

31,5 – 20 – 40 + 28,5 = 0;  0=0

 

2.     Делим балку по длине на участки. Границей участка являются: точка приложения сосредоточенной силы (R_А, F, R_B); точка приложения сил (М); начало и конец распределенной нагрузки (q). Получилось 5 участков: I, II, III, IV, V.

3.     На каждом участке определяем величину поперечной силы Q:

←

←                                                                            Q

←

→

→

 

Строим эпюру Q, соединяя найденные пограничные значения прямой (т.к. зависимость в уравнениях линейная).

Проверяем эпюру:

в месте приложения сосредоточенной силы должен быть скачок, равный величине этой силы.

 

4.   На каждом участке определяем величину изгибающего момента М:

                                                                                                                            М

←

←

←

←

←

 

(qх – заменяем распределенную нагрузку на отрезке Х на сосредоточенную, приложенную в середине этого участка; - плечо силы qх).

 

Строим эпюру М. На I, II, IV, V участках это прямые (зависимость линейная), соединяющие значения М в начале и конце участка. На участке III – парабола (в уравнении М^III есть Х²).

Определяем, есть ли в параболе точка экстремума. Она есть, если на этом участке есть Q=0 (см. эпюру Q, пересечение Q^III с нулевой линией).

Приравняем уравнение для Q^III к нулю и находим, при каком Х Q^III=0:

- 28,5 +10 х =0;  х = 2,85

 

Подставляем найденное значение Х в уравнение М^III и находим значение М_экстр.:

 

Практическая работа №15 «Расчёты на прочность при изгибе».

Тема: Сопротивление материалов. Деформация изгиба.

 

Цель работы: Научиться построению эпюр изгибающих моментов и поперечных сил и производить расчеты на прочность при изгибе.

 

Задание: Для заданной расчетной схемы оси определить реакции опор, построить эпюры поперечных сил и изгибающих моментов, подобрать диаметр оси из условия прочности при изгибе. Номер варианта принять согласно номеру студента в списке по журналу. Для расчетов принять: материал оси — сталь 40, допускаемое напряжение на изгиб .

 

Порядок выполнения.

 

1. Изобразить расчетную схему.

2. Выписать исходные данные из таблицы.

3. Заменить действие опор на балку силами реакций.

4. Составить уравнение равновесия для плоской системы параллельных сил:

  

5. Найти из уравнений равновесия неизвестные силы реакций.

6. Определить поперечную силу в каждом из характерных сечений, как сумму внешних сил, приложенных по одну сторону от сечения.

7. Построить эпюру поперечных сил.

8. Определить величину изгибающего момента для каждого характерного сечения, как сумму моментов внешних сил, приложенных по одну сторону от сечения, относительно центра тяжести этого сечения.

9. Построить эпюру изгибающих моментов.

10. Выбрать наиболее нагруженное сечение, где Mu=max.

11. Записать уравнение условия прочности при изгибе:

12. Найти требуемую величину осевого сопротивления сечения:

;   из выражения; .

13. Определить диаметр наиболее нагруженного поперечного сечения оси:

14. Округлить диаметр до ближайшего стандартного значения из ряда R40 по таблицы 2

15. Вывод

 

Задания к практической работе № 8

 

1	2
3	4
5	6
7	8
9	10

 

Практическая работа № 16 «Выбор рационального сечения балки».

 

Основные положения и расчётные формулы

Геометрические характеристики круга и кольца

Круг (рисунок 10.1)

- круг;

Рисунок 10.1

Кольцо (рисунок 10.2)

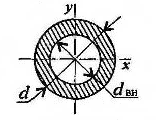
Рисунок 10.2

Моменты сопротивления:

Площади сечения

Условие прочности при совместном действии изгиба и кручения.

Эквивалентные моменты

 

 

Расчетно-графическая работа

Для промежуточного вала редуктора, передающего мощность Р при угловой скорости ω, определить вертикальную и горизонтальную составляющие реакции подшипников, построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях. Определить диаметры вала по сечениям, приняв [σ] – 60 МПа и полагая F_T- 0,364 F_t. Расчёт произвести по гипотезе максимальных касательных напряжений.

 

Рисунок 10.3

 

Указание: Окружную силу определить по формуле

Приложение № 1

Сталь горячекатная. Швеллеры.

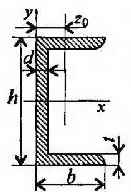
Обозначение:

h- высота швеллера; b- ширина швеллера

d- толщина стенки; t-средняя толщина полки

А- площадь швеллера

J- момент инерции

W- момент сопротивления

i – радиус инерции

S – статический момент полусечения

Z₀- расстояние от оси у до наружной грани стенки

Таблица 1

 

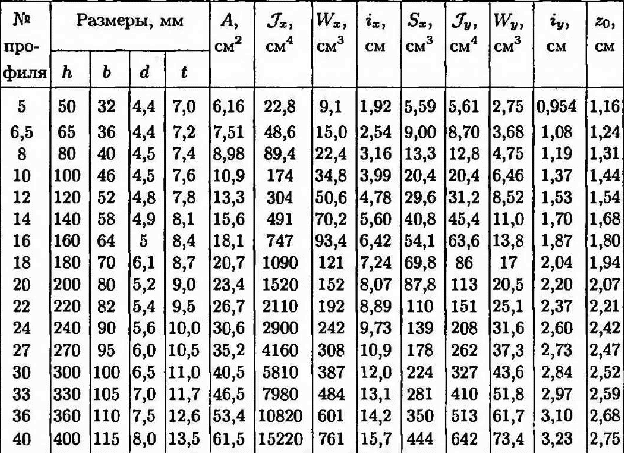
Сталь горячекатная. Балки двутавровые.

Обозначение: 

h- высота балки ;b- ширина балки

d- толщина стенки; t-средняя толщина полки

А- площадь сечения; J- момент инерции

W- момент сопротивления

i – радиус инерции

S – статический момент полусечения

Таблица 2

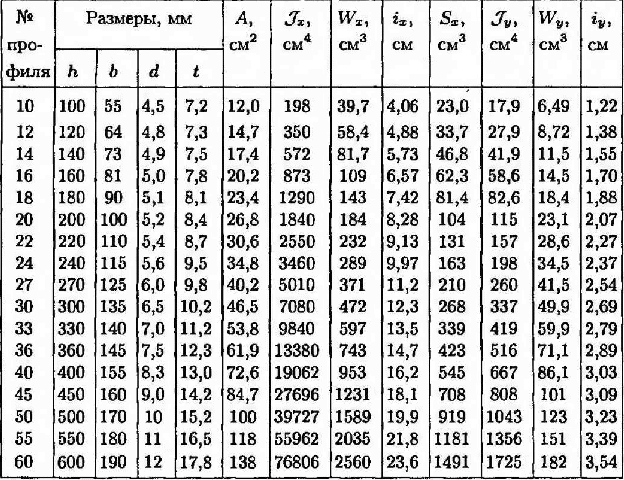
Сталь прокатная угловая равнополочная.

Обозначение: 

b- ширина полки;

d- толщина полки;

А- площадь уголка;

W- момент сопротивления

i – радиус инерции

Z₀- расстояние от оси у до наружной грани полки

J- момент инерции

 

Таблица 3

 

 

 

 

 

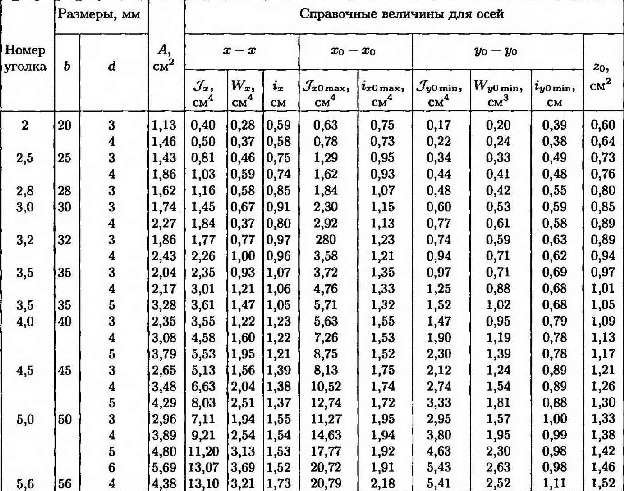
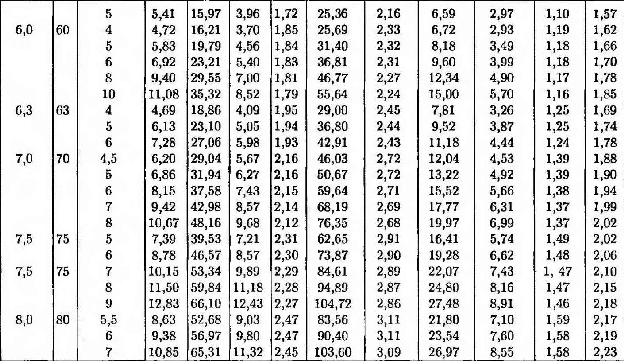
Продолжение таблицы 3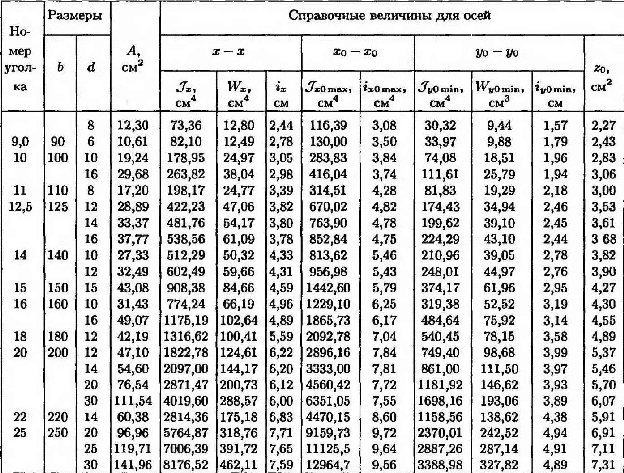

 

 

Практическая работа №17 «Расчёт вала на изгиб и кручение».

Основные понятия. Крутящий момент

Под кручением понимается такой вид деформации, когда в поперечных сечениях бруса действует только крутящий момент M_k, (другое обозначение T, M_z), а остальные силовые факторы (нормальная и поперечная силы и изгибающие моменты) отсутствуют.

Или другое определение кручением называют деформацию, возникающую при действии на стержень пары сил, расположенной в плоскости, перпендикулярной к его оси (рис. 5.1).

Кручение возникает в валах, винтовых пружинах, в элементах пространственных конструкций и т.п.

Деформация кручения наблюдается если прямой брус нагружен внешними моментами (парами сил M), плоскости действия которых перпендикулярны к его продольной оси

В чистом виде деформация кручения встречается редко, обычно присутствуют и другие внутренние силовые факторы (изгибающие моменты, продольные силы).

Стержни круглого или кольцевого сечения, работающие на кручение, называют валами.

Внешние крутящие моменты передаются на вал в местах посадки на него шкивов, зубчатых колес, там, где поперечная нагрузка смещена относительно оси вала.

Мы будем рассматривать прямой брус только в состоянии покоя или равномерного вращения. В этом случае алгебраическая сумма всех внешних скручивающих моментов, приложенных к брусу, будет равна нулю.

При расчете брусьев, испытывающий деформацию кручения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от M_k), возникающих в брусе, и нахождение угловых перемещений в зависимости от внешних скручивающих моментов.

При расчете валов обычно бывает известна мощность, передаваемая на вал, а величины внешних скручивающих моментов, подлежат определению. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п.

В ряде случаев величины внешних крутящих моментов определяются по величине потребляемой мощности и по скорости вращения вала. Если вал делает в минуту nоборотов, то угол поворота вала за 1 сек, выраженный в радианах, равен  Работа крутящего момента M_k за 1 сек, т. е. мощность N, передаваемая валом, равна произведению величины момента на угол поворота вала (в радианах) за 1 сек:

где мощность N  выражена в кГ∙м/сек.

Если мощность N задана в лошадиных силах (л.с.), то

Если мощность N  задана в киловаттах, то, учитывая, что 1 л.с. равна 0,736 кВт, получаем

 

Построение эпюр крутящих моментов

Для определения напряжений и деформаций вала необходимо знать значения внутренних крутящих моментов M_k  (M_z) в поперечных сечениях по длине вала. Диаграмму, показывающую распределение значений крутящих моментов по длине бруса, называют эпюрой крутящих моментов. Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала.

В простейшем случае, когда вал нагружен только двумя внешними моментами (эти моменты из условия равновесия вала ΣM_z=0 всегда равны друг другу по величине и направлены в противоположные стороны), как показано на рис. 5.1, крутящий момент M_z в любом поперечном сечении вала (на участке между внешними моментами) по величине равен внешнему моменту |M₁|=|M₂|.

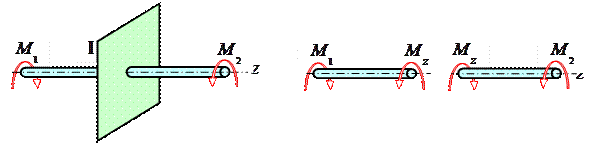
Рис. 5.1

 

В более сложных случаях, когда к валу приложено несколько внешних моментов, крутящие моменты M_k  в поперечных сечениях различных участков вала неодинаковы.

На основании метода сечений крутящий момент в произвольном поперечном сечении вала численно равен алгебраической сумме внешних скручивающих моментов, приложенных к валу по одну сторону от рассматриваемого сечения.

При расчетах на прочность и жесткость знак крутящего момента не имеет никакого значения, но для удобства построения эп. M_k примем следующее правило знаков: крутящий момент считается положительным, если при взгляде в торец отсеченной части вала действующий на него момент представляется направленным по ходу часовой стрелки (рис.5.2).

В технике употребляется терминология « винт с правой нарезкой» или «…с левой нарезкой…», причем правый винт наиболее распространен, являясь стандартом. Полезно заметить, что при навинчивании гайки на правый винт мы прикладываем положительный момент M_кр , а при свинчивании гайки – отрицательный.

Рис. 5.2

 

При наличии распределенной моментной нагрузки m (рис.5.3) крутящие моменты М_К связаны дифференциальной зависимостью

из которой вытекает следующая формула:

где  – крутящий момент в начале участка.

Согласно формуле (5.2) на участках с равномерно распределенной нагрузкой m крутящий момент изменяется по линейному закону. При отсутствии погонной нагрузки (m = 0) крутящий момент сохраняет постоянное значение  (М_К = М_Ко = const). В сечениях, где к валу приложены сосредоточенные скручивающие моменты, на эпюре М_К возникают скачки, направленные вверх, если моменты направлены против часовой стрелки, либо вниз – при обратном направлении моментов.

Рис. 5.3

 

На рис. 5.4, а изображен стержень, жестко защемленный в правом концевом сечении, к которому приложены три внешних скручивающих момента.

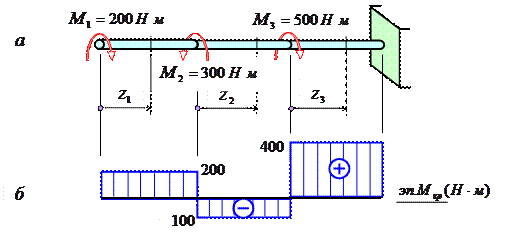
Рис. 5.4

 

В нашем случае крутящие моменты в их поперечных сечениях удобно выражать через внешние моменты, приложенные со стороны свободного конца бруса.

Это позволяет определять крутящие моменты, не вычисляя реактивного момента, возникающего в заделке.

Крутящий момент M_z1 в сечении I численно равен M₁=200 нм и, согласно принятому правилу знаков, положителен.

Крутящий момент M_z2 в сечении II численно равен алгебраической сумме моментов M₁ и M₁, т.е. M_z2 =200-300=-100 нм, а его знак зависит от соотношения этих моментов.

Аналогичным образом вычисляется крутящий момент M_z3 в сечении III: M_z3 =200-300+500=400 нм.

Изменение крутящих моментов по длине вала покажем с помощью эпюры крутящих моментов. На рис. 5.4, б показана такая эпюра для стержня, изображенного на рис. 5.4, а.

Каждая ордината эп. M_k в принятом масштабе равна величине крутящего момента, действующего в том поперечном сечении бруса, которому соответствует эта ордината.

В сечении, в котором к брусу приложен внешний скручивающий момент, ордината эпюры изменяется скачкообразно на величину, равную значению этого момента.

Следует учитывать, что наибольший внешний скручивающий момент, приложенный к брусу, не всегда равен наибольшему крутящему моменту, по которому ведется расчет бруса на прочность и жесткость.

 

Пример 1.

Построить эпюру крутящих моментов для жестко защемленного стержня (рис.5.4.1, а).

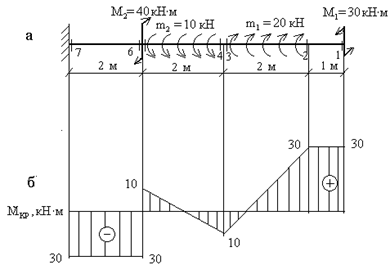
Рис.5.4.1

 

Решение.

Следует отметить, что алгоритм и принципы построения эпюры крутящих моментов полностью совпадают с алгоритмом и принципами построения эпюры продольных сил.

1. Намечаем характерные сечения.

2. Определяем крутящий момент в каждом характерном сечении.

3. По найденным значениям строим эпюру  (рис.5.4.1, б).

 

Пример 2.

Рассмотрим расчетную схему ва­ла, нагруженного двумя сосредоточенными моментами М и 2М и распределенными по длине: т (рис. 5.4.2).

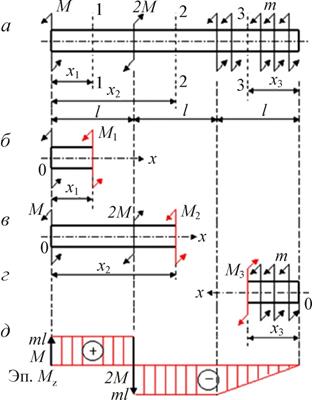
Рис. 5.4.2. Построение эпюры внутренних крутящих моментов:

а – расчетная схема; б – первый участок, левая часть; в – второй участок, левая часть;

г – третий участок, правая часть; д – эпюра внутренних крутящих моментов

 

Решение.

В исходных сечениях 1–1; 2–2; 3–3 задаются положительными зна­чениями внутренних крутящих мо­ментов М₁, М₂, М₃. Пусть .

Для первого участка (рис. 5.4.2, б):

ΣM_k = M₁ + M = 0;

M₁ = –M = ml = const.

Для второго участка (рис. 5.4.2, в):

Для третьего участка (рис. 5.4.2, г):

Границы измерения параметра х₃ в следующей системе координат:

Тогда

Отмеченные значения ординат откладываются на эпюре внутренних крутящих моментов (рис. 5.4.2, д).

 

 

 

 

Практическая работа №18 «Расчёт на устойчивость

Цель: Провести расчет на устойчивость сжатых стержней

 

1. Получение сведений о материале стержня для определения предельной гибкости стержня расчетным путем или по таблице:

2. Получение сведений о геометрических размерах поперечно­го сечения, длине и способах закрепления концов для определения категории стержня в зависимости от гибкости:

где А — площадь сечения; J_min— минимальный момент инерции (из осевых);

μ — коэффициент приведенной длины.

3. Выбор расчетных формул для определения критической силы и критического напряжения.

 

4. Проверка и обеспечение устойчивости.

При расчете по формуле Эйлера условие устойчивости:

F — действующая сжимающая сила; [s_у] — допускаемый коэффици­ент запаса устойчивости.

При расчете по формуле Ясинского

где a, b — расчетные коэффициенты, зависящие от материала (величины ко­эффициентов приводятся в таблице 36.1)

В случае невыполнения условий устойчивости необходимо уве­личить площадь поперечного сечения.

Иногда необходимо определить запас устойчивости при задан­ном нагружении:

При проверке устойчивости сравнивают расчетный запас вынос­ливости с допускаемым:

Примеры решения задач

 

Пример 1. Рассчитать гибкость стержня. Круглый стержень диаметром 20 мм закреплен так, как показано на рис. 37.1.

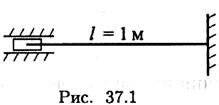 Решение

1. Гибкость стержня определяется по формуле

2. Определяем минимальный радиус инерции для круга. 

Подставив выражения для J_min и А (сечение круг)

получим

1. Коэффициент приведения длины для данной схемы крепле­ния μ= 0,5.
2. Гибкость стержня будет равна

Пример 2. Как изменится критическая сила для стержня, ес­ли изменить способ закрепления концов? Сравнить представленные схемы (рис. 37.2)

 

Решение

 

 

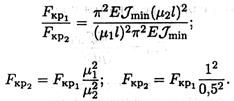
Критическая сила увеличится в 4 раза. 

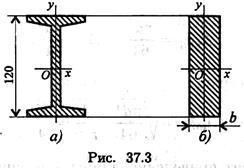 Пример 3. Как изменится критическая сила при расчете на устойчивость, если стержень двутаврового сечения (рис. 37.3а, дву­тавр № 12) заменить стержнем прямоугольного сечения той же пло­щади (рис. 37.3б)? Остальные параметры конструкции не меняются. Расчет выполнить по формуле Эйлера.

Решение

 

1. Определим ширину сечения прямоугольника, высота сечения равна высоте сечения двутавра. Геометрические параметры двутавра № 12 по ГОСТ 8239-89 следующие:

площадь сечения А₁ = 14,7см²;

минимальный из осевых моментов инерции . 

По условию площадь прямоугольного сечения равна площади сечения двутавра. Определяем ширину полосы при высоте 12 см.

2. Определим минимальный из осевых моментов инерции.

3. Критическая сила определяется по формуле Эйлера:

4. При прочих равных условиях отношение критических сил рав­но отношению минимальных моментов инерции:

5. Таким образом, устойчивость стержня с сечением двутавр № 12 в 15 раз выше, чем устойчивость стержня выбранного пря­моугольного сечения.

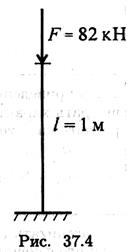 Пример 4. Проверить устойчивость стержня. Стержень длиной 1 м защемлен одним концом, сечение — швеллер № 16, материал — СтЗ, запас устойчивости трехкратный. Стержень нагружен сжима­ющей силой 82 кН (рис. 37.4).

Решение

 

1. Определяем основные геометрические пара­метры сечения стержня по ГОСТ 8240-89. Швеллер № 16: площадь сечения 18,1см²; минимальный осевой момент сечения 63,3 см⁴; мини­мальный радиус инерции сечения г_т;_п = 1,87см.

2. Определяем категорию стержня в зависимости от гибкости.

Предельная гибкость для материала СтЗ λ_пред = 100.

Расчетная гибкость стержня при длине l = 1м = 1000мм

Рассчитываемый стержень — стержень большой гибкости, рас­чет ведем по формуле Эйлера.

3. Допускаемая нагрузка на стержень

4. Условие устойчивости

82кН < 105,5кН. Устойчивость стержня обеспечена.

Практическая работа №19 «Механические передачи. Расчёт привода».

Цель:Сформировать умения, по выполнению расчетов для определения совместного действия изгиба и кручения на валу.

Пример выполнения задания

Из условия прочности рассчитать необходимый диаметр вала . На валу установлены два колеса. На колеса действуют две окружные силы F_t1=1,2 кН   F_t2=2кН, и две радиальные силы F_r1=0,43 кН    F_r2=0,72кН. Диаметры колес соответственно равны d₁=0,1м ,   d₂=0,06м,  [σ]=50Мпа.

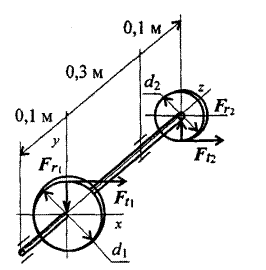
Решение

1.Составим расчетную схему вала.

 

     2.Определим крутящий момент на валу

М_к=М_вр=F_t1=F_t2

М_к=1,2₌0,06кН*м=60 Н*м

3. Изгиб рассматриваем в двух плоскостях:  горизонтальной  (плоскость Н) и вертикальной (плоскостьV)

      В горизонтальной плоскости определяем реакции в опоре

=F_t1*a-R_B^H(a+b)+F_t2(a+b+c)=0

1,2*0,1-R_B^H*0,4+2*0,5=0

R_B^H=2,8кН

= R_А^H(а+b)-F_t1*b+F_t2*c=0

R_А^H*0,4-1,2*0,3+2*0,1=0

R_А^H=0,4кН

 Определяем изгибающие моменты в точках В и С

М_С^Н=400*0,1=40 Н*м

М_В^Н=-2000*0,1=200 Н*м

    В вертикальной плоскости определяем реакции в опоре

= F_r1*a-R_B^V(a+b)-F_r2(a+b+c)=0

-R_B^V*0,4+0,43*0,1-0,72*0,5=0

R_B^V=-0,79кН

= R_А^V(a+b)- F_r1*b-F_r2*c=0

    R_А^V*0,4-0,43*0,3-0,72*0,1=0

R_А^V=0,5кН

   Определяем изгибающие моменты в точках С и В

М_С^V= R_А^V*aМ_С^V=500*0.1=50 Н*м

М_B^V= F_r2*cМ_B^V=720*0.1=72 Н*м

    Определяем суммарные изгибающие моменты в точках В и С

М_С= =63 Н*м

М_В==215 Н*м

   В точке В максимальный изгибающий момент, здесь же действует и крутящий момент.

    Расчет диаметра вала ведем по наиболее нагруженному сечению.

 

 

 

 

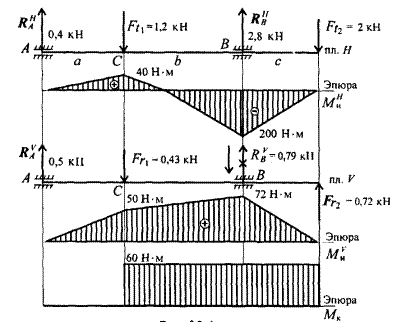
4.Эквивалентный момент в точке В по третьей теории прочности

М_{экв 111}=

М_{экв 111}==223 Н*м

 

5. Определяем диаметр вала  круглого поперечного сечения из условия прочности

σ_экв=≤[σ], W_х=0,1d³,≤[σ]

d ≥  d≥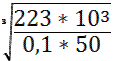=35,5мм

Округляем полученную величину: d=36мм

6. Определяем необходимые размеры вала кольцевого сечения при с=0,8

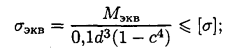
W_х=0,1d³(1-с⁴) – кольцо

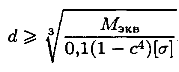
Диаметр вала кольцевого сечения можно определить по формуле

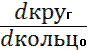=d_кольцо=d_круг⁴

 

d_кольцо=36⁴       d ≥42,5мм

Примем d=42мм

Перегрузка незначительная d_вн=0,8d=0,8*42=33,6мм≈33мм

7. Сравним затраты металла  по площадям сечения вала в обоих  случаях

       Площадь поперечного сечения сплошного вала

     А_1круга===1018мм²

       Площадь поперечного сечения полого вала

 А_{2кольца}=(d²-d²_внутр)

         А_{2кольца}==530мм

      Площадь поперечного сечения сплошного вала почти в два раза больше вала кольцевого сечения

=≈2

Задание: решить самостоятельно по вариантам

Вариант 2

 

Вариант 3

Содержание отчета

1. Наименование работы.

2. Цель работы.

3. Номер варианта.

4.Расчеты

5. Вывод

Контрольные вопросы:

1. Что такое сложное сопротивление?

2.Какие виды деформации бруса называют сложным со­противлением? 

3. Какой изгиб называется косым?

4. Сформулируйте принципы,  на  которых строится  рас­чет брусьев при сложном сопротивлении?

5.  Какие внутренние усилия возникают в стержне в  случае сложного сопротивления?

6. По каким формулам определяются нормальные напряжения при косом изгибе?

7.Когда возникает косой изгиб? 

 

Практическая работа №20 «Прямозубая передача».

Учебная цель: Произвести расчет цилиндрической прямозубой передачи.

 

Образовательные результаты, заявленные во ФГОС третьего поколения:

Студент должен

уметь:

- рассчитывать цилиндрическую зубчатую передачу;

- строить эвольвентное зацепление зубчатой передачи;

знать:

- классификацию зубчатых передач

- расчетные формулы.

 

Краткие теоретические и учебно-методические материалы по теме практической работы

В зависимости от относительного расположения геометрических осей ведущего и ведомого валов различают: зубчатые передачи цилиндрическими колесами (рис.1),применяемые при параллельных осях валов; зубчатые передачи коническими колесами (рис.2), применяемые при пересекающихся осях валов; зубчатые передачи винтовыми и гипоидными колесами, применяемые при скрещивающихся осях валов.

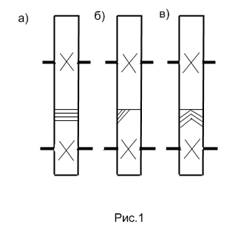
По расположению зубьев относительно образующей цилиндрические зубчатые колеса подразделяются на (см.рис.1): прямозубые (а), косозубые (б) и шевронные (в).

Конические зубчатые колеса бывают (см. рис.2): прямозубые (а), косозубые (б) и с круговым зубом (в).

Цилиндрические колеса могут быть с внешним  и с внутренним  зацеплением.

Если ведущий и ведомый валы находятся на значительном расстоянии друг от друга, передача осуществляется последовательным рядом зубчатых колес.

Рисунок 2

 

Общее передаточное число такого ряда зубчатых колес равно отношению числа зубьев последнего зубчатого колеса ряда к числу зубьев первого; промежуточные зубчатые колеса («паразитные») не влияют на величину передаточного числа, от их количества зависит лишь направление ведомого колеса. При нечетном числе промежуточных колес ведущее и ведомое зубчатые колеса имеют одинаковые направления вращения:

i = ω₁/ ω_n = u = z_n / z₁

 

Пример по выполнению практической работы

Что делать

Чем руководствоваться

1.      Определить угловую скорость тихоходного или быстроходного вала в зависимости от известной угловой скорости и заданного передаточного числа. Во избежание получения больших габаритов передачи не следует применять i >6 для механических передач и i >10-12 для ручных. При необходимости создания передачи с большими значениями i следует применять двух- или трехступенчатые передачи 2.    Выбрать материал шестерни и колеса. Определить σв, σт, σ-1 и твердость НВ 3.    Определить допускаемые контактные напряжения для колеса (материал колеса менее прочен, чем материал шестерни ) 4.      Выбрать коэффициент ширины венца колеса φа = b / aω 5.      Выбрать (предварительно) коэффициент нагрузки К После определения размеров зубчатых колес следует уточнить коэффициент нагрузки. При этом:    а) коэффициент динамичности определяется в зависимости от степени точности зацепления, твердости поверхности зубьев колеса окружной скорости   б) коэффициент концентрации нагрузки определяется в зависимости от степени точности зацепления, расположения зубчатых колес относительно ширины зубчатых колес, характера нагрузки и твердости поверхности зубьев 6.      Определить расчетный момент на валу шестерни в зависимости от предаваемой мощности и угловой скорости       7.      Определить межосевое расстояние аω 8.      Определить ширину венцов зубчатых колес. 9.      Задаться модулем зубьев. По ГОСТ 9563-60 принять стандартное значение модуля 10.  Определить: а) суммарное число зубьев передачи б) число зубьев колеса в) число зубьев колеса Число зубьев шестерни в некорригированной передаче должно быть не менее zmin≥17. Большие числа зубьев обеспечивают   более плавную работу передачи 11.  Уточнить межосевое расстояние. 12.  Сравнить прочность на изгиб зубьев шестерни и колеса. При нереверсивной работе передачи берут допускаемые напряжения [σ0]и, а при реверсивной [σ-1]и, которые в 1,4 раза меньше  [σ0]и. Если зубья шестерни окажутся прочнее зубьев колеса, дальнейшей расчет ведется для зубьев колеса (или наоборот)                         13.  Произвести проверочный расчет зубчатой передачи: а) на контактную прочность       б) на изгиб     14.  Определить основные размеры шестерни и колес

ω2 = ω1 / i, или ω1 =  ω2 i, или n2 = n1 / i, или  n1 = n2 i                 См. табл.1,2     [σ]к = 2,75 НВ     См. табл. 3     К = Кдин Ккнц   В начале расчета можно принимать К≈1,3 при симметричном расположении зубчатых колес и К≈1,5 при несимметричном или консольном расположении колес относительно опор  См. табл. 4   См. табл. 5         МБр = МБ К, где МБ – номинальный момент на валу шестерни МБ = NБ / ω1, где МБ   Н∙м, NБ  Вт, ω1 рад/c                                          МБр аω = 48,7 (и + 1) ∙ 3√ ──────,                                          [σ]к2φаи где и = z2 / z1, МБ   Н ∙ мм, [σ]к Н / мм2, аω мм   b = φa aω   m = (0,01 ÷ 0,02) aω       zc = 2aω / m   zш = z1 = zc / (и + 1) zк = z2 = иz1           aω = m (z1 + z2) / 2 для шестерни                                   σ-1                              у1[σ0]и = у1 ∙ 1,4 ────;        [n]kσ для колеса                         σ-1 у2 [σ0]и = у2 ∙ 1,4 ────;                            [n]kσ у1 и у2 принимают по табл. 7; [n] – требуемый коэффициент запаса прочности; [n] ≈1,5-2 (большие значения для более прочной стали); kσ – действительный (эффективный) коэффициент концентрации напряжений у корня зуба; kσ = 1,6-1,8 (для стальных зубчатых колес).    Уточненные значения kσ и [n] см. в табл. 8 и 9                          340        МБр(и + 1)3 σк = ──── ∙ √─────── ≤ [σ]к                         аω              bu       2 МБр u σu = ───── ≤ [σ]u y2z2bm2   d1 = mz1;                                d2 = mz2; da1 = d1 + 2m = m (z1+2); da2 = d2 + 2m = m (z2+2); df1 = d1 - 2,5m = m (z1-2,5); df2 = d2 – 2,5m = m (z1-2,5);

 

Таблица 1 - Рекомендуемые сочетания марок стали шестерни и колеса при твердости < НВ350

Шестерня	Колесо	Шестерня	Колесо	Шестерня	Колесо	Шестерня	Колесо
45	35 35Л	50	Ст5 35 45Л	55	Ст6 45 55Л	50Г	Ст 6 45 55Л
40Х	50 55 40ГЛ	30ХГС	35Х 40Х 40ГЛ	40ХН	35Х 40Х 40ГЛ	-	-

 

 

Таблица 2 - Рекомендуемые сочетания марок стали шестерни и колеса при твердости > НВ350

Шестерня	Колесо	Шестерня	Колесо
45; 50 55; 50Г 35Х; 40Х	35; 40 40; 45; 50 50; 55	40ХН 15Х; 20Х 12ХНЗА	35Х; 40Х 15Х; 20Х 12ХНЗА

 

Таблица 3 - Значения коэффициента ширины венца зубчатого колеса

Колеса	φа
Прямозубые Косозубые Шевронные	0,12-0,14 0,2-0,6 0,4-1,2

 

Таблица 4 - Значения коэффициента К_дин для расчета прямозубых цилиндрических колес

Степень точности зацепления	Твердость поверхности зубьев большого колеса, НВmin	Наибольшая допустимая окружная скорость, м/c	Кдин при окружной скорости, м /с
			До 3	3-8	8-12
7       8       9	До 200 200-350 Более 350   До 200 200-350 Более 350   До 200 200-350	12     8       3	1,5 1,2 1,2   1,4 1,3 1,3   1,5 1,4	1,5 1,4 1,3   1,6 1,5 1,4   - -	1,6 1,5 1,4   -       - -

 

Таблица 5 - Значение коэффициента концентрации нагрузки К_кнц

Твердость поверхности зубьев	Степень точности	Ккнц
>НВ350 обоих зубчатых колес пары       < НВ350 хотя бы одного из колес пары	6 7 8 9	θ 1,1θ 1,2θ 1,3θ θ(1-φ)+φ

 

     Значение вспомогательного коэффициента θ берется из табл.6; φ-вспомогательный коэффициент, зависящий от характера изменения нагрузки: при постоянной нагрузке он равен 1,0; при незначительных колебаниях нагрузки – 0,6; при значительных ее колебаниях – (0,25-0,3)

 

Таблица 6 - Значение вспомогательного коэффициента θ

Расположение зубчатых колес	Форма зубьев	Отношение b/d1 (для конических колес по среднему диаметру)
		≤1,1	1-1,6	1.6-1,8	1,8
Симметричное Несимметричное или консольное хотя бы одного из колес	Любая Косые β<20º Шевронные β<20º Прямые	1,1 1,4 1,3 1.3	1,2 1,4 1,4 1,3	1,3 1,5 1,4 1,4	1,4 1,5 1,5 1,5

 

Таблица 7 - Значение коэффициента у для эвольвентного наружного зацепления при α = 20º

Число зубьев	у	Число зубьев	у	Число зубьев	у
12 14 16 18 20	0,304 0,324 0,339 0,354 0,372	24 28 30 35 40	0,395 0,411 0,416 0,431 0,442	50 65 100 300 рейка	0,457 0,472 0,481 0,496 0,523

 

Таблица 8 - Значения эффективного коэффициента концентрации напряжений k_σ y корня зуба

Материал и термообработка	kσ
Стальные зубчатые колеса, подвергнутые нормализации или улучшению Стальные зубчатые колеса, зубья, подвергнутые объемной закалке Стальные зубчатые колеса, зубья, подвергнутые цементации, азотированию или цианированию Чугунные зубчатые колеса	1,4-1,6 1,8   1,2 1,2

 

Таблица 9 - Рекомендуемые значения коэффициента запаса прочности [n] дл расчета на изгиб зубьев цилиндрических и конических зубчатых колес

Материал и термообработка	[n]
Отливки стальные и чугунные, термически не обработанные Отливки стальные и чугунные, подвергнутые отжигу нормализации или улучшению Поковки стальные, подвергнутые нормализации или улучшению Поковки стальные, подвергнутые объемной закалке	1,9   1,7 1,5 1,8

 

Задания для практического занятия:

 

Произвести расчет цилиндрической прямозубой передачи

 

№ вари анта	N	i	ω
	кВт		Рад/c
1	8	2	80
2	6	4	100
3	10	6	120
4	11	7	90
5	15	8	130

 

Контрольные вопросы

 

1. Обеспечивают ли зубчатые передачи постоянство передаточного отношения?

2.  Какая величина является основной характеристикой размера зубьев?

3.  Габариты какой передачи (прямозубой или косозубой) при прочих равных условиях меньше?

 

 

Практическая работа №21 «Косозубая и шевронная передача».

Цель: закрепление теоретических знаний по теме «Механические передачи» и приобретение практических умений в проведении проектировочных и проверочных расчетов зубчатых передач.

Задание. Рассчитать одноступенчатый цилиндрический редуктор по данным, приведенным в таблиц

 

Вариант

Передаваемая мощность Р_1, кВт

Частота вращения ведущего вала, n₁, об/мин

Передаточное число i

Тип передачи

Материал

шестерни

Материал колеса

1

4,5

780

4

прямозубая

Сталь 45

Сталь 35

2

14

960

4

прямозубая

Сталь40Х

Сталь 45

3

20

960

5

косозубая

Сталь50Г

Сталь 45

4

25

1440

4,5

косозубая

Сталь40ХН

Сталь40Х

5

35

960

5

прямозубая

Сталь40ХН

Сталь 50

6

40

1140

4

прямозубая

Сталь40ХН

Сталь35Х

7

45

960

5

прямозубая

Сталь40ХН

Сталь35Х

8

50

960

4

косозубая

Сталь40ХН

Сталь40Х

9

10

730

2

косозубая

Сталь 55

Сталь 45

10

20

960

3

косозубая

Сталь 50Г

Сталь 40

11

30

1440

5

шевронная

Сталь 40Х

Сталь 45

12

40

960

6

шевронная

Сталь 40Х

Сталь 45

13

50

960

4

шевронная

Сталь40ХН

Сталь40Х

14

60

735

5

шевронная

Сталь40ХН

Сталь40Х

15

70

960

6

шевронная

Сталь 40Х

Сталь 45

16

80

960

5

шевронная

Сталь 40Х

Сталь 45

17

7

1460

3

прямозубая

Сталь 50

Сталь 35

18

14

960

5

прямозубая

Сталь 50

Сталь 35

19

17

730

4

прямозубая

Сталь 50

Сталь 35

20

20

960

4

косозубая

Сталь 50Г

Сталь 45

21

24

720

6

косозубая

Сталь 50Г

Сталь 45

22

30

940

5

косозубая

Сталь 50Г

Сталь 45

23

40

1460

6

шевронная

Сталь30ХГС

Сталь40Х

24

45

960

6,5

шевронная

Сталь30ХГС

Сталь40Х

25

50

730

5

шевронная

Сталь 40ХН

Сталь40Х

26

60

960

4,5

шевронная

Сталь 40ХН

Сталь40Х

27

7

960

5

косозубая

Сталь 40Х

Сталь 45

28

10

1440

4

косозубая

Сталь 40Х

Сталь 45

29

14

730

6

косозубая

Сталь 40Х

Сталь 45

30

7

1440

6

прямозубая

Сталь 45

Сталь 45

 

Материал шестерни улучшен, материал колеса нормализован. Срок службы редуктора неограничен. Характер нагрузки – спокойная с незначительными колебаниями. Для косозубых и шевронных передач углом наклона зубьев задаться.

 

Расчет закрытой цилиндрической прямозубой передачи.

1. Определить передаточное число и.

2. В зависимости от условий работы передачи выбрать материалы колес, назначить термическую обработку и значения твердости рабочих поверхностей зубьев.

 

Предпочтительные марки сталей для изготовления зубчатых колес

Термическая обработка

Твердость НВ (HRC)

d, мм

Любой

315

200

125

80

b, мм

Любая

200

125

80

50

Нормализация, улучшение

179-207 235-262 269-302

45

45 35ХМ

45

40Х

35ХМ

45

45

40Х

45

45

45

Поверхностная закалка ТВЧ

(45-50) (50-56)

—

—

35ХМ 50ХМ

35ХМ 50ХМ

35ХМ 50ХМ

Цементация

Нитроцементация Азотирование

(56-63) (56-63) (50-56)

—

—

20ХН2М 25ХГТ 40ХН2МА

20ХН2М 25ХГТ 40ХН2МА

20ХН2М 25ХГТ 40ХН2МА

 

3. Определить базу испытаний N_HO, расчетную циклическую долговечность N_H, вычислить коэффициенты и допускаемые напряжения изгиба.

4. Выбрать коэффициент длины зуба (ширины венца колеса) и рассчитать.

5. Определить межосевое расстояние из условия контактной прочности и округлить его значение до стандартного.

Для стандартных редукторов расчетное значение а_ш округляют доближайшего большего значения: 40, 50, 63, 80, 100, 125, (140), 160, (180), 200, (225), 250, (280), 315, (335), 400, (450), 500, (560), 630, (710), 800, (900), 1000 и т. д. до 25 000 (в скобках значения по 2-му ряду стандарта для ).

6. Задать модуль из соотношения  и округлить его значение до ближайшего стандартного. При этом в силовых передачах желательно, чтобы модуль был не менее 1,5—2 мм.

7. Определить суммарное число зубьев , передачи, числа зубьев шестерни и колеса.

8. Выбрать коэффициенты формы зубьев Y_Fi и Y_F2 для шестерни и колеса.

9. Проверить прочность зубьев по напряжениям изгиба. При неудовлетворительных результатах ( или ) необходимо путем соответствующего изменения числа зубьев и модуля; при том же межосевом расстоянии добиться уменьшения напряжений изгиба, не нарушая при этом условия контактной прочности.

10. Произвести геометрический расчет передачи.

11. Определить окружную скорость колеса v и назначить соответствующую степень точности зацепления.

 

Значения окружной скорости колес

Вид передачи

Форма зубьев

Твердость поверхностей зубьев колеса (большего) НВ

Окружная скорость v (м/с, не более) при степени точности

6

7

8

9

Цилиндрическая

Прямые

 

Не прямые

До 350

Св. 350

До 350

Св. 350

18

15

36

30

12

10

25

20

6

5

12

9

4

3

8

6

Коническая

Прямые

До 350

Св. 350

10

9

7

6

4

3

3

2,5

Примечание. Во избежание получения чрезмерно высоких значений коэффициентов нагрузки рекомендуется степень точности назначать на единицу выше, чем указано в таблице.

 

Расчет открытых передач. Иногда открытые передачи рассчитывают так же, как закрытые. Рекомендуется следующая последовательность расчета.

1. Определить передаточное число и.

2. В зависимости от условий работы передачи выбрать материалы колес, назначить их термическую обработку и значения твердости рабочих поверхностей зубьев.

3. Определить расчетную долговечность, вычислить коэффициенты режима работы и определить допускаемые напряжения изгиба.

4. Задать число зубьев шестерни  и по передаточному числуопределить число зубьев колеса z₂.

5. Определить коэффициенты формы зуба Y_F.

6. Выбрать коэффициент длины зуба (ширины венца колеса ).

7. Из условия прочности на изгиб определить модуль передачи т и округлить его до ближайшего большего стандартного значения.

8. Произвести геометрический расчет передачи.

9. Определить окружную скорость колес и соответствующую ее степень точности зацепления.

Последовательность расчета закрытой цилиндрической косозубой передачи.

1. Определить передаточное число .

2. В зависимости от условий работы передачи выбрать материалы колес, назначить термическую обработку и твердость рабочих поверхностей зубьев.

3. Определить базовое число циклов , расчетную циклическую долговечность, определить допускаемые напряжения изгиба и контактные напряжения.

4. Выбрать коэффициент  длины зуба (ширины венца колеса).

5. Определить межосевое расстояние из условия контактной прочности.

6. Задать значение нормального модуля из соотношения и округлить его до ближайшего стандартного значения. При этом для силовых передач желательно иметь модуль не менее 1,5—2 мм.

7. Задать угол наклона зубьев  и определить суммарное число зубьев , передачи, числа зубьев шестерни и колеса  и .

8. Определить эквивалентные числа зубьев  и  и коэффициенты формы зуба  и .

9. Проверить прочность зубьев по напряжениям изгиба. При неудовлетворительных результатах ( или ) необходимо путем соответствующего изменения числа зубьев и модуля при том же межосевом расстоянии добиться определенного изменения напряжения изгиба, не нарушая условия контактной прочности.

10. Произвести геометрический расчет передачи. Определить окружную скорость колес и назначить соответствующую степень точности, выбрать.

Расчет открытых передач (часто открытые передачи рассчитывают так же, как закрытые).

1. Определить передаточное число и.

2. В зависимости от условий работы передачи выбрать материалы для колес, назначить их термическую обработку и твердость рабочих поверхностей зубьев.

3. Определить базу испытаний базового числа циклов , расчетную циклическую нагрузку, вычислить коэффициенты и определить допускаемые напряжения изгиба.

4. Задать угол наклона зубьев  и число зубьев шестерни 

5. Определить число зубьев колеса 

6. Определить числа зубьев эквивалентных колес, шестерни и колеса  и по табл.6 коэффициенты формы зуба  и .

7. Выбрать — коэффициент длины зуба (ширины венца).

8. Из условия прочности на изгиб определить значение нормального модуля  и округлить до ближайшего большего стандартного значения.

9. Произвести геометрический расчет передачи.

10. Определить окружную скорость колес  и назначить соответствующую ей степень точности.

 

VII Контрольные вопросы.

1. Каковы основные достоинства и недостатки зубчатых передач по сравнению с другими передачами?

2.По каким признакам классифицируют зубчатые передачи?

3.Чем отличается закрытая передача от открытой?

4.Перечислите достоинства зубчатой передачи по сравнению с фрикционной передачей.

5.Почему в зубчатых передачах сохраняется постоянным передаточное отношение?

6.Что такое эвольвента окружности и какими свойствами, полезными для зубчатых зацеплений, она обладает?

7.Какие окружности называют начальными, какие делительными?

8.Что называется шагом, модулем и углом зацепления?

9.Какие факторы влияют на выбор степени точности зубчатых передач? Какие степени точности передач применяют в общем машиностроении? Какие нормы характеризуют степень точности? Для чего необходим боковой зазор в зубчатой передаче?

10.С какой целью производят смазывание зубчатых передач?

11.Какие основные факторы влияют на КПД зубчатых передач?

12.Каковы области применения прямозубых и косозубых передач?

13.Каковы сравнительные достоинства прямозубых и косозубых колёс?

14.Как определяется передаточное отношение и передаточное число?

15.Каковы главные виды разрушений зубчатых колёс?

16.Какие силы действуют в зубчатом зацеплении?

17.Какие допущения принимаются при расчёте зубьев на контактную прочность?

18.По какой расчётной схеме выполняется расчёт зубьев на изгиб?

19.Где применяются прямозубые цилиндрические передачи?

20.Каким образом в прямозубой передаче можно уменьшить контактные напряжения?

21.Почему для изготовления шестерни берут более твердый материал, чем для изготовления колес? В каких случаях это обосновано?

22.Почему в шевронных передачах угол наклона зубьев выше, чем в косозубых?

23.Почему косозубые передачи прочнее, чем прямозубые?

 

 

 

Перечень рекомендуемой основной и дополнительной литературы, Интернет–ресурсов, необходимых для освоения дисциплины

Основные источники:

1.         Кривошапко, С. Н. Сопротивление материалов. Практикум : учебное пособие для СПО / С. Н. Кривошапко, В. А. Копнов. – 4–е изд., испр. и доп. – М. : Издательство Юрайт, 2017. – 353 с. (ЭБС Юрайт).

2.         Асадулина, Е. Ю. Сопротивление материалов. Конспект лекций : учебное пособие для СПО / Е. Ю. Асадулина. – 2–е изд., испр. и доп. – М. : Издательство Юрайт, 2017. – 254 с. (ЭБС Юрайт).

3.         Техническая механика : учебник / Г.Г. Сафонова, Т.Ю. Артюховская, Д.А. Ермаков. – М. : ИНФРА-М, 2017. — 320 с. (ЭБС Знаниум).

Дополнительные источники:

1.         Родионов, В. Н. Физика : учебное пособие для СПО / В. Н. Родионов. – 2–е изд., испр. и доп. – М. : Издательство Юрайт, 2017. – 295 с. (ЭБС Юрайт).

2.         Физика : учебник / А.А. Пинский, Г.Ю. Граковский ; под общ. ред. Ю.И. Дика, Н.С. Пурышевой. — 4-е изд., испр. — М. : ФОРУМ : ИНФРА-М, 2017. — 560 с. (ЭБС Знаниум).

3.         Горлач, В. В. Физика : учебное пособие для СПО / В. В. Горлач.– М. : Издательство Юрайт, 2017. – 175 с. (ЭБС Юрайт).

Интернет–ресурсы:

1.         ЭБС Юрайт https://www.biblio–online.ru/

2.         ЭБС Знаниум https://www.znanium.com

3.         ЭБС Лань https://e.lanbook.com/

4.         ЭБС Консультант студента www.studentlibrary.ru/

5.         Естественнонаучный образовательный портал: http://en.edu.ru

6.         Министерство образования Российской Федерации: http://www.ed.gov.ru

7.         Российский общеобразовательный портал: http://www.school.edu.ru

 

 

Скачано с www.znanio.ru