С. И. Волкова                                                  

Математика

и конструирование

                ШКОЛА РОССИИ                     ФГОС

С. И. Волкова

Математика

и конструирование

удк 373.167.1:51 ББК 22.1я72

вы

Серия «Школа России» основана в 2001 году

Данное пособие предназначено для учащихся общеобразовательных организаций.

В пособии представлен учебный материал, соответствующий программе авторского курса «Математика и конструирование», который создаёт условия для расширения, углубления и совершенствования геометрических представлений, знаний и умений учащихся, помогает формировать элементы конструкторских и графических умений, развивать воображение и логическое мышление детей.

Все тексты предназначены для чтения взрослыми.

Учебное издание

Серия «Школа России»

Волкова Светлана Ивановна

МАТЕМАТИКА И КОНСТРУИРОВАНИЕ

1 класс

Учебное пособие для общеобразовательных организаций

Руководитель проекта оформления

Юлиан Маркаров

Авторы проекта оформления и художники

Нина Санадзе и Анна Терентьева (Тию)

Центр начального образования

РеДакция естестВенно-математических преДметоВ

Руководитель Центра М К. Антошин

Заведующий редакцией О. А. ПоДымоВа Редактор Т. Б. Бука

Ответственный за выпуск Т. Б. Бука

Обложка Е. Н. ГруДиной

Художественные редакторы А. В. КрикуноВ, И. Н. ВасильеВ

Технический редактор Л. В. Марухно Корректор И. А. ГригалашВили

Налоговая льгота — Общероссийский классификатор продукции ОК 005-93—953000. Изд. лиц. Серия ИД № 05824 от 12.09.01. Подписано в печать 07.07.15. Формат 60х90 ¹ Л. Бумага офсетная. Гарнитура Букварная. Печать офсетная. Уч.-изд. л. 20,51. Доп. тираж 4000 экз. Заказ № 345.

Акционерное общество «Издательство «Просвещение». 127521, г. Москва, 3-й проезд Марьиной рощи, д. 41.

Отпечатано по заказу АО «ПолиграфТрейд» в филиале «Тверской полиграфический комбинат детской литературы» ОАО «Издательство «Высшая школа». 170040, г. Тверь, проспект 50 лет Октября, д. 46. тел.: +7 (4822) 44-85-98. Факс: +7 (4822) 44-61-51.

lSBN 978-5-09-038428-5 © Издательство «Просвещение», 2000 С) Художественное оформление.

Издательство «Просвещение», 2000, 2015

Все права защищены

Интегрированный курс «Математика и конструирование» объединяет в единый учебный предмет два разноплановых по способу овладения ими учебных предмета: математику и трудовое обучение. Такое объединение поможет повысить качество обучения и развития учащихся, так как создаёт условия для осуществления органического единства мыслительной и конструкторско-практической деятельности детей во всём многообразии их взаимного влияния друг на друга и взаимодействия: математические знания и мыслительная деятельность учащихся (умение проводить сравнение, анализ, обобщение и т.п.) служат базой для овладения курсом, специальным образом организованная на её основе конструкторско-практическая деятельность детей даёт возможность формировать элементы конструкторского МЫШЛения, отрабатывать трудовые и конструкторские навыки, проводить анализ предстоящей работы, а всё, вместе взятое, позволяет развивать пространственное и логическое мышление учащихся, актуализировать математические знания за счёт их целенаправленного использования в новых для детей условиях.

Основная цель курса «Математика и конструирование» в начальных классах состоит как в том, чтобы обеспечить высокий уровень математической грамотности учащихся (научить их счёту, сформировать умения выполнять арифметические действия, решать текстовые задачи и др.) и развить трудовые умения и навыки, так и в том, чтобы познакомить с основами конструкторско-практической деятельности и сформировать элементы конструкторского мышления, графической грамотности и технических умений и навыков у учащихся.

Идея интеграции двух учебных предметов и сформулированные цели построения курса определяют и его содержание, основными положениями которого являются:

—преемственность с курсом математики в начальных классах, особенно с его арифметической линией, содержание которой обеспечивает числовую грамотность учащихся, умения решать текстовые задачи, изучение величин и др.; изучение арифметического материала в силу сказанного может быть организовано, например, по новым учебникам и учебно-методическим пособиям по математике авторского коллектива М.И. Моро, МА. Бантова, Г.В. Бельтюкова, С.И. Волкова, СВ. Степанова;

—существенное усиление геометрического содержания начального курса математики, реализуемого в виде практической геометрии и обеспечивающего расширение геометрических представлений, знаний и умений учащихся, развитие их пространственного воображения и логического мышления; блок практической геометрии включает в себя знакомство с основными линейными и плоскостными геометрическими фигурами, их свойствами, а также с некоторыми многогранниками и телами вращения, что создаёт основу, на базе которой у учащихся формируются элементы конструкторского мышления и умений;

—значительное усиление графической линии курса трудового обучения, которая обеспечивает формирование умений и навыков изображать на бумаге в форме схематического рисунка, эскиза, чертежа сначала элементарные геометрические фигуры и различные объекты, а затем и более сложные объекты или части конструируемых объектов, а также формирование умений понимать, читать и использовать чертёж, устанавливать смысловые связи между его элементами, соотносить объекты и их изображения на чертеже, вносить в чертёж нужные изменения и реализовывать их в конструируемом объекте;

З

4-

—расширение содержания курса за счёт привлечения дополнительного материала, связанного с идеей интеграции двух учебных предметов, в частности материала, который обеспечивает представления и знания о точности вычислений, измерений и построений.

Одной из основных особенностей курса «Математика и конструирование» является его геометрическая направленность, реализуемая в ходе практической деятельности учащихся, направленная на расширение, обогащение и углубление геометрических представлений и знаний детей и на создание прочной основы для развития графической грамотности, конструкторского мышления и конструкторских умений и навыков.

Изложение геометрического материала в курсе проводится в наглядно-практических заданиях и упражнениях в русле исторического процесса развития геометрических понятий, когда основу их освоения составляют наблюдения, сравнения и практическая деятельность учащихся. При отборе материала, входящего в геометрическое содержание курса «Математика и конструирование»,

мы исходили из того, что он должен обеспечивать реализацию поставленных целей, учитывать геометрический опыт детей, полученный в дошкольный период, быть интересным и доступным для понимания, укладываться в форму практических заданий, способствовать развитию воображения и мышления детей.

Изучение геометрического материала происходит в процессе специально организуемой конструкторско-практической деятельности учащихся и включает в себя работу с линейными, плоскостными и пространственными объектами, степень трудности при изготовлении которых растёт

постепенно, по мере продвижения по изучаемому материалу.

Система заданий и задач геометрического содержания выстраивается в органичном единстве с арифметическим материалом, дополняя и обогащая его и представления детей о математической       науке, которая изучает как количественные, так и пространственные отношения между объектами действительного мира.

Основой освоения геометрического содержания курса является систематическая конструкторско-практическая деятельность учащихся, включающая в себя воспроизведение изучаемых объектов в форме моделей и их свойств, доконструирование объектов, трансформацию одного объекта в другой, конструирование объектов по эскизу, чертежу, описанию. Большое внимание в курсе уделяется поэтапному формированию навыков самостоятельного выполнения заданий, когда ученики знакомятся со свойствами фигур в результате выполнения задания, формулируют их, проверяют правильность своих формулировок, решают, пусть и небольшие, проблемы, возникающие перед ними.

В методике проведения уроков по курсу или использованию материала курса          на интегрированных уроках учитываются возрастные особенности детей младшего школьного возраста, в связи с чем большое место в процессе изучения курса должны занять такие методы,    как наглядные и практические, метод дидактической игры и эвристической беседы, выполнение творческих заданий и др.

Так, при первичном введении основных геометрических понятий (точка, линия, плоскость) используются способы создания наглядного образа изучаемой фигуры, а также выполнение несложных практических работ, в ходе которых дети устанавливают новые свойства изучаемого объекта. Система специально разработанных практических заданий предполагает: изготовление модели изучаемой геометрической фигуры, выявление ее основных свойств, распознавание изучаемой фигуры среди предметов, окружающих детей, связь с ранее изученными фигурами— общее и отличное, использование изучаемой геометрической фигуры для конструирования новых, более сложных объектов. Для выполнения заданий такого характера используются счётные

палочки, прямоугольные и произвольные листы бумаги и картона, модели геометрических фигур,          мягкая проволока, пластилин и др. Дети знакомятся и учатся работать с основными геометрическими и чертёжными инструментами: линейкой, угольником, циркулем и пр. Так, после введения в 1 классе одной из важнейших геометрических фигур—отрезка—предлагается целая серия специальных заданий на проведение сравнения длин отрезков, на взаимное расположение отрезков, на использование отрезков для построения каркасов многоугольников на плоскости и многогранников в пространстве. Многие задания требуют доконструирования или переконструирования заданных фигур в другие как с сохранением числа использованных отрезков,

так и с изменением (увеличением или уменьшением) их числа. В ряде случаев дети производят графическую фиксацию полученного результата в форме рисунка, эскиза, чертежа.

Аналогично выстраиваются в методическом плане и линии с конструированием и последующим использованием плоскостных фигур и пространственных тел. На этом этапе работа дополняется заданиями на разбиение геометрических фигур на части, обладающие заданными свойствами, на составление названной фигуры из частей или других фигур.

Изученные геометрические фигуры используются для различных аппликаций (сюжетные картинки, транспортные средства и др.), а также для конструирования различных объектов (модель платяного шкафа, карандашница, коробочка для семян, грузовик, гараж и др.).

В результате такой работы, с одной стороны, существенно расширяются геометрические представления, знания и умения детей, а с другой — формируются умения использовать полученные знания для моделирования и конструирования новых объектов, совершенствуются умения и навыки изображать геометрические фигуры и композиции из них на бумаге в форме рисунка, чертежа, умения читать и преобразовывать чертёж по заданным условиям.

Программа интегрированного курса «Математика и конструирование» составлена для начальной школы в соответствии со следующим учебным планом: 5 ч, 5 ч, 5 ч и 5 ч.

Недельное число часов по курсу «Математика и конструирование» в каждом классе начального обучения складывается следующим образом: к числу часов, отводимых в начальной школе на математику (4, 4, 4, 4), добавляется 1 ч — половина учебного времени, отводимого на трудовое обучение (вторая половина учебного времени по этому предмету используется, как известно, для реализации другого интегрированного курса — «ИЗО и художественный труд»).

Материал интегрированного курса «Математика и конструирование» может изучаться как на отдельном уроке, проводимом один раз в неделю, так и на каждом уроке математики, при этом на него отводится примерно 10 — 15 мин урока, на котором занятия идут с использованием учебника математики для начальных классов и альбомов по курсу «Математика и конструирование».

Содержание курса 1 класса включает в себя знакомство с геометрическими фигурами:

точкой, линией (прямая, кривая), отрезком, лучом, ломаной, углом, многоугольником, в том числе прямоугольником (квадратом); обозначение геометрических фигур буквами, построение прямоугольника (квадрата) на клетчатой бумаге.

В пособии есть также 7 приложений, материал которых используется для проведения практических работ.

Кроме того, данная тетрадь содержит дополнительный материал (ещё 4 приложения): — задания на составление сложных геометрических узоров и изображений; — упражнения по складыванию фигурок из бумаги («Оригами»).

Материал пособия разбит на уроки, что удобно, если учитель проводит отдельный урок геометрического содержания (один раз в неделю). Если материал тетради включается в каждый урок математики и конструирования, то учитель выбирает по 2-3 задания, отводя на их выполнение по 10 — 15 мин. При этом задания выполняются последовательно, без пропусков.

Естественно, что учитель может дополнить предложенные упражнения своими заданиями.

Требования к знаниям, умениям и навыкам учащихся к концу первого года обучения сформулированы в программе курса «Математика и конструирование».

Авторы

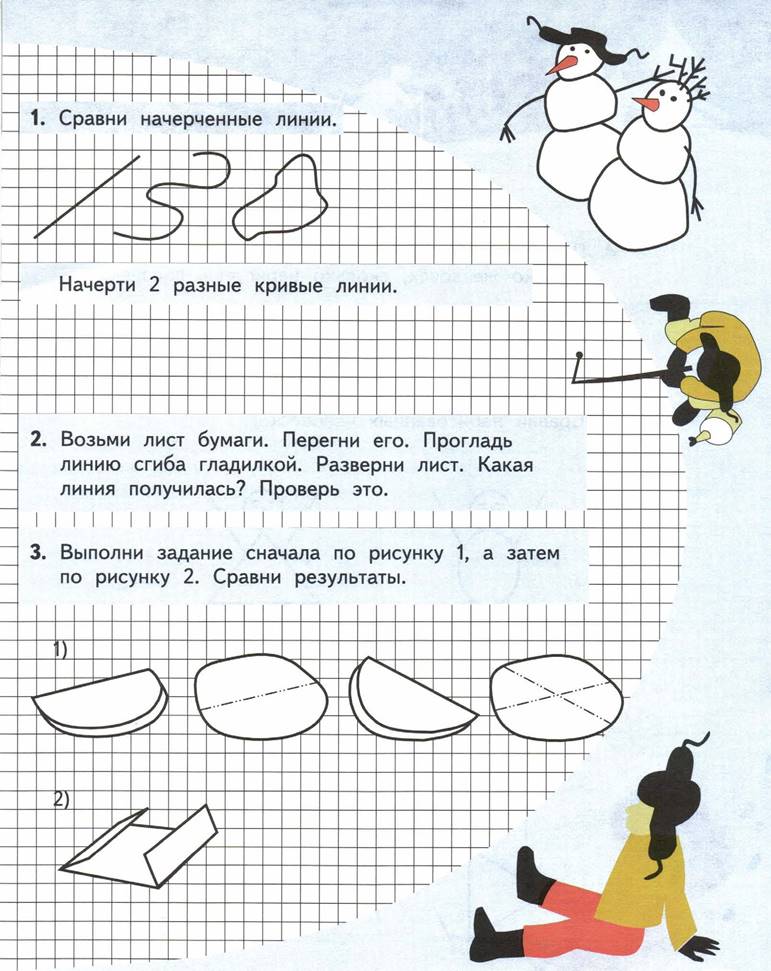
З. Точка    след, который оставляет на бумаге, например, остро отточенный карандаш.

Поставь несколько точек.

Держи карандаш правильно.

4.      Соедини точки с помощью карандаша.

Ты получил линии. Нарисуй свою линию.

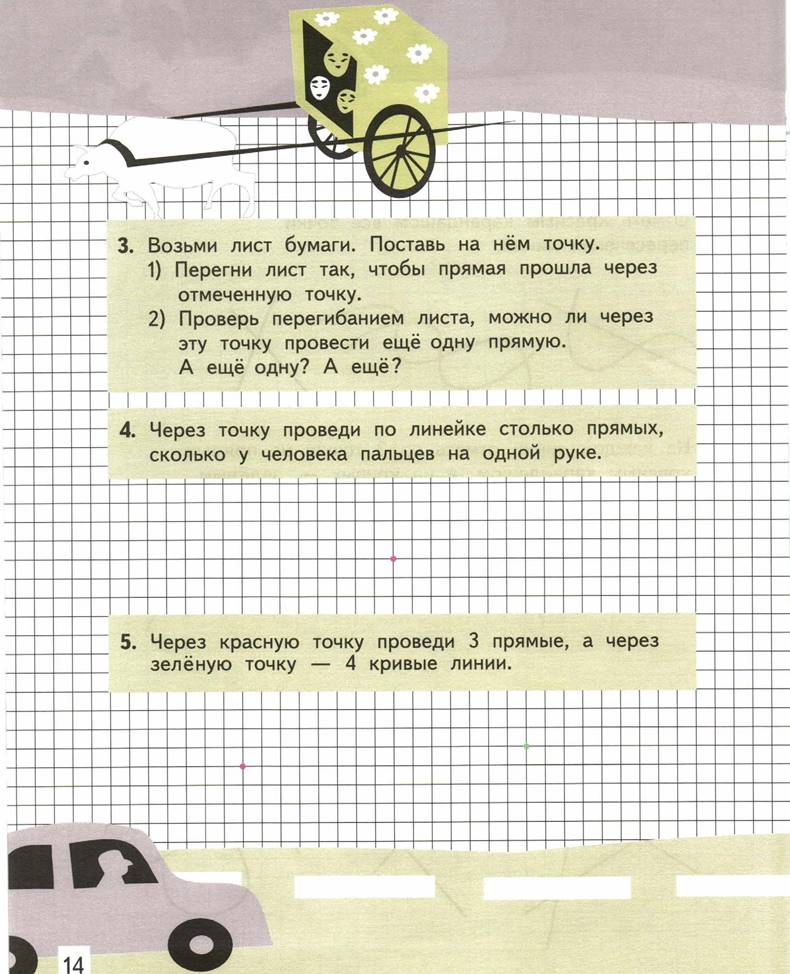
5.      Поставь точку красным карандашом; слева от неё поставь точку зелёным карандашом, а справа синим. Сколько точек получилось?

Через точку проведена линия.

Любую линию можно провести, не отрывая карандаша от бумаги. Через каждую точку проведи по одной линии.

Прямая. Кривая линия

1.      Номера прямоугольников, на которых начерченные линии пересекаются, обведи красным карандашом, а те, на которых не пересекаются, синим.

2.      Отметь точки пересечения линий на клетчатой разлиновке по правилу, заданному в каждом ряду.

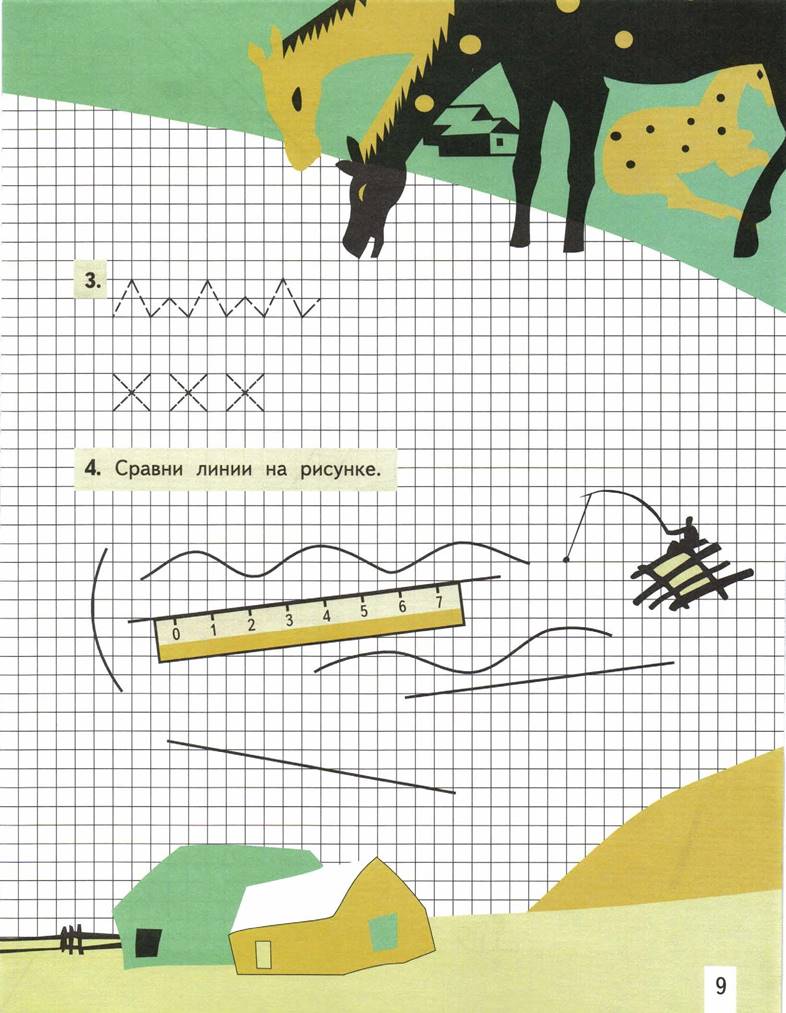
4.       Продолжи узор до конца строки, нарисовав столько же точек, сколько нарисуешь палочек.

5.      
Сравни нарисованных человечков.

                                       Коля 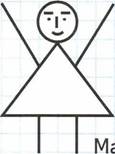            Маша

Из данных геометрических фигур составь и нарисуй такого человечка, который будет отличаться от Коли и Маши.

6.       Отметь красным карандашом все точки пересечения линий.

1.     

2.      На каждом рисунке отметь красным карандашом все точки пересечения линий.

2. Проведи прямую с помощью линейки и каранДаија через 2 точки на каждом рисунке. '?Biiiiii

З. Рассмотри рисунки. Линия, которая начерчена на рисунке 1, проходит горизонтально, а линия на рисунке 2 вертикально.

Через каждые 2 точки проведи прямую.

RiinE•

1.       Через 2 точки проведи прямую.

Отметь: 1) ещё 2 точки на прямой; 2) З точки над прямой; З) 4 точки под прямой.

2.       Проведи через З точки, где сможешь, прямую.

випт

Всегда ли через З точки можно провести прямую?

ДА НЕТ

З. Найди на рисунке: вертикальные прямые и отметь их кружком (О); горизонтальные прямые и отметь их галочкой (V).

4. Продолжи узор.

Отрезок

1.      «Без конца и края линия прямая.

«Хоть сто лет по ней идти, не найти конца пути!»

Ограничь путь Карандаша, отметь на прямой 2 точки. Ты получил отрезок прямой. Коротко его называют отрезок.

2.      Соедини отрезком точки каждой пары.

Обведи овалом (О) вертикальный отрезок.

З. Назови фигуры, изображённые на рисунке. Сравни их.

Обозначение геометрических фигур буквами

1.     В геометрии принято точку обозначать одной большой буквой латинского алфавиты. На рисунке изображены и обозначены точки А, В, С, D, Е.

С помощью линейки соедини отрезком точки А и В. Получился отрезок АВ. Начерти отрезки Е), ЕС, DC.

2.     Обозначь буквами точки и отрезки.

З. На каждом рисунке проведи недостающие отрезки так, чтобы получились рисунки известных тебе предметов.

4.      Соедини отрезком каждую пару точек.

Латинский алфавит приведён в Приложении 12.

5.      Кенгурёнок и медвежонок взялись за разные концы скакалки. Нарисуй разными цветными карандашами, как это может быть. Покажи 2 варианта.

6.      Продолжи узор.

Работа по разрезанию листа бумаги.

Помни! Работая с ножницами, надо быть очень осторожным. При разрезании лист должен лежать на парте.

7.      Разрежь заготовку (Приложение 1) по прямой, начерченной пунктиром. Возьми 2 полученные полоски. Одну полоску перегни так, чтобы получились 2 полоски одинаковой длины. Вторую полоску перегни так, чтобы получились 2 полоски разной длины: одна длиннее другой.

О

опп

4.       Обозначь точки буквами. Через одну пару

« точек проведи отрезок, а через другую прямую. Сравни полученные фигуры. 1 т

5.       Начерти отрезок. Отметь на нём точку, которая не совпадает ни с одним из концов отрезка. Сколько отрезков на чертеже? Запиши. Е]

6.       Сравни пары отрезков.

7.       Продолжи узор.

Практические работы

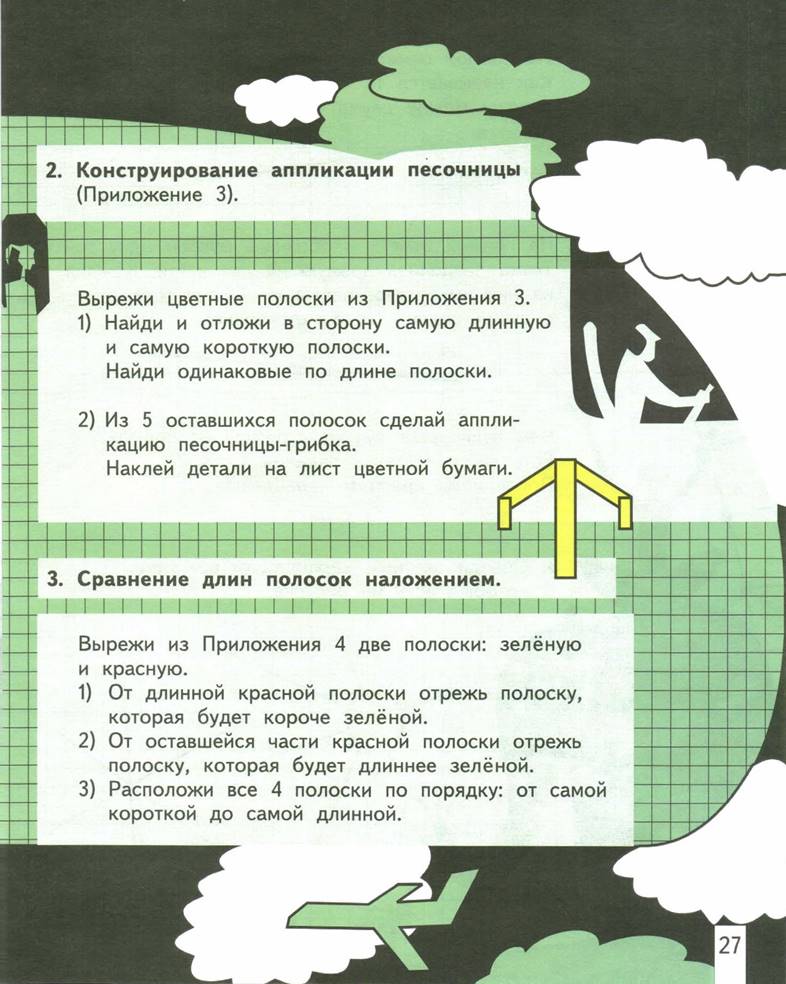
1. Конструирование модели самолёта из полосок бумаги (Приложение 2).

Рассмотри рисунок и выполни следующие задания:

—Назови основные детали, составляющие самолёт.

—Посчитай, сколько их.

—Сравни детали самолёта по длине и выдели равные. —Сколько полосок надо иметь, чтобы сконструировать такую модель самолёта?

—Сколько полосок у тебя? (Приложение 2.) Как надо поступить, чтобы количество полосок и количество деталей самолёта стало одинаковым? —Найди полоску, из которой будешь делать крылья. -—Выполни действия по чертежу.

Наклей детали на лист цветной бумаги так, чтобы получить аппликацию «Самолёт».

-——••iiiiil

1.     На прямой отметь и обозначь буквами две точки. Как называется та часть прямой, которая расположена между двумя её точками?

2.     На прямой отметь и обозначь буквой одну точку. Точка разделила прямую на две части. Каждая из них имеет своё название — луч (сравни с лучом солнца, лучом фонарика).

Чем отличается луч от отрезка? от прямой?

Есть ли на чертеже задания 1 лучи? Проведи их красным карандашом.

З. Обведи цветным карандашом все лучи, которые есть на рисунке.

о

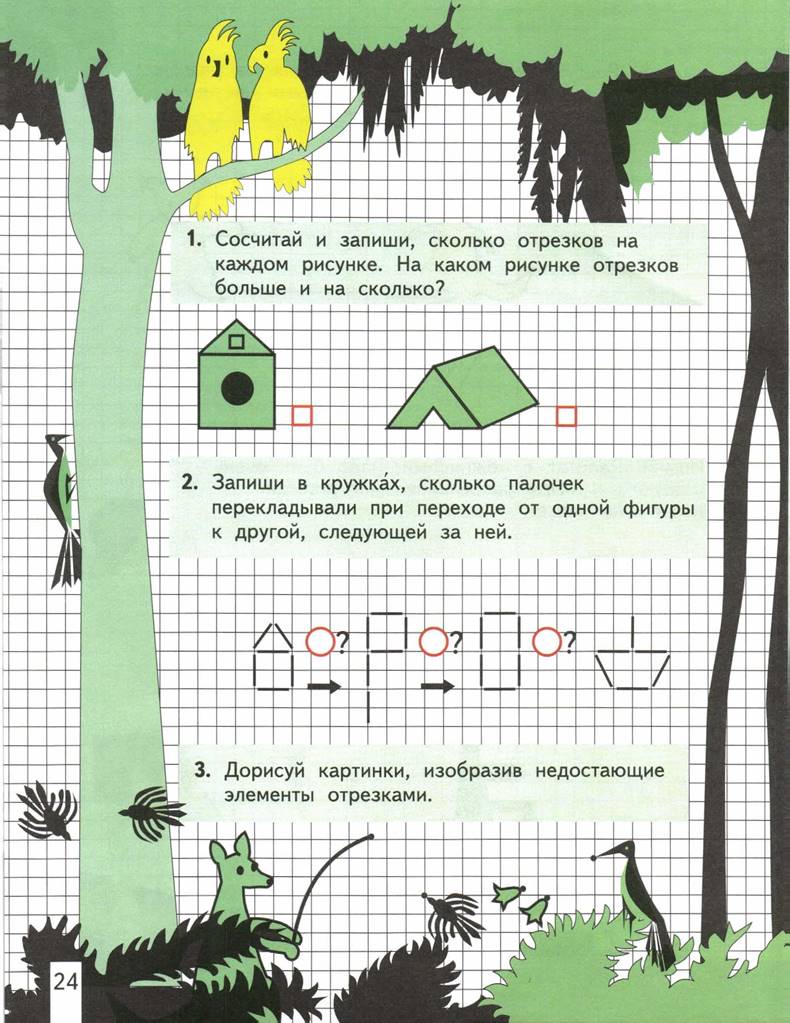
4.       Сколько отрезков на рисунке?

5.       Сколько отрезков на каждом рисунке?

6.       Соедини отрезком точки с номерами: 1 и 2; 1 и З; 1 и 4; З и 4. Получившийся вертикальный отрезок отметь синим кружком, а горизонтальный зелёным.

7.       Сколько счётных палочек надо переложить, чтобы совок «смотрел» в другую сторону?

8.       Сравни на глаз, какой отрезок длиннее, и отметь его.

пплплт•пптпп»_

1. Прочерти отрезки красным карандашом, лучи синим, а прямые зелёным.

5.      Сравни отрезки на глаз, а затем проверь себя с помощью циркуля. Проведи стрелки так, чтобы каждый следующий отрезок был короче предыдущего.

6.      Сравни отрезки, используя циркуль.

Обведи красным карандашом равные отрезки.

аа а а • •

7.       Коля выше Васи, но ниже Пети. Кто выше: Вася или Петя? Подчеркни имя. Покажи это с помощью отрезков. мааг

8.       Нарисуй то, что недорисовал художник.

,зз

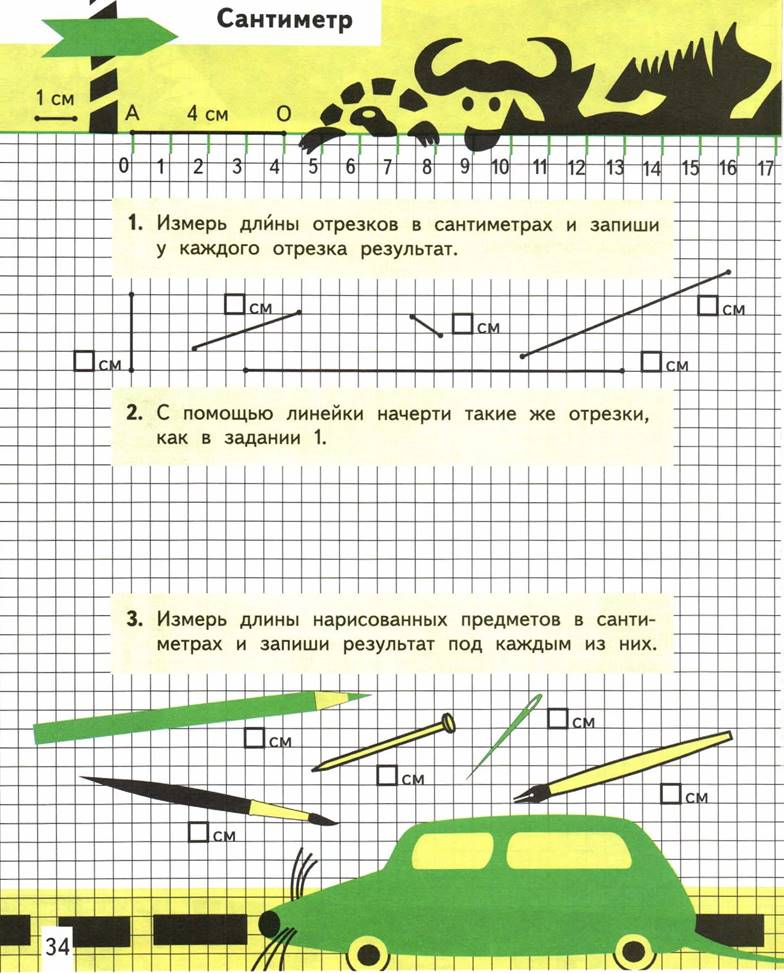
1     2                     3 4 5 6 7 8 9 10 11

7. Измерь отрезки и запиши, отрезок короче второго.

                Первый отрезок короче второго на         см.

8. Начерти 2 отрезка так, чтобы один из них был длиннее другого на З см.

1.      Начерти отрезок длиной 8 см. Обозначь его. Отметь на отрезке точку М так, чтобы она разделила его на 2 отрезка: один длиной 5 см, другой длиной З см.

2.     

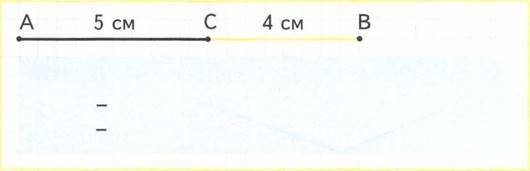
З. Обозначь отрезки буквами. Сделай записи к данному чертежу, как в задании 2.

37

6.      Начерти на одной прямой один за другим отрезки длиной 2 см, З см,

Обозначь все полученные отрезки. Найди длину каждого отрезка. Запиши это, например, так: АВ = 2 см.

7.      Таня, Лена, Оля и Катя начертили по одному отрезку. Отрезки у Тани и Лены одинаковой длины. Отрезок у Лены длиннее, чем у Оли, а

Угол

Сказка о том, как образовался угол

Как-то проказница-Точка подкралась к спящей прямой, взобралась на неё и начала подпрыгивать. Сначала она прыгала осторожно, чтобы не разбудить прямую. И некоторое время ей это удавалось. Но затем малышка-Точка забыла об осторожности да так подпрыгнула, что прямая не выдержала её сильного прыжка и сломалась. Вместо прямой стало две её части. Эти две части не разлетелись в разные стороны только потому, что Точка успела схватить их. Сначала она соединила их, как на рисунке 1, а затем, как на рисунке 2. Так появилась на свет новая геометрическая фигура, которую называют угол. Фигуру, изображ нную на рисунке 1, называют развёрнутым углом.

Место, где точка сводит и держит части развалившейся прямой, называют вершиной угла, а части прямой сторонами угла.

1.      Начерти угол. Отметь его вершину синим карандашом, а стороны красным.

Угол можно обозначить одной буквой (по его вершине) или тремя буквами (при этом в середине всегда записывают букву, обозначающую вершину угла). Например, угол на рисунке 1 можно назвать А, или ВАС, или САВ.

2.      1) Как можно назвать второй угол на рисунке 1?

2) Обозначь каждый угол на рисунке 2 и выпиши его названия.

О

З. Продолжи узор.

4.       Сделай несколько рисунков к стихотворению:

От вершины по лучу,

Словно с горки, покачу.

Только луч теперь «она»: Он зовется «сторона».

5.       Возьми лист бумаги и перегни его два раза так, чтобы получились углы. Сколько углов получилось?

6.       Отсчитай 11 счётных палочек и выложи домик, как на рисунке. Домик «смотрит» влево. Переложи одну палочку так, чтобы домик «повернулся» в другую сторону.

7.       Выпиши названия всех углов на чертеже.

8.       Продолжи узор.

Прямой угол. Виды углов: прямой, тупой, острый

„а-

1. Возьми лист бумаги непрямоугольной формы и выполни по чертежу шаг за шагом следующие операции.

Получились 4 равных угла. Эти углы называют прямыми. Для построения прямых углов можно использовать чертёжный треугольник.

Эти углы прямые.             Эти углы не прямые.

1.      Рассмотри рисунок. Сравни изображённые на н ё М УГЛЫ.

Угол, который меньше прямого (рис. 2), называется острым, а угол, который больше прямого угла, но меньше развёрнутого,— тупым (рис. 3).

а•аь

2.      Рассмотри рисунок. Выпиши номера прямых, острых и тупых углов.

Прямые углы:

Острые углы: Тупые углы:

lza

zn

З. Соедини отрезками точки в порядке возрастания их номеров: 1-ю со 2-й, 2-ю с 3-й и т. д.

Сколько углов в полученной фигуре? Найди в ней и отметь прямые, острые и тупые углы разными цветными карандашами: прямые красным, острые синим, тупые    зелёным карандашом.

•iiiiiiiiiiiiiiii•••••••••••••••••••••••••

6.      Подпиши, кто какой угол начертил, если угол Саши меньше угла, начерченного Севой, но больше угла, начерченного Димой.

7.      Продолжи узор.

а Ломаная.

Длина ломаной

1.      Сделай из деталей конструктора фигуру, как на рисунке 1. Это модель ломаной.

Рассмотри, как ломаная изображается на чертеже (рис. 2). Эта ломаная состоит из трёх звеньев.

2.      Найди на рисунке ломаные и обведи их номера кружк5ми.

З. Соедини точки в порядке увеличения их номеров. Сравни полученные фигуры.

7. Отсчитай З счётные палочки. Выложи первую фигуру, а затем, перекладывая палочки, выкладывай следующие за ней фигуры. Назови каждую из полученных фигур.

1.       Обозначь буквами каждую ломаную. Измерь и выпиши длины звеньев каждой ломаной. Длина какой ломаной больше?

2.       Соедини точки отрезками так, чтобы получилась ломаная: а) из двух звеньев; б) из трёх звеньев.

З. Начерти ломаные: 1) из двух звеньев длиной 5 см и З см; 2) из трёх звеньев длиной 1 см, З см, 6 см. Найди длину каждой ломаной. Сравни их.

4.       Найди длину ломаной АВС.

Начерти: 1) отрезок такой же длины, как длина ломаной АВС; 2) двузвенную ломаную такой же длины, как заданная, но со звеньями другой длины.

5.       Начерти отрезок АВ длиной 8 см. Раздели его на три отрезка длиной 2 см, 1 см и 5 см. Будет ли полученная фигура ломаной? Закрась ответ: почему?

Начерти ломаную с такими звеньями.

6.       Найди длину каждой ломаной.

7.       Раскрась тот домик, от которого длина пути до школы короче.

школа

1. Какие фигуры изображены на чертеже? В каждой фигуре соедини отрезком точки А и В. Каждая фигура — замкнутая ломаная, или многоугольник.

1.      Сделай из деталей конструктора четырёхзвенную ломаную. Преобразуй («замкни») её так, как показано на рисунке. Ты получил четырёхугольник.

2.      Закрась красным карандашом окошки с номерами прямых углов.

З. Рассмотри чертёж и раскрась на нём все многоугольники. Назови каждый из них.

4.       Рассмотри рисунок и назови все многоугольники, какие найдёшь на нём.

5.       Выложи на парте из палочек фигуру, как на чертеже. Это особый треугольник: у него все стороны одинаковой длины.

Увеличь количество палочек на 2 и выложи из них треугольник. Можно ли выложить треугольник из четырёх СЧёТНЫХ палочек?

6.       Сравни начерченные фигуры. Что у них общего? Как назвать эти фигуры одним словом?

7.       1) Отсчитай 5 счётных палочек и выложи фигуру, как на рисунке 1. Переложи 2 палочки так, чтобы получить 2 одинаковых треугольника.

2) Отсчитай 10 счётных палочек и выложи фигуру, как на рисунке 2. Переложи 4 палочки так, чтобы получить 4 одинаковых треугольника.

4.       Сосчитай, сколько нужно палочек, чтобы выложить фигуру, как на рисунке. Возьми нужное количество палочек и выложи такую же фигуру. Сколько получилось прямоугольников?

Убери 2 палочки так, чтобы остался один прямоугольник.

5.       Сосчитай, сколько треугольников на рисунке. Запиши их количество около каждого большого треугольника.

дол, да

—•иииммн•••

6.       Раскрась квадраты так, как показано на рисунке. оЕЬ

пап апа ооа

1. Маленькие отрезки и предметы измеряют в сантиметрах. Для измерения более крупных предметов и более длинных отрезков применяется ещё одна мера длины дециметр.

В 1 дециметре 10 сантиметров.

Начерти 2 отрезка: один длиной 1 см, другой длиной 1 дм.

68

2. Начерти: отрезок, который будет длиннее 1 дм на З см; отрезок, длина которого на 6 см меньше, чем 1 дм.

З. Начерти прямоугольник со сторонами 5 см и 2 см.

Проведи в нём один отрезок так, чтобы получить квадрат. Какой длины будет сторона квадрата?

Практическая работа «Изготовление геометрического набора треугольников». Аппликации

Рассмотри Приложение 5. Назови все фигуры, которые видишь. Вырежи их. Выложи из них представленные на рисунках фигуры: домик и чайник, используя все 8 треугольников. zrw Сохрани вырезанные треугольники.

Упражнения для закрепления

1.      1) Измерь стороны начерченного прямоугольника. Проведи в нём один отрезок так, чтобы он разделил его на квадрат и прямоугольник. Запиши длины сторон полученного квадрата и прямоугольника.

1

     Длина стороны квадрата        см.

       Длины сторон прямоугольника           см и        см.

2) Проведи:

в квадрате один отрезок так, чтобы он разделил его на 2 равных треугольника; в маленьком прямоугольнике один отрезок так, чтобы он разделил его на 2 равных квадрата.

73

2.      Начерти несколько таких двузвенных ломаных, чтобы длина каждой из них была равна 6 см. Рассуждай так: «6 это 1 и 5. Начертим ломаную, у которой длина одного звена 1 см, а другого — 5 см. Далее, 6 это...»

О

vzzauv;v

З. Отсчитай 16 счётных палочек и выложи фигуру, как на рисунке. Переложи З палочки так, чтобы стало 4 квадрата.

4.       Из треугольников геометрического набора (Приложение 5) выложи такую ракету.

5.       Начерти справа такую же фигуру, какая начерчена слева.

6.       Петя и Саша одинакового роста. Толя ВЫИје Пети, а Саша выше Игоря. Кто выше: Толя или Игорь? Покажи это на отрезках.

7.       Продолжи узор.

8.       Среди данных отрезков отметь тот, которым можно дополнить рисунок.

9.       Измерь и запиши длины сторон:

1) прямоугольника ABCD; 2) к адрата EkMN.

17.     Закрась все прямоугольники жёлтым карандашом. Обведи номера тех прямоугольников, которые являются квадратами.

18.     Сколько квадратов на рисунке? Сосчитай и запиши.

19.     Начерти квадрат со стороной З см. Проведи в нём отрезок так, чтобы он разделил квадрат на 2 равных треугольника.

Приложение 11.

Оригами

Оригами искусство складывания изделий из бумаги. Родина оригами Япония. «Ори» означает «сложенный», а «гами» «бумага».

Заготовкой для оригами служит квадрат.

Гриб

Заготовка: 2 квадрата один коричневого или красного цвета размером 8 х 8 см, а другой белого или жёлтого цвета размером 6 х 6 см.

1.        Изготовление шляпки гриба.

2.        Изготовление ножки гриба.

линия сгиба

З. У полученного треугольника склей внутренние стороны.

4.       У полученного прямоугольника склей внутренние стороны.

5.       У основания треугольника сделай надрез (рис. З).

6.       Вставь ножку гриба в его шляпку (рис. 4).

Приложение 11 составлено по книге Т. И. Тарабариной «Оригами и развитие ребёнка» (Ярославль: Академия развития, 1997).

Бабочка

Заготовка: квадрат цветной бумаги со стороной 10—12 см.

Усики для бабочки вырезаются отдельно.

Бабочку каждый может раскрасить по-своему.

Рыбка

Заготовка: квадрат светлых тонов со стороной 10—12 см.

З. Нарисуй на полученной заготовке хвост и плавники.

4.       Вырежи хвост и плавники по нарисованным линиям.

5.       Нарисуй глаз и укрась рыбку.

Заготовка: квадрат серого, или белого, или пёстрого цвета со стороной 10—15 см.

          np 0            1一7

Приложение 1

Приложение 2

Приложение З

Приложение 4 Приложение 5

Приложение 6

Приложение 7