
5 МНОГОМЕРНАЯ ЛОКАЛЬНАЯ БЕЗУСЛОВНАЯ ОПТИМИЗАЦИЯ
5.1 Детерминированные прямые методы
5.1.1 Метод Гаусса – Зейделя
Метод Гаусса – Зейделя относится, с одной стороны, к классу прямых методов оптимизации, а с другой стороны – к классу детерминированных методов оптимизации. Метод предназначен для решения многомерной задачи безусловной оптимизации (точнее говоря, многомерной задачи локальной безусловной оптимизации): найти минимум критерия оптимальности f(x), определенного в n-мерном арифметическом пространстве. На каждой итерации метода Гаусса – Зейделя последовательно решается n одномерных задач безусловной оптимизации, имеющих целью отыскание локальных минимумов соответствующих одномерных функций вдоль координатных направлений.
При решении сложных задач автоматизированного проектирования чаще всего приходится иметь дело с математическими моделями, в которых нет аналитических зависимостей для первых производных минимизируемой функции f(x). Поэтому поиск локального минимума в этом случае приходится вести по результатам вычислений только значений функции f(x) – с помощью прямых методов оптимизации.
Рассматривается следующая многомерная задача безусловной оптимизации
(точнее говоря, задача многомерной локальной безусловной оптимизации): найти
минимум критерия оптимальности f(x), определенного в n-мерном
евклидовом пространстве ![]() ,
,
![]() (5.1)
(5.1)
При решении задачи (5.1) методом Гаусса – Зейделя (методом покоординатного спуска, методом циклического покоординатного спуска) используются следующие итерационные формулы:
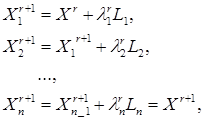 (5.2)
(5.2)
где вектор Li определяет направление вдоль i-й координатной оси и представляет собой n-мерный вектор с компонентами
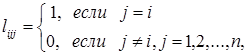
а величины ![]() – определяются из условий
– определяются из условий
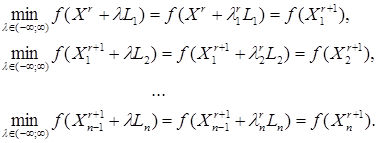 (5.3)
(5.3)
Другими словами, величина ![]() представляет
собой длину шага, минимизирующего функцию f(x) в направлении Li
на итерации номер r, исходя из точки, полученной
на предыдущем шаге.
представляет
собой длину шага, минимизирующего функцию f(x) в направлении Li
на итерации номер r, исходя из точки, полученной
на предыдущем шаге.
Если положить ![]() , то формулы (5.2), (5.3)
можно записать в виде
, то формулы (5.2), (5.3)
можно записать в виде
![]() (5.4)
(5.4)
![]() (5.5)
(5.5)
Таким образом, каждая итерация по методу Гаусса – Зейделя включает в себя n шагов. Каждая последующая итерация начинается из точки, полученной на последнем шаге предыдущей итерации. Поиск заканчивается при выполнении одного из стандартных условий окончания итераций:
![]() (5.6)
(5.6)
![]() (5.
(5.![]() )
)
Заметим, что задачи (5.5) даже в случае одноэкстремальной функции f(x) могут быть задачами многоэкстремальной оптимизации и могут быть решены рассмотренными в главе 3 методами решения задач одномерной оптимизации.
Алгоритм метода Гаусса – Зейделя
Шаг 1. Задаем начальную точку X0 и полагаем r = 0 , i = 1.
Шаг 2. Последовательно для i = 1,2,...,n решаем задачи (5.5), т.е. исходя из предыдущей точки отыскиваем минимум функции f(x) вдоль i-го координатного направления.
Шаг 3. Если условие окончания поиска (5.6) или (5.6') выполнено, то
полагаем ![]() и заканчиваем вычисления. Иначе
полагаем r = r + 1 и переходим к шагу 2.
и заканчиваем вычисления. Иначе
полагаем r = r + 1 и переходим к шагу 2.
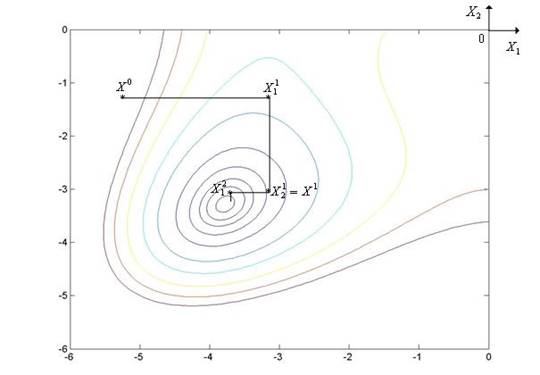 |
Рис. 5.1. Траектория поиска минимума неовражной функции Химмельблау методом Гаусса – Зейделя
Метод Гаусса – Зейделя иллюстрирует рис. 5.1, на котором показан фрагмент
линий уровня функции Химмельблау (является одной из широко известных двумерных
тестовых функций и определяется следующим образом:![]() ).
На рис. 5.1 точка
).
На рис. 5.1 точка ![]() представляет собой локальный
минимум функции f(x)
вдоль оси X1 при исходной точке X0.
Точка
представляет собой локальный
минимум функции f(x)
вдоль оси X1 при исходной точке X0.
Точка ![]() представляет собой локальный
минимум функции f(x)
вдоль оси X2 при исходной точке
представляет собой локальный
минимум функции f(x)
вдоль оси X2 при исходной точке ![]() .
Отыскание точки
.
Отыскание точки ![]() завершает первую итерацию.
Следующая итерация начинается из точки X1=
завершает первую итерацию.
Следующая итерация начинается из точки X1=![]() и т.д.
и т.д.
Метод Гаусса – Зейделя медленно сходится на овражных функциях (многомерный критерий оптимальности f(x) называется «овражным» в своей области допустимых значений вектора варьируемых переменных D, если в этой области имеют место слабые изменения частных производных функции f(x) по одним направлениям и значительные изменения этих производных по другим направлениям), в которых овраг не ориентирован в направлении какой-либо из координатных осей (рис. 5.2). На рисунке показаны линии уровня функции Розенброка (n = 2).
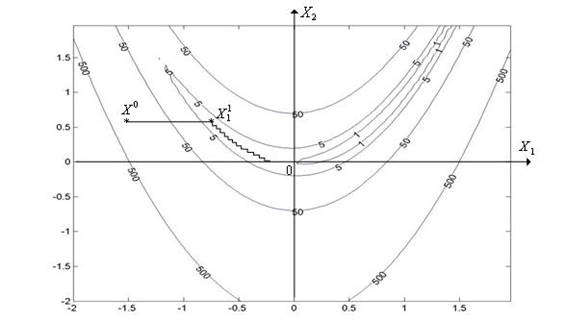 |
Рис. 5.2. Траектория поиска минимума овражной функции Розенброка методом Гаусса – Зейделя. Текущая точка быстро (в данном случае – за один шаг) «скатывается» на дно оврага и очень медленно движется по дну оврага к минимуму функции f(x)
5.1.2 Метод Хука – Дживса
Метод Хука – Дживса относится, с одной стороны, к классу прямых методов оптимизации, а с другой стороны – к классу детерминированных методов оптимизации. Метод предназначен для решения многомерных задач локальной безусловной оптимизации. Метод требует задания величин пробных шагов Δi по каждому из координатных направлений 0x1, x2,..., 0xn. Каждая итерация метода состоит из двух этапов. Рассмотрим для примера первую итерацию (последующие итерации выполняются по такой же схеме). На первом этапе из текущей точки X0 делаются пробные шаги величиной (+Δi), (–Δi) по всем указанным координатным направлениям и в полученных точках вычисляются значения критерия оптимальности f(x). Принимаются те шаги, которые привели к уменьшению значения функции f(x) по сравнению с ее значением в точке X0. В результате получается точка X1. На втором этапе делается шаг длиной α1 и в направлении (X1 – X0). Величины αi, где i = 1, 2,..., называются ускоряющими множителями и могут определяться различными способами, например, из условия локального минимума функции f(x) вдоль соответствующего направления.
Рассмотрим следующую многомерную задачу локальной безусловной оптимизации (если задача оптимизации является задачей безусловной оптимизации и отыскивается любой локальный минимум критерия оптимальности f(x), то эта задача оптимизации называется задачей локальной безусловной оптимизации): найти минимум критерия оптимальности f(x), определенного в n-мерном евклидовом пространстве Rn,
![]() (5.7)
(5.7)
При решении задачи (5.7) методом Хука – Дживса (методом конфигураций, методом пробных шагов) используются итерационные формулы, аналогичные формулам, используемым в методе Гаусса – Зейделя
![]() (5.7′)
(5.7′)
где принято ![]() , вектор Li
определяет направление вдоль i-й координатной
оси и представляет собой n-мерный вектор с
компонентами
, вектор Li
определяет направление вдоль i-й координатной
оси и представляет собой n-мерный вектор с
компонентами
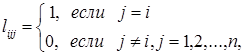
величины ![]() – определяются из условий
если
– определяются из условий
если
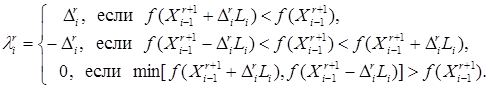 (5.8)
(5.8)
После завершения n шагов выполняется спуск
в направлении вектора (![]() ) по формуле
) по формуле
![]() (5.9)
(5.9)
где ![]() – ускоряющий множитель. В
различных модификациях метода Хука –Дживса множитель
– ускоряющий множитель. В
различных модификациях метода Хука –Дживса множитель ![]() может:
может:
приниматься постоянным (обычно равным 2),
выбираться из условия f(Xr+1) < f(Xr),
находиться из условия локального минимума функции f(x) при движении из точки Xr
в направлении вектора (![]() ):
):
![]() (5.10)
(5.10)
Заметим, что задачи (5.10) даже в случае одноэкстремальной функции f(x) могут быть многоэкстремальными задачами оптимизации и могут быть решены рассмотренными в главе 3 методами решения задач одномерной оптимизации.
Итерации заканчиваются при выполнении одного из стандартных условий
окончания итераций (5.6) и (5.![]() ).
).
Вектор ![]() является вектором
свободных параметров метода – вектором «пробных шагов» по всем n координатным осям.
является вектором
свободных параметров метода – вектором «пробных шагов» по всем n координатным осям.
Алгоритм метода Хука – Дживса
Шаг 1. Задаем начальную точку Х0, вектор «пробных»
шагов ![]() и полагаем r
= 0.
и полагаем r
= 0.
Шаг 2. Последовательно для i =
1,2,... по формулам (5.7) и (5.8) находим точки ![]()
Шаг 3. Если ![]() , то переходим к шагу 4.
Иначе уменьшаем длины «пробных» шагов
, то переходим к шагу 4.
Иначе уменьшаем длины «пробных» шагов ![]() ,
например, вдвое и переходим к шагу 2.
,
например, вдвое и переходим к шагу 2.
Шаг 4. Если условие окончания поиска (5.6) или (5.6') выполнено, то
полагаем ![]() и заканчиваем вычисления. Иначе
выполняем спуск в направлении вектора
и заканчиваем вычисления. Иначе
выполняем спуск в направлении вектора ![]() по
формуле (5.9), в которой ускоряющий множитель находится, например, из условия
(5.10). Полагаем r = r + 1 и переходим к шагу 2.
по
формуле (5.9), в которой ускоряющий множитель находится, например, из условия
(5.10). Полагаем r = r + 1 и переходим к шагу 2.
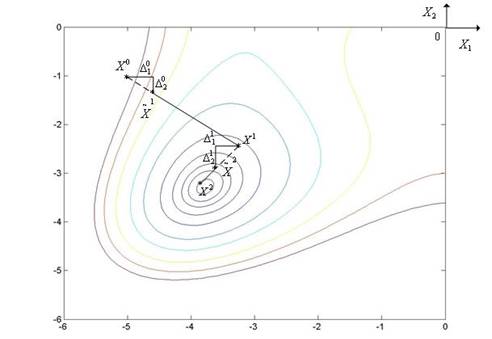 Метод Хука – Дживса иллюстрирует рис.
5.3, на котором показаны линии уровня функции Химмельблау (n = 2). Ускоряющий множитель
Метод Хука – Дживса иллюстрирует рис.
5.3, на котором показаны линии уровня функции Химмельблау (n = 2). Ускоряющий множитель ![]() находиться
из условия локального минимума функции f(x) при движении из точки Xr
в направлении вектора
находиться
из условия локального минимума функции f(x) при движении из точки Xr
в направлении вектора ![]() .
.
Рис. 5.3. Траектория поиска минимума неовражной функции Химмельблау методом Хука – Дживса
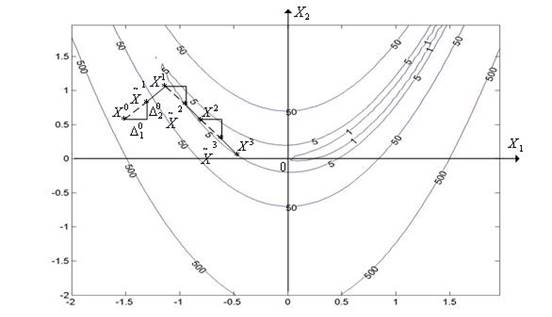 |
Рис. 5.4. Траектория поиска минимума овражной функции Розенброка методом Хука – Дживса. Ускоряющий множитель αr принят равным двум
Метод Хука – Дживса имеет высокую эффективность в случае, если функция f(x) имеет прямолинейный овраг (не обязательно ориентированный вдоль одного из координатных направлений, как в методе Гаусса – Зейделя). При минимизации овражных функций, имеющих не прямолинейный овраг, процесс поиска может сильно замедлиться и закончиться далеко от точки истинного минимума (рис. 5.4). На рисунке показаны линии уровня функции Розенброка (n = 2).
5.1.3 Метод Розенброка
Метод Розенброка относится, с одной стороны, к классу прямых методов оптимизации, а с другой стороны – к классу детерминированных методов оптимизации. Метод предназначен для решения многомерных задач локальной безусловной оптимизации. Каждая итерация метода Розенброка состоит из двух этапов. В зависимости от модификации метода первый этап может выполняться с использованием различных методов, например, с помощью метода Гаусса –Зейделя. В этом случае первый этап метода состоит в выполнении одного шага метода Гаусса – Зейделя. На втором этапе выполняется преобразование системы координат таким образом, чтобы в новой системе координат одна из осей совпадала с направлением шага на предыдущем этапе. Остальные оси новой системы координат обычно находят с помощью процедуры ортогонализации Грамма – Шмидта.
Рассмотрим следующую задачу локальной безусловной оптимизации: найти минимум критерия оптимальности f(x), определенного в n-мерном евклидовом пространстве Rn:
![]() (5.11)
(5.11)
Ортогонализация Грамма – Шмидта
При решении задачи (5.11) методом Розенброка (методом вращающихся координат) используется преобразование на каждой итерации системы координат таким образом, чтобы в новой системе координат одна из осей совпадала с направлением предыдущего шага. Остальные оси новой системы координат обычно находят с помощью процедуры ортогонализации Грамма –Шмидта.
Рассмотрим произвольный набор векторов p1, p2,…, pn пространства Rn. Поставим задачу построить на основе этих векторов ортонормированный набор векторов e1, e2,…, en того же пространства Rn. Напомним, что набор векторов e1, e2,…, en называется ортонормированным, если для любых двух векторов из этого набора выполняется условие
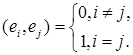 (5.12)
(5.12)
Или, другими словами, набор векторов e1, e2,…, en ортонормирован, если эти векторы линейно независимы и скалярное произведение любых двух из них равно единице.
Для построения векторов e1, e2,…, en применим индуктивный подход. Положим, что
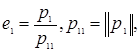 (5.13)
(5.13)
где ![]() – символ евклидовой нормы. Полагая
векторы e1, e2,…,
en уже
построенными, будем искать вектор ek в виде
– символ евклидовой нормы. Полагая
векторы e1, e2,…,
en уже
построенными, будем искать вектор ek в виде
![]() (5.14)
(5.14)
Для отыскания неизвестных множителей pik умножим (5.14) скалярно на вектор ej, j = 1,2,…, k – 1:
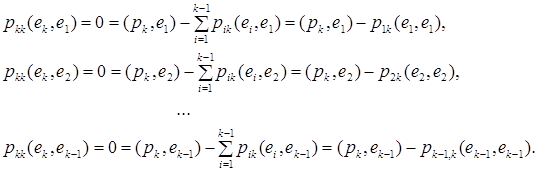
Поскольку (ej,ej) = 1, имеем
![]() (5.15)
(5.15)
Множитель pkk найдем из условия
![]() = 1:
= 1:
![]() (5.16)
(5.16)
Определение. Процесс перехода от векторов p1, p2,…, pn к векторам q1, q2,…, qn согласно формулам (5.13)–(5.16) называется ортогонализацией Грамма – Шмидта.
Алгоритм метода Розенброка
Каждая итерация метода Розенброка состоит из двух этапов. В зависимости от модификации метода первый этап может выполняться с использованием различных методов. Рассмотрим применение на первом этапе итерационной формулы метода Гаусса – Зейделя. Приведем формулировку этой формулы, несколько отличную от формулировки, рассмотренной в пункте 5.1.
Положим ![]() и пусть
и пусть ![]() – орты системы координат,
используемой на r-й итерации. Тогда итерационную
формулу метода Гаусса – Зейделя можно записать в виде
– орты системы координат,
используемой на r-й итерации. Тогда итерационную
формулу метода Гаусса – Зейделя можно записать в виде
![]() (5.17)
(5.17)
где коэффициенты
![]() находятся из условий
находятся из условий
![]() (5.18)
(5.18)
На втором этапе каждой из итераций система векторов ![]() с использованием ортогонализации
Грамма – Шмидта заменяется новой системой линейно независимых векторов
с использованием ортогонализации
Грамма – Шмидта заменяется новой системой линейно независимых векторов ![]() .
.
Шаг 1. Задаем начальную точку Х0, полагаем r = 0, i = 1, и орты исходной системы координат обозначаем ![]() .
.
Шаг 2. Исходя из точки Xr по
формулам (5.17) и (5.18) выполняем одну итерацию по методу Гаусса – Зейделя –
получаем точку Xr+1 и
совокупность векторов ![]() .
.
Шаг 3. Если одно из стандартных условий окончания итераций
![]() (5.19)
(5.19)
![]() . (5.1
. (5.1![]() )
)
выполнено, то
полагаем ![]() и заканчиваем вычисления. Иначе
переходим к шагу 4.
и заканчиваем вычисления. Иначе
переходим к шагу 4.
Шаг 4. На основе векторов ![]() находим векторы
находим векторы
![]() :
:
![]() (5.20)
(5.20)
Шаг 5. С помощью процедуры ортогонализации Грамма – Шмидта
(5.13)–(5.16) выполняем переход от системы векторов ![]() к
системе векторов
к
системе векторов ![]() , полагаем r = r +
1 и переходим к шагу 2.
, полагаем r = r +
1 и переходим к шагу 2.
Заметим, что из формулы (5.20) следует равенство ![]()
По сравнению с методом Гаусса – Зейделя и методом Хука – Дживса метод Розенброка имеет, как правило, более высокую эффективность на овражных функциях с непрямолинейным оврагом.
Метод Розенброка иллюстрирует рис. 5.5, на котором показаны линии уровня функции Химмельблау (n = 2).
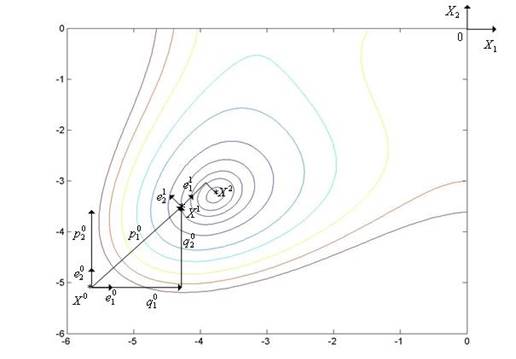
Рис. 5.5. Траектория поиска минимума функции Химмельблау методом Розенброка
5.1.4 Метод сопряженных направлений
Метод сопряженных направлений относится, с одной стороны, к классу прямых методов оптимизации, а с другой стороны – к классу детерминированных методов оптимизации. Метод предназначен для решения многомерных задач локальной безусловной оптимизации. Каждая итерация метода состоит из двух этапов. Рассмотрим содержание этих этапов для первой итерации метода. Остальные итерации выполняются по такой же схеме. На первом этапе, исходя из текущей точки х0, выполняется одна итерация по методу Гаусса – Зейделя – определяется точка х1. На втором этапе решается одномерная задача безусловной оптимизации вдоль направления (х1 – х0).
Рассмотрим следующую задачу локальной безусловной оптимизации: найти минимум критерия оптимальности f(x), определенного в n-мерном евклидовом пространстве Rn (5.11).
Введем прежде следующие понятия: векторы p1,
p2,…, pk,
принадлежащие пространству Rn,
называются векторами сопряженными относительно матрицы A (n*n) (A –
ортогональными векторами), если (Api,pj) для всех ![]()
В методе сопряженных направлений применяется итерационная формула метода Гаусса – Зейделя в виде, близком к использованному в пункте 5.3.
Положим ![]() и пусть e1, e2,…,
en – орты используемой системы
координат. Тогда итерационную формулу метода Гаусса – Зейделя можно записать в
виде
и пусть e1, e2,…,
en – орты используемой системы
координат. Тогда итерационную формулу метода Гаусса – Зейделя можно записать в
виде
![]() (5.21)
(5.21)
где коэффициенты
![]() находятся из условий
находятся из условий
![]() (5.22)
(5.22)
Алгоритм метода сопряженных направлений
Шаг 1. Задаем начальную точку х0 и полагаем r = 0, i = 1.
Шаг 2. Последовательно для i =
1,2,...,n по формулам (5.21), (5.22) находим
точки ![]() .
.
Шаг 3. Исходя из точки ![]() , еще раз
находим минимум функции f(x)
вдоль первого координатного направления – вычисляем координаты точки
, еще раз
находим минимум функции f(x)
вдоль первого координатного направления – вычисляем координаты точки
![]() ,
(5.23)
,
(5.23)
где коэффициент ![]() находится из условия
находится из условия
![]() (5.24)
(5.24)
Шаг 4. Исходя из точки ![]() , находим
минимум функции f(x)
вдоль вектора
, находим
минимум функции f(x)
вдоль вектора ![]() – вычисляем
– вычисляем
![]() (5.25)
(5.25)
где коэффициент ![]() находится из условия
находится из условия
![]() (5.26)
(5.26)
Шаг 5. Если одно из стандартных условий окончания итераций
![]() (5.27)
(5.27)
![]() (5.2
(5.2![]() )
)
 выполнено, то полагаем
выполнено, то полагаем ![]() , и заканчиваем вычисления. Иначе
полагаем r = r + 1 и переходим к шагу 2.
, и заканчиваем вычисления. Иначе
полагаем r = r + 1 и переходим к шагу 2.
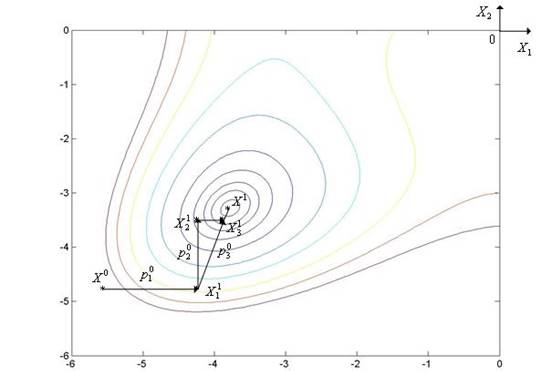
Рис. 5.6. Траектория поиска минимума функции Химмельблау методом сопряженных направлений
Метод сопряженных направлений иллюстрирует рис. 5.6, на котором показаны линии уровня функции Химмельблау (n = 2).
5.1.5 Симплекс-метод
Симплекс-метод относится, с одной стороны, к классу прямых методов оптимизации, а с другой стороны – к классу детерминированных методов оптимизации. Метод предназначен для решения многомерной задачи локальной безусловной оптимизации. Одна итерация простейшего варианта симплекс-метода состоит из следующих шагов. 1 Вычисляем значение минимизируемой функции f(x) во всех вершинах текущего симплекса, в которых эти значения не были вычислены на предыдущих итерациях. 2 Среди значений функции f(x) во всех вершинах текущего симплекса находим максимальное значение. Положим, что это значение достигается в вершине xk. 3 Выполняем отражение вершины xk текущего симплекса (т.е. выполняем операцию отражения вершины симплекса).
Рассмотрим следующую задачу локальной безусловной оптимизации: найти минимум критерия оптимальности f(x), определенного в n-мерном евклидовом пространстве Rn (5.11).
Регулярный симплекс и некоторые операции над ним
Регулярным симплексом в пространстве Rn называется правильный многогранник, образованный (n + 1)-й равноотстоящими друг от друга вершинами. Для случая n = 2 – это равносторонний треугольник, для случая n = 3 – тетраэдр.
Если в пространстве Rn
необходимо построить регулярный симплекс, одна из вершин которого находится в
точке ![]() , то координаты вершин такого
симплекса удобно задавать с помощью n*(n + 1) матрицы
, то координаты вершин такого
симплекса удобно задавать с помощью n*(n + 1) матрицы
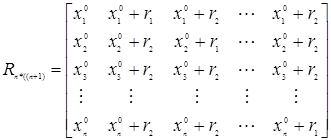 . (5.28)
. (5.28)
Здесь i-й столбец представляет собой
координаты i-й вершины симплекса, ![]()
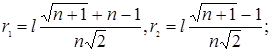 (5.29)
(5.29)
l – длина ребра симплекса.
Например, регулярный симплекс в двумерном пространстве R2 с одной из вершин в начале координат (когда
![]() ) определяется (2*3) матрицей
) определяется (2*3) матрицей
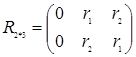
и имеет вид, представленный на рис. 5.7.
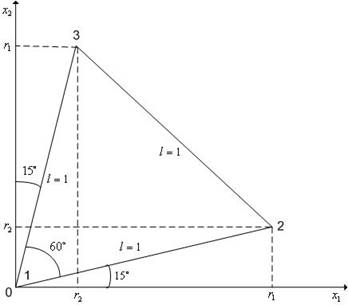 |
Рис. 5.7. Регулярный симплекс в пространстве R2 с одной из вершин в начале координат
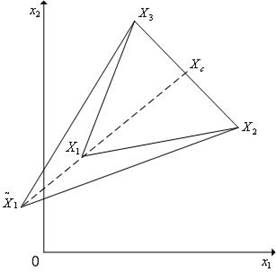
В алгоритме симплекс-метода используется следующее важное свойство регулярного симплекса: если одну из вершин регулярного симплекса перенести на надлежащее расстояние вдоль прямой, соединяющей данную вершину и центр тяжести оставшихся вершин, то вновь получится регулярный симплекс (рис. 5.8).
Будем называть эту процедуру отражением вершины симплекса относительно центра тяжести остальных вершин.
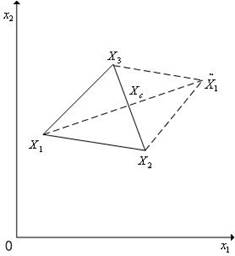 |
Рис. 5.8. Отражение вершины X1 регулярного симплекса в пространстве R2 относительно центра тяжести Xc остальных вершин
Пусть ![]() – векторы координат вершин
регулярного симплекса. Тогда при выполнении операции отражения k-й вершины симплекса имеет место следующая связь
координат этой вершины и новой вершины:
– векторы координат вершин
регулярного симплекса. Тогда при выполнении операции отражения k-й вершины симплекса имеет место следующая связь
координат этой вершины и новой вершины:
![]() (5.30)
(5.30)
Здесь
![]() (5.31)
(5.31)
вектор координат центра тяжести остальных вершин симплекса (за исключением отраженной вершины k).
Таким образом, после отражения k-й вершины
симплекса с координатами вершин ![]() получаем новый
симплекс с координатами вершин
получаем новый
симплекс с координатами вершин
![]() . (5.32)
. (5.32)
Кроме операции отражения вершины симплекса симплекс-метод может использовать операцию редукции симплекса (рис. 5.9) – уменьшение длин всех ребер симплекса на одну и ту же величину.
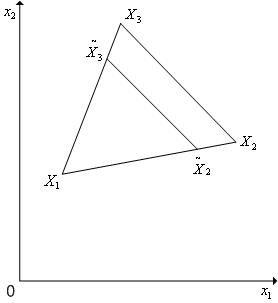 |
Рис. 5.9 Редукция вершин регулярного симплекса в пространстве R2 к вершине X1
Пусть ![]() – векторы координат вершин
регулярного симплекса. Тогда при выполнении операции редукции вершин этого
симплекса к вершине xk новые
координаты остальных вершин симплекса определяются по формуле
– векторы координат вершин
регулярного симплекса. Тогда при выполнении операции редукции вершин этого
симплекса к вершине xk новые
координаты остальных вершин симплекса определяются по формуле
![]()
где ![]() – коэффициент редукции.
Рекомендуется использовать
– коэффициент редукции.
Рекомендуется использовать ![]() .
.
Таким образом, после редукции вершин симплекса ![]() к вершине xk получаем новый симплекс с координатами вершин
к вершине xk получаем новый симплекс с координатами вершин
![]() . (5.33)
. (5.33)
Алгоритм простейшего варианта симплекс-метода
Суть симплекс-метода раскрывает его простейший вариант.
Шаг 1. Задаем начальную точку x0, длину ребра симплекса l и полагаем r = 0.
Шаг 2. По формулам (5.28) и (5.29) находим координаты ![]() всех вершин симплекса.
всех вершин симплекса.
Шаг 3. Вычисляем значения ![]() минимизируемой
функции во всех вершинах симплекса.
минимизируемой
функции во всех вершинах симплекса.
Шаг 4. Находим максимальное из значений функции f(x) в вершинах симплекса ![]() :
:
![]()
Шаг 5. По формулам (5.31), (5.32) отражаем вершину ![]() относительно центра тяжести
остальных вершин симплекса – получаем новый симплекс с координатами вершин
относительно центра тяжести
остальных вершин симплекса – получаем новый симплекс с координатами вершин ![]() .
.
Шаг 6. Вычисляем значение ![]() минимизируемой
функции в новой вершине симплекса.
минимизируемой
функции в новой вершине симплекса.
Шаг 7. Если условие окончания итераций (5.34) выполнено, то в качестве
приближенного значения точки минимума функции f(x) принимаем ту вершину симплекса ![]() , в которой f(x) имеет минимальное значение, и заканчиваем вычисления.
Иначе полагаем r = r + 1 и переходим к шагу 4.
, в которой f(x) имеет минимальное значение, и заканчиваем вычисления.
Иначе полагаем r = r + 1 и переходим к шагу 4.
Поскольку размер симплекса в простейшем варианте симплекс-метода фиксирован, в качестве условия окончания итераций в данном случае можно использовать условие
![]() , (5.34)
, (5.34)
где ![]() – требуемая точность решения по
– требуемая точность решения по ![]() – номер произвольной вершины
симплекса. Отметим, что выражение в левой части неравенства (5.34) есть
максимальная разность значений функции f(x) в двух вершинах симплекса
– номер произвольной вершины
симплекса. Отметим, что выражение в левой части неравенства (5.34) есть
максимальная разность значений функции f(x) в двух вершинах симплекса ![]() .
.
Простейший вариант симплекс-метода иллюстрирует рис. 5.10, на котором показаны линии уровня функции Химмельблау (n = 2).
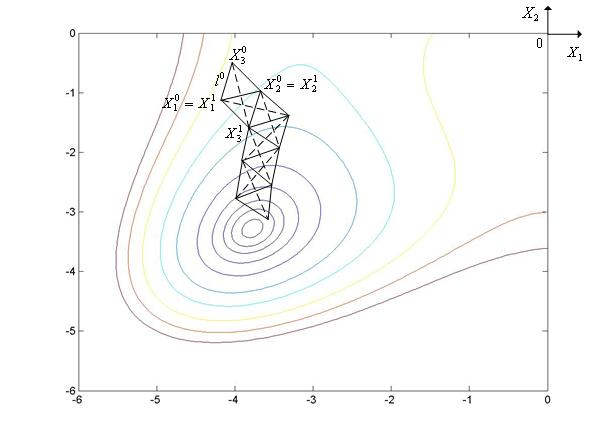
Рис. 5.10. Траектория поиска минимума функции Химмельблау простейшим симплекс-методом
5.1.6 Метод деформируемого многогранника (Нелдера – Мида)
Метод Нелдера – Мида относится, с одной стороны, к классу прямых методов оптимизации, а с другой стороны – к классу детерминированных методов оптимизации. Метод является развитием симплекс-метода решения многомерных задач безусловной оптимизации. В дополнение к процедуре отражения вершины симплекса, которая используется в симплекс-методе, в методе Нелдера-Мида используются процедуры редукции симплекса, сжатия симплекса, растяжения симплекса и, быть может, процедура восстановления симплекса.
Рассмотрим следующую задачу локальной безусловной оптимизации: найти минимум критерия оптимальности f(x), определенного в n-мерном евклидовом пространстве Rn (5.11).
В случае если функция f(x) является овражной функцией, эффективность симплекс-метода при решении задачи (5.11) значительно снижается в силу того, что регулярный симплекс нельзя «вытянуть» вдоль оврага. Метод Нелдера – Мида (метод деформируемого многогранника) является развитием симплекс-метода и использует в процессе поиска деформацию (изменение размеров и формы) текущего симплекса (не обязательно регулярного).
Метод использует следующие операции над симплексами:
- отражение;
- редукция;
- сжатие;
- растяжение.
Отражением вершины симплекса относительно центра тяжести остальных вершин называется перенос одной из его вершин на надлежащее расстояние вдоль прямой, соединяющей данную вершину и центр тяжести оставшихся вершин.
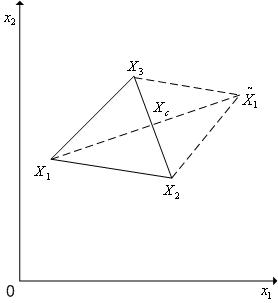 |
Рис. 5.11. Отражение вершины X1 симплекса в пространстве R2 относительно центра тяжести Xc остальных вершин
В результате отражения k-й вершины
симплекса с координатами вершин ![]() получаем новый
симплекс с координатами вершин
получаем новый
симплекс с координатами вершин
![]() (5.35)
(5.35)
где
![]() (5.36)
(5.36)
вектор координат центра тяжести остальных вершин симплекса (за исключением отраженной вершины k).
Редукции симплекса – уменьшение длин всех ребер симплекса в одно и
то же количество раз. В результате выполнения редукции вершин симплекса ![]() к вершине xk
получаем новый симплекс с координатами вершин
к вершине xk
получаем новый симплекс с координатами вершин
![]() , (5.37)
, (5.37)
где ![]() – коэффициент редукции.
– коэффициент редукции.
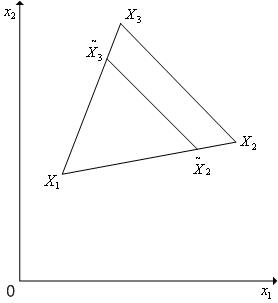 |
Рис. 5.12. Редукция вершин симплекса в пространстве R2 к вершине X1
Сжатие симплекса (рис. 5.13). В результате выполнения сжатия
симплекса ![]() в направлении
в направлении ![]() получаем новый симплекс с
координатами вершин
получаем новый симплекс с
координатами вершин
![]() (5.38)
(5.38)
где ![]() – коэффициент сжатия,
– коэффициент сжатия, ![]() – вектор координат центра тяжести
остальных вершин симплекса.
– вектор координат центра тяжести
остальных вершин симплекса.
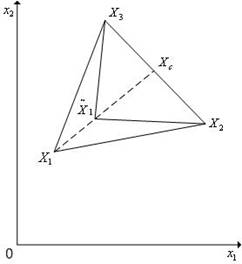
Рис. 5.13. Сжатие симплекса в пространстве R2 в направлении (X1 – Xc)
Растяжение симплекса (рис. 5.14). В результате выполнения
растяжения симплекса ![]() в направлении
в направлении ![]() получаем новый симплекс с
координатами вершин
получаем новый симплекс с
координатами вершин
![]() (5.39)
(5.39)
 где
где ![]() –
коэффициент растяжения,
–
коэффициент растяжения, ![]() – вектор
координат центра тяжести остальных вершин симплекса.
– вектор
координат центра тяжести остальных вершин симплекса.
Рис. 5.14. Растяжение симплекса в пространстве R2 в направлении (X1 – Xc)
Алгоритм метода Нелдера – Мида
Симплекс с вершинами ![]() обозначим Sr.
обозначим Sr.
Шаг 1. Задаем начальную точку x0, длину ребра симплекса l и полагаем r = 0.
Шаг 2. Находим координаты ![]() всех вершин
регулярного симплекса S0 с длиной
ребра l. Вычисляем значения
всех вершин
регулярного симплекса S0 с длиной
ребра l. Вычисляем значения ![]() минимизируемой функции во всех
вершинах симплекса.
минимизируемой функции во всех
вершинах симплекса.
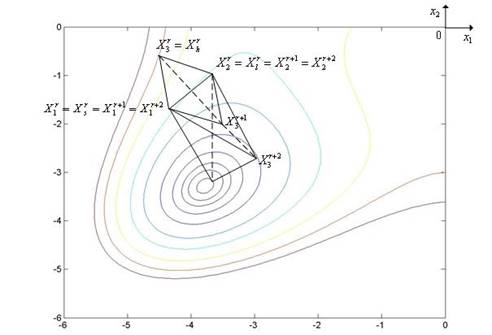
Шаг 3. Среди вершин симплекса Sr
находим вершины ![]() , в которых функция f(x) принимает,
соответственно, наименьшее, наибольшее и следующее за максимальным значения, а
также находим значения функции f(x) в этих точках:
, в которых функция f(x) принимает,
соответственно, наименьшее, наибольшее и следующее за максимальным значения, а
также находим значения функции f(x) в этих точках:
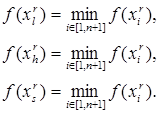
 Шаг 4. По формулам (5.35), (5.36)
выполняем отражение вершины симплекса
Шаг 4. По формулам (5.35), (5.36)
выполняем отражение вершины симплекса ![]() относительно
центра тяжести остальных вершин симплекса – получаем новый симплекс Sr+1. Вычисляем значение
относительно
центра тяжести остальных вершин симплекса – получаем новый симплекс Sr+1. Вычисляем значение ![]() минимизируемой функции в новой
вершине симплекса.
минимизируемой функции в новой
вершине симплекса.
Рис. 5.15. Ситуация, когда метод Нелдера – Мида использует успешное растяжение симплекса
Шаг 5. Если условие окончания итераций (5.40) выполнено, то в качестве приближенного значения точки минимума функции f(x) принимаем ту вершину симплекса Sr+1, в которой f(x) имеет минимальное значение, и заканчиваем вычисления.
Шаг 6. Если ![]() и
и ![]() , то переходим к шагу 7 (растяжению
симплекса) (рис. 5.15). Если
, то переходим к шагу 7 (растяжению
симплекса) (рис. 5.15). Если ![]() , но
, но ![]() , то переходим к шагу 3 (отражению)
(рис. 5.16).
, то переходим к шагу 3 (отражению)
(рис. 5.16).
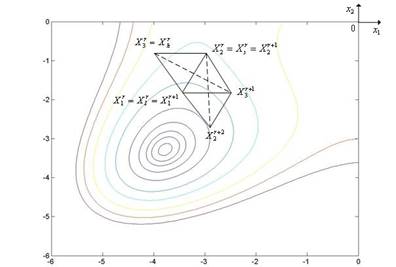 |
Рис. 5.16. Ситуация, когда метод Нелдера – Мида использует успешное отражение симплекса
Если ![]() , то переходим к шагу 8 (сжатию
симплекса) (рис. 5.17 и рис. 5.18).
, то переходим к шагу 8 (сжатию
симплекса) (рис. 5.17 и рис. 5.18).
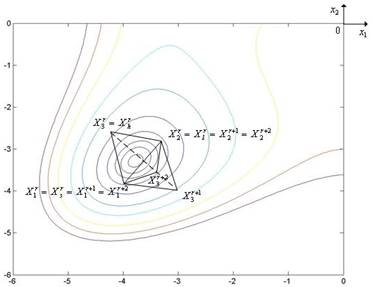 |
Рис. 5.17. Ситуация, когда метод Нелдера – Мида использует успешное сжатие симплекса
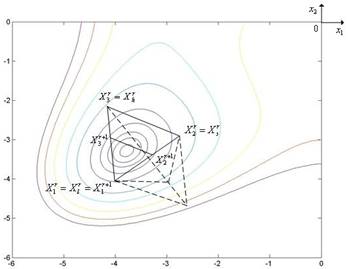 |
Рис. 5.18. Ситуация, когда метод Нелдера – Мида использует редукцию после неудачного сжатия симплекса. Пунктиром показаны отвергнутые (неудачные) итерации
Шаг 7. Ситуация ![]() и
и ![]() . По формуле (5.39) выполняем
растяжение симплекса Sr+1
в направлении
. По формуле (5.39) выполняем
растяжение симплекса Sr+1
в направлении![]() – получаем новый симплекс Sr+2. Вычисляем значение
минимизируемой функции в новой вершине симплекса
– получаем новый симплекс Sr+2. Вычисляем значение
минимизируемой функции в новой вершине симплекса ![]() .
Если
.
Если ![]() , то полагаем r
= r + 2 и переходим
к шагу 3 (отражению вершины симплекса). Иначе полагаем r
= r + 3 и переходим
к шагу 3 (отражению вершины симплекса) с симплексом Sr
(т.е. не используем результаты растяжения).
, то полагаем r
= r + 2 и переходим
к шагу 3 (отражению вершины симплекса). Иначе полагаем r
= r + 3 и переходим
к шагу 3 (отражению вершины симплекса) с симплексом Sr
(т.е. не используем результаты растяжения).
Шаг 8. Ситуация ![]() . По формуле (5.38)
выполняем сжатие симплекса Sr+1
в направлении
. По формуле (5.38)
выполняем сжатие симплекса Sr+1
в направлении ![]() – получаем новый
симплекс Sr+2. Вычисляем
значение минимизируемой функции в новой вершине симплекса
– получаем новый
симплекс Sr+2. Вычисляем
значение минимизируемой функции в новой вершине симплекса ![]() . Если
. Если ![]() ,
то полагаем r = r + 2 и переходим к шагу 3 (отражению вершины симплекса).
Иначе по формуле (5.37) выполняем редукцию симплекса Sr к вершине
,
то полагаем r = r + 2 и переходим к шагу 3 (отражению вершины симплекса).
Иначе по формуле (5.37) выполняем редукцию симплекса Sr к вершине ![]() –
получаем новый симплекс Sr+1.
Вычисляем значение минимизируемой функции во всех новых вершинах симплекса Sr+1. Полагаем r
= r + 1 и переходим
к шагу 3 (отражению симплекса).
–
получаем новый симплекс Sr+1.
Вычисляем значение минимизируемой функции во всех новых вершинах симплекса Sr+1. Полагаем r
= r + 1 и переходим
к шагу 3 (отражению симплекса).
На рис. 5.14–5.18 минимизируемой функцией f(x) является функция Химмельблау.
В качестве условия окончания итераций в методе Нелдера – Мида можно использовать условие
![]() , (5.40)
, (5.40)
где ![]() – требуемая точность решения по f,
– требуемая точность решения по f, ![]() – номер
произвольной вершины симплекса. Можно также завершать итерации, когда длина
максимального из ребер текущего симплекс станет меньше или равна
– номер
произвольной вершины симплекса. Можно также завершать итерации, когда длина
максимального из ребер текущего симплекс станет меньше или равна ![]() – требуемой точности решения по x.
– требуемой точности решения по x.
Изложенная схема метода Нелдера – Мида имеет тот недостаток, что для сильно овражных функций может происходить вырождение («сплющивание») симплекса. Поэтому к рассмотренному алгоритму метода Нелдера – Мида добавляется этап периодического (через N итераций) восстановления симплекса, который заключается в следующем:
- в текущем симплексе выбираются две «лучшие» вершины и определяется
расстояние между ними ![]() ;
;
- исходя из «лучшей» вершины текущего симплекса строится новый симплекс,
длина ребра которого принимается равной ![]() .
.
5.2 Детерминированные методы первого и второго порядка
5.2.1 Метод наискорейшего спуска. Метод дробления шага
Рассматривается следующая многомерная задача локальной безусловной оптимизации: найти минимум критерия оптимальности f(x), определенного в n-мерном евклидовом пространстве Rn (5.11).
Положим, что функция f(x) всюду дифференцируема в n-мерном евклидовом пространстве Rn.
Направление спуска в градиентных методах оптимизации совпадает с направлением антиградиента минимизируемой функции f(x). Итерационная формула градиентных методов оптимизации имеет вид
![]() (5.41)
(5.41)
Здесь ![]() – длина шага на r-й итерации в направлении sr,
где
– длина шага на r-й итерации в направлении sr,
где
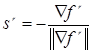 – (5.42)
– (5.42)
единичный вектор
направления антиградиента функции f(x) в точке xr, ![]() – некоторая векторная норма,
например, евклидова. Напомним, что градиент функции f(x) в точке xr
есть значение вектора частных производных этой функции в точке xr:
– некоторая векторная норма,
например, евклидова. Напомним, что градиент функции f(x) в точке xr
есть значение вектора частных производных этой функции в точке xr:
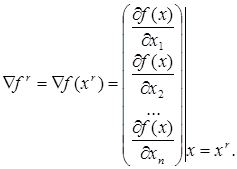
Различные градиентные методы оптимизации отличаются между собой правилами
выбора длины шага ![]() .
.
Градиентный метод наискорейшего спуска предназначен для решения многомерных задач локальной безусловной оптимизации. Метод относится, с одной стороны, к классу методов оптимизации первого порядка (к классу градиентных методов оптимизации), а с другой стороны – к классу детерминированных методов оптимизации. Одна итерация метода состоит из следующих шагов: определение в текущей точке направления антиградиента минимизируемой функции f(x); решение каким-либо методом одномерной задачи локальной безусловной оптимизации в этом направлении.
Градиентный метод наискорейшего спуска в качестве длины шага ![]() использует величину, при которой
достигается минимум функции f(x) в направлении sr:
использует величину, при которой
достигается минимум функции f(x) в направлении sr:
![]() (5.43)
(5.43)
Задача (5.41) есть одномерная задача локальной безусловной оптимизации, которая может быть решена рассмотренными в главе 3 методами, например, методом Паулла (параграф 3.6).
Алгоритм схемы метода
Шаг 1. Задаем начальную точку x0 и полагаем счетчик числа итераций r = 0.
Шаг 2. По формуле (5.42) вычисляем компоненты вектора sr.
Шаг 3. Каким-либо методом решаем одномерную задачу безусловной оптимизации (5.43) – определяем точку xr+1.
Шаг 4. Вычисляем величину f(xr+1) – значение функции f(x) в точке xr+1.
Шаг 5. Проверяем условие окончания поиска (5.44)–(5.46). Если условие
окончания поиска выполнено, то полагаем ![]() и
завершаем итерации. Иначе – полагаем r = r + 1, переходим к шагу 2.
и
завершаем итерации. Иначе – полагаем r = r + 1, переходим к шагу 2.
В качестве критерия окончания поиска можно использовать одно из стандартных условий окончания итераций
![]() (5.44)
(5.44)
![]() (5.45)
(5.45)
В качестве критерия окончания поиска можно использовать также условие
![]() (5.46)
(5.46)
где ![]() – константа, определяющая
требуемую точность решения по градиенту функции f(x).
– константа, определяющая
требуемую точность решения по градиенту функции f(x).
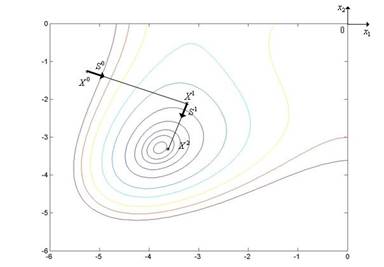
Рис. 5.19. Траектория поиска минимума функции Химмельблау градиентным методом наискорейшего спуска
Градиентный метод наискорейшего спуска иллюстрирует рис. 5.19, на котором показан фрагмент линий уровня функции Химмельблау.
Градиентный метод с дроблением шага предназначен для решения многомерных задач локальной безусловной оптимизации. Метод относится, с одной стороны, к классу методов оптимизации первого порядка (к классу градиентных методов оптимизации), а с другой стороны – к классу детерминированных методов оптимизации. Одна итерация метода состоит из следующих шагов: определение в текущей точке хr направления антиградиента минимизируемой функции f(x); выполнение в этом направлении шага длиной λr, зависящей от модуля градиента функции f(x) в точке хr.
В данном методе точка xr+1 определяется по формуле
![]() (5.47)
(5.47)
где величина шага λr находится из условия
![]() (5.48)
(5.48)
Алгоритм метода
Шаг 1. Задаем начальную точку x0,
начальную величину шага λr и коэффициент дробления шага ![]() . Полагаем счетчик числа итераций r = 0.
. Полагаем счетчик числа итераций r = 0.
Шаг 2. По формуле (5.47) вычисляем компоненты вектора xr+1.
Шаг 3. Вычисляем величину f(xr+1) – значение функции f(x) в точке xr+1.
Шаг 4. Если условие (5.48) выполнено, то переходим к следующему шагу. Иначе – переходим к шагу 6.
Шаг 5. Полагаем ![]() и переходим к шагу 2.
и переходим к шагу 2.
Шаг 6. Проверяем условие окончания поиска (5.44)–(5.46). Если условие
окончания поиска выполнено, то полагаем ![]() и
завершаем итерации. Иначе – полагаем r = r +
1 и переходим к шагу 2.
и
завершаем итерации. Иначе – полагаем r = r +
1 и переходим к шагу 2.
Градиентный метод дробления шага иллюстрирует рис. 5.20, на котором показан фрагмент линий уровня функции Химмельблау.
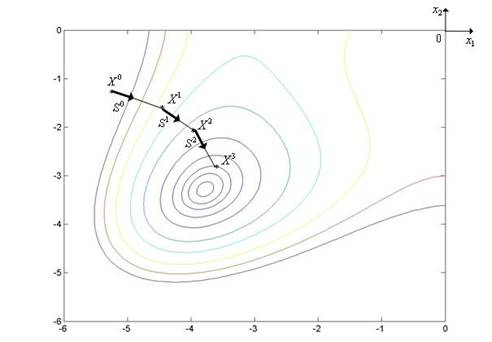
Рис. 5.20. Траектория поиска минимума функции Химмельблау градиентным методом дробления шага
Пример. Выполнить несколько итераций (не менее двух) решения двумерной задачи локальной безусловной оптимизации
![]() (5.49)
(5.49)
где ![]() (5.50)
(5.50)
градиентным
методом с дроблением шага, исходя из точки ![]() .
.
Принять ![]() , в качестве нормы
вектора градиента использовать евклидову норму.
, в качестве нормы
вектора градиента использовать евклидову норму.
Траекторию поиска изобразить на рис. 5.21, на котором приведены линии уровня квадратичной функции (5.50), полученные с помощью MATLAB.
Итерация градиентного метода с дроблением шага для задач (5.49), (5.50) имеет вид
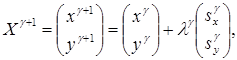 (5.51)
(5.51)
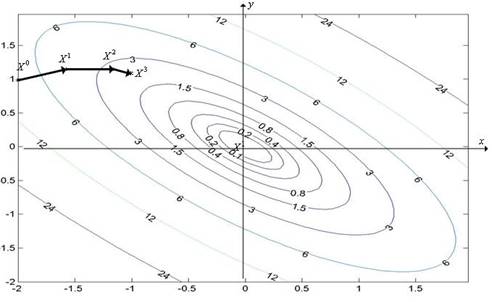
Рис. 5.21. Фрагмент (три итерации) траектории поиска минимума функции (5.50) градиентным методом с дроблением шага
где 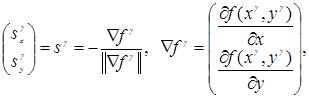 (5.52)
(5.52)
а величина шага ![]() находится из условия
находится из условия
![]()
![]() (5.53)
(5.53)
Найдем явные выражения для частных производных функции (5.50):
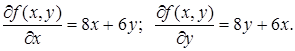 (5.54)
(5.54)
Таким образом, из (5.51), (5.52), (5.54) имеем искомую итерационную формулу градиентного метода с дроблением шага для задачи (5.49), (5.50).
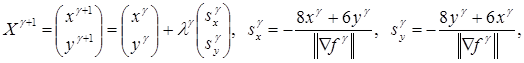
![]() (5.55)
(5.55)
Первая итерация (r = 0)
Из формул (5.54), (5.55) последовательно имеем
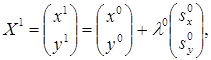
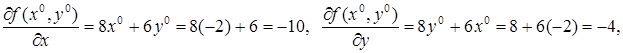
![]()
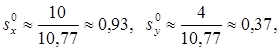
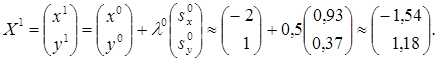
Таким образом, 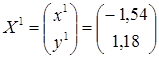 (рис.
5.20).
(рис.
5.20).
Условие (5.53) на первой итерации имеет
вид ![]()
![]()
Поскольку
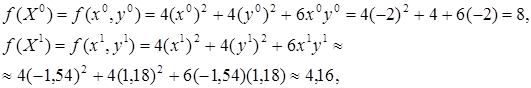
левая часть этого неравенства равна ![]() . Его правая часть, легко видеть,
равна 0,52 · 10,77 = 2,69.
. Его правая часть, легко видеть,
равна 0,52 · 10,77 = 2,69.
Таким образом, на первой
итерации условие (5.53) выполняется и величина шага ![]() должна
быть изменена:
должна
быть изменена:![]()
Вторая итерация (r = 1).
Аналогично первой итерации последовательно имеем
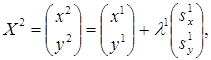
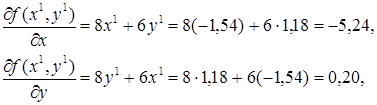
![]()
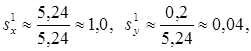
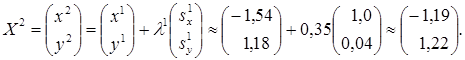
Таким образом, 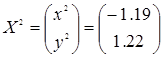 (рис.
5.20).
(рис.
5.20).
Условие (5.53) на первой итерации имеет
вид ![]()
![]()
Поскольку
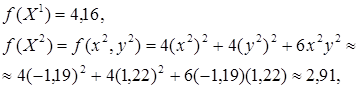
левая часть этого неравенства равна ![]() . Его правая часть, легко видеть,
равна 0,5 · 0,35 · 5,24 = 0,92.
. Его правая часть, легко видеть,
равна 0,5 · 0,35 · 5,24 = 0,92.
Таким образом, на второй
итерации условие (5.53) выполняется и величина шага ![]() должна
быть изменена:
должна
быть изменена:![]()
Третья итерация (r = 2).
Аналогично первой итерации последовательно имеем
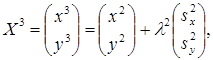
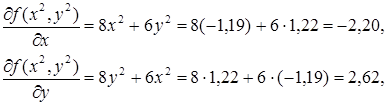
![]()
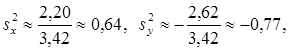
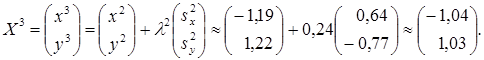
Таким образом, 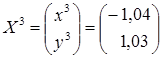 (рис.
5.21).
(рис.
5.21).
Условие (5.53) на первой итерации имеет
вид ![]()
![]()
Поскольку
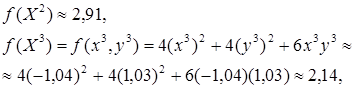
левая часть этого неравенства равна ![]() . Его правая часть, легко видеть,
равна 0,5 · 0,24 · 3,42 = 0,41.
. Его правая часть, легко видеть,
равна 0,5 · 0,24 · 3,42 = 0,41.
Таким образом, на третьей
итерации условие (5.53) выполняется и величина шага ![]() должна
быть изменена:
должна
быть изменена:![]()
5.2.2 Метод оптимизации Ньютона
Метод оптимизации Ньютона предназначен для решения многомерных задач локальной безусловной оптимизации. Метод относится, с одной стороны, к классу методов оптимизации k-го порядка, где k = 2 (т.е. к классу методов оптимизации второго порядка), а с другой стороны – к классу детерминированных методов оптимизации. Одна итерация метода требует вычисления в текущей точке компонент вектора градиента минимизируемой функции, а также компонент матрицы Гессе в этой точке. Матрицей Гессе H(х) функции f(x) называется (n*n)-матрица вторых частных производных этой функции. Здесь n – размерность вектора x.
Положим, что функция f(x) всюду дважды дифференцируема в n-мерном евклидовом пространстве Rn.
Рассмотрим следующую многомерную задачу локальной безусловной оптимизации: найти минимум критерия оптимальности f(x), определенного в n-мерном евклидовом пространстве Rn,
![]() (5.56)
(5.56)
Обоснование метода оптимизации Ньютона
Рассмотрим первые три члена разложения функции f(x) в ряд Тейлора в окрестности точки xr:
![]() (5.57)
(5.57)
Здесь H(x) – матрица Гессе
функции f(x). Из
(5.57) следует, что градиент функции ![]() равен
равен
![]() (5.58)
(5.58)
Если матрица Гессе H(xr)
положительно определена, то функция ![]() достигает
минимума в точке, в которой градиент этой функции равен нулевому вектору.
достигает
минимума в точке, в которой градиент этой функции равен нулевому вектору.
Таким образом, в точке xr+1
минимума функции ![]() справедливо равенство
справедливо равенство
![]() (5.59)
(5.59)
где 0 – n-мерный вектор нулей. Отсюда получаем итерационную формулу
![]() (5.60)
(5.60)
для отыскания очередного приближения к точке минимума функции f(x). Здесь
![]() (5.61)
(5.61)
Выражение (5.60) представляет собой итерационную формулу решения системы уравнений (5.59) широко известным методом касательных (методом Ньютона). Этим фактом объясняется название рассматриваемого метода оптимизации.
Найдем скалярное произведение градиента функции f(x) в точке xr и
вектора ![]() :
:
![]() (5.62)
(5.62)
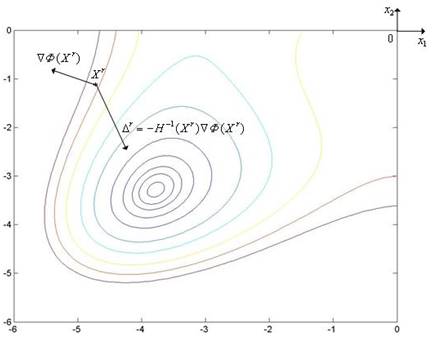 Последнее неравенство справедливо в
силу постулируемой положительной определенности матрицы Гессе в точке xr. Геометрически неравенство (5.62) означает,
что вектор
Последнее неравенство справедливо в
силу постулируемой положительной определенности матрицы Гессе в точке xr. Геометрически неравенство (5.62) означает,
что вектор ![]() образует тупой угол с градиентом
целевой функции f(x)
в точке xr (рис. 5.22). Таким
образом, при минимизации овражных функций вектор
образует тупой угол с градиентом
целевой функции f(x)
в точке xr (рис. 5.22). Таким
образом, при минимизации овражных функций вектор ![]() может
составлять с осью оврага меньший угол, чем вектор антиградиента. Эта
особенность делает метод оптимизации Ньютона, вообще говоря, более эффективным,
чем градиентный метод наискорейшего спуска.
может
составлять с осью оврага меньший угол, чем вектор антиградиента. Эта
особенность делает метод оптимизации Ньютона, вообще говоря, более эффективным,
чем градиентный метод наискорейшего спуска.
Рис. 5.22. К обоснованию метода многомерной оптимизации Ньютона
Отметим трудности, которые могут возникать при использовании итерационной формулы (5.60):
1 Если размерность пространства Rn велика, то обращение на каждой итерации матрицы Гессе H(xr) может потребовать значительных вычислительных ресурсов.
2 Значение минимизируемой функции f(x) в точке ![]() может
превышать значение функции в предыдущей точке xr
вследствие того, что направление
может
превышать значение функции в предыдущей точке xr
вследствие того, что направление ![]() ведет к
уменьшению f(x),
но величина шага слишком велика.
ведет к
уменьшению f(x),
но величина шага слишком велика.
3 Направление спуска, определяемое вектором ![]() ,
ведет к убыванию целевой функции только при положительной определенности
матрицы Гессе H(xr).
Это приводит к тому, что на каждой итерации необходимы вычислительные затраты
на проверку обусловленности этой матрицы. Указанная матрица может быть плохо
обусловленной. Более того, указанная матрица может быть вырожденной и поэтому
не иметь обратной матрицы.
,
ведет к убыванию целевой функции только при положительной определенности
матрицы Гессе H(xr).
Это приводит к тому, что на каждой итерации необходимы вычислительные затраты
на проверку обусловленности этой матрицы. Указанная матрица может быть плохо
обусловленной. Более того, указанная матрица может быть вырожденной и поэтому
не иметь обратной матрицы.
Вследствие этих трудностей итерационная формула (5.60) в «чистом» виде не используется в вычислительной практике.
Для того чтобы избежать обращения матрицы Гессе, на практике вектор ![]() находят обычно из следующей
системы линейных алгебраических уравнений (СЛАУ), вытекающей из равенства (5.61):
находят обычно из следующей
системы линейных алгебраических уравнений (СЛАУ), вытекающей из равенства (5.61):
![]() (5.63)
(5.63)
СЛАУ (5.63) может быть решена различными численными методами (например, прямыми методами, итерационными методами).
Величина шага в направлении ![]() , которая
приводит к убыванию функции f(x), может быть обеспечена путем добавления в итерационную
формулу (5.60) коэффициента
, которая
приводит к убыванию функции f(x), может быть обеспечена путем добавления в итерационную
формулу (5.60) коэффициента ![]() , т.е. путем
использования вместо формулы (5.60) итерационной формулы
, т.е. путем
использования вместо формулы (5.60) итерационной формулы
![]() , (5.64)
, (5.64)
где коэффициент ![]() выбирают тем или иным способом
так, чтобы обеспечить условие
выбирают тем или иным способом
так, чтобы обеспечить условие ![]()
Для того чтобы направление спуска независимо от определенности матрицы
Гессе H(xr)
вело к убыванию функции f(x),
в качестве вектора ![]() можно использовать
вектор
можно использовать
вектор
![]() (5.65)
(5.65)
где I – (n*n) – единичная матрица, а ![]() –
параметр, выбираемый так, чтобы матрица
–
параметр, выбираемый так, чтобы матрица ![]() являлась
положительно определенной.
являлась
положительно определенной.
Алгоритм метода оптимизации Ньютона
Рассмотрим алгоритм одной из модификаций метода оптимизации Ньютона, в
которой используется итерационная формула (5.64) и вектор ![]() находят путем решения на каждой
итерации СЛАУ (5.63).
находят путем решения на каждой
итерации СЛАУ (5.63).
Шаг 1. Задаем начальную точку x0,
начальную величину шага ![]() и коэффициент
дробления шага
и коэффициент
дробления шага ![]() . Полагаем счетчик числа
итераций r = 0.
. Полагаем счетчик числа
итераций r = 0.
Шаг 2. Вычисляем в точке xr
вектор градиента ![]() и матрицу Гессе H(xr).
и матрицу Гессе H(xr).
Шаг 3. Решаем СЛАУ (5.63) и находим вектор ![]() .
.
Шаг 4. По формуле (5.64) вычисляем компоненты вектора xr+1.
Шаг 5. Вычисляем величину f(xr+1) – значение функции f(x) в точке xr+1.
Шаг 6. Проверяем условие окончания поиска (5.66). Если условие окончания
поиска выполнено, то полагаем ![]() и завершаем
итерации. Иначе – переходим к следующему шагу.
и завершаем
итерации. Иначе – переходим к следующему шагу.
Шаг 7. Если f(xr+1)
< f(xr),
то полагаем r = r + 1 и переходим к шагу 2. Иначе
– фиксированное число раз полагаем ![]() и переходим к
шагу 4.
и переходим к
шагу 4.
В качестве условия окончания поиска можно использовать одно из стандартных условий окончания итераций:
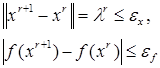
или условие (5.66)
![]()
где ![]() – константа, определяющая
требуемую точность решения по градиенту функции f(x).
– константа, определяющая
требуемую точность решения по градиенту функции f(x).
5.3 Методы случайного поиска
5.3.1 Метод с возвратом при недостаточном шаге. Метод наилучшей пробы
Метод с возвратом при неудачном шаге предназначен для решения многомерных задач локальной безусловной оптимизации. Метод относится, с одной стороны, к классу прямых методов оптимизации, а с другой стороны – к классу стохастических методов оптимизации. Метод является одношаговым методом оптимизации. Идея метода состоит в следующем: на каждой итерации, исходя из текущей точки хr, делается шаг длиной λr в случайном направлении; в полученной точке вычисляется значение минимизируемой функции f(x); если это значение меньше значения f(xr), то полученная точка становится следующей текущей точкой; иначе – делается следующий шаг в новом случайном направлении; если фиксированное количество таких попыток не привело к уменьшению функции f(x), то длина шага λr уменьшается и рассмотренные шаги метода повторяются.
Рассматривается задача (5.56). При ее решении методом с возвратом при неудачном шаге (одношаговый метод оптимизации) используется итерационная формула
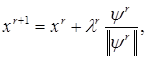 (5.67)
(5.67)
где ![]() – величина шага
на r-й итерации,
– величина шага
на r-й итерации, ![]() –
реализация n-мерного случайного вектора,
–
реализация n-мерного случайного вектора, ![]() –
некоторая векторная норма. Обычно в качестве координат вектора
–
некоторая векторная норма. Обычно в качестве координат вектора ![]() используют независимые случайные
величины, равномерно распределенные в интервале [–1;1].
используют независимые случайные
величины, равномерно распределенные в интервале [–1;1].
Шаг 1. Задаем начальную
точку х0, начальную длину шага ![]() и
полагаем счетчик числа итераций r = 0.
и
полагаем счетчик числа итераций r = 0.
Шаг 2. Задаем начальное значение счетчика числа неудачных попыток k = 1.
Шаг 3. Получаем
реализацию случайных чисел ![]() – компонент вектора
– компонент вектора
![]() и по формуле (5.67) находим пробную
точку xr+1.
и по формуле (5.67) находим пробную
точку xr+1.
Шаг 4. Вычисляем значение f(xr+1) функции f(x) в точке xr+1.
Шаг 5. Если f(xr+1) < f(xr), то полагаем r = r + 1и переходим к шагу 3. Иначе – переходим к шагу 6.
Шаг 6. Полагаем k = k + 1. Если k < K, то переходим к шагу 3. Иначе – переходим к шагу 7. Здесь K – предельное количество неудачных попыток (свободный параметр метода). Рекомендуется K = 3n.
Шаг 7. Проверяем
условие окончания поиска (5.68). Если условие окончания поиска выполнено, то
полагаем ![]() и завершаем итерации. Иначе –
полагаем r = r +
1,
и завершаем итерации. Иначе –
полагаем r = r +
1, ![]() и переходим к шагу 2. Здесь
и переходим к шагу 2. Здесь ![]() – коэффициент уменьшения шага
(свободный параметр метода).
– коэффициент уменьшения шага
(свободный параметр метода).
В качестве условия окончания поиска можно использоваться одно из стандартных условий окончания итераций:
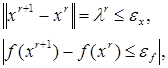 (5.68)
(5.68)
где ![]() –
константа, определяющая требуемую точность решения по x;
–
константа, определяющая требуемую точность решения по x;
![]() –
константа, определяющая требуемую точность решения по f.
–
константа, определяющая требуемую точность решения по f.
Данный метод иллюстрирует рис. 5.23, на котором показан фрагмент линий уровня функции Химмельблау.
![]()
Рис. 5.23. Траектория поиска минимума функции Химмельблау методом с возвратом при неудачном шаге. Пунктиром на рисунке показаны неудачные шаги
Модификацией метода с возвратом при неудачном шаге является метод наилучшей пробы (также одношаговый метод оптимизации).
Метод наилучшей пробы предназначен для решения многомерных задач локальной безусловной оптимизации. Метод относится, с одной стороны, к классу прямых методов оптимизации, а с другой стороны – к классу стохастических методов оптимизации. Метод является модификацией метода с возвратом при неудачном шаге и, так же как этот метод, является одношаговым методом оптимизации. Идея метода состоит в следующем: на каждой итерации, исходя из текущей точки хr, делается фиксированное количество шагов длиной λr в случайных направлениях; в полученных точках вычисляются значения минимизируемой функции f(x) и находится минимальное из них; если это значение меньше значения f(xr), то соответствующая точка x становится следующей текущей точкой; иначе – длина шага λr уменьшается, и рассмотренные шаги метода повторяются.
Шаг 1. Задаем начальную
точку x0,
начальную длину шага ![]() и полагаем счетчик числа
итераций r = 0.
и полагаем счетчик числа
итераций r = 0.
Шаг 2. Генерируем M
случайных векторов ![]() и по формуле (5.67)
находим пробные точки
и по формуле (5.67)
находим пробные точки ![]() .
.
Шаг 3. Вычисляем
значения ![]() функции f(x)
в пробных точках
функции f(x)
в пробных точках ![]() и находим минимальное из
этих значений
и находим минимальное из
этих значений ![]()
Шаг 4. Если f(xr+1) < f(xr), то полагаем r = r + 1 и переходим к шагу 2. Иначе – переходим к шагу 5.
![]()
Рис. 5.24. Траектория поиска минимума функции Химмельблау методом наилучшей пробы. Пунктиром на рисунке показаны неудачные пробы
Шаг 5. Проверяем
условие окончания поиска (5.68). Если условие окончания поиска выполнено, то
полагаем ![]() и завершаем итерации. Иначе –
полагаем r = r +
1,
и завершаем итерации. Иначе –
полагаем r = r +
1, ![]() и переходим к шагу 2. Здесь
и переходим к шагу 2. Здесь ![]() – коэффициент уменьшения шага
(свободный параметр метода).
– коэффициент уменьшения шага
(свободный параметр метода).
Метод наилучшей пробы иллюстрирует рис. 5.24, на котором показан фрагмент линий уровня функции Химмельблау.
5.3.2 Метод комплексов
Метод комплексов используется при решении многомерных задач локальной безусловной оптимизации. Метод относится, с одной стороны, к классу стохастических методов оптимизации, а с другой стороны – к классу прямых методов оптимизации. Метод основан на использовании операции отражения вершины комплекса с растяжением и операции сжатия комплекса.
Комплексом называется многогранник с N > n + 1 вершинами (необязательно выпуклый). Рекомендуется N = 2n. Вообще говоря, комплексом в комбинаторной топологии называется геометрическая фигура, которая может быть разбита на более элементарные фигуры. В нашем случае такими элементарными фигурами являются симплексы. Поэтому, говоря более строго, в данном параграфе рассматриваются симплициальные комплексы. В комбинаторной топологии комплексом называется геометрическая фигура, которая может быть разбита на более элементарные фигуры. Таким образом, симплициальный комплекс – это комплекс, который может быть разбит на симплексы. В курсе «Методы оптимизации» термин комплекс синонимичен термину симплициальный комплекс. Комплексы используются, например, при решении многомерных задач локальной безусловной оптимизации методом комплексов.
При решении задачи (5.56) методом комплексов используются следующие операции:
- генерация случайного комплекса;
- отражение вершины комплекса с растяжением;
- сжатие комплекса.
Генерация случайного комплекса. В пространстве Rn координаты вершин случайного комплекса с N вершинами могут быть найдены по формуле
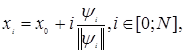 (5.69)
(5.69)
где x0 –
произвольная начальная точка, i – номер вершины
комплекса, l – скаляр, определяющий размеры
комплекса, ![]() – реализация n-мерного
случайного вектора,
– реализация n-мерного
случайного вектора, ![]() – некоторая векторная норма. Обычно в качестве координат вектора
– некоторая векторная норма. Обычно в качестве координат вектора ![]() используют независимые случайные
величины, равномерно распределенные в интервале [–1;1].
используют независимые случайные
величины, равномерно распределенные в интервале [–1;1].
![]() Отражение
вершины комплекса с растяжением. Положим, что в пространстве Rn тем или иным способом задан комплекс Cr с N вершинами
Отражение
вершины комплекса с растяжением. Положим, что в пространстве Rn тем или иным способом задан комплекс Cr с N вершинами ![]() , и его вершину
, и его вершину ![]() необходимо отразить через центр
тяжести комплекса с растяжением. В новом комплексе Cr+1
все вершины, кроме k-й, совпадают с соответствующими
вершинами исходного комплекса Cr, а k-я вершина находится на прямой, проходящей через центр
тяжести этого комплекса и его вершину
необходимо отразить через центр
тяжести комплекса с растяжением. В новом комплексе Cr+1
все вершины, кроме k-й, совпадают с соответствующими
вершинами исходного комплекса Cr, а k-я вершина находится на прямой, проходящей через центр
тяжести этого комплекса и его вершину ![]() (рис.
5.25).
(рис.
5.25).
Рис. 5.25. Отражение вершины ![]() комплекса Cr через центр его тяжести с растяжением.
Пунктиром показан новый комплекс Cr+1
комплекса Cr через центр его тяжести с растяжением.
Пунктиром показан новый комплекс Cr+1
Обозначим координаты вершин нового комплекса ![]() .
Тогда имеем
.
Тогда имеем
![]() (5.70)
(5.70)
где ![]() –
коэффициент растяжения комплекса (рекомендуемое значение – 1,3);
–
коэффициент растяжения комплекса (рекомендуемое значение – 1,3);
![]() –
вектор координат центра тяжести комплекса Cr:
–
вектор координат центра тяжести комплекса Cr:
![]() (5.71)
(5.71)
Сжатие комплекса. Положим, что в пространстве Rn
тем или иным способом задан комплекс Cr с N вершинами ![]() и его вершину
и его вершину ![]() необходимо переместить ближе к
центру тяжести комплекса Cr – выполнить сжатие
комплекса. В новом комплексе Cr+1
все вершины, кроме k-й, совпадают с
соответствующими вершинами исходного комплекса Cr,
а k-я вершина находится на прямой, проходящей
через центр тяжести этого комплекса и его вершину
необходимо переместить ближе к
центру тяжести комплекса Cr – выполнить сжатие
комплекса. В новом комплексе Cr+1
все вершины, кроме k-й, совпадают с
соответствующими вершинами исходного комплекса Cr,
а k-я вершина находится на прямой, проходящей
через центр тяжести этого комплекса и его вершину ![]() (рис.
5.26). Обозначим координаты вершин нового комплекса
(рис.
5.26). Обозначим координаты вершин нового комплекса ![]() .
Тогда имеем
.
Тогда имеем
![]() (5.72)
(5.72)
где ![]() –
коэффициент сжатия комплекса (рекомендуемое значение – 2),
–
коэффициент сжатия комплекса (рекомендуемое значение – 2), ![]() – вектор координат центра тяжести комплекса Cr.
– вектор координат центра тяжести комплекса Cr.
![]()
Рис. 5.26. Сжатие комплекса Cr. Пунктиром показан новый комплекс Cr
Алгоритм простейшего варианта метода комплексов
Шаг 1. Задаем начальную точку ![]() ,
исходя из которой должен быть построен комплекс C0,
начальное значение величины l = l0 и полагаем счетчик числа итераций r = 0.
,
исходя из которой должен быть построен комплекс C0,
начальное значение величины l = l0 и полагаем счетчик числа итераций r = 0.
Шаг 2. Генерируем N случайных векторов ![]() и по формуле (5.69) находим
координаты
и по формуле (5.69) находим
координаты ![]() вершин комплекса Cr.
вершин комплекса Cr.
Шаг 3. Вычисляем значения ![]() функции
f(x) во всех
вершинах комплекса Cr.
функции
f(x) во всех
вершинах комплекса Cr.
Шаг 4. Находим максимальное из значений функции f(x) в вершинах комплекса Cr
![]()
Шаг 5. По формулам (5.70), (5.71) для комплекса Cr
выполняем отражение вершины комплекса с растяжением ![]() – получаем вершину
– получаем вершину ![]() и новый комплекс Cr+1.
и новый комплекс Cr+1.
Шаг 6. Вычисляем значение ![]() функции
f(x) в вершине
функции
f(x) в вершине ![]() .
.
Шаг 7. Если ![]() >
>![]() , то полагаем r = r +
1 и переходим к шагу 8. Иначе – по формулам (5.71), (5.72) выполняем сжатие
симплекса Cr+1 в
направлении
, то полагаем r = r +
1 и переходим к шагу 8. Иначе – по формулам (5.71), (5.72) выполняем сжатие
симплекса Cr+1 в
направлении ![]() , полагаем r
= r + 2 и переходим
к шагу 6.
, полагаем r
= r + 2 и переходим
к шагу 6.
Шаг 8. Проверяем условие окончания поиска (см. ниже). Если условие окончания поиска выполнено, то в качестве точки x* полагаем вершину комплекса Cr, в которой функция f(x) имеет наименьшее значение и завершаем итерации. Иначе – переходим к шагу 4.
В качестве критерия окончания поиска может использоваться следующее
условие: максимальная длина ребра комплекса Cr
не превышает ![]() –
требуемую точность решения по x. Может использоваться
также следующее аналогичное условие: максимальная разность значений функции f(x) в двух вершинах
комплекса Cr не превышает
–
требуемую точность решения по x. Может использоваться
также следующее аналогичное условие: максимальная разность значений функции f(x) в двух вершинах
комплекса Cr не превышает ![]() – требуемую точность
решения по f.
– требуемую точность
решения по f.
![]() Метод комплексов
иллюстрирует рис. 5.27, на котором показан фрагмент линий уровня функции
Химмельблау. На рисунке исходный комплекс Cr
имеет вершины
Метод комплексов
иллюстрирует рис. 5.27, на котором показан фрагмент линий уровня функции
Химмельблау. На рисунке исходный комплекс Cr
имеет вершины ![]() . После отражения с
растяжением вершины
. После отражения с
растяжением вершины ![]() этого
комплекса, в которой функция имеет максимальное значение, получаем комплекс Cr+1 с вершинами
этого
комплекса, в которой функция имеет максимальное значение, получаем комплекс Cr+1 с вершинами ![]() . После отражения с растяжением
вершины
. После отражения с растяжением
вершины ![]() комплекса
Cr+1, в которой функция
имеет максимальное значение, получаем комплекс Cr+2
с вершинами
комплекса
Cr+1, в которой функция
имеет максимальное значение, получаем комплекс Cr+2
с вершинами ![]() .
.
Рис. 5.27. Траектория поиска минимума функции Химмельблау методом комплексов
Известно множество модификаций рассмотренного метода комплексов, направленных, в частности, на преодоление «уплощения» комплекса в процессе поиска. С этой целью через фиксированное количество итераций находятся максимальная и минимальная диагонали комплекса и, если их отношение превышает заданное, то по рассмотренной схеме производится построение нового комплекса.
5.3.3 Метод повторяющегося случайного поиска
Метод повторяющегося случайного поиска используется при решении многомерных задач локальной безусловной оптимизации. Метод относится, с одной стороны, к классу стохастических методов оптимизации, а с другой стороны – к классу прямых методов оптимизации и является многошаговым методом оптимизации (точнее – 3 шаговым методом). Если xr – текущая точка, то в данном методе следующая точка находится по формуле xr + λr · Δr, где λr – величина шага (скаляр) на r-й итерации, Δr = β · sr + (1 – β)pr – направление шага на r-й итерации. Здесь sr – нормализованный вектор «предыстории», определяющий среднее направление поиска на двух предыдущих шагах; pr – нормализованный вектор псевдослучайных чисел, равномерно распределенных в интервале [0,1]; β – скалярный коэффициент, задающий относительные веса детерминированной и случайной компонент в векторе Δr.
Рассматривается задача (5.56).
В методе повторяющегося случайного поиска (трехшаговый метод) используется итерационная схема (рис. 5.27)
![]() (5.73)
(5.73)
где ![]() – величина шага (скаляр) на r-й итерации,
– величина шага (скаляр) на r-й итерации, ![]() – вектор,
определяющий направление шага на r-й итерации:
– вектор,
определяющий направление шага на r-й итерации:
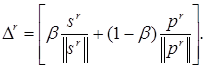 (5.74)
(5.74)
Здесь ![]() – вектор «предыстории»,
определяющий среднее направление поиска на двух предыдущих шагах;
– вектор «предыстории»,
определяющий среднее направление поиска на двух предыдущих шагах; ![]() – некоторая векторная норма; pr – n-мерный вектор псевдослучайных чисел, равномерно
распределенных в интервале [1;0]; скаляр
– некоторая векторная норма; pr – n-мерный вектор псевдослучайных чисел, равномерно
распределенных в интервале [1;0]; скаляр ![]() –
коэффициент, задающий относительные веса детерминированной и случайной
компонент в векторе
–
коэффициент, задающий относительные веса детерминированной и случайной
компонент в векторе ![]() (свободный параметр
метода); скаляр
(свободный параметр
метода); скаляр ![]() – коэффициент, задающий
относительные веса векторов sr-1,
sr-2 в векторе (свободный
параметр метода).
– коэффициент, задающий
относительные веса векторов sr-1,
sr-2 в векторе (свободный
параметр метода).
![]() Заметим,
что отношение
Заметим,
что отношение ![]() представляет собой
единичный вектор направления sr, а
отношение
представляет собой
единичный вектор направления sr, а
отношение ![]() – единичный вектор направления.
– единичный вектор направления.
Рис. 5.28. К итерационной схеме метода повторяющегося случайного поиска
Принято ![]() так что
так что ![]() и
и 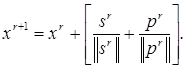
Упрощенный алгоритм метода повторяющегося случайного поиска
Шаг 1. Задаем начальную точку x0,
начальный шаг ![]() , значения коэффициентов
, значения коэффициентов ![]() и полагаем счетчик числа итераций r = 2.
и полагаем счетчик числа итераций r = 2.
Шаг 2. Тем или иным способом, например с помощью одношагового метода наилучшей пробы, определяем точки x1, x2 – этап «разгона» метода.
Шаг 3. Генерируем n-мерный случайный вектор pr и по формулам (5.73), (5.74) вычисляем координаты точки xr+1 и значение f(xr+1) функции f(x) в этой точке.
Шаг 4. Если f(xr+1)<
f(xr),
то проверяем условие окончания итераций (см. ниже). Если условие окончания
выполнено, то полагаем ![]() и завершаем итерации.
Если условие окончания итераций не выполнено, то некоторому правилу увеличиваем
длину шага
и завершаем итерации.
Если условие окончания итераций не выполнено, то некоторому правилу увеличиваем
длину шага ![]() , например, полагая
, например, полагая ![]() , принимаем r
= r + 1 и переходим
к шагу 3. Если f(xr+1)
, принимаем r
= r + 1 и переходим
к шагу 3. Если f(xr+1)![]() f(xr), то переходим к шагу 5.
f(xr), то переходим к шагу 5.
Шаг 5. Некоторое фиксированное количество раз делаем попытку, исходя из
той же точки xr, не меняя длины шага ![]() , добиться уменьшения значения
функции f(x)
путем только изменения вектора pr,
т.е. не меняя xr и
, добиться уменьшения значения
функции f(x)
путем только изменения вектора pr,
т.е. не меняя xr и ![]() , переходим к шагу 3. Если это
фиксированное количество попыток не привело к успеху, то, исходя из той же
точки xr, по некоторому правилу
уменьшаем длину шага
, переходим к шагу 3. Если это
фиксированное количество попыток не привело к успеху, то, исходя из той же
точки xr, по некоторому правилу
уменьшаем длину шага ![]() , например, полагая
, например, полагая ![]() , и переходим к шагу 3.
, и переходим к шагу 3.
В качестве условия окончания поиска можно использоваться одно из стандартных условий окончания итераций
![]()
где ![]() – константа, определяющая
требуемую точность решения по x;
– константа, определяющая
требуемую точность решения по x;
![]()
![]() где
где ![]() –
константа, определяющая требуемую точность решения по f.
–
константа, определяющая требуемую точность решения по f.
Рис. 5.29. Траектория поиска минимума функции Химмельблау методом повторяющегося случайного поиска
Известно множество модификаций рассмотренной простейшей схемы метода
повторяющегося случайного поиска. Например, в процессе поиска могут изменяться
по некоторым правилам не только длина шага ![]() ,
но и коэффициенты
,
но и коэффициенты ![]() .
.
Метод повторяющегося случайного поиска иллюстрирует рис. 5.29, на котором показан фрагмент линий уровня функции Химмельблау.
5.3.4 Метод случайного поиска с постоянным радиусом и случайными направлениями
Метод случайного поиска с постоянным радиусом поиска и случайными направлениями используется при решении многомерных задач локальной безусловной оптимизации. Метод относится, с одной стороны, к классу стохастических методов оптимизации, а с другой стороны – к классу прямых методов оптимизации. Метод является одношаговым методом оптимизации. Пусть xr – текущая точка. Тогда основные шаги метода имеют следующее содержание: генерируется некоторое фиксированное количество случайных точек y1, y2,..., равномерно распределенных по поверхности гиперсферы радиуса Rr с центром в точке xr; в каждой из этих точек вычисляются значения минимизируемой функции f(x); находится минимальное из вычисленных значений (пусть это будет значение, соответствующее точке yk); каким-либо из одномерных методов оптимизации (например, методом Паулла) находим минимум функции f(x) в направлении (yk – xr); соответствующая точка x принимается за следующую текущую точку.
Рассматривается задача (5.56).
Данный метод использует процедуру генерации случайных точек, равномерно
распределенных по поверхности гиперсферы в пространстве Rn.
Пусть ![]() –
вектор координат центра гиперсферы,
–
вектор координат центра гиперсферы, ![]() – радиус
гиперсферы, R – вектор с началом в точке xc и концом в искомой точке на поверхности
гиперсферы,
– радиус
гиперсферы, R – вектор с началом в точке xc и концом в искомой точке на поверхности
гиперсферы, ![]() – углы между вектором R и ортами координатных осей
– углы между вектором R и ортами координатных осей ![]() .
.
Во введенных обозначениях алгоритм генерации случайных точек, равномерно
распределенных по поверхности гиперсферы радиуса ![]() ,
может быть представлен в следующем виде:
,
может быть представлен в следующем виде:
- генерируем n случайных чисел, равномерно
распределенных в интервале ![]() ;
;
- вычисляем направляющие косинусы ![]() вектора
R;
вектора
R;
- находим координаты искомой точки ![]() .
.
Упрощенный алгоритм метода случайного поиска с постоянным радиусом поиска и случайными направлениями.
Шаг 1. Задаем начальную точку x0,
начальный радиус гиперсферы ![]() , и полагаем
счетчик числа итераций r =
0.
, и полагаем
счетчик числа итераций r =
0.
Шаг 2. Генерируем случайные точки ![]() равномерно
распределенные по поверхности гиперсферы радиуса
равномерно
распределенные по поверхности гиперсферы радиуса ![]() с
центром в точке xr. Здесь N – количество точек – свободный параметр метода.
с
центром в точке xr. Здесь N – количество точек – свободный параметр метода.
Шаг 3. Вычисляем значения минимизируемой функции ![]() в
полученных точках и находим точку, в которой достигается минимальное значение
функции f(x):
в
полученных точках и находим точку, в которой достигается минимальное значение
функции f(x):
![]()
Шаг 4. Каким-либо из рассмотренных в главе 3 одномерных методов
оптимизации (например, методом Паулла) находим минимум функции f(x) в направлении ![]() :
:
![]()
![]()
Шаг 5. Проверяем условие окончания итераций (см. ниже). Если условие
окончания выполнено, то полагаем ![]() и завершаем
итерации. Иначе – принимаем r =
r + 1 и переходим к шагу
2.
и завершаем
итерации. Иначе – принимаем r =
r + 1 и переходим к шагу
2.
В качестве условия окончания поиска можно использовать одно из стандартных условий окончания итераций:
![]()
где ![]() – константа, определяющая
требуемую точность решения по x;
– константа, определяющая
требуемую точность решения по x;
![]()
где ![]() – константа, определяющая
требуемую точность решения по f.
– константа, определяющая
требуемую точность решения по f.
Могут быть использованы также другие критерии окончания поиска, например,
условие не превышения текущим радиусом гиперсферы величины ![]() :
:
![]()
В процессе поиска радиус гиперсферы может меняться, увеличиваясь при удачных шагах (вдали от точки x*) и уменьшаясь при неудачных шагах (вблизи от точки x*).
Поиск может быть ускорен, если точки на гиперсфере выбирать (случайным образом) в некотором секторе по отношению к предыдущему направлению. Угол раскрыва этого сектора может меняться в процессе поиска.
![]()
Рис. 5.30. Траектория поиска минимума функции Химмельблау методом случайного поиска с постоянным радиусом поиска и случайными направлениями (n = 2)
Метод случайного поиска с постоянным радиусом поиска и случайными направлениями иллюстрирует рис. 5.30, на котором показан фрагмент линий уровня функции Химмельблау.
На рисунке точки, лежащие на окружности с центром в точке xr, соответствуют случайным точкам![]() .
.
Примечание. Одна итерация по методу случайного поиска с постоянным радиусом поиска и случайными направлениями может привести к уменьшению минимизируемой функции в большей степени, чем один шаг поиска в направлении антиградиента этой функции. Данное утверждение иллюстрирует рис. 5.31, на котором показаны линии уровня двумерной квадратичной функции
![]()
![]() (см. параграф
5.1.4).
(см. параграф
5.1.4).
Рис. 5.31. Один шаг поиска в направлении антиградиента минимизируемой функции (∇f(xr)) приводит на линию уровня (1.5). В то же время одна итерация по методу случайного поиска с постоянным радиусом поиска и случайными направлениями – на линию уровня ~0,2. Точки на окружности с центром в точке xr соответствуют случайным точкам. Любое направление поиска в секторе β лучше, чем направление антиградиента
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.