Многопрофильная олимпиада школьников «Будущее Арктики»

Отборочный тур

Математика. Решения задач 5 класса^[1]

Задача1. Сумма 2019 натуральных чисел равна 2020. Найдите произведение этих чисел. Не забудьте обосновать свой ответ.

Решение. Наименьшее натуральное число равно 1. Если все 2019 чисел равны 1, то их сумма равна 2019, что меньше 2020. Значит, среди данных чисел есть число A, которое больше 1. (Заметим, что мы не знаем, такое число одно или их несколько.)

Если число A не меньше чем 3 (A > 3), то сумма оставшихся 2018 натуральных чисел не превосходит 2020 − 3 = 2017. С другой стороны, сумма этих 2018 не меньше, чем 2018 · 1 = 2018. Получили противоречие. Значит, A = 2.

Если одно из чисел равно 2, то сумма оставшихся 2018 натуральных чисел равна 2018. Это означает, что все оставшиеся числа равны 1. Таким образом, искомое произведение

                                                                               2 1} = 2.

Ответ. Произведение чисел равно 2.

Критерии оценивания. Правильный ответ без пояснения — 4 балла. Обоснование ответа оценивается дополнительно от 1 до 3 баллов в зависимости от полноты. 7 баллов за задачу можно поставить даже в том случае, когда обоснование не является абсолютно полным.

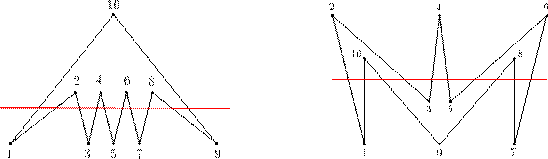
Задача2. Существует ли 10-угольник, который одной прямой можно разбить на 6 частей?

Решение. Существует. См. примеры на рис.

Задача3. Несколько мальчиков встретились на автобусной остановке, чтобы поехать в зоопарк. При встрече все они поздоровались друг с другом за руку. Сколько мальчиков поехали в зоопарк, если всего было 15 рукопожатий?

Решение. Найдем число рукопожатий для 6 мальчиков.

Способ I. Каждый из шести мальчиков протянет руку 5 раз. Значит, руки

протягивали всего 6·5 = 30 раз. Заметим, что в любом рукопожатии участвует две руки, поэтому рукопожатий в два раза меньше. Таким образом, число рукопожатий пяти мальчиков равно 30 : 2 = 15.

Способ II. Пусть сначала первый мальчик поздоровается со всеми своими друзьями. Получим 5 рукопожатий. Затем второй мальчик протянет руку всем кроме первого (так как с первым он уже поздоровался). Получим ещё 4 рукопожатия. И так далее третий поздоровается с тремя (четвертым, пятым, шестым), четвёртый — с двумя (пятым и шестым), пятый — с одним (шестым мальчиком). Шестой мальчик уже успел со всеми поздороваться. Всего получим 5 + 4 + 3 + 2 + 1 = 15 рукопожатий.

Способ III. Понять, что в случае шести мальчиков будет 15 рукопожатий, помогает наглядная схема (граф). Точки обозначают мальчиков, а отрезки, соединяющие эти точки, соответствуют рукопожатиям.

Заметим, что если мальчиков меньше 6, то рукопожатий меньше 15, а если больше 6, то больше 15. Таким образом, в зоопарк поехали 6 мальчиков.

Ответ. 6 мальчиков.

Критерии оценивания. Правильный ответ без пояснения — 4 балла. Показано, что у шести мальчиков будет 15 рукопожатий — ещё 3 балла.

Задача4. Семья ночью подошла к мосту. Папа может перейти его за 1 минуту, мама — за 2, малыш — за 5, а бабушка — за 10 минут. У них есть один фонарик. Мост выдерживает только двоих. Как им перейти мост за 17 минут? (Если переходят двое, то они идут с меньшей из их скоростей. Двигаться по мосту без фонарика нельзя. Светить издали нельзя. Носить друг друга на руках нельзя.)

Решение. Приведем два возможных решения.

Способ I.

папа с мамой — 2 мин, папа обратно с фонариком — 1 мин, малыш с бабушкой — 10 мин, мама обратно с фонариком — 2 мин, папа с мамой — 2 мин.

Всего 17 минут!

Способ II.

папа с мамой — 2 мин, мама обратно с фонариком — 2 мин, малыш с бабушкой — 10 мин, папа обратно с фонариком — 1 мин, папа с мамой — 2 мин.

Чтобы придумать решение этой задачи, важно понять, что двое самых медленных должны идти вместе.

Математика. Решения задач 6 класса

Задача1. Если бы у красного дракона было на 6 голов больше, чем у зеленого, то у них было бы 34 головы на двоих. Но у красного дракона на 6 голов меньше, чем у зеленого. Сколько голов у красного дракона?

Решение. Из первого условия находим, что число голов у зелёного дракона равно (34 − 6) : 2 = 14. Так как у красного дракона на 6 голов меньше, чем у зеленого, то у него 14 − 6 = 8 голов.

Ответ. 8 голов.

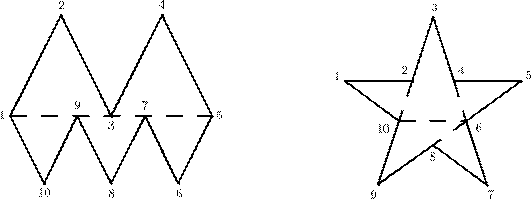
Задача2. Существует ли 10-угольник, который можно разрезать на 5 треугольников?

Решение. Существует. См. примеры на рис.

Задача3. Четыре друга участвовали в олимпиаде. Витя решил больше всех задач — восемь, а Петя меньше всех — пять задач. Каждая задача олимпиады была решена ровно тремя из друзей. Сколько задач было на олимпиаде?

Решение. По условию каждая задача олимпиады была решена ровно тремя из друзей. Значит, общее число решений делится на 3. Так как Витя решил больше всех задач — восемь, а Петя меньше всех — пять задач, то оставшиеся два друга могли решить: 1) по 6 задач каждый; 2) 6 и 7 задач; 3) по 7 задач. Только в третьем случае количество решенных задач делится на 3. Значит, друзья Вити и Пети решили по 7 задач каждый, и всего на олимпиаде было (5 + 7 + 7 + 8) : 3 = 9 задач.

Ответ. 9 задач.

Задача4. Охотник встретил двух пастухов. У одного пастуха было три куска хлеба, у второго — пять кусков. Все куски хлеба одинакового размера. Все трое разделили и съели весь хлеб поровну. Охотник дал пастухам после еды 8 монет на двоих. Как пастухи разделили эти деньги?

Решение. Так как всего было 3 + 5 = 8 кусков хлеба, и хлеб поделили поровну, то каждый съел по  куска. У первого пастуха было 3 куска хлеба, следовательно, он отдал охотнику  куска. Второй пастух отдал охотнику  куска хлеба. Таким образом, второй пастух отдал в 7 раз больше хлеба, чем первый. Следовательно, он должен получить в 7 раз больше монет. Охотник заплатил всего 8 монет, поэтому первый получил 1 монету, а второй — 7 монет.

Ответ. Первый пастух — 1 монету, второй — 7 монет.

Математика. Решения задач 7 класса

Задача1. Говядина без костей стоит 450 рублей за килограмм, говядина с костями — 390 рублей за килограмм, а кости без говядины — 75 рублей за килограмм. Сколько костей в килограмме говядины?

Решение. Пусть в килограмме говядины x кг костей, тогда говядины без костей — (1 − x) кг. Таким образом, «вклад» костей в стоимость говядины

75x рублей, а «вклад» самой говядины 450(1−x) рублей. Получим уравнение

75x + 450(1 − x) = 390.

Решив данное уравнение, найдем x = 0,16. Таким образом, в одном килограмме говядины 160 г костей.

Ответ. 160 грамм.

Задача2. Выступая на арене с 10 львами и 15 тиграми, дрессировщик Вася потерял над ними контроль, и звери начали пожирать друг друга. Лев насытится, если съест трёх тигров, а тигр — если съест двух львов. Определите, какое наибольшее число зверей могло насытиться, и как это могло произойти?

Решение. Так как на арене было 10 львов, то насытиться могли только 10 : 2 = 5 тигров. Аналогично, наесться могли не более, чем 15 : 3 = 5 львов. 5 львов и 5 тигров вместе насытиться не могут, так как в этом случае должны быть съедены все животные. Тот, кто ел последним, должен остаться на арене. Следовательно, количество насытившихся хищников не превосходит

9.

Покажем, как 9 зверей могут насытиться. Сначала 3 льва съедают 9 тигров. После этого останутся 6 тигров и 10 львов, среди которых 3 сытых. Затем 4 тигра съедают 8 львов так, что остаются 2 голодных льва. Оставшиеся 2 льва съедают 6 тигров. Таким образом, насытились 3+2 = 5 львов и 4 тигра, то есть, 9 хищников.

Замечание. Существуют и другие способы, которыми могут насытиться 9 хищников.

Ответ. 9 хищников.

Критерии оценивания. Правильный ответ без пояснений — 2 балла. Если доказано, что насытиться могут не более 9 хищников, при этом нет примера — 5 баллов. Пример, как могут насытиться 9 зверей, оценивается ещё 2 баллами.

Задача3. Вася утверждает, что он может нарисовать шестиугольник и, проведя прямую через две его вершины, отрезать от него семиугольник. Не ошибается ли Вася?

Решение. Вася прав. См. пример на рис.

Задача4. В многодетной семье у каждого ребёнка спросили: «Сколько у тебя братьев?» Каждый из детей назвал одно натуральное число, а сумма всех названных чисел оказалась равной 35. Сколько детей в семье, если все дети ответили правильно?

Решение. Пусть в семье n мальчиков и k девочек. У каждого мальчика (n−1) брат, а у каждой девочки n братьев. Имеем, что n(n−1)+k ·n = 35, откуда n(n + k − 1) = 35. Значит, число n является делителем 35.

Если n = 1, то в этом случае единственному мальчику придется сказать, что у него 0 братьев. По условию задачи все дети назвали натуральное число, а число 0 не является натуральным. Значит, n = 1̸ .

Если n = 5, то n + k − 1 = 7, откуда k = 3.

Если n = 7, то k = −1, а если n = 35, то k = −33. Таким образом, n = 7̸ и n = 35̸ .

Мы перебрали все делители числа 35. Единственный возможный случай n = 5, k = 3. Значит, в семье n + k = 5 + 3 = 8 детей.

Ответ. В семье 8 детей.

Математика. Решения задач 8 класса

Задача1. Вася вырезал из бумаги многоугольник, а Петя разрезал его на треугольник и четырехугольник. Сколько сторон могло быть в Васином многоугольнике? Найдите все возможные варианты и обоснуйте, почему нет других.

Решение. Поскольку все вершины Васиного многоугольника являются вершинами треугольника или вершинами четырёхугольника, то в нём не более 7 вершин. Примеры для многоугольников, имеющих от 3 до 7 сторон, приведены на рис.

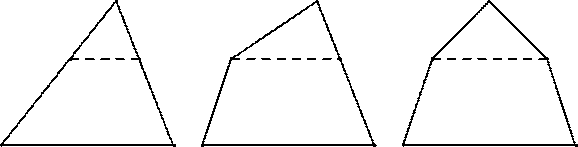
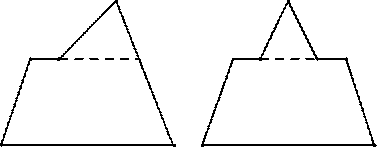
Ответ. 3, 4, 5, 6 или 7 сторон.

Критерии оценивания. Рассмотрены 3 многоугольника из 5 возможных — 3 балла; рассмотрены все 5 многоугольников — 5 баллов; доказано, что число сторон исходного многоугольника не превосходит 7 — добавляются ещё 2 балла.

Задача2. Выступая на арене с 10 львами и 15 тиграми, дрессировщик Вася потерял над ними контроль, и звери начали пожирать друг друга. Лев насытится, если съест трёх тигров, а тигр — если съест двух львов. Определите, какое наибольшее число зверей могло насытиться, и как это могло произойти?

Решение. Так как на арене было 10 львов, то насытиться могли только 10 : 2 = 5 тигров. Аналогично, наесться могли не более, чем 15 : 3 = 5 львов. 5 львов и 5 тигров вместе насытиться не могут, так как в этом случае должны быть съедены все животные. Тот, кто ел последним, должен остаться на арене. Следовательно, количество насытившихся хищников не превосходит

9.

Покажем, как 9 зверей могут насытиться. Сначала 3 льва съедают 9 тигров. После этого останутся 6 тигров и 10 львов, среди которых 3 сытых. Затем 4 тигра съедают 8 львов так, что остаются 2 голодных льва. Оставшиеся 2 льва съедают 6 тигров. Таким образом, насытились 3+2 = 5 львов и 4 тигра, то есть, 9 хищников.

Замечание. Существуют и другие способы, которыми могут насытиться 9 хищников.

Ответ. 9 хищников.

Критерии оценивания. Правильный ответ без пояснений — 3 балла. Если доказано, что насытиться могут не более 9 хищников, при этом нет примера — 5 баллов. Пример, как могут насытиться 9 зверей, оценивается ещё 2 баллами.

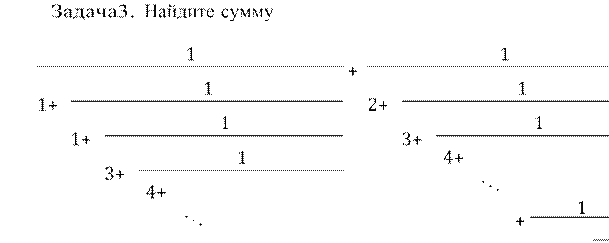1 2019 +

                                                                     +                                                               2020

2019 +

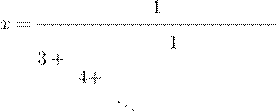
Решение. Обозначим

.

1

+

2019 +

Искомая сумма примет вид

.

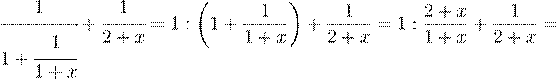
Ответ. Сумма равна 1.

Задача4. Кассир продал все билеты в первый ряд кинотеатра, причем по ошибке на одно из мест было продано два билета. Сумма номеров мест на всех этих билетах равна 857. На какое место продано два билета?

Решение. Докажем вспомогательное утверждение.

Лемма. .

Доказательство леммы. Обозначим S = 1 + 2 + 3 + ... + (n − 1) + n.

Запишем сумму этих же слагаемых, но в обратном порядке. Получим S = = n+(n−1)+(n−2)+...+3+2+1. Сложим обе записанные суммы (первое слагаемое первой суммы с первым слагаемым во второй, второе слагаемое со вторым и т.д.). Тогда

2S = (1 + n) + (2 + n − 1) + (3 + n − 2) + ... + (n − 1 + 2) + (n + 1).

Заметим, что все выражения в скобках равны (n + 1), а число таких

слагаемых равно n. Значит, 2S = n(n + 1), откуда . Лемма доказана.

Перейдем к решению задачи.

Выясним, сколько мест могло быть в первом ряду.

Если мест не менее 41, то .

Значит, количество мест в первом ряду меньше 41.

Если количество мест равно 39 (или меньше). Так как 1 + 2 + ... + 39 =

=  = 780, то даже после прибавления к этой сумме числа 39, результат будет меньше 857. Значит, число мест должно быть больше 39.

Таким образом, в первом ряду ровно 40 мест.

Теперь несложно определить, на какое место был продан лишний билет.

Так как сумма номеров всех мест на первом ряду

= 820, то номер места, на которое продано два билета, равен разности 857 − 820 = 37.

Ответ. На тридцать седьмое место было продано два билета.