Книга содержит два раздела. В первом разделе представлены задачи и решения отборочного и заключительного этапа многопрофильной олимпиады школьников "Будущее Арктики" по математике для 5-8 классов за 2016-2018 гг. Также включены задания олимпиады, проводимой ИМИКТ САФУ им. М. В. Ломоносова. Во втором разделе "Математический факультатив" представлены материалы для изучения и проработки некоторых наиболее часто используемых методов классической олимпиадной математики.

Е. В. Михайлов

Многопрофильная олимпиада школьников

«Будущее Арктики»

Математика

5 – 8 классы

Архангельск

Издательство «КИРА»

2018

УДК 373(072+51(075.3)

ББК 74.262.21+22.1я721

М 69

Авторы: Е. В. Михайлов

Рецензенты:

кандидат педагогических наук, доцент кафедры экспериментальной математики и информатизации образования Северного (Арктического) федерального университета имени М. В. Ломоносова Н. Н. Патронова;

старший преподаватель Северного (Арктического) федерального университета имени М. В. Ломоносова В. В. Тепляков

Михайлов, Евгений Владимирович.

М 69 Многопрофильная олимпиада школьников «Будущее Арктики». Математика : 5 – 8 классы / Е. В. Михайлов. – Архангельск : КИРА, 2018. – 183 с. : табл., рис.

ISBN 978-5-98450-594-9

Пособие состоит из двух разделов. Первый раздел включает в себя задачи, решения и ответы отборочного и очного туров многопрофильной олимпиады школьников «Будущее Арктики» по математике для 5 - 8 классов. Во втором разделе «Математический факультатив» представлены материалы для изучения и проработки некоторых наиболее часто используемых методов классической олимпиадной математики.

Сборник рассчитан на широкий круг читателей, интересующихся математикой.

УДК 373(072+51(075.3)

ББК 74.262.21+22.1я721

ISBN 978-5-98450-594-9

Предисловие

Предлагаемая читателю книга содержит задачи по математике многопрофильной олимпиады школьников «Будущее Арктики». Первая такая олимпиада прошла в 2016 году. Её организатором является ФГАОУ ВО «Северный (Арктический) федеральный университет им. М. В. Ломоносова». Основная цель олимпиады — развитие и стимулирование интереса у школьников к научноисследовательской деятельности и формирование целостного представления о приоритетных направлениях социально-экономического развития страны и мотивации к поступлению на приоритетные направления подготовки в университет.

Олимпиада проводится в два этапа: отборочный тур (школьный этап) и очный тур (заключительный этап). Отборочный тур проходит в форме выполнения олимпиадных заданий в очной форме в образовательных организациях. Он рассчитан на 90 минут. Это повлияло на выбор заданий и их количество. Задачи отборочного тура значительно легче, чем задачи заключительного этапа. Очный тур проводится в очной форме на базе Высшей школы информационных технологий и автоматизированных систем. Время выполнения заданий 235 минут.

В олимпиаде «Будущее Арктики» традиционно принимают участие школьники из Архангельска, Северодвинска, Новодвинска, Лешуконского, Пинежского, Онежского, Приморского, Вельского, Плесецкого и других районов Архангельской области. Отдельные площадки олимпиады работали в Коряжме и Нарьян-Маре.

В настоящее время большинство вузов страны проводят собственные олимпиады. Хорошие результаты дают участникам дополнительные баллы при поступлении. Для успешного выполнения таких заданий требуется серьезная подготовка, начинать которую можно уже с 5–8 класса.

В первый раздел книги вошли задания по математике для школьников 5–8 классов отборочных и очных туров олимпиады «Будущее Арктики» прошедшие в 2016–2018 гг. Также в книгу добавлены задания олимпиад проводимые ВШ ИТиАС (в то время Институт математики, информационных и космических технологий) в 2014 и 2015 гг.

Ко всем задачам первого раздела даны ответы и подробные решения. Если Ваш ответ не сходится с представленным в книге, не огорчайтесь и не торопитесь смотреть решение. Отложите эту задачу на некоторое время и постарайтесь решить ее позже. Решение многих задач требует длительных размышлений и оригинальных идей. Приведем здесь слова известного советского математика Н. Я. Виленкина: “Решение трудной математической проблемы можно сравнить с взятием крепости.” Если Вам все-таки не удалось найти решение и «взять эту крепость», то постарайтесь разобрать решение, которое приведено автором.

Для понимания условий и решений олимпиадных задач вполне достаточно знаний школьного курса математики. Однако для их решения требуются неожиданные и оригинальные подходы, используются методы непривычные для школьной практики. Такие приемы относятся к классической олимпиадной тематике. Во втором разделе книги «Математический факультатив» представлены материалы для изучения и проработки некоторых наиболее часто используемых методов.

В конце книги приведен список литературы, использованной автором, а также рекомендуемая литература для дальнейшего изучения.

Пособие адресовано как школьникам, которые только начинают участвовать в математических олимпиадах, так и более подготовленным учащимся. Также книга может быть полезной студентам педагогических специальностей, учителям математики, которые могут использовать материал книги в индивидуальной работе со способными учениками, а также всем любителям математики.

В заключение приведем несколько советов тем, кто «завтра» станет участником олимпиады.

Советы участнику олимпиады

• Перед олимпиадой обязательно нужно выспаться! При этом желательно встать не впритык, а за 2-3 часа до тура. Вашей голове нужно успеть «проснуться» и войти в ритм. • Есть некоторые «легальные допинги» для мозга. Тут на вкус и цвет, например, для этих целей подойдет кофе и горький шоколад. • Наблюдайте, в каком состоянии вы решаете лучше всего. Например, кому-то волнение помогает, а кому-то наоборот вредит. Учитесь менять своё состояние. Например, чтобы успокоить нервы, можно выпить воды или же выполнить дыхательные упражнения.

• Внимательно прочитайте условия задач и определите порядок, в котором будете их решать (лучше начинать с легких задач, которые, как правило, размещены в начале).

• Если условие задачи можно понять по разному, то не выбирайте удобную для себя трактовку, а обратитесь за консультацией к членам жюри.

• Если задача не решается — попробуйте ее упростить (взять меньшие числа, рассмотреть частные случаи и т.д.). • Разбейте задачу на несколько подзадач (например, необходимость и достаточность).

• Преобразуйте или переформулируйте условие задачи на более понятном языке (например, введите переменные, нарисуйте схему, граф и т.д.).

• Если неясно, верно ли некоторое утверждение, попробуйте его доказать или опровергнуть.

• Не зацикливайтесь на одной задаче. Если нет идеи решения, то задачу лучше (хотя бы на время) отложить.

• Если устали, отвлекитесь на несколько минут (посмотрите в окно или просто отдохните).

• Решив задачу, сразу оформляйте решение. Это поможет проверить его правильность и освободит внимание для других задач. • На олимпиадах как правило учитываются любые продвижения в решении. Даже если Вы не решили задачу, но у Вас есть какие-то идеи или соображения, запишите их в чистовик. Возможно, среди них есть правильные, за которые Вам поставят несколько баллов. • Каждый, даже очевидный, шаг решения нужно записывать. Громоздкие решения лучше записывать в виде нескольких утверждений (лемм).

• Перед тем, как сдать работу, перечитайте её «глазами членов жюри» — смогут ли они в ней разобраться?

РАЗДЕЛ ПЕРВЫЙ

Условия задач

2016 год. Отборочный тур

5 класс

1. Деревянный кубик с ребром 4 сантиметра окрасили в желтый цвет, а затем распилили на одинаковые кубики с ребром 1 сантиметр. Сколько получилось маленьких кубиков с одной цветной гранью?

2. Для нумерации страниц книги потребовалось всего 1392 цифры. Сколько страниц в этой книге?

3. Из числа 10...0 (25 нулей) вычли число 25. Чему равна сумма цифр полученной разности?

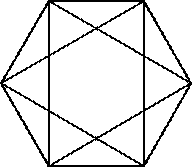
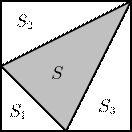
4. Сколько треугольников в фигуре, изображенной на рисунке?

5. Часы отбивают каждый час положенное число ударов и в половину каждого часа — один удар (и в два часа ночи, и в два часа дня они бьют два раза). Сколько ударов пробьют часы за сутки?

6. Полный бидон с молоком весит 20 кг, а наполненный молоком наполовину, весит 14 кг. Сколько будет весить бидон, если наполнить его молоком на треть?

6 класс

1. Опытный дрессировщик может вымыть слона за 40 минут, а его сыну для этого потребуется 2 часа. За сколько времени они вымоют трех слонов, работая вдвоем?

2. На доске в строчку написаны двадцать пятерок. Поставив между некоторыми из них знак «+», Вася обнаружил, что сумма равна 1000. Сколько плюсов поставил Вася?

3. Ужасный антивирус пожирает память компьютера. За первую секунду он управился с половиной памяти, за вторую секунду — с одной третью оставшейся части, за третью — с четвертью того, что сохранилось, за четвертую — с одной пятой остатка. И тут его настиг могучий Антивирус. Какая часть памяти уцелела?

4. В классе 27 учеников. Из них 19 посещают математический кружок, 6 — химический, а 5 учеников не посещают эти кружки. Сколько химиков увлекается математикой?

6. Имеется 5 чемоданов и к ним 5 ключей. Но ключи перемешались. Сколько испытаний в худшем случае нужно провести, чтобы подобрать для каждого из чемоданов его ключ?

7 класс

1. Сколько существует четырехзначных чисел, у которых сумма цифр равна 4, а произведение цифр равно 0?

2. В классе 27 учеников. Из них 19 посещают математический кружок, 6 — химический, а 5 учеников не посещают эти кружки. Сколько химиков увлекается математикой?

3. Имеются кубики с ребром 1 и 2 сантиметра. Нужно наполнить коробку со сторонами 8, 5 и 3 сантиметра так, чтобы не осталось пустого места и было использовано наименьшее количество кубиков. Сколько потребуется кубиков?

4. Определите, чему равен угол между часовой и минутной стрелкой в 23 часа 45 минут.

5. Имеется 5 чемоданов и к ним 5 ключей. Но ключи перемешались. Сколько испытаний в худшем случае нужно провести, чтобы подобрать для каждого из чемоданов его ключ?

6. В ряд стоят три коробки, в каждой по 111 конфет. Ксюша берет по одной конфете из каждой в таком порядке: левая, центральная, правая, центральная, левая, центральная и так далее до тех пор, пока в центральной коробке не закончатся конфеты. В одной из двух крайних коробок осталось больше конфет. Сколько и в какой коробке?

8 класс

1. Параллелепипед с ребрами 4, 6, 9 составлен из кубиков с ребром 1. Сколько маленьких кубиков надо удалить, чтобы убрать весь внешний слой толщиной в один кубик?

2. Электронные часы показывают время в стандартном формате (например, 20:27). Найдите наибольшее возможное значение произведения цифр на таких часах.

3. Сократите дробь

4. Площадь правильного треугольника равна 36. Отрезали от каждой вершины по маленькому правильному треугольнику так, чтобы остался правильный шестиугольник (шестиугольник, у которого все стороны и углы равны). Какова площадь этого шестиугольника?

5. В ряд стоят три коробки, в каждой по 111 конфет. Ксюша берет по одной конфете из каждой в таком порядке: левая, центральная, правая, центральная, левая, центральная и так далее до тех пор, пока в центральной коробке не закончатся конфеты. В одной из двух крайних коробок осталось больше конфет. Сколько и в какой коробке?

6. Сколько различных значений можно получить, расставляя скобки в выражении −1 − 1 − 1 − ... − 1 (2016 единиц)?

2016 год. Очный тур

5 класс

1. Сколько раз к наибольшему двузначному числу нужно прибавить наибольшее трехзначное число, чтобы получить наибольшее пятизначное?

2. Докажите, что из трех натуральных чисел всегда можно найти два, сумма которых делится на 2.

3. Длина крокодила от головы до хвоста в три раза меньше десяти кэн, а от хвоста до головы равна трем кэн и двум сяку. Известно, что одна сяку равна 30 см. Найдите длину крокодила в метрах. (Кэн и сяку — японские единицы длины.)

4. Можно ли число 2016 представить в виде суммы нескольких натуральных чисел так, чтобы произведение всех этих чисел тоже было равно 2016?

5. Как имея два сосуда вместимостью 5 л и 7л, налить из водопроводного крана 6л?

6. Как разрезать прямоугольник, длина которого 16 см, а ширина 9 см, на две равные части, из которых можно составить квадрат?

6 класс

1. Какое из чисел больше:

1 − 2 + 3 − 4 + 5 − ... + 99 − 100

или

1 + 2 − 3 + 4 − 5 + 6 − ... − 99 + 100?

2. Малыш и Карлсон съели бочку варенья и корзину печенья,начав и закончив одновременно. Сначала Малыш ел печенье, а Карлсон — варенье, потом (в какой-то момент) они поменялись. Карлсон и варенье, и печенье ел в три раза быстрее Малыша. Какую часть варенья съел Карлсон, если печенья они съели поровну?

3. Хулиганы Ваня и Женя порвали стенгазету, при этом Ванярвал каждый кусок на три части, а Женя — на семь частей. Устыдившись своего поступка, они решили собрать все обрывки, чтобы склеить стенгазету, при этом они собрали 2016 обрывков. Установите, все ли обрывки были найдены.

4. Можно ли число 2016 представить в виде суммы несколькихнатуральных чисел так, чтобы произведение всех этих чисел тоже было равно 2016?

5. На доске написано 10 последовательных чисел. Когда одно изних стерли, то сумма оставшихся оказалась равна 2020. Какие числа остались на доске?

6. Хозяйка испекла торт для гостей, но не знает, сколько всегобудет человек — трое или четверо. Какое наименьшее число разрезов она должна сделать, чтобы в любом случае все могли получить торта поровну?

7 класс

1. Определите количество цифр числа: 4⁵· 5¹³.

2. В классе число отсутствующих учеников составляет 1/6 часть от числа присутствующих. После того как из класса вышел один ученик, число отсутствующих стало равно 1/5 числа присутствующих. Сколько учеников учатся в этом классе?

3. В формулу линейной функции y = kx + b вместо букв k и b впишите числа от 1 до 20 (каждое по одному разу) так, чтобы получилось 10 функций, графики которых проходят через одну и ту же точку.

4. Дан прямоугольный треугольник, один из углов которого равен 30^◦. Из середины его гипотенузы восстановлен перпендикуляр к ней. Докажите, что длина отрезка этого перпендикуляра, лежащего внутри треугольника, равна трети длины большего катета.

5. Про различные числа a и b известно, что .

Найдите .

6. Десять друзей отправили друг другу поздравительные открытки. Каждый послал 5 открыток. Докажите, что найдутся два человека, которые взаимно поздравили друг друга.

8 класс

1. Сравните числа:

A = 2015 · 20162016 · 201720172017

B = 2017 · 20152015 · 201620162016.

2. Числа a, b и c отличны от нуля и выполняются равенства:

Докажите, что ab + bc + ca = 0.

3. Три пирата вечером поделили добытые за день бриллианты: по двенадцать Биллу и Сэму, а остальные — Джону, который считать не умел. Ночью Билл у Сэма, Сэм у Джона, а Джон у Билла украли по одному бриллианту. В результате средняя масса бриллиантов у Билла уменьшилась на один карат, у Сэма уменьшилась на два карата, зато у Джона увеличилась на четыре карата. Сколько бриллиантов досталось Джону? (Карат — единица измерения массы, равная 200 мг (0,2 грамма). Применяется в ювелирном деле для выражения массы драгоценных камней и жемчуга.)

4. Боковая сторона трапеции равна одному основанию и вдвое меньше другого. Докажите, что вторая боковая сторона перпендикулярна одной из диагоналей трапеции.

5. Натуральное число n делится на 18 и имеет 14 различных положительных делителей. Найдите число n.

2017 год. Отборочный тур

5 класс

1. На одной чашке весов лежат 6 апельсинов, а на другой — 2 дыни. Если добавить одну такую же дыню к апельсинам, то весы уравновесятся. Сколько апельсинов уравновесят дыню?

2. Электронный будильник показывает часы (две цифры, от 00 до 23) и минуты (две цифры). Сколько раз между 00:01 и 23:59 показания часов будут читаться одинаково слева направо и справа налево?

3. На большом клетчатом листе бумаги нарисовали “по клеточкам” квадрат 100 × 100 клеток. Сколько клеток к нему примыкает снаружи (соприкасается с ним хотя бы по одной вершине)?

4. Делимое в 6 раз больше делителя, а делитель в 6 раз больше частного. Чему равны делимое, делитель и частное?

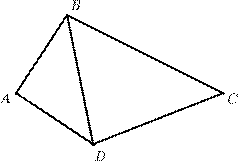
5. Диагональ делит четырехугольник с периметром 31 см на два треугольника с периметрами 21 см и 30 см. Определите длину этой диагонали.

6 класс

1. Сказочный замок имеет форму большого куба, склеенного из одинаковых маленьких кубиков. Внутри замка часть кубиков убрали, и получилась пустая комната размерами 10 × 10 × 10 кубиков. Сколько кубиков примыкает снаружи к этой комнате (соприкасается с ней хотя бы по одной вершине)?

2. 2 землекопа выкопают 2 метра канавы за 2 часа. Сколько метров канавы выкопают 3 землекопа за 3 часа?

3. См. задачу 5 для 5 класса.

4. Поезд проходит мост длиной 250 метров за 1 минуту, а мимо телеграфного столба он проходит за полминуты. Какова длина поезда?

5. Есть 6 карточек с цифрами 1, 2, 3, 4, 5, 6. Используя их можно составить два трехзначных числа, например, 645 и 321. Вася составил эти числа так, что их разность оказалась самой маленькой из всех возможных. Чему равна эта разность?

7 класс

1. Вычислите:

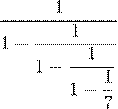2. В квадрате со стороной a середины двух смежных сторон

соединены между собой и с противоположной вершиной квадрата. Вычислите площадь полученного треугольника.

3. В нашей компании 5 человек. У нас есть некоторое количество денег, в среднем по 8 рублей на человека. У меня 10 рублей. Сколько в среднем денег у остальных четырех членов компании?

4. Начнём считать пальцы на правой руке. Первым будет большой, вторым — указательный, третьим — средний, четвёртым — безымянный, пятым — мизинец, шестым — снова безымянный, седьмым — средний, восьмым — указательный, девятым — большой, десятым — указательный, и так далее. Какой палец получит номер 2017?

5. Допуская, что стрелки часов движутся с постоянной скоростью, узнайте, через сколько минут после того, как часы показывали 3 часа, минутная стрелка догонит часовую?

8 класс

1. В нашей компании 5 человек. У нас есть некоторое количество денег, в среднем по 8 рублей на человека. У меня 10 рублей. Сколько в среднем денег у остальных четырех членов компании?

2. В равнобедренном треугольнике ABC угол B равен 30^◦, AB = = BC = 6. Проведены высота CD треугольника ABC и высота DE треугольника BDC. Найдите BE.

3. Известно, что. Чему равно ?

4. Допуская, что стрелки часов движутся с постоянной скоростью, узнайте, через сколько минут после того, как часы показывали 3 часа, минутная стрелка догонит часовую?

5. Петя, Коля и Вася решали задачи из задачника и решили вместе 100 задач, при этом каждый из них решил ровно 60 задач. Будем называть задачу, которую решили все трое, легкой, а задачу, которую решил только один из ребят — трудной. Каких задач было больше, легких или трудных, и на сколько?

2017 год. Очный тур

5 класс

1. Как разделить круглую головку сыра тремя прямолинейными разрезами на 8 равных частей?

2. Клоуны Бам, Бим и Бом вышли на арену в красной, синей и зелёной рубашках. Их туфли были тех же трёх цветов. Туфли и рубашка Бима были одного цвета. На Боме не было ничего красного. Туфли Бама были зелёные, а рубашка нет. Каких цветов били туфли и рубашка у Бома и Бима?

3. На прямой отмечено несколько точек так, что среди расстояний между ними встречаются 1 см, 2 см, 3 см, 4 см, 5 см, 6 см, 7 см и 8 см. Какое наименьшее число точек могло быть отмечено?

4. Ваня и Федя вышли навстречу друг другу с постоянной скоростью. Ваня вышел в 10:00 из деревни Ванино и пришел в деревню Федино в 15:00. Федя вышел из деревни Федино в 11:00 и пришел в Ванино в 16:00. В какое время они встретились?

5. Коля заплатил в кассу столовой за три блюда, а Саша — за два блюда (все пять блюд — одинаковой стоимости). Только они сели за стол, как к ним присоединился Юра, и они втроем съели поровну все пять блюд. При расчете приятелей между собой выяснилось, что Юра должен заплатить за съеденное им 5 рублей. Сколько из этих денег должен взять Коля и сколько Саша?

6. Отличник Поликарп заполнил клетки таблицы цифрами так, что сумма цифр, стоящих в любых трех соседних клетках, равнялась 15, а двоечник Колька стёр почти все цифры. Сможете ли вы восстановить таблицу?

6 класс

1. Клоуны Бам, Бим и Бом вышли на арену в красной, синей и зелёной рубашках. Их туфли были тех же трёх цветов. Туфли и рубашка Бима были одного цвета. На Боме не было ничего красного. Туфли Бама были зелёные, а рубашка нет. Каких цветов били туфли и рубашка у Бома и Бима?

2. Найдите наибольшее число, у которого каждая цифра, начиная с третьей, равна сумме двух предыдущих цифр.

3. В прямоугольнике провели два отрезка, которые разбили его на четыре прямоугольника. Три из них имеют периметры 11, 13 и 15 см. Каким может быть периметр четвертого прямоугольника?

4. Имея полный бак топлива, катер может проплыть 75 км против течения реки или 150 км по течению. На какое наибольшее расстояние против течения реки он может отплыть при условии, что топлива должно хватить и на об-ратный путь?

5. Сколько трёхзначных чисел имеют ровно две различные цифры?

6. Найдите такое натуральное число x, что

НОД(x, 9) + НОК(x, 9) = 2017.

7 класс

1. Вычислите:

2. Можно ли в квадрат со стороной 1 поместить несколько неперекрывающихся квадратов с суммой периметров 100?

3. Чему равно n, если 1 · 2 · 3 · ... · n = 2¹⁵· 3⁶· 5³· 7²· 11 · 13?

4. Непослушный ребёнок находится от отца на расстоянии 26 своих шагов. В то время как он сделал 4 шага, отец успевает 3, но отец проходит за 2 своих шага столько же, сколько ребёнок за 3.

Через сколько шагов отец догонит ребёнка?

5. Найдите такое натуральное число x, что

НОД(x, 9) + НОК(x, 9) = 2017.

6. Брат и сестра измерили шагами длину и ширину огорода прямоугольной формы. Когда брат шел по длинной стороне, а сестра по короткой стороне прямоугольника, они сделали вместе 270 шагов. Потом брат шел по короткой стороне, а сестра по длинной стороне огорода, и тогда они сделали вместе 290 шагов. Длина шага брата равна 0,8 м, а сестры 0,6 м. Найдите площадь огорода.

8 класс

1. Сравните числа a и b , если 5 · (a − 1) = a²+ b.

2. Сколько решений в натуральных числах имеет уравнение x2y3 = 612?

3. Трапеция, длины сторон которой равны 1, 1, 1 и 2, разбита на четыре одинаковые трапеции. В результате верхняя сторона разделена на четыре отрезка. Найдите отношение длины большего из них к меньшему.

4. Брат и сестра измерили шагами длину и ширину огорода прямоугольной формы. Когда брат шел по длинной стороне, а сестра по короткой стороне прямоугольника, они сделали вместе 270 шагов. Потом брат шел по короткой стороне, а сестра по длинной стороне огорода, и тогда они сделали вместе 290 шагов. Длина шага брата равна 0,8 м, а сестры 0,6 м. Найдите площадь огорода.

5. В вершинах шестиугольника ABCDEF записаны соответственно числа 2, 7, 9, 10, 3, 12. За один шаг к двум соседним вершинам можно прибавить или вычесть одно и то же число. Можно ли за несколько шагов из указанной последовательности чисел получить следующую: 5, 11, 6, 15, 8, 14, сохраняя соответствия чисел вершинам?

6. На плоскости взяли 2017 различных точек. Докажите, что через одну из них можно провести прямую так, что в каждой из двух полуплоскостей будет ровно по 1008 точек.

2018 год. Отборочный тур

5 класс

1. Часы бьют три, и, пока они бьют, проходит 3 секунды. Сколько времени пройдет, пока часы будут бить семь?

2. В очереди в школьный буфет стоят Юра, Миша, Вова, Олег и Саша. Юра стоит впереди Миши, но после Олега. Вова и Олег не стоят рядом, а Саша не находится рядом ни с Олегом, ни с Юрой, ни с Вовой. В каком порядке стоят ребята?

3. Решите ребус:

УРАН

+ УРАН

НАУКА

4. Прямоугольник на рисунке составлен из 7 квадратов. Сторона черного квадрата равна 1 см, а сторона серого квадрата равна 3 см.

Чему равна площадь всего прямоугольника?

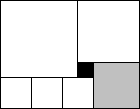
5. В 120-ти квартирном доме два 60-ти квартирных подъезда. Все жильцы купили новые таблички с номерами квартир, при этом таблички для двузначных номеров стоили вдвое, а для трехзначных — втрое дороже однозначных. Жильцы второго подъезда израсходовали на таблички 846 рублей. Сколько израсходовали жильцы первого подъезда?

6 класс

1. На батоне колбасы нарисованы тонкие поперечные кольца. Если разрезать по красным, получится 5 кусков, если по желтым — 7 кусков, если по зеленым — 11 кусков. Сколько кусков колбасы получится, если разрезать по кольцам всех трех цветов?

2. В лесу растёт дерево. В первый день его росток показался над землёй и к концу недели поднялся на 10 сантиметров. За вторую неделю оно стало в полтора раза выше, за третью в 1 раза, за четвертую — в 1 раза, за пятую — в 1 раза, за шестую — в 1

раза ...И так далее. Какой высоты достигнет дерево за 99 недель, если скорость роста будет сокращаться по той же логике?

3. В 120-ти квартирном доме два 60-ти квартирных подъезда.

Все жильцы купили новые таблички с номерами квартир, при этом таблички для двузначных номеров стоили вдвое, а для трехзначных — втрое дороже однозначных. Жильцы второго подъезда израсходовали на таблички 846 рублей. Сколько израсходовали жильцы первого подъезда?

4. Прямоугольник на рисунке разрезан на квадраты. Длина выделенной ломанной равна 63 сантиметра. Чему равна площадь прямоугольника?

5. Мартышка, Осёл и Козёл затеяли сыграть трио. Уселись чинно в ряд, Мартышка справа. Ударили в смычки, дерут, а толку нет. Поменялись местами, при этом Осёл оказался в центре. А трио всё нейдёт на лад. Пересели ещё раз. При этом оказалось, что каждый из трёх «музыкантов» успел посидеть и слева, и справа, и в центре. Кто где сидел на третий раз?

7 класс

1. У дороги из Ёлкино в Палкино растёт дуб, от которого до Ёлкино вдвое ближе, чем до Палкино. Федя, едущий с постоянной (и большей 0) скоростью из Ёлкино в Палкино, в 12.00 был вдвое ближе к дубу, чем к Ёлкино. В 12.40 снова оказалось, что Федя вдвое ближе к дубу, чем к Ёлкино. Когда Федя приедет в Палкино?

2. Лесоруб одним ударом топора разбивает любой чурбак или полено на три части. Он хочет разбить чурбак на 33 части. Сколько ударов ему понадобится?

3. Решите уравнение:

(100 − (99 − (98 − (97 − ... − (2 − (1 + x)))))...) = x.

4. В таблицу 3 × 3 записаны числа. Сумма трех чисел в каждой строке, в каждом столбце и на каждой диагонали равна 111. Найдите число в центральной клетке таблицы.

5. Петя сбегает с четвертого этажа на первый на 2 секунды быстрее, чем мама едет на лифте. Мама едет на лифте с четвертого этажа на первый на 2 секунды быстрее, чем Петя сбегает с пятого этажа на первый. За сколько секунд Петя сбегает с четвертого этажа на первый? (Длины пролетов лестницы между всеми этажами одинаковы).

8 класс

1. На каждой перемене Робин-Бобин съедал по шоколадке. Уроки были каждый день недели, кроме воскресенья, всего 29 уроков. Сколько шоколадок на переменах съел Робин-Бобин за неделю?

2. Пять положительных чисел a, b, c, d и e таковы, что ab = 2, bc = 3, cd = 4, de = 5 . Чему равно

3. В треугольнике ABC медиана BE перпендикулярна биссектрисе AD.Найдите длину AB, если AC = 12.

4. План города имеет схему, изображенную на рисунке. На

всех улицах введено одностороннее движение: можно ехать только «вверх» или «вправо». Сколько есть способов добраться из «левого нижнего» угла в «правый верхний»?

5. Коля и Вася за осень получили по 60 оценок, причем Коля получил пятерок столько же, сколько Вася четверок, четверок столько же, сколько Вася троек, троек столько же, сколько Вася двоек, и двоек столько же, сколько Вася пятерок. При этом средний балл у них одинаковый. Сколько двоек за осень получил Коля?

2018 год. Очный тур

5 класс

1. Дата 21.02.2012 читается одинаково слева направо и справа налево. А будут ли ещё после неё такие даты в нашем столетии?

2. Собираясь в школу, Миша нашёл под подушкой, под диваном, на столе и под столом всё необходимое: тетрадь, шпаргалку, плеер и кроссовки. Под столом он нашёл не тетрадь и не плеер. Мишины шпаргалки никогда не валяются на полу. Плеера не оказалось ни на столе, ни под диваном. Что где лежало, если в каждом из мест находился только один предмет?

3. Будильник спешит на 9 минут в сутки. Ложась спать в 22:00, на нём установили точное время. На какое время надо завести звонок, чтобы будильник зазвенел ровно в 6:00?

4. 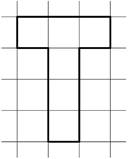У буквы Т на рисунке ширина 3 клетки, высота — 4 клетки, а толщина палочек — одна клетка. Сколько клеточек в букве Т, у которой ширина 13 клеток, высота — 20 клеток, а толщина палочек — 3 клетки?

5. Чтобы построить поросячий домик, Ниф-Нифу не хватало 400 кирпичей, Нуф-Нуфу не хватало 300 кирпичей, а Наф-Нафу не хватало всего 200 кирпичей. Когда они сложили все свои кирпичи вместе, оказалось, что они как раз могут построить один домик на троих. Сколько кирпичей нужно для одного поросячьего домика?

6. Есть 30 гирек , которые весят 1 г, 2 г, 3 г, ..., 30 г. Можно ли разложить их на три кучки одинакового веса по 10 гирь в каждой?

6 класс

1. Если из спичек сложить клетчатый квадрат 2 × 2, то потребуется 12 спичек (см. рисунок). Сколько спичек потребуется, чтобы сложить клетчатый квадрат 12 × 12?

2. Каждому из двух муравьев, Толстому и Тонкому, нужно перенести по 150 г груза из точки A (где они сейчас находятся) в точку B, расстояние между которыми равно 15 метров. Толстый муравей ходит со скоростью 3 м/мин, но может унести 5 г груза. Тонкий — со скоростью 5 м/мин, но может унести лишь 3 г груза. Кто из них быстрее доставит весь свой груз в точку B? Скорость муравья с грузом не отличается от скорости муравья без груза.

3. Площадь прямоугольника — 1 кв. дм. Может ли его периметр быть больше 1 км?

4. Девять голодных школьниц за час набирают корзину клубники и наедаются досыта. Сытые школьницы клубнику не едят, поэтому набирают корзину за час вшестером. Сколько голодных школьниц можно накормить досыта корзиной клубники?

5. После возвращения цирка с гастролей знакомые расспрашивали дрессировщика Казимира Алмазова о «пассажирах» его автофургона: «Тигры были?». — «Да, причём их было в семь раз больше, чем не тигров». «А обезьяны?» — «Да, их было в семь раз меньше, чем не обезьян». «А львы были?» Ответьте за Казимира Алмазова.

6. Шестизначное число делится на 8. Какую наибольшую сумму цифр оно может иметь?

7 класс

1. Числа от 1 до 10 разбили на две группы так, что произведение чисел в первой группе нацело делится на произведение чисел во второй. Какое наименьшее значение может быть у частного от деления первого произведения на второе?

2. Некто обычно поднимался по движущемуся вверх эскалатору, шагая со скоростью одна ступенька в секунду. Сделав 20 шагов, он оказывался наверху. Однажды он торопился, шагал через ступеньку (две ступеньки в секунду) и оказался наверху, пройдя 32 ступеньки. Сколько ступенек в эскалаторе?

3. По кругу стоит 101 коробка. В каждой коробке лежат чёрные и белые шарики, а на коробке написано, сколько в ней чёрных шариков и сколько белых. Петя хочет переложить из каждой коробки по одному шарику в следующую по часовой стрелке коробку так, чтобы обе надписи на каждой из коробок стали неверными. Сможет ли он это сделать?

4. 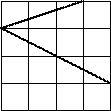На стандартном тетрадном листе в клетку нарисован угол (см. рисунок). Найдите его величину, не используя измерительные инструменты. Ответ обоснуйте.

5. Найти все тройки простых чисел a, b, c таких, что

7a − bc = 105.

6. Для каждого числа от 1 до 99 выписали сумму его цифр.

Чему равна сумма всех выписанных чисел?

8 класс

1. На круговом маршруте работают два автобуса, которые курсируют с одинаковой скоростью и интервалом движения в 21 минуту. Каким будет интервал движения, если на этом маршруте будут работать 3 автобуса с той же одинаковой скоростью?

2. В треугольнике ABC медиана BM в два раза меньше стороны AB и образует с ней угол 40^◦. Найдите угол ABC.

3. Все натуральные числа, сумма цифр в записи которых делится на 5, выписывают в порядке возрастания: 5, 14, 19, 23, 28, 32, .... Чему равна самая маленькая положительная разность между соседними числами в этом ряду? Приведите пример и объясните, почему меньше быть не может.

4. Решите уравнение

x²+ x = 1111111122222222.

5. Для каждого числа от 1 до 999 выписали сумму его цифр. Чему равна сумма всех выписанных чисел?

6. У Васи есть 9 палочек по 5 см и 9 палочек по 6 см. Он хочет, разломав несколько палочек, сложить из всех получившихся кусков равносторонний 11-угольник. Каким наименьшим количеством разломов он может обойтись?

2014 год. Олимпиада ИМИКТ

7 класс^{^[1]}

1. От потолка комнаты вертикально вниз по стене поползли две мухи. Спустившись до пола, они поползли обратно. Первая муха ползла в оба конца с одной и той же скоростью, а вторая, хотя и поднималась вдвое медленней первой, но зато спускалась вдвое быстрее. Какая из мух раньше приползет обратно?

2. Выписаны подряд все натуральные числа:

1234567891011121314151617181920...

Какая цифра стоит на 2014-м месте?

3. Путешественник, сняв в гостинице комнату на неделю, предложил хозяину в уплату цепочку из семи серебряных колец — по кольцу за день, с тем, однако, условием, что будет рассчитываться ежедневно. Хозяин согласился, оговорив со своей стороны, что можно распилить только одно кольцо. Как путешественнику удалось расплатиться с хозяином гостиницы?

4. Из квадратного листа бумаги в клетку, содержащего целое число клеток, вырезали квадрат, содержащий целое число клеток так, что осталось 124 клетки. Сколько клеток мог содержать первоначальный лист бумаги?

5. На скамейке сидят десять школьников, мальчики и девочки. Может ли быть так, что между каждыми двумя мальчиками сидит четное число школьников, а между каждыми двумя девочками — нечетное?

6. Имеется 19 гирек с массами 1, 2, 3, ..., 19 г. Девять из них — железные, девять — бронзовые и одна — золотая. Известно, что общий вес всех железных гирек на 90 г больше, чем общий вес бронзовых. Найдите вес золотой гирьки.

7. Точки E и F — середины сторон BC и CD квадрата ABCD. Отрезки AE и BF пересекаются в точке K. Что больше: площадь треугольника AKF или площадь четырехугольника KECF?

8. Клетки квадратной таблицы 15 × 15 раскрашены в красный, синий и зеленый цвета. Докажите, что найдутся, по крайней мере, две строки, в которых клеток хотя бы одного цвета поровну.

8–9 класс^{^[2]}

1. Средний возраст школьников одного класса равен их количеству. Пятнадцатилетний школьник этого класса уехал на олимпиаду по математике в другой город. После чего средний возраст оставшихся школьников снова равнялся их количеству. Сколько школьников первоначально было в классе?

2. Радиус описанной около треугольника окружности равен 2, а длины всех высот являются целыми числами. Найдите стороны треугольника.

3. Имеется 19 гирек с массами 1, 2, 3, ..., 19 г. Девять из них — железные, девять — бронзовые и одна — золотая. Известно, что общий вес всех железных гирек на 90 г больше, чем общий вес бронзовых. Найдите вес золотой гирьки.

4. Можно ли представить число

1²+ 2²+ 3²+ ... + 2014²

в виде суммы квадратов 2013 различных натуральных чисел?

6. Найдите геометрическое место точек пересечения медиан всех треугольников вписанных в данную окружность.

7. Таблица n×n заполнена числами. Оказалось, что сумма чисел в любом “кресте” (объединении некоторой вертикали и некоторой горизонтали) равна нулю. Верно ли, что все числа равны нулю?

8. Можно ли на гранях куба расставить числа 1, 2, 3, 4, 5, 6 так, чтобы каждое число являлось делителем суммы своих соседей?

9. Сумма трех неотрицательных чисел x₁, x₂, x₃не превосходит

. Докажите, что .

10. При каком наибольшем n числа от 1 до n можно расположить на окружности так, чтобы сумма любых двух соседних, делилась на третье число по ходу часовой стрелки.

2015 год. Олимпиада ИМИКТ

6 класс^{^[3]}

1. Прямоугольник разделён двумя вертикальными и двумя горизонтальными отрезками на девять прямоугольных частей. Площади

некоторых из получившихся частей указаны на рисунке. Найдите площадь верхней правой части.

2. Электронные часы показывают время от 00.00.00 до 23.59.59. Сколько времени в течение суток на табло часов горят ровно три цифры 7?

3. Сумма пяти натуральных чисел равна 200. Докажите, что их произведение не может оканчиваться на 2015.

4. В выражении1 : 2 : 3 : 4 : 5 : 6 : 7 : 8 : 9 расставить скобки так, чтобы результат был: а) минимален; б) максимален.

5. По дороге идут два туриста. Один из них делает шаги на 10% короче и в то же время на 10% чаще, чем другой. Кто из туристов идет быстрее и почему?

6. Можно ли испечь такой торт, который может быть разделён одним прямолинейным разрезом на 4 части?

7. В стране Непедагогии дети врут только родителям, а родители — только детям (но уж врут всегда). В семье, кроме мамы и папы, трое детей. Боря сказал Даше, показав на Галю: «Но я же старше неё!», а потом Инне, показав на Ваню: «Но я же старше него!» Как зовут папу и маму?

8. Семь грибников собрали вместе 100 грибов, причем никакие двое не собрали по одинаковому числу грибов. Доказать, что есть трое грибников, собравших вместе не менее 50 грибов.

9. Может ли сумма цифр полного квадрата равняться 555?

7 класс

некоторых из получившихся частей указаны на рисунке. Найдите площадь верхней правой части.

2. Электронные часы показывают время от 00.00.00 до 23.59.59. Сколько времени в течение суток на табло часов горит число, которое одинаково читается слева направо и справа налево?

3. В три магазина привезли 1990 книг. В первые три дня первый магазин продал соответственно полученных им книг; второй магазин — полученных им книг; третий —

и . Выясните, сколько книг получили первый, второй и третий магазины.

4. В клетчатом квадрате закрасили меньший квадрат. Незакрашеных клеток осталось 79. Могут ли все углы большого квадрата оказаться незакрашенными?

5. В стране Непедагогии дети врут только родителям, а родители — только детям (но уж врут всегда). В семье, кроме мамы и папы, трое детей. Боря сказал Даше, показав на Галю: «Но я же старше неё!», а потом Инне, показав на Ваню: «Но я же старше него!» Как зовут папу и маму?

6. Может ли сумма цифр полного квадрата равняться 555?

7. Доказать, что не существует таких целых чисел n и m, что

(m²+ m + 1)²− (n²− n + 1)²= 2015.

8–9 класс^{^[4]}

1. Плоскость раскрашена в 4 цвета (т.е. разбита на четыре непустых множества). Доказать, что существует прямая, содержащая точки не менее чем трёх цветов.

2. Доказать, что не существует двух трапеций (отличных от параллелограммов) таких, что боковые стороны каждой из них равны соответственно основаниям другой.

3. Может ли сумма цифр полного квадрата равняться 555?

4. Может ли король, совершая ходы по шахматным правилам,обойти всю доску, сделав при этом не более 13 поворотов? (Король ходит на любую соседнюю клетку. Соседние клетки — это клетки, у которых есть хотя бы одна общая точка.)

5. Найти все натуральные числа x, y, z, удовлетворяющие уравнению

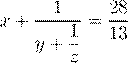6. Мышка грызет куб с ребром равным 3, разбитый на 27 единичных кубиков. Когда мышка съедает кубик она переходит к другому, имеющему общую грань с предыдущим. Может ли мышка съесть весь куб, кроме центрального кубика?

7. Семь грибников собрали вместе 100 грибов, причем никакие двое не собрали по одинаковому числу грибов. Доказать, что есть трое грибников, собравших вместе не менее 50 грибов.

8. Доказать, что если ab+cd делится нацело на a+c, то ad+bc делится на a + c. (a, b, c, d натуральные числа)

9. Пловец плывет вверх против течения Невы. Возле Республиканского моста он потерял флягу. Проплыв еще 20 минут против течения, он заметил свою потерю и вернулся догонять флягу; догнал ее возле моста Лейтенанта Шмидта. Определить скорость течения Невы, если расстояние между мостами 2 км.

10. Докажите, что если многочлен с целыми коэффициентами в нуле и единице принимает значения равные 1, то у него нет целых корней.

РЕШЕНИЯ

Первое условие, которое надлежит выполнять в математике, — это быть точным, второе — быть ясным и, насколько можно, простым.

Л. Карно

2016 год. Отборочный тур

5 класс

1. Рассмотрим любую из граней большого кубика. Каждая такая грань состоит из 16 граней маленьких кубиков с ребром 1 см. Только 4 кубика из 16 имеют ровно одну окрашенную грань в желтый цвет. У куба 6 граней,следовательно, число маленьких кубиков с одной цветной гранью равно 6 · 4 = 24.

2. Для нумерации страниц с 1 по 9 понадобится 9 цифр, для страниц 10–99 требуется 90 · 2 = 180 цифр, тогда на страницы с трехзначными числами было использовано 1392 − 9 − 180 = 1203 цифры. Следовательно, таких страниц 1203 : 3 = 401. 401 страница и еще 99 страниц c однозначными и двухзначными номерами дают ответ 500 страниц.

3. Преобразуем данную разность

= 9|9{..z.9} 74 + 1 = 9|9{..z.9} 75.

23девятки 23девятки Сумма цифр полученной разности равна 23 · 9 + 7 + 5 = 219.

4. На рисунках ниже изображены 12 «простых» треугольников, 12 «двойных» (состоящих из двух треугольников), 6 «тройных» треугольников и два «больших», всего — 32 треугольника.

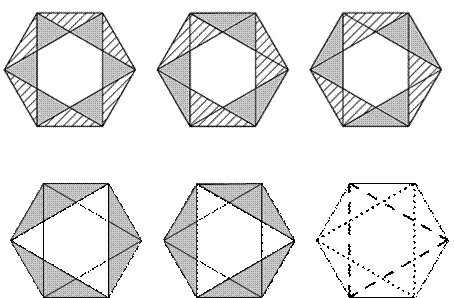
5. За первые 12 часов часы пробьют 1+2+...+12 = 78 — раз в целое число часов и еще 12 раз за каждые полчаса. Итого за сутки часы сделают (78 + 12) · 2 = 180 ударов.

6. Вес молока, заполняющего половину бидона, равен 20−14 = = 6 кг. Поэтому вес молока, заполняющего бидон полностью, равен 6 · 2 = 12 кг, а вес бидона равен 20 − 12 = 8 кг. Значит, вес бидона, заполненного на треть, равен 8 + 12 : 3 = 8 + 4 = 12 кг.

6 класс

1. Дрессировщик за 1 минуту может вымыть сын . Значит, за одну минуту вместе они вымоют =

= слона. Таким образом, чтобы помыть одного слона им потребуется 30 минут, а на помывку трех — 90 минут.

2. Предположим, что трехзначного числа 555 нет. Тогда максимальная сумма не превосходит 10·55 = 550, противоречит условию. Значит, одно из чисел 555 (два числа 555 в сумме дадут больше 1000). Таким образом, из оставшихся 17-и пятерок образованы числа, сумма которых равна 445. Следовательно, требуется найти такие числа n и m, что 5n + 55m = 445, а n + 2m = 17. Из первого уравнения находим, что n+11m = 89. Далее можно свести к уравнению или найти подбором по m (m может принимать значение не больше чем 8). Единственно возможные значения m = 8, n = 1. Таким образом, 20 пятерок разбиты на числа: 555, 5 и восемь раз по 55; всего 9 знаков «+».

3. За первую секунду уничтожено и осталось после первой секунды памяти. За вторую секунду уничтожено . После второй секунды остается памяти. Далее, за третью секунду уничтожено , а после третьей секунды осталось

. Наконец, за четвертую секунду уничтожено , после четвертой секунды останется .

Таким образом, осталась часть памяти.

4. Так как в классе 27 учеников, а 6 из них данные кружки не посещают, то количество учеников, увлеченных математикой и химией равно 21. Только 19 из 21 ученика занимаются математикой. Значит, 3 ученика занимаются химией, но не математикой. Всего кружок по химии посещают 6 человек, таким образом, трое посещают и химический, и математический кружки.

5. См. решение задачи 5 для 5 класса.

6. Возьмем любой из 5-ти чемоданов. Если первые четыре ключа не подойдут, то пятый ключ подойдет обязательно. Значит, для подбора ключа к первому чемодану достаточно сделать 4 попытки. Останется четыре чемодана. Чтобы подобрать ключ к одному из них (фиксированному) потребуется 3 попытки и т. д. Ключ к последнему чемодану подходит автоматически. Итого потребуется 4+3+2+1 = = 10 попыток, чтобы подобрать все ключи к чемоданам.

7 класс

1. Так как сумма цифр равна 4, а произведение равно 0, то одна из цифр равна 0. Сумма оставшихся трех цифр равна 4. Если самая большая цифра равна 4, то остальные три — нули, и получается всего одно число: 4000. Если наибольшая цифра — 3, то среди остальных — одна единица и два нуля. Таких чисел 6: 3100, 3010, 3001, 1300, 1030, 1003. Если же наибольшая цифра — 2, то остальные цифры — это либо еще одна двойка и два нуля, либо две единицы и один ноль. Получим еще 12 чисел: 2200, 2020, 2002, 2110, 2101, 2011, 1210, 1120, 1201, 1102, 1021, 1012. Всего получается 1 + 6 + 12 = 19 чисел.

2. См. решение задачи 4 для 6 класса.

3. В данную коробку поместятся только 8 кубиков с ребром 2. Остальное пространство заполним кубиками с ребром 1. Число таких кубиков равно объему незаполненной части коробки:

8 · 5 · 3 − 8 · 2³= 120 − 64 = 56.

Таким образом, потребуется 8 больших и 56 маленьких кубиков, всего 8 + 56 = 64 кубика.

4. Угол между минутной стрелкой и отметкой «12» на циферблате равен 90^◦. Так как в 23:45 до 00:00 осталось четверть часа, то угол между часовой стрелкой и отметкой «12» равен угла

◦

между «11» и «12», т. е. равен. Тогда искомый угол равен 90^◦− 7,5^◦= 82,5^◦.

5. См. решение задачи 6 для 6 класса.

6. Пусть Ксюша последовательно вынимает первую, вторую, третью и т. д. конфеты. Заметим, что все конфеты с четными номерами она берет из средней коробки, а с нечетными номерами — из левой и правой коробок. Таким образом, она остановится, взяв 222-ю конфету. Т. е. Ксюша вытащила 111 конфет из средней коробки и 111 из левой и правой вместе.

Так как Ксюша брала конфеты, начиная с левой коробки, то из нее достали не меньше конфет, чем из правой. Значит, из левой коробки взято 56 конфет, а из правой 55. Таким образом, в правой коробке осталось больше конфет, чем в левой, и их количество равно 111 − 55 = 56.

8 класс

1. Параллелепипед состоит из 4 · 6 · 9 = 216 кубиков. Длина ширина и высота параллелепипеда внутри (если убрать внешний слой) на 2 кубика меньше. Поэтому внутренний параллелепипед содержит 2 · 4 · 7 = 56 кубиков. Таким образом, необходимо убрать 216 − 56 = 160 кубиков.

2. Наибольшее произведение первых двух цифр равно 1 · 9 = 9, когда часы показывают 19 часов. Наибольшее произведение двух последних цифр равно 5 · 9 = 45, когда часы показывают 59 минут. Таким образом, наибольшее произведение всех четырех цифр равно 1 · 9 · 5 · 9 = 405.

3. Заметим, что x < 0 и y < 0. Преобразуем числитель дроби

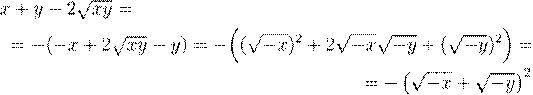Тогда

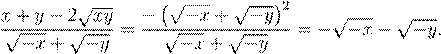
4. Так как △AA₁A₂равносторонний, то A₁A₂= AA₂.

Шестиугольник A₁A₂B₁B₂C₁C₂правильный, поэтому

A1A2 = A2B1 = B1B2.

△BB₁B₂равносторонний, следовательно, B₁B₂= BB₁.

Из указанных равенств следует, что AA₂= A₂B₁= B₁B.

Таким образом, точки A₂и B₁делят сторону AB на три равные части.

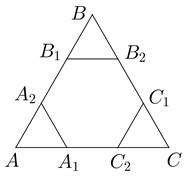
Имеем, что △AA₁A₂подобен △ABC с коэффициентом подобия

. Отношение площадей, двух подобных треугольников, равно квадрату коэффициента подобия. Значит, S_AA₁_A₂= k²· S_ABC=

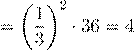(кв. ед.)

Так как треугольники AA₁A₂, BB₁B₂и CC₁C₂равны, то площадь шестиугольника равна

SA₁A₂B₁B₂C₁C₂= SABC−SAA₁A₂−SBB₁B₂−SCC₁C₂= 36−4−4−4 = 24.

5. См. решение задачи 6 для 7 класса.

6. Рассмотрим какую-то (правильную) расстановку скобок. Не вычисляя значения внутри скобок, раскроем их. Получим выражение, состоящее из 2016 единиц, перед которыми стоят знаки «плюс» или «минус». Другими словами, с помощью расстановки скобок мы можем некоторые минусы, заменить на плюсы.

Самое маленькое число, которое можно получить, это −2016 (если скобки не ставить вообще). Это число четное. При замене одного любого минуса на плюс сумма увеличивается на 2. Значит, все числа, которые мы можем получить, будут четными.

Все знаки минус заменить на плюс, расставляя скобки, не возможно. Поэтому самое большое число, которое можно получить, равно −(1 − 1 − 1 − ... − 1) = 2014.

Осталось показать, что можно получить все четные числа от −2016 до 2014. Действительно, перемещая левую скобку в выражении −(1 − 1 − 1 − ... − 1) вправо, значение уменьшается на 2:

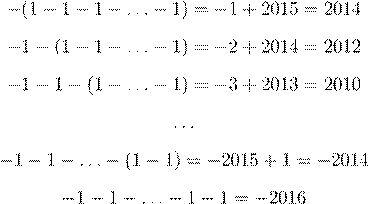
Таким образом, можно получить 1008 отрицательных чисел, нуль и 1007 положительных чисел, т. е. всего 2016 различных значений.

Замечание. В условии задачи предполагается, что расстановки скобок вида

−1(−1 − 1 − ... − 1) или (−1 − 1)(−1 − 1 − ... − 1)

не возможны. Мы не можем считать, что отсутствие знака арифметической операции означает умножение.

2016 год. Очный тур

5 класс

1. Наибольшее двухзначное число — 99,наибольшее трехзначное число — 999, а наибольшее пятизначное число — 99999. Поэтому к числу 99 необходимо прибавить (99999 − 99) : 999 = 99900 : 999 = = 100 чисел.

2. Среди любых трех чисел обязательно найдутся либо два четных, либо два нечетных числа. Их сумма делится на два.

3. По условию, утроенная длина крокодила равна 9 кэн и 6 сяку или 10 кэн. Следовательно, 1 кэн = 6 сяку = 180 см. Длина крокодила равна 3 кэн 2 сяку, то есть 600 см.

4. .

1006 чисел 1006 чисел

Заметим, что существуют и другие способы решения данной задачи.

5. Запишем решение задачи в виде таблицы.

Ход	1	2	3	4	5	6	7	8	9	10
5 л.	0	5	0	2	2	5	0	4	4	5
7 л.	7	2	2	0	7	4	4	0	7	6

6. Решение представлено на рисунке.

6 класс

1. Первый способ. Первое число равно

(1 − 2) + (3 − 4) + (5 − 6) + ... + (99 − 100) = −50,

так как разность чисел в каждой скобке равна (–1), а всего таких скобок 50. Аналогично, второе число равно

(1 + 2) + (−3 + 4) + ... + (−99 + 100) = 3 + 49 = 52.

Поэтому второе число больше первого.

Второй способ. Объединяя слагаемые попарно так же, как выше, получим, что первое число отрицательно (сумма отрицательных чисел). Сумма двух данных чисел равна

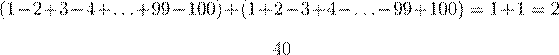, остальные слагаемые взаимно уничтожаются. Так как сумма двух чисел положительна, а первое число — отрицательно, то второе число положительно и, поэтому, больше первого.

2. Так как Малыш и Карлсон съели печенья поровну, а Карлсон ест в три раза быстрее, то Малышу на поедание печенья нужно было в три раза больше времени, чем Карлсону. Поскольку они начали и закончили одновременно, то Карлсон ел варенье столько же времени, сколько Малыш ел печенье (и наоборот). Значит, Карлсон ел варенье в три раза дольше, чем его ел Малыш, и в три раза быстрее, поэтому он съел варенья в 9 раз больше, чем Малыш. Таким образом, Карлсон съел всего варенья.

3. Вначале стенгазета была одним «куском». Каждый раз, когда кусок рвет Ваня, добавляется 2 куска. Когда кусок рвет Женя, добавляется 6 кусков. Т. е. общее число кусков должно всегда быть нечетным, но 2016 — четное, значит, не все обрывки были найдены. 4. См. решение задачи 4 для 5 класса.

5. Пусть x — наименьшее из написанных чисел. Обозначим через x + y вычеркнутое число (0 6 y 6 9). Тогда

x+(x+1)+(x+2)+(x+3)+(x+4)+(x+5)+(x+6)+(x+7)+

+ (x + 8) + (x + 9) − (x + y) = 2020,

то есть 9x = 1975+y. Число 1975+y делится на 9 только при y = 5. Значит, x = 1980 : 9 = 220, а y = 5. Значит, на доске остались числа 220, 221, 222, 223, 224, 226, 227, 228 и 229.

6. Для того, чтобы разрезать торт на четыре равные части мож-но провести два взаимно перпендикулярных разреза через центр.

Чтобы получить треть торта , к куску A (образу-

ет сектор с углом 90^◦) нужно добавить кусок с углом 30^◦. Поэтому проведем третий разрез. При таком разрезании куски A+B, D +E и C + F равны.

Двух разрезов недостаточно: с одной стороны, все получающи-

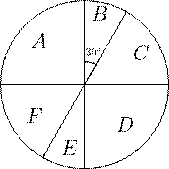
еся при этом части должны быть равными по четверти торта, с другой стороны, некоторые из них — по трети торта.

7 класс

1. Выполним необходимые преобразования. Имеем 4⁵5¹³= (2²)⁵5¹³= 2¹⁰5¹⁰5³= 125 10¹⁰= 12500...0. {нулейz }

Таким образом, данное число состоит из 13 цифр.

2. Пусть в классе первоначально отсутствовали x учеников. Тогда присутствовали 6x школьников. Общее число учеников в классе — 7x. После того как из класса вышел один ученик, число отсутствующих стало равно x+1, а число присутствующих — 6x−1. Так как после выхода ученика число отсутствующих стало равно 1/5 числа присутствующих, составим уравнение

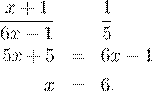
Значит, в классе учатся 7x = 7 · 6 = 42 ученика.

3. Первый способ. Графики функции y = 1x + 20, y = 2x + 19, y = 3x + 18, ..., y = 9x + 12, y = 10x + 11 проходят через одну точку (1, 21), причем все натуральные числа от 1 до 20 выписаны по одному разу.

Второй способ. Графики функции y = 1x + 2, y = 3x + 4, y = 5x + 6, ..., y = 17x + 18, y = 19x + 20 проходят через одну точку (−1, 1), причем все натуральные числа от 1 до 20 выписаны по одному разу.

4. Рассмотрим треугольник ABC с ∠A = 30^◦. Точка E середина гипотенузы AB, EF ⊥ AB.

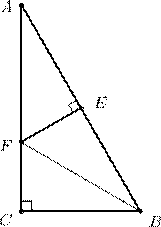
Пусть длина отрезка EF = x. Так как △AEF — прямоугольный, ∠A = 30^◦, то AF = 2x (катет, лежащий напротив угла 30^◦равен половине гипотенузы).

В треугольнике ABC угол C — прямой, а ∠A = 30^◦, значит

Так как BC = EB, а FB — общая сторона △FBC и △FBE, то эти треугольники равны по катету и гипотенузе.

Так как △FBC = △FBE получим, что FC = FE = x. Значит, AC = AF +FC = 2x+x = 3x = 3EF. Что и требовалось доказать.

5. Из данного равенства имеем . Выполним преобразования

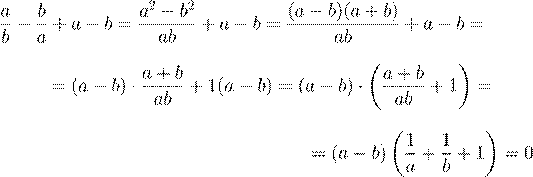Так как разность a − b = 0̸ (числа a и b различные), а произведение

то .

6. Первый способ. Всего было послано 50 открыток. Число 10 · 9

«неориентированных» пар школьников равно = 45, поэтому

на какую-то пару приходится не менее двух открыток.

Второй способ. Всего было отправлено 50 открыток. Значит, существует участник, который получил не менее пяти открыток (если бы каждый получил не более четырёх, то всего было бы отправлено не более 40 открыток). Таким образом, он послал открытки пятерым участникам и получил открытки не менее чем от пяти участников. Поскольку, кроме него, имеется лишь 9 участников, то хотя бы один другой участник входит в обе пятерки.

8 класс

1. Преобразуем оба числа:

A = 2015 · 2016 · 10001 · 2017 · 100010001;

B = 2017 · 2015 · 10001 · 2016 · 100010001.

Таким образом, видим, что числа равны.

2. Имеем: .

Аналогично получим, что ab = a − c и bc = b − a. Сложим три полученных равенства

ab + bc + ac = a − c + b − a + c − b = 0.

3. Количество бриллиантов у каждого пирата за ночь не изме-нилось. Так как у Билла — 12 бриллиантов, а их средняя масса уменьшилась на 1 карат, то сумма их масс уменьшилась на 12 каратов. Аналогично, сумма масс бриллиантов Сэма уменьшилась на 24 карата. Поскольку масса бриллиантов Билла и Сэма уменьшилась на 36 каратов, то у Джона она на те же 36 каратов увеличилась. Так как средняя масса его бриллиантов увеличилась на 4 карата, то у него было 36 : 4 = 9 бриллиантов.

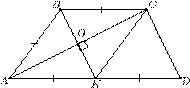
Рис. 8.1

Способ I. Пусть K — середина большего основания AD трапеции

ABCD, в которой (рис. 8.1). Тогда ABCK — ромб, поэтому BK ⊥ AC. Так как BC = KD и BC ∥ KD, то BCDK — параллелограмм. Тогда BK ∥ CD. Имеем, что BK ⊥ AC и BK ∥ CD, следовательно, CD ⊥ AC.

Способ II. Так как AK = KD и четырехугольник ABCK — ромб, то AK = KD = KC (рис. 8.1). Это означает, что в треугольнике ACD медиана CK равна половине стороны AD. Отсюда следует, что ∠ACD = 90^◦.

Способ III. Продолжим стороны AB и до пересечения в точке

M (рис. 8.2). Имеем, что , тогда из подобия треугольников BMC и AMD следует, что: 1) AB = BM; 2)

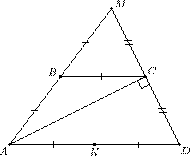
Рис. 8.2

MC = CD. Из первого равенства имеем AM = 2AB = AD, т.е. △AMD равнобедренный, а из второго равенства следует, что AC — медиана треугольника AMD. Так как в равнобедренном треугольнике медиана, проведенная к основанию, является высотой, то AC ⊥ CD.

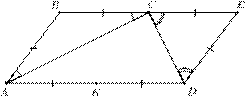
Рис. 8.3

Способ IV. Продлим сторону BC так, что BE = 2BC (рис. 8.3).

Тогда — параллелограмм.

△ABC — равнобедренный, значит, ∠ACB = ¹⁸⁰₂− ∠^B= 90^◦−

Аналогично, △C — равнобедренный, следовательно,

Имеем, что

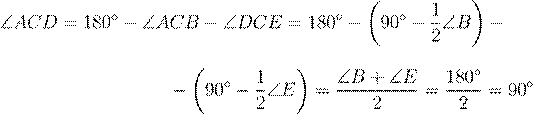(∠B + ∠E = 180^◦, т.к. ABED — параллелограмм.)

5. Если число n = p^k, где p — простое, то оно имеет (k + 1) делитель. Это числа 1, p, p², ..., p^k.

Если n = p^kq^m, где p и q простые числа, то оно имеет

(k + 1) · (m + 1) делителей, которые получаются произведением делителя числа p^kна делитель числа q^m.

По условию задачи число n делится на 18 = 2¹· 3²и имеет 14 делителей. Рассмотрим несколько случаев.

I. Если n = 2^k·3^m. Тогда k > 1, m > 2, причем (k +1)(m+1) = = 2 · 7. Значит, k = 1, m = 6. Получим, что n = 2¹· 3⁶= 1458.

II. Если n = 2^k·3^m·x, где k > 1, m > 2, а множитель x больше 1, не делится ни на 2, ни на 3. Пусть число x имеет l делителей (l > 2 т.к. N делится на 1 и на само себя). Тогда количество делителей числа n равно (k + 1)(m + 1) · l. В этом случае равенство

(k + 1)(m + 1) · l = 2 · 7

не возможно.

Таким образом, единственное значение n = 1458.

6. См. решение задачи 6 для 7 класса.

2017 год. Отборочный тур

5 класс

1. Из условия задачи следует, что две дыни уравновешиваются одной дыней и шестью апельсинами. Значит, одна дыня весит столько же, сколько 6 апельсинов.

2. Выпишем показания часов, которые читаются одинаково слева направо и справа налево: 01:10, 02:20, 03:30, 04:40, 05:50, 10:01, 11:11, 12:21, 13:31, 14:41, 15:51, 20:02, 21:12, 22:22, 23:32. Всего получили 15 различных показаний.

3. Способ I. Квадрат 100×100 состоит из 10000 клеток. Окружив этот квадрат по периметру полоской толщиной в одну клетку, получим новый большой квадрат размером 102×102. В этом новом квадрате 102 · 102 = 10404 клетки. Таким образом, к исходному квадрату примыкает 10404 − 10000 = 404 клетки.

Способ II. К каждой из четырех сторон квадрата примыкает по 100 клеток. Еще по одной клетке соприкасается с каждой вершиной квадрата. Итого получим 4 · 100 + 4 = 404 клетки.

4. Так как делимое в шесть раз больше делителя, то частное равно 6. Известно, что делитель в шесть раз больше частного. Поэтому, делитель равен 6 · 6 = 36. И, наконец, так как делимое в шесть раз больше делителя, то делимое равно 6 · 36 = 216.

5. Общий периметр двух треугольников равен 31см + 20см = = 51см, и он равен периметру четырехугольника плюс удвоенная длина диагонали (т.к. диагональ входит в два треугольника). Таким образом, диагональ равна (51см − 31см) : 2 = 10см.

6 класс

1. Пустая комната содержала 10 · 10 · 10 = 1000 кубиков. Представим, что эту комнату со всех сторон окружает слой кубиков толщиной в один кубик. Тогда комната находится внутри большого куба размером 12×12×12. Этот большой куб состоит из 12 · 12 · 12 = 1728 маленьких кубиков. Поэтому, снаружи комнаты в замке примыкает 1728 − 1000 = 728 кубиков.

2. Так как землекопа выкопают метра канавы за 2 часа, то 1 землекоп выкопает за 2 = часа 1 метр канавы. Отсюда получаем, что один землекоп за 1 час выкопает в 2 раза меньше, метра канавы. Таким образом, 3 землекопа за 3 часа выкопают

метра.

3. См. решение задачи 5 для 5 класса.

4. Способ I. За одну минуту голова поезда проходит всю длину моста и ещё всю длину поезда. Поскольку мимо телеграфного столба поезд проходит за полминуты, то за полминуты он проходит всю длину поезда, а на прохождение длины моста у него остается еще полминуты. Получается, что длина поезда равна длине моста и равна 250 метров.

Способ II. Пусть x метров — длина поезда. Тогда за 1 минуту поезд проходит (x + 250) метров. Известно, что за полминуты он проходит мимо телеграфного столба. Поэтому, за 1 минуту — 2x метров. Составим уравнение: 2x = x + 250, откуда x = 250.

5. Первые цифры у полученных чисел должны отличаться на единицу. Далее, двузначное число, образованное второй и третьей цифрой, у уменьшаемого должно быть как можно меньше, то есть 12. А у вычитаемого — как можно больше, то есть 65. Остаются цифры 4 и 3 для первых цифр. Таким образом, минимальная разность будет у чисел 412 и 365, при этом она равна 412−365 = 47.

7 класс

1. Будем производить вычисления с конца. Тогда

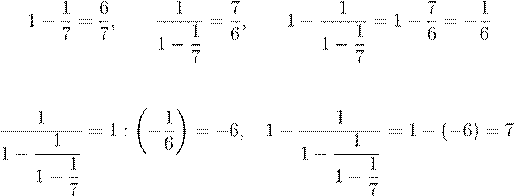Окончательно получим, что

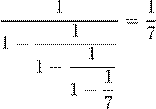2. Вычислим площадь трех треугольников, которые дополняют построенный треугольник до квадрата. Получим, что

Таким образом, площадь выделенного треугольника

3. Общее количество денег в компании равно 5·8 = 40 рублей. У рассказчика 10 рублей, следовательно, у четырех оставшихся ребят вместе 40 − 10 = 30 рублей. Вычислим сколько денег в среднем у каждого из оставшихся членов компании. Получим 30 : 4 = 7,5 рублей.

4. Большой палец получил номер 1. Пройдя 8 пальцев (указательный, средний, безымянный, мизинец, безымянный, средний, указательный, большой) счет снова попадет на большой палец. Таким образом, большой палец получит номера 1, 9, 17, 25, .... Так как 1 + 252 · 8 = 2017, то номер 2017 получит большой палец.

5. Способ I. Пусть минутная стрелка догнала часовую через t минут.

◦

Минутная стрелка за одну минуту поворачивается на, а за t минут — на 6t градусов.

Часовая стрелка сделает полный оборот за 12 ч = 12 · 60 мин = 720 мин, значит, за t минут повернулась на градусов.

Так как в три часа угол между стрелками равнялся 90^◦, то получим уравнение

откуда

Таким образом, минутная стрелка догонит часовую через 16 минуты.

Способ II. Данную задачу можно решить без уравнения. За одну минуту минутная стрелка поворачивается на 6^◦. Часовая стрелка «убегает» вперед со скоростью в 12 раз меньшей. Получим, что

стрелки часов за одну минуту сближаются на .

Так как в три часа угол между стрелками равнялся 90^◦, то стрелки совместятся через 90 : = 16 минуты.

8 класс

1. См. решение задачи 3 для 7 класса.

2. В прямоугольном треугольнике BCD катет CD лежит напро-

тив угла 30^◦, следовательно,.

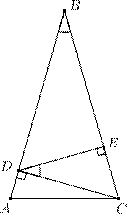
∠CDE = ∠B = 30^◦так как это углы со взаимно перпендикулярными сторонами. Значит, в прямоугольном треугольнике CDE катет.

Таким образом, BE = BC − EC = 6 − 1,5 = 4,5.

3. Возведем равенство в квадрат. Получим, что

откуда

4. См. решение задачи 5 для 7 класса.

5. Пусть среди решенных задач было x трудных, y средней сложности (те задачи, которые решили ровно двое из трех ребят) и z легких задач.

Так как каждый из ребят решил по 60 задач, то x + 2y + 3z = = 180. Всего Петя, Коля и Вася решили решили 100 задач, значит, x + y + z = 100.

Домножим второе из полученных уравнений на два и вычтем из него первое равенство. Получим, что

2(x + y + x) − (x + 2y + 3z) = 2 · 100 − 180,

откуда x−z = 20. Таким образом, трудных задач было на 20 больше, чем легких.

2017 год. Очный тур

5 класс

1. Можно провести два перпендикулярных вертикальных разреза через центр головки сыра и один горизонтальный разрез посередине.

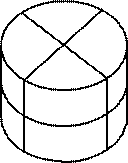
При таком разрезании куски сыра не перекладываются.

Если же перед каждым разрезом можно переставлять куски сыра наиболее удобным образом, то тремя разрезами сыр можно разрезать по-другому. Для этого один из двух кусков, получившихся после первого вертикального разреза, нужно поставить на другой, провести еще один разрез, взять одну из «двухэтажных» половин, поставить на другую и провести третий разрез. После третьего разреза головка сыра окажется разделенной на 8 одинаковых порций.

2. Составим таблицу:

	Бам	Бим	Бом
рубашка	не зеленая	одинаковый	не красная
туфли	зеленые	одинаковый	не красные

Из последней строчки таблицы видим, что у Бама зеленые туфли, поэтому двум другим клоунам остаются синие и красные. На Боме нет ничего красного, значит, у него синие туфли, а красные у Бима. Тогда рубашка у Бима тоже красная.

	Бам	Бим	Бом
рубашка	не зеленая	красная	не красная
туфли	зеленые	красные	синие

Из первой строчки второй таблицы видим, что рубашка Бама не зеленая и не красная. Значит, Бам вышел в синей рубашке, а Бом в зеленой.

	Бам	Бим	Бом
рубашка	синяя	красная	зеленая
туфли	зеленые	красные	синие

Таким образом, у Бома: рубашка — зеленая, туфли — синие, а у Бима: рубашка и туфли красные.

3. Если расположить пять точек A, B, C, D и E (например, слева направо) так, что AB = BC = 1 см и CD = DE = 3 см, то отрезки AB, AC, CD, BD, AD, CE, BE и AE имеют требуемые длины. Легко проверить, что меньшим число точек быть не может (можно построить всего 6 отрезков с концами в четырех отмеченных точках).

4. Заметим, что Ваня и Федя были в пути по 5 часов. Значит, скорости ребят одинаковы, и за час каждый из них проходил одну пятую расстояния между деревнями. Ваня за первый час прошел одну пятую всего пути. Поэтому, когда вышел Федя, до встречи им вместе осталось пройти четыре пятых пути. Это расстояние навстречу друг другу они пройдут за 2 часа. Таким образом, ребята встретились в 13:00.

5. Юра заплатил за свою долю обеда 5 руб. Следовательно, полная стоимость всего обеда равна 5 · 3 = 15 руб. Так как было куплено 5 одинаковых блюд, то стоимость одного блюда равна 15 : 5 = 3 руб. Коля заплатил в кассу 3 · 3 = 9 руб, а Саша — 3 · 2 = 6 руб. Следовательно, Юра должен отдать: Коле 9 − 5 = 4 руб, Саше 6 − 5 = 1 рубль.

6. Так как сумма первого, второго и третьего числа равна сумме второго, третьего и четвертого, то первое число и четвертое совпадают. Аналогично можно показать, что равны между собой все числа, стоящие на местах 1, 4, 7, 10, 13. Таблица примет вид:

Также можно показать, что равны между собой все числа, стоящие на местах 3, 6, 9, 12, 15. Так как на 6 месте стоит число 4, то заполним таблицу дальше:

Числа, стоящие на местах 2, 5, 8, 11, 14 тоже равны между собой и должны быть равны 5, чтобы соблюдалось условие о сумме 15.

Окончательное решение приведено в таблице

6 класс

1. См. решение задачи 2 для 5 класса.

2. Число будет тем больше, чем больше в нём цифр. А всего цифр будет тем больше, чем меньше первые две цифры. Проверим. Если первые цифры 1 и 0, то получаем 10112358. Если первые цифры будут 1 и 1, то получим 112358, если 2 и 0, то получим 202246. Итак, искомое число 10112358.

Замечание. Для полного решения проверка случаев, когда первые цифры равны 11 или 20 обязательна.

3. Заметим, что суммарные периметры противоположных прямоугольников равны. Тогда периметр четвертого прямоугольника может равняться:

• 11 + 13 − 15 = 9 см;

• 11 + 15 − 13 = 13 см;

• 13 + 15 − 11 = 17 см.

4. На 1 км против течения расходуется бака, а на 1 км по течению — бака. Таким образом, чтобы проплыть 1 км туда и

обратно будет израсходовано бака топлива. Поэтому, имея полный бак топлива, катер может проплыть 50 км туда и обратно.

5. Будем рассматривать числа в зависимости от количеством нулей.

Существует всего 9 трёхзначных чисел, в записи которых ровно 2 нуля: 100, 200, 300, ..., 900. Все такие числа удовлетворяют условию.

Если в записи числа один ноль, то оставшиеся две цифры должны быть одинаковыми, причем одна из них должна стоять на первом месте. Таких возможностей всего 9 (по числу ненулевых

цифр), каждая из них дает два числа вида a0a и aa0. Значит, получим еще 18 чисел, удовлетворяющих условию задачи.

Наконец, если в записи числа нулей нет, то каждая пара ненулевых цифр a и b дает по 6 вариантов: .

Остается заметить, что таких пар можно составить . Итак, этот случай дает 36 · 6 = 216 чисел.

Всего можно составить 9 + 18 + 216 = 243 числа.

6. Поскольку НОД(x, 9) является делителем 9, то возможно 3 случая: I) НОД(x, 9) = 1, II) НОД(x, 9) = 3 и III) НОД(x, 9) = 9.

Рассмотрим эти случаи по отдельности.

I) Если НОД(x, 9) = 1, то НОК(x, 9) = 2016. Так как числа x и 9 взаимно простые, то x = 2016 : 9 = 224. Заметим, что НОД(224, 9) = 1.

II) Если НОД(x, 9) = 3, то НОК(x, 9) = 2013. Противоречие. Число 2013 не делится на 9, поэтому не может быть общим кратным чисел x и 9.

III) Если НОД(x, 9) = 9, то НОК(x, 9) = 2008. Снова противоречие. Число 2008 не делится на 9.

Таким образом, единственное возможное значение x = 224.

7 класс

1. Обозначим:. Тогда

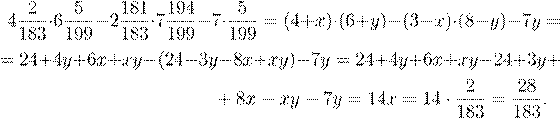
2. Разобьем квадрат 1 × 1 на 100 × 100 квадратиков со стороной . Строго внутрь каждого такого квадратика поместим еще меньший квадратик со стороной в два раза меньше. Тогда получим, что внутри квадрата со стороной 1 расположено 100 · 100 непересекающихся маленьких квадратиков со стороной .

Сумма их периметров будет равна .

3. Ясно, что n меньше, чем 17 (ведь простой множитель у 17 отсутствует). В то же время n должно быть не меньше, чем 15, поскольку множитель 5 входит в произведение в третьей степени (значит, должны быть множители 5, 10 и 15).

Итак, n равно 15 или 16. Эти случаи могут отличаться только суммарной степенью двойки. Проверяем, что условию задачи удовлетворяет n = 16.

4. Пусть x (см) длина шага ребенка, а y (см) длина шага отца. Обозначим n — число шагов отца, за которое он догонит ребенка. Так как за то время как ребенок сделает 4 шага, отец успевает 3, то ребенок пробежит шагов до встречи с отцом. Получим

соотношение:.

Известно, что отец проходит за 2 своих шага столько же, сколько ребёнок за 3, поэтому . Тогда получим:

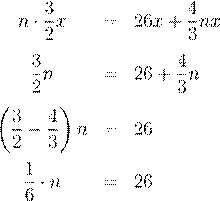
n = 156.

Таким образом, отец сделает 156 шагов, прежде чем догонит ребенка.

5. См. решение задачи 6 для 6 класса.

6. Пусть брат делает a и b шагов, а а сестра x и y шагов по длинной стороне прямоугольника и короткой, соответственно.

Получим следующие соотношения

a + y = 270,

b + x = 290,

0,8a = 0,6x,

0,8b = 0,6y.

Из двух последних уравнений находим, что .

Подставим в первые два уравнения.Получим систему:

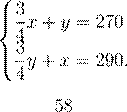Из первого уравнения полученной системы выразим переменную y и подставим во второе уравнение.

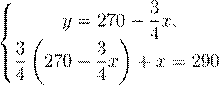Решим последнее уравнение.

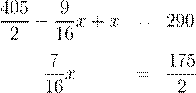
x = 200.

Таким образом, получим

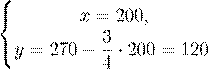Длина участка — 0,6x = 0,6 · 200 = 120 (м), а ширина — 0,6y = = 0,6 · 120 = 72 (м).

Площадь участка — 120 · 72 = 8640 (м²).

8 класс

1. Так как 5 · (a − 1) = a²+ b, то a − b = a²− 4a + 5 = a²− 4a + 4 + 1 = (a − 2)²+ 1 > 0.

Таким образом, a > b

2. Так как x²y³= 2¹²· 3¹², то y = 2^a· 3^b, где a и b целые неотрицательные числа. Тогда x²· 2^3a· 3^3b= 2¹²· 3¹², откуда x²= = 2^12−3a·3^12−3b. Таким образом, произведение 2^12−3a·3^12−3bявляется точным квадратом. Это возможно, если числа a и b принимают значения 0, 2 или 4. Следовательно, уравнение имеет 3 · 3 = 9 решений в натуральных числах. Выпишем эти решения: (2⁶· 3⁶, 1), (2³· 3⁶, 2²), (3⁶, 2⁴), (2⁶· 3³, 3²), (2³· 3³, 2²· 3²), (3³, 2⁴· 3²), (2³, 3⁴), (2³, 2²· 3⁴), (1, 2⁴· 3⁴).

Верхняя сторона состоит из одного большого и трёх маленьких отрезков. Если длину маленького отрезка обозначить через x, то длина большого отрезка будет равна 1 − 3x. Поскольку нижняя сторона состоит из трёх больших отрезков и одного маленького, то 3(1 − 3x) + x = 2, откуда . Значит, длина большого отрезка равна , а отношение большего отрезка к меньшему равно

4. См. решение задачи 6 для 7 класса.

5. Пусть вершины A, C, E — нечетные, а вершины B, D и F — четные. Найдем суммы S₁и S₂чисел в нечетных вершинах и четных вершинах, соответственно.

В начале: S₁= 2 + 9 + 3 = 14, S₂= 7 + 10 + 12 = 29.

Если за несколько шагов из данной последовательности чисел получим следующую: 5, 11, 6, 15, 8, 14, то в результате: S₁= 5+6+ 8 = 19, S₂= 11 + 15 + 14 = 40.

Заметим, что в указанном процессе прибавления (вычитания) одного и того же числа к двум соседним вершинам разность S₂−S₁на каждом шаге остается постоянной (инвариант).

Для исходной последовательности S₂− S₁= 29 − 14 = 15, а для конечной S₂− S₁= 40 − 19 = 21. Таким образом, с помощью указанных операций из первой последовательности нельзя получить вторую.

6. Рассмотрим все прямые, соединяющие пары данных точек. Существует такая прямая l, которая не параллельна ни одной из этих прямых, причем все 2017 точек находятся в одной из полуплоскостей относительно этой прямой. Будем передвигать эту прямую параллельно первоначальному положению в сторону данных точек. Пряма l каждый раз проходит не более чем через одну из них. Когда она будет проходить через 1009-ю точку, то в каждой из двух полуплоскостей будет ровно по 1008 точек.

2018 год. Отборочный тур

5 класс

1. Пока часы бьют три проходит два промежутка между ударами, а когда семь, то 6 таких же промежутков. Следовательно, чтобы пробить 7, потребуется в 3 раза большее время, т.е. 3·3 = 9 секунд.

2. Имеются три условия, чтобы определить порядок детей в очереди:

1. Юра стоит впереди Миши, но после Олега;

2. Вова и Олег не стоят рядом;

3. Саша не стоит рядом ни с Олегом, ни с Юрой, ни с Вовой.

Из первого условия получим, что Олег стоит раньше Юры, а Юра — впереди Миши. Изобразим это на схеме:

Буфет ←− О Ю М

(Мальчики обозначены первой буквой своего имени, а прочерки соответствуют местам, которые могут занять оставшиеся ребята.)

Из третьего условия делаем вывод, что Саша может стоять только рядом с Мишей. Значит, Саша — последний в очереди:

Буфет ←− О Ю МС

Из второго условия заключаем, что Вова стоит между Юрой и Мишей. Получаем ответ:

Буфет ←− ОЮВМС

Замечание. Если указан только ответ, то решение не может считаться полным. Необходимо показать, что указанный порядок мальчиков в очереди удовлетворяет всем условиям (это сделать легко), и никакой другой порядок школьников не удовлетворяет тем же ограничениям (это уже сложнее).

3. Сумма двух четырехзначных чисел равна пятизначному. Это

УРА1 + возможно если буква Н обозначает 1: УРА1 .

1АУКА

УР21

Значит, буква А обозначает цифру 2: УР21 .

12УК2

Далее определяем, что буква У обозначает цифру 6, а буква K —

6Р21

4: .

Таким образом, буква Р обозначает цифру 3. Окончательно

6321

получаем, что .

4. Из условия задачи получаем, что сторона каждого из трех квадратов снизу равна 3см − 1см = 2см, а стороны двух верхних квадратов равны 5 см и 4 см. Таким образом, длина прямоугольника — 9 см, а его ширина — 7 см. Осталось вычислить площадь S = 9см · 7см = 63см².

5. Пусть x рублей стоил однозначный номер, тогда двузначные и трехзначные номера стоят 2x и 3x рублей соответственно. Во втором подъезде 99−60 = 39 квартир с двузначными номерами (61, 62, ..., 99) и 120−99 = 21 квартира с трехзначным номером. Известно, что жители второго подъезда заплатили 846 рублей. Значит,

39 · 2x + 21 · 3x = 846,

откуда x = 6.

В первом подъезде 9 однозначных номеров и 60 − 9 = 51 трехзначный номер. Следовательно, жители первого подъезда израсходовали на таблички

9x + 51 · 2x = 111x = 111 · 6 = 666 рублей.

6 класс

1. Чтобы разрезать батон колбасы на 5 кусков, необходимо сделать 4 разреза. Значит, красных колец 4. Аналогично желтых колец 6, а зеленых — 10. Следовательно, всего на колбасе нарисовано 4 + 6 + 10 = 20 колец. Разрезав по ним, получим 20 + 1 = 21 кусок.

2. Чтобы получить высоту дерева по прошествии 99-й недели, нужно умножить 10 см на 1 — и так далее вплоть до 1.

Это можно записать так:

Заметим, что числитель каждого дробного множителя сокращается со знаменателем следующей дроби. Получается, что вместо того, чтобы перемножать все числа, выражение можно упростить до: 10·

= 500. Таким образом, высота дерева после 99-й недели станет равна 500 см.

3. См. решение задачи 5 для 5 класса.

4. Пусть x см сторона самого маленького квадратика. Тогда

второй по величине квадратик имеет сторону 2x см, а самый большой квадрат — 3x см. Найдем длину выделенной ломанной.

Получим, что

x + x + 2x + 2x + 2x + 2x + 2x + 3x + 3x + x + x + x = 63,

откуда 21x = 63, x = 3.

Стороны прямоугольника равны x+2x+2x+2x = 7x = 7·3 = = 21 (см), и x + x + 3x = 5x = 5 · 3 = 15 (см). Таким образом, площадь прямоугольника равна 21см · 15см = 315см².

5. Мартышка не сидела в центре ни в первый, ни во второй раз, значит, сидела там в конце. Осёл не сидел справа ни в первый, ни во второй раз, значит, сидел там в конце. Козлу остаётся место слева.

7 класс

1. По условию задачи расстояние от дуба до Ёлкино в два раза меньше, чем расстояние от дуба до Палкино. Таким образом, если ЕД = x, то ДП = 2x (см. рис). В 12:00 Федя находился вдвое ближе

к дубу, чем к Елкино (точка Ф₁). Значит, ЕФ, а Ф.

В 12:40 Федя снова находился вдвое ближе к дубу, чем к Елкино (точка Ф₂). Это означает, что точка Д является серединой отрезка ЕФ₂. Следовательно, ЕД = ДФ₂= Ф₂П = x.

Имеем, что Федя за 40 минут проехал расстояние Ф, откуда найдем, что на расстояние x он тратит минут. Так как после 12:40 ему осталось проехать отрезок Ф₂П = x, то Федя приедет в Палкино в 13:10.

2. При каждом ударе число частей увеличивается на 2. Лесоруб хочет увеличить число частей на 33−1 = 32. Для это надо ударить 32 : 2 = 16 раз.

3. Перед числом 99 стоит один знак минус, перед числом 98 — 2, перед 97 — 3 и т.д. Т. е. перед нечетным числом стоит нечетное число минусов, а перед четным — четное (очевидно, что происходит чередование). Перед неизвестной переменной x стоит столько же минусов, сколько и перед числом 1, т.е. нечетное число знаков «−».

Таким образом, раскрыв скобки, получим

100 − 99 + 98 − 97 + 96 − 95 + ... + 2 − 1 − x = x

(100 − 99) + (98 − 97) + (96 − 95) + ... + (2 − 1) − x = x

50 − x = x

2x = 50 x = 25.

4. Сначала сложим суммы трех столбцов (или трех строк). Получим, что сумма всех записанных в таблицу чисел равна 333. Сложим теперь строку, столбец и две диагонали, проходящие через центр. Сумма равна 444. В эту сумму центральное число входит четыре раза, а остальные — ровно по одному разу. Центральное число, сложенное само с собой три раза, дает избыток в 444−333 = = 111. Значит, число в центральной клетке равно 111 : 3 = 37.

5. Между первым и четвертым этажами 3 пролета, а между пятым и первым — 4. Согласно условию, Петя 4 пролета пробегает на 2 секунды дольше, чем мама едет на лифте, а три пролета — на 2 секунды быстрее мамы. Значит, за 4 секунды Петя пробегает один пролет. Тогда с четвертого этажа на первый (т.е. на 3 пролета) Петя сбегает за 4 · 3 = 12 секунд.

8 класс

1. Между 29 уроками 28 промежутков. Промежуток — это перемена или ночь. Между 6 учебными днями было 5 ночей. Значит, перемен (и съеденных на них шоколадок) было 28 − 5 = 23.

2. Пусть A = bcde = bc · de = 3 · 5 = 15, а B = ab · cd = 2 · 4 = 8.

Тогда

3. Так как BE медиана

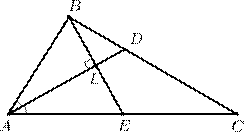
биссектриса AL является высотой, следовательно, △ABE — равнобедренный, AB = AE = 6.

4. Найдем число способов доехать до каждого перекрестка. Для этого воспользуемся следующим наблюдением: число различных маршрутов в точку C равно числу маршрутов в точку A плюс число маршрутов в точку B (рис. 8.1). Действительно, чтобы из левого нижнего угла попасть в точку C необходимо сначала доехать до точек A или B, а затем проехать еще один квартал (т.е. отрезок AC или BC). Используя это правило, последовательно заполним схему

(рис. 8.2).

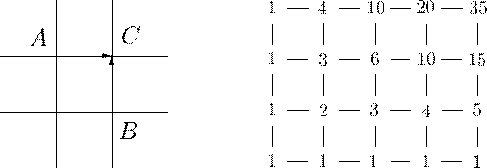
Рис. 8.1 Рис. 8.2

Число на каждом перекрестке показывает количество способов до него доехать из левого нижнего угла. Таким образом, в правый верхний угол ведут 35 различных маршрутов.

5. Введем переменные, показывающие количество различных отметок у мальчиков. Для удобства обозначения занесем в таблицу.

	5	4	3	2
Коля	x	y	z	t
Вася	t	x	y	z

Так как количество отметок и средний балл у мальчиков одинаковый, то

5x + 4y + 3z + 2t = 5t + 4x + 3y + 2z.

Из этого равенства следует, что

3t = x + y + z,

или

4t = x + y + z + t.

Известно, что оба мальчика получили по 60 отметок, значит, x+y+ z+t = 60. Таким образом, 4t = 60, t = 15, и Коля получил 15 двоек.

2018 год. Очный тур

5 класс

1. Такие даты, конечно, будут. Можно даже их все перечислить:

~~01.02.2010~~ (предшествует 2012 году), 02.02.2020, 03.02.2030,

04.02.2040, ..., 09.02.2090, ~~10.02.2001~~, ~~11.02.2011~~, 12.02.2021, 13.02.2031, 14.02.2041, ..., 19.02.2091, ~~20.02.2002~~, ~~21.02.2012~~, 23.02.2032, ...28.02.2082, 29.02.2092 (заметим, что 2092 високосный). Всего 24 даты с указанным свойством в этом столетии, которые позже 21.02.12.

2. По условию плеер нашёлся не под столом, не на столе и не под диваном. Значит, плеер мог быть только под подушкой. Поэтому шпаргалка под подушкой лежать не могла. Но она не валялась и на полу (т.е. её не было ни под столом, ни под диваном). Следовательно, шпаргалка лежала на столе. Тетрадь не лежала под столом, значит ей осталось только место под диваном. Тогда под столом могли быть только кроссовки.

3. За сутки (24 часа) будильник уйдет вперед на 9 минут, поэтому за 8 часов с 22:00 до 6:00 он уйдет вперед на 3 минуты, т.е. в 06:00 будет показывать 06:03.

4. Разобьем букву Т на два прямоугольника: горизонтальную полоску сверху и вертикальную ножку. Первый прямоугольник имеет размер 3×13, поэтому в нем 3·13 = 39 клеток. Ножка буквы состоит из 20 − 3 = 17 клеток и имеет размер 17 × 3. Значит, во втором прямоугольнике 17 · 3 = 51 клетка, а общее число клеток равно 39 + 51 = 90.

5. Ниф-Нифу, Нуф-Нуфу и Наф-Нафу вместе не хватает 900 кирпичей, чтобы построить три домика, а не один. А количество имеющихся кирпичей у Ниф-Нифа, Нуф-Нуфа и Наф-Нафа хватит на постройку одного домика. Следовательно, на два домика понадобилось бы как раз 900 кирпичей. А значит, один поросячий домик строится из 450 кирпичей.

6. Можно. Объединим сначала гирьки в пары: первая с последней, вторая с предпоследней и т. д. Получится 15 пар, каждая весом 31 г. Теперь достаточно в каждую кучку поместить по 5 указанных пар произвольным образом.

6 класс

1. В каждом горизонтальном ряду по 12 спичек. Всего горизонтальных рядов 13. Значит, число спичек, лежащих горизонтально, равно 12 · 13 = 156. Столько же спичек расположены вертикально.

Следовательно, всего потребуется 156 + 156 = 312 спичек.

2. Покажем, что толстый муравей справится на 2 мин раньше.

I способ. Чтобы донести груз, Толстому нужно сделать 30 рейсов из точки A в точку B и 29 обратных рейсов из точки B в точку A. На один рейс у него уходит 5 минут, а на весь путь уйдет 5·(30+29) = = 295 мин. Тонкому муравью нужно сделать 50 рейсов из точки A в точку B и 49 обратных рейсов из точки B в точку A. У него на один рейс уходит 3 минуты, а на весь путь уйдет 3 · (50 + 49) = 297 мин. Поэтому Толстый окончит свою работу раньше.

II способ. Если бы оба муравья находились в точке B, то они бы выполнили работу за одинаковое время: Толстому нужно было сделать 60 рейсов по 5 минут, а тонкому 100 рейсов по 3 минуты. Так как муравьи уже находятся в точке A, время Толстого уменьшается на 5 минут, а время Тонкого — на 3 минуты. Значит, Толстый окончит работу раньше.

3. Возьмем длину прямоугольника 500 м = 5000 дм. Тогда

ширина прямоугольника равна дм = 0,02 мм. При этом

5000

периметр прямоугольника P = 2·500 м+2·0,02 мм > 1000 м = 1 км.

4. I способ. Так как шесть сытых школьниц за 1 час набирают одну корзину, то одна школьница наполняет корзину на , а остальную часть собранных ягод съедает (если она голодная). Таким образом, если бы 9 школьниц были сытыми, то они набрали бы за 1 час корзины. Значит, 9 голодных школьниц наелись досыта, съев корзины ягод, а целой корзины хватило бы на 18 школьниц.

II способ. Разделим корзину на 18 кружек (18=НОК(6, 3)). Тогда голодная школьница за час набирает в корзину две кружки клубники и сколько-то съедает. А сытая школьница набирает три кружки. Значит, голодная школьница успевает съесть одну кружку и наесться. Поэтому корзиной можно накормить 18 голодных школьниц.

5. Так как тигров в семь раз больше, чем не тигров, то тигры составляют от всех животных.

Так как обезьян было в семь раз меньше, чем не обезьян, то обезьяны составляют всех животных.

Заметим, что = 1, следовательно, других животных не было.

6. Можно заметить, что число 999000 делится на 8. К этому числу необходимо прибавить такое трехзначное число, которое делится на 8 и имеет наибольшую сумму цифр.

У трехзначного числа, сумма цифр не превосходит 27. Если сумма цифр равна 27, то это число 999, но оно не делится на 8.

Если у искомого числа сумма цифр 26, то это одно из чисел: 998, 989,899. Ни одно из этих чисел не делится на 8.

Если сумма цифр 25. Указанную сумму цифр имеют числа 997, 979, 799, 988, 898, 889, но они не делятся на 8.

Если сумма цифр 24, то число 888 делится на 8.

Таким образом, сумма цифр шестизначного числа, которое делится на 8, не больше, чем 9 + 9 + 9 + 24 = 51. Указанная сумма цифр достигается у числа 999888.

7 класс

1. Среди чисел от 1 до 10 на 7 делится только сама семерка. Значит, она должна входить в первую группу, и частное не меньше

Приведём пример, когда частное равно 7: . Заметим, что есть и другие примеры. · · · ·

Таким образом, наименьшее значение частного равно 7.

2. Пусть эскалатор за 1 секунду поднимается на n ступенек.

Так как при первом подъеме человек шагал со скоростью одна ступенька в секунду и сделал 20 шагов, то он затратил 20 секунд. Значит, число ступеней на эскалаторе равно 20 + 20n.

Во второй раз человек поднялся, сделав 32 шага со скоростью 2 шага в секунду. В этом случае он потратил на подъем 16 секунд. Поэтому число ступеней на эскалаторе равно 32 + 16n. Составим уравнение:

20 + 20n = 32 + 16n.

Решив данное уравнение, найдем, что n = 3, а число ступенек равно 20 + 20 · 3 = 80.

3. Предположим, что Пете удалось переложить шары так, что условия задачи выполнены. Занумеруем по кругу все коробки числами от 1 до 101, начиная с некоторой. Пусть из первой коробки во вторую переложен белый шарик. (Случай, когда из первой коробки во вторую переложен черный шар, разбирается аналогично.) Тогда из второй в третью должен быть переложен черный шарик, иначе обе надписи на второй коробке останутся верными. Так как в третью коробку переложили черный шар, то в четвертую можно переложить только белый и т.д. Таким образом, цвета переложенных шариков должны чередоваться. Так как количество коробок нечетное число, то из 101-й и 1-й коробки были переложены шары одного цвета. Противоречие. Таким образом, Петя не сможет переложить шары.

4. Ответ: 45^◦.

Способ I. Введем обозначения как показано на рис.

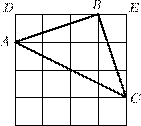
Проведем отрезок BC.

1) △ABD = △BCE (по двум катетам), следовательно, AB = BC, а треугольник ABC равнобедренный.

2) Треугольник ADB — прямоугольный, ∠D = 90^◦, тогда

∠DAB + ∠DBA = 90^◦.

Из равенства треугольников ABD и BCE следует, что ∠DAB = ∠CBE. Таким образом,

∠CBE + ∠DBA = 90^◦.

3) ∠DBE — развернутый, поэтому

∠ABC = 180^◦− (∠CBE + ∠DBA) = 180^◦− 90^◦= 90^◦.

Значит, △ABC — равнобедренный прямоугольный, а тогда

∠A = ∠C = 180◦ 2− ∠B = 45◦.

Способ II. Проведем отрезок BC. Заметим, что AB = BC, так как это диагонали прямоугольников 3 × 1. Тогда треугольник ABC — равнобедренный и ∠A = ∠C = x.

Рассмотрим точку M и соединим ее с вершиной B (см. рис.).

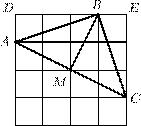
Отрезки AM, BM и CM равны, так как это диагонали прямоугольников размером 2 × 1. Тогда треугольники ABM и BCM равнобедренные, причем

∠A = ∠ABM = x и ∠C = ∠CBM = x.

По теореме о сумме углов треугольника ∠A + ∠ABC + ∠C = ∠A + ∠ABM + ∠CBM + ∠C = x + x + x + x = 4x = 180^◦, откуда ∠A = x = 45^◦.

Замечание. Приведенное решение можно немного сократить. Заметим, что BM — медиана в равнобедренном треугольнике ABC, следовательно, BM — высота. Таким образом, △ABM — равнобедренный прямоугольный, а ∠A = 45^◦.

5. Ответ: a = 17, b = 7, c = 2 или a = 17, b = 2, c = 7.

Имеем, что bc = 7a − 105 = 7(a − 15). Так как b и c простые числа, то либо b = 7, либо c = 7.

Если b = 7, то c = a − 15. Так как числа a и c простые, то a − 15 — четное. Единственное четное простое число — 2. Поэтому c = 2, a = 17.

Аналогично разбирается случай, когда c = 7. Получим, что b = = 2, a = 17.

6. Цифры 0 на сумму не влияют, а каждая не нулевая цифра 10 раз встречается в разряде единиц и 10 раз в разряде сотен. Поэтому сумма всех цифр равна

20(1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9) = 20 · 45 = 900.

8 класс

1. Так как интервал движения при двух автобусах на маршруте составляет 21 минуту, то длина маршрута «в минутах» составляет 42 минуты. Следовательно, интервал движения при трех автобусах на маршруте составляет 42 : 3 = 14 минут.

2. Способ I. Пусть N — середина стороны AB. Ток как AB = = 2BM, то BN = BM, т.е. △BMN равнобедренный. Значит, ∠NMB = ∠MNB = (180^◦− ∠NBM)/2 = (180^◦− 40^◦)/2 = 70^◦.

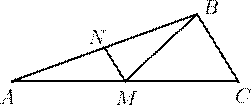
Отрезок MN — средняя линия треугольника ABC, следовательно, MN ∥ BC, а ∠MBC = ∠NMB = 70^◦как накрест лежащие углы.

Тогда ∠ABC = ∠ABM + ∠MBC = 40^◦+ 70^◦= 110^◦.

Способ II. Продлим медиану BM так, что BM = MD. Так как AB = 2BM, то получим, что AB = BD, а △ABD — равнобедренный.

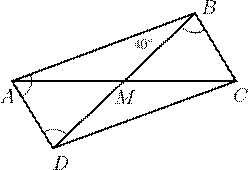
Значит, .

Четырехугольник ABCD является параллелограммом, так как его диагонали точкой пересечения делятся пополам. Следовательно,

∠DBC = ∠ADB = 70^◦, а ∠ABC = ∠ABD + ∠DBC = 40^◦+ 70^◦=

110^◦.

3. Понятно, что если два соседних числа отличаются только в разряде единиц, то разность между ними равна 5 (например, 523 и 528). Значит, нужно, чтобы числа отличались и в других разрядах. Можно попробовать взять большее число круглым, тогда числа будут отличаться минимум в двух разрядах. Возьмем, например, 50, предыдущее число 46, а разность равна 4. Если взять 500, то предыдущее число 497 и разность равна 3. Осталось подобрать такое число нулей, чтобы разность была равна 1. Получим, что наименьшая разность равна 1, например, между числами 49999 и

50000.

4. Имеем, что

1111111122222222 = 11111111 · 100000000 + 2 · 11111111 =

= 11111111 · 100000002.

Так как сумма цифр числа 100000002 делится на 3, то и само число делится на 3. Действительно,

100000002 = 99999999 + 3 = 3 · (33333333 + 1) = 3 · 33333334. Таким образом, x(x + 1) = 11111111 · 3 · 33333334 = 33333333 · 33333334.

Заметим, что число x₁= 33333333 является корнем уравнения. Второй корень можно найти по теореме Виета. Получим x₂= = −33333334.

5. Цифры 0 на сумму не влияют, а каждая не нулевая цифра 100 раз встречается в разряде единиц, 100 раз в разряде десятков и

100 раз в разряде сотен. Поэтому сумма всех цифр равна 300(1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9) = 300 · 45 = 13500.

6. Покажем, что Вася может сделать всего 7 разломов.

Общая длина всех палочек составляет 99 см, поэтому стороны 11-угольника должны быть по 9 см. Разломаем 3 шестисантиметровых палочки пополам и приставим по кусочку к 6 оставшимся шестисантиметровым палочкам. Получим шесть девятисантиметровых сторон. Теперь отломаем от 4 пятисантиметровых палочек по куску длиной 1 см. Все отломанные куски приложим к одной из оставшихся пятисантиметровых палочек, а оставшиеся четырёхсантиметровые куски — по одному к остальным оставшимся пятисантиметровым палочкам. Получим 11 девятисантиметровых сторон. (Есть и другой способ разлома палочек.)

Покажем, что 6 разломов не хватит. В самом деле, если мы сделали 6 разломов, то по крайней мере 12 палочек остались целыми. Значит, в составе по крайней мере одной из сторон 11-угольника окажется хотя бы две целых палочки. Но суммарная длина любых двух целых палочек больше 9см.

2014 год. Олимпиада ИМИКТ

7 класс

1. Так как вторая муха поднималась вдвое медленней, то только на подъем она потратила такое же время, какое первая потратила на путь вниз и вверх. Таким образом, первая муха приползла раньше.

Данное решение можно оформить алгебраически. Пусть x (м/с) — скорость первой мухи, а h (м) — высота комнаты.

Тогда время первой мухи секунд, а время второй мухи

. Очевидно, что время движения

второй мухи больше, чем время первой.

2. Сначала записано 9 однозначных чисел. Затем последовательно выписываются 90 двузначных чисел, т.е. числа от 10 до 99. Для этого потребовалось 90 · 2 = 180 цифр. Значит, для записи первых 99 натуральных чисел было использовано 9 + 180 = 189 цифр. Дальше идут трехзначные числа. Так как 2014 − 189 = = 1825 = 3 · 608 + 1, то 2013 цифр потребуется для записи первых 608-ми натуральных чисел, а с 2014-й цифры начинается запись следующего трехзначного числа 609. Таким образом, 2014-я цифра это 6.

3. Путешественник может распилить только третье кольцо цепи. Тогда у него будет одно кольцо, которое он распилил, и две цепочки длинами два и четыре кольца.

В первый день он отдает одно кольцо. Во второй — отдает цепочку из двух, но одно кольцо, которое отдал в первый день, забирает назад. В третий день — снова отдает хозяину одно кольцо. В четвертый день — путешественник отдает цепочку из четырех колец, при этом забирает одно кольцо и цепочку из двух колец себе обратно. В пятый день —отдает одно кольцо. В шестой — отдает цепочку из двух колец и забирает одно кольцо, которым расплатится за седьмой день проживания.

4. Пусть квадратный лист имел размер n×n. Тогда он содержал n²клеток. Если из этого квадрата вырезать меньший квадрат размером m×m, то в оставшемся куске будет n²−m²клеток. Таким образом, получим уравнение с двумя переменными

n²− m²= 124.

Разложим левую и правую части полученного равенства на множители. Имеем

(n − m) · (n + m) = 2 · 2 · 31.

Так как числа n−m и n+m натуральные, причем n−m < n+m, то получим следующие возможные случаи:

Решив эти системы уравнений, получим, что решения первой и третьей системы не являются натуральными числами. Оставим это в качестве упражнения читателю. Решим вторую систему методом сложения. Получим, 2n = 64, откуда n = 32, а m = 30. Таким образом, первоначальный лист бумаги содержал 32²= 1024 клетки.

Замечание. Заметим, что числа n−m и n+m одной четности (например, так как (n−m)+(n+m) = 2n — четное число), поэтому, системы 1) и 3) можно было не рассматривать.

5. Занумеруем все места на скамейке последовательно числам от 1 до 10. Так как между любыми двумя девочками сидит нечетное число школьников, то все девочки сидят на местах с одинаковой четностью.

Первый случай. Если девочки сидят только на местах с четными номерами (но, возможно, что не все четные места заняты девочками). Тогда все нечетные места заняты мальчиками, и между любой такой парой мальчиков, сидящих на нечетных местах, нечетное число школьников. Противоречие, так как между любыми двумя мальчиками должно сидеть четно число школьников.

Второй случай. Если девочки сидят только на местах с нечетными номерами (но не обязательно, что все нечетные места занимают девочки). Тогда все четные места заняты мальчиками, и между любой парой мальчиков, сидящих на четных местах, нечетное число школьников. Противоречие.

Таким образом, школьники так сидеть не могут.

6. Заметим, что общий вес девяти самых тяжелых гирек массами 11 г, 12 г, ..., 19 г ровно на 90 г больше, чем общий вес девяти самых легких гирек массами 1 г, 2 г, ..., 9 г. Поэтому, железные гирьки имеют массу 11 г, 12 г, ..., 19 г, а бронзовые гирьки — 1 г, 2 г, ..., 9 г. Действительно, если хотя бы одна бронзовая гирька имеет вес больше 9 грамм, то общий вес всех бронзовых гирек больше, чем 1 + 2 + ... + 9 = 45, а тогда общий вес всех железных гирек больше, чем 45 + 90 = 135, чего быть не может (т.к. девять самых тяжелых весят вместе 135 г). Аналогично можно показать, что никакая железная гирька не может иметь массу меньше чем 11 г. Значит, золотая гирька весит 10 грамм.

7. Пусть площадь квадрата ABCD равна 4S. Тогда площадь каждого из треугольников ABE, BCF и AED равна S.

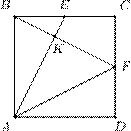
Имеем, что S_KECF= S_BCF−S_BEK= S−S_BEK< S. Причем для суммы площадей треугольника AKF и четырехугольника KECF выполняется равенство

SAKF + SKECF = SABCD − SABE − SAFD = 4S − S − S = 2S.

Таким образом, S_AKF> S, и, следовательно, S_AKF> S_KECF.

8. Предположим, что это не так. Тогда в любых двух строчках количество клеток каждого цвета различное, а общее число клеток не менее чем

3 · (0 + 1 + 2 + ... + 14) = 315.

Пришли к противоречию. В квадрате 15×15 всего 15²= 225 клеток. Полученное противоречие показывает, что найдутся две строчки, в которых клеток хотя бы одного цвета поровну.

8–9 класс

1. Пусть x лет общий возраст всех одноклассников школьника, который уехал на олимпиаду, а n — число учеников в классе. Тогда получим два равенства:

Выразим из этих равенств переменную x и приравняем. Получим, что n²− 15 = (n − 1)², откуда n = 8.

Таким образом, в классе первоначально было 8 школьников.

Замечание. Если продолжить решение, то получим, что x = 49, а средний возраст оставшихся школьников равен 7. Такая ситуация абсурдна с точки зрения здравого смысла. В одном классе найдутся два ученика, возраст одного из которых не более 7 лет, а возраст другого 15 лет. Дело в том, что первоначально в условии задачи фигурировали студенты-заочники, а возраст отбывшего студента был другим. Авторы хотели адаптировать условие на школьников, в результате чего возникла такая курьезная ситуация.

2. Введем стандартные обозначения: h_a, h_b, h_c— высоты треугольника, опущенные на стороны a, b и c соответственно. Пусть

S S S

S — площадь треугольника, тогда.

В любом треугольнике высоты меньше диаметра описанной окружности. Следовательно, h_a< 2R = 4, h_b< 4 и h_c< 4.

Известно, что длины всех высот выражаются натуральными числами. Рассмотрим несколько случаев.

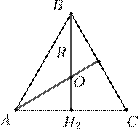
Случай I. Все высоты равны. Пусть h_a= h_b= h_c= h. Имеем, что треугольник равносторонний. Тогда

(т.к. медианы точкой пересечения делятся в отношении 2:1, считая от вершины), откуда h = 3. При этом

Такой треугольник удовлетворяет всем условиям задачи.

Осталось показать, что другие случаи не возможны.

Случай II. Среди высот есть различные (т.е. треугольник не равносторонний). Можем считать, что h_a6 h_b6 h_c< 4. Для удобства обозначим S = 3x.

В этом случае имеем следующие возможные ситуации (подслучаи)

h_a	h_b	h_c	a = 6x/h_a	b = 6x/h_b	c = 6x/h_c	a < b + c
1	1	2	6x	6x	3x
1	1	3	6x	6x	2x
1	2	2	6x	3x	3x	6x ≮ 3x + 3x
1	2	3	6x	3x	2x	6x ≮ 3x + 2x
1	3	3	6x	2x	2x	6x ≮ 2x + 2x
2	2	3	3x	3x	2x
2	3	3	3x	2x	2x

Из таблицы видим, что в трех случаях не выполняется неравенство треугольника. Осталось рассмотреть оставшиеся 4 варианта.

1. Если h_a= 1, h_b= 1, h_c= 2. Тогда △ABC — равнобедренный, a = b. Из равенства h_c= R = 2 следует, что центр описанной окружности совпадает с серединой основания AB, тогда △ABC — равнобедренный прямоугольный, что не верно.

2. Если h_a= h_b= 1, h_c= 3. Тогда a = b = 6x, c = 2x. Применим формулу. Учитывая, что S = 3x имеем

откуда . Но тогда.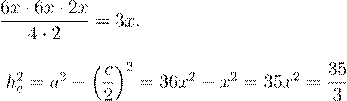

Противоречие, так как h_c= 3.

Аналогично можно показать, что оставшиеся два случая также не удовлетворяют условию.

Таким образом, a = b = c = 2√3.

3. См. решение задачи 6 для 7 класса.

4. Имеем, что 3²+4²= 5², тогда (3·403)²+(4·403)²= (5·403)².

Заменим в числовом выражении

1²+ 2²+ 3²+ ... + 2014²

два слагаемых 1209²и 1612²одним — их суммой 2015². Таким образом, получим представление данного числа в виде суммы квадратов 2013 различных натуральных чисел.

5. См. решение задачи 5 для 7 класса.

6. Докажем, что геометрическое место точек пересечения медиан всевозможных треугольников, вписанных в данную окружность, есть внутренность круга, ограниченного данной окружностью. Точка пересечения медиан каждого такого треугольника лежит внутри него и, значит, внутри его описанной окружности.

Пусть M — произвольная точка внутри описанной окружности. Проведем через M диаметр и пусть A — ближайший к точке M конец этого диаметра (т.е. AM 6 AO). Отложим на продолжении отрезка AM отрезок . Очевидно, что точка лежит внутри круга. Проведём через хорду BC, перпендикулярную AO.

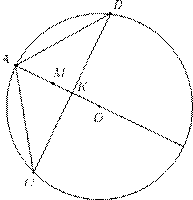
При этом точка будет серединой этой хорды, а M — точкой пересечения медиан треугольника ABC.

7. Введем обозначения: a_i— сумма чисел, стоящих в i-й строке, b_j— сумма чисел в j-м столбце, x_ij— число, стоящее на пересечении i-й строки и j-го столбца. Так как сумма чисел в любом “кресте”

равна нулю, то a_i+ b_j− x_ij= 0, откуда

x_ij= a_i+ b_j. (∗)

Рассмотрим произвольную i-ю строку таблицы и распишем каждый ее элемент по формуле (∗). Имеем

xi1 = ai + b1, xi2 = ai + b2,

...

xin = ai + bn.

Сложим все эти равенства. Получим

a_i= n · a_i+ S,

где S = b₁+ b₂+ ... + b_n— сумма всех чисел в таблице. Тогда

Последнее равенство показывает, что все числа a_iравны между собой, т.е..

Аналогичным образом получим, что.

Используя данные равенства и формулу (∗), можем записать,что

Таким образом, мы показали, что все числа таблицы равны .

Так как в таблице всего n²чисел, а их сумма равна S, то

откуда S = 0 и x_ij= 0.

Значит, все числа в таблице равны 0.

8. Предположим, что такая расстановка существует.

Сначала заметим, что сумма чисел, записанных на гранях, равна 1 + 2 + 3 + 4 + 5 + 6 = 21 — нечетное число.

Пусть на одной из граней куба написано число a, а на противоположной грани — число b. Тогда сумма соседних чисел для a и для b равна 21−(a+b). Если оба числа a и b четные, то сумма их соседей 21−(a+b) — нечетное число, и она не может делится ни на a, ни на b. Таким образом, напротив четного числа стоит нечетное. Значит, числа 1, 2, 3, 4, 5, 6 разбились на пары чисел разной четности, стоящих на противоположных гранях куба. Покажем, что число 5 не может стоять в паре ни с одним четным числом. Действительно: 1) 5 не стоит в паре с 2, так как 21−(5+2) = 14 не делится на 5; 2) 5 не стоит в паре с 4, так как 21 − (5 + 4) = 12 не делится на 5; 3) 5 не может стоять в паре с 6, так как 21 − (5 + 6) = 10 не делится на 6. Получили, что у числа 5 нет парного. Значит, предположение не верно, и указанной расстановки чисел на гранях куба не существует. 9. Преобразуем левую часть доказываемого неравенства

(1−x₁)(1−x₂)(1−x₃) = 1−(x₁+x₂+x₃)+(x₁x₂+x₂x₃+x₁x₃−x₁x₂x₃).

Так как, то .

Выражение x1x2 + x2x3 + x1x3 − x1x2x3 = x1x2 + x2x3 + x1x3(1 − x2) > 0,

так как это сумма трех неотрицательных чисел x₁x₂, x₂x₃и x₁x₃(1 − x₂).

Таким образом,

Неравенство доказано.

10. Если n = 3, то подходит любая расстановка чисел. Предположим, что при некотором n > 3 существует расстановка, удовлетворяющая условию задачи. Тогда перед каждым четным числом по ходу часовой стрелки стоят два числа одной четности (сумма двух чисел разной четности нечетна и не может делиться на четное число). Рассмотрим два случая. 1) Хотя бы для одного четного числа оба его «предшественника» четны. Тогда рассмотрим ближайшее к ним против хода часовой стрелки нечетное число. Следующие за ним по ходу часовой стрелки два числа четны, но «нечетное»+«четное» не может делиться на «четное». 2) Для каждого четного числа оба его «предшественника» нечетны. Тогда между каждыми двумя четными числами стоит, по крайней мере, два нечетных числа. Если четных чисел на окружности k, то нечетных — не меньше 2k. Но разность между количеством нечетных чисел и количеством четных чисел не больше 1, следовательно k 6 1, тогда n 6 3.

Таким образом, n = 3 — наибольшее число, для которого существует расстановка чисел, удовлетворяющая условию задачи.

2015 год. Олимпиада ИМИКТ

6 класс

1. Пусть x площадь верхней средней части прямоугольника.

Тогда x : 30 = 35 : 21. Значит, x = 50. Обозначим y — площадь верхней правой части (искомая), тогда y : 50 = 8 : 10.

Следовательно y = 40.

2. Пусть часы показывают время ab.cd.ef. Тогда

0 6 a 6 2, 0 6 b 6 9, 0 6 c 6 5, 0 6 d 6 9, 0 6 e 6 5, 0 6 f 6 9.

Таким образом, три цифры 7 могут гореть только вместо цифр b,

d и f. Тогда время на часах a7.c7.d7. Так как b = 7, то a = 0 или a = 1. Значит, a может принимать 2 значения, а d и f по 6. Получим 2 · 6 · 6 = 72 различных комбинаций с тремя цифрами 7. Каждая такая комбинация горит ровно 1 секунду, поэтому искомое время 72 секунды.

3. Предположим, что произведение a₁· a₂· a₃· a₄· a₅= ...2015. Тогда все 5 чисел являются нечетными. Но сумма 5 нечетных чисел — нечетна, она не может равняться 200.

4. Как бы ни расставляли скобки, число 1 окажется в числителе, а число 2 в знаменателе.

а).

б) .

5. Пусть первый турист за 1 час делает n шагов длинной l. Значит, путь, проходимый за час, равен nl. Второй турист за 1 час сделает 1,1n шагов длинной 0,9l, а расстояние, которое он пройдет за час равно 1,1n · 0,9l = 0,99nl. Поэтому, первый турист идет быстрее.

6. Торт можно испечь в виде буквы Ш или Е (см. рисунок).

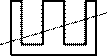
7. В семье двое мужчин: отец и сын. Рассмотрим 2 случая.

I случай. Боря — отец, Ваня — сын.

Боря, сказав Инне, показав на Ваню: «Но я же старше него!» говорит правду. Значит, Инна — мама. Тогда Даша и Галя дочери. Боря, сказав, Даше, что он старше Гали, говорит правду. Противоречие. Отец сказал правду своей дочери. Значит, Боря не может быть отцом.

II случай. Боря — сын, Ваня — отец.

Боря, сказав Инне, показав на Ваню: «Но я же старше него!» говорит ложь. Значит, Инна — мама. В первом высказывании Боря говорит Даше, что он старше Гали. Это может быть правдой. Боря не врет своей сестре. Здесь противоречия нет.

Таким образом, Ваня — отец, Инна — мама.

8. Пусть 7 грибников собрали x₁< x₂< x₃< x₄< x₅< x₆< x₇грибов. Рассмотрим 2 случая.

I случай. x₅> 16. Тогда, x₆> 17, x₇> 18. Отсюда x₅+x₆+x₇> 51. Нашлась тройка, собравшая не менее 50 грибов.

II случай. x₅< 16. Тогда x₅6 15, x₄6 14, x₃6 13, x₂6 12, x₁6 11. Значит, x₁+x₂+x₃+x₄6 14+13+12+11 = 50. Но тогда x₅+ x₆+ x₇> 50.

Таким образом, в обоих случаях нашлась тройка грибников, собравших вместе не менее 50 грибов.

9. Пусть сумма цифр полного квадрата равна 555. Тогда это число делится на 3, но оно не делится на 9. Поэтому данное число не может быть полным квадратом.

7 класс

1. См. решение задачи 1 для 6 класса.

2. Пусть часы показывают время ab.cc.ba. Если a = 0, то b и c могут принимать 6 значений (0, 1, 2, 3, 4, 5). Получим 36 возможных комбинаций.

Если a = 1, то b и c могут принимать 6 значений (0, 1, 2, 3, 4, 5). Снова получаем 36 возможных комбинаций.

Если a = 2, то b может принимать значения 0, 1, 2, 3 — четыре варианта, а c может принимать значения 0, 1, 2, 3, 4, 5. Таким образом, получим еще 24 дополнительных комбинации.

Значит, искомая комбинация цифр горит 36 + 36 + 24 = 96 секунд.

3. Пусть x, y, z — количество книг, поступивших в первый второй и третий магазины соответственно.

Так как первый магазин продавал полученных им книг, то количество поступивших в него книг делится на НОК(37,11,2) = = 814. Значит, x^...814.

Аналогично y ^...171, а z ^...150, так как НОК(57,9,3) = 171, а НОК(25,30,10) = 150.

Таким образом, x = 814n, y = 171m, z = 150k, где n, m, k — натуральные числа. Известно, что в магазины завезли всего 1990 книг, поэтому

814n + 171m + 150k = 1990. (∗)

Так как 814 · 3 > 1990, то n < 3.

Рассмотрим два случая.

Случай I. Если n = 1, тогда 171m + 150k = 1176. Поделив обе части равенства на 3, получим

57m + 50k = 392.

Так как числа 50k и 392 четные, то m — четно.

392 − 57m

Имеем, что k = .

Если m = 2 или m = 4, то k не является целым.

Если .

Если m > 6, то k отрицательное.

Таким образом, получили одно из возможных решений: n = 1, m = 6, k = 1.

Случай II. Если n = 2, тогда 171m + 150k = 362. При m = 1 или m = 2 получим, что число k не является целым. Если m > 2, то k отрицательное.

Значит, уравнение (∗) имеет единственное решение n = 1, m = 6, k = 1. Следовательно, в первый магазин завезли 814 · 1 = 814 книг, во второй — 171 · 6 = 1026 книг, а в третий — 150 · 1 = 150 книг.

4. Пусть квадратный лист имел размер n×n. Тогда он содержал n²клеток. Если в этом квадрате закрасить меньший квадрат размером m×m, содержащий m²клеток, то в незакрашенном куске будет n²− m²клеток. Таким образом, получим уравнение с двумя переменными

n²− m²= 79.

Разложим левую часть данного равенства на множители. Имеем

(n − m) · (n + m) = 79.

Так как числа n − m и n + m натуральные, причем n − m < n + m, а 79 — простое число, то

{

n − m = 1, n + m = 79.

Сложив уравнения системы, получим 2n = 80, а n = 40. Затем, из первого уравнения находим m = 39.

Таким образом, в квадрате 40 × 40 закрасили квадрат 39 × 39, поэтому хотя бы один угол будет закрашен.

5. См. решение задачи 7 для 6 класса.

6. См. решение задачи 9 для 6 класса.

7. Имеем, что m²+ m + 1 = m(m + 1) + 1. Числа m и m + 1 разной четности, поэтому произведение m(m+1) — четное, а число m²+ m + 1 — нечетное.

Аналогично n²− n + 1 = n(n − 1) + 1 — нечетное число.

Таким образом, выражение (m²+ m + 1)²− (n²− n + 1)²представляет собой разность квадратов двух нечетных чисел. Очевидно, что эта разность — четное число. Значит, не существует таких целых чисел n и m, что

(m²+ m + 1)²− (n²− n + 1)²= 2015.

8. См. решение задачи 8 для 6 класса.

8–9 класс

1. Рассмотрим две точки 1 и 2, окрашенные в первый и второй цвета. Проведем через эти точки прямую a. Возможно два случая.

Случай I. На прямой a найдется хотя бы одна точка, окрашенная в третий или четвертый цвет. Тогда прямая a — искомая. Она содержит точки не менее чем трех цветов.

Случай II. Все точки прямой a окрашены в первый или второй цвета. Рассмотрим на плоскости еще две точки 3 и 4, окрашенные в третий и четвертый цвета соответственно. Проведем через эти точки прямую b. Снова возможно два случая.

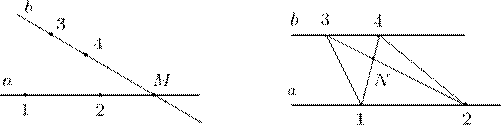
Рис. 1.1 Рис. 1.2

Случай II.1. Прямые a и b пересекаются в точке M (рис. 1.1).

Так как M ∈ a, то M — либо первого, либо второго цвета. Тогда прямая b содержит точки не менее чем трех цветов. Действительно, на этой прямой лежат точки 3, 4 и M, окрашенные в три разных цвета.

Случай II.2. Прямые a и b параллельны (рис. 1.2). Рассмотрим трапецию с вершинами в точках 1, 3, 4, 2. Пусть N — точка пересечения диагоналей трапеции. Тогда в зависимости от цвета точки N хотя бы одна из диагоналей содержит точки не менее чем трех цветов.

Цвет точки N	искомая прямая

Например, если точка N окрашена в третий цвет, то прямая, проходящая через точки 1 и 4 (в таблице обозначена 1N4), содержит точки 1, 4 и N, окрашенные в три разных цвета.

Таким образом, во всех случаях существует прямая, содержащая точки не менее чем трёх цветов.

2. Покажем, что в любой трапеции разность длин оснований больше разности длин ее боковых сторон. Рассмотрим трапецию ABCD (BC ∥ AD) и докажем, что |AD − BC| > |CD − AB|.

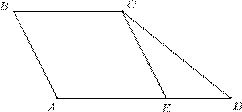
Если трапеция равнобедренная, то указанное неравенство, очевидно, выполняется.

Пусть CD > AB. Проведем через точку C прямую CE так, что CE параллельна AB. Четырехугольник ABCE является параллелограммом, поэтому AE = BC, AB = CE. В этом случае

AD − BC = AD − AE = DE > CD − CE = CD − AB.

(Неравенство DE > CD−CE следует из неравенства треугольника для △CDE.)

Таким образом, если в трапеции ABCD стороны AB и CD — боковые, а BC и AD — основания, то трапеции, в которой BC и AD — боковые стороны, а AB и CD — основания, не существует.

3. См. решение задачи 9 для 6 класса.

4. Да, может. Маршрут короля показан на рисунке 4.1 (при этом на некоторых клетках король будет дважды). Всего он совершил 13 поворотов в вершинах 1, 2, ..., 13.

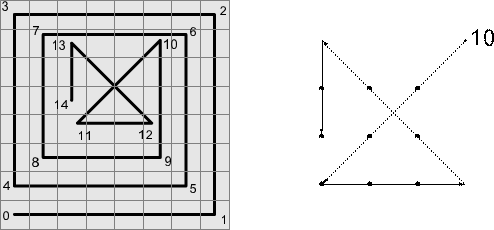
Рис. 4.1 Рис. 4.2

После того как в указанном маршруте дошли до точек 9 и 10, подсказкой к дальнейшему пути (а именно, расположение вершин 10, 11 и т.д.) может служить следующая известная задача: соединить девять точек четырьмя прямыми линиями не отрывая карандаша от листа бумаги (см. рис. 4.2).

5. Так как y и z натуральные числа, то

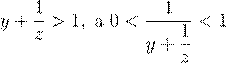Поэтому из равенства

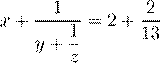
следует, что

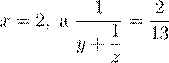“Перевернув” дроби во втором равенстве, получим

Так как y — натуральное число, а , то, откуда z = 2. Таким образом, x = 2, y = 6, z = 2.

6. Предположим, что мышка съела все кубики сыра кроме центрального.

Раскрасим кубики в белый и чёрный цвета в шахматном порядке (см. рис.), а именно, пусть белыми будут 12 кубиков, расположенных в серединах рёбер большого куба (то есть кубики, ровно две грани каждого из которых расположены на поверхности большого куба), а остальные 14 кубиков пусть будут чёрными.

Когда мышка переходила от одного съеденного кубика к другому, то цвета кубиков чередовались. Поэтому она съела 13 черных и 13 белых кусочков. Пришли к противоречию, в большом кубе 14 черных и 12 белых кусков.

Значит, Мышка не сможет съесть указанные 26 кубиков.

7. См. решение задачи 8 для 6 класса.

8. Воспользуемся тождеством ad + bc = (a + c)(b + d) − (ab + cd).

Так как оба числа (a+c)(b+d) и (ad+cd) делятся нацело на a+c, то и их разность делится нацело на a + c.

9. Заметим, что пловец удаляется от фляги и догоняет флягу с одной и той же скоростью (собственная скорость пловца в стоячей воде). Поэтому он догонит флягу за 20 минут. Значит, течение за 40 минут снесло флягу на 2 км. Так как 40 мин = ч, то скорость течения реки равна 2 км : км/ч.

10. Пусть многочлен P(x) имеет вид

P(x) = a_nxⁿ+ a_n−1xⁿ⁻¹+ ... + a₂x²+ a₁x + a₀.

Так как P(0) = 1, то a₀= 1.

Так как P(1) = 1, то a_n+ a_n−1 + ... + a₂+ a₁+ 1 = 1, откуда

a_n+ a_n−1 + ... + a₂+ a₁= 0.

Значит, среди коэффициентов a₁, a₂, ..., a_n−1, a_nчетное число нечетных чисел. Поэтому при любом целом значении x сумма

anxn + an−1xn−1 + ... + a2x2 + a1x

является четным числом, а значение многочлена

P(x) = (a_nxⁿ+ a_n−1xⁿ⁻¹+ ... + a₂x²+ a₁x) + 1 — нечетное число.

Таким образом, многочлен P(x) при целых x принимает нечетные значения, а потому он не может иметь целых корней.

ОТВЕТЫ

2016 год. Отборочный тур 5 класс

1. 24 кубика. 2. 500 страниц. 3. 219. 4. 32 треугольника. 5. 180 ударов. 6. 12 кг.

6 класс

1. 90 минут. 2. 9 плюсов. 3. 3 химика увлекаются математикой. 5. 180 ударов. 6. 10.

7 класс

1. 19 чисел. 2. 3 химика увлекаются математикой. 3. 64 кубика.

4. 82,5^◦. 5. 10. 6. 56 конфет останется в правой коробке.

8 класс

1. Надо убрать 160 кубиков. 2. 405. 3. −√−x − √−y. 4. 24. 5.

56 конфет останется в правой коробке. 6. 2016.

2016 год. Очный тур 5 класс

1. 100 чисел. 3. 600 см. 4. Можно. 6 класс

1. Второе число больше первого. 2. . 3. Не все обрывки были найдены. 4.Можно. 5. На доске остались числа 220, 221, 222, 223,

224, 226, 227, 228 и 229. 6. 3 разреза.

7 класс

1. 13 цифр. 2. 42 ученика. 5. −1. 8 класс

1. A = B. 3. 9 бриллиантов. 5. n = 1458.

2017 год. Отборочный тур 5 класс

1. 6 апельсинов. 2. 15 раз. 3. 404 клетки. 4. Частное — 6, делитель — 36, делимое — 216. 5. 10 см.

6 класс

1. 728 кубиков. 2. 3 метра. 3. 10 см. 4. 250 метров. 5. 412−365 =

47.

7 класс

1. рублей. 4. Большой палец. 5. Минутная

стрелка догонит часовую через 16 минуты.

8 класс

1. 7,5 рублей. 2. 4,5. 3. 119. 4. Минутная стрелка догонит часовую через минуты. 5. Трудных задач было на 20 больше, чем легких.

2017 год. Очный тур 5 класс

2. У Бома: рубашка — зеленая, туфли — синие, а у Бима: рубашка и туфли красные. 3. 5 точек. 4. В 13:00. 5. Коле 4 рубля,а Саше 1 рубль. 6. Восстановленная таблица приведена ниже.

6 класс

1. У Бома: рубашка — зеленая, туфли — синие, а у Бима: рубашка и туфли красные. 2. 10112358. 3. 9 см, 13 см и 17 см. 4.

50 км. 5. 243 числа. 6. 224.

7 класс

1. 156 шагов. 5. 224. 6. 8640 м². 8 класс

1. a > b. 2. 9 решений. 3. 5. 4. 8640 м². 5. Нельзя.

2018 год. Отборочный тур 5 класс

6321

+ 1. 9 секунд. 2. Олег, Юра, Вова, Миша, Саша. 3. .

4. 63см². 5. 666 рублей.

6 класс

1. 21 кусок. 2. 500 см. 3. 666 рублей. 4. 315см². 5. Слева направо:

Козёл, Мартышка, Осёл.

7 класс

1. 13:10. 2. 16 ударов. 3. x = 25. 4. 37. 5. 12 секунд.

8 класс

1. 23 шоколадки. 2. 35 способов. 5.

15 двоек.

2018 год. Очный тур 5 класс

1. Да, например, 12.02.2021. 2. Тетрадь была под диваном, шпаргалка — на столе, плеер — под подушкой, кроссовки — под столом. 3. На 6 часов и 3 минуты. 4. 90 клеток. 5. 450 кирпичей. 6.

Можно.

6 класс

1. 312 спичек. 2. Толстый муравей справится на 2 мин раньше. 3. Да, может. 4. 18 школьниц. 5. Львов не было. 6. Наибольшая сумма цифр равна 51 у числа 999888.

7 класс

1. 7. 2. 80 ступенек. 3. Не сможет. 4. 45^◦. 5. a = 17, b = 7, = 2 или a = 17, b = 2, = 7. 6. 900.

8 класс

1. 14 минут. 2. 110^◦. 3. Наименьшая разность равна 1, например, между числами 49999 и 50000. 4. x₁= 33333333, x₂= −33333334.

5. 13500. 6. 7 разломов.

2014 год. Олимпиада ИМИКТ 7 класс

1. Первая муха приползет раньше. 2. Цифра 6 стоит на 2014-м месте. 4. 1024 клетки. 5. Не может. 6. 10 грамм. 7. S_AKF> S_KECF. 8–9 класс

1. 8 школьников. 2. a = b = c = 2√3. 3. 10 грамм. 4. Можно.

5. Не может. 6. ГМТ — внутренность круга, ограниченного данной окружностью. 7. Верно. 8. Нельзя. 10. n = 3.

2015 год. Олимпиада ИМИКТ 6 класс

1. 40. 2. 72 секунды. 5. Первый турист идет быстрее. 7. Отец —

Иван, мама — Инна. 9. Не может.

7 класс

1. 40. 2. 96 секунд. 3. В первый магазин привезли 814 книг, во второй — 1026, в третий — 150. 4. Не могут. 5. Отец — Иван, мама —

Инна. 6. Не может.

8–9 класс

3. Не может. 4. Может. 5. x = 2, y = 6, z = 2. 6. Мышка не сможет съесть весь куб, кроме центрального кубика. 9. 3 км/ч.

РАЗДЕЛ ВТОРОЙ

Математический факультатив

Тема 1. Принцип Дирихле

Принцип Дирихле достаточно прост и очевиден, иногда им пользуются из соображения логики, даже не зная его формулировки. Но зная этот, принцип проще догадаться в каких задачах его можно применить. В наиболее простой шуточной формулировке он утверждает: «Если в пяти клетках сидят шесть кроликов, то найдется клетка, в которой сидит не менее чем два кролика».

Обратим внимание, что согласно принципу Дирихле мы не можем сказать точно в какой клетке сидят сразу несколько кроликов, и не знаем какое точное число кроликов сидит в такой клетке. По принципу Дирихле мы можем лишь быть уверены, что такая клетка существует.

Приведем более общие формулировки.

Принцип Дирихле: если в N клетках не менее N +1 кроликов, то в какой-то клетке сидят хотя бы 2 кролика.

Обобщённый принцип Дирихле: если в N клетках не менее kN + 1 кроликов, то хотя бы в одной клетке сидит не менее чем k + 1 кролик.

Доказательство принципа Дирихле простое, но заслуживает внимания, поскольку похожие рассуждения часто встречаются. Приведем доказательство методом от противного для обобщенного принципа Дирихле.

Доказательство. Предположим, что в каждой клетке сидит не более чем k кроликов. Тогда всего кроликов не более kN, а по условию их не меньше чем kN +1. Получили противоречие, которое опровергает наше предположение.

Удивительно, что на основе такого простого и понятного принципа удается решать весьма сложные содержательные задачи из различных разделов математики. Главное — понять, что в задаче «клетки», а что «кролики». Часто в этом и заключается творческая часть решаемой задачи.

Пример1. В школе 400 учеников. Докажите, что хотя бы двое из них родились в один день года.

Решение. В качестве «клеток» выступают дни в году (их не более 366), а в качестве «кроликов» школьники. Т.е. так как различных дат в календаре не более 366, а школьников 400, то по меньшей мере двое из них родились в один день.

Задача2. В клетках таблицы 3 × 3 расставлены числа −1, 0, 1. Докажите, что какие-то две из 8 сумм по всем строкам, всем столбцам и двум главным диагоналям будут равны.

Решение. Эти суммы могут принимать лишь 7 разных значений: от −3 до 3. Значит, какие-то две из них равны.

Пример3. В классе 30 учеников. В диктанте Вова сделал 13 ошибок, а остальные ученики — меньше. Докажите, что по крайней мере три ученика сделали ошибок поровну.

Решение. Каждый из остальных 29 учеников сделал не более 12 ошибок. Пусть имеется 13 комнат («клетки») с табличками 0, 1, 2, ..., 12. Каждого школьника («кролика») попросим зайти в комнату с такой табличкой, сколько у него ошибок. Так как 29 > 2 · 13, то в какую-то комнату войдет не менее трех человек.

Пример4. Докажите, что в любой компании из 10 человек есть двое, имеющие одинаковое число знакомых в этой компании.

Решение. В компании из 10 человек у каждого участника может быть от 0 до 9 знакомых. Рассмотрим 10 комнат с табличками 0, 1, 2, ..., 9. Каждого участника попросим зайти в комнату с такой табличкой, сколько у него знакомых. На первый взгляд кажется, что принцип Дирихле здесь не поможет, имеется 10 человек и 10 комнат. Однако заметим, что комнаты с номерами 0 и 9 не могут быть заняты одновременно. Поэтому все 10 человек зашли не более чем в 9 комнат. Следовательно, по крайней мере два человека вошли в одну комнату, а это означает что у них одинаковое число знакомых.

Пример5. На координатной плоскости отмечено 5 целочисленных точек (обе координаты каждой точки — целые числа). Докажите, что середина хотя бы одного из отрезков, соединяющих какие-то две из этих точек, также является целочисленной точкой.

Решение. Заметим, что середина отрезка с концами в точках

(a; b) и (c; d) имеет вид . Для координат любой

целочисленной точки есть четыре возможности: (Ч; Ч), (Ч; Н), (Н; Ч), (Н; Н). Здесь Ч обозначает четную координату, а Н — нечетную. Так как точек 5, то найдутся, по крайней мере, две точки, которые имеют одинаковый вид — они и будут искомыми.

Пример6. Внутри равностороннего треугольника со стороной 1 расположено 5 точек. Доказать, что расстояние между некоторыми двумя из них меньше 0,5.

Решение. Проведем средние линии в этом треугольнике. Они разбивают его на четыре маленьких равносторонних треугольника со стороной 0,5. Назовём их «клетками», а точки будем считать «кроликами». По принципу Дирихле из пяти точек хотя бы две окажутся в одном из четырёх треугольников (см. рисунок). Расстояние

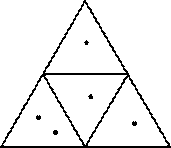
между этими точками меньше 0,5, поскольку точки не могут лежать в вершинах маленьких треугольников. (Здесь использована известная лемма о том, что длина отрезка, расположенного внутри треугольника, меньше длины его наибольшей стороны.)

Пример7. Докажите, что из 100 целых чисел можно выбрать одно или несколько чисел так, чтобы их сумма оканчивалась двумя нулями.

Решение. Пусть даны числа x₁, x₂, ..., x₁₀₀. Рассмотрим другие 100 чисел: x₁, x₁+x₂, ..., x₁+x₂+...+x₁₀₀и их остатки при делении на 100. Если один из остатков ноль, то искомая сумма найдена. В противном случае, две суммы дают одинаковый остаток от деления на 100. Пусть это суммы

x₁+ x₂+ ... + x_mи x₁+ x₂+ ... + x_k,

причем m < k. Тогда их разность

(x₁+ x₂+ ... + x_k) − (x₁+ x₂+ ... + x_m) = x_m₊₁+ x_m₊₂+ ... + x_n

делится на 100.

Приведем еще несколько различных формулировок принципа Дирихле.

Непрерывный принцип Дирихле: Если n кроликов съели S

кг травы, то какой-то кролик съел не меньше кг и какой-то съел n

не больше кг.

Более строго этот принцип можно записать так:

Если среднее арифметическое нескольких чисел равно a, то либо все они равны a, либо среди этих чисел найдутся два числа, одно из которых больше a, а другое меньше a.

Принцип Дирихле для длин и площадей:

1.Если на отрезке длины L расположено несколько отрезков с суммой длин больше L, то хотя бы два из них имеют общую точку.

2.Если внутри фигуры площади S находится несколько фигур, имеющих сумму площадей больше S, то хотя бы две из них имеют общую точку.

3.Если на отрезке длины L расположено несколько отрезков, сумма длин которых больше k · L, то по крайней мере одна точка покрыта не менее чем k + 1 из этих отрезков.

4.Если внутри фигуры площади S находится несколько фигур, сумма площадей которых больше k · S, то из этих фигур можно выбрать по крайней мере k + 1, которые имеют общую точку.

Принципнедостаточности: Если в n клетках сидит менее n(n − 1) кроликов, то найдутся две клетки, в которых одинаковое

2 количество кроликов (может быть, ни одного).

Пример8. К празднику 10 мальчиков надули 44 шарика, среди них 11 красных, а остальные — других цветов. Докажите, что:

а) найдется мальчик, надувший по крайней мере два красных шарика;

б) найдется мальчик, надувший по крайней мере 5 шариков;

в) найдутся два мальчика, надувшие одинаковое количество шариков (может быть, ни одного).

Решение. а) Так как мальчиков 10, а красных шариков 11, то по принципу Дирихле найдется мальчик, надувший не менее двух шариков.

б) Так как мальчиков («клетки») 10, а шариков («кроликов») 44,

причем 44 > 4 · 10, то какой-то мальчик надул не менее 5 шариков.

в) Если бы мальчики надули разное количество шариков, то шариков было бы не менее 0+1+2+...+9 = 45, а их 44. (Принцип недостаточности.) Значит, какие-то два мальчика надули одинаковое количество шариков.

Пример9. В квадрате площадью S расположены 2018 фигур, сумма площадей которых больше 2017S. Докажите, что у всех этих фигур есть общая внутренняя точка.

Решение. Утверждение данной задачи непосредственно следует из принципа Дирихле для площадей. Однако мы приведем более подробное доказательство.

Пусть S₁, S₂, ..., S₂₀₁₈— площади данных фигур, а S₁, S₂, ...,

S₂₀₁₈— площади фигур, дополняющих их до квадрата. Понятно, что

S_k+ S_k= S. По условию S₁+ S₂+ ... + S₂₀₁₈> 2017S, поэтому

Таким образом, сумма площадей дополняющих фигур меньше площади квадрата, и, значит, они не могут покрыть весь квадрат, т.е. найдётся точка, не принадлежащая ни одной из них. Тогда эта точка принадлежит каждой из исходных фигур и является искомой.

Задача 10. Даны 7 отрезков. Длина каждого больше 10 см и меньше 1 м. Докажите, что из каких-то трех можно составить треугольник.

Решение. Расположим отрезки по величине: a₁6 a₂6 ... 6 a₇. Из отрезков можно составить треугольник тогда и только тогда, когда найдется такое k, что a_k+ a_k₊₁> a_k₊₂. Предположим, утверждение задачи неверно. Значит, a_k+ a_k₊₁6 a_k₊₂(k = 1, 2, ..., 5.) Но тогда a₃> 20, a₄> 30, ..., a₇> 130 см. Противоречие.

Пример11. Докажите, что в каждом девятиугольнике есть пара диагоналей, угол между которыми меньше 7^◦.

Решение. Докажем сначала вспомогательную лемму.

n(n − 3)

Лемма: Число диагоналей n-угольника равно .

Доказательство. В качестве первого конца диагонали можно взять любую из n вершин, а в качестве второго — любую из n − 3 вершин, отличной от выбранной и двух соседних с ней. Получим n(n−3) варианта соединить вершины многоугольника. Однако, при таком подсчете каждая диагональ учитывается дважды, следоваn(n − 3)

тельно, число диагоналей равно . Лемма доказана.

9 · 6

По доказанной лемме у девятиугольника = 27 диагоналей.

Через произвольную точку плоскости проведем 27 прямых параллельно этим диагоналям. Получим 54 угла. Если каждый из этих углов не меньше 7^◦, то их сумма не меньше 54 · 7^◦= 378^◦> 360^◦, что невозможно.

Пример12. В классе 22 ученика. Когда каждому выставили годовые оценки по всем 10 предметам (тройку, четверку или пятёрку), оказалось, что у любых двух учеников хотя бы по одному предмету оценки различаются. Докажите, что можно найти двух таких учеников и два таких предмета, что по первому предмету лучше успевает первый ученик, а по второму — второй.

Решение. Рассмотрим сумму оценок каждого ученика по всем 10 предметам. Наименьшее значение, которое может принимать эта сумма, равно 30, а наибольшее — 50. Таким образом, сумма всех оценок может принимать только 21 различное значение. Так как в классе учатся 22 ученика, то по принципу Дирихле найдутся по крайней мере два ученика, у которых суммарные оценки одинаковы. По условию задачи у этих учеников оценки отличаются хотя бы по одному предмету — пусть оценка первого выше. Тогда по какому-то другому предмету оценка первого должна быть ниже, чем у второго.

Пример13. Петя нарисовал окружность и отметил на ней 25 точек. Потом Витя провёл какие-то 6 отрезков с концами в этих точках. Докажите, что после этого Петя сможет провести ещё один такой отрезок, не имеющий общих точек ни с одним из проведенных Витей.

Решение. Когда Витя проводил шесть отрезков, он занял не более 6·2 = 12 точек из двадцати пяти имеющихся на окружности. Эти точки разбили окружность не более чем на 12 дуг.Осталось по меньшей мере еще 13 «свободных» точек, как-то распределенных по этим дугам. По принципу Дирихле хотя бы в одну дугу попадет не менее двух точек. Петя может их соединить, и этот отрезок не будет пересекать ни один из ранее проведённых.

Пример14. Дано 11 различных натуральных чисел, не больших 20. Докажите, что из них можно выбрать два числа, одно из которых делится на другое.

Замечание. Данную задачу можно сформулировать в общем виде. Если из множества {1, 2, 3, ..., 2n} выбрать любые n + 1 число, то среди них найдутся два таких числа, что одно делит другое.

Решение. Способ I. Разобьем числа от 1 до 20 на 10 множеств (наборов чисел), в каждом из которых в любой паре чисел одно делится на другое: {11}, {13}, {15}, {17}, {19}, {1,2,4,8,16}, {3,6,12}, {5,10,20}, {7,14}, {9,18}. Так как нам дано 11 чисел, то какие-то два числа принадлежат одному множеству, а тогда одно из них делится на другое.

Способ II. Приведем доказательство для задачи в общем виде. Представим каждое из данных n+1 чисел в виде 2^k·m, где k — целое неотрицательное число, а m — нечетное число, 1 6 m 6 2n−1. Так как среди чисел от 1 до 2n только n нечетных, то среди данных чисел должны найтись два числа с одинаковыми нечетными делителями.

Поэтому одно из них делится на другое.

Задачи для самостоятельного решения

Задача1. Докажите, что среди любых шести целых чисел найдутся два числа, разность которых кратна 5.

Задача 2. 100 человек сидят за круглым столом, причем более половины из них — мужчины. Докажите, что какие-то двое мужчин сидят друг напротив друга.

Задача 3. 10 школьников на олимпиаде решили 35 задач. Среди них есть школьники, решившие ровно одну задачу, школьники, решившие ровно две задачи, и школьники, решившие ровно три задачи. Докажите, что есть школьник, решивший не менее пяти задач.

Задача 4. Цифры 1, 2, ..., 9 разбили на три группы. Докажите, что произведение чисел в одной из групп не меньше 72.

Задача 5. Докажите, что равносторонний треугольник нельзя покрыть двумя меньшими равносторонними треугольниками.

Задача 6. В ковре размером 4 м× 4 м моль проела 15 дырок. Докажите, что из него можно вырезать коврик размером 1 м× 1 м, не содержащий внутри себя дырок. (Дырки считайте точечными.)

Задача 7. На картине 20 см × 15 см сидят 40 комаров. Докажите, что за один удар можно прихлопнуть не менее четырех комаров круглой мухобойкой радиусом 5 см.

Задача 8. Докажите, что существует число вида 222...2, которое делится на 2018.

Задача 9. Докажите, что существует степень тройки, оканчивающаяся на 001.

Задача 10. Имеется 101 пуговица одного из 11 цветов. Докажите, что либо среди этих пуговиц найдутся 11 пуговиц одного цвета, либо 11 пуговиц разных цветов.

Задача 11. В классе 25 человек. Известно, что среди любых трёх из них есть двое друзей. Докажите, что есть ученик, у которого не менее 12 друзей.

Тема 2. Принцип крайнего

При решении многих задач бывает полезно рассмотреть некоторую крайнюю или экстремальную величину (элемент, характеристику), связанную с задачей. Крайними свойствами может обладать и объект, с виду расположенный в середине (узкое место).Этот метод решения задач называется принципом (правилом) крайнего.

Пример1. В 100-угольнике каждый угол равен полусумме соседних. Докажите, что все углы равны.

Решение. Рассмотрим наибольший угол α многоугольника (любой из них, если несколько). Так как он является средним арифметическим двух соседних, то он не больше каждого из них. Тогда, соседние углы тоже равны α. Аналогичным образом, рассматривая соседние углы к соседним и т.д., двигаясь по цепочке, доказываем, что все углы равны.

Замечание. Ключевая идея в решении данной задачи — рассмотреть самый большой угол многоугольника. Этот угол и является «крайним» элементом.

Пример2. На каждой из 15 планет, расстояния между которыми попарно различны, находится по астроному, который наблюдает ближайшую к нему планету. Докажите, что некоторую планету никто не наблюдает.

Решение. Так как расстояния между планетами попарно различные, то рассмотрим две планеты, расстояние между которыми наименьшее среди всех попарных расстояний. Ясно, что астрономы, находящиеся на этих двух планетах, смотрят друг на друга. Рассмотрим оставшиеся 13 планет. Если хотя бы один из астрономов с этих планет смотрит на одну из двух выбранных планет, то на все 13 планет не хватит наблюдателей, т.е. среди этих планет найдется та, которую никто не наблюдает. Если же ни на одну из выбранных двух планет никто не смотрит, то эти две планеты можно не рассматривать и повторить все рассуждения для 13 планет.

Рассуждая так и далее, мы найдем планету, которую никто не наблюдает (используем, что 15 — нечетное число).

Пример3. Докажите, что числа от 1 до 16 можно записать в строку, но нельзя записать по кругу так, чтобы сумма любых двух соседних была квадратом натурального числа.

Решение. Рассмотрим самое большое число 16 («крайний» элемент) и найдем числа, которые могут стоять с ним рядом.

Пусть рядом с числом 16 стоит число x. Тогда

16 + 1 6 16 + x = a²6 16 + 15,

откуда a²= 25, а x = 9. Таким образом, мы получили, что у числа 16 не более одного соседа, и удовлетворяющее условию расположение чисел по кругу не возможно.

Приведем пример расположения чисел в строку: 16, 9, 7, 2, 14, 11, 5, 4, 12, 13, 3, 6, 10, 15, 1, 8.

Пример4. Можно ли натуральные числа от 1 до 99 выписать в строку так, чтобы разность любых двух соседних (из большего вычитается меньшее) была не меньше 50? Тот же вопрос для чисел от 1 до 100?

Решение. Число 50 делит числа от 1 до 99 на 2 равные части, т.е. число 50 стоит посередине. Заметим, что рядом с этим числом нельзя поставить никакое другое так, чтобы было выполнено условие задачи. Значит, указанным образом числа расставить нельзя.

Для ответа на второй вопрос сначала заметим, что у чисел 50 и 51 может быть только один сосед 100 и 1 соответственно. Поэтому эти числа стоят крайними слева и справа. Далее приведем пример, показывающий, что требуемая расстановка возможна: 51, 1, 52, 2, 53, 3, ..., 99, 49, 100, 50.

Пример5. На тарелке лежат 9 разных кусочков сыра. Всегда ли можно разрезать один из них на две части так, чтобы полученные 10 кусочков делились бы на две порции равной массы по 5 кусочков в каждой?

Решение. Расположим кусочки в порядке возрастания массы: m₁< m₂< ... < m₉. В одну порцию положим 1-й, 3-й, 5-й и 7-й кусочки, в другую — 2-й, 4-й, 6-й и 8-й. Тогда

m₁+ m₃+ m₅+ m₇< m₂+ m₄+ m₆+ m₈.

Добавим теперь 9-й кусочек в первую порцию. Так как m₉> m₈, m₇> m₆, m₅> m₄, m₃> m₂, а m₁> 0, то m₁+ m₃+ m₅+ m₇+ m₉> m₂+ m₄+ m₆+ m₈.

Следовательно, достаточно разрезать 9-й кусочек. Более строго от

9-го кусочка необходимо отрезать кусок массой

и положить его во вторую порцию.

Пример6. Докажите, что число

, (n > 2)

не является целым.

Решение. Рассмотрим знаменатели всех дробей, входящих в сумму S. Среди этих знаменателей найдется число вида 2^k, где k — максимальное, т.е. 2^k6 n < 2^k⁺¹. Заметим, что среди чисел от 1 до n только одно делится нацело на 2^k(само число 2^k). Действительно, предположим, что есть еще ходя бы одно такое число a. Тогда

2^k< a 6 n < 2^k⁺¹. При этом разность a − 2^k< 2^k⁺¹− 2^k= 2^k

^k. Пришли к противоречию, так как 0 < a − 2^k< 1. делится на 2

Приведем все слагаемые в сумме S к наименьшему общему знаменателю. Во все дроби, кроме , число 2 войдет как дополнительный множитель, а у этой дроби дополнительным множителем обязательно будет нечетное число. У всей дроби S знаменатель, конечно, является четным числом, а числитель, как мы видим, состоит из суммы некоторого числа четных чисел и одного нечетного.

Следовательно, числитель — нечетное число, а потому вся дробь не может быть целой.

Пример7. На каждой стороне произвольного четырехугольника, как на диаметре, построена окружность. Доказать, что четыре построенных круга полностью покроют четырехугольник.

Решение. Обозначим данный четырехугольник ABCD (заметим, что приведенное решение проходит и для невыпуклого четырехугольника). Пусть M — произвольная точка внутри четырехугольника. Рассмотрим максимальный угол среди углов AMB, BMC, CMD, DMA. Пусть это будет, например, угол AMB (см.

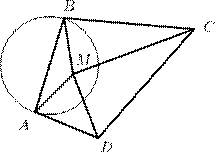
рис.). Тогда ∠AMB > 90^◦(в противном случае ∠AMB +∠BMC +

+ ∠CMD + ∠DMA < 4 · 90^◦= 360^◦). Следовательно точка M покроется кругом, построенном на отрезке AB, как на диаметре.

Пример8. Из точки внутри выпуклого многоугольника опускают перпендикуляры на его стороны или их продолжения. Докажите, что хотя бы один перпендикуляр попадет на сторону.

Решение. Предположим, что внутри некоторого выпуклого многоугольника нашлась точка O такая, что все перпендикуляры опущенные на прямые, содержащие стороны падают на продолжения сторон. Рассмотрим наименьший перпендикуляр. Пусть он опущен на сторону AB (см. рис.). Перпендикуляр OH к прямой AB пересекает прямую, содержащую сторону BC, в точке K. Но тогда расстояние от точки O до этой прямой меньше, чем длина отрезка OK, который в свою очередь короче отрезка OH, а значит прямая, содержащая сторону AB, не была ближайшей к точке O.

Противоречие.

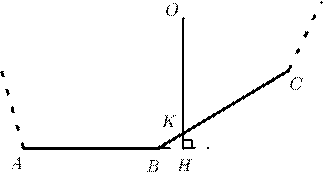
Замечание. У данной задачи есть механическое решение. Представим, что многоугольник вырезан из листа пенопласта некоторой толщины. Поместим в этот многоугольник один или несколько маленьких грузиков так, чтобы центр масс системы совпадал с точкой O. Если поставить такой многоугольник (призму) на горизонтальную поверхность, то он будет бесконечно катится по этой поверхности, так как перпендикуляр из точки O (центра масс) всегда падает не на сторону, а на ее продолжение. Получим вечный двигатель, чего, как известно, не существует.

Пример9. Докажите, что у многогранника есть две грани с одинаковым числом сторон.

Решение. Рассмотрим грань многогранника с наибольшим числом сторон, равным n. К этой грани примыкает ровно n его различных граней, следовательно, всего у данного многогранника имеются не менее чем n+1 граней. Осталось заметить, что количество возможных вариантов числа сторон у грани равно n−2, так как меньше трех сторон у каждой из них быть не может. Следовательно, найдутся по крайней мере две грани с равным числом сторон (принцип Дирихле).

Пример10. В некоторой стране 100 аэродромов, причем все попарные расстояния между ними различны. С каждого аэродрома поднимается самолет и летит на ближайший к нему аэродром. Докажите, что ни на один аэродром не может прилететь больше пяти самолетов.

Решение. Если самолеты из точек A и B прилетели в точку O, то AB — наибольшая сторона треугольника AOB, т. е. ∠AOB > 60^◦. Предположим, что в точку O прилетели самолеты из точек A₁, ...,

A_n. Тогда один из углов A_iOA_jне превосходит . Поэтому

т. е. n < 6.

Задачи для самостоятельного решения

Задача1. По кругу выписано 2018 чисел, каждое из которых равно среднему арифметическому своих соседей. Докажите, что все числа равны.

Задача2. Среднее арифметическое десяти различных натуральных чисел равно 15. Найдите наибольшее значение наибольшего из этих чисел.

Задача3. Докажите, что если длины всех сторон треугольника меньше 1, то его площадь меньше .

Задача4. Легко распилить кубик 3 × 3 × 3 на 27 кубиков шестью распилами. Можно ли уменьшить число распилов, если части разрешается перекладывать и пилить по несколько частей сразу?

Задача5. По окружности записаны 30 чисел. Каждое из этих чисел равно модулю разности двух чисел, стоящих после него по часовой стрелке. Сумма всех чисел равна 1. Найти эти числа.

Задача6. В течение дня в библиотеке побывало 100 читателей. Оказалось, что в тот день из любых трёх читателей двое в библиотеке встретились. Докажите, что сотрудник библиотеки мог сделать важное сообщение в такие два момента времени, чтобы все 100 человек его услышали. (Каждый читатель побывал в библиотеке только один раз.)

Задача7. На плоскости задано множество точек. При этом каждая точка этого множества является серединой отрезка двух каких-то других точек этого множества. Докажите, что множество — бесконечное.

Задача8. На небе бесконечное число звёзд. Астроном приписал каждой звезде пару натуральных чисел, выражающую яркость и размер. При этом каждые две звезды отличаются хотя бы в одном параметре. Докажите, что найдутся две звезды, первая из которых не меньше второй как по яркости, так и по размеру.

Задача9. Гости за круглым столом ели изюм из корзины с 2019 изюминками. Оказалось, что каждый съел либо вдвое больше, либо на 6 меньше изюминок, чем его сосед справа. Докажите, что были съедены не все изюминки.

Задача10. В городе N с каждой станции метро на любую другую можно проехать. Доказать, что одну из станций можно закрыть на ремонт без права проезда через неё так, чтобы с любой из оставшихся станций можно было по-прежнему проехать на любую другую.

Тема 3. Инвариант и полуинвариант

Инвариантом некоторого преобразования называется величина или свойство, не изменяющееся при этом преобразовании.

В качестве инварианта могут выступать: четность, остатки от деления, алгебраическое выражение от данных задачи, выделенная часть объекта, раскраска и др.

На самом деле школьники знакомятся с понятием инварианта на уроках физики когда изучают законы сохранения энергии и импульса. Полная механическая энергия и импульс замкнутой системы тел является инвариантом при их взаимодействии.

Полуинвариантом называется величина, значение которой изменяется монотонно (не убывает или не возрастает) при заданных преобразованиях.

Понятие полуинварианта часто используется при доказательствах остановки процессов.

Пример1. На доске написаны шесть чисел: 1, 2, 3, 4, 5, 6. За один ход разрешается к любым двум из них одновременно добавлять по единице. Можно ли за несколько ходов все числа сделать равными?

Решение. Нет. Сумма написанных чисел нечётна. За каждый ход эта сумма увеличивается на 2, т.е. всегда остаётся нечётной, а сумма шести равных чисел всегда чётна. Инвариантом данного преобразования является четность суммы всех чисел.

Замечание. Если выбранный инвариант даёт одинаковые значения для двух объектов, это ещё не значит, что один можно получить из другого указанными операциями!

Пример2. На доске написаны числа 1, 2, ..., 2018. Разрешается стереть любые два числа и вместо них написать их разность. Повторив эту операцию 2017 раз, мы получим одно число. Докажите, что это число не может быть нулем.

Решение. Пусть на некотором шаге стерли 2 числа a и b, a > b. Перед этим сумма всех чисел была равна S + a + b, а потом

S + a − b = (S + a + b) − 2b,

где S — сумма оставшихся на доске чисел, кроме a и b.

Таким образом, четность суммы на каждом шаге не меняется. Осталось заметить, что первоначальная сумма 1 + 2 + ... + 2018 состоит из 1009 четных и 1009 нечетных чисел, следовательно, она нечетна. Значит, последнее число не может быть ноль.

Пример3. 100 фишек выставлены в ряд. Разрешено менять местами две фишки, стоящие через одну фишку. Можно ли с помощью таких операций переставить все фишки в обратном порядке?

Решение. Так как разрешено менять местами фишки, стоящие через одну, то фишки которые стояли на нечетных местах при всех таких операциях останутся на местах с нечетными номерами.

Значит, первая фишка не может оказаться на 100 месте.

Пример4. На чудо дереве растет 49 апельсинов и 50 бананов. Разрешено срывать одновременно два фрукта. Если срывают два одинаковых фрукта, то вместо них мгновенно вырастает один банан. Если же срывают два разных фрукта, то вместо них мгновенно вырастает один апельсин. Через некоторое время на дереве остался один фрукт. Что это за фрукт — банан или апельсин?

Решение. Если с дерева сорвать два одинаковых фрукта, то число апельсинов либо не изменяется, либо уменьшается на два. Если же с дерева сорвать два разных фрукта, то число апельсинов не меняется. Таким образом, инвариантом данного преобразования является четность числа апельсинов. Так как число апельсинов вначале было нечетным, то последний сорванный фрукт — апельсин.

Пример5. а) На столе стоят 7 стаканов дном вверх. Разрешено переворачивать одновременно любые два стакана. Можно ли поставить все стаканы дном вниз? б) Тот же вопрос для 7 стаканов, но переворачиваются любые 6. в) То же для 8 стаканов, переворачиваются — 7.

Решение. а) Способ I. Если стакан переворачивается четное число раз, то он оказывается в начальном положении. Поэтому чтобы поставить все стаканы дном вниз, нужно каждый стакан перевернуть нечетное число раз. Общее количество переворачиваний также будет нечетным (сумма семи нечетных слагаемых). Но по условию за один раз переворачивается 2 стакана, значит, общее количество переворачиваний — четное.

Способ II. Поставим в соответствие каждому стакану, стоящему дном вверх, число 0, а стоящему дном вниз — число 1. Рассмотрим сумму всех чисел, соответствующих любому положению. При переворачивании любых двух стаканов эта сумма либо изменяется на 2, либо не меняется. Таким образом, остаток от деления указанной суммы на два является инвариантом. В начальном положении, соответствующая сумма и остаток равны 0, а стаканам, стоящим дном вниз, соответствует сумма 7, остаток от деления на 2 — 1.

Поэтому поставить дном вниз все стаканы не возможно.

б) Ответ: нельзя. Решение аналогично пункту а).

в) Ответ: можно. Первый раз переворачиваем все стаканы кроме первого, второй раз — кроме второго, ..., восьмой раз — все кроме восьмого. Таким образом, каждый стакан будет перевернут 7 раз, поэтому окажется в положении «дном вниз», что и требовалось.

Пример6. Набор чисел a, b, c каждую секунду заменяется на a + b − c, b + c − a, c + a − b. В начале имеется набор чисел 2016, 2018, 2019. Может ли через некоторое время получиться набор 2017, 2018, 2019.

Решение. Не может. Инвариант — сумма трех чисел.

Пример7. На доске написаны числа 1, 2, 3, ..., 19, 20. Разрешается стереть любые два числа a и b и вместо них написать число а) a+b−1; б) ab+a+b. Какое число может остаться на доске после 19 таких операций?

Решение. а) Способ I. После каждой такой операции сумма всех выписанных на доске чисел уменьшается на 1 (полуинвариант). Поэтому после 19 операций на доске останется число

1 + 2 + ... + 19 + 20 − 19 = 191.

Данная задачу полезно решить, используя понятие инвариант.

Способ II. Рассмотрим величину X равную сумме всех чисел, уменьшенную на их количество. Пусть на доске было n чисел, а с числами a и b провели указанную операцию. Обозначим: S — сумма всех чисел на доске, кроме a и b. Тогда до преобразования величина X равнялась S + a + b − n, а после преобразования X = S + + (a + b − 1) − (n − 1) = S + a + b − n. Значит, значение величины

X при указанных преобразованиях не меняется, она — инвариант. Вначале X = 1+2+3+...+19+20−20 = 190. Значит, и после 19 операций, когда на доске останется одно число x, X = x − 1 = 190, откуда x = 191.

б) Идеей для поиска инварианта является следующее тождество: ab + a + b + 1 = (a + 1)(b + 1).

Пусть в какой-то момент времени на доске записаны числа a₁, a₂, ..., a_n. Рассмотрим произведение Π всех чисел, увеличенных на

Π = (a₁+ 1)(a₂+ 1)(a₃+ 1) · ... · (a_n+ 1).

Без ограничения общности можем считать, что мы стерли два числа a₁и a₂, и вместо них записали новое число a₁a₂+ a₁+ a₂. Тогда на доске будет n − 1 число:

a₁a₂+ a₁+ a₂, a₃, ..., a_n,

которым соответствует произведение

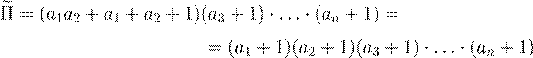Как мы видим, Π = Πe, т.е. произведение всех чисел, увеличенных на единицу, является инвариантом.

Пусть на доске осталось последнее число x. Тогда x + 1 = (1 + 1)(2 + 1)(3 + 1) · ... · (20 + 1),

откуда x = 21! − 1.

Пример8. Вася разорвал листок бумаги на 10 частей, некоторые из получившихся кусков он снова разорвал на 10 частей и т.д. Мог ли он получить 2018 кусков бумаги?

Решение. Вася забирает один кусок а добавляет 10, таким образом, каждый раз количество кусков увеличивается на 9. Инвариантом такого преобразования является остаток от деления числа кусков на 9. Для числа 1 этот остаток равен 1, а для числа 2018 он равен 2. Значит, 2018 кусочков бумаги получиться не могло.

Пример9. На столе лежит куча из 637 ракушек. Из нее убирают одну ракушку и кучу делят на две (не обязательно поровну). Затем из какой-нибудь кучи, содержащей больше одной ракушки, снова убирают одну ракушку и снова кучу делят на две. И так далее. Можно ли через несколько ходов оставить на столе только кучи, состоящие из трех ракушек?

Решение. Заметим, что сумма числа ракушек и числа кучек является инвариантом. Вначале значение этого инварианта равно 637+1 = 638. Допустим, что через несколько ходов на столе осталось n кучек, состоящих из трех ракушек. При этом значение инварианта равно 3n + n = 4n. Таким образом, должно выполняться равенство

4n = 638.

Пришли к противоречию, 638 не делится на 4. Значит, мы не можем получить кучки, состоящие из трех камней.

Пример10. На 44 деревьях, расположенных по окружности, сидели 44 веселых чижа (на каждом дереве по чижу). Время от времени два чижа одновременно перелетают на соседние деревья в разных направлениях (один - по часовой стрелке, другой - против). Докажите, что чижи не смогут собраться на одном дереве.

Решение. Занумеруем деревья по порядку, начиная с некоторого дерева. Для каждого чижа рассмотрим номер дерева, на котором он сидит, и сложим эти 44 номера. Заметим, что в процессе перелетания чижей эта сумма либо не менятся, либо меняется на 44. Следовательно, остаток от деления данной суммы на 4 остается неизменным. Вначале сумма номеров деревьев равна 1+2+...+44 =

, что дает остаток 2 от деления на 4. Если

предположить, что все чижи перелетели на одно дерево с номером n, то рассматриваемая сумма станет равной 44n, т.е. станет делиться на 4. Тем самым, получено противоречие.

Пример11. В десяти сосудах содержится 1, 2, 3, ..., 10 литров воды. Разрешается перелить из сосуда A в сосуд B столько воды, сколько имеется в B. Можно ли добиться, чтобы после нескольких переливаний в 5 сосудах оказалось 3 литра, а в остальных 6, 7, 8, 9, 10?

Решение. Нельзя. Предложенная операция обладает полуинвариантом: при любом переливании число нечетных сосудов (содержащих нечетное число литров воды) не увеличивается. Количество таких сосудов уменьшается при переливании из нечетного сосуда в нечетный, а в остальных случаях не изменяется. Следовательно, переход из состояния 1, 2, ..., 10 в состояние 3, 3, 3, 3, 3, 6, ..., 10 невозможен, поскольку он увеличивает число нечетных сосудов.

Пример12. Вокруг поляны стоят 12 домиков, покрашенные в белый и красный цвета, в которых поселилось 12 гномов. У каждого гнома нечетное число друзей. В январе первый гном красит свой дом в тот цвет, в который окрашены дома большинства его друзей. В феврале это же делает второй (по часовой стрелке) и т.д. Докажите, что наступит момент, после которого цвет дома у каждого гнома перестанет меняться.

Решение. Рассмотрим число пар гномов-друзей, у которых дома разного цвета. Каждый месяц это число не увеличивается. Действительно, если цвет дома сохраняется, то число не меняется, если же цвет дома меняется, то это число уменьшается. Так как это число неотрицательно, оно не может бесконечно уменьшаться, значит, с того момента, когда оно перестанет меняться, каждый гном будет красить свой дом в один и тот же цвет.

Пример13. На плоскости дано 2n точек. Докажите, что эти точки можно соединить n непересекающимися отрезками.

Решение. Пусть точки попарно соединены отрезками произвольным образом. В качестве полуинварианта рассмотрим сумму длин этих отрезков. Если никакие два не имеют общих точек, то задача решена. В противном случае найдутся два отрезка, имеющих общую точку. Если эти отрезки лежат на одной прямой, то заменим их на непересекающиеся отрезки меньшей общей длины с концами в этих же точках. Пусть отрезки AB и CD не лежат на одной прямой и пересекаются в точке M (см. рис.). Тогда по неравенству

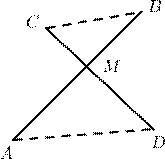
треугольника для △AMD и △BMC имеем:

AM + MD > AD,

BM + MC > CB.

Сложим полученные неравенства, тогда

AB + CD > AD + BC,

и сумма длин всех проведенных отрезков уменьшилась. Так как точек конечное число, то и способов их соединить отрезками конечно. Значит, в некоторый момент эта сумма длин перестанет уменьшатся, т.е. никакие два отрезка не пересекаются.

Пример14. Квадратное поле разбито на 100 одинаковых квадратных участков, девять из которых поросли бурьяном. Известно, что бурьян за год распространяется на те и только те участки, у каждого из которых не менее двух соседних участков уже поросли бурьяном (участки соседние, если они имеют общую сторону). Докажите, что это поле никогда не зарастет бурьяном полностью.

Решение. Не сложно проверить, что длина границы заросшего бурьяном участка (или нескольких участков) при указанных преобразованиях не возрастает (полуинвариант). В начальный момент она не превосходит 9 · 4 = 36, поэтому в конечный момент длина границы не может быть равной 40, т.е. периметру всего поля.

Пример15. Каждая из расположенных по кругу 12 ламп может находиться в одном из двух состояний: гореть или не гореть. За один ход можно изменить состояние любых трех ламп, расположенных подряд. Вначале горит только одна лампа. Можно ли добиться того, чтобы горели все 12 ламп?

Решение. Занумеруем лампы, начиная с горящей, по кругу числами от 1 до 12. Рассмотрим лампы с номерами 1, 2, 4, 5, 7, 8, 10, 11. Изменяя состояние любых трех ламп, мы изменим состояние ровно двух ламп из рассматриваемых. Среди них изначально горит одна лампа. Поскольку меняем каждый раз состояние ровно двух ламп из указанных, количество горящих ламп среди них всегда будет оставаться нечетным. Таким образом, все 12 ламп гореть не могут.

Задачи для самостоятельного решения

Задача1. Каждое число от 1 до 1000000 заменили суммой его цифр. С полученным набором чисел проделали то же самое, и так до тех пор, пока не получилось 1000000 однозначных чисел. Каких чисел получилось больше: единиц или двоек?

Задача2. На доске написаны 15 плюсов и 10 минусов. Разрешается стереть любые два знака и записать вместо них плюс, если они одинаковы, и минус, если они различны. Какой знак останется на доске после выполнения 24 таких операций?

Задача3. Можно ли накрыть доминошками (по 2 клетки) шахматную доску с вырезанными клетками a1 и h8? (Подсказка. См. Тема 4. Раскраски.)

Задача4. На прямой сидят три кузнечика, каждую секунду прыгает один кузнечик. Он прыгает через какого-нибудь кузнечика (но не через двух сразу). Докажите, что через 2019 секунд они не могут вернуться в исходное положение.

Задача5. В одной клетке квадратной таблицы 4 × 4 стоит минус, а в остальных плюсы. Разрешается одновременно менять знак во всех клетках, расположенных в одной строке или в одном столбце. Докажите, что сколько бы мы ни проводили таких перемен знака, нам не удастся получить таблицу из одних плюсов.

Задача6. На доске написано число 8ⁿ. У него вычисляется сумма цифр, у полученного числа вновь вычисляется сумма цифр, и так далее, до тех пор, пока не получится однозначное число. Что это за число, если n = 2018?

Задача7. Дана тройка чисел . Разрешается любые два числа заменить на следующие два числа: их сумму, деленную

на √2, и их разность, деленную на √2. Можно ли, проделав эту

операцию несколько раз, получить тройку чисел 1, √2, 1 − √2?

Задача8. На столе лежит куча из 1001 камня. Ход состоит в том, что из какой-либо кучи, содержащей более одного камня, выкидывают камень, а затем одну из куч делят на две. Можно ли через несколько ходов оставить на столе только кучки, состоящие из трех камней?

Задача9. В парламенте у каждого его члена не более трех врагов. Докажите, что парламент можно разбить на две палаты так, что у каждого парламентария в одной с ним палате будет не более одного врага.

Задача10. Написанное на доске четырехзначное число можно заменить на другое, прибавив к двум его соседним цифрам по единице, если ни одна из этих цифр не равна 9; либо, вычтя из соседних двух цифр по единице, если ни одна из них не равна 0. Можно ли с помощью таких операций из числа 1234 получить число 2018?

Тема 4. Раскраска

Иногда для решения задачи необходимо исследуемый объект раскрасить (может быть в несколько цветов).

Пример1. На каждой клетке доски 5 × 5 сидит жук. В некоторый момент все жуки взлетают и приземляются на соседние по стороне клетки. Докажите, что, по крайней мере, одна клетка останется пустой.

Решение. Раскрасим доску в шахматном порядке. Жуки с

черных клеток сядут на белые и наоборот. Так как всего имеется 13 черных клеток и 12 белых, то, по крайней мере, одна (черная) клетка останется пустой.

Пример2. Можно ли из 13 кирпичей 1 × 1 × 2 сложить куб 3 × 3 × 3 с дыркой 1 × 1 × 1 в центре?

Решение. Раскрасим маленькие кубики 1 × 1 × 1, из которых состоят куб и кирпичи, в белый и черный цвет в шахматном порядке. В 13 кирпичах поровну (по 13) черных и белых кубиков, а в кубе без центра одних — 12, а других — 14.

Пример3. Можно ли доску 10 × 10 разрезать на фигурки из четырёх клеток в форме буквы Г?

Решение. Воспользуемся «матрасной» раскраской доски 10 × 10 (т.е. покрасим столбцы через один в черный цвет). При такой раскраске получим 50 белых и 50 черных клеток. Каждая буква «Г» занимает нечётное число (1 или 3) черных клеток. Поэтому если бы доску можно было разрезать на 25 фигурок в виде буквы «Г», то черных клеток на доске было бы нечётное число (сумма 25 нечётных

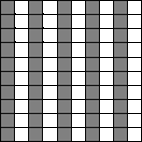
чисел). Пришли к противоречию, доску 10×10 разрезать на фигурки в виде буквы «Г» нельзя.

Пример4. Докажите, что доску размером 10 × 10 нельзя разрезать на прямоугольники 1 × 4.

Решение. Приведем несколько раскрасок, каждая из которых решает задачу.

В каждом способе предполагаем, что разрезать удастся, тогда число маленьких прямоугольников будет равно 100 : 4 = 25.

Способ I. Покрасим доску так, как изображено на рисунке 4.1. Тогда в каждом прямоугольнике 1×4 будет ровно одна закрашенная клетка, а значит должно быть ровно 25 закрашенных клеток. А их 26 штук. Противоречие.

Рис. 4.1 Рис. 4.2

Способ II. Покрасим доску так, как изображено на рисунке 4.2. Тогда в каждом прямоугольнике 1×4 будет ровно две закрашенные клетки, а значит должно быть ровно 25·2 = 50 закрашенных клеток.

А их 52 штуки. Противоречие.

Способ III. Покрасим доску так, как изображено на рисунке 4.3. Тогда в каждом прямоугольнике 1 × 4 будет либо одна, либо три закрашенные клетки, а значит закрашенных клеток должно быть нечетное количество (т.к. это сумма 25-ти нечетных чисел). А их 42 штуки. Противоречие.

Рис. 4.3 Рис. 4.4

Способ IV. Покрасим доску так, как изображено на рисунке 4.4. Тогда в каждом прямоугольнике 1 × 4 будет либо ноль, либо две закрашенные клетки, а значит закрашенных клеток должно быть четное количество. Ho всего имеется 25 черных клеток. Поэтому доску 10 × 10 нельзя разрезать на прямоугольники 1 × 4.

Способ V. Применим диагональную раскраску поля 10 × 10 в четыре цвета (см. пример 5). Тогда в каждом прямоугольнике 1×4 будут по одной клетке каждого цвета. Значит, количество клеток каждого цвета одинаково. Приходим к противоречию. Клеток первого и третьего цветов по 25, клеток второго цвета —26, а клеток четвертого цвета — 24.

Пример5.

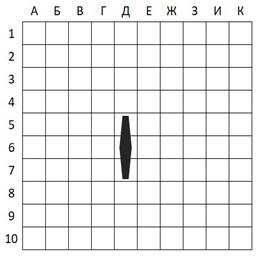
На поле размером 10 × 10 клеток для игры в «Морской бой» поставили корабль в прямоугольник размером 1×3 клетки. Можно ли, сделав 33 выстрела, наверняка в него попасть?

Решение. Способ I. Применим диагональную раскраску поля 10×10 в три цвета (рис. 5.1). На рисунке цвета обозначены цифрами 1, 2 и 3. Любой прямоугольник 1×3 содержит ровно по одной клетке каждого цвета. Заметим, что клеток первого цвета — 34, второго и третьего — по 33. Таким образом, выстрелив 33 раза во все клетки цвета 2 (или 3), мы однозначно попадем в корабль.

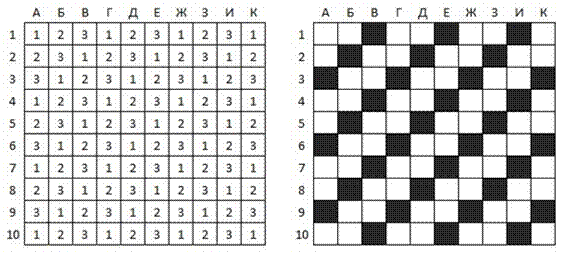
Рис. 5.1 Рис. 5.2

Способ II. Раскрасим поле 10×10 в два цвета (рис. 5.2). Любой прямоугольник 1 × 3 содержит ровно одну клетку черного цвета. Следовательно, выстрелив во все закрашенные клетки, мы однозначно попадем в корабль. Осталось посчитать число закрашенных клеток, их как раз 33.

Пример6. Для игры в классики на земле нарисованы клетки с числами от 1 до 10 (см. рис). Маша прыгнула снаружи в клетку

1, затем попрыгала по остальным клеткам (каждый прыжок — на соседнюю по стороне клетку) и выпрыгнула наружу из клетки 10.

Известно, что на клетке 1 Маша была 1 раз, на клетке 2 — 2 раза, ..., на клетке 9 — 9 раз. Сколько раз побывала Маша на клетке 10?

Решение. Покрасим клетки в шахматном порядке: клетки с нечетными числами будут белыми, а с четными — черными. Каждым прыжком Маша меняет цвет клетки. Более того, она начинает движение с белой клетки, а заканчивает на черной. Значит, клеток черного и белого цвета на её маршруте будет поровну. В белых клетках она побывает 1 + 3 + 5 + 7 + 9 = 25 раз, а в черных, кроме 10-ой клетки, 2 + 4 + 6 + 8 = 20 раз. Значит, в 10-ой клетке она побывает 5 раз. Можно построить соответствующий пример:

12323434545456565676767678787878989898989X9X9X9X9X,

где X = 10.

Пример7. На клетчатой бумаге отмечены произвольным образом 2000 клеток. Докажите, что среди них всегда можно выбрать 500 клеток, попарно не соприкасающихся друг с другом.

Решение. Покрасим бумагу в 4-цветную решетку (в каждом квадратике 2 × 2 содержатся клетки всех четырех цветов).

1	2	1	2	···
3	4	3	4	···
1	2	1	2	···
3	4	3	4	···
...	...	...	...	...

Клетки одного цвета между собой не соприкасаются. Клеток какого-то цвета отмечено хотя бы 500. Действительно, в противном случае всех отмеченных клеток было бы не более 499 · 4 = 1996 < 2000 (принцип Дирихле).

Пример8. Из листа клетчатой бумаги размером 29×29 клеточек вырезали 99 квадратиков 2 × 2 (режут по линиям). Доказать, что из оставшейся части листа можно вырезать ещё хотя бы один такой же квадратик.

Решение. Закрасим квадратики 2×2 как показано на рисунке. Заметим, что всего закрашено 10 · 10 = 100 таких квадратиков. Вырезая из исходного квадрата 29 × 29 любой квадратик 2 × 2, мы «задеваем» ровно один заштрихованный квадратик. Следовательно, после 99 таких операций один из них останется нетронутым.

Пример9. В спортклубе тренируются 100 толстяков весом от 1 до 100 кг. На какое наименьшее число команд их можно разделить так, чтобы ни в одной команде не было двух толстяков, один из которых весит вдвое больше другого?

Решение. Заметим, что наличие толстяков одинакового веса только упрощает задачу. Действительно, с каждым толстяком можно поместить в команду всех толстяков того же веса. При этом условие задачи по-прежнему будет выполнено. Значит, можно считать, что все 100 толстяков разного веса.

В частности, у каждого толстяка есть не более чем один товарищ, который вдвое легче него, и не более чем один, который вдвое тяжелее него.

Теперь заставим наших толстяков взяться за руки: каждый из них подаст левую руку тому, который вдвое тяжелее него (если такой есть), а правую — тому, который вдвое легче него (если такой есть).

Получится, что вся сотня разобьётся на непересекающиеся «цепочки». Причём в каждой цепочке самый правый — это самый лёгкий, а самый левый — это самый тяжёлый.

Раскрасим каждую цепочку в два цвета в шахматном порядке, начиная с самого лёгкого. Теперь сформируем две искомые команды по «цветному» признаку. Таким образом, всех толстяков можно распределить на две команды.

Задачи для самостоятельного решения

Задача1. Можно ли ходом коня обойти все клетки шахматной доски, начав с клетки а1, закончив в клетке h8 и на каждой клетке доски побывав ровно один раз?

Задача2. На каждой клетке доски 7 × 7 сидит жук. а) По команде все жуки одновременно переползают на соседние по стороне клетки. Докажите, что при этом хотя бы в одной клетке будет несколько жуков. б) По команде все жуки переползают в одну из соседних по диагонали клеток. Докажите, что после этого найдётся 7 свободных клеток.

Задача3. Ване дали целый ящик с фигурками в виде «пьедестала» (см. рисунок).

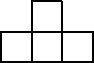
а) Сможет ли он замостить ими шахматную доску 8 × 8?

б) А доску 10 × 10?

Задача4. Из шахматной доски (размером 8 × 8) вырезали центральный квадрат размером 2 × 2. Можно ли оставшуюся часть доски разрезать на равные фигурки в виде буквы «Г», состоящие из четырёх клеток?

Задача5. Какое наибольшее количество прямоугольников 4×1 можно разместить в квадрате 6 × 6 (не нарушая границ клеток)?

Задача6. Замок имеет форму правильного треугольника, разбитого на 49 залов, каждый из которых тоже имеет форму правильного треугольника. В стене между любыми двумя залами есть дверь. Путник хочет обойти как можно больше залов, не заходя ни в один дважды. Какое наибольшее количество залов ему удастся обойти?

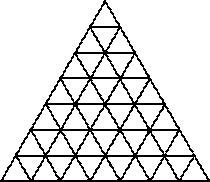
Задача7. Дно прямоугольной коробки выложено плитками размером 2 × 2 и 1 × 4. Плитки высыпали из коробки и потеряли одну плитку 2×2. Вместо нее достали плитку 1×4. Докажите, что выложить дно коробки плитками теперь не удастся.

Тема 5. Игры и стратегии

В данной теме рассмотрим задачи, в которых речь идет о достижении цели с помощью последовательности ходов. Как правило в таких задачах требуется выяснить, кто из игроков побеждает в той или иной игре. Решение такой задачи требует описания стратегии, правила выбора ходов, обеспечивающего достижение цели; в задачах про игры при этом требуется доказать, что стратегия обеспечивает выигрыш при любом поведении партнера.

Задачи по теме «игры и стратегии» условно можно разделить на три группы:

1) задачи в которых выигрышная стратегия базируется на идее симметрии или дополнения;

2) задачи, в которых рассуждения ведутся с конца, для отыскания начальных выигрышных позиций;

3) задачи, в которых результат игры не зависит от обоих игроков.

Следует отметить: в задачах с участием игроков, игроки ходят поочерёдно, пропускать ход запрещено.

Рассмотрим несколько игр, в который выигрышная стратегия базируется на идее симметрии или дополнения.

Пример1. Двое кладут по очереди пятаки на круглый стол. Проигрывает тот, кто не сможет положить очередной пятак. Кто выигрывает?

Решение. В этой игре выигрывает первый, независимо от размеров стола. Первым ходом он кладет пятак в центр стола так, чтобы их центры совпадали. После этого на каждый ход второго игрока начинающий отвечает симметричным ходом относительно центра стола. Важно заметить, что при такой стратегии после каждого хода первого игрока расположение монет на столе симметрично. Поэтому если возможен очередной ход второго игрока, то возможен и симметричный ему ход первого. Следовательно, он побеждает.

Пример2. Перед Бабой Ягой и Кащеем Бессмертным лежат две кучи мухоморов, в одной 100 штук, а в другой 150 штук. Эти персонажи по очереди берут грибы из куч, за один раз можно взять любое ненулевое число грибов из одной из куч. Пропускать ход нельзя, выигрывает тот, после хода которого грибов не останется. Первой ходит Баба Яга. Кто из игроков выиграет при правильной игре?

Решение. У Бабы Яги есть выигрышная стратегия. Первым ходом она уравнивает число мухоморов в обоих кучах (т.е. берет 50 мухоморов из второй кучи), а затем повторяет ход Кащея Бессмертного, только берет столько же мухоморов из соседней кучи. После каждого хода Бабы Яги в обоих кучках остается равное количество мухоморов.

Пример3. 1) На столе в ряд лежат 100 пирожных. За ход можно съесть одно пирожное или два, лежащих рядом. Проигрывает тот, кто не может сделать хода. Кто выиграет при правильной игре? 2) Кто выиграет, если пирожных не в ряд, а по окружности? 3) Рассмотрите оба способа расположения в случае 99 пирожных.

Решение. 1) У первого игрока есть выигрышная стратегия.

Своим первым ходом он съедает два пирожных в центре, то есть 50-е и 51-е пирожные. При этом ряд из пирожных разделился на два равных набора по 49 штук. Далее, после любого хода противника, начинающий съедает пирожные стоящие на тех же местах, на которых стояли пирожные, съеденные вторым игроком, только берет их из другого набора. Заметим, что после каждого хода первого игрока остаются два одинаковых набора пирожных.

Ответим сразу и на третий вопрос для случая, когда 99 пирожных расположены в ряд. Снова выиграет первый игрок, только своим первым ходом он должен съесть не два, а одно пирожное, стоящее в центре. Далее он повторяет ходы второго игрока.

2) В этом случае выиграет второй игрок.

Первый способ. После первого хода первого игрока «окружность

из пирожных» разрывается, и на столе останутся либо 99, либо 98 пирожных. Можем считать, что оставшиеся пирожные уже лежат в ряд. Затем, второй игрок, съедая одно или два пирожных (в зависимости от числа оставшихся пирожных), разбивает этот ряд на два одинаковых набора. Таким образом, он может на любой ход противника отвечать аналогичным ходом, но в другом наборе.

Заметим, что такая стратегия обеспечивает выигрыш второго игрока и для случая с 99-ю пирожными. Тем самым мы ответили на вторую часть третьего вопроса.

Второй способ. В случае 100 пирожных второй игрок может обеспечить себе выигрыш, пользуясь центрально симметричной стратегией, т.е. на каждый ход первого игрока он может ответить центрально симметричным ходом. Однако эта стратегия не подойдет для случая 99 пирожных.

Пример4. а) На столе лежит 20 спичек. Играющие по очереди могут взять одну, две или три спички. Кто не может сделать ход (спичек не осталось) проигрывает. б) Кто выиграет, если спичек не 20, а 21?

Решение. а) Заметим, что сколько бы спичек ни взял первый, второй может дополнить ход до четырех спичек (если первый взял одну, то второй берет четыре и т.п.). Тогда после хода второго игрока сначала останется 16 спичек, затем 12, затем, 8, 4 и , наконец, 0 — первый игрок проиграл.

б) В этом случае выиграет первый: первым ходом он должен взять одну спичку, а затем дополнять ход второго игрока до четырех.

Пример5. Ладья стоит на поле a1. За ход разрешается сдвинуть ее на любое число клеток вправо или на любое число клеток вверх. Выигрывает тот, кто поставит ладью на поле h8.

Решение. В этой игре побеждает второй игрок. Его стратегия такова: каждым своим ходом он возвращает ладью на диагональ a1 − h8. Первый игрок каждый раз вынужден будет уводить ладью с этой диагонали, а второй игрок после этого будет иметь возможность вернуть ладью на линию a1 − h8. Так как поле h8 принадлежит диагонали, то на него сумеет встать именно второй игрок.

В примерах 4 и 5 мы нашли выигрышную стратегию для одного из игроков. Но как до этого догадаться? Иногда выигрышную стратегию можно найти, проанализировав игру «с конца». Для этого необходимо выделить классы выигрышных и проигрышных позиций обладающих следующими свойствами:

’

1) завершающая игру позиция является выигрышной;

2) за ход из одной выигрышной позиции нельзя попасть в другую;

3) из любой невыигрышной позиции за один ход можно попасть в какую-то выигрышную.

Нахождение таких классов выигрышных и проигрышных позиций для игры равносильно ее решению. Действительно, к победе ведет такая стратегия: ходи в выигрышную позицию. Если исходная позиция выигрышная, то выигрывает второй (т.к. первый игрок, сделав один ход, попадает в проигрышную позицию). В противном случае выигрывает первый.

Проанализируем еще раз оба решения примеров 4 и 5.

Решение примера 4 а). Рассмотрим таблицу из 20 столбцов, соответствующим спичкам, лежащим на столе. Определим с конца выигрышные и проигрышные позиции. При этом выигрышную позицию будем обозначать знаком «+», а проигрышную — знаком «−».

Так как завершающая позиция выигрышная, то клетке с номером 20 соответствует знак «+». Предыдущие три спички является проигрышным позициями, т.е. если игрок завершает свой ход, взяв 17-ю, 18-ю или 19-ю спичку, то он проиграл. Поставим в эти клетки знак «−».

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
																			+

− − −

Если какой-то игрок взял 16-ю спичку, то его соперник попадет в одну из проигрышных позиций (17-ю, 18-ю или 19-ю), таким образом, 16-й клетке соответствует знак «+». Продолжая такой анализ, заполним таблицу полностью.

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
			+				+				+				+				+

− − − − − − − − − − − − − − −

Из этой таблицы видим, что т.к. начальная позиция проигрышная, то первый игрок, при правильной игре второго, проигрывает. Причем второй игрок может обеспечить себе выигрыш каждый раз, забирая спичку с номером, кратным четырем.

Решение примера 5). Завершающая позиция игры (ладья стоит на поле h8) — выигрышная. Поставим в эту клетку знак «+».

Позиции, из которых ладья может за один ход попасть на выигрышное поле h8 — проигрышные. Поэтому в остальных клетках верхней горизонтали и правой вертикали должен стоять знак «−»

(рис. 5.1).

Рис. 5.1 Рис. 5.2 Рис. 5.3

Далее замечаем, что позиция g7 выигрышная, поскольку любой ход из нее приводит противника в проигрышную позицию. Другие позиции на этой горизонтали или вертикали проигрышные, так как из них можно перевести ладью на поле g7 (рис. 5.2).

Далее все аналогично: позиция f6 — выигрышная, так как любой ход вверх или вправо ведет противника в проигрышную позицию. Остальные клетки на этой горизонтали или вертикали соответствуют проигрышной позиции. Позиция e5 снова выигрышная, остальные — проигрышные, и так далее (рис.5.3).

Таким образом, можем сделать вывод. Так как в начале игры ладья стоит в выигрышной позиции, то выигрывает второй игрок. Действительно, первый игрок своим первым ходом попадает в проигрышную позицию, а второй игрок всегда может поставить ладью обратно на диагональ с выигрышными позициями.

Решим еще несколько задач, связанных с анализом позиций.

Пример6. Ферзь стоит на поле 1 шахматной доски. За ход его можно передвинуть на любое число полей вправо, вверх, или по диагонали вправо-вверх. Выигрывает тот, кто поставит ферзя на клетку h8. Кто выигрывает при правильной игре?

Решение. Определим выигрышные позиции. Как обычно, завершающая позиция игры (ферзь стоит на h8) — выигрышная. Поставим в эту клетку знак «+». Позиции, из которых ферзь может за один ход попасть на выигрышное поле h8 — проигрышные. Поэтому в остальных клетках верхней горизонтали a8 − h8, правой вертикали h1−h8 и диагонали a1−h8 должен стоять знак «−» (см.

рис. 6.1). С позиций f7 и g6 за один ход можно попасть только

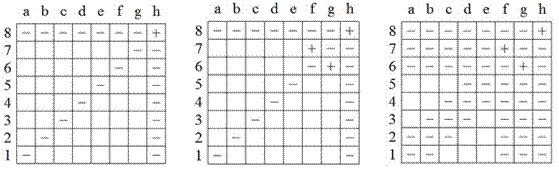
Рис. 6.1 Рис. 6.2 Рис. 6.3

на проигрышные поля. В эти клетки поставим знак «+» — они выигрышные (см. рис. 6.2). Только что полученные выигрышные позиции порождают набор новых проигрышных позиций (см. рис.

6.3). Продолжим аналогичным образом (см. рис. 6.4, 6.5). После того как получим очередной набор минусов отметим плюсом те поля, из которых каждый ход ведет в проигрышную позицию. После этого отмечаем минусом те поля, из которых есть хотя бы один ход в выигрышную позицию. В результате этого процесса плюсы и минусы будут расставлены так, как показано на рисунке 6.6. Так как

Рис. 6.4 Рис. 6.5 Рис. 6.6

первоначально ферзь стоит в проигрышной позиции c1, то первый игрок выиграет, причем у него есть три варианта первого хода: на поля c5, d1 и e3.

Пример7. Игра начинается с числа 2. За ход разрешается прибавить к имеющемуся числу любое натуральное число, меньшее его. Выигрывает тот, кто получит 1000.

Решение. Применяя метод «анализ с конца», найдем выигрышные и проигрышные позиции. Если игрок назвал число 1000, то он выиграл, значит, 1000 — выигрышная позиция. За один ход 1000 можно получить из чисел 501, 502, 503, ..., 999. Этим числам соответствует проигрышная позиция. Далее заметим, что число 500 можно перевести только в одну из проигрышных позиций, полученных на предыдущем шаге. Таким образом, 500 — выигрышная позиция. Продолжая этот анализ, получим, что выигрышными позициями являются числа: 1000, 500, 250, 125, 62, 31, 15, 7, 3. Поэтому первый игрок выиграть. Первым ходом он называет число 3, а затем, любое число названное вторым игроком, он может перевести в выигрышную позицию.

Следующие две игры (пример 8 и 9) относятся к категории «играм-шутка» или «псевдоигры». Результат игры-шутки определен заранее, он не зависит от того, как играют соперники. Что бы ни делали игроки, либо всегда выигрывает первый игрок, либо всегда выигрывает второй. Для решения такой игры не нужно указывать выигрышную стратегию. Достаточно лишь доказать, что выигрывает тот или иной игрок (независимо от того, как будет играть).

Пример8. Двое по очереди ломают шоколадку 6×8 долек. За ход разрешается сделать прямолинейный разлом любого из кусков вдоль углубления. Проигрывает тот, кто не сможет сделать ход.

Решение. Заметим, что после каждого хода количество кусков увеличивается ровно на 1. Сначала был один кусок, а в конце игры, когда нельзя сделать ни одного хода, шоколадка разломана на 48 маленьких долек. Таким образом, игра будет продолжаться ровно 47 ходов. Последний, 47-й ход (нечетный по счету ход), сделает первый игрок. Поэтому он в этой игре побеждает, причем независимо от того, как будут играть он и соперник.

Пример9. Два гроссмейстера по очереди ставят на шахматную доску ладьи (за один ход — одну ладью) так, чтобы они не били друг друга. Тот, кто не сможет поставить ладью, проигрывает. Кто выиграет при правильной игре — первый или второй гроссмейстер?

Решение. Поставить ладью на некоторое поле можно тогда и только тогда, когда ни на горизонтали, ни на вертикали, содержащей это поле, не стоит ладьи. Поэтому описанная выше игра равносильна следующей: гроссмейстеры по очереди вычеркивают из набора букв a, b, ..., h и цифр 1, 2, ..., 8 по одной букве и цифре. Очевидно, что как бы ни ходили игроки, после восьмого хода все буквы и цифры будут вычеркнуты. Восьмой ход принадлежит второму, поэтому первый не сможет сделать следующего хода.

В завершение рассмотрим еще несколько примеров на разные виды игр.

Пример10. На шахматной доске стоит фишка. Двое по очереди передвигают фишку на соседнюю по стороне клетку. При этом запрещается ставить фишку на поле, где она уже побывала. Проигрывает тот, кто не может сделать очередной ход. Кто выигрывает при правильной игре?

Решение. Разобьем доску на доминошки 1 × 2 клетки. Стратегия первого будет состоять в следующем: если перед ходом первого фишка стоит в одной из клеток, принадлежащих какой-то доминошке, то своим ходом первый игрок передвигает ее в другую клетку этой же доминошки. Заметим, что после хода первого для каждой доминошки выполнено одно из условий: в каждой клетке этой доминошки фишка уже побывала; ни в одной из клеток этой доминошки фишка еще не побывала. Это означает, что первый игрок всегда сможет сделать ход, придерживаясь своей стратегии, и следовательно, он не проиграет.

Пример11. Дана полоска клетчатой бумаги длиной в 100 клеток. Двое играющих по очереди красят клетки в черный цвет, причем первый всегда красит четыре подряд стоящие клетки, а второй — три подряд стоящие. Уже покрашенную клетку второй раз красить нельзя. Проигрывает тот, кто не может сделать очередной ход. Кто выигрывает при правильной игре: первый или второй?

Решение. При правильной игре выигрывает второй игрок.

Своим первым ходом второй игрок закрашивает три клетки, отступив на три клетки от одного из краев полосы (см. рис.) и объявив три не закрашенные крайние клетки «заповедником».

В дальнейшем второй игрок может делать любые возможные ходы, не вторгаясь в заповедник. Если таких ходов у него больше не осталось, то он закрашивает клетки заповедника. Разумеется, у первого игрока в такой ситуации ответного хода нет.

Пример12. В одной куче 18 конфет, а в другой — 23. Двое по очереди съедают одну из куч, а другую делят ещё на две кучи. Тот, кто не сможет поделить кучу (если там одна конфета), проигрывает. Как должен играть начинающий, чтобы выиграть?

Решение. Первым ходом первому нужно съесть кучу из 23 конфет, а кучу из 18 конфет разделить на две кучи с нечетным числом конфет. После этого второй съест одну из куч, а другую кучу разделит на две кучи, в одной из которых четное число конфет, а в другой — нечетное. Теперь перед первым игроком ситуация, аналогичная начальной — имеются две кучи, в одной из которых четное число конфет, а в другой — нечетное. Первый снова должен съесть «нечетную» кучу, а «четную» кучу поделить на две нечетных, и т.д. Как бы ни ходил второй, после его хода остается две кучи, одна из которых имеет четное (а, следовательно, большее 1) число конфет. Поэтому после хода второго первый может сделать свой ход. Таким образом, если первый будет придерживаться описанной выше стратегии, то он победит.

Задачи для самостоятельного решения

Задача1. Двое по очереди закрашивают на белой доске 8 × 8 квадрат 2 × 2 черной краской. Красить уже покрашенную клетку запрещается. Проигрывает тот, кто не может сделать хода. Кто выиграет при правильной игре?

Задача2. На доске написано число 1. Два игрока по очереди прибавляют любое число от 1 до 5 к числу на доске и записывают вместо него сумму. Выигрывает игрок, который первый запишет на доске число тридцать. Кто выиграет при правильной игре?

Задача3. Числа от 1 до 20 выписаны в строчку. Игроки по очереди расставляют между ними плюсы и минусы. После того, как все места заполнены, подсчитывается результат. Если он чётен, то выигрывает первый игрок, если нечётен, то второй. Кто выиграет?

Задача4. На окружности расставлено 2018 точек. За ход разрешается соединить любые две из них отрезком, не пересекающим отрезков, проведенных ранее. Проигрывает тот, кто не может сделать ход.

Задача5. В левом нижнем углу шахматной доски стоит «хромой король». За ход его модно подвинуть вправо или вверх на одну клетку. Проигрывает тот, кто не может сделать хода. Кто выиграет при правильной игре?

Задача6. Король стоит на поле a1 шахматной доски. За ход разрешается сдвинуть его на одну клетку вправо, или на одну клетку вверх, или на одну клетку по диагонали вправо-вверх. Выигрывает тот, кто поставит короля на клетку h8. Кто выигрывает при правильной игре?

Задача7. Имеется три кучки камней: в первой — 10, во второй — 15, в третьей — 20. За ход разрешается разбить любую кучку на две меньшие; проигрывает тот, кто не сможет сделать ход.

Задача8. В чашке сидит 105 микробов. За ход разрешается вытащить 2, 3 или 5 микробов. Проигрывает тот, кто не может сделать очередной ход.

Задача9. В коробке лежит 300 спичек. За ход разрешается взять из коробка не более половины имеющихся в нем спичек. Проигрывает тот, кто не может сделать ход.

Задача10. Двое играют в следующую игру. Каждый игрок по очереди вычеркивает 9 чисел (по своему выбору) из последовательности 1,2,...,100,101. После одиннадцати таких вычеркиваний останутся 2 числа. Первому игроку присуждается столько очков, какова разница между этими оставшимися числами. Доказать, что первый игрок всегда сможет набрать по крайней мере 55 очков, как бы ни играл второй.

Тема 6. Метод математической индукции

Метод математической индукции

Пусть требуется установить справедливость бесконечной последовательности утверждений, занумерованных натуральными числами: P(1), P(2), P(3), ..., P(n), .... И пусть первое утверждение P(1) верно, и мы умеем доказывать, что из верности утверждения P(k) следует верность следующего утверждения P(k+1). Тогда все утверждения в этой последовательности верны.

В самом деле, из утверждения P(1) следует P(2), из утверждения P(2) следует P(3), и так далее, в итоге мы получем, что верно утверждение P(n) при любом натуральном значении n. Наглядно принцип математической индукции можно пояснить так: выстроим рядом друг за другом кости домино (см. рис.). Если толкнуть одну доминошку, то за ней повалится вся цепочка: падая, каждая костяшка толкает следующую.

Определения

Базой индукции называется утверждение P(1). Иногда базой индукции называют утверждение P(m), при некотором m, или несколько первых утверждений P(1), P(2), ..., P(m).

Предположением индукции называется предположение о том, что утверждение P(n) верно для n = k.

Шагом индукции (индукционным переходом) называется доказательство того, что из верности утверждения P(k) следует верность утверждения P(k + 1).

Логическим основанием для этого метода доказательства служит так называемая аксиома индукции, пятая из аксиом Пеано, определяющих натуральные числа. Верность метода индукции эквивалентна тому, что в любом непустом подмножестве натуральных чисел существует минимальный элемент.

В некоторых случаях для доказательства утверждения P(k + 1) приходится использовать не только утверждение P(k), но и все предыдущие утверждения.

Принцип полной математической индукции

Пусть имеется последовательность утверждений P(1), P(2), P(3), .... Пусть также для любого натурального k мы умеем доказывать, что из верности утверждений P(1), P(2), ..., P(k) следует верность следующего утверждения: P(k + 1). Тогда все утверждения в этой последовательности верны.

Принцип полной математической индукции также эквивалентен аксиоме индукции в аксиомах Пеано.

Осознание метода математической индукции как отдельного важного метода восходит к Блезу Паскалю и Герсониду, хотя отдельные случаи применения встречаются ещё в античные времена у Прокла и Эвклида. Современное название метода было введено де Морганом в 1838 году.

Пример1. В клетчатом квадрате 64 × 64 вырезали одну из клеток. Докажите, что оставшуюся часть квадрата можно разрезать на уголки из трех клеток.

Решение. Докажем общее утверждение для квадрата размером 2ⁿ× 2ⁿклеток с вырезанной клеткой.

База. Для n = 1 это утверждение очевидно: если из квадрата 2 × 2 вырезана одна клетка,то оставшаяся часть квадрата — это уголок из трех клеток.

Предположение индукции. Предположим, что утверждение верно для n = k, то есть квадрат размером 2^k×2^kклеток с вырезанной одной клеткой можно разрезать на уголки из трех клеток.

Шаг индукции. Упражнение. Чтобы понять суть доказательства рассмотрите отдельно переход от квадрата 2 × 2 к квадрату 4 × 4 и переход от квадрата 4 × 4 к квадрату 8 × 8.

Докажем, что утверждение верно для n = k + 1. Итак, пусть в квадрате 2^k⁺¹× 2^k⁺¹клеток вырезана одна из клеток. Разрежем этот квадрат на 4 квадрата 2^k× 2^kклеток. Вырезанная клетка попала в один из этих четырех квадратов. Из остальных трех квадратов можно вырезать по одной угловой клетке так, чтобы они образовывали уголок из трех клеток (см. рис.). Вырежем этот

уголок. Оставшаяся часть представляет собой четыре квадрата 2ⁿ× 2ⁿклеток, в каждом их которых вырезано по одной клетке.

По предположению индукции каждый из этих квадратов можно разрезать на уголки. Тем самым, и квадрат 2ⁿ⁺¹× 2ⁿ⁺¹клеток с вырезанной клеткой можно разрезать на уголки.

Таким образом, мы доказали, что любой квадрат размером 2ⁿ× 2ⁿс одной вырезанной клеткой можно разрезать на уголки из трех клеток.

Очень часто метод математической индукции применяется для доказательства тождеств, зависящих от натурального параметра.

Пример2. Докажите тождества:

2).

Решение. 1) База. Если n = 1, то 1 = . Значит, при n = 1 утверждение верно.

Предположение индукции. Пусть утверждение верно при n = k, т.е.

Шаг индукции. Докажем утверждение для n = k + 1. Имеем

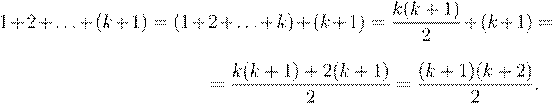
Таким образом, индукционный переход доказан, а вместе с ним и первое тождество.

Замечание. Очень часто при решении задач методом математической индукции используется сокращенная запись. Доказывают базу индукции и индукционный переход от n к n + 1. При этом индукционное предположение отдельно не выписывается, но его считают верным.

12(1 + 1)2

2) База. Если n = 1, то 13 = , равенство верно.

Индукционный переход. Пусть утверждение верно для n. Докажем, что оно верно для (n + 1).

Имеем следующую цепочку равенств

1³+ 2³+ ... + (n + 1)³= (1³+ 2³+ ... + n³) + (n + 1)³=

Тождество доказано.

Заметим, что из первого и второго тождества следует, что

1³+ 2³+ ... + n³= (1 + 2 + ... + n)².

Пример3. Пусть x > −1, n — натуральное число. Докажите что, (1 + x)ⁿ> 1 + nx (неравенство Бернулли).

Решение. Применим метод математической индукции.

База. При n = 1 неравенство очевидно (оно обращается в верное равенство).

Шаг индукции. Пусть уже доказано, что (1 + x)ⁿ> 1 + nx .

Тогда

(1 + x)ⁿ⁺¹= (1 + x) · (1 + x)ⁿ> (1 + x)(1 + nx) =

= 1 + (n + 1)x + nx²> 1 + (n + 1)x.

Пример4. Известно, что — целое число. Докажите, что — также целое при любом целом n.

Решение. Обозначим. Так как A(−n) = A(n), то достаточно провести доказательство для натуральных значений n. Применим метод математической индукции.

База индукции. При n = 0 утверждение очевидно, а при n = 1 дано в условии.

Предположение индукции. Пусть число A(k) является целым при всех натуральных значениях k 6 n.

Шаг индукции. Докажем, что число A(k+1) — целое. Для этого рассмотрим произведение

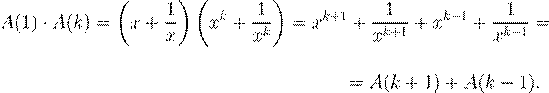
Таким образом, A(k+1) = A(1)·A(k)−A(k−1) — целое как разность двух целых чисел A(1) · A(k) и A(k − 1).

Пример5. Доказать , что при любом натуральном n число

3²ⁿ⁺¹+ 2ⁿ⁺²делится на 7.

Решение. Применим метод математической индукции.

Обозначим A(n) = 3²ⁿ⁺¹+ 2ⁿ⁺².

База индукции. Если n = 1, то A(1) = 3³+ 2³= 35 и, очевидно, делится на 7.

Предположение индукции. Пусть A(k) делится на 7.

Шаг индукции. Докажем, что A(k + 1) делится на 7, то есть справедливость утверждения задачи при n = k + 1.

A(k+1) = 32(k+1)+1+2(k+1)+2 = 32k+1·32+2k+2·21 ^{= 9}·32k+1⁺²·2k+2 = = 9·32k+1+(9−7)·2k+2 = 9·(32k+1+2k+2)−7·2k+2 = 9·A(k)−7·2k+2.

Последнее число делится на 7, так как представляет собой разность двух целых чисел, делящихся на 7. Следовательно, 3²ⁿ⁺¹+ 2ⁿ⁺²делится на 7 при любом натуральном n.

Пример6. Несколько прямых делят плоскость на части. Докажите, что эти части можно раскрасить в 2 цвета так, что граничащие части будут иметь разный цвет.

Решение. Применим принцип математической индукции по количеству прямых n.

База индукции. При n = 1 утверждение задачи очевидно: достаточно покрасить две полуплоскости, на которые одна прямая делит плоскость, в разные цвета.

Предположение индукции. Пусть утверждение задачи верно для k прямых.

Шаг индукции. Рассмотрим некоторые k + 1 прямые. Уберем временно (k + 1)-ю прямую (т.е. любую из прямых). Оставшиеся k прямых разобьют плоскость на несколько частей. По предположению индукции их можно раскрасить в два цвета так, что граничащие области будут иметь разный цвет. Снова вернем убранную прямую, при этом появятся новые части. Однако, части, граничащие по этой новой прямой, будут иметь одинаковый цвет. Перекрасим все области, расположенные по одну из сторон относительно (k + 1)-й прямой, в противоположный цвет. Полученная в результате раскраска удовлетворяет условию задачи.

Таким образом, утверждение верно для любого числа прямых.

Пример7. Докажите, что квадрат можно разрезать на n квадратов для любого n, начиная с шести.

Решение. Применим в этой задаче метод математической индукции, но в измененном виде.

База индукции. В качестве базы возьмем не одно, а целых три утверждения, т.е. покажем, что квадрат можно разрезать на 6, 7 и 8 частей (см. рис.).

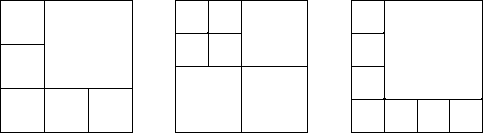
Индукционный переход. Покажем, что если квадрат можно разрезать на k квадратов, то его можно разрезать и на k + 3 квадрата. Для этого достаточно взять один из квадратов и разрезать его на 4.

Тем самым, мы доказали, что квадрат можно разрезать на любое количество квадратов, начиная с 6. Действительно, из индукционного перехода получим, что утверждение верно для следующих чисел:

6 → 9 → 12 → 15 → 18 → ...,

7 → 10 → 13 → 16 → 19 → ..., 8 → 11 → 14 → 17 → 20 → ....

Любое натуральное число n, где n > 6, появится в одной из этих последовательностей.

Пример8. На кольцевой автомобильной дороге стоят несколько одинаковых автомобилей. Известно, что если весь бензин, находящийся в автомобилях, слить в один из них, то этот автомобиль сможет проехать по всей кольцевой дороге и вернуться на прежнее место. Докажите, что хотя бы один из этих автомобилей может проехать по всей кольцевой дороге в заданном направлении, забирая по пути бензин у остальных автомобилей.

Решение. Применим индукцию по числу автомобилей n. Случай n = 1 очевиден. Предположим, что для n автомобилей утверждение доказано. Рассмотрим случай, когда число автомобилей равно n + 1. Тогда среди них найдется такой автомобиль A, который может, используя лишь имеющийся в нем бензин, доехать до следующего автомобиля B (иначе бензина во всех автомобилях не хватило бы для того, что бы проехать один раз по всей кольцевой дороге). Выльем из автомобиля B бензин в A, и уберем B с дороги. Среди оставшихся n автомобилей, по предположению индукции, найдется такой, который может объехать всю дорогу, забирая по пути бензин у остальных автомобилей. Ясно, что тот же автомобиль может сделать это и в первоначальной ситуации, когда на дороге n + 1 автомобиль: на участке от A до B у него заведомо хватит бензина (из машины A), а на остальных участках у него ровно столько же бензина, сколько в случае n машин.

Пример9. Доказать, что при любом натуральном значении n

Решение. Сразу применить метод математической индукции не удастся. Из неравенства S_n< 2, где

не понятно, как доказать, что .

Чтобы провести доказательство по индукции, мы, как это часто делают, усилим доказываемое утверждение. Докажем, что при всех натуральных значениях n

База. Если.

Предположение индукции. Пусть.

Шаг индукции. Докажем, что. Имеем

Необходимо доказать неравенство

. (∗)

Выполнив равносильные преобразования, получим

, .

Домножим левую и правую части неравенства на положительное число (n + 1)², тогда

, .

Неравенство (∗) доказано, а вместе с ним доказаны шаг индук-

ции и неравенство S_n< 2.

Пример10. В плоскости проведено n прямых, из которых никакие две не параллельны и никакие три не проходят через одну точку. На сколько частей разбивают плоскость эти прямые.

Решение. Выполнив несколько чертежей, находим, что одна прямая разбивает плоскость на 2 части, две прямые — на 4 части, три прямые — на 7 частей, четыре прямые — на 11 частей.

Обозначим через N(n) число частей, на которые n прямых разбивают плоскость. В условии задачи (в отличие от примера 2) нам не дана формула для N(n), которую надо доказать. Это приводит к некоторым трудностям. Однако, рассмотрев несколько отдельных случаев, мы можем предположить такую формулу, а затем ее доказать.

Можно заметить, что

N(1) = 2

N(2) = N(1) + 2 = 2 + 2, N(3) = N(2) + 3 = 2 + 2 + 3,

N(4) = N(3) + 4 = 2 + 2 + 3 + 4.

Естественно предположить, что

N(n) = N(n − 1) + n = 2 + 2 + 3 + 4 + 5 + ... + n,

или, как легко установить, воспользовавшись формулой 1) примера 2 (сумма n первых членов арифметической прогрессии),

Докажем справедливость этой формулы методом математической индукции.

Для n = 1 формула уже проверена.

Сделав предположение индукции, рассмотрим k + 1 прямых, удовлетворяющих условию задачи. Выделим из них произвольным образом k прямых. По предположению индукции они разобьют

плоскость на 1+k(k+1)/2 частей. Оставшаяся (k+1)-я прямая разобьётся выделенными k прямыми на k + 1 частей и, следовательно, пройдёт по (k+1)-й части, на которые плоскость уже была разбита, и каждую из этих частей разделит на 2 части, то есть добавится ещё k + 1 часть. Итак,

что и требовалось доказать.

Задачи для самостоятельного решения Задача1. Докажите тождество:

Задача2. Докажите, что при любом натуральном n число: а) 4ⁿ+ 15n − 1 делится на 9;

б) 2³n + 1 делится на 3ⁿ⁺¹и не делится на 3ⁿ⁺².

Задача3. а) Докажите, что число 111...11 (27 единиц) делится на 27. б) Докажите, что число 111...11 (3ⁿединиц) делится на 3ⁿ.

Задача3. а) Имеется очень много купюр достоинства 3 и 5 тугриков. Докажите, что этими купюрами можно выдать любое количество тугриков больше восьми.

б)Кусок бумаги разрешается рвать на 4 или 6 кусков. Докажите, что по этим правилам его можно можно разорвать на любое число кусков, начиная с девяти.

Задача4. Докажите, что правильный треугольник можно разрезать на n правильных треугольников для любого n, начиная с шести.

Задача5. Доказать, что при любом натуральном n большем 1 справедливо неравенство

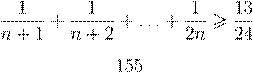Задача6. Докажите, что любое натуральное число можно представить в виде суммы нескольких различных членов последовательности Фибоначчи. (Последовательность Фибоначчи {a_n} определяется условиями a₁= 1, a₂= 2, a_n₊₂= a_n₊₁+ a_n.)

Задача7. Ученик Коля Васин при помощи метода математической индукции смог доказать, что в любом табуне все лошади одной масти. Если есть только одна лошадь, то она своей масти, так что база индукции верна. Для индуктивного перехода предположим, что есть n лошадей (с номерами от 1 до n). По индуктивному предположению лошади с номерами от 1 до n−1 одинаковой масти. Аналогично лошади с номерами от 2 до n также имеют одинаковую масть. Но лошади с номерами от 2 до n − 1 не могут менять свою масть в зависимости от того как они сгруппированы — это лошади, а не хамелеоны. Поэтому все n лошадей должны быть одинаковой масти. Есть ли ошибка в этом рассуждении, и если есть, то какая?

Задача8. У бородатого многоугольника во внешнюю сторону растет щетина. Его пересекает несколько прямых, на каждой из которых с одной из сторон тоже растет щетина (см. рис.).

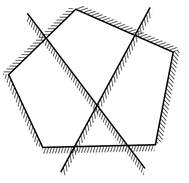
В результате многоугольник оказался разбитым на некоторое число частей. Докажите, что хотя бы одна из частей окажется бородатой снаружи.

Задача9. В прямоугольнике 3 × n (3 строки, n столбцов) расставлены фишки трёх цветов по n штук каждого цвета. Докажите, что переставляя фишки в строчках, можно сделать так, чтобы в каждом столбце были фишки всех трёх цветов.

Тема 7. Комбинаторика

Комбинаторика— это раздел математики, изучающий методы решения задач на подсчет числа различных комбинаций.

В комбинаторике есть два важных правила, часто применяемых при решении комбинаторных задач.

Основные правила комбинаторики

Правило произведения. Пусть требуется выполнить одно за другим какие-то k действий, причем 1-е действие можно выполнить n₁способами, 2-е – n₂способами и т. д. до k-го действия, которое можно выполнить n_kспособами, причем количество способов выполнить каждое действие не зависит от того, какими были предыдущие действия. Тогда все k действий можно выполнить n₁· n₂· ... · n_kспособами.

Пример1. В магазине есть 5 разных видов чашек и 4 вида блюдец. Сколькими способами можно составить комплект из чашки с блюдцем?

Решение. Для того чтобы составить комплект из чашки и блюдца необходимо выполнить 2 действия: первое — выбрать чашку, второе — выбрать блюдце. Заметим, что количество способов выбрать блюдце не зависит от того, какую чашку выбрали в первом действии. Таким образом, по правилу произведения комплект из чашки и блюдца можно составить 5 · 4 = 20 способами.

Замечание. Очень важно полностью разобраться почему здесь надо умножать. Объясним это более подробно.

Рассмотрим таблицу, в которой каждая строка соответствует одной из пяти имеющихся чашек, а каждый столбец — одному из четырех блюдец.

Каждая клетка такой таблицы соответствует одному из способов составить комплект из чашки и блюдца. Например, выделенная в таблице ячейка соответствует комплекту из третьей чашки и второго блюдца.

	Б₁	Б₂	Б₃	Б₄
Ч₁
Ч₂
Ч₃		X
Ч₄
Ч₅

Таким образом, число различных наборов их чашки с блюдцем равно числу клеток в таблице, а этих клеток — 5 · 4 = 20.

Еще один способ понять, почему необходимо умножать количество чашек на количество блюдец, это составить дерево комбинаций. Каждой ветке такого дерева соответствует ровно один комплект из

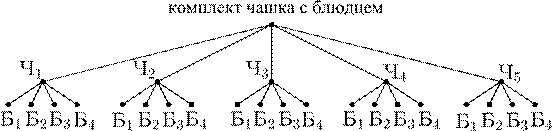
чашки и блюдца.

Пример2. Шарль «перенумеровал» все свои книги с помощью трёхбуквенного кода, используя все 26 букв (латинского) алфавита: AAA, AAB, AAC, ..., AAZ, ABA, ABB, .... У него 680 книг. Каков код последней из его книг?

Решение. Найдем число книг, код которых начинается с буквы A. На втором и третьем месте может стоять любая из 26 букв. По правилу произведения получим, что 26 · 26 = 676 книг имеют код, начинающийся с буквы A. Таким образом, 676-я книга получила код AZZ, 677-я — BAA, 678-я — BAB, 679-я — BAC, а 680-я — BAD. Значит, код последней книги — BAD.

Правило суммы. Пусть требуется выполнить одно из какихлибо k действий, взаимно исключающих друг друга. Если 1-е действие можно выполнить n₁способами, 2-е – n₂способами и

т. д. до k-го действия, которое можно выполнить n_kспособами, то выполнить одно из этих k действий можно (n₁+ n₂+ ... + n_k) способами.

Пример3. На подносе лежат 5 яблок и 4 груши. Сколькими способами можно выбрать фрукт с подноса?

Решение. В данной задаче, в отличие от предыдущей, выбирается только один фрукт. Если первое действие — выбор яблока, а второе — выбор груши, то необходимо выполнить ровно одно из этих двух взаимно исключающих действий. По правилу суммы выбрать фрукт с подноса можно 5 + 4 = 9-ю способами. Действительно, на подносе всего 9 фруктов и один из них можно выбрать 9 способами.

Правило сложения, как правило, используется тогда, когда все комбинации можно разбить на непересекающиеся классы. Чтобы найти общее число комбинаций необходимо подсчитать число комбинаций в каждом классе (например, по правилу умножения), а затем сложить эти количества. Использование такой простой идеи — «разделяй (на классы) и влавствуй» — оказывается чрезвычайно полезным при решении задач.

Заметим, что в некоторых задачах приходится использовать оба комбинаторных правила — умножения и сложения — вместе.

Пример4. Сколькими способами можно посадить шестерых школьников на скамейку так, чтобы Коля и Оля оказались рядом.

Решение. Способ I. Будем считать, что на скамейке шесть пустых мест. Посадить на одно из них Колю можно шестью различными способами, после чего посадить рядом с ним Олю можно либо одним, либо двумя различными способами. Это зависит от того, Куда мы посадим Колю — на крайнее место или нет. Применим правило сложения. Для этого разобьем все искомые комбинации на два непересекающихся класса:

1-й класс: Коля сидит на краю скамейки, Оля рядом с ним; 2-й класс: Коля сидит где-то в середине, Оля рядом с ним.

Заметим, что эти классы не пересекаются и исчерпывают все комбинации.

Посчитаем число комбинаций в 1-м классе. Место для Коли можем выбрать двумя способами, после этого место для Оли уже будет определено (никакого выбора нет, один способ). После этого останется 4 свободных места и 4 школьника. Эти места можно занять 4·3·2·1 способом (на первое место можно посадить любого из четырех школьников, на второе — любого из трех оставшихся, на третье — любого из двух оставшихся, наконец, последнее место занимает последний ученик). Значит, в 1-м классе 2·1·4·3·2·1 = 48 комбинаций.

Найдем число исходов во 2-м классе. Место для Коли можно выбрать четырьмя способами, после чего Олю можно посадить рядом с ним двумя способам (либо справа от Коли, либо слева). Затем снова останутся 4 школьника и 4 свободных места. Их можно занять 4·3·2·1 способами. Значит, во 2-м классе 4·2·4·3·2·1 = 192 комбинации.

Итого по правилу сложения существует 48+192 = 240 способов посадить школьников так, чтобы Коля и Оля оказались рядом.

Способ II. См. пример 5.2.

Основные понятия комбинаторики

Пусть даны n различных элементов и мы составляем из них какую-то комбинацию из k элементов (т.е. выбираем k элементов).

Эти комбинации могут отличаться:

• составом элементов;

• порядком следования элементов;

• возможностью повтора элементов в комбинации.

В соответствии с этим выделяют следующие виды комбинаций.

Перестановкой из n элементов называется комбинация, в которой все эти n элементов расположены в определенном порядке.

Таким образом, перестановки отличаются друг от друга только порядком расположения элементов.

Пример5.1). Сколькими способами шесть учеников могут выстроиться в очередь в столовую?

Решение. Первое место в очереди может занимать любой из шести учеников, на второе место в очереди уже можно поставить любого из пяти оставшихся школьников, на третье место — любого из четырех, на четвертое — любого из трех, на пятое — любого из двух и, наконец, последнее место займет оставшийся ученик. Заметим, что количество способов выбрать следующего ученика, чтобы поставить в очередь, не зависит от того, какие ученики были выбраны раньше. Таким образом, по правилу произведения число различных очередей равно 6 · 5 · 4 · 3 · 2 · 1 = 720.

Для таких произведений введено специальное обозначение

6! = 1 · 2 · 3 · 4 · 5 · 6 = 720,

читается 6-факториал.

Дадим строгое определение факториала.

Определение. Факториалом натурального числа n, где n > 2, называется произведение всех натуральных чисел от 1 до n включительно n! = 1 · 2 · 3 · ... · n, (читается n − факториал).

Отдельно введем 0! = 1! = 1.

Ниже нам пригодится понятие двойного факториала.

Определение. Двойной факториал числа n обозначается n!! и представляет собой произведение всех натуральных чисел от 1 до n той же самой четности, что и число n.

• n!! = 2 · 4 · 6 · ... · n для четного числа n;

• n!! = 1 · 3 · 5 · ... · n для нечётного числа n.

Например: 7!! = 1 · 3 · 5 · 7 = 105, 10!! = 2 · 4 · 6 · 8 · 10 = 3840.

Утверждение. Число всех перестановок из n элементов обозначается P_nи вычисляется по формуле:

P_n= n!.

Доказательство данного утверждения аналогично решению примера 5.1.

Пример5.2. Шесть учеников, среди которых есть Оля и Коля, выстраиваются в очередь в столовую (см. пример 5.1). В скольких способах Оля стоит рядом с Колей. (Сравни с примером 4.)

Решение. Будем считать, что вместо двух учеников Оли и Коли стоит одна пара. Значит, вместо шести школьников очередь образуют пять «элементов»: четыре школьника и одна пара. Эти 5 элементов можно переставить P₅= 5! = 120 способами, но Олю и Колю в паре можно поставить P₂= 2 способами (Оля стоит раньше Коли, или Коля стоит раньше Оли). Таким образом, по правилу произведения число очередей, в которых Оля стоит рядом с Колей равно

P₅· P₂= 120 · 2 = 240.

Пример6. Сколько различных слов можно получить переставляя буквы слова 1) “ВЕКТОР” 2) “ПАРАБОЛА”?

Решение. 1) Так как все буквы слова различны, то всего можно получить 6! = 720 слов. 2) Считая три буквы А этого слова различными (А₁, А₂, А₃), получим 8! разных слов. Однако слова, отличающиеся лишь перестановкой букв А, на самом деле одинаковы. Поскольку буквы А₁, А₂, А₃можно переставлять 3! способами, все 8! слов разбиваются на классы слов по 3! одинаковых. Поэтому всего различных слов 8!/3! = 6720.

Размещением из n элементов по k (k 6 n) называется комбинация, в которой какие-то k из этих n элементов расположены в определенном порядке. Таким образом, размещения отличаются друг от друга не только порядком расположения элементов, но и тем, какие именно k элементов выбраны в комбинацию.

Пример7. На 9-ти карточках написано по одной цифре от 1 до 9 без повторений. Располагая любые три карточки в строку, мы получим трехзначное число. Сколько различных трехзначных чисел можно получить при помощи этих 9-ти карточек?

Решение. Применим правило произведения. Первое цифру можем выбрать 9 способами. Затем, вторую цифру можем выбрать восемью способами (любая карточка кроме той, которую уже взяли). Наконец, в качестве третьей цифры можем использовать любую из 7 оставшихся карточек. Таким образом, количество различных трехзначных чисел равно 9 · 8 · 7 = 504.

Утверждение. Число всех размещений из n элементов по k обозначается A^k_n(читается «а из эн по ка») и вычисляется по формуле:

Доказательство. Каждое размещение представляет собой упорядоченный набор из k элементов. Первый элемент можем выбрать n способами, второй — n−1 способом, ..., k-й — n−k+1 способом.

Таким образом, по правилу произведения

Пример8. Сколькими способами можно случайным образом из 25 учеников класса выбрать 2-х для дежурства в столовой и гардеробе?

Решение. Так как в данном случае важно, не только какие 2 ученика будут выбраны из 25 (состав элементов), но и кто из них будет помогать в столовой, а кто — в гардеробе (порядок следования элементов), то общее число комбинаций будет числом размещений из 25 по 2. Таким образом, искомое число способов равно:

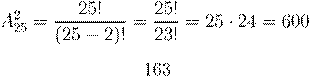Сочетанием из n элементов по k (k 6 n) называется комбинация, в которой из этих n элементов выбраны любые k без учета их порядка в комбинации. Таким образом, для сочетания имеет значение только состав выбранных предметов, а не их порядок. Другими словами, сочетание не что иное, как любое k-элементное подмножество n-элементного множества.

Пример9. Из класса, в котором учатся 25 учеников, нужно выбрать троих для участия в школьной олимпиаде. Сколькими способами это можно сделать?

Решение. Каждая такая комбинация из трех учеников является сочетанием из 25 учеников по 3. Если бы порядок учеников в тройке был важен, то они представляли бы собой размещения из 25 человек по 3. Всего таких упорядоченных троек

= 23 · 24 · 25 = 13800. Однако, в данном случае не важно, кто из трех школьников первый, кто второй, а кто третий. Поэтому все эти размещения разбиваются на классы (группы, множества) комбинаций. В один класс попадают все размещения, отличающиеся друг от друга только порядком расположения школьников. Например, случаю, в котором на олимпиаду отправляются Иванов, Петров и Сидоров, соответствуют 3! = 6 различных размещений, составляющих один класс:

Иванов–Петров–Сидоров, Иванов–Сидоров–Петров,

Петров–Иванов–Сидоров, Петров–Сидоров–Иванов, Сидоров–Иванов–Петров, Сидоров–Петров–Иванов.

Легко понять, что все размещения распределены в классы по 6! комбинаций, а число таких классов равно числу сочетаний и равно

Утверждение. Число всех сочетаний из n элементов по k обозначается (читается «це из эн по ка») и вычисляется по формуле:

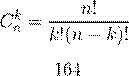Доказательство. Формулу для числа сочетаний выведем из формулы для числа размещений. При подсчете размещений из n по k мы считали число способов, которыми можно выбрать k предметов из n с учетом их порядка. Каждое сочетание учитывается при этом столько раз, сколько существует способов переставить выбранные k предметов, то есть k! раз. Значит, чтобы найти число сочетаний, нужно поделить число размещений на k!. Получим, что

Пример10. Сколько диагоналей в выпуклом n-угольнике?

Решение. Решим задачу двумя способами.

Первый способ. В качестве первого конца диагонали можно взять любую из n вершин, а в качестве второго – любую из n − 3 вершин, отличных от выбранных и двух соседних с ней. При таком подсчете каждая диагональ учитывается дважды, поэтому число n(n − 3)

диагоналей равно .

Второй способ. Рассмотрим n вершин многоугольника. Проведем все отрезки, которые соединяют любые две вершины. Число таких отрезков равно C_n²= − . Каждый из этих отрезков, за ⁿ^{(n 1)}

исключением n сторон, является диагональю. Таким образом, число диагоналей равно C_n²− n = − − n = − .

n(n 1) n(n 3)

2 2

Рассмотренные выше комбинации относятся к так называемому выбору без возвращения — входящие в их состав элементы не повторяются.

Кроме того, комбинаторика рассматривает и случаи с повторением элементов, входящих в рассматриваемые комбинации — так называемый выбор с возвращением — размещения, сочетания и перестановки из n элементов по k, в которых некоторые элементы (или все) могут быть одинаковыми.

Далее будем считать, что нам даны элементы n различных

видов (типов), причем элементов каждого типа найдется любое необходимое количество. Во всех случаях мы будем осуществлять выборку объема k, т.е. будем составлять комбинации из k элементов.

Перестановки с повторениями — это комбинации, в которых все k элементов расположены в определенном порядке и относятся к одному из n видов, причем элемент первого вида a₁повторяется k₁раз, элемент второго вида a₂повторяется k₂раз, ..., элемент n-го типа a_nповторяется k_nраз. Число всех перестановок с повторениями обозначают P^¯_k(k₁,k₂,...,k_n).

Утверждение. Число всех перестановок с повторениями может быть вычислено по формуле:

где k = k₁+ k₂+ ... + k_n.

Доказательство. Рассмотрим одну перестановку с повторениями и заменим в ней все одинаковые элементы разными. Число различных перестановок без повторений, которые можно составить из рассматриваемой нами перестановки с повторениями, равно k₁! · k₂!·...·k_n!. Проделав это для каждой перестановки с повторениями, получим все k! перестановок без повторений. Следовательно,

P¯_k(k₁,k₂,...,k_n) · k₁!k₂! · ... · k_n! = k!,

из чего следует доказываемая формула.

Пример11. Сколько различных слов можно получить переставляя буквы слова 1) «МАМА» (Выпишите все эти слова) 2) «МАТЕМАТИКА»? (Сравни с примером 6.)

Решение. 1) , мама, ммаа, маам, амам, аамм, амма.

2) .

Размещения с повторениями. Пусть даны элементы n различных видов. Любая комбинация, содержащая k элементов, расположенных в определенном порядке, в которой элемент любого вида может повторяться несколько раз, называется размещением с повторениями из n элементов по k.

Еще раз заметим, что здесь n не число различных элементов, из которых осуществляется выбор объема k, а число различных видов (типов) элементов, причем элементов каждого типа найдется любое необходимое количество.

Число всех размещений с повторениями из n элементов по k обозначают .

Утверждение. Число всех размещений с повторениями из n элементов по k определяется по формуле:

Доказательство. Каждое размещение представляет собой упорядоченный набор из k элементов. Первый элемент можем выбрать n способами, второй — n способами, ..., k-й — n способами. Таким образом, по правилу произведения .

Пример12. Сколько различных чисел может быть на экране калькулятора, имеющего 5 регистров?

Решение. В каждом из регистров калькулятора может быть любая цифра из 10 имеющихся: от 0 до 9. (Заметим, что это не количество пятизначных чисел, и в первой ячейке может быть 0, он просто не отображается). Очевидно, что цифры в регистрах могут повторяться, причем нам важен порядок их следования. Таким образом, здесь необходимо использовать формулу размещений с повторениями. Значит искомое количество различных чисел равно

Сочетания с повторениями. Пусть даны элементы n различных видов. Любая комбинация, содержащая k элементов, расположенных без учета порядка, в которой элемент любого вида может повторяться несколько раз, называется сочетанием с повторениями из n элементов по k.

Число всех сочетаний с повторениями из n элементов по k обозначают .

Пример13. В кондитерской продают 4 вида пирожных: наполеоны, эклеры, тирамису и корзиночки. Сколькими способами можно купить 7 пирожных?

Решение. Ясно, что пирожные могут повторяться, но использовать формулу размещений с повторениями не получится — так как, порядок, в котором пирожные лежат в коробке, — несущественен (в отличие от набранных цифр на калькуляторе в примере 12, где, например, 11115 и 51111 — разные числа). Таким образом, каждая покупка является сочетанием с повторениями из 4 по 7.

Отсортируем пирожные в покупке, выложив их в ряд по типам: сначала выложим наполеоны, затем эклеры и тирамису, а в конце корзиночки. Например, запись «ннэээтк», означает, что были куплены 2 пирожных наполеон, 3 эклера, одно тирамису и одна корзинка. Закодируем эту покупку с помощью двух символов. Символ ◦ будет обозначать пирожное, а символ | — разделитель (перегородка) между пирожными разных видов. Например, покупке «ннэээтк» соответствует код ◦ ◦ | ◦ ◦ ◦ | ◦ |◦. Может случиться так, что пирожное какого-то вида в покупке нет. В этом случае два или несколько разделителей стоят рядом. Например, если были куплены «ннээккк», то соответствующий код — ◦ ◦ | ◦ ◦|| ◦ ◦◦. В этом коде между двумя рядом стоящими перегородками нет символов ◦, так как пирожных тирамису в покупке нет.

Таким образом, любая покупка будет закодирована 10-ю символами: семь ◦ и три разделителя |. Ясно, что различным вариантам покупки будут соответствовать разные комбинации из семи ◦ и трех перегородок. Верно и обратное. Чтобы составить комбинацию указанного вида, необходимо из 10 мест (позиций для ◦ и перегородок) выбрать без учета порядка 7 мест для ◦, или три места для перегородок. Значит, число способов купить 7 пирожных равно

Прием, описанный при решении этой задачи, называется методом шаров и перегородок.

Аналогичным образом можно вывести формулу для числа сочетаний с повторениями в общем виде.

Утверждение. Число всех сочетаний с повторениями C¯_n^kиз n элементов по k определяется по формуле:

Пример14. 1) Шесть ящиков занумерованы числами от 1 до 6. Сколькими способами можно разложить по этим ящикам 20 одинаковых шаров так, чтобы ни один ящик не оказался пустым?

2) Найти число решений уравнения

x₁+ x₂+ ... + x_k= n, (n > k)

в натуральных числах.

Решение. 1) Выложим шары в ряд. Для определения расклада шаров по шести ящикам разделим ряд пятью перегородками на шесть групп: первая группа для первого ящика, вторая — для второго и так далее. Таким образом, число вариантов раскладки шаров по ящикам равно числу способов разложения пяти перегородок. Перегородки могут стоять на любом из 19 мест (между 20 шарами — 19 промежутков). Поэтому число их возможных расположений равно.

2) Представим, что у нас имеется n шаров, которые необходимо разложить по k ящикам так, чтобы ни один из ящиков не оказался пустым. Обозначим x_iчисло шаров в i-м ящике. Тогда задача сводится к числу решений уравнения x₁+ x₂+ ... + x_k= n в натуральных числах. Таким образом, число решений уравнения и число разложений шаров по ящикам совпадают.

Дальше решение совпадает с решением п. 1. Имеется n шаров, между ними (n − 1) промежуток. Требуется поставить (k − 1) перегородку в какие-то из этих промежутков. Получим различных разложений шаров, которые соответствуют решениям уравнения.

Пример15. 1) Шесть ящиков занумерованы числами от 1 до 6. Сколькими способами можно разложить по этим ящикам 20 одинаковых шаров (на этот раз некоторые ящики могут оказаться пустыми)?

2) Найти число решений уравнения

x₁+ x₂+ ... + x_k= n

в неотрицательных целых числах.

Решение. 1) Для того, чтобы разложить шары по ящикам, необходимо из чисел 1, 2, 3, 4, 5, 6 выбрать 20, естественно с повторениями и без учета порядка. Каждой такой выборке соответствует разложение шаров по ящикам. Числу единиц в выборке соответствует число шаров в первом ящике, числу двоек — число шаров во втором ящике и т. д. Таким образом, число разложений шаров по ящикам равно числу сочетаний с повторениями из 6 элементов по 20, т. е. равно.

2) Представим, что у нас имеется n шаров, которые необходимо разложить по k ящикам, причем некоторые ящики могут оказаться пустыми. Обозначим x_iчисло шаров в i-м ящике. Тогда задача сводится к числу решений уравнения x₁+ x₂+ ... + x_k= n в целых неотрицательных числах. Таким образом, число решений уравнения равно числу разложения шаров, которое можно сделать

Замечание. Достаточно много задач комбинаторики можно свести к решению уравнения вида x₁+x₂+...+x_k= n в натуральных или целых неотрицательных числах. Формулы для числа решений таких уравнений очень полезны для решения многих задач.

Рассмотрим еще несколько комбинаторных задач разного вида.

Пример16.1. В классе 15 мальчиков и 15 девочек. Сколькими способами их можно рассадить их за пятнадцатью партами так, чтобы за каждой партой мальчик сидел слева, а девочка справа?

Решение. Начнем с мальчиков: за первую парту можно посадить любого из 15, за вторую — любого из 14 оставшихся и т. д. Получим 15! способов рассадки мальчиков. Для девочек совершенно аналогично получается 15! способов. Общее число способов рассадки равно 15! · 15! = (15!)².

Пример16.2. В классе 15 мальчиков и 15 девочек. Сколькими способами их можно рассадить их за пятнадцатью партами так, чтобы за каждой партой мальчик сидел за одной партой с девочкой?

Решение. Ясно, что ответ предыдущей задачи нужно увеличить в 2¹⁵раза, потому что каждую пару, получающуюся в предыдущей задаче, можно посадить 2 способами: один раз мальчик слева, другой — справа. Получаем 15!·2¹⁵способов. Решим задачу другим способом. Начнем с мальчиков. Первого из них можно посадить на любое из 30 мест в классе, второго — на одно из 28 оставшихся (его нельзя сажать за парту, где уже сидит первый), третьего — на одно из 26 оставшихся и т. д., вплоть до пятнадцатого мальчика, которому остается 2 свободных места. Получаем 30 · 28 · 26 · ... · 4 · 2 = 30!! способов рассадить мальчиков. Для девочек остается 15 свободных мест, которые они могут занять 15! способами. Общее число способов рассадки равно 30!! · 15!. (Заметим, что оба ответа совпадают, хотя они записаны разными формулами.)

Пример16.3. В классе 15 мальчиков и 15 девочек. Сколькими способами их можно разбить на пары танцевать вальс на концерте?

Решение. Берем мальчика — он может танцевать с любой из 15 девочек, второй мальчик может танцевать с любой из 14 оставшихся девочек и т. д. Всего получим 15! способов разбить учеников на пары для танца.

Пример16.4. В классе 30 учеников. Сколькими способами их можно разбить на пары для дежурства в классе в течении 15 дней (одна пара дежурит один день)?

Решение. Представим себе, что мы выполняем обязанности старосты и должны составить список дежурств и повесить его в классе. В этом списке 30 пустых строчек–позиций (в первый день дежурят 1 и 2, во второй день 3 и 4 и т. д.). В первую строчку вписываем любого из 30 членов класса, во вторую — одного из 29 оставшихся и т. д. Это можно сделать 30! способами. Однако при этом каждую пару мы считали дважды, поэтому число способов разбить учеников на пары для дежурства равно .

Пример16.5. В классе 30 учеников. Сколькими способами их можно разбить на пары для сбора макулатуры?

Решение. Первый способ. В предыдущей задаче пары были неодинаковы — там был важен порядок заступления на дежурство. В данном случае пары одинаковы, нет ни первых, ни последних пар. Поэтому 30!/2¹⁵способов разбиения на неодинаковые пары мы должны разделить на 15!. Получим способов разбить класс для сбора макулатуры. Второй способ.· Берем любого члена класса и назначаем ему напарника. Это можно сделать 29 способами. Остается 28 человек, опять берем любого и назначаем напарника 27 способами и т. д. Получаем 29 · 27 · 25 · ... · 3 · 1 = 29!! способов.

Пример17. 1) Семь девушек водят хоровод. Сколькими различными способами все они могут образовать круг?

2) Сколько ожерелий можно составить из семи различных бусинок?

Решение. 1) Представим себе на время, что хоровод неподвижен. Тогда девушки могут образовывать круг P₇способами. Однако, любое расположение хоровода и 6 вариантов, получающихся из него поворотами, следует считать одним и тем же вариантом хоровода. Потому число различных хороводов P₇/7 = P₆= 6! = 120. 2) Ожерелье, в отличие от хоровода, можно не только вращать по кругу, но и перевернуть. Поэтому число ожерелий в два раза меньше числа хороводов. Значит, число ожерелий равно 120 : 2 = 60.

Пример18. 1) Сколькими способами Дима сможет покрасить пять елок в серебристый, зеленый и синий цвета, если количество краски у него неограничено, а каждую елку он красит только в один цвет?

2) У Димы есть пять шариков: красный, зеленый, желтый, синий и золотой. Сколькими способами он сможет украсить ими пять елок, если на каждую требуется надеть ровно один шарик?

3) А если можно надевать несколько шариков на одну елку (и все шарики должны быть использованы)?

Решение. 1) Каждую из пяти елок можно покрасить в один из трех цветов, поэтому всего различных способов существует 3⁵= 243. 2) На первую елку можно надеть любой из пяти шариков, на вторую елку — любой из оставшихся четырех, и так далее; всего получаем 5! = 120 способов. 3) Каждый из шариков можно надеть на любую елку, поэтому в этом случае ответ — 5⁵= 3125.

Пример19. 1) В заборе 20 досок, каждую надо покрасить в синий, зеленый или желтый цвет, причем соседние доски должны быть покрашены в разные цвета. Сколькими способами это можно сделать? 2) А если требуется еще, чтобы хотя бы одна из досок обязательно была синей?

Решение. 1) Первую доску покрасим любым из трех цветов, а каждую следующую можно покрасить двумя способами в любой цвет кроме того, которым покрашена предыдущая доска. Таким образом, существует 3 · 2¹⁹различных раскрасок. 2) Существует всего 2 способа раскрасить забор в зеленый и желтый цвета так, чтобы цвета чередовались. В остальных 3·2¹⁹−2 способах покраски хотя бы одна доска будет синего цвета.

Пример20. У людоеда в подвале томятся 25 пленников. 1) Сколькими способами он может выбрать трех из них себе на завтрак, обед и ужин? 2) А сколько есть способов выбрать троих, чтобы отпустить на свободу?

Решение. 1) В первом случае важен порядок выбранных пленников. Поэтому на завтрак, обед и ужин людоед может выбрать трех пленников способами. 2) В данном случае порядок выбранных пленных не важен. Значит, людоед может отпустить трех человек на свободу способами.

Пример21. На полке стоит 12 книг. Сколькими способами можно выбрать из них 5 книг, никакие две из которых не стоят рядом?

Решение. Рассмотрим 7 оставшихся на полке книг. Между каждыми двумя соседними (и справа и слева от крайних) либо есть пустое место (от одной вынутой книги) либо нет. Набор пустых мест однозначно определяет комплект вынутых книг. Таким образом, получим число искомых комбинаций .

Пример22. Сколько существует различных прямоугольников со сторонами, идущими по линиям сетки прямоугольника 6 × 8?

Решение. Любой прямоугольник определяется парой горизонтальных и парой вертикальных сторон. Горизонтальные стороны

можно выбрать способом, а вертикальные

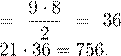способами. Значит, число прямоугольников равно

Пример23. Имеется 6 различных красок: белая, черная, красная, желтая, зеленая и синяя. Сколькими геометрически различными способами можно раскрасить ими куб в 6 цветов? (Два способа раскраски геометрически одинаковы, если они могут быть переведены друг в друга движением куба.)

Решение. Узнаем сначала, сколько способов раскраски куба геометрически неотличимы от данного. Пусть куб раскрашен какимто образом. Грань, окрашенную в белый цвет, можно или оставить на месте, или перевести в любую из остальных 5 граней. Всего получается выбор из 6 возможностей. Если этот выбор уже произведен, то существуют 4 самосовмещения куба, при которых белая грань сохраняет выбранное положение: куб можно вращать на углы 0, 90, 180 и 270^◦вокруг оси, проходящей через его центр перпендикулярно к выбранной грани. По правилу произведения получаем, что каждый класс геометрически одинаковых раскрасок куба насчитывает 6 · 4 = 24 способа раскраски. А так как общее число способов покрасить 6 граней куба в 6 цветов равно 6! = 720, то число геометрически различных способов равно 720 : 24 = 30. Итак, куб можно раскрасить 30 геометрически различными способами.

Пример24. По прямой в одном направлении на некотором расстоянии друг от друга движутся 2014 одинаковых шариков, а навстречу им движутся 2015 таких же шариков. Скорости всех шариков одинаковы. При столкновении любых двух шариков они разлетаются в противоположные стороны с той же скоростью, с какой двигались до столкновения. Сколько всего столкновений произойдет между шариками?

Решение. После столкновения шарики разлетаются с той же скоростью, поэтому ситуация не изменится. если мы разрешим шарикам при столкновении проскакивать друг сквозь друга, сохраняя скорость. Тогда каждый шарик, катящийся «справа », встретит по одному разу каждый из шариков, катящихся «слева», т.е. встреч будет 2014 · 2015 = 4058210.

Задачи для самостоятельного решения

Задача1. В автомобиле пять мест. Сколькими способами пять человек могут занять в нем места для поездки, если водить машину могут только трое из них.

Задача2. Сколько трехзначных чисел содержат ровно одну цифру 7?

Задача3. Студент Илья записал на клочке бумажки семизнач-

ное число (важный телефонный номер) и пролил на неё чай. В итоге на бумажке можно было прочитать лишь следующее: ∗ ∗ ∗ − 1 ∗ − ∗ ∗. Илья вспомнил про номер лишь то, что если вычислить это выражение, то получится ноль. Сколько различных телефонных номеров можно восстановить по этим данным?

Задача4. Таблицу размером 3 × 3 надо заполнить числами 2014, 2015 и 2016 так, чтобы сумма чисел в каждой строке была одинаковой. Сколькими различными способами можно это сделать?

Задача5. Сколько различных чисел можно составить из цифр 1, 2, 3, ..., 9 (каждая цифра используется ровно один раз) таких, чтобы никакие две нечётные цифры не стояли рядом?

Задача6. Сколькими способами можно посадить за круглый стол 5 мужчин и 5 женщин так, чтобы никакие два лица одного пола не сидели рядом?

Задача7. Сколькими способами можно посадить на карусель 5 мужчин и 5 женщин так, чтобы никакие два лица одного пола не сидели рядом. Способы, переходящие друг в друга при вращении карусели, считаются совпадающими.

Задача8. В группе 18 мальчиков и 2 девочки. Сколько способов выбрать 10 человек для работы в столовой, если хоть одна девочка должна работать?

Задача9. В классе, в котором учатся Петя и Ваня — 17 человек. Сколькими способами можно выбрать из класса команду для игры в «Что? Где? Когда?» (6 человек) так, чтобы Петя и Ваня не входили в команду одновременно?

Задача10. Сколькими способами можно разбить 24 школьников на две команды, в одной из которых — 15 человек, а в другой — 9 человек?

Задача11. Сколькими способами можно разбить 24 школьников на две команды по 12 человек?

Задача12. Сколькими способами можно разбить 24 школьников на четыре команды по 6 человек?

Задача13. Найдите сумму всех семизначных чисел, которые могут быть получены перестановками цифр 1, 2, ..., 7.

Задача14. Найдите число всевозможных «слов» из букв слова «зоология». Сколько таких слов, в которых 3 буквы «о» стоят рядом?

Задача15. Старуха Шапокляк решила обзавестись коллекцией из 50 саквояжей. В магазине ей на выбор предложили оранжевые, зеленые, фиолетовые и голубые саквояжи. Сколькими способами она может сделать покупку? Саквояжи одного цвета считаются идентичными.

Задача16. Пассажир оставил вещи в автоматической камере хранения, а когда пришел получать вещи, выяснилось, что он забыл номер. Он только помнит, что в номере были числа 23 и 37. Чтобы открыть камеру, нужно правильно набрать пятизначный номер. Каково наименьшее количество номеров нужно перебрать, чтобы наверняка открыть камеру? (Числа 23 и 37 можно увидеть и в числе

237.)

Ответы

Литература

1. Агаханов Н. Х., Богданов И. И., Кожевников П. А. и др. Математика. Областные олимпиады. 8-11 классы. — М.: Просвещение, 2010. — (Пять колец).

2. Агаханов Н. X., Подлипский О.К. Математика. Районные олимпиады. 6-11 классы. — М.: Просвещение, 2010. — (Пять колец).

3. Агаханов Н. X., Подлипский О.К., Рубанов И. С. Математика. Всероссийские олимпиады. Вып. 3. — М.: Просвещение, 2011. — 207 с.

4. Алфутова Н. Б., Устинов А. В. Алгебра и теория чисел. Сборник задач для математических школ. — М.: МЦНМО, 2009.

5. Антипов М.А., Кноп К.А., Порецкий А.М., Солынин А.А. Семь шагов. Олимпиады Юношеской математической школы 2008 - 2014 годов. — М.: МЦНМО, 2016.

6. Арнольд В. И. Задачи для детей от 5 до 15 лет. — М.: МЦНМО, 2004. — 16 с.

7. Балаян Э.Н. 1000 лучших олимпиадных и занимательных задач по математике: 5-11 классы. — Ростов н/Д : Феникс, 2015.

8. Балаян Э.Н. 1001 олимпиадная и занимательная задачи по математике. — Ростов н/Д : Феникс, 2008. — (Библиотека учителя).

9. Баранова Т. А., Блинков А. Д., Кочетков К. П., Потапова М. Г., Семёнов А. В. Весенний Турнир Архимеда. Олимпиада для 5– 6 классов. Задания с решениями, технология проведения. — М.: МЦНМО, 2003.

10. Блинков А. Д. Избранные задачи окружных олимпиад по математике в Москве/ Составитель А. Д. Блинков. — М.: МЦНМО,

2015.

11. Блинков А. Д., Горская Е. С., Гуровиц В. М. Московские математические регаты. — М.: МЦНМО, 2007.

12. Васильев Н. Б., Гутенмахер В. Л., Раббот Ж.М., Тоом А. Л. Заочные математические олимпиады. — М.: Наука, 1986.

13. Васильев Н. Б., Савин А.П., Егоров А.А. Избранные олимпиадные задачи. Математика. — М.: Бюро Квантум, 2007. (Библиотечка “Квант”. Вып. 100. Приложение к журналу “Квант” № 2/2007.)

14. Галкин Е. В. Нестандартные задачи по математике. Алгебра: Учеб. пособие для учащихся 7-11 кл. — Челябинск: Взгляд, 2004.

15. Галкин Е. В. Нестандартные задачи по математике. Задачи с целыми числами: Учеб. пособие для учащихся 7-11 кл. — Челябинск: Взгляд, 2005.

16. Генкин С. А., Итенберг И. В., Фомин Д. В. Ленинградские математические кружки. — Киров: АСА, 1994.

17. Горбачёв Н. В. Сборник олимпиадных задач по математике. —

М.: МЦНМО, 2004.

18. Гуровиц В. М., Ховрина В. В. Графы. — М.: МЦНМО, 2017. — (Школьные математические кружки)

19. Дынкин Е. Б., Молчанов С. А., Розенталь А. Л. Математические соревнования. Арифметика и алгебра. — М.: Просвещение, 1970.

20. Евдокимов М.А. От задачек к задачам. — М.: МЦНМО, 2004.

21. Егоров А.А., Раббот Ж.М. Олимпиады «Интеллектуальный марафон». Математика. — М.: Бюро Квантум, 2006. — (Библиотечка “Квант”. Вып. 97. Приложение к журналу “Квант” № 5/2006.)

22. Екимова М.А., Кукин Г.П. Задачи на разрезание. — М.: МЦНМО, 2002.

23. Ибатулин И. Ж. Математические олимпиады: теория и практика. Основная школа. — М.: БИНОМ. Лаборатория знаний, 2013.

24. Игнатьев Е. И. В царстве смекалки. — М.: Наука, 1978.

25. Канель-Белов А. Я., Ковальджи А. К. Как решают нестандартные задачи. — М.: МЦНМО, 2008.

26. Канель-Белов А. Я., Трепалин А. С., Ященко И. В. Олимпиадный ковчег. — М.: МЦНМО, 2014.

27. Козлова Е. Г. Сказки и подсказки (задачи для математического кружка). — М.: МЦНМО, 2004. — 165 с.

28. Кордемский Б. А. Математическая смекалка. М.: Издательство технико-теоретической литературы, 1957.

29. Крижановский А. Ф. Математические кружки. 5–7 классы. —

М.: ИЛЕКСА, 2016.

30. Кузьмин О. В. Комбинаторные методы решения логических задач: учеб. пособие. — М.: Дрофа, 2006. — 192 с.

31. Кузьмин О. В. Перечислительная комбинаторика: учеб. пособие. — М.: Дрофа, 2005. — 112 с.

32. Лазаров Б., Михайлов Е. В. «Черноризец Храбр»: турнир по математике и информатике: задачи, решения, материалы для подготовки. Архангельск: КИРА, 2015.

33. Лепехин Ю. В. Математика. 7-8 классы: задания для подготовки к олимпиадам. — Волгоград: Учитель, 2011. — 296 с.

34. Лепехин Ю. В. Олимпиадные задания по математике. 5-6 классы. — Волгоград: Учитель, 2011. — 236 с.

35. Медников Л. Э. Чётность. — М., МЦНМО, 2009. — (Школьные математические кружки)

36. Михайлов Е. В., Патронова Н. Н., Тепляков В. В. Теория вероятностей в примерах и задачах: Часть 1. Комбинаторика. Случайные события и их вероятности. — Архантельск: САФУ,

2013.

37. Прасолов В. В. Задачи по алгебре, арифметике и анализу. — М.: МЦНМО, 2011.

38. Прасолов В. В. Задачи по планиметрии. — М.: МЦНМО,2001.

39. Раскина И.В., Шноль Д.Э. Логические задачи. — М.: МЦНМО, 2018. — (Школьные математические кружки)

40. Спивак А. В. Тысяча и одна задача по математике. —

М.:Просвещение, 2002.

41. Тепляков В. В. Открытые олимпиады по математике ПГУ– САФУ имени М. В. Ломоносова 2009–2013. Архангельск: САФУ,

2013.

42. Уфнаровский В. А. Математический аквариум. — М.: МЦНМО,

2010.

43. Фарков А. В. Математические олимпиады в школе. 5–11 классы. — М.: Айрис-пресс, 2009.

44. Федоров Р. М., Канель-Белов А. Я., Ковальджи А. К., Ященко И. В. Московские математические олимпиады 1993-2005 г./ Под ред. В. М. Тихомирова. — М.: МЦНМО, 2006.

45. Чулков П.В. Арифметические задачи. — М.: МЦНМО, 2017. — (Школьные математические кружки)

46. Шаповалов А.В., Ященко И.В. Вертикальная математика для всех. Готовимся к задаче С6 ЕГЭ с 6-го класса. — М.: МЦНМО,

2014.

47. Шарыгин И. Ф., Ерганжиева Л. Н. Наглядная геометрия. 5-6 кл.: Пос. для общеобр. уч. завед. — М.: Дрофа, 1998.

48. Шень А. Игры и сттратегии с точки зрения математики. — М.: МЦНМО, 2008.

49. Шень А. Математическая индукция. — М.: МЦНМО, 2007.

50. Яковлев И. В. Комбинаторика для олимпиадников. — М.: МЦНМО, 2016. — 80 с.

51. Ященко И. В. Приглашение на Математический праздник. — М.: МЦНМО, 2009.

Интернет ресурсы:

52. geometry.ru

53. zaba.ru

54. problems.ru (Самая большая база олимпиадных задач, большая часть из которых с решениями.)

Многопрофильная олимпиада школьников "Будущее Арктики". Математика: 5-8 классы.

Предисловие

Советы участнику олимпиады

5 класс

6 класс

7 класс

8 класс

5 класс

6 класс

7 класс

8 класс

5 класс

6 класс

7 класс

8 класс

5 класс

6 класс

7 класс

8 класс

5 класс

6 класс

7 класс

8 класс

5 класс

6 класс

7 класс

8 класс

7 класс[1]

8–9 класс[2]

6 класс[3]

7 класс

8–9 класс[4]

РЕШЕНИЯ

5 класс

6 класс

7 класс

8 класс

5 класс

6 класс

7 класс

8 класс

5 класс

6 класс

7 класс

8 класс

5 класс

6 класс

7 класс

8 класс

5 класс

6 класс

7 класс

8 класс

5 класс

6 класс

7 класс

8 класс

7 класс

8–9 класс

6 класс

7 класс

8–9 класс

ОТВЕТЫ

2016 год. Отборочный тур 5 класс

6 класс

7 класс

8 класс

2016 год. Очный тур 5 класс

7 класс

2017 год. Отборочный тур 5 класс

6 класс

7 класс

8 класс

2017 год. Очный тур 5 класс

6 класс

7 класс

2018 год. Отборочный тур 5 класс

6 класс

8 класс

2018 год. Очный тур 5 класс

7 класс^{^[1]}

8–9 класс^{^[2]}

6 класс^{^[3]}

8–9 класс^{^[4]}