Моделирование логических устройств для решения прикладных задач

Методическая разработка урока «Моделирование логических устройств для решения прикладных задач»

Корчецева Любовь Ивановна учитель информатики        МОУ СОШ № 56

Ярославль

2024

Методическая разработка урока

«Моделирование логических устройств для решения прикладных задач»

Цель урока: Создание условий для развития способностей обучающихся самостоятельно решать прикладные задачи в различных сферах деятельности на основе освоенного им опыта.

Задачи урока:

·        повторить основные этапы компьютерного моделирования;

·        повторить алгоритм получения формулы по таблице истинности, упрощение логических функций;

·        предоставить учащимся разнообразные задачи прикладного характера на моделирование логических устройств по заданному результату;

·        смоделировать логические устройства с помощью среды LogМodel.

·        показать учащимся экономное и рациональное воплощение устройств в «железе»

Требования к знаниям и умениям:

Учащиеся должны знать:

- определения элементарных дизъюнкций и конъюнкций, ДНФ И КНФ, СДНФ и СКНФ;

- алгоритмы получения функции по таблице истинности.

Учащиеся должны уметь:

-  решать задачи на конструирование логических схем по заданному результату.

Этапы урока:

I.                   Повторение 10 мин

I.                   Решение задач на построение логических схем по таблице истинности и их моделирование их в среде LogModel 30 мин.

II.                Подведение итогов урока 5 мин.

Набор прикладных задач для моделирования устройств:

1.      Освещение 2-х этажного дома по «евростандарту»

2.      Голосование жюри «Минута славы»

3.      Автомат размена наличных денег

4.      Отбор задач для олимпиады

Ход урока

В жизни  же часто возникает ситуация, когда известен результат и для его реализации необходимо построить устройство.

Рассмотрим следующую задачу:

Задача. В двухэтажном доме лестница освещается одной лампой Х. На первом этаже установлен один выключатель А, на втором этаже - выключатель В. Если включают А, то лампа загорается. При поднятии на второй этаж и включении В лампа гаснет. Если кто-то выходит и нажмет В, то лампа включается, при спуске на первый этаж и нажатии А лампа должна погаснуть.

Алгоритм решения:

·         Составить таблицу истинности по условию задачи.

·         Определить логическую функцию по таблице.

·         Построить логическую схему.

Чтобы решить данную задачу необходимо повторить основные понятия, а именно:

·         этапы моделирования;

·         алгоритмы получения формулы по таблице истинности

·         построение логической схемы по формуле

I.      Повторение:

1.     Этапы моделирования:

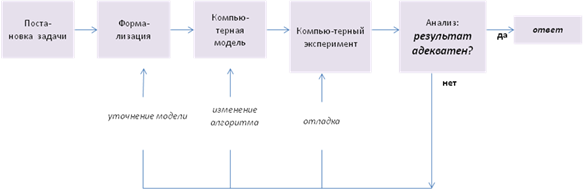
2.     Алгоритмы получения формулы по таблице истинности:

3.     Решение задач на конструирование логических схем

Для заданной таблице истинности построить логическую схему:

Запишем элементарные конъюнкции и, перед построением логической схемы, упростим СДНФ:

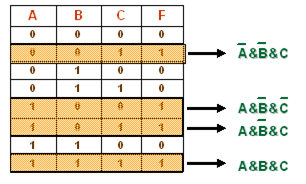
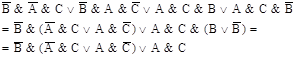                                                                                     3)

II.                                                   Решение задач на построение логических схем по таблице истинности и их моделирование их в среде LogModel

Вернёмся к нашей задаче:

 Задача 1. «Освещение подъезда по «евростандарту»: В двухэтажном доме лестница освещается одной лампой Х. На первом этаже установлен выключатель А, на втором этаже - выключатель В. Если включают А, то лампа загорается. При поднятии на второй этаж и включении В лампа гаснет. Если кто-то выходит и нажмет В, то лампа включается, при спуске на первый этаж и нажатии А лампа должна погаснуть.

1.     Постановка задачи: лампа горит, когда выключатели в разных позициях.

2.     Формализация: построим ТИ по условию задачи, и по ней составим СДНФ или СКНФ

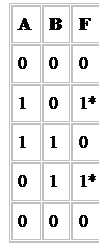
Определим логическую функцию по таблице истинности. Пометим те строки, выходы в которых равны, и количество которых меньше, т.е. с выходом =1. Воспользуемся сначала 1-ым алгоритмом получения СДНФ функции по таблице истинности. Выпишем для каждой отмеченной строки комбинацию переменных через знак &  и расставим знаки операции отрицания: F=.

Теперь воспользуемся 2-ым алгоритмом и получим СКНФ функции. Для каждого набора переменных, на которых функция принимает значение логической 1, запишем конъюнкции, которые объедим дизъюнкцией:

3.     Компьютерная модель и эксперимент

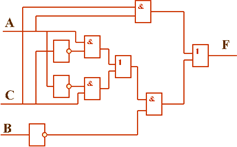
Построим логические схемы по полученным функциям:

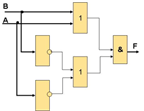
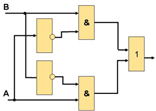
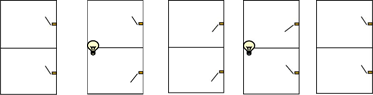
Реализуем  и проверим с помощью среды LogModel полученные логические схемы:

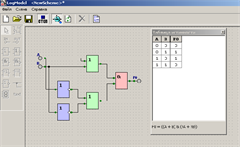
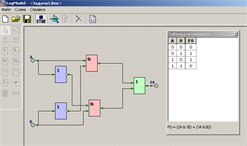
4.     Анализ: модель работает в обоих случаях;  в обоих случаях используется четыре логических элемента и на экономичное воплощение устройства в «железе» не отразится.

Задача2 «Минута славы» Смоделировать устройство, которое можно было бы использовать для голосования членам жюри: артист проходит в следующий тур конкурса, если за него проголосовало не менее двух человек из жюри.

1.     Формализация: построим ТИ по условию задачи, и по ней, в зависимости от рациональности, составим СДНФ или СКНФ

2.     Компьютерная модель и компьютерный эксперимент: Функциональная схема и реализация её в среде LogModel.

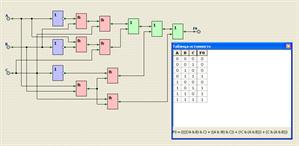
3.   Анализ: модель работает, но если упростить полученную формулу, то воплощение устройства в «железе» будет белее экономичным.

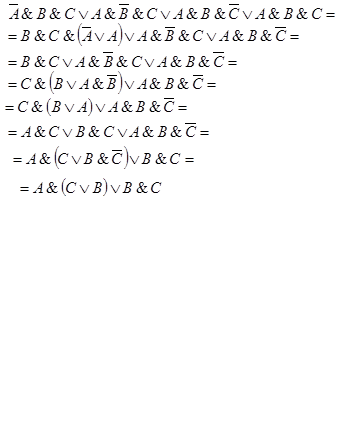
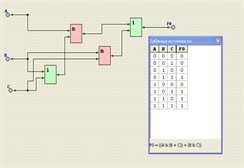
Задача3 Автомат размена наличных денег. Построить логическую схему для автомата по размену наличных денег. Автомат может разменять одну купюру 10 рублей двумя монетами по 5 рублей или одну купюру 50 рублей пятью купюрами по 10 рублей или одну купюру 100 рублей двумя купюрами по 50 рублей или 10 купюрами по 10 рублей.

1.     Постановка задачи:

1. Сколько различных вариантов решения предусматривает условие задачи и почему?
2. Какие исходные данные должен иметь такой автомат для работы и какие данные должны быть на выходе?

3. Какой вариант решения задачи проще (на первый взгляд и после анализа) и соответственно выгоднее для реализации “в металле”?

Задание предусматривает 2 варианта решения:

Первая реализация: “или” в задании используется в разделяющей форме, т.е. нельзя, например, разменять за один раз 2 купюры: одну – 10 рублей и одну – 50 рублей.

Вторая реализация: “или” используется в объединяющей форме, т. е. за один раз можно разменять любую комбинацию из трёх купюр: 10 рублей, 50 рублей и 100 рублей.

2.     Формализация:

Обозначения:

Входы:

А: “наличие купюры 10 рублей”;

В: “наличие купюры 50 рублей”;

С: “наличие купюры 100 рублей”;

D: “вид размена при наличии купюры 100 рублей”:0 – по 50 рублей,1 – по 10 рублей.

Выходы:

F₀:“выдать две монеты по 5 рублей”;

F₁: “выдать 10 купюр по 10 рублей”;

F₂: “выдать 5 купюр по 10 рублей”;

F₃: “выдать две купюры по 50 рублей”.

3.     Компьютерная модель и компьютерный эксперимент:

Первая реализация:

“или” в задании используется в разделяющей форме, т.е. нельзя, например, разменять за один раз 2 купюры: одну – 10 рублей и одну – 50 рублей.

Построить сразу формулы для функций выходов сложно, поэтому нужно сначала составить таблицу истинности, в которой предусмотреть все возможные варианты.

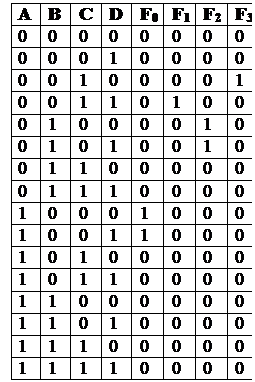
Некоторые формулы необходимо упростить перед построением схемы.

Построим логическую схему в среде LogModel и сравним результат:

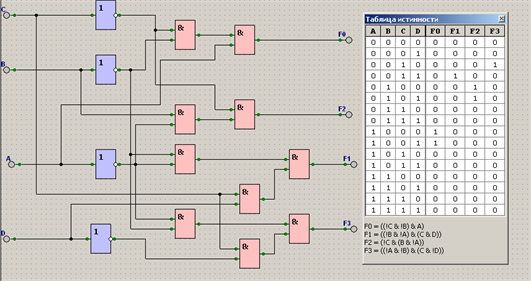
Вторая реализация:

“или” используется в объединяющей форме, т. е. за один раз можно разменять любую комбинацию из трёх купюр: 10 рублей, 50 рублей и 100 рублей.

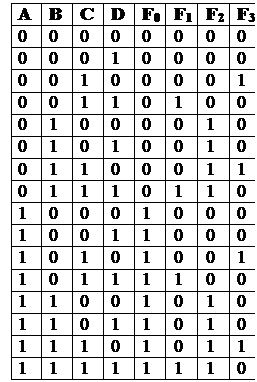
Некоторые формулы необходимо упростить перед построением схемы:

Построим логическую схему и реализуем её в среде LogModel и сравним результат:

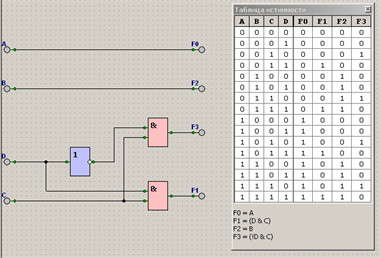
·        Анализ: оказывается, что этот вариант более простой в реализации, так как зависимость функций F0, F1, F2, F3 более простая (в первой реализации эти функции зависят не напрямую от наличия сигнала на соответствующих входах, но и от отсутствия сигналов на других входах – реализация более жёсткая).

I.  

II.  

III. Домашнее задание

1)    По заданной таблице истинности составьте СКНФ, упростите её, если это возможно, и постройте логическую схему:

2) По заданной таблице истинности составьте СДНФ, упростите её, если это возможно, и постройте логическую схему

3) Задача4. Отбор задач для олимпиады Три преподавателя отбирают задачи для олимпиады. Задач несколько. По каждой из задач каждый из преподавателей высказывает свое мнение: легкая задача (0) или трудная (1). Задача включается в олимпиадное задание, если не менее 2 преподавателей отметили ее как трудную, но если все три преподавателя считают ее трудной, то такая задача не включается в олимпиадное задание как слишком трудная. Требуется составить функциональную схему устройства, которое на выходе выдавало бы 1, если задача включается в олимпиадное задание, и 0, если не включается.

Алгоритм решения:

·          Составить таблицу истинности.

·          Определить логическую функцию.

·          Построить логическую схему.

·          Проверить устройство в среде LogModel

IV. Итог урока:

·        повторили основные этапы компьютерного моделирования, алгоритм получения формулы по таблице истинности, упрощение логических функций;

·        на основе полученных ранее знаний решали разнообразные задачи прикладного характера на моделирование логических устройств по заданному результату и реализовали их решение в среде LogМodel.

·        Увидели возможности экономного и рационального воплощения устройств в «железе»

Список литературы:

1)    Босова Л.Л., Босова А.Ю. Информатика. 10 класс. Базовый уровень — М : Бином. Лаборатория знаний, 2021 — 288с.

2)    Поляков. К.Ю., Еремин Е.А. Информатика (базовый и углубленный уровени). 10 класс. Ч.1 — М: Бином. Лаборатория знаний2019 — 352с.

3)    http://www.getsoft.ru/users/32238/programs/?platform=9x - Агафонников В. под руководством Коршунова А. Д., программа для моделирования логических схем «LogModel», физический факультет ИГУ, г. Иркутска, программа является бесплатной,

4)    http://festival.1september.ru/ - Фестиваль педагогических идей «Открытый урок»

5)    http://www.uchenik.vofka.ru/my_files/indx.htm - Учимся информационным технологиям, Моделирование информационных процессов на уроках информатики

1)       

Скачано с www.znanio.ru