
Исследовательский проект
«МОДУЛЬ ЧИСЛА»
2024 г.
Модуль – одна из самых интересных и многогранных тем в математике. Понятие «модуль» широко применяется во многих разделах школьного курса математики, например, в изучении абсолютной и относительной погрешностей приближенного числа; в геометрии и физике будут изучаться понятия вектора и его длины (модуля вектора). Понятия модуля применяется в курсах высшей математики, физики и технических наук, изучаемых в высших учебных заведениях.
Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это слово имеет множество значений и применяется не только в математике, физике и технике, но и в архитектуре, программировании и других точных науках.
Считают, что термин предложил использовать Котс, ученик Ньютона. Знак модуля был введен в XIX веке Вейерштрассом.
В архитектуре модуль – исходная единица измерения, устанавливаемая для данного архитектурного сооружения.
В технике – это термин, применяемый в различных областях техники, служащий для обозначения различных коэффициентов и величин, например, модуль упругости, модуль зацепления...
Начав
подготовку к ОГЭ по математике, я обнаружил, что работы содержат задания с
модулем (уравнения, графики, неравенства). В первой части содержатся задания на
нахождение значений иррациональных выражений, например: 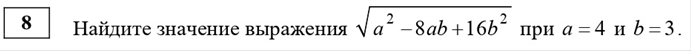 ,
,
На первый взгляд задание не сложное: я увидела формулу квадрата разности, смело убрала корень, и в результате получила -8.
Моё решение:![]() =
= ![]() .
.
Если a=4, b=3, то ![]() = 4 –
4 · 3= - 8.
= 4 –
4 · 3= - 8.
Конечно, при проверке решения, выяснилось, что я забыл, что имею дело с корнем (подкоренное выражение не отрицательное!), а про модуль в данном примере я совсем не вспомнил. Во второй части ОГЭ задание на построение графика «пугает» одним видом:
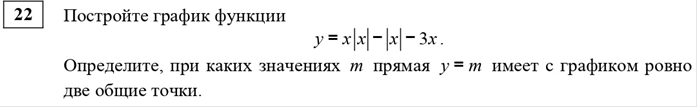
Проблемный вопрос: почему задания с модулем так сложны для восприятия? Как помочь себе, моим одноклассникам и другим ребятам преодолеть «страх модуля»?
Цель работы: получение расширенной информации о модуле числа, его применении, а также о различных способах решения уравнений, неравенств и построения графиков функций, содержащих знак абсолютной величины.
Действия по решению данной проблемы:
1. Изучить литературу по данной теме.
2. Провести исследование и анализ имеющихся способов решения заданий с модулем.
3. Выбрать из найденных способов решения наиболее оптимальные.
4. Провести обобщение и систематизацию имеющего материала.
Методы работы: Сбор информации и ее анализ.
В ходе решения данной проблемы, я поставил перед собой следующие ЗАДАЧИ:
- Научиться решать уравнения, неравенства с модулем.
- Научиться строить графики с модулем.
- Научиться самостоятельно овладевать новыми знаниями.
- Учиться получать информацию, пользуясь ресурсами Интернета.
- Научиться представлять математический текст в компьютерной форме, пользуясь специальными редакторами и компьютерными программами.
Практическая направленность проекта
Данную работу можно использовать в качестве учебного пособия для учащихся.
Модуль числа – это такая забавная концепция в математике, с пониманием которой у многих людей возникают трудности. Но, чтобы её понять,попробую разобраться, зачем и кому он нужен.
Ситуация первая
В жизни, часто встречаются ситуации, где отрицательные числа не имеют никакого практического смысла.
Например, мы не можем проехать на машине «минус 70 километров» (мы проедем 70 километров, не важно, в каком направлении), как и не можем купить «минус 5 кг апельсинов». Эти значения всегда должны быть положительными.
Именно для обозначения таких ситуаций математики придумали специальный термин – модуль или абсолютная величина.
Ситуация вторая
Ты покупаешь пакет чипсов «Lay’s». На пакете написано, что он весит 100 грамм. Но, если ты начнешь взвешивать пакеты, вряд ли они будут весить ровно 100 грамм. Какой-то из них будет весить 101 грамм, а какой-то 99.
И что, можно идти судиться с компанией «Lay’s», если они тебе недовесили?
Нет. Потому что «Lay’s» устанавливает допуск и говорит, что пакет будет весить 100 грамм, плюс-минус 1 грамм. Вот это «плюс-минус» – это и есть модуль.
Ситуация третья
В жизни вообще не бывает 100% точных величин. Всегда есть вот такие допуски. В зарплате, например: «Я согласен работать за 250 тыс рублей в месяц, плюс-минус 20 тыс!» 20 тысяч – это и есть модуль.
А вообще для простоты надо запомнить, что модуль это расстояние от точки отсчета в любую сторону.Теперь подробнее…
Модуль числа - коротко о главном.
Что же такое модуль числа?
Представь, что это ты.

Предположим, что ты стоишь на месте и можешь двигаться как вперёд, так и назад. Обозначим точку отправления 0.

Итак, ты делаешь 3 шага вперёд и оказываешься в точке с координатой 3.
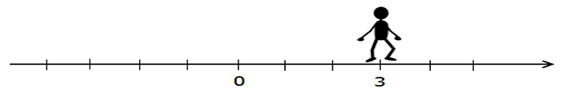
Это означает, что ты удалился от места, где стоял на 3 шага (3 единичных отрезка).
То есть, расстояние от начала движения до точки, где ты в итоге оказался, равно 3.
Но ведь ты же можешь двигаться и назад!
Если
от отправной точки с координатой 0 сделать 3 шага в обратную сторону, то окажешься в точке с
координатой −3.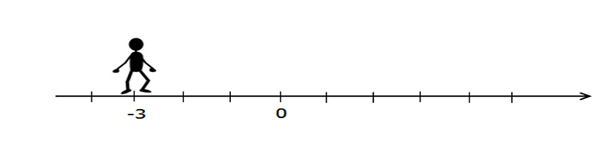
Какое расстояние было пройдено в первом и во втором случае?
Конечно же, расстояние, пройденное в первом и во втором случае, будет одинаковым и равным трем, ведь обе точки (3 и −3), в которых ты оказался одинаково удалены от точки, из которой было начато движение (0).
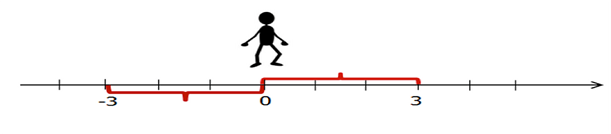
Таким образом, мы приблизились к понятию модуля.
Получается, что модуль показывает расстояние от любой точки на координатном отрезке до точки начала координат.
Так, модулем числа 5 будет 5. Модуль числа −5 также равен 5.
Потому что расстояние не может быть отрицательным! Модуль – это абсолютная величина.
Обозначается модуль просто:|a|, (a — любое число).
Модулем действительного числа x называется само число x, если оно неотрицательно, и – x, если x – отрицательное число.
|x|=
x, если х ≥ 0
–х, если х < 0.
Расстояние между двумя точками на прямой.
Рассмотрим координатную прямую, на которой отмечены 2 точки: A и B . Чтобы найти расстояние между этими точками, нужно найти длину отрезка AB. Это делается при помощи следующей формулы: AB=∣a−b∣, где a , b — координаты этих точек на прямой (координатной прямой).
Ввиду того, что в формуле присутствует модуль, при решении не принципиально, из какой координаты какую вычитать (так как берётся абсолютная величина этой разности).То есть ∣a−b∣=∣b−a∣.
Пример. Найти расстояние между точками L(-3) и M(5), отмеченными на координатной прямой.

Решение. Чтобы найти расстояние между точками L и M надо из координаты точки L вычесть координату точки M или наоборот, а в качестве ответа взять модуль полученного результата: LM =|-3 - 5| = |-8| = 8 или LM =|5 - (-3)| = |5 + 3| = 8.
Тема «Модуль действительного числа» является составной частью курса алгебры и является необходимым его компонентом. Тема представлена в таких разделах школьного курса математики, как арифметика, алгебра и геометрия. Содержание раздела «Арифметика» служит базой для дальнейшего изучения учащимися математики, способствует развитию их логического мышления, формированию умения пользоваться алгоритмами, а также приобретению практических навыков, необходимых в повседневной жизни. Тема «Модуль действительного числа» рассматривается после изучения положительных и отрицательных чисел, понятие используется при сравнении чисел и нахождении расстояния между точками.
Содержание раздела «Алгебра» способствует формированию математического аппарата для решения задач из разных разделов математики, смежных предметов. В разделе «Алгебра» понятие модуля встречается при решении уравнений и неравенств, которые содержат переменную под знаком модуля, а также при тождественных преобразованиях.
Содержание раздела «Функции» нацелено на получение конкретных знаний о функции как важнейшей математической модели для описания и исследования разнообразных процессов. В разделе «Функции» представлен график функции
![]() , его
преобразования, исследуются свойства функции.
, его
преобразования, исследуются свойства функции.
Тема «Модуль действительного числа» впервые встречается в 6 классе, далее в 7-9 классе идёт расширение знаний по этой теме.
Я провела анализ изложения темы «Модуль» в школьных учебниках, по которым училась, для того, чтобы вспомнить, обобщить и систематизировать полученные в процессе обучения знания, умения и навыки по данной теме.
Изложение темы «Модуль действительного числа» в учебно-методическом комплекте А.Г. Мерзляка 7-9 класс, Г.В.Петерсона 6 класс.
|
6 класс |
Тема «Модуль числа» рассматривается в разделе «Рациональные числа». Понятие «модуль» автор предлагает рассмотреть через расстояние: «Расстояние от начала отсчёта до точки, обозначающей данное число, называют модулем этого числа»(от латинского modus – мера, величина). Далее предлагается ряд свойств: ·
Модуль числа a
обозначается символом ·
Так как противоположные числа находятся на одинаковом расстоянии
от начала отсчёта, то их модули равны ·
Модуль числа 0 считается равным 0: это число находится на
«нулевом расстоянии» от самого себя: ·
Как и любое расстояние между двумя точками, модуль не может быть
отрицательным. Таким образом, для любого числа a
выполняется неравенство: Далее в теме «Сравнение чисел» автор даёт понятие модуля, как разветвлённого алгоритма[1].Задания в данном учебнике располагаются по уровню сложности, от простого к сложному. Сначала автор предлагает задания на нахождения значений выражений с модулем, затем решение уравнений, решение неравенств с модулем с помощью координатной прямой и задания на тождественные преобразования. |
|
7 класс |
Тема «Модуль действительного числа» не представлена в данном учебнике отдельным параграфом, но данную тему автор включает в такие темы как «Линейное уравнение с одной переменной», «Тождественное равные выражения. Тождества», «Линейная функция, ее график и свойства», «Уравнения с двумя переменными», «Система уравнений с двумя переменными».[2] В теме «Уравнения» А.Г. Мерзляк предлагает простейшие уравнения с модулем, при том что автор в начале параграфа предлагает разобранный пример с решением. Уравнения в параграфе располагаются по возрастанию уровня сложности. Далее в теме «Тождества» учащимся предлагаются тождества с модулем. Задания располагаются также по уровню сложности, но стоит заметить, что заданий мало. В теме «Линейная функция» встречается упражнение на построение графика модуля, но стоит отметить, что автор не включает в объяснение процесс построения самого графика. Тема «Уравнения с двумя переменными» требует от учащихся решение
уравнений с помощью построения графика функции. В теме «Система уравнений с двумя переменными» предлагается решить систему уравнений с двумя переменными, одно из уравнений которой с модулем, с помощью построения графика. Заданий в параграфе представлено мало и задания, как показывают авторы учебника «со звездочкой», то есть повышенного уровня сложности. |
|
8 класс |
Тема «Модуль действительного числа» не представлена как
самостоятельная, но встречается в темах «Рациональные дроби», «Функция В теме «Рациональные дроби» встречаются задания на нахождение допустимых значений выражения. Также построение графика функции и решение уравнения с модулем. В теме «Функция Тема «Свойства арифметического корня» затрагивает тему «Модуль», именно там закладываются новые методы решения уравнений. В теоретической части параграфа разобраны примеры с решением, что поможет учащимся самостоятельно разобрать тему и применить свои знания на практике. В данной теме представлены задания, где необходимо «увидеть» модуль, так как в заданиях в явном виде он не представлен. В теме «Квадратные уравнения» А.Г. Мерзляк предлагает учащимся решить уравнения с помощью нового подхода к понятию модуля. |
|
9 класс |
Задания с модулем встречаются в главе «Неравенства»[4].Также автор предлагает решение уравнений и построение графиков функций В главе «Квадратичная функция» есть задания с модулем. · Нахождение области определения/значений функции; · Построение
графика функции В теме «Квадратичная функция, ее свойства и график» А.Г. Мерзляк приводит правила построения графиков функций 1.
2.
В данной теме учащимся предлагаются задания, в достаточном количестве, на построения графика функции с модулем. |
По окончанию анализа учебников математики Г.В. Петерсона 6 класс и А.Г. Мерзляка для 7-9 классов можно сделать вывод, что тема «Модуль действительного числа» раскрыта достаточно полно. Авторы предлагают 1 способ решения уравнений и неравенств с модулем, основанный на понятии «расстояния». Построение графиков функций, содержащих модуль также показано одним способом по «разветвлённому» определению. Хотя в учебнике 9 класса есть интересная рубрика «Когда сделаны уроки», в которой показан новый способ построения графиков, использую сдвиги «основного» графика.
Для себя я отметила, что переходя из класса в класса понятие «модуль» «повзрослело» вместе со мной, но навык решения таких заданий постепенно теряется. Мне бы хотелось иметь всегда под рукой «помощника» по способам и методам решения уравнений и неравенств с модулем, а также способами построения графиков с модулями. Поэтому я решила:
- изучить «лайфхаки» решений заданий с модулями, кроме данных в учебниках, существуют;
- составить памятку-«помощницу», в которой соберу и оформлю всю найденную и полезную информацию;
- провести опрос среди учащихся 7-9 классов (больше, конечно, меня будут интересовать одноклассники): «посчитали бы они для себя мои «находки» полезными и значимыми»?
Способы построения графиков функций, содержащих модуль.
С сайтом «Решу ОГЭ»[5] Д.Д.Гущина я познакомилась ещё в 7 классе при подготовке к ВПР[6] по математике (и по другим предметам тоже). Навигация очень удобная, разобраться в использовании нетрудно.
На сайте все разбито "по полочкам", т.к. каждое задание соответствует определенной теме. Поэтому, можно найти все, что нужно - выучить теорию и нарешивать тренировочные тесты, так сказать "набивать руку". В этом помогает «Каталог заданий». Здесь можно прорешать все аналоги каждого задания.
Также на сайте содержится много полезной информации, например, если вы зайдете на вкладку "Об экзамене", то можно найти всю актуальную информацию про экамен вашего года. А еще очень важная информация, составители сайта - те, кто является составителем самих экзаменационных работ. Также, есть вкладка "Справочник", т.к. там только нужная информация.
Меня интересовали задания по теме модуль.Просмотрев каталог заданий, я не нашла в первой части заданий с модулями, зато во второй части обнаружила 19 заданий на построение графиков с решениями (задание 22 ОГЭ)[7].
![]()
![]()
![]()

Для себя сделала вывод: построение графиков, содержащих модуль, осуществляется двумя способами:
1. На основании определения модуля
Построение
графика функции![]()
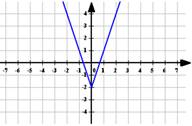
![]()
Приведем
пример построения графика функции ![]()
![]()
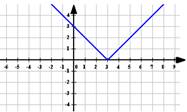 Построение
графика функции
Построение
графика функции ![]()
![]()
Приведем
пример построения графика функции ![]()
![]()
2. На основании правил геометрического преобразования графиков функций.
Какие геометрические преобразования, можно использовать при построении графиков функций? (параллельный перенос вдоль осей ОХ и ОУ, симметричное отображение относительно осей или точки)
Построение
графика ![]() .
.
![]()
 Чтобы
построить график функции
Чтобы
построить график функции ![]() , если
известен график функции
, если
известен график функции ![]() ,
нужно оставить на месте ту его часть, где
,
нужно оставить на месте ту его часть, где ![]() , и
симметрично отобразить относительно оси Х другую его часть, где
, и
симметрично отобразить относительно оси Х другую его часть, где ![]() .
.
Алгоритм построения графика:
1.
Построить график функции ![]() ,
,
2.
Часть графика ![]() ,
лежащая над осью ОХ, сохраняется, а часть его, лежащая под осью ОХ,
отображается симметрично относительно оси ОХ.
,
лежащая над осью ОХ, сохраняется, а часть его, лежащая под осью ОХ,
отображается симметрично относительно оси ОХ.
Построение
графика ![]() .
.
![]()
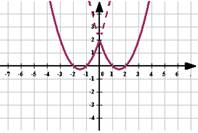 Чтобы
построить график функции
Чтобы
построить график функции ![]() , если
известен график функции
, если
известен график функции ![]() ,
нужно оставить на месте ту его часть, где
,
нужно оставить на месте ту его часть, где ![]() , а
при
, а
при ![]() отобразить
построенную часть симметрично относительно оси ОУ.
отобразить
построенную часть симметрично относительно оси ОУ.
Алгоритм построения графика:
Построить
график функции ![]() ,
,
При ![]() график
сохраняется, а при
график
сохраняется, а при ![]() отображается
построенная часть симметрично относительно оси ОУ.
отображается
построенная часть симметрично относительно оси ОУ.
Нашла ещё один интересный способ:
***Рассмотрим функцию y = |x + 1| – |x – 2|.
Решение.
Раскрывая знак модуля, необходимо рассмотреть всевозможную комбинацию знаков подмодульных выражений.
Возможны четыре случая:
{x + 1 – x + 2 = 3, при x ≥ -1 и x ≥ 2;
{-x – 1 + x – 2 = -3, при x < -1 и x < 2;
{x + 1 + x – 2 = 2x - 1, при x ≥ -1 и x < 2;
{-x – 1 – x + 2 = -2x + 1, при x < -1 и x ≥ 2 – пустое множество.
Тогда исходная функция будет иметь вид:
{3, при x ≥ 2;
y = {-3, при x < -1;
{2x – 1, при -1 ≤ x < 2.
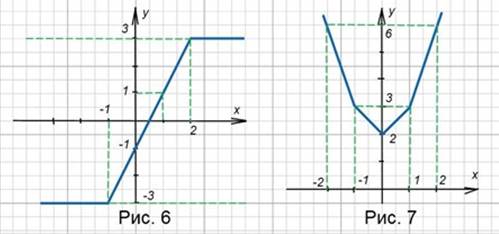
Получили кусочно-заданную функцию, график которой изображен на рисунке 6.
.
3*** Алгоритм построения графиков функций вида
y = a1|x – x1| + a2|x – x2| + … + an|x – xn| + ax + b.
В предыдущем примере было достаточно легко раскрыть знаки модуля. Если же сумм модулей больше, то рассмотреть всевозможные комбинации знаков подмодульных выражений проблематично. Как же в этом случае построить график функции?
Заметим, что графиком является ломаная, с вершинами в точках, имеющих абсциссы -1 и 2. При x = -1 и x = 2 подмодульные выражения равны нулю. Практическим путем мы приблизились к правилу построения таких графиков:
Графиком функции вида y = a1|x – x1| + a2|x – x2| + … + an|x – xn| + ax + b является ломаная с бесконечными крайними звеньями. Чтобы построить такую ломаную, достаточно знать все ее вершины (абсциссы вершин есть нули подмодульных выражений) и по одной контрольной точке на левом и правом бесконечных звеньях
Задача.
Построить график функции y = |x| + |x – 1| + |x + 1| и найти ее наименьшее значение.
Решение:
Нули подмодульных выражений: 0; -1; 1. Вершины ломаной (0; 2); (-1; 3); (1; 3). Контрольная точка справа (2; 6), слева (-2; 6). Строим график (рис. 7). min f(x) = 2.
Рассмотренные преобразования справедливы для всех видов функций.
Вывод:
|
Функция |
Преобразование |
Пример |
|
y = f(|x|) |
1) Для x ≥ 0, y = f(x) 2) Для x < 0 – преобразование симметрии относительно Oy графика y = f(x), для x ≥ 0 симметричные части графика из правой полуплоскости в левую |
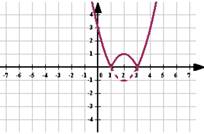
y = x2 – 8|x| + 12. 1.Определим четность функции. Значение для y(-x) совпадает со значением для y(x), поэтому данная функция четная. Тогда ее график симметричен относительно оси Oy. 2.Строим график функции y = x2 – 8x + 12 для x ≥ 0 и симметрично отображаем график относительно Oy для отрицательных x (рис. 1). |
|
y =|f(x)| |
1) Для f(x) ≥ 0, |f(x)| = f(x) 2) Для f(x) < 0, |f(x)| = -f(x) Симметричное отображение части графика из нижней полуплоскости в верхнюю относительно Ox |
y = |x2 – 8x + 12|. 1.область значений предложенной функции: y ≥ 0. 2. график расположен над осью абсцисс или касаясь ее. 3. строим график функции y = x2 – 8x + 12, оставляют часть графика, которая лежит над осью Ox, без изменений, а часть графика, которая лежит под осью абсцисс, симметрично отображают относительно оси Ox (рис. 2) |
|
y = |f(|x|)| |
f(x) → f(|x|) → |f(|x|)|. |
y = |x2 – 8|x| + 12| 1. проводим комбинацию преобразований: y = x2 – 8x + 12 → y = x2 – 8|x| + 12 → y = |x2 – 8|x| + 12|. (рис.3) |
|
|
||
Методы и способы решения уравнений , содержащих модуль.
Решение уравнений, содержащих переменную под знаком модуля, не менее сложная тема. Попробую разобраться, с чем же это связано? Почему, например, квадратные уравнения большинство щёлкает, как орешки, а с таким, далеко не самым сложным понятием, как модуль, имеет столько проблем?
На мой взгляд, все эти сложности связаны с отсутствием четко сформулированных правил для решения уравнений с модулем. Так, решая квадратное уравнение, ученик точно знает, что ему нужно сначала применять формулу дискриминанта, а затем формулы корней квадратного уравнения. А что делать, если в уравнении встретился модуль? Постараюсь составить необходимый план действий на случай, когда уравнение содержит неизвестную под знаком модуля. К каждому случаю приведу несколько примеров:
1. Рассмотрим уравнение вида |x| = с, где с – действительное число. Это уравнение можно решить с помощью определения модуля.
Все действительные числа разобьем на три группы: те, что больше нуля, те, что меньше нуля, и третья группа – это число 0. Запишем решение в виде схемы:
{±c, если с > 0
Если |x| = c, то x = {0, если с = 0
{нет корней, если с < 0
Примеры:
1) |x| = 5, т.к. 5 > 0, то x = ±5;
2) |x| = -5, т.к. -5 < 0, то уравнение не имеет корней;
3) |x| = 0, то x = 0.
2. Уравнение вида |f(x)| = b, где b > 0. Для решения данного уравнения необходимо избавиться от модуля. Делаем это так: f(x) = b или f(x) = -b. Теперь необходимо решить отдельно каждое из полученных уравнений. Если в исходном уравнении b< 0, решений не будет.
Примеры:
1) |x + 2| = 4, т.к. 4 > 0, то
x + 2 = 4 или x + 2 = -4
x = 2 x = -6
Ответ: -6;2
2) |x2 – 5| = 11, т.к. 11 > 0, то
x2 – 5 = 11 или x2 – 5 = -11
x2 = 16 x2 = -6
x = ± 4 нет корней
Ответ: -4;4
3) |x2 – 5x| = -8 , т.к. -8 < 0, то уравнение не имеет корней.
3. Уравнение вида |f(x)| = g(x). По смыслу модуля такое уравнение будет иметь решения, если его правая часть больше или равна нулю, т.е. g(x) ≥ 0. Тогда будем иметь:
f(x) = g(x) или f(x) = -g(x).
Примеры:
1) |2x – 1| = 5x – 10. Данное уравнение будет иметь корни, если 5x – 10 ≥ 0. Именно с этого и начинают решение таких уравнений.
1. О.Д.З: 5x – 10 ≥ 0
5x ≥ 10
x ≥ 2.
2. Решение:
2x – 1 = 5x – 10 или 2x – 1 = -(5x – 10)
3x = 9 7x = 11
x = 3 x = 11/7
3. Объединяем О.Д.З. и решение, получаем:
Корень x = 11/7 не подходит по О.Д.З., он меньше 2, а x = 3 этому условию удовлетворяет.
Ответ: 3
2) |x – 1| = 1 – x2.
1. О.Д.З: 1 – x2 ≥ 0. Решим методом интервалов данное неравенство:
(1 – x)(1 + x) ≥ 0
-1 ≤ x ≤ 1
2. Решение:
x – 1 = 1 – x2 или x – 1 = -(1 – x2)
x2 + x – 2 = 0 x2 – x = 0
x = -2 или x = 1 x = 0 или x = 1
3. Объединяем решение и О.Д.З.:
Подходят только корни x = 1 и x = 0.
Ответ: 0; 1.
4. Уравнение вида |f(x)| = |g(x)|. Такое уравнение равносильно двум следующим уравнениям f(x) = g(x) или f(x) = -g(x).
Пример:
1) |x2 – 5x + 7| = |2x – 5|. Данное уравнение равносильно двум следующим:
x2 – 5x + 7 = 2x – 5 или x2 – 5x +7 = -2x + 5
x2 – 7x + 12 = 0 x2 – 3x + 2 = 0
x = 3 или x = 4 x = 2 или x = 1
Ответ: 1; 2; 3; 4
5. Уравнения, решаемые методом подстановки (замены переменной). Данный метод решения проще всего объяснить на конкретном примере. Так, пусть дано квадратное уравнение с модулем:
x2 – 6|x| + 5 = 0. По свойству модуля x2 = |x|2, поэтому уравнение можно переписать так:
|x|2 – 6|x| + 5 = 0. Сделаем замену |x| = t, t ≥ 0, тогда будем иметь:
t2 – 6t + 5 = 0. Решая данное уравнение, получаем, что t = 1 или t = 5. Вернемся к замене:
|x| = 1 или |x| = 5
x = ±1 x = ± 5
Ответ: -5; -1; 1; 5
Рассмотрим еще один пример:
x2 + |x| – 2 = 0. По свойству модуля x2 = |x|2, поэтому
|x|2 + |x| – 2 = 0. Сделаем замену |x| = t, t ≥ 0, тогда:
t2 + t – 2 = 0. Решая данное уравнение, получаем, t = -2 или t = 1. Вернемся к замене:
|x| = -2 или |x| = 1
Нет корней x = ± 1
Ответ: x = -1, x = 1.
6. Еще один вид уравнений – уравнения со «сложным» модулем. К таким уравнениям относятся уравнения, в которых есть «модули в модуле». Уравнения данного вида можно решать, применяя свойства модуля.
Примеры:
1) |3 – |x|| = 4. Будем действовать так же, как и в уравнениях второго типа. Т.к. 4 > 0, то получим два уравнения:
3 – |x| = 4 или 3 – |x| = -4.
Теперь выразим в каждом уравнении модуль х, тогда |x| = -1 или |x| = 7.
Решаем каждое из полученных уравнений. В первом уравнении нет корней, т.к. -1 < 0, а во втором x = ±7.
Ответ -7; 7.
2) |3 + |x + 1|| = 5. Решаем это уравнение аналогичным образом:
3 + |x + 1| = 5 или 3 + |x + 1| = -5
|x + 1| = 2 |x + 1| = -8
x + 1 = 2 или x + 1 = -2. Нет корней.
x = 1 x = -3
Ответ: -3; 1.
7. Возведение обеих частей уравнения в квадрат:
![]()
![]()
Отсюда: ![]()
![]()
Ответ: 1; 5.
8.Графический.
Пример 1:![]()
Построим в одной системе координат графики функций ![]() и
и ![]() Абсциссы
точек пересечения графиков будут являться корнями уравнения.
Абсциссы
точек пересечения графиков будут являться корнями уравнения.
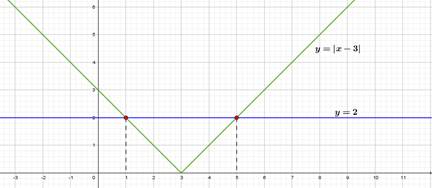
Отсюда получаем ![]()
Ответ: 1; 5.
Пример 2: ![]()
Построим в одной системе координат графики функций ![]() и
и ![]() .
.
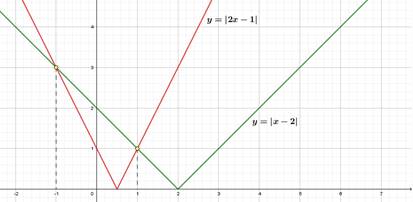
Ответ: -1; 1.
Существует еще и универсальный метод решения уравнений с модулем. Это метод интервалов.[8]
Метод интервалов позволяет решать любые уравнения, содержащие модуль. Суть этого метода в том, чтобы разбить числовую ось на несколько участков (интервалов), причем разбить ось нужно именно нулями выражений, стоящих в модулях. Затем на каждом из получившихся участков всякое подмодульное выражение либо положительно, либо отрицательно. Поэтому каждый из модулей может быть раскрыт или со знаком минус, или со знаком плюс. После этих действий остается лишь решить каждое из полученных простых уравнений на рассматриваемом интервале и объединить полученные ответы.
Рассмотрим данный метод на конкретном примере.
|x + 1| + |2x – 4| – |x + 3| = 2x – 6.
1) Найдем нули выражений, стоящих в модулях. Для этого нужно приравняем их к нулю, и решить полученные уравнения.
x + 1 = 0 2x – 4 = 0 x + 3 = 0
x = -1 2x = 4 x = -3
x = 2
2) Расставим получившиеся точки в нужном порядке на координатной прямой.
Они
разобьют всю ось на четыре участка. 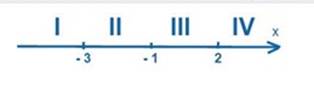
3) Определим на каждом из получившихся участков знаки выражений, стоящих в модулях. Для этого подставляем в них любые числа с интересующих нас интервалов. Если результат вычислений – число положительное, то в таблице ставим «+», а если число отрицательное, то ставим «–». Это можно изобразить так:
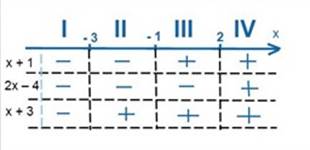
4) Теперь будем решать уравнение на каждом из четырех интервалов, раскрывая модули с теми знаками, которые проставлены в таблице. Итак, рассмотрим первый интервал:
I интервал (-∞; -3). На нем все модули раскрываются со знаком «–». Получим следующее уравнение:
-(x + 1) – (2x – 4) – (-(x + 3)) = 2x – 6. Приведем подобные слагаемые, раскрыв предварительно скобки в полученном уравнении:
-x – 1 – 2x + 4 + x + 3 = 2x – 6
-4x = -12
x = 3.
Полученный ответ не входит в рассматриваемый интервал, поэтому в окончательный ответ писать его не надо.
II интервал [-3; -1). На этом интервале в таблице стоят знаки «–», «–», «+». Именно так и раскрываем модули исходного уравнения:
-(x + 1) – (2x – 4) – (x + 3) = 2x – 6. Упростим, раскрыв при этом скобки:
-x – 1 – 2x + 4 – x – 3 = 2x – 6. Приведем в полученном уравнении подобные:
-5x = -6
x = 6/5. Полученное число не принадлежит рассматриваемому интервалу, поэтому оно не является корнем исходного уравнения.
III интервал [-1; 2). Раскрываем модули исходного уравнения с теми знаками, которые стоят на рисунке в третьей колонке. Получаем:
(x + 1) – (2x – 4) – (x + 3) = 2x – 6. Избавимся от скобок, перенесем слагаемые, содержащие переменную x в левую часть уравнения, а не содержащие x в правую. Будем иметь:
x + 1 – 2x + 4 – x – 3 = 2x – 6
-4x = -8
x = 2.
В рассматриваемый интервал число 2 не входит.
IV интервал [2; +∞). Все модули раскрываем со знаком «+». Получим:
(x + 1) + (2x – 4) – (x + 3) = 2x – 6.
x + 1 + 2x – 4 – x – 3 = 2x – 6
0 = 0.
После преобразований уравнение превратилось в верное равенство. Это говорит о том, что любое число из рассматриваемого интервала будет являться решением исходного уравнения. Значит ответом, как на этом интервале, так и во всем уравнении является множество чисел, удовлетворяющих условию x ≥ 2.
Ответ: x ≥ 2.
Метод интервалов хоть и является универсальным методом решения уравнений с модулем, его применение не всегда оправдано. Порой решить уравнение выходит гораздо быстрее, используя, например, определение модуля или какие-то другие методы.
Вывод:
|
|
Методы решения |
Алгоритм |
Пример |
|
1 |
По определению модуля. |x| = с, где с – действительное число |
решение в виде схемы: {±c, если с > 0 {0, если с = 0 {нет корней, если с < 0 |
4 -
х=3 или х= -3 Ответ: -3; 3 |
|
2 |
По определению модуля. |f(x)| = b, где b > 0. |
1.необходимо избавиться от модуля: f(x) = b или f(x) = -b. 2.решить отдельно каждое из полученных уравнений. *Если в исходном уравнении b< 0, решений не будет. |
х-5 = 4 или х-5 = -4 х=9 х=1
Ответ: 1; 9
|
|
3 |
По определению модуля. |f(x)| = g(x). |
По смыслу модуля: уравнение будет иметь решения, если g(x) ≥ 0. Тогда будем иметь: f(x) = g(x) или f(x) = -g(x). * если g(x) < 0, то решений не будет. |
|2x – 1| = 5x – 10. Данное уравнение будет иметь корни, если 5x – 10 ≥ 0. Именно с этого и начинают решение таких уравнений. 1) О.Д.З: 5x – 10 ≥ 0 5x ≥ 10 x ≥ 2. 2) Решение: 2x – 1 = 5x – 1 или 2x – 1 = -(5x – 10) 3x = 9 7x = 11 x = 3 x = 11/7 3) Объединяем О.Д.З. и решение, получаем: Корень x = 11/7 не подходит по О.Д.З., он меньше 2, а x = 3 этому условию удовлетворяет. Ответ: 3 |
|
4 |
По определению модуля. |f(x)| = |g(x)|. |
равносильно двум следующим уравнениям: f(x) = g(x) или f(x) = -g(x). |
|x2 – 5x + 7| = |2x – 5|. Данное уравнение равносильно двум следующим: 1)x2 – 5x + 7 = 2x – 5 x2 – 7x + 12 = 0 x = 3 ; x=4 или 2)x2 – 5x +7 =-2x + 5 x2 – 3x + 2 = 0 x = 2 ; x = 1 Ответ: 1; 2; 3; 4 |
|
5 |
Метод замены переменной.
|
a|x|2 + b|x| + c = 0. 2.сделаем замену |x| = t, t ≥ 0, тогда будем иметь:at2 +bt + c = 0. 3.Решаем данное уравнение. 4. Вернемся к замене. |
x2 – 6 | x | + 8 = 0 Пусть | x | = y, y ≥ 0 Получим: y2 – 6y + 8 = 0, y1 = 2; y2 = 4. Вернёмся к замене: | x | = 2 или | x | = 4, x = ± 2. x = ± 4. Ответ: -4; -2; 2;4.
|
|
6 |
*«Сложный модуль» (модуль в модуле) |a – |x|| = b. |
1.при условии b≥0, по определению модуля, «убираем» внешний модуль: a – |x|= b или a – |x|= - b. 2.используя свойства модуля, сводим решение данных уравнений к методу 1. |
|3 + |x + 1|| = 5 1) 3 + |x + 1| = 5 |x + 1| = 2 х+1=2 или х+1= -2 х=1 х= -3 или 2) 3 + |x + 1| = -5 |x + 1| = -8 Нет корней. Ответ: -3; 1.
|
|
7 |
Возведение обеих частей в квадрат |f(x)| = |g(x)| или |f(x)| = g(x). |
1.при
условии: g(x) ≥ 0, используя свойство f2(x) = g2(x). 2. решаем полученное квадратное уравнение. |
Отсюда: (х-3-2)(х-3+2)=0 (х-5)(х-1) = 0 х-5 =0 или х-1 =0 х=5 х=1 Ответ: 1; 5.
|
|
8 |
Графический
|
1.«разбиваем» уравнение на «знакомые» функции; 2.в одной системе координат строим графики функций; 3.находим координаты точек пересечения графиков; 4.записываем только абсциссы точек пересечения графиков |
Построим
в одной системе координат графики функций
Ответ: -1; 1 |
|
9 |
Метод интервалов* |
1.приравниваем к нулю выражения, стоящие под знаком модуля; 2.полученные значения отмечаем на координатной прямой, которая при этом разбивается на интервалы(промежутки), в каждом из которых свой знак подмодульного выражения; 3. решаем полученные уравнения в каждом из интервалов. *Применяется, когда уравнение содержит более одного модуля
***ТРУДОЁМКИЙ
|
|x + 1| + |2x – 4| – |x + 3| = 2x – 6
1) Найдем нули выражений, стоящих в модулях: x + 1 = 0 2x – 4 = 0 x + 3 = 0 x = -1 2x = 4 x = -3 x = 2 2) Определим знаки подмодульных выражений на каждом промежутке:
3) I интервал (-∞; -3). все выражения со знаком «–»: -(x + 1) – (2x – 4) – (-(x + 3)) = 2x – 6. -x – 1 – 2x + 4 + x + 3 = 2x – 6 -4x = -12 x = 3. 3 не принадлежит интервалу (-∞; -3). II интервал [-3; -1). Выражения имеют знаки «–»,«–»,«+»: -(x + 1) – (2x – 4) – (x + 3) = 2x – 6. -x – 1 – 2x + 4 – x – 3 = 2x – 6. -5x = -6 x = 6/5 = 1,2 1,2 не принадлежит [-3; -1). III интервал [-1; 2). Выражения имеют знаки «+»,«–»,«+»:
(x + 1) – (2x – 4) – (x + 3) = 2x – 6. x + 1 – 2x + 4 – x – 3 = 2x – 6 -4x = -8 x = 2. 2 не принадлежит [-1; 2). IV интервал [2; +∞). Все выражения со знаком «+»: (x + 1) + (2x – 4) – (x + 3) = 2x – 6. x + 1 + 2x – 4 – x – 3 = 2x – 6 0 = 0. Верное равенство. Значит ответом, являтся множество чисел: x ≥ 2. Ответ: [2; +∞). |
Решение неравенств, содержащих переменную под знаком модуля.
Теперь рассмотрим три простейших вида неравенств с модулями:
1. НЕРАВЕНСТВО |x |< a ("КОЗА НА ВЕРЕВОЧКЕ").
Такое неравенство требует от нас, чтобы число x было удалено от нуля не больше, чем на a единичных отрезков, будто x — это коза, привязанная к нулю на веревочке длины a. При этом уходить можно как влево, так и вправо. Графически это можно проиллюстрировать так:
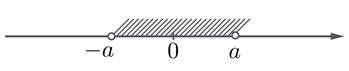
И решением этого неравенства будет промежуток ( -a ; a) . В случае нестрогого неравенства числа -a и a входили бы в множество решений, и изображались бы жирными точками, а в ответе стояли бы квадратные скобки.
2. НЕРАВЕНСТВО |x | > a ("ВОЛК ЗА ЗАБОРОМ").
Такое неравенство, наоборот, требует от нас, чтобы число x не приближалось к нулю ближе, чем на a единичных отрезков, как если бы x был волком, от которого мы защищались бы забором на расстоянии a от нуля. При этом "бегать за забором" можно как слева, так и справа, главное — достаточно далеко. Иллюстрация будет такая:
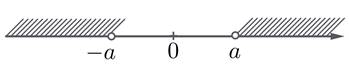
И ответ будет таким: ( -∞; -a) ᴗ (a ;+∞)
Аналогично в случае нестрогого неравенства точки были бы жирными, а скобки при
-a и a — квадратными.
3. НЕРАВЕНСТВО a<|x |< b ("ФРЕНДЗОНА").
В этом случае числу x не позволено удаляться от нуля дальше, чем на b единичных отрезков, но и приближаться ближе, чем на a тоже нельзя. Можно представить, что ноль - это девушка, а x — это юноша попавший в френдзону: и близко не подпускает, но и уходить далеко тоже нельзя.
Иллюстрация для этого неравенства выглядит так:
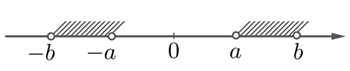
И ответ таков: (- b; - a) ᴗ (a ; b).
Знаков неравенства здесь было использовано два, и если один из них сделать нестрогим, соответствующие числа попадут в ответ с квадратной скобкой и превратятся в жирные точки на оси (причем сразу и с плюсом, и с минусом).
Подведем итог: выпишем решения простейших неравенств с модулями:
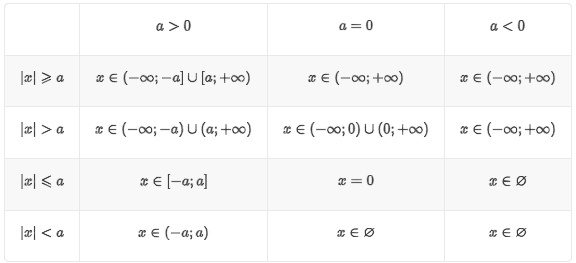
Алгоритм решения неравенств с модулями:
1. Найти в неравенстве все выражения, содержащиеся под знаком модуля.
2. Найти, при каких значениях переменной они обращаются в нуль.
3. Разбить найденными значениями числовую прямую на непересекающиеся промежутки.
4. Определить для каждого числового промежутка, чему равно значение каждого модуля: самому выражению, содержащемуся под знаком модуля, или противоположному ему.
5. Для каждого числового промежутка записать и решить исходное неравенство без знаков модуля.
6. Найти пересечение полученных множеств решений и соответствующих числовых промежутков.
7. В ответе записать объединение всех получившихся множеств решений.
Приложение 1.
Задания школьного курса по теме «Модуль»
6 класс (Г.В. Петерсон) «Разветвлённое понятие модуля»
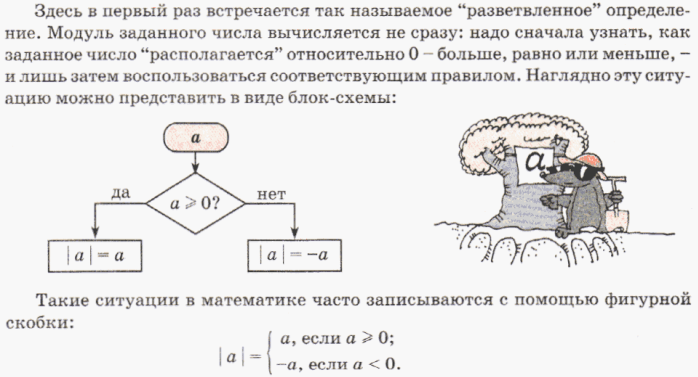
Типы заданий:
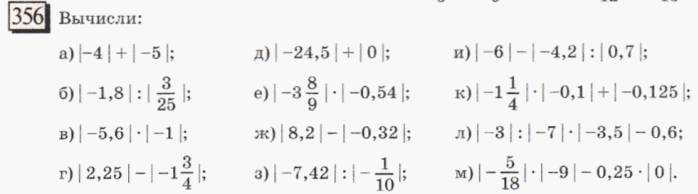
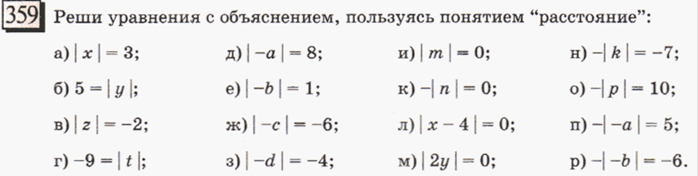





7 класс (А.Г.Мерзляк)
Тема «Линейное уравнение с одной переменной»:
![]()
![]()

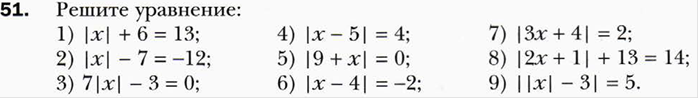
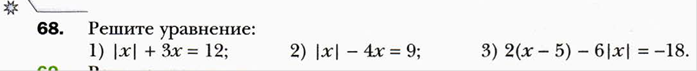
Тема «Целые выражения.Тождества»
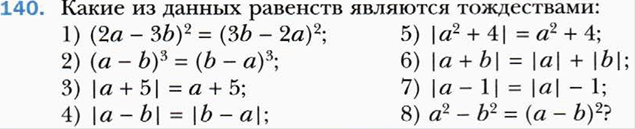
Тема «Функции.Линейная функция, её график и свойства»
![]()
Тема «Системы линейных уравнений с двумя переменными.Уравнения с двумя переменными и его график»
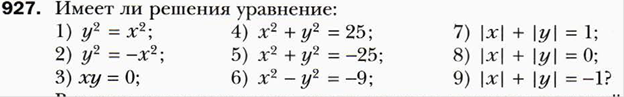


8 класс (А.Г. Мерзляк)
Тема «Рациональные выражения.Рациональные дроби».
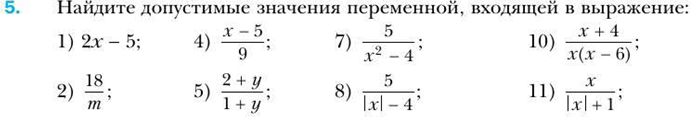
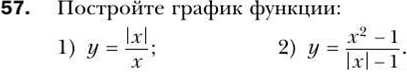
![]()
Тема «Квадратные корни.Свойства арифметического квадратного корня».




![]()
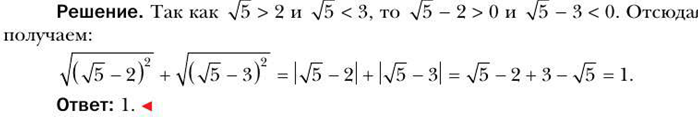
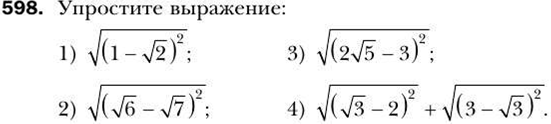
Тема «Квадратные уравнения».
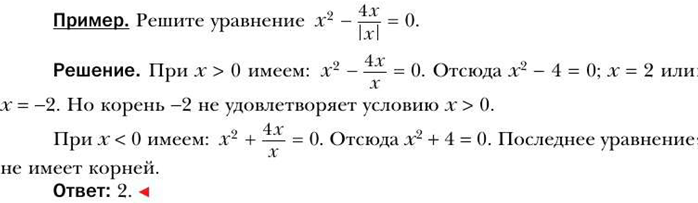
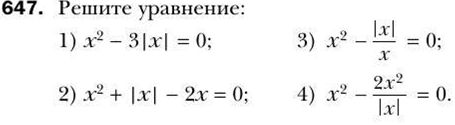
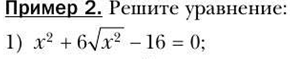

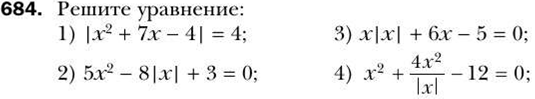
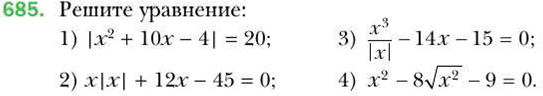
9 класс (А.Г.Мерзляк)
Тема «Неравенства»
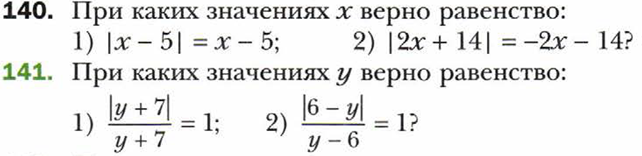

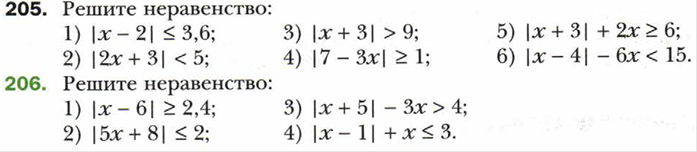
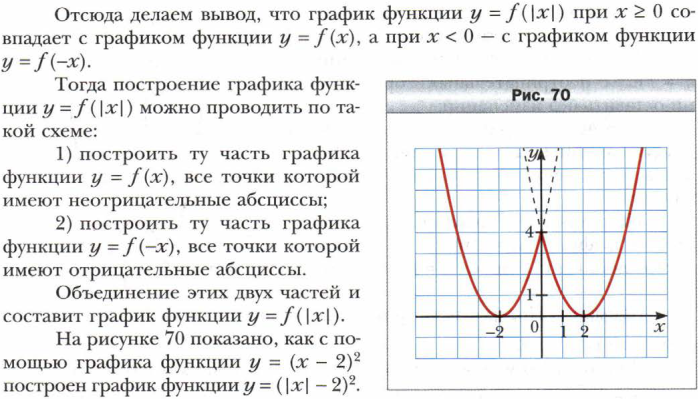
Тема «Квадратичная функция»

Рубрика «Когда сделаны уроки. О некоторых преобразованиях графиков функций».



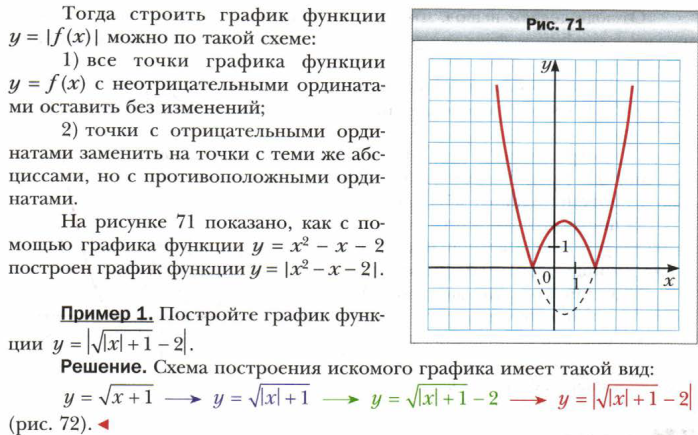
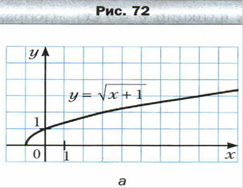
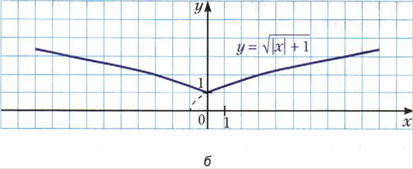
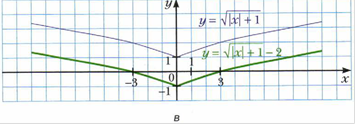
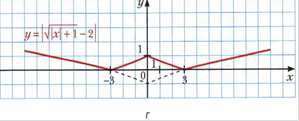

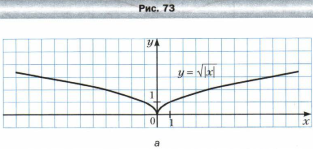
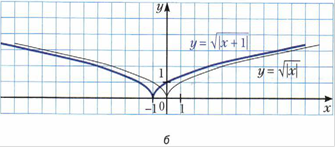
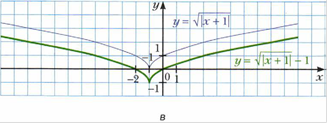
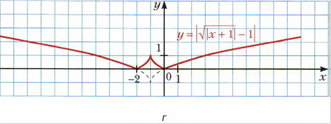

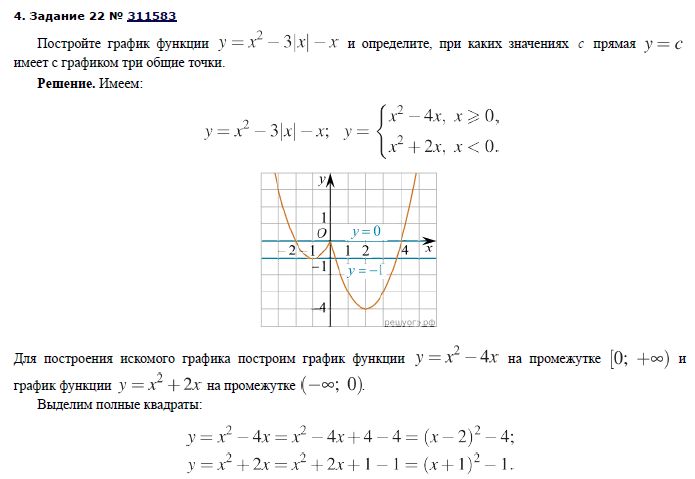
Приложение 2
Способы построения графиков функций, содержащих модуль
(https://oge.sdamgia.ru/)


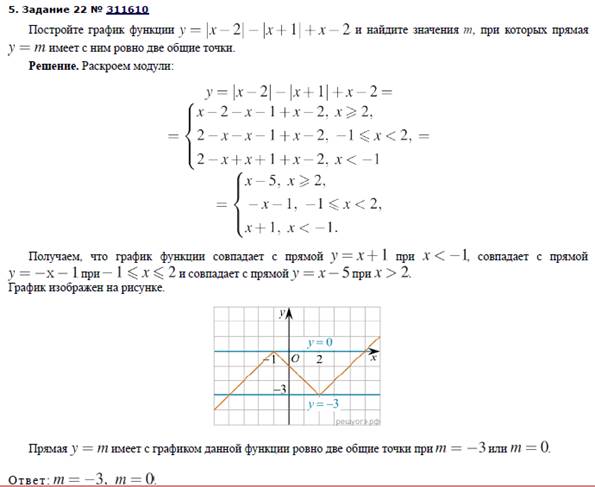
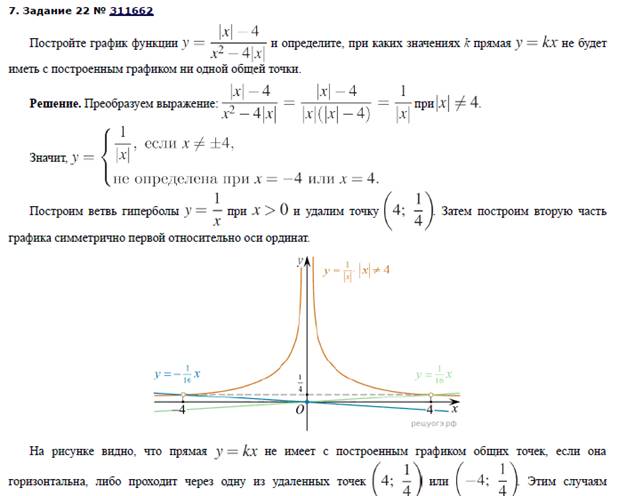
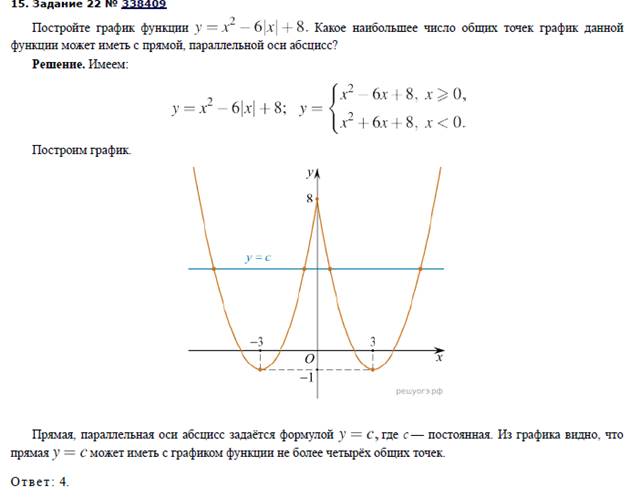

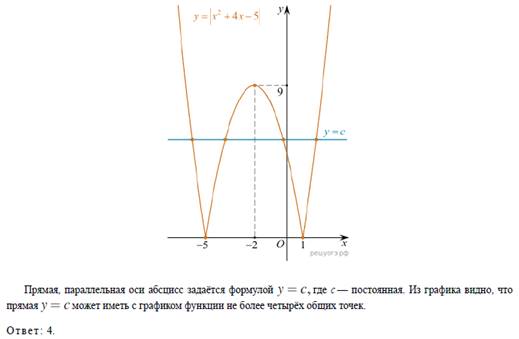
Приложение 3
Задания ВПР 6 класса (https://vpr.sdamgia.ru/)
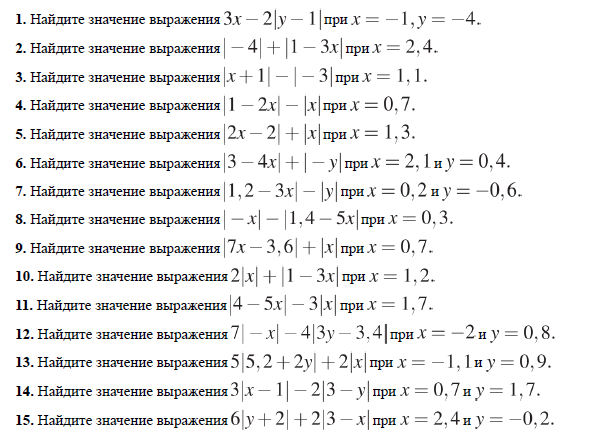

Анкета (на входе)
для учащихся 7 – 11 классов
Ответьте, пожалуйста, на вопросы, отмечая подходящий для вас вариант ответа +
1. Какая тема алгебры вам кажется наиболее трудной? (поставьте +)
А) задачи _____
Б) построение графиков функций ____
В) модуль числа _____
Г) уравнения ____
2. Укажите неверное равенство: (поставьте +)
А) ![]() ____
____
Б) ![]() ____
____
В) ![]() ____
____
Г) ![]() ____
____
3. Решите уравнение: ![]() (поставьте +)
(поставьте +)
А) -40 ____
Б) 40 ____
В) -40 или 40 ____
4. Что такое модуль числа? (поставьте +)
А) знак ![]() ____
____
Б) знак, который убирает знак минус ____
В) расстояние от начала отсчёта до точки, с данной координатой ____
5. Почему тема «Модуль» для многих кажется трудной? (поставьте +)
А) плохо запоминают материал с урока _____
Б) нет под рукой подсказок (забывают, с чего начать действовать) _____
В) модуль вводит многих ( и меня тоже) в «ступор» _____
Мной было опрошено 33 ученика 7 – 11 классов. Результаты опроса:
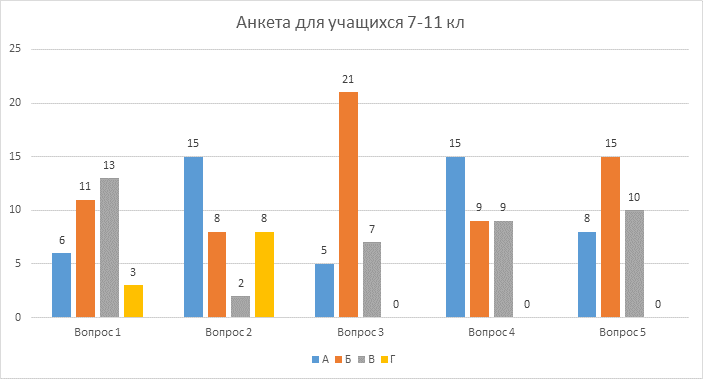
Вывод: Большинство ребят считают самыми сложными в алгебре темы «Построение графиков функций» «Модуль числа», хотя значение модуля многие вычислили верно. Определение модуля вспомнили немногие, поэтому, наверно, и выбрать верно корни уравнения смогли тоже немногие. Проанализировав результат опроса, я подумала, что результат моей исследовательской работы будет полезен не только мне, но и многим ребятам, заинтересованным в хорошей отметке по математике.
Анкета (на выходе)
для учащихся 9 - 11 классов
Ответьте, пожалуйста, на вопросы, отмечая подходящий для вас вариант ответа +. Можно выбрать несколько вариантов ответа.
1. Пользуетесь ли вы какими-нибудь пособиями, справочными материалами для подготовки к ОГЭ (ЕГЭ)?
А) мало, т.к. необходимый материал разбирается на уроке _____
Б) пользуюсь, ищу разборы заданий в Интернете _____
В) ничем не пользуюсь _____
2. Хотели бы вы иметь универсальное пособие, особенно по сложным темам всегда под рукой?
А) конечно хочу: открыл, нашёл , повторил нужный материал _____
Б) нет, мне не нужны ______
В) скорее да, т.к. не всегда (особенно на уроке) можно сразу найти нужную информацию в Интернете ______
3. Оцените, пожалуйста, моё пособие на тему «Модуль – просто о сложном»
А) заинтересовало, можно воспользоваться при случае ____
Б) нужная информация, изложена понятно и доступно ____
В) хотела бы иметь такое под рукой, т.к тема «Модуль» для меня –«тёмный лес» ____
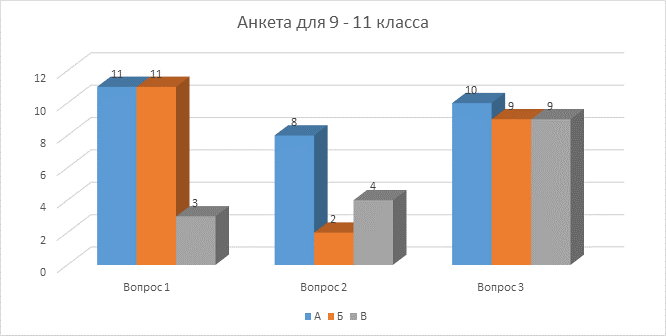
Вывод: большинство ребят считают, что всё-таки лучше иметь «синицу в руках», ведь ресурсы Интернета не всегда бывают доступны на уроке. Результат моей работы заинтересовал ребят, особенно тех, кто имеет хорошие результаты по математике. Думаю, что в ходе подготовки к экзаменам они будут пользоваться моей памяткой – помощницей. Удачи нам!
Памятка «Модуль – просто о сложном»
|
Модуль действительного числа
|
|
Геометрический смысл модуля
|
|
Свойства модуля действительного числа:
|
|
Расстояние между двумя точками AB=∣a−b∣=∣b−a∣, где a , b — координаты этих точек на прямой (координатной прямой). Пример:
LM =|-3 - 5| = |-8| = 8 или LM =|5 - (-3)| = |5 + 3| = 8.
|
Способы построения графиков, содержащих модуль
|
Функция |
Преобразование |
Пример |
|
y = f(|x|) |
1) Для x ≥ 0, y = f(x) 2) Для x < 0 – преобразование симметрии относительно Oy графика y = f(x), для x ≥ 0 симметричные части графика из правой полуплоскости в левую |
y = x2 – 8|x| + 12. 1.Определим четность функции. Значение для y(-x) совпадает со значением для y(x), поэтому данная функция четная. Тогда ее график симметричен относительно оси Oy. 2.Строим график функции y = x2 – 8x + 12 для x ≥ 0 и симметрично отображаем график относительно Oy для отрицательных x (рис. 1). |
|
y =|f(x)| |
1) Для f(x) ≥ 0, |f(x)| = f(x) 2) Для f(x) < 0, |f(x)| = -f(x) Симметричное отображение части графика из нижней полуплоскости в верхнюю относительно Ox |
y = |x2 – 8x + 12|. 1.область значений предложенной функции: y ≥ 0. 2. график расположен над осью абсцисс или касаясь ее. 3. строим график функции y = x2 – 8x + 12, оставляют часть графика, которая лежит над осью Ox, без изменений, а часть графика, которая лежит под осью абсцисс, симметрично отображают относительно оси Ox (рис. 2) |
|
y = |f(|x|)| |
f(x) → f(|x|) → |f(|x|)|. |
y = |x2 – 8|x| + 12| 1. проводим комбинацию преобразований: y = x2 – 8x + 12 → y = x2 – 8|x| + 12 → y = |x2 – 8|x| + 12|. (рис.3) |
|
|
||
Решение уравнений с модулем
|
|
Методы решения |
Алгоритм |
Пример |
|
1 |
По определению модуля. |x| = с, где с – действительное число |
решение в виде схемы: {±c, если с > 0 {0, если с = 0 {нет корней, если с < 0 |
4 -
х=3 или х= -3 Ответ: -3; 3 |
|
2 |
По определению модуля. |f(x)| = b, где b > 0. |
1.необходимо избавиться от модуля: f(x) = b или f(x) = -b. 2.решить отдельно каждое из полученных уравнений. *Если в исходном уравнении b< 0, решений не будет. |
х-5 = 4 или х-5 = -4 х=9 х=1
Ответ: 1; 9
|
|
3 |
По определению модуля. |f(x)| = g(x). |
По смыслу модуля: уравнение будет иметь решения, если g(x) ≥ 0. Тогда будем иметь: f(x) = g(x) или f(x) = -g(x). * если g(x) < 0, то решений не будет. |
|2x – 1| = 5x – 10. Данное уравнение будет иметь корни, если 5x – 10 ≥ 0. Именно с этого и начинают решение таких уравнений. 1) О.Д.З: 5x – 10 ≥ 0 5x ≥ 10 x ≥ 2. 2) Решение: 2x – 1 = 5x – 1 или 2x – 1 = -(5x – 10) 3x = 9 7x = 11 x = 3 x = 11/7 3) Объединяем О.Д.З. и решение, получаем: Корень x = 11/7 не подходит по О.Д.З., он меньше 2, а x = 3 этому условию удовлетворяет. Ответ: 3 |
|
4 |
По определению модуля. |f(x)| = |g(x)|. |
равносильно двум следующим уравнениям: f(x) = g(x) или f(x) = -g(x). |
|x2 – 5x + 7| = |2x – 5|. Данное уравнение равносильно двум следующим: 1)x2 – 5x + 7 = 2x – 5 x2 – 7x + 12 = 0 x = 3 ; x=4 или 2)x2 – 5x +7 =-2x + 5 x2 – 3x + 2 = 0 x = 2 ; x = 1 Ответ: 1; 2; 3; 4
|
|
5 |
Метод замены переменной.
|
a|x|2 + b|x| + c = 0. 2.сделаем замену |x| = t, t ≥ 0, тогда будем иметь:at2 +bt + c = 0. 3.Решаем данное уравнение. 4. Вернемся к замене. |
x2 – 6 | x | + 8 = 0 Пусть | x | = y, y ≥ 0 Получим: y2 – 6y + 8 = 0, y1 = 2; y2 = 4. Вернёмся к замене: | x | = 2 или | x | = 4, x = ± 2. x = ± 4. Ответ: -4; -2; 2;4.
|
|
6 |
*«Сложный модуль» (модуль в модуле) |a – |x|| = b. |
1.при условии b≥0, по определению модуля, «убираем» внешний модуль: a – |x|= b или a – |x|= - b. 2.используя свойства модуля, сводим решение данных уравнений к методу 1. |
|3 + |x + 1|| = 5 1) 3 + |x + 1| = 5 |x + 1| = 2 х+1=2 или х+1= -2 х=1 х= -3 или 2) 3 + |x + 1| = -5 |x + 1| = -8 Нет корней. Ответ: -3; 1.
|
|
7 |
Возведение обеих частей в квадрат |f(x)| = |g(x)| или |f(x)| = g(x). |
1.при
условии: g(x) ≥ 0, используя свойство f2(x) = g2(x). 2. решаем полученное квадратное уравнение. |
Отсюда: (х-3-2)(х-3+2)=0 (х-5)(х-1) = 0 х-5 =0 или х-1 =0 х=5 х=1 Ответ: 1; 5.
|
|
8 |
Графический
|
1.«разбиваем» уравнение на «знакомые» функции; 2.в одной системе координат строим графики функций; 3.находим координаты точек пересечения графиков; 4.записываем только абсциссы точек пересечения графиков |
Построим
в одной системе координат графики функций
Ответ: -1; 1 |
|
9 |
Метод интервалов* |
1.приравниваем к нулю выражения, стоящие под знаком модуля; 2.полученные значения отмечаем на координатной прямой, которая при этом разбивается на интервалы(промежутки), в каждом из которых свой знак подмодульного выражения; 3. решаем полученные уравнения в каждом из интервалов. *Применяется, когда уравнение содержит более одного модуля
***ТРУДОЁМКИЙ
|
|x + 1| + |2x – 4| – |x + 3| = 2x – 6
1) Найдем нули выражений, стоящих в модулях: x + 1 = 0 2x – 4 = 0 x + 3 = 0 x = -1 2x = 4 x = -3 x = 2 2) Определим знаки подмодульных выражений на каждом промежутке:
3) I интервал (-∞; -3). все выражения со знаком «–»: -(x + 1) – (2x – 4) – (-(x + 3)) = 2x – 6. -x – 1 – 2x + 4 + x + 3 = 2x – 6 -4x = -12 x = 3. 3 не принадлежит интервалу (-∞; -3). II интервал [-3; -1). Выражения имеют знаки «–»,«–»,«+»: -(x + 1) – (2x – 4) – (x + 3) = 2x – 6. -x – 1 – 2x + 4 – x – 3 = 2x – 6. -5x = -6 x = 6/5 = 1,2 1,2 не принадлежит [-3; -1). III интервал [-1; 2). Выражения имеют знаки «+»,«–»,«+»:
(x + 1) – (2x – 4) – (x + 3) = 2x – 6. x + 1 – 2x + 4 – x – 3 = 2x – 6 -4x = -8 x = 2. 2 не принадлежит [-1; 2). IV интервал [2; +∞). Все выражения со знаком «+»: (x + 1) + (2x – 4) – (x + 3) = 2x – 6. x + 1 + 2x – 4 – x – 3 = 2x – 6 0 = 0. Верное равенство. Значит ответом, являтся множество чисел: x ≥ 2. Ответ: [2; +∞). |
Решение неравенств с модулем
|
Вид неравенства |
Алгоритм |
Пример |
|
|x |< a "КОЗА НА ВЕРЕВОЧКЕ"
|
Число x должно быть удалено от нуля не больше, чем на a единичных отрезков, будто x — это коза, привязанная к нулю на веревочке длины a. При этом уходить можно как влево, так и вправо.
Ответ: ( -a ; a) * В случае нестрогого неравенства числа -a и a входили бы в множество решений, и изображались бы жирными точками, а в ответе стояли бы квадратные скобки. |
|2x + 3 |< 5 -5 < 2x + 3 < 5 -5 – 3 < 2x + 3 -3 < 5 - 3 -8 < 2x < 2 -8 : 2< 2x : 2< 2 : 2 -4 < x < 1
Ответ: ( -4 ; 1)
|
|
|x | > a "ВОЛК ЗА ЗАБОРОМ"
|
Число x не должно приближаться
к нулю ближе, чем на a единичных отрезков, как если бы x был волком, от
которого мы защищались бы забором на расстоянии a от нуля. При этом
"бегать за забором" можно как слева, так и справа Ответ: ( -∞; -a) ᴗ (a ;+∞) *В случае нестрогого неравенства точки были бы жирными, а скобки при -a и a — квадратными |
|7 - 3x | ≥ 1 7-3x ≥1 или 7-3x≤-1 -3x ≥1-7 -3x≤-1-7 -3x≥-6 -3x≤-8 x≤-6:(-3) x≥-8:(-3) x≤ 2 x≥
Ответ: x≤ 2 ; x≥
|
|
a<|x |< b "ФРЕНДЗОНА"
|
Числу
x не позволено удаляться от нуля дальше, чем на b единичных отрезков, но и приближаться ближе, чем
на a тоже нельзя. Можно
представить, что ноль - это девушка, а x — это юноша попавший в френдзону: и близко не подпускает, но и
уходить далеко тоже нельзя. Ответ: (- b; - a) ᴗ (a ; b). *Если один из них сделать нестрогим, соответствующие числа попадут в ответ с квадратной скобкой и превратятся в жирные точки на оси (причем сразу и с плюсом, и с минусом). |
- 3,6 < |x - 2 |< 9 1) -9 < x - 2 < 3,6 -9+2 < x -2+2 <3,6+2 -7 < x < 5,6
2) – 3,6 < x - 2 < 9 -3,6+2 < x -2+2 < 9+2 - 1,6< x < 11
Ответ:(-7;5,6)ᴗ(-1,6;11). |
В ходе работы над проектом попыталась выяснить: почему задания с модулем так сложны для восприятия? Как помочь себе, моим одноклассникам и другим ребятам преодолеть «страх модуля»?
В ходе решения данной проблемы, поставила перед собой следующие задачи:
- Научиться решать уравнения, неравенства с модулем.
- Научиться строить графики с модулем.
- Научиться самостоятельно овладевать новыми знаниями.
- Учиться получать информацию, пользуясь ресурсами Интернета.
- Научиться представлять математический текст в компьютерной форме, пользуясь специальными редакторами и компьютерными программами.
Изучила много методической литературы по данной теме,провела исследование и анализ имеющихся способов решения заданий с модулем,выбрала из множества найденных способов решения наиболее оптимальные, провела обобщение и систематизацию имеющего материала.
Среди ребят 7- 11 классов провела опрос о значимости данной темы. Большинство ребят считают самыми сложными в алгебре темы «Построение графиков функций» «Модуль числа», хотя значение модуля многие вычислили верно. Определение модуля вспомнили немногие, поэтому, наверно, и выбрать верно корни уравнения смогли тоже немногие. Ребята считают тему «Модуль» сложной и пугающей, т.к. им не хватает наглядной информации под рукой. Многие считают, что если бы была возможность повторить материал «здесь и сейчас», то они бы правильно ответили на все вопросы анкеты. Проанализировав результат опроса, подумала, что результат моей исследовательской работы будет полезен не только мне, но и многим ребятам, заинтересованным в хорошей отметке по математике.
На занятии по подготовке к экзамену предложила ребятам 9 -11 класса оценить «продукт» моей работы: «Памятку «Модуль – просто о сложном»». Большинство ребят считают, что всё-таки лучше иметь «синицу в руках», ведь ресурсы Интернета не всегда бывают доступны на уроке. Результат моей работы заинтересовал ребят, особенно тех, кто имеет хорошие результаты по математике. Думаю, что в ходе подготовки к экзаменам они будут пользоваться моей памяткой – помощницей.
Считаю,что данную работу можно использовать в качестве учебного пособия для учащихся для самостоятельной подготовки к экзаменам и как методический материал для учителя.
В процессе работы получила для себя много новой информации о модуле числа, его применении, а также о различных способах решения уравнений, неравенств и построения графиков функций, содержащих знак абсолютной величины.
Поставленная мной цель была успешно выполнена.
1. Дорофеев Г.В., Петерсон Л.Г. Математика (в 3 частях): 6 класс: учебник / Г.В Дорофеев, Л.Г. Петерсон.- М. : Бином, 2020. : ил.
2. Мерзляк А.Г. Алгебра: 7 класс: учебник для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. - М. : Вентана-Граф, 2021. - 272 с. : ил.
3. Мерзляк А.Г. Алгебра: 8 класс: учебник для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. - М. : Вентана-Граф, 2020. - 256 с. : ил.
4. Мерзляк А.Г. Алгебра: 9 класс: учебник для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. - М. : Вентана-Граф, 2020. - 314 с. : ил.
Интернет-ресурсы
https://youclever.org/book/ «Учебник по подготовке к ОГЭ и ЕГЭ/ ЮКлэва»
https://oge.sdamgia.ru/
https://vpr.sdamgia.ru/
https://100ballnik.com/
https://infourok.ru/
https://uchi.ru/
https://foxford.ru/
http://spacemath.xyz/modul_chisla/
https://mathematichka.ru/school/functions/Function_Graph_Modul.html
https://youclever.org/book/
Скачано с www.znanio.ru
[1] Приложение 1
[2] Приложение 1
[3] Приложение 1
[4] Приложение 1
[5] https://oge.sdamgia.ru/
[6] https://vpr.sdamgia.ru/
[7] Приложение 2
[8] https://blog.tutoronline.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.