Поделиться
Практикум для 7-10классов.Модули в школе..docx
ПРАКТИКУМ ДЛЯ 7-11 КЛАССОВ. МОДУЛИ
I. Примеры (из централизованных тестов)
П-1. Найти сумму корней уравнения 8 класс
| x2+3x | = 4
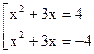
1) x2+3x-4=0; x1 = 1; x2 = -4;
2) x2+3x+4=0;
D=9-16 < 0; 
Сумма корней: 
.
Ответ: -3
П-2. Найти сумму корней уравнения 7-8 класс
| 2x-3 | = | x-1 |
(2x-3)2-(x-1)2=0
(2x-3-x+1)*(2x-3+x-1)=0
(x-2)*(3x-4)=0 x=2
и x=
; 
. Ответ: 3
П-3. Найти
сумму корней 7-8 класс
| x2-2x | = | 1-2x |
(x2-2x)2-(1-2x)2=0
(x2-2x-1+2x)*(x2-2x+1-2x)=0
(x2-1)*(x2-4x+1)=0
x2-1=0 или x2-4x+1=0
x1,2=
D=16-4=12
x3=
x3=2+
x4=
x4=2-
1-1+2+
+2-
=4 
. Ответ: 4
П-4. Произведение корней 8-9 класс
| x2+x-3 | = x
1) 
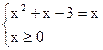2) 
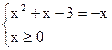
x2=3; x1,2=
x2+x-3=0
x1=
; x3=1
x2=
- не удов. x
x4=-3
– не удов. x
Ответ: x1=
; x2=1;
x1*x2=
*1=
П-5. Произведение корней 8-9 класс
| 3x2-x | = 8+x
Решение
1) 
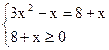2)
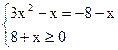
Решаем первую систему:
3x2-2x-8=0
x1=2
и x2=
Оба корня удовлетворяют
неравенству 8+x
0,
а значит, являются решениями исходного уравнения.
Вторая система решений не имеет. Следовательно, произведение корней равно:
2*
=
.
Ответ: 
П-6. Найти сумму корней уравнения 9-10 класс
| x+3 | + | 2x-1 | = 8
Решение
1) Найдем нули подмодульных выражений: x+3=0;
x=-3; , 2x-1=0;
x=
2) Они разбивают числовую ось на три промежутка. Решаем данное уравнение на каждом промежутке.
 |
-3
x
3)
|
|
x<-3 |
-3 |
x |
|
x+3 |
- |
+ |
+ |
|
2x-1 |
- |
- |
+ |
|
|
-x-3-2x+1=8
|
x+3-2x+1=8
|
x+3+2x-1=8
|
Сумма корней: 
. Ответ: 
П-7. Произведение корней 10-11 класс
| x-2 | * x2 = 10-5x
Решение
| x-2
| = 
1) 
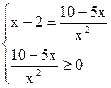
Найдем ОДЗ:
+ +
-
Т.к.
, то
0
2 x
10-5x
0
2-x0
Решим уравнение системы:
(x-2)*x2=10-5x,
x
0
10-5x=x3-2x2
x=2
x3-2x2+5x-10=0
x3-2x2+5x-10
x-2
x3-2x2 x2+5
5x-10
5x-10
0
(x-2)*(x2+5)=0
x=2 или
x2-5
x=2 уд. ОДЗ
x1=2 является корнем исходного уравнения
2) 
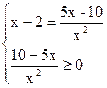
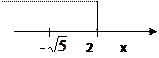
Решим уравнение системы:
5x-10=x2*(x-2), x0
5x-10-x3+2x2=0
-x3+2x2+5x-10=0
x3-2x2-5x+10=0
x=2; 8-8-10+10=0
x3-2x2-5x+10 x-2
x3-2x2 x2-5
-5x-10
-5x-10
0
(x-2)*(x2-5)=0 
x=2; x=
; x=
x=
ОДЗ.
Следовательно, x2=
Произведение
корней равно: x2*x2=2*(
). Ответ: -2
П-8. Найти среднее арифметическое всех корней данного уравнения 9-10 класс
| x2-x-1 | = x2+2x+1
1) 
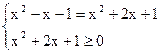
3x+2=0.
x=
ОДЗ
x2+2x+1
x
(x+1)
2=0
x=-1,
x
R
2) x2-x-1=-x2-2x-1
2x2+x=0
x*(2x+1)=0
x=0 или x=
Оба корня удовлетворяют ОДЗ. Следовательно, среднее арифметическое всех корней уравнения равно:
=
=
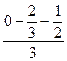. Ответ: 
П-9. Найти произведение корней уравнения 9 класс
x2+3x+| x+3 | = 0
Решение
| x+3 | = -x2-3x
1) 
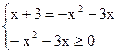
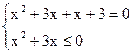
x=-1, x=-3
+ -
+ -3 0 x
-1ОДЗ; -3ОДЗ
2) 
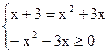
x2+2x-3=0 , x1=1; x2=-3 1ОДЗ -3ОДЗ
Следовательно, корнями данного уравнения являются: -1 и -3
Произведение корней равно: (-1)*(-3)=3. Ответ: 3
П-10. Найти среднее арифметическое всех корней уравнения 9 класс
| x-1 | + 2 * | x+3| = 5
Решение
1) Найдем нули подмодульных выражений: x-1=0, x=1
x+3=0, x=-3
-3 1 x
2) Числа -3 и 1 разбивают числовую прямую на три интервала. Решаем уравнение на каждом интервале
3)
|
|
x<-3 |
-3 |
x |
|
x-1 |
- |
- |
+ |
|
x+3 |
- |
+ |
+ |
|
|
1-x-2*(x+3)=5 1-x-2x-6=5 -3x-10=0 x= -3 x= |
1-x+2*(x+3)=5 1-x+2x+6=5 x+7-5=0 x=-2 x=-2 корень |
x-1+2*(x+3)=5 x-1+2x+6=5 3x+5=5 3x=0 x=0 нет корней |
Среднее арифметическое корней:
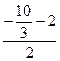=-5:2=
:2=
; -3ОДЗ. Ответ: 
П-11. Найти среднее арифметическое всех корней 9-10 класс
| | 3x-1 | - 3 | = 2
Решение
1) | 3x-1 | - 3 = 2
| 3x-1 | = 5
3x-1=5 3x-1=-5
3x=6 3x=-4
x1=2 x2=
2) | 3x-1 | - 3 = -2
| 3x-1 | = 1
3x-1=1 3x-1=-1
3x=2 3x=0
x3=
x4=0
Среднее арифметическое всех корней:
(2++0-):4=(2-):4=:4=. Ответ:
П-12. Найти произведение корней уравнения 9-10 класс
| 2x-1 | + | x+1 | = 2x+1
Решение
Найдем нули:
1) 2x-1=0, x=, x+1=0,х = -1
2) 2x+1
x+1
x
-1 
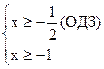
x
x
x
Решим на промежутках:
2) x<-1 решений
нет, т.к. x
-
1-2x+x+1=2x+1
-3x=-1
x=
x1= - корень уравнения
x>
2x-1+x+1=2x+1
x=1
)
x2=1
– корень уравнения. 4) Произведение корней равно: 
.
Ответ:
II. Упрощение выражений с модулем.
Применяем определение модуля или свойства модуля.
1) | a | =
2) a2= | a |2; | -a | =a, | a-b | = | b-a |
| ab
| = | a | * | b
| и | 
|
= 
Другие свойства модуля будут указаны в процессе решения задач.
Задачи с модулем. (Упрощения)
(9-11 классы)
З-1. Упростить выражение
ОДЗ:
дробь определена для любых значений a.
1) при
a0
2) при a<0
II способ
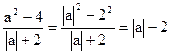
Ответ:
при a
,
a-2
при a
,
-(a+2)
3-2. Упростить выражение
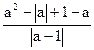ОДЗ:
дробь определена для a1
1) Нули подмодульных выражений: 0 и 1 делят числовую ось на промежутки:
(-
;0),
[0;1), (1;+)
2) Упростить дробь на каждом из промежутков
|
a<0 |
0 |
a>1 |
|
|
|
|
Ответ: при a(-;0), 
;
при a[0;1), 1-a;
при a(1;+), a-1.
З-3. Упростить выражение
Решение
ОДЗ:
выражение определено для всех значений x-1
1) Найдем нули подмодульных выражений: -1 и 1. Они разбивают числовую ось на промежутки:
(-;-1), (-1;1), [1;+)
2) Упростим выражение на каждом промежутке
a) x<-1
б) -1<x<1
в)
x1
Ответ:
при x(-;-1), 1; при x(-1;1), 
при x[1;+), 3.
З-4. Упростить выражение.
Решение
Дробь определена на R, кроме 0
x
+x+1=(x+)+
при любых x
Дробь примет вид
1) Найдем нули
подмодульных выражений: -1; 0; 1. Они разбивают числовую ось на промежутки: (-;-1), [-1;0), (0;1), [1;+).
2) Упростим выражение на каждом промежутке
при x <-1
при -1
и 0<
x <1
при x
Ответ: при x<-1, -1
при x
при x
1
З-5. Решить уравнение. Найти сумму корней.
Решение
Дробь
определена при x
|x-1|
; 
1) Найдем нули подмодульных выражений:
x-1=0, x=1 и x=0
 |
2) Решим уравнение на каждом из промежутков:
|
x<0 |
0 |
x |
|
Решений нет |
5=x x
x x Следовательно,
x=-2+ корень уравнения |
5-(4x-x 5-2x+x
x x Следовательно, x=3 |
3) Сумма корней уравнения равна:
-2+
Ответ: 1+
Пример для самостоятельной работы:
Ответ: 1) 
при
x
2)
при
x
;
3) 
при
x
4) 
при
x
З-6. Упростить выражение (Математика №23, 2004 г.)
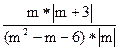
Решение. Разложим квадратный трехчлен на множители:
m2-m-6=(m+2)*(m-3)
Дробь примет вид:
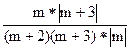
Дробь определена на R, кроме
-2 0 3 x
1) при m<-2 и -2<m<0, тогда
2) при 0<m<3
;
3)
при m3
Ответ:
при m(-;-2)
(-2;0)
(3;+), 
; при m(0;3), 
З-7. Упростить выражение (Математика №23, 2004 г.)
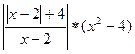
Решение
2 x
Область
определения дроби R, кроме 
Рассмотрим
промежутки (-;2) и (2;+)
1) x<2 
2) x>2
Ответ:
при x(-;2), x2-4x-12;
при x(2;+), (x+2)2
Для самостоятельной работы:
З-8. Упростить
Ответ: при x(-;-3),
; при x(-3;+),
З-9. Упростить
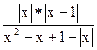
Ответ: при x[0;1), 
; при x(1;+),
З-10. Упростить
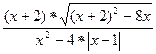
Ответ: при x(-;1), 
;
при
x[1;2),
;
при
x(2;+), 
Решение неравенств.
| x |
-a a x
-a
[-a; a]
| x |<a, a>0 -a a x
-a < x < a, (-a; a)
| x |
0 x
x=0
| x |<-a, нет решений
| x |
a>0 -a a x
x
| x |
x
– любое
(-
)
x
| x |>0
x
x<0;
x>0, (-
)
(0;+)
Примеры.
П-1. Найти наибольшее целое решение неравенства.
|x - 4| > 2x-1
Решение
1)
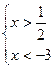
2) 
3) Общее
решение x
-3 1 
Ответ. Наибольшее целое решение -это 1
П-2. Найти число целых решений неравенства.
1
Решение
1
;
т.к. 
1) 
2 4 x
2) |x-3|3
0 6 x
3) Общее решение: [0;2]
[4;6]
0 2 4 6 x
Целые решения: 0,1,2,4,5,6. Ответ: 6
П-3. Найти наименьшее целое положительное решение неравенства.
Решение
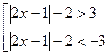
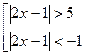
1) 
2) 
не имеет решения
3) Общее решение: (-;-2)
(3;+)
-2 3
4 x
Наименьшее положительное целое решение равно 4. Ответ: 4
П-4. Найти наименьшее целое положительное решение неравенства. 8-9 класс
Решение
1) 
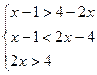
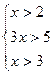
x>3
Значит, наименьшее целое решение неравенства: 4. Ответ: 4
П-5. Решить неравенство (квадратичная функция) 9-10 класс
Решение
1) 3x2-x-1>1
3x2-x-2>0
3x2-x-2=0
x1=1,
x2=
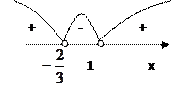3*(x-1)*(x
)>0
2) 3x2-x-1<-1
3x2-x<0
3x2-x=0
x*(3x-1)=0
x=0;
x=
3x*(x-)<0
0
x*(3x-1)<0
x
3) Общее решение: объединим эти решения
|
Ответ: (-;-)
(0;) 
(1;+)
П-6. Решить неравенство 9-10 класс
Решение
Данное неравенство
равносильно неравенству (x2-5x-6)*(x2-5x+6)0,
которое решим методом интервалов:
x2-5x-6=0 x2-5x+6=0
x1=-1; x2=6 x1=2; x2=3
(x+1)*(x-6)*(x-2)*(x-3)
(Можно решить и
алгебраически)
+ - + - +
-1 2 3 6 x
Ответ: [-1;2]
[3;6]
П-7. Решить неравенство 9-10 класс
Решение
(x-2)2-(x+4)2
(x-2-x-4)*(x-2+x+4)
(Можно решить методом
промежутков)
-6*(2x+2)
-3*(x+1)
x+1
0
x-1
Ответ: [-1;+
)
П-8. Решить неравенство 9-11 класс
(Можно решить методом
промежутков)
Решение
1) Найдем нули подмодульных выражений
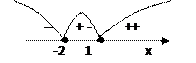x=-2;
x=1
x
-x-2-(1-x)<x-
-x-2-1+x<x-
-3<x<
; x>-1,5
– нет решений, т.к. x<-2
x-
>0; x>
2) -2<x<1
x+2+x-1<x-1,5; x<-2,5 – нет решений
3) x1
x+2-x+1<x-1,5; x>4,5; (4,5;+)
Ответ: (4,5;+)
П-9. Решить неравенство 8-9 класс
Решение
1) x
0
x2+5x+6<0
x2+5x+6=0
x1=-2; x2=-3
+ - +
|
(-3;-2)
2) x>0
x2-5x+6<0
x2-5x+6=0
x1=2; x2=3
(2;3)
3) Общее решение: (-3;-2)
(2;3). Ответ: (-3;-2)
(2;3)
П-10. Решить неравенство
Решение
-5<x2-4x<5
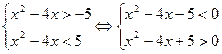
x2-4x-5<0 x2-4x+5>0
x2-4x-5=0 x2-4x+5=0
D<0 x1=-1; x2=5
 |
Ответ: (-1;5) Можно и графически
П-11. Решить неравенство
Решение
1) Нули подмодульных выражений:
x2-2x=0; x=0; x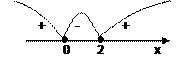=2
2)
3) a.
Если x
,
то
2x-x2<x
0 3 x
x2-3x<0
x*(x-3)<0
0<x<3
Т.к. x<0, то нет решений.
б. Если 0<x<2, то
0
1 2 x
-x2+2x-x<0
x2-x>0
x*(x-1)>0
x
(1;2)
в. Если x2, то
2 1 x
x2-2x<x
x2-3x<0
0<x<3,
но x2,
поэтому
x
[2;3)
Ответ: (1;3)
П-12. Решить уравнение
x2-4*
+5x+3=0
x+10; x-1
x2-4*(x+1)+5x+3=0
x2-4x-4+5x+3=0
x2+x-1=0
D=1+4=5
x1=
; x2=
1) 
уд. усл. x
2) 
=
=
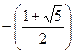Оценим: 
2<
<3
-3<-
<-2
-
<-
<-1
-2<-
<-1,5
- не уд. усл. x
Следовательно, корнем явл. x=
II. x+1<0; x<-1
x2-4*(-x-1)+5x+3=0
x2+4x+4+5x+3=0
x2+9x+7=0
D=81-28=53
x1=
; x2=
a)
-
не явл. решением 
7,2801098
7<
<8
-2<-9+
<-1
-1<
<-
x<-1
б) 
- явл. решением
7<
<8, -8<-
<-7
-17<-9-
<-16 , -8,5<
<-8 
x<-1
Ответ:
и 
Для самостоятельной работы
В1.
1. Решить уравнение
а) 
Т.к. 2x-3 и 3-2x противоположны, поэтому
3-2x0 (только ), тогда
-2x-3
x
б) 
Ответ:
1
2. Решить уравнение
Ответ:
[-1,5;0]
В2. 1. Решить уравнение
а) 
Ответ: x
б) 
Ответ: 3,5;
0,5
2. Решить уравнение
Ответ: -2; 4
В3. 1. Решить уравнение
а) 
Ответ: 
; -4,5
б) 
Ответ:
x1,2
2. Решить уравнение
Ответ: 
; -1; -
В4. 1. Решить уравнение
а) 
Ответ: 
б) 
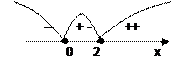
Решаем методом интервалов
1) x<0
-x-(2-x)=2
-x-2+x=2
-2=2 – неверно 
2) 0x<2
x-(2-x)=2
x-2+x=2
2x=4
x=2
[0;2)
3) x2
x-(x-2)=2
x-x+2=2
0=0 – верно 
x2
Ответ: x2
2. Решить уравнение
Решение
1) x<1
, 
, x=
(входит в рассмотр.
промежуток)
2) x1
, 
, x=-3
.
Ответ: 
П-1. Решить уравнение
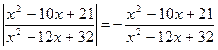
Решение
+ - + - +
3 4 7 8 x
Ответ: [3;4)
[7;8)
П-2. Решить уравнение
Решение
; 
; 
, не удовлетворяет
, 
,
x1=-4, x2=4
Ответ: -4; 4
П-3. Решить уравнение
Решение
Пусть 
=y0,
тогда
y2-5y+6=0, y1=3, y2=2
Значит:
1. 
а) 
,
б) 
,
D<0, решений нет
2. 
а) 
,
б) 
,
D<0, решений нет
Ответ: 
;
4; 1
П-4. Решить уравнение
Решение
Во-первых, x
Тогда 
,
, 
Т.к. x
, то x+3=3x-1,
x=2
Ответ: 2
П-5. Решить уравнение
Решение
, т.к. D<0,
значит, 
 |
-1 1 x
1) x-1, 
, x=2
( неудовл. усл. x1)
2) -1<x1, 
, 
, 
(оба 
(-1;1]), 3) x>1
, x=2
(2
(1;+)). Ответ: 0; ; 2
Учитель
математики – Кобаидзе Н.И. «Исследователи-энциклопедисты»
гимназии
№ 5 г. Владикавказа, РСО-Алании 
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
