НАУЧНО-МЕТОДИЧЕСКАЯ РАЗРАБОТКА ПО ТЕМЕ: «ЗАДАЧИ КАК СРЕДСТВО ОБУЧЕНИЯ И ВОСПИТАНИЯ ОБУЧАЮЩИХСЯ НА ЗАНЯТИЯХ ПО ФИЗИКЕ»

НАУЧНО-МЕТОДИЧЕСКАЯ РАЗРАБОТКА

ПО ТЕМЕ: «ЗАДАЧИ КАК СРЕДСТВО ОБУЧЕНИЯ И

ВОСПИТАНИЯ ОБУЧАЮЩИХСЯ НА ЗАНЯТИЯХ ПО

ФИЗИКЕ»

СОДЕРЖАНИЕ

1. Понятие задачи в психологии и дидактике. Значение решения задач в процессе обучения физики

2. Состояние методики формирования умений решать задачи в теории и практике

3. Методы решения задач

4. Виды задач по физике

5. Теоретические основы методики обучения обучающихся умению решать задачи

6. Методика обучения обучающихся решению задач по физике

7. Литература

ПОНЯТИЕ ЗАДАЧИ В ПСИХОЛОГИИ И ДИДАКТИКЕ.
ЗНАЧЕНИЕ РЕШЕНИЯ ЗАДАЧ В ПРОЦЕССЕ ОБУЧЕНИЯ

ФИЗИКЕ

Понятие «задача» весьма широкое и многогранное, поэтому в педагогической и психологической литературе нет его единого определения. Некоторые авторы, говоря о задаче в широком смысле слова, рассматривают ее как определенную ситуацию. Задача в самом общем смысле - это ситуация, определяющая действие некоторой решающей системы. «Задача-ситуация, требующая от субъекта некоторого действия» - Леонтьев А.Н. Эти дефиниции охватывают все ситуации и включают учебные, дидактические, экономические, социальные и другие задачи. В приведенных определениях центральным является понятие действия, а действие предусматривает выделение цели, предмета, мотива, способа. Другие авторы отождествляют задачи с системами, обладающими свойствами. «Задача, - пишет, например, А.Ф.Эсаулов,- это более или менее определенные системы информационных процессов, несогласованное или даже противоречивое соотношение между которыми вызывает потребность в их преобразовании». (5)

В более узком плане термин «задача» употребляется в следующих двух значениях: первое - это любое задание, выполнение которого требует осуществления какого-либо познавательного акта; второе - не всякое задание, а именно «задача», которую часто принято обозначать через понятие «познавательная задача», и решение которой приводит учащихся к приобретению новых для них знаний и навыков. «Познавательная задача» представляет собой ситуацию, в которой на основании одних (заданных) признаков системы объектов надлежит сделать заключение о каких-либо других (искомых) признаках (свойствах)» - Сохор А.М.(4). Простое определение задачи подобного рода было давно С.О. Шатуновским. Оно гласит: задача есть изложение требования «найти по «данным» вещам другие «искомые» вещи, находящиеся друг к другу и к данным вещам в указанных соотношениях. При этом предполагается, что понятие «вещь», «найти», «данные», «искомые» в каждом отдельном случае особо определяется. ( Фридман Л.М.) (8)

В «Педагогической энциклопедии» познавательная задача характеризуется наличием у обучающихся определенной цели, учетом имеющихся условий и требований, необходимых для решения задачи, применением соответствующих данной цели и условиям способов или приемов решения.

По способу постановки познавательная задача может быть представлена как в качестве проблемной, так и не проблемной. Она не будет проблемной, если новый способ или принцип решения учащиеся поймут из объяснения учителя, без самостоятельного поиска. Она станет проблемной, если педагог предложит учащимся самостоятельно вывести правило на основе анализа приведенных примеров.

Одним из условий обеспечения глубоких и прочных знаний у учащихся является организация их деятельности по решению задач.

Прежде чем обсуждать вопрос о формировании у обучающихся умения их решать, рассмотрим содержание понятия «физическая задача» в пособиях по методике преподавания физики.

В методической литературе продолжительное время пользовались терминами «задача», «физическая задача», без их определения. Одно из первых определений физической задачи дали С.Е. Каменецкий и В.П. Орехов в пособии для учителей «Методика решения задач по физике в средней школе».(3) «Физической задачей, - пишут они, - в учебной практике обычно называют небольшую проблему, которая в общем случае решается с помощью логических умозаключений, математических действий и эксперимента на основе законов и методов физики. В методической же и учебной литературе под задачами обычно понимают целесообразно подобранные упражнения, главное назначение которых заключается в изучении физических явлений, формирования понятий, развитии физического мышления учащихся и привитии им умений применять свои знания на практике».

Анализируя многие определения этого понятия, можно сделать вывод, что физическая задача - это ситуация (совокупность определенных факторов), требующая от учащихся мыслительных и практических действий на основе законов и методов физики, направленных на овладение знаниями по физике и на развитие мышления.

В колледже процесс решения задач служит одним из средств овладения системой научных знаний по тому или иному учебному предмету. Особо велико его значение в овладении системой понятий. Особую роль процессу решения задач отводят в усвоении понятий о физических явлениях и величинах.

Неоценима роль этого процесса в овладении умениями и навыками познавательного и практического характера.

Развитие творческого мышления и самостоятельности, подготовка школьников к участию в рационализаторстве и к творческим поискам путей повышения производительности труда также возможны только при условии систематического решения задач.

Важное значение имеют задачи как средство диагностики умственного развития и специальных способностей учащихся.

Их решение имеют большое воспитательное значение, так как с помощью задач можно познакомить учащихся с достижениями науки и техники; воспитать трудолюбие, настойчивость, волю, характер, целеустремленность.

Процесс решения задач также является средством контроля за знаниями, умениями и навыками учащихся.

Решение задач является условием предупреждения формализма в знаниях учащихся и условием выработки у них умения применять знание на практике. Научить учащихся решать физические задачи - сложная педагогическая проблема.

СОСТОЯНИЕ МЕТОДИКИ ФОРМИРОВАНИЯ УМЕНИЙ
РЕШАТЬ ЗАДАЧИ В ТЕОРИИ И ПРАКТИКЕ

Проведенные исследования показали, что успех обучения решению задач в значительной мере зависит от применяемой преподавателем методики обучения: учащиеся пользуются обобщенным методом решения или каждая частная задача решается своим методом.

Обучение учащихся умению решать задачи предполагает знание преподавателем различных способов обучения этому умению, из которых он может выбрать наиболее рациональный. Теория и практика обучения обучающихся умению решать задачи позволяют в настоящее время выделить три основных способа.

Первый способ традиционный. Он состоит из следующих элементов:

1. Объяснение преподавателем подхода к решению задач данного вида; иллюстрация решения одной или двух конкретных задач.

2. Коллективное решение задач, при котором выделенный подход осуждается со всей группой. Один обучающийся решает задачу у доски, а все остальные списывают решение; при этом лишь немногие пытаются решить предлагаемые задачи самостоятельно.

3. Самостоятельное решение задач в связи с выполнением домашних заданий.

4. Самостоятельное решение задач в связи с выполнением контрольных работ. Второй способ включает два новых элемента: полусамостоятельное и самостоятельное решение задач. Процесс обучения при этом ведется по следующей схеме.

1. Раскрытие преподавателем общего подхода к решению задач данного вида на примере решения одной-двух частных задач.

2. Коллективное решение небольшого количества задач с использование общего подхода.

3. Полусамостоятельное решение задач с учетом коллективного анализа их условий и решения, а также самостоятельной работы по реализации намеченного плана.

4. Самостоятельное решение задач, включающее самостоятельный анализ условия, его краткую запись, разработку плана решения, его реализацию, анализ ответа, проверку правильности решения.

5. Самостоятельная работа по решению задач в связи с выполнением домашних заданий.

6. Самостоятельная работа по решению задач в связи с выполнением

контрольных работ.

Третий способ алгоритмический.

Под алгоритмом понимают точное предписание для совершения некоторой последовательности элементарных действий над исходными данными любой задачи. Процесс обучения решению задач в данном случае идет в определенной последовательности.

1. Коллективное решение задач, относящихся к данному классу (множеству) задач.

2. Выдвижение проблемы отыскания общего метода решения задач данного класса.

3. Отыскание обучающимися (под руководством преподавателя) общего метода решения задач данного класса, «создание» алгоритма решения задач.

4. Усвоение структуры алгоритма и отдельных операций, из которых слагается решение, в процессе коллективного решения задач.

5. Самостоятельное решение задач, включающее самостоятельный анализ

условия, выбор способа краткой его записи, применение найденного

алгоритма решения к конкретной ситуации, анализ и проверка полученного решения.

6. Самостоятельная работа по решению задач в связи с выполнением домашних заданий.

7. Самостоятельная работа по решению задач в связи с выполнением контрольных работ.

В методической литературе описаны первые два способа. Третий способ может быть осуществлен при условии, если преподаватель будет располагать алгоритмами решения физических задач.

Следует различать общий алгоритм решения задач и алгоритмы решения по контрольным темам (разделам) курса физики и частные с помощью которых могут быть усвоены отдельные действия (например, алгоритм преобразования едениц физических величин).

Умение решать задачи следует отнести к сложному познавательному умению, усвоение которого, с одной стороны, предполагает условие большого количества операций и частных умений, с другой стороны, выступает как критерий усвоения различных элементов знаний. Поэтому так часто задача выступает как один из элементов проверочных и контрольных работ. Степень овладения умением решать задачи определяет качество знаний учащихся, возможность осуществления самостоятельной познавательной деятельности. Все это определяет особое значение умения решать задачи среди других познавательных умений.

Неумение решать задачи является одной из основных причин снижения успеха в изучении физики.

МЕТОДЫ РЕШЕНИЯ ЗАДАЧ

Применяемые при рассмотрении вычислительных задач логические операции определяют - метод решения - аналитический и синтетический (в чистом виде каждый из них встречается редко), чаще всего используется аналитико-синтетический.

Аналитический метод состоит в расчленении данной задачи на ряд более простых (анализ), т.е. решение начинается с искомой величины или отыскания закономерности, которая дает непосредственный ответ на вопрос задачи. Анализируя условия, обучающиеся находят закономерность, которая связывает искомую величину с другими; если выражающая эту закономерность формула содержит, кроме искомой, еще неизвестную величину, то находят другую закономерность, связывающую ее с известными из условия; так поступают до тех пор, пока искомая величина не будет полностью выражена через известные.

Синтетический метод предполагает последовательное выяснение связей величин, данных в условии, с другими до тех пор, пока в уравнение в качестве одного неизвестного не войдет искомая величина. Таким образом, решение задачи при синтетическом методе в противоположность аналитическому начинается, как правило, не с искомой величины.

Оба метода правомерны, однако в дидактическом плане они имеют свои особенности, которые нужно учитывать в учебном процессе. Аналитический метод более «целеустремлен»: нахождение правильной исходной формулы сразу ведет к цели, внимание учеников не задерживается на промежуточных этапах, но это не всегда хорошо, так как слабые ученики недостаточно полно усваивают физическое содержание и количественные характеристики рассматриваемых в задаче явлений. Синтетический способ (очевидно, что в нем присутствует анализ) позволяет подробно рассматривать промежуточные этапы решения, количественные характеристики явлений, наименование физических величин. Он показывает преподавания, ближе конкретно-образному мышлению учащихся, и поэтому к нему ученики обращаются «спонтанно», в то время как аналитическому методу решения их, как правило, необходимо учить. Дело в том, что синтетический способ подобен методу проб и ошибок, а аналитический предъявляет повышенные требования к уровню логического мышления и их математической подготовки.

Аналитико-синтетический метод решения задач. При решении задач анализ и синтез неразрывно связаны между собой, т.е. применяется единый аналитикосинтетический метод.

ВИДЫ ЗАДАЧ ПО ФИЗИКЕ

Задачи можно классифицировать по различным признакам: по способу выражения условия задачи, по способу решения, степени трудности, характеру содержания и т.д.

По способам выражения условия различают задачи текстовые, графические, задачи-рисунки, экспериментальные задачи.

По степени сложности различают простые и сложные задачи, а также трудные. Простыми будем называть такие задачи, решение которых осуществляется в одно-два действия, или умозаключения.

По характеру и методу исследования вопросов выделяют качественные и количественные задачи. Решение качественных задач предполагает построение умозаключений на основе применения физических теорий и законов, без применения математического аппарата. К количественным задачам относятся задачи, ответы которых не могут быть найдены без выполнения математических преобразований и вычислений.

По содержанию различают абстрактные и конкретные задачи с производственным и историческим содержанием, а также занимательные.

По основному способу решения без применения которого нельзя получить ответ на вопрос задачи. Различают вычислительные, экспериментальные и логические задачи. При решении физических задач применяются логический, математический, экспериментальный способы. По виду используемого раздела математики различают арифметический, алгебраический, геометрический, координатный и графический способы (рис.1).

Логический способ позволяет объяснить заданную ситуацию, осуществить решение задачи на качественном уровне. Применение определенного вида математического способа позволяет произвести анализ существующих зависимостей между физическими величинами на количественном уровне.

По роли в формировании физических понятий различают следующие виды задач:

1. задачи, в процессе решения которых осуществляется уточнение признаков понятий. К ним относят задачи простые и абстрактные;

2. задачи, в процессе решения которых осуществляется уточнение объема и конкретизация понятий. К ним относятся задачи вида «где наблюдается?», «где применяется?»...;

3. задачи, основной целью которых является дифференцировка понятий. Сюда относятся логические задачи по выявлению общих черт и существенных различий; сравнение предметов и явлений в качественном и количественном отношениях;

4. задачи, основной целью которых является установление и закрепление нового понятия. К ним относятся все вычислительные, графические задачи, задачи-рисунки, доказательства, логические задачи, вида «что нужно сделать для того, чтобы...»;

5. задачи, целью которых является систематизация понятий и формирование у учащихся умения классифицировать их, правильно соотносить друг с другом;

6. задачи, целью которых является формирование у учащихся умения применять понятия в различных ситуациях, для объяснения и предсказания явлений. К данному типу задач необходимо отнести задачи с конкретным содержанием, а также задачи по данным лабораторных работ.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ МЕТОДИКИ ОБУЧЕНИЯ
ОБУЧАЮЩИХСЯ УМЕНИЮ РЕШАТЬ ЗАДАЧИ.

Структурный анализ процесса решения задач. Чтобы формировать у обучающихся обобщенное умение решать задачи, необходимо знать структуру процесса решения задач. Проведем структурный анализ процесса решения учебных задач. Структура решения задач включает в себя следующие этапы:

1- ый этап - ознакомление с условием задачи;

2- ой этап - составление плана решения задачи;

3- ий этап - осуществление решения;

4- ый этап - проверка правильности решения задачи.

Каждый этап осуществляется определенными действиями. Действия для каждого этапа:

ориентировка - уточнение характеристики цели действия, выделение свойств объектов, в отношении которых нужно произвести преобразование; планирование - определение состава и последовательности преобразования; исполнение - осуществление этих преобразований; контроль - проверка достижения цели действия.

Структура деятельности преподавателя по обучению обучающихся умению решать задачи. В деятельности преподавателя по обучению обучающихся умению решать задачи можно выделить две структурные части: теоретическую, которая включает овладение теорией, и практическую. При этом решаются такие педагогические задачи, как определение объема знаний, которые должны быть усвоены учениками под руководством преподавателядавателя, состава умений, необходимых для решения задач, и последовательность формирования у обучающихся умения выполнять отдельные операции.

Теоретическая подготовка преподавателя должна обеспечить:

1. Четкое представление о методах решения физических задач. В методике преподавания физики выделяют аналитический, синтетический, аналитикосинтетический методы решения задач.

2. Знание способов решения задач по физике. Еще больше противоречивых мнений на определение способа решения задачи. Чаще всего метод определяют через способ. Однако в теории обучения обучающихся умению решать задачи эти два понятия надо разграничивать. Под способом решения физической задачи следует понимать совокупность средств реализации того или иного метода.

3. Знание содержания и структуры способа решения задачи. Способ решения учебной задачи также имеет свою структуру, познанную на определенном уровне. Этой структуре надо обучать учащихся. Структура задачи и структура способа ее решения должны стать объектом обучения.

4. Структура задачи, по В.М. Глушкову, представлена на рис. 1.

5. Л.М. Фридман выделяет аналогичные части учебной задачи, но связи между ними устанавливает несколько по другому, рис.2.

6. В структуре способа решения учебной задачи в настоящее время можно выделить четыре основных этапа: ознакомление с условиями задачи, составление плана ее решения, осуществление этого плана и проверка полученного решения.

ЗАДАЧА

ЗАДАННАЯ

СИСТЕМА

РЕШАЮЩАЯ

СИСТЕМА

ПРЕДМЕТ

ДЕЙСТВИЯ.

ТРЕБОВАНИЯ

СПОСОБЫ РЕШЕНИЯ ЗАДАЧ.

СРЕДСТВА РЕШЕНИЯ ЗАДАЧ

РИС. 1

ЗАДАЧА

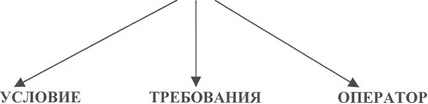
ПРЕДМЕТНАЯ ОТНОШЕНИЯ

РИС.2

4. Овладение общим алгоритмом решения физической задачи. Общий алгоритм решения физической задачи определяет структуру деятельности обучающихся по отысканию решения любой вычислительной задачи. Структура деятельности представляет собой реализацию основных этапов решения через определенные действия.

5. Рассмотрение алгоритма решения задач определенного класса как конкретизацию общего алгоритма для определенного раздела или темы курса физики.

6. Умение выделить в алгоритме решения задач определенного класса его структурные элементы и содержание отдельных действий. Преподавателю необходимо уметь анализировать и оценивать различные учебные алгоритмы.

7. Умение верно определять рациональный способ введения алгоритма в учебный процесс.

Практическая часть деятельности по обучению обучающихся умению решать

задачи включает следующие элементы:

1. вооружение обучающихся знанием содержания и общей структуры задач, а также задач различных видов, их классификаций;

2. вооружение обучающихся знанием структуры процесса решения учебной задачи;

3. обучение обучающихся общей структуре решения физических задач;

4. обучение обучающихся особенностям решения задач различных видов (вычислительных, логических, экспериментальных, графических, задач- рисунков);

5. «выработка» алгоритмов решения задач по конкретным темам и на их основе формулирование общего алгоритма решения учебных задач;

6. проведение специальной работы по усвоению обучающимися алгоритма, раскрытие перед ними содержания отдельных действий;

7. определение последовательности решения задач по конкретной теме, чтобы в процессе решения первых задач отрабатывались конкретные операции, а затем осуществлялось свертывание их в обобщенные действия;

8. обеспечение реализации обучающимися всех этапов решения задач в процессе решения.

Структура учебного алгоритма.

Алгоритмы нашли широкое применение в процессе обучения. В учебной практике известно большое количество различных конкретных алгоритмов и алгоритмических предписаний.

К основным свойствам алгоритмов относятся их детерминированность, результативность, массовость.

Алгоритм выполняет функцию модели деятельности. Учебная деятельность заключается в описании наблюдаемого, в организации поиска ответа на поставленный вопрос, в объяснении наблюдаемых фактов и в исполнении намеченного плана.

Познание любого процесса (явления или предмета) начинается с описания наблюдаемого. На основе описания отыскивается первоначальная структура деятельности (эвристика), которая становится основой создания предписания. Полученное предписание, как правило, недостаточно детерминирует процесс познания. Алгоритм можно рассматривать как более познанную структуру деятельности.

Общий алгоритм решения задач.

1. Внимательно прочитайте условия задачи и уясните основной вопрос; представьте процессы и явления, описанные в задаче.

2. Повторно прочитайте содержание задачи для того, чтобы четко представить основной вопрос задачи, цель ее решения, заданные величины, опираясь на которые можно вести поиски решения.

3. Произведите краткую запись условия задачи с помощью общепринятых буквенных обозначений.

4. Выполните рисунок или чертеж к задаче.

5. Определите, каким методом будет решаться задача; составьте план ее решения.

6. Запишите основные уравнения, описывающие процессы; предложенные заданной системой.

7. Найдите решение в общем виде, выразив искомые величины через заданные.

8. Проверьте правильность решения задачи в общем виде, произведя действие с наименованиями величин.

9. Произведите вычисления с заданной точностью.

10. Произведите оценку реальности полученного решения.

11. Запишите ответ.

Критерии и уровни сформированности умения решать задачи по физике.

Зная критерии и уровни сформированности умения решать задачи, можно оценить знания и умения обучающихся, а также методику применяемую преподавателем при обучении. С другой стороны, это позволяет определять и научно основывать содержание соответствующих этапов обучения, на которых формируется умение до заданного уровня. Определение верхнего (высшего) уровня необходимо для осознанной, целенаправленной работы преподавателя по формированию умения до заданного уровня, видение перспективы в развитии данного умения.

На основе знаний структуры деятельности и состава операций определяются критерии, а на основе критериев определяются уровни сформированности умения решать задачи.

Основные критерии сформированности умения решать физические задачи:

1. Знание основных операций, из которых складывается процесс решения задач, и умение их выполнять.

2. Усвоение структуры совокупности операций.

3. Перенос усвоенного метода решения задач по одному разделу на решение задач по другим разделам и предметам.

МЕТОДИКА ОБУЧЕНИЯ ОБУЧАЮЩИХСЯ РЕШЕНИЮ ЗАДАЧ

ПО ФИЗИКЕ

Управление любым процессом предполагает перевод объекта из одного заданного состояния в другое. Чтобы это положение применить к процессу обучения обучающихся общим методам решения задач, необходимо знать уровень сформированности этого умения у них к началу изучения курса физики. Затем должны быть четко определены (сформулированы) требования к знаниям обучающихся об общих методах решения задач и к уровню сформированности этого умения к моменту окончания средней школы. Третья проблема, которую должен решать преподаватель, - это проблема поиска рациональных способов обучения методам решения задач.

В процессе решения математических и физических задач имеются общие операции. Поэтому возможно осуществить перенос умения решать математические задачи на решение физических задач. Так, обучающиеся к началу обучения уже владеют вычислительными умениями, а также умением построения графика. Но есть и такие операции, содержание которых в математике и физике неидентично (например, действия с именованными величинами).

К окончанию средней школы у обучающихся должны быть сформированы общие методы решения задач. Процесс усвоения обучающимися методов решения задач идет довольно сложно.

Наблюдения за деятельностью обучающихся, изучение их знаний о методах решения задач на основе анализа письменных работ позволяет предположить, что усвоение общих методов идет путем усвоения содержания отдельных операций, из которых складывается деятельность обучающихся. На основе сравнения методов решения в различных классах, применяемых обучающимися можно судить о том, как происходит свертывание операций в определенную структуру, познание самой структуры. В настоящее время представляется возможным выделить следующие основные этапы овладения обучающимися методами решения задач:

1. выработка умения анализировать условие задачи;

2. выработка умения выполнять отдельные операции, общие для большого класса задач;

3. овладение конкретными методами решения задач по определенной теме и определенного вида;

4. овладение предписаниями алгоритмического типа по решению задач определенных видов (вычислительных, логических, экспериментальных);

5. усвоение общего предписания алгоритмического типа по решению физической задачи.

Аналогично названным этапам можно выделить основные этапы деятельности преподавателя по руководству процессом выработки у обучающихся общих методов решения физических задач. Этапы формирования у обучающихся умения решать задачи:

Первый этап. Процесс анализа конкретных физических задач довольно сложен. Он начинается с восприятия условия задачи, заданной определенным кодом. Текстовый код (как более распространенный способ предъявления физической задачи) оказывается трудно воспринимаемым для образного представления содержания задачи. Поэтому процесс восприятия конкретной задачи сопровождается перекодированием ее условия с помощью кода более высокого порядка. Первой формой перекодирования задачи является форма краткой записи ее условия через буквенные и знакомые обозначения с соответствующими индексами, а также выполнение рисунков, чертежей, схем, электрических цепей.

На данном этапе обучающиеся овладевают и другими формами дальнейшего перекодирования и кодами более высокого порядка, например, использованием аналитической формы записи для графического кодирования сил.

Второй этап начинается с выявления структуры процесса решения задачи. На первых порах происходит нечеткое (диффизнорассеянное) восприятие самой структуры, но основное внимание обращается на содержание общих операций по решению любой физической задачи; идет процесс усвоения этих операций. Особое внимание должно быть уделено формированию таких операций, как выбор рациональных способов решения задачи, выполнение приближенных вычислений, выполнение действий с именными величинами, преобразование единиц величин, применению различных способов проверки и анализ результата.

Названные операции отрабатываются в процессе решения конкретных задач. При этом учащиеся решают задачи различными методами, реализуя их через определенные способы. Наряду с использованием, усвоением отдельных операций, которые являются общими для решения большого класса физических задач, учащиеся овладевают методами и способами решения конкретных задач.

На третьем этапе происходит усвоение общей структуры решения класса задач по конкретной теме, на применение конкретных физических законов. На данном этапе усвоение учащимися общих методов решения задач данного класса усвоенные ранее операции выстраиваются в строгую систему, которую можно рассматривать как предписание алгоритмического типа для решения задач по определенным темам.

Четвертый этап процесса усвоения учащимися методов решения физических задач заключается в том, что предписания алгоритмического типа для решения задач определенного вида по конкретным темам и на конкретные законы обобщаются в общие предписания алгоритмического типа задач этого вида.

На пятом этапе происходит дальнейшее обобщение предписаний алгоритмического типа, при этом вырабатывается общее предписание алгоритмического типа для решения любой физической задачи.

Скачано с www.znanio.ru