Научно – практическая работа написана на тему: «Свойство биссектрисы треугольника».

Несколько решений одной задачи.

Свойство биссектрисы треугольника.

Абстракт:

    Научно – практическая работа написана на тему: «Свойство биссектрисы треугольника».

Объектом исследования данной работы являются различные доказательства теоремы о свойстве биссектрисы треугольника.

Целью работы является попытка выявить более лёгкое доказательство свойства;

показать, что теорему о свой­стве биссектрисы треугольника можно доказывать различными способами с опорой на новую тео­рию в процессе изучения всего кур­са планиметрии;

расширить знания учащихся, изучив аналогичную теорему о бис­сектрисе внешнего угла треуголь­ника.

Гипотеза: так как в учебнике «Геометрия 9» дан 1^ый способ доказательства, то он наверное  и является более лёгким.

Этапы исследования:

1.     Работа с литературой.

2.     Нахождение способов поставленной цели.

3.     Обработка результатов.

Работа носила исследовательско - практический характер. Все доказательства были рассмотрены самостоятельно, при этом использовались формулы площади треугольника, косинус острого угла, подобие треугольников, обобщённая теорема Фалеса.

Работа состоит из введения, двух глав (1глава – доказательства теоремы, 2 глава - геометрический практикум), заключения, списка используемой литературы.

1

Аннотация научного проекта, написанного на тему:

«Свойство биссектрисы треугольника».

Целью исследования стала попытка выявить более лёгкое доказательство теоремы о свойстве биссектрисы треугольника и показать её применение на практике.

Новизна исследования в том, что в данной работе рассматриваются всевозможные доказательства данного свойства: с помощью формул площади треугольника, теоремы Фалеса, теоремы косинусов, признаков подобия фигур.

Ученица, рассмотрела способы доказательства теоремы, проделав предварительную работу по их отбору и классификации.

Проведенные исследования помогают автору приобрести новые знания, умения  и навыки при работе со справочной литературой.

Отмечается хорошее знание автором учебного материала, умение доказывать, делать выводы.

Работа выполнена грамотно с соблюдением всех необходимых требований.

2

Введение

          Часто полезнее решить одну и ту же задачу тремя способами, чем решить три-четыре различные задачи. Решая одну задачу различ­ными методами, можно пу­тем сравнений выяснить, какой из них короче и эф­фективнее. Так вырабатыва­ется опыт.

                                                                                                                    У. Сойер

О существовании этой важной теоремы учащиеся быстро забыва­ют, так как в учебниках она, как и другие, формулируется и доказы­вается один раз, и задач, решаемых с применением этого свойства, очень мало. А это, конечно, сказы­вается на результатах олимпиад и вступительных экзаменов в вузы.

Полученные знания позволили найти формулу длины биссектри­сы треугольника; выразить длину отрезка, на которые биссектриса делит противоположную сторону треугольника; выразить отно­шение отрезков, на которые делят­ся биссектрисы точкой их пересечения, через стороны треугольни­ка.

Решение одной и той же зада­чи различными методами дает воз­можность полнее исследовать свой­ства геометрической фигуры и вы­явить наиболее простое решение. Решая задачу подходящим методом, иногда удается попутно «открыть» свойство фигуры, о ко­тором в задаче ничего не говорит­ся, или получить интересное обоб­щение задачи. Нередко найденный способ решения может быть в даль­нейшем использован для решения более трудных задач, сходных с решенной задачей.

3

Глава I

Теорема о свойстве биссектрисы треугольника.

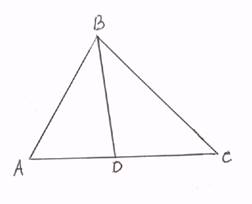
Биссектриса BD любого угла треугольника ABC делит проти­воположную сторону АС на час­ти AD и DC, пропорциональные прилежащим сторонам.

Очевидно, если АВ = ВС, то теорема верна. Поэтому будем счи­тать, что АВ ВС.

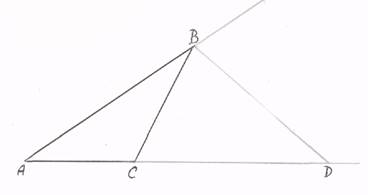
Биссектриса ВD внешне­го угла треугольника пересека­ет продолжение его стороны АС в точке  D, расстояния от которой до концов этой стороны А и С пропорциональ­ны соответственно прилежа­щим сторонам треугольника  АВ и ВС.

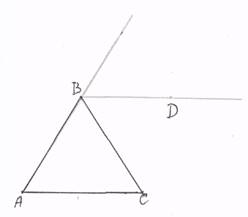
Известно, что если  АВ = ВС, то BD || АС.

Рассмотрим несколько доказательств теорем о свойстве биссектрисы треугольника: биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам.

4

1. Шыныбеков А.Н. «Геометрия – 9»

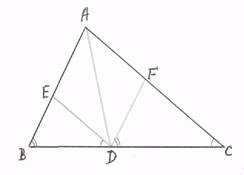
Проведем через точку D прямые, параллельные сторонам АВ и АС треугольника ABC. Построим параллелограмм AEDF, являющийся ромбом, поскольку диагональ AD -биссектриса углов А и D ромба. Во-вторых, так как соответству­ющие его стороны параллельны, то треугольники ABC, BED и DFC  подобны друг другу. Поэтому             получаем равенства     

                                            и                     

 или ВСDЕ=АСВD и BCDF=ABDC. Отсюда, учитывая, что

DE=DF, получим АС • BD=AB • DC.  Откуда вытекает, что .

2. А.В. Погорелов «Геометрия 7-11» (прямоугольные треугольники подобны, если они имеют по равному острому углу)

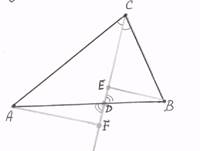
Пусть CD — биссектриса треугольника ABC

(рис. 2). Если треугольник ABC равнобедренный с основанием АВ, то указан­ное свойство биссектрисы очевидно, так как в этом случае бис­сектриса CD является и медианой.

                                    Рассмотрим общий случай, когда АСВС.

 Опустим пер­пендикуляры AF и BE из вершин А и В на прямую CD.

Прямоугольные треугольники ACF и ВСЕ  подобны, так как у них равны острые углы при вершине С. Из подобия треуголь­ников следует пропорциональность сторон:         .

Прямоугольные треугольники ADF и BDE тоже подобны. У них  углы  при  вершине D  равны  как  вертикальные.  Из  подобия треугольников следует

пропорциональность сторон:  .

Сравнивая это равенство с предыдущим, получим:  или ,

т.е. отрезки AD и BD пропорциональны сторонам АС и ВС, что и требовалось доказать.

5

3. Используется обобщённая теорема Фалеса: параллельные прямые, пересекающие стороны угла, отсекают на  них пропорциональные отрезки:

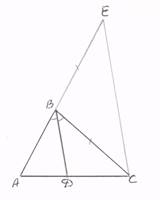
 Продолжим сторону АВ за вершину В и проведём СЕ║ВD, тогда треугольник ВСЕ равнобедренный, в котором ВС=ВЕ. Но по обобщённой теореме Фалеса

. Следовательно, .

          Рис 3

4. Используется признак подобия треугольников по двум углам: если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

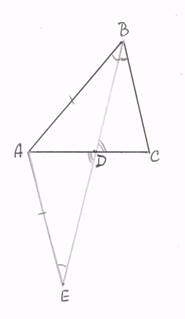
Продолжим биссектрису BD до пересечения в точке Е с прямой АЕ║ВС, тогда АЕD=DBC=DBA, а значит, треугольник АВЕ – равнобедренный и АВ=АЕ. Поскольку вертикальные углы ADE и BDC равны, то треугольники ADE и CDB подобны по двум углам и тогда , следовательно, .

5.  

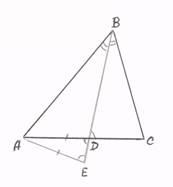
Продолжим биссектрису BD и на луче BD отметим точку Е такую, чтобы АЕ=AD, тогда AED=ADE=BDC. Следовательно, треугольника АВЕ и CBD подобны по двум углам. А это значит, что , то есть .

                                                                6

6. Используются формулы площади треугольника: площадь треугольника равна половине произведения его стороны на высоту, проведённую к этой стороне.

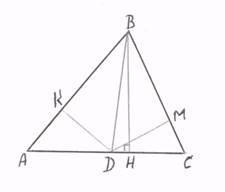
Треугольники ABD и DBC имеют общую высоту ВН. Тогда отношение их площадей равно отношению . Но по свойству биссектрисы эти треугольники имеют равные высоты, проведённые соответственно к сторонам АВ и ВС. Тогда .

7. Площадь треугольника равна половине произведения двух сторон треугольника на синус угла  между ними.

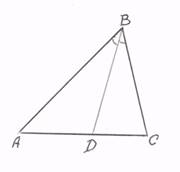
         ADBDsinADB, DCBDsinCDB. Так как синусы смежных углов равны, то

                                       .  (1)

С другой стороны, ABBDsinABD и BCBDsinCBD. Так как ABD=CBD (BD –  биссектриса), то   

                                                                               .   (2)

Учитывая равенства (1) и (2), получим .

7

Глава II

Геометрический практикум

1. Формула длины биссектрисы треугольника (используется теорема косинусов и свойство биссектрисы треугольника)

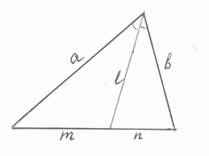Применим теорему косинусов к треугольникам с равными углами. Выра­зив косинусы этих углов и приравняв их, получим уравнение

откуда       b(l² + a² - т²) = а(l² + b² - п²) или

 l²(b -a) - аb(b - а) = (тb)т - (ап)п. Из свойства биссектрисы, записанного в виде равенства an = mb,

получим (b- а)(l² - аb) = атп - bтп или (b - а)(1² - аb) = -тп(b - а). Разделив обе части уравнения на (b - а), имеем l² = аb - тп.

2. Формула нахождения длин отрезка, на которые биссектриса делит противоположную сторону треугольника.

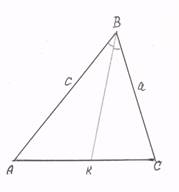Найдем  длину  отрезка АК.   По  свойству  биссектрисы  ВК  получим  или, откуда  или , тогда , то есть

.  Следовательно, AK=AC . Если стороны треугольника обозначить ВС = а, АС = b, АВ = с, то формула записывается и запоминается легче:  АК=.

3. Нахождение отношения длин отрезков биссектрисы, на которые она делится точкой их пересечения.

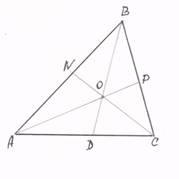
По  свойству биссектрисы АО в треугольнике ABD  

. Воспользовавшись доказанной выше формулой и обозначением сторон треугольника, получаем . Поэтому .

                                                                                    8

                                                         Заключение.

При выполнении работы было найдено 7 способов доказательства теоремы о свойстве биссектрисы треугольника. На мой взгляд, наиболее лёгким является доказательство, основанное на обобщённой теореме Фалеса.

Полученные знания позволили найти формулу длины биссектри­сы треугольника; выразить длину отрезка, на которые биссектриса делит противоположную сторону треугольника, через стороны треугольника; выразить отно­шение отрезков, на которые делят­ся биссектрисы точкой их пересечения, через стороны треугольни­ка.

9

Список литературы:

1. Г.И. Глейзер «История математики в школе»   Москва «Просвещение» 1964год

2. А.В.Погорелов «Геометрия 7-11»

3. А.Н. Шыныбеков «Геометрия 9»

4. Газета «Математика в школе» приложение к 1 сентября  №1 2005год.

10

         Содержание

1.     Абстракт………………………………………………….1

2.     Этапы исследования……………………………………..1

3.     Аннотация………………………………………………..2

4.     Введение………………………………………………….3

5.     Глава I……………………………………………………..4

6.     Глава II…………………………………………………….8

7.     Заключение ……………………………………………….9

8.     Список литературы………………………………………10

ГУ «Верх - Убинская средняя школа»

   Несколько решений

одной задачи.

Свойство биссектрисы

треугольника.

Исследовательская работа

по математике:

                                                              Выполнила:         Бояринова Татьяна

                                                                                                 ученица 9класса

                                                              Руководитель:     Позднякова О.А.                                           

с. Верх – Уба

2008 г.