ГБОУ АО «АЛГ»   

                                          Секция: Геометрия

                                                     Тема

                      ФАНТАСТИЧЕСКИЕ ФИГУРЫ, ИХ СВОЙСТВА

                     И ГЕОМЕТРИЯ, В КОТОРОЙ ОНИ ОБИТАЮТ

                                                  Выполнил:

                                           Конев Владимир Дмитриевич, 7 Б класс,

                                           ГБОУ АО “Астраханская лингвистическая гимназия”

 научный руководитель : О.М .Гиллер, учитель математики ГБОУ АО  «Астраханская лингвистическая  гимназия»

                                        2020

             Оглавление

1. Введение………………………………………. 3               

 2. Евклидова геометрия……………………......  4     

  3. Неевклидова геометрия……………………... 5                

  4. Параллельные линии…………………………. 6          

   5. Теорема о сумме углов треугольника………...8         

   6. Неевклидова геометрия в жизни……………10             

  7. Заключение……………………………………13 

                           Введение

    Все привыкли к обычным фигурам, как квадрат, треугольник, пятиугольник, линия… Мы знаем, что сумма углов треугольника равна 180°, параллельные линии никогда не пересекаются. Но, что если я скажу вам, что параллельные линии могут пересекаться, существует треугольник с сумой углов больше 180°? Вы не поверите? Посмотрим!

     Цель моего исследования: узнать, как работает геометрия на шаре, определить, чем она отличается от геометрии на плоскости и как Неевклидова геометрия применяется в реальной жизни

    Задачи:

1.Узнать об использовании неевклидовой геометрии в жизни.

2. Исследовать свойства Фигур в неевклидовом пространстве

3.Провести эксперименты.

    Гипотеза: Необычные условия, как сфера могут повлиять на свойства геометрических фигур

   Актуальность проекта: Самолёты летают по сфере, а не плоскости и для экономии топлива полёт должен происходить по кратчайшему пути, а на сфере кратчайший путь отличается от кратчайшего пути на плоскости.

    Методы исследования: Изучение литературы, эксперименты, сравнение результатов экспериментов. 

           Евклидова геометрия

Евклидова геометрия построена на 5 аксиомах, описанных в труде Евклида «Начала», и на Теоремах, основанных на аксиомах. Что же такое Аксиома? Аксиома или постулат – утверждение, не требующие каких-нибудь доказательств и является истиной.

Основные постулаты Евклида:
1.Из каждой точки ко всякой другой точке можно провести прямую;

I постулат. Требуется, чтобы от каждой точки ко всякой другой точке можно было провести прямую линию.
2.Каждую ограниченную прямую можно продолжить неопределённо;

II постулат.И чтобы каждую прямую можно было неограниченно продолжить.
3.Из любого центра можно описать окружность любого радиуса;

III постулат. И чтобы из любого центра можно было описать окружность любого радиуса.
4.Все прямые углы равны;

IV постулат. И чтобы все прямые углы были равны.
5.Через точку не лежащую на данной прямой можно провести прямую, параллельную данной и только одну.

V постулат. И чтобы всякий раз, когда прямая при пересечении с двумя другими прямыми образует с ними односторонние углы, сумма которых меньше двух прямых, эти прямые пересекались с той стороны от секущей, с которой эта сумма меньше двух прямых углов.

Был мудрым Евклид,

Но его параллели,

Как будто бы вечные сваи легли.

И мысли его, что как стрелы летели,

Всегда оставались в пределах Земли.

А там, во вселенной, другие законы,

Там точками служат иные тела.

И там параллельных лучей миллионы

Природа сквозь Марс, может быть, провела.

 И правда, 4 аксиомы Евклида до сих пор остаются истиной и неприкасаемыми. Но прошли тысяча лет и в «истинности» 5 постулата усомнились. Чем же провинился 5 постулат? По сравнению с остальными постулатами 5 постулат звучал неожиданно сложно.

Если на плоскости при пересечении двух прямых третьей сумма внутренних односторонних углов меньше 180°, то эти прямые при достаточном продолжении пересекаются, и притом с той стороны, с которой эта сумма меньше 180°.

Так звучит Современный вариант 5 постулата.

Многие умы за тысячу лет пытались заменить 5 постулат на более лёгкий, но равноценный с ним.

           Неевклидова геометрия

На плоскости Евклидова геометрия работала безоговорочно, но когда люди работали с ней в астрономии, то классическая геометрия давала сбой.

Первый вклад в неевклидовую геометрию совершил русский математик и астроном Лексель Андрей Иванович. Он изучал свойства кругов на сфере. Он первый опубликовал результаты своих работ по сферической геометрии и использовал их для изучения орбит планет. Дело Лекселя продолжил его соотечественник – Фусс. Он разрешил несколько проблем сферической геометрии, преимущественно занимаясь сферическим эллипсом. За рубежом Сферической геометрией занимался великий немецкий математик Бернхард Риман. Но только во второй середине 19 века была основана геометрия на сфере, какой мы знаем её сейчас. Первым попытавшимся основать её был Штейнер с его работами о разделении сферических фигур. В этих работах Штейнер доказывает гипотезу, схожую с теоремой Фусса, и находит две дуги круга.

               Параллельные линии

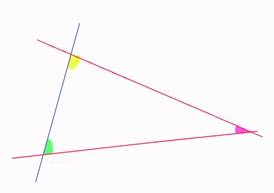
Попробуем посмотреть на аксиому о параллельных прямых на сфере, а не на плоскости. Поначалу кажется, что никаких разногласий нет, но при детальном разборе обнаруживается 2 противоречия аксиоме!

1. По условию прямые при достаточном продолжении пересекутся, если сумма внутренних углов меньше 180°, но на сфере пересечение возможно с суммой внутренних углов равна 180°.

2. Также по условию линии пересекаются с той стороны, с которой эта сумма меньше 180°, но на сфере можно продолжить с противоположной стороны и прямые также пересекутся, что не возможно на плоскости.

Видно, что аксиома не работает должным образом на сфере, но что это значит?

Это значит, что теоремы, связанные с 5 постулатом будут другими или рушатся.

Например, первая теорема о Параллельных прямых в учебнике Геометрии 7 класса А.Г Мерзляка:

«Две прямые, перпендикулярные третьей прямой, параллельны»  

Т.е Если a ⊥ x и b ⊥ x, то a ∥ b

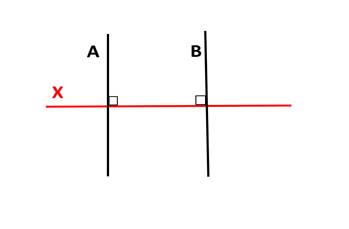
В Евклидовой геометрии теорема доказывается, но на сфере линии не будут параллельными.

На сфере можно нарисовать две прямые, перпендикулярные третьей, но не параллельные.

Теорема о сумме углов треугольника

   «Сумма углов одинакова у всех треугольников.»

Так звучит равноценная пятому постулату Евклида формулировка. По теореме о сумме углов треугольника у любого треугольника сумма углов равна 180°, что соответствует формулировке пятого постулата.

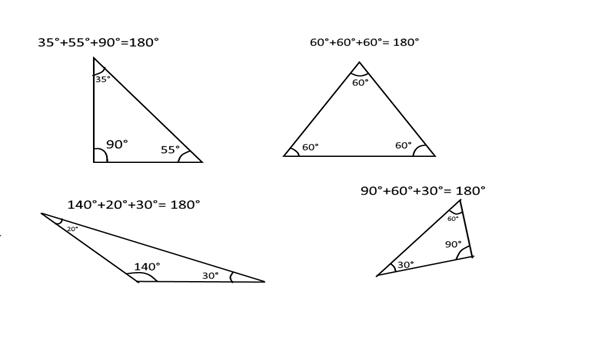
    На этом рисунке изображены разные треугольники с суммой углов 180 градусов

    На неевклидовой плоскости сумма углов не постоянная, но если в геометрии Лобачевского сумма углов всегда меньше 180°, то в сферической геометрии сумма углов всегда больше 180°. Попробуем это доказать.

1. Пусть боковые стороны равнобедренного треугольника ABC пересекают основание треугольника, так что образуют перпендикуляр.

2. По теореме перпендикулярных прямых ÐA и ÐC равны 90°.

3.Сумма углов ÐA и ÐС равна 180°, значит, при любом значении ÐB, кроме 0, сумма углов ÐABC будет больше, чем 180° ч.т.д.

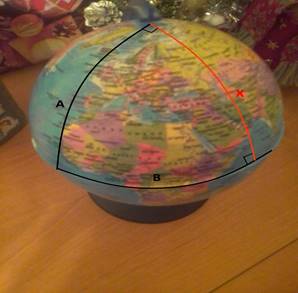
На этом рисунке изображён треугольник на сфере с суммой углов больше 180 градусов

Например, если провести боковые стороны от Гринвича до линии Перемены дат на глобусе, то сумма углов будет равняться 270, а если от Гринвича до Гринвича, то сумма будет 540.

Разница суммы углов треугольника противоречит равноценному аналогу Пятого постулата, что снова доказывает несостоятельность аксиомы о параллельности Прямых.

      Неевкдидова Геометрия в Жизни

Геодезические линии являются кратчайшими линиями на сфере в отличии от евклидового пространства, где кратчайшие линии – прямые.

Геодезические линии – дуги кругов, делящие шар на пополам.

Геодезические линии особенно важны в авиаперелётах. Если поездка на машине, то искривление не заметно, а на самолёте, где счёт идёт на тысячи километров искривление играет важную роль.

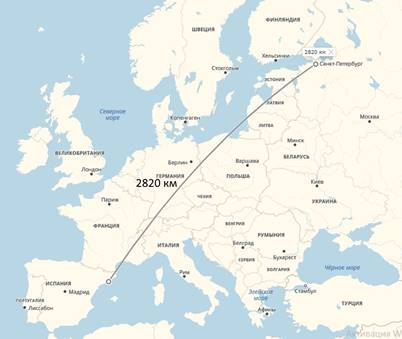
      По геодезической линии расстояние между                     

    Санкт-Петербургом и Барселоной равна 2820 км

Но что если измерить расстояние не учитывая кривизну Земли? А получится существенная разница между неправильным ответом и правильным, что приведёт к серьёзной ошибке.

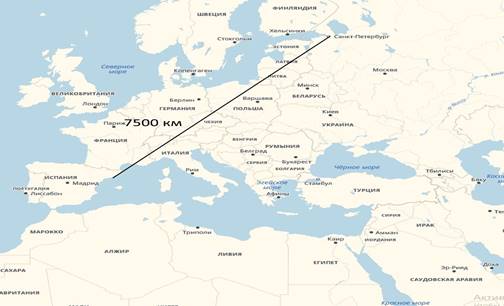
Измерив по линейке и умножив на масштаб получилось 7500 км. Разница правильного и неправильного результата составляет 4680 км!

Но можно не волноваться ,сейчас в большинстве картах давно учитывается искривлённость Земли.

Кстати при помощи Антипод можно найти место, куда ты попадёшь если прокапаешь сквозь землю.

1. Ставим точку на ваш город или ваше местоположение.

2. Чертим под любым углом первую линию, что бы она пересекала точку

3. Чертим также вторую линию, что бы она пересекала точку

4. Ищем точку пересечения

Готово! Вы нашли то место. Я попробовал так с нашим городом Астрахань, и антипод оказался на юго-востоке Тихого океана.

                 Заключение

Я узнал, как ведут себя геометрические фигуры на шаре, и насколько отличаются их свойства в двух геометриях. Я смог доказать отличия в привычных теоремах на шаре и на плоскости. Я узнал как можно применить Неевклидову геометрию и узнал больше о геометрии, как науке. Также узнал историю Геометрии, о которой не говорят в школьной программе.

                                                            Список литературы

 1.Александров П. С. Что такое неевклидова геометрия. – М.: УРСС, 2007.

 2. Башмакова И.Г. Как возникла геометрия. В кн. ДЭ, 2-е изд. Т.2 1964. С.293-299.

3.Иовлев Н. Н. Введение в элементарную геометрию и тригонометрию Лобачевского. — М.-Л.: Гиз., 1930.

4.Каган В.Ф. Лобачевский и его геометрия. – М: Гостехиздат, 1955. 5.Кадомцев С.Б. Геометрия Лобачевского и физика. – М.: Изд-во «Знание», 1984.

6.Клайн М. Математика. Поиск истины. – М.: «Мир», 1988.

7. Кутузов Б.В. Геометрия Лобачевского и элементы оснований геометрии. – М.: Учпедгиз, 1950.

8.Сосов Е.Н. Геометрия Лобачевского и её применение в специальной теории относительности. – Казань: 2012.

9.Фок В. А. Теория пространства, времени и тяготения / 2-е изд. М.: ГИФМЛ, 1961.