О построении графиков сложных функций на основе свойства монотонности

О построении графиков сложных функций на основе свойства монотонности.

Кобаидзе Нина Ивановна,
учитель математики.

     Умения строить графики функций и читать их, т. е. определять промежутки монотонности, экстремальные значения и другие характеристики функции по её графику, - важный элемент математической культуры. Эти умения необходимы будущему экономисту, программисту и даже врачу. Во многих задачах график является лишь вспомогательным элементом решения. Отсюда появляется необходимость познакомить учащихся с различными простыми приёмами построения графиков. Мы предлагаем простую и компактную схему построения графиков вида y=f(v(x)) без использования производной. Эта схема может быть использована на занятиях кружка, на факультативах или в работе с сильными учащимися на уроках. Рассмотрим примеры.

1. Построить график функции y= arctg 2^x.

Решение. Данная функция является композицией двух функций: v=2^x и y= arctgv (рис. 1)

Функцию v=v(x) назовём внутренней, y=y(v) – внешней. Внутренняя функция является строго возрастающей: при возрастании х от  до +  v(x) возрастает от 0 до +.
По графику внешней функции определим, что такому изменению v соответствует y возрастает от 0 до . График такой монотонной функции легко начертить (рис. 2); Контрольная точка: при х=0 и у = /4. Предварительно следует напомнить ученикам о существовании горизонтальных и вертикальных асимптот графиков некоторых функций, например у = 1/х, у = arctgх, у =

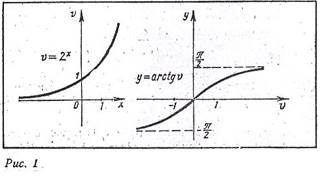
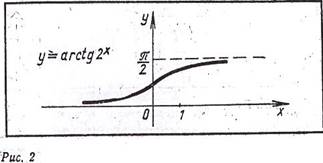
Пример-1. y= arctg 2^x.

2. Построить график функции у = 2^1\х.

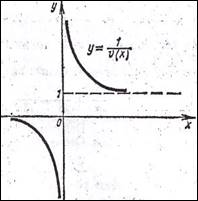
Решение. Строим графики внутренней и внешней функций (рис.3). Выделяем промежутки монотонности внутренней функции:  (- и (0; +

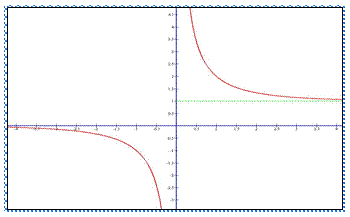
При возрастании х от  до +   v(x) убывает от 0 до - . Такому изменению v соответствует убывание у от 1 до 0. В системе координат хОу для x (-; 0) чертим соответствующую кривую (рис. 4). Если х возрастает от 0 до +, то v(x) убывает от + до 0, а у убывает от + до 1.Теперь изобразим соответствующую кривую при x  (0; +

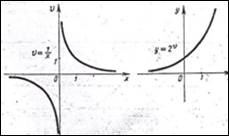  рис.3     рис.4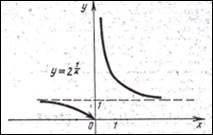

Пример - 2. у = 2^1\х.

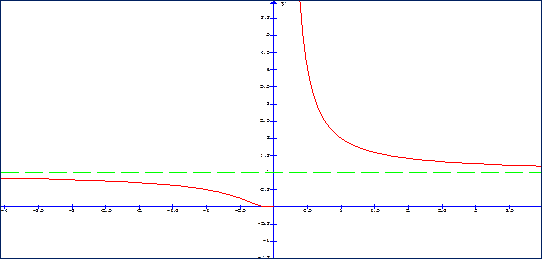
Для более точного построения графика следует использовать контрольные точки, выбирая те значения аргумента х, при которых легко вычислить точные значения у(х): у(1)=2, у(0,5)=4, у(-1)=0,5.

Таким образом, построение графика сложной функции y=f(v(x)) в некоторых случаях можно осуществить по следующему плану: 1. Начертить графики внутренней функции

v = v(x) и внешней y = f (v) функций в системе координат хОу.

2. Определить промежутки монотонности внутренней функции v = v(x) и отметить их на оси Ох плоскости хОу.

3. На каждом промежутке определить границы изменения v = v(x) и выбрать те значения

v(x), которые попадают в область определения функции y = f (v).

4. По графику внешней функции y = f (v) найти характер изменения функции у.

5. В системе координат хОу начертить график у = у(х).

Работая по этой схеме, учащиеся постоянно обращаются к графикам основных элементарных функций, учатся по графику следить за изменением функции при изменении аргумента и, наоборот, по заданному изменению функции строить её график. При этом график воспринимается не как статичный образ, а как отражения движения.

Это движение следует постоянно подчёркивать, показывая ученикам именно возрастание или убывание переменной величины.

Такое представление особенно важно формировать при изучении пределов функции.

элементарными способами строить графики сложных функций, учащиеся получат большой запас иллюстраций свойств непрерывности, различных видов разрывов, односторонних пределов и т. п. Овладев этой методикой, наиболее подготовленные ученики, только глядя на формулу, определяющую функцию, сразу же рисуют эскиз графика.

Используя схему построения графика функции у = у(х), ученики овладевают также умением представлять сложную функцию в виде композиции двух функций – внутренней и внешней, навыком «видеть» эти две функции, без чего нельзя обойтись при изучении дифференцирования сложных функций.

3. Построить график функции у = .

Решение приведено на рис. 5. Если х возрастает от 0 до + , то v(x) возрастает от 1 до +.

Этому изменениюv соответствует убывание у от 1 до 0. Изображаем график функции

у = у (х) при х0, а затем используем чётность данной функции.

При построении графиков следует иметь в виду, что область определения сложной функции y = f (v(х)) может быть уже области определения внутренней функции.

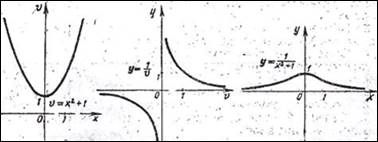     Рис. 5

  Пример – 3.  у = .

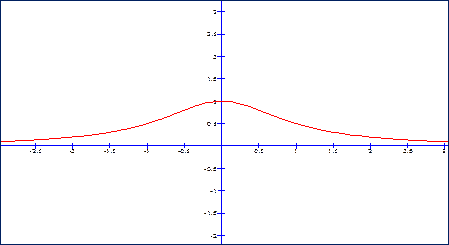 Пример -3.

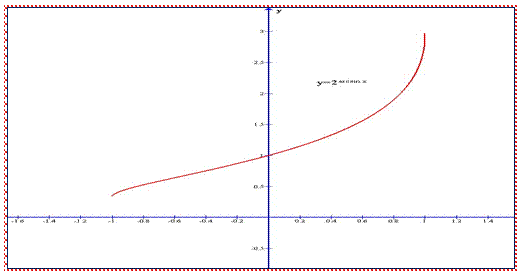
4. Построить график функции y =  (Рис. 6-7)

На рисунке 6 приведён график внутренней и внешней функций.

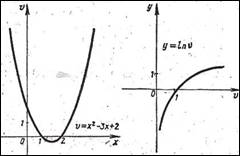 рис. 6  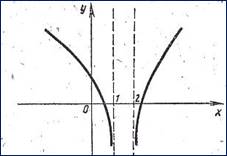     рис.7

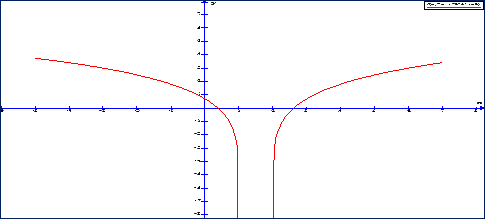
Пример – 4.  у =

 Пример – 4.

Если х возрастает от - до 1, то v(x) убывает от + до 0, а у при этом убывает

 от +  до - . При х  v(x) 0, и при этих значениях х функция y = f (v(х)) не определена. Если х возрастает от 2 до + , то v возрастает от 0 до + , а у при этом возрастает от -  до + . График данной сложной функции изображён на рисунке 7.

5. Построить график функции y = .  (Рис. 8 а, б, в)

Здесь (как всегда в случае периодической функции) вначале достаточно построить график на отрезке, длина которого равна периоду функции.

Предложенная схема применима и тогда, когда сложная функция является композиций не двух, а большего числа функций, графики которых известны.

y =  - (рис 8а, б, в).

рис. 8 - а                                           рис. 8 - б

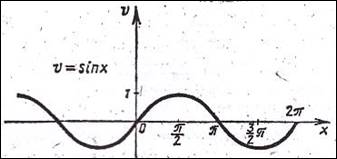
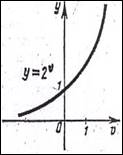
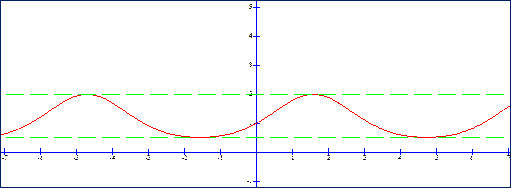
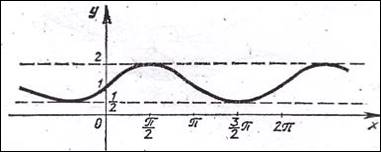  рис. 8 – в.

Пример – 5.   y =

 Пример -5.

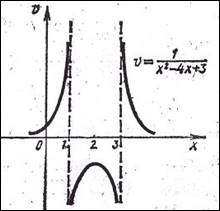
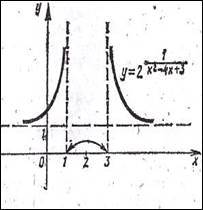
6. Построить график функции y =

Данная функция является композицией трёх функций: u = х² – 4х +3, v = , y = .

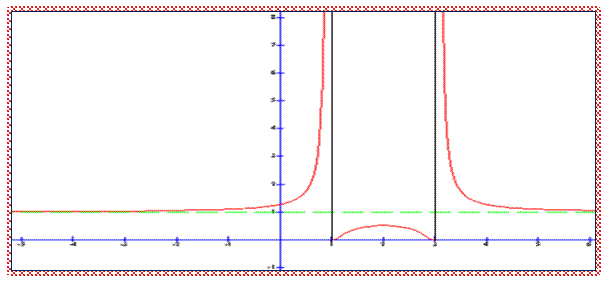
Отсюда последовательно получаем три графика (рис. 9 а, б, в). Здесь мы обошлись без графиков функций: v = 1/u и y = 2^v, свойства, монотонности которых хорошо известны.

     Рис. 9а                                               рис. 9б                                            рис. 9в

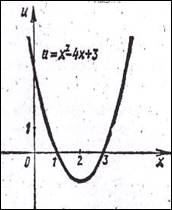
Конечно, при построении сложных функций надо использовать весь арсенал элементарных средств: переносы, отражения, сложение графиков и т. д.

Пример – 6.    y =

7. Построить график функции у =   .

Последовательные этапы построения показаны на рисунке 10.

         Рис. 10 - а                                                            рис. 10 - б

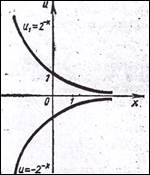
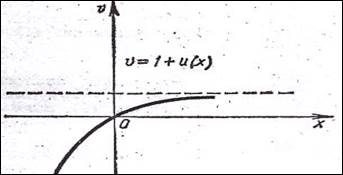
 Рис. 10 – в                                    Пример-7.    у =  ^.

Пример - 8. y = .

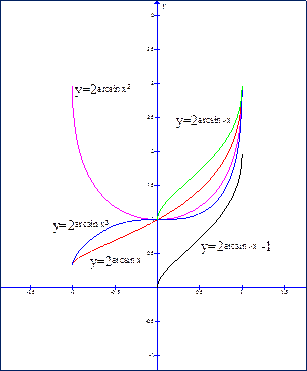
П - 9. y = ;

П - 10. y = ;

П - 11. y = ;

П - 12. y =  - 1.

Для овладения указанной методикой предлагаем построить с учащимися графики сложных функций:

у = arctg, у = arctg(х²+4х+5),

у = 2^tgx и т. д.