
Урок обобщения и систематизации знаний по теме «Интеграл и его применение»
Цели:
· формирование учебно-познавательной и информационной компетенций, посредством обобщения, систематизации знаний по теме «Первообразная. Интеграл», формирования навыков нахождения площади криволинейной трапеции несколькими способами.
· формирование информационной, общекультурной компетенций через развитие познавательной активности, интереса к предмету, творческих способностей учащихся, расширение кругозора, развитие математической речи.
· формирование коммуникативной компетенции и компетенции личностного самосовершенствования, посредством работы над коммуникативными навыками, умением работать в сотрудничестве, над воспитанием таких личностных качеств, как организованность, дисциплинированность.
Девиз урока: “Математика – язык, на котором говорят все точные науки” Н.И. Лобачевский
Ход урока
I. Организационный момент. Эмоциональный настрой на урок.
Здравствуйте, ребята! Я рада приветствовать вас на уроке.
2.Мотивация урока.
Мощным средством исследования в математике, физике, механике и других дисциплинах является определенный интеграл – одно из основных понятий математического анализа. Геометрический смысл интеграла – площадь криволинейной трапеции. Физический смысл интеграла – 1) масса неоднородного стержня с плотностью, 2) перемещение точки, движущейся по прямой со скоростью за промежуток времени.
А знаете ли вы?
Что интегралы используются при:
· решении задач из области физики;
· решении экономических задач (на оптимизацию работы фирмы в условиях конкуренции, расчет о доходности потребительского кредита);
· решении социально - демографических задач (математическая модель народонаселения Земли и др.).
Цель нашего урока - обобщить, систематизировать знания по теме «Первообразная и интеграл», подготовиться к предстоящему зачету.
Мы совершим необычное восхождение на вершину «Пика знаний».
3. Актуализация опорных знаний. Проверка домашнего задания: «Проверим рюкзаки»
Перед дальней дорогой нужно проверить насколько хорошо вы подготовились к восхождению. Проверим домашнее задание, которое было задано на предыдущем уроке:
Работа в группах «Кроссворд»
Вопросы к кроссворду
1. Как называется функция F(x)? 2. Что является графиком функции y = ax + b? 3. Самая низкая школьная оценка. 4. Какой урок проходит обычно перед зачетом? 5. Синоним слова «дюжина». 6. Есть в каждом слове, у растения и может быть у уравнения.
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7. Что можно вычислить при помощи интеграла? 8. Одно из важнейших понятий математики. 9. Форма урока, на котором проводится проверка знаний. 10. Немецкий ученый, в честь которого названа формула, связывающая площадь криволинейной трапеции и интеграл. 11. Конь - лошадь- жеребенок, бык - корова - теленок, король - королева- принц, граф - графиня - .... 12. Соответствие между множествами X и Y, при котором каждому значению из множества Х поставлено в соответствии единственное значение из множества Y, носит название ....
Ответы
1. Первообразная. 2. Прямая. 3. Единица. 4. Контрольная. 5. Двенадцать.
6. Корень. 7. Площадь. 8. Интеграл. 9. Зачет. 10. Лейбниц. 11. График. 12. Функция.
4. Обобщение и систематизация знаний по теме «Интеграл и его применение»
1 задание: «Дальше, дальше...» Каждый учащийся пишет ответы в своей тетради.
1. Что называется интегралом?
2. Что называется первообразной?
3. Как читается основное свойство первообразной?
4. Верно ли, что интеграл от любой степенной функции будет снова степенной функцией?
5. F'(х) — f(x) - как это можно прочесть?
6. Как можно вычислить площадь криволинейной трапеции при помощи интеграла?
2 задание. Работа у доски. Запишите с помощью интегралов площадь фигур, изображенных на рисунках:
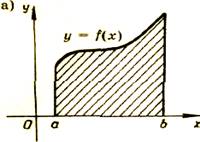
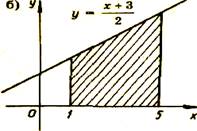
Для функции f(х) = ![]() найти первообразную, график которой
проходит через точку М(1;3).
найти первообразную, график которой
проходит через точку М(1;3).
а) F(х) =4 +![]() ; б) F(х) =
; б) F(х) = ![]() - 5; в) F(х) = -
- 5; в) F(х) = -![]() + 4; г) F{х) =x3 - 4.
+ 4; г) F{х) =x3 - 4.
Вычислите
определенный интеграл: ![]() .
.
Математический привал.
«Счастливая случайность выпадает лишь на долю подготовленных умов» (Луи Пастер)
Зачитываются сведения учащимися из истории интегрального исчисления
Символ интеграла введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы S (первой буквы слова сумма). Само слово интеграл придумал Я. Бернулли (1690 г.). Вероятно, оно происходит от латинского integero, которое переводится, как приводить в прежнее состояние, восстанавливать. (Действительно, операция интегрирования “восстанавливает” функцию, дифференцированием которой получена подынтегральная функция.) Возможно происхождение слова интеграл иное: слово integer означает целый.
В ходе переписки И. Бернулли и Г. Лейбниц согласились с предложением Я. Бернулли. Тогда же, в 1696г., появилось и название новой ветви математики - интегральное исчисление (calculus integralis), которое ввел И. Бернулли.
Возникновение задач интегрального исчисления связано с нахождением площадей и объемов. Ряд задач такого рода был решен математиками древней
Греции. Античная математика предвосхитила идеи интегрального исчисления в значительно большей степени, чем дифференциального исчисления. Большую роль при решении таких задач играл исчерпывающий метод, созданный
Евдоксом Книдским (ок. 408 - ок. 355 до н. э.) и широко применявшийся
Архимедом (ок. 287 - 212 до н. э.).
В XVII веке были сделаны многие открытия, относящиеся к интегральному исчислению. Так, П. Ферма уже в 1629 году решил задачу квадратуры любой кривой. Однако при всей значимости результатов, полученных математиками
XVII столетия, исчисления еще не было. Необходимо было выделить общие идеи, лежащие в основе решения многих частных задач, а также установить связь операций дифференцирования и интегрирования, дающую достаточно точный алгоритм. Это сделали Ньютон и Лейбниц, открывшие независимо друг от друга факт, известный вам под названием формулы Ньютона - Лейбница.
В развитии интегрального исчисления приняли участие русские математики М. В. Остроградский (1801 - 1862 гг.), В. Я. Буняковский Строгое изложение теории интеграла появилось только в прошлом веке,
Решение этой задачи связано с именами О. Коши, одного из крупнейших математиков немецкого ученого Б. Римана (1826 - 1866 гг.), французского математика Г. Дарбу (1842 - 1917).
Ответы на многие вопросы, связанные с существованием площадей и объемов фигур, были получены с созданием К. Жорданом (1826 - 1922 гг.) теории меры.
Различные обобщения понятия интеграла уже в начале нашего столетия были предложены французскими математиками А. Лебегом (1875 - 1941 гг.) и
А. Данжуа (1884 - 1974) советским математиком А. Я. Хичиным (1894 -1959 гг.)
3 задание: Вычислить устно. Найти первообразные для функций:
а) 10х; в) sin x2; д) х4; б) х2; г) соs х; е) 3x2.
4 задание: Работа в парах. Истинны ли равенства?
а) 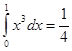 ; б)
; б) 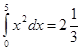 ; в)
; в) ![]() ;
;
г) 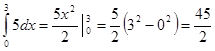 ;
;
д) 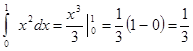 ;
;
е) 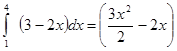 ?
?
5 задание: Работа в группах. «Спешите видеть»
Каждая группа за 5 минут должна изобразить криволинейную трапецию, ограниченную:
а) графиком функции у = (х + 1)2, осью Ох и прямой у = 1 - х;
б) графиком функции у = 4х - х2, осью Ох и прямой у = 4 - х;
5. Зарядка для глаз.
6. Самостоятельная работа. Тест.
1. Множество всех
первообразных функции ![]() имеет вид …
имеет вид …
A. ![]() ; Б.
; Б. ![]() ; В.2; Г.
; В.2; Г. ![]() ; Д. 2+
; Д. 2+![]() .
.
2. Операция нахождения неопределённого интеграла от некоторой функции называется…
A. интегрированием; Б. дифференцированием; В. логарифмированием;
Г. возведением в степень; Д. извлечением корня.
3. Множество всех
первообразных функции ![]() имеет вид …
имеет вид …
A. ![]() ; Б.
; Б. ![]() ; В.
; В.![]() ; Г.
; Г. ![]() ; Д.
; Д.![]() .
.
4. Закончите определение:
Неопределённым интегралом от функции y = f(x) называется:
A. производная функции F(x); Б. совокупность всех первообразных функции y = f(x);
B. совокупность всех производных функции y = f(x); Г. знак вида ò.
5. Множество всех
первообразных функции ![]() имеет вид …
имеет вид …
A. ![]() ; Б.
; Б.![]() ; В.
; В. ![]() ; Г.
; Г. ![]() .
.
6. Выберите
правильный вариант ответа:![]() …
…
A.
![]() ; Б.
; Б. ![]() ; В.
; В. ![]() ; Г.
; Г.![]() .
.
7. Формула Ньютона-Лейбница:
A.
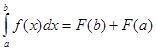 ; Б.
; Б. 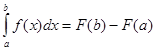 ;
;
B. 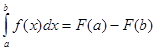 ; Г.
; Г. 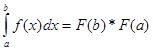 .
.
8. Закончите определение:
Дифференцируемая функция F(x) называется первообразной для функции f(x) на промежутке Х, если в каждой точке этого промежутка…
A.
![]() ; Б.
; Б. ![]() ; В.F(x) = f(x)+C;
; В.F(x) = f(x)+C;
Г. Предел от функции F(x) при х®0 равен нулю.
9. Выберите
правильный вариант ответа: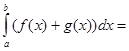
A.
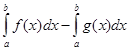 ; Б.
; Б. 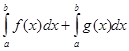 ;
;
B.
![]() ; Г.
; Г. 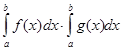 .
.
10. Для функции f(х) = еx найти первообразную, график которой проходит через точку М(0; 2).
А. F(х) = е + 3; Б. F(х) = еx; В. F(х) = ex +1; Г. F{х) =ex -1.
В «Листе учета знаний» суммируются все плюсы и выводится оценка за урок.
7.Рефлексия. Учащиеся отвечают на вопрос «Чему вы научились при изучении, данной темы?»
8. Итог урока. Д/з. В «Листе учета знаний» суммируются все плюсы и выводится оценка за урок.
«Мышление начинается с удивления», – заметил 2 500 лет назад Аристотель. Наш соотечественник Сухомлинский считал, что «чувство удивления – могучий источник желания знать; от удивления к знаниям – один шаг». А математика замечательный предмет для удивления.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.