
Обратные тригонометрические функции.
Рассмотрим пример 1: sin
x =![]() .
.
Данному значению синуса соответствуют два
значения угла: x
= ![]() и x
=
и x
= ![]()
Пример 2 : cos
x =![]() .
.
Данному значению косинуса соответствуют
два значения угла: x
= ![]() и x
=
и x
= ![]()
Для того, чтобы такого типа задачи решались однозначно, существуют обратные тригонометрические функции:
у = arcsin a, у = arccos a, у = arctg a, у = arcctg a,
Читаются: арксинус числа а, арккосинус числа а, арктангенс числа а, арккотангенс числа а.
(аrcus в переводе с латинского значит дуга, сравните со словом арка, угол).
Определение.
Если ![]() arcsin a – это такое число на отрезке
arcsin a – это такое число на отрезке
[![]() ;
;![]() ] , синус
которого равен а.
] , синус
которого равен а.
Если ![]() arcсоs
a – это такое число
на отрезке
arcсоs
a – это такое число
на отрезке
[![]() ;
;![]() ] , косинус которого
равен а.
] , косинус которого
равен а.
arctg a
– это такое число на интервале (![]() ;
;![]() ) , тангенс которого
равен а.
) , тангенс которого
равен а.
arcсtg
a – это такое число
на интервале (![]() ;
;![]() ) , котангенс которого
равен а.
) , котангенс которого
равен а.
arcsin a ![]() [
[![]() ;
;![]() ], т.е. угол
находится в I или IV четверти.
], т.е. угол
находится в I или IV четверти.
arcsin a, если а > 0, находится в I четверти.
arcsin a, если а < 0, находится в IV четверти.
arcsin (- a) = - arcsin a.
arcсоs a ![]() [
[![]() ;
;![]() ] т.е. угол
находится в I или II четверти.
] т.е. угол
находится в I или II четверти.
arccos a, если а > 0, находится в I четверти.
arccos a, если а < 0, находится в II четверти.
arccos (-a) = ![]() .
.
arctg a ![]() (
(![]() ;
;![]() ), т.е.
угол находится в I или IV четверти.
), т.е.
угол находится в I или IV четверти.
arctg a, если а > 0, находится в I четверти.
arctg a, если а < 0, находится в IV четверти.
arctg (- a) = - arctg a.
arcсtg a ![]() (
(![]() ;
;![]() ) т.е. угол
находится в I или II четверти.
) т.е. угол
находится в I или II четверти.
arcctg a, если а > 0, находится в I четверти.
arcctg a, если а < 0, находится в II четверти.
arcctg (-a) = ![]() .
.
Рассмотрим примеры на вычисление значений обратных тригонометрических функций.
1. аrcsin
![]() =
=
![]() =60°
=60°
2. аrcsin
(- ![]() =
-
=
- ![]() =
-60°
=
-60°
3. аrcsin
1
= ![]() =90°
=90°
4. аrcsin 0 = 0 =0°
5. аrcsin
(
-1) = ![]() =
-90°
=
-90°
6. аrccos
![]() =
=
![]() =45°
=45°
7. аrccos
( - ![]() )=
π
-
)=
π
- ![]() =
=
![]() = 135°
= 135°
8. аrccos 1 = 0 =0°
9. аrccos (-1) = π =180°
10.
аrccos 0 = ![]() =90°
=90°
11.
аrctg 1
= ![]() =45°
=45°
12. аrctg
(-1) = - ![]() =
- 45°
=
- 45°
13. аrctg 0 = 0 = 0°
14.
аrcctg 1
= ![]() =
45°
=
45°
15. аrcctg (- 1) = аrctg (-1) = 135°
16. sin (аrccos
![]() ) = sin
) = sin
![]() =
=![]() .
.
17. cos (аrctg
(-1)) = cos ( - ![]() )
= 1
)
= 1
18. √3 ctg(аrcsin
(- ![]() +
+
![]() аrctg
√3 +
аrctg
√3 + ![]() аrccos
( -
аrccos
( - ![]() )
)
Выполнить самостоятельную работу.
«Обратные тригонометрические функции».
Вариант 1.
Вычислить значение выражения. Ответ в каждом задании записать в радианной и градусной мере угла .
1. arc
sin ![]() .
.
2. arc
sin 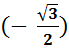 .
.
3. arc cos 0 + arc sin 0 + arc ctg 0.
4. arc
cos 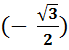 .
.
5. arc tg (-1).
6. arc ctg (-1).
7. 2 arc cos (-1) +3 arc sin (-1).
8. 3
arc sin![]() )
+ 2 arc ctg (-√3) - arc cos
)
+ 2 arc ctg (-√3) - arc cos 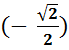 .tg
(arc sin
.tg
(arc sin 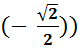 .
.
Ответ в следующих заданиях записать в виде числа.
9. √2cos( arc ctg (-1)).
10. 8 sin(arc sin (-1)).
11.
cos ( 2 arc sin![]() ).
).
12. tg (3 arc cos (-1))
13. sin ( 2 arc cos ![]() -
arc ctg 0 ).
-
arc ctg 0 ).
Вариант 2.
Вычислить значение выражения. Ответ в каждом задании записать в радианной и градусной мере угла.
1. arc sin (-1).
2. arc cos (-1).
3. arc
ctg 0 + arc ctg ![]() +
arc tg 0.
+
arc tg 0.
4. arc
cos ![]() .
.
5. arc
sin 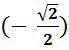 .
.
6. arc ctg (- √3).
7. 7 arc cos 0 – 2 arc cos 1 - 3 arc sin 1.
8. arc
cos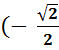 )
- arc ctg
)
- arc ctg ![]() +
2 arc sin 0.
+
2 arc sin 0.
Ответ в следующих заданиях записать в виде числа.
9. Ctg (arc tg (-1)).
10. 5
sin (arc cos 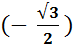 .
.
11. ![]() cos
cos
![]() arc
sin
arc
sin 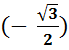 .
.
12. . ctg (3 arc sin (-1)).
13. sin
(2 arc cos ![]() -
arc ctg 0 ).
-
arc ctg 0 ).
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.